Optimization of Robust LMI-Control Systems for Unstable Vertical Plasma Position in D-Shaped Tokamak
Abstract
:1. Introduction
1.1. Tokamak Plasma Vertical Position Control and LMI
1.2. Paper Structure
2. Statement of the Control Problem
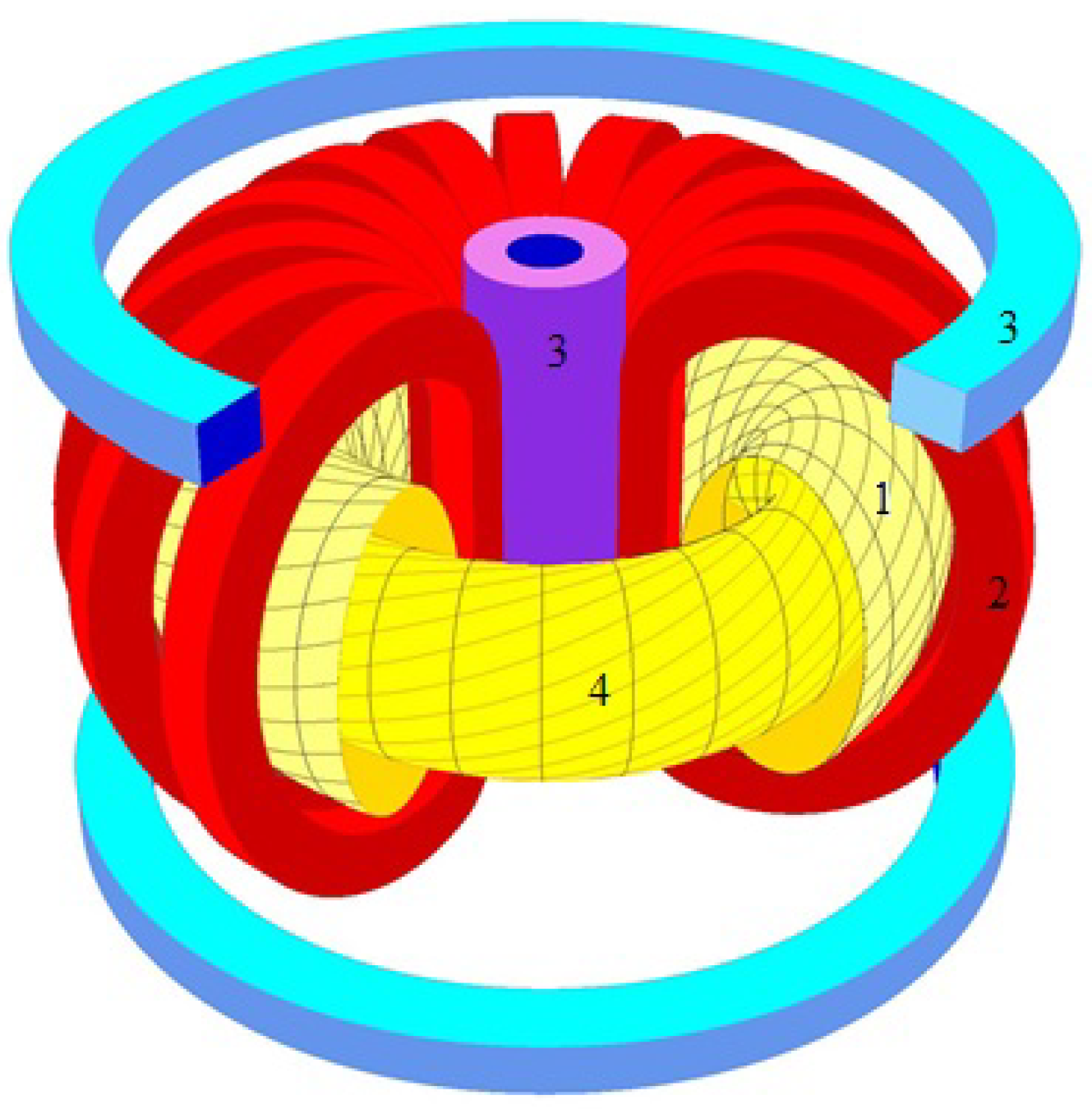
2.1. Tokamak T-15MD
2.2. Model of the Plant under Control and the Work Goal
2.3. Dynamical Model of Vertical Plasma Displacement in a Tokamak
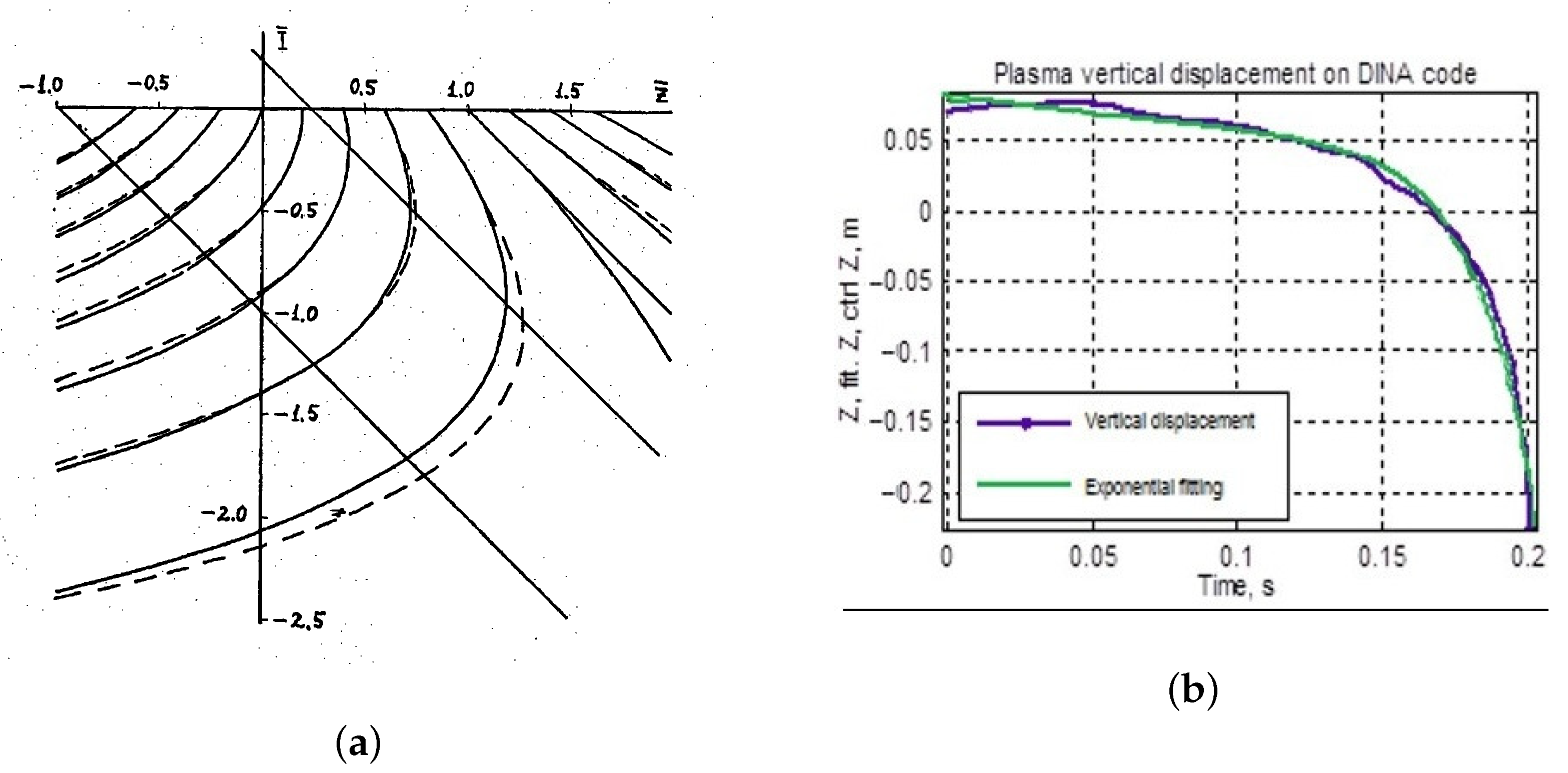
3. Acceptable Disturbance Estimation
4. -Stabilization for LMI Region
4.1. Region
4.2. Region
5. Stabilization
6. Design with Desired Pole Region and Triple Pole Controller
7. Robust State Feedback Control
7.1. Robust Control
7.2. Robust Control
8. Stabilizing Output Feedback: Linear Dynamical Controller
9. Robust Stability Radius
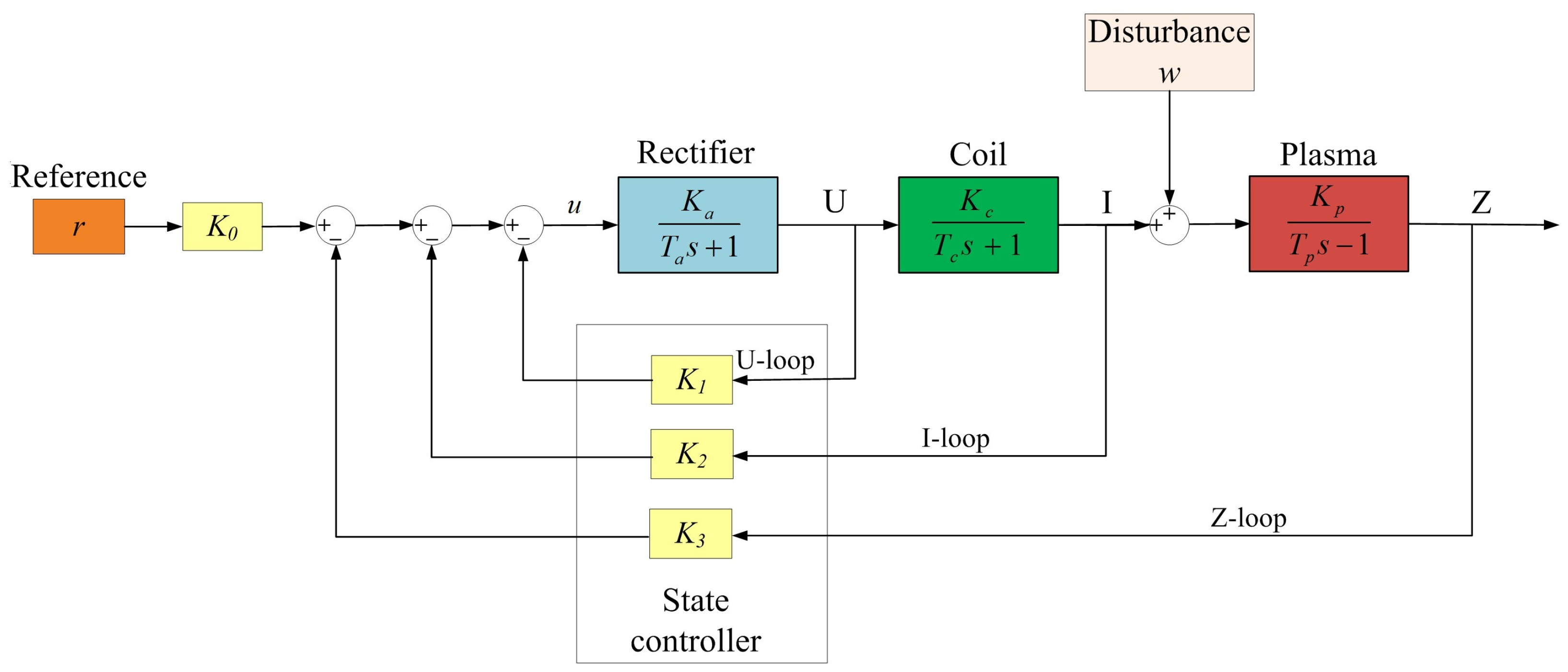
9.1. The Three-Loop Control System
9.2. The One-Loop Control System
9.3. The Robust Stability Radii for Three-Loop and One-Loop Control Systems
10. Comparative Analysis of Closed-Loop Vertical Position Plasma Control Systems
- Mathematical modeling and analysis of physical phenomena, and selection of sensors and actuators;
- Designing a control system that provides a given behavior, satisfies the imposed constraints, and minimizes the resources consumed;
- Verification of control efficiency using simulation studies on plant models (including the real-time simulation on digital platforms specifically “digital twins”) [5];
- Practical implementation in a real experiment or production process.
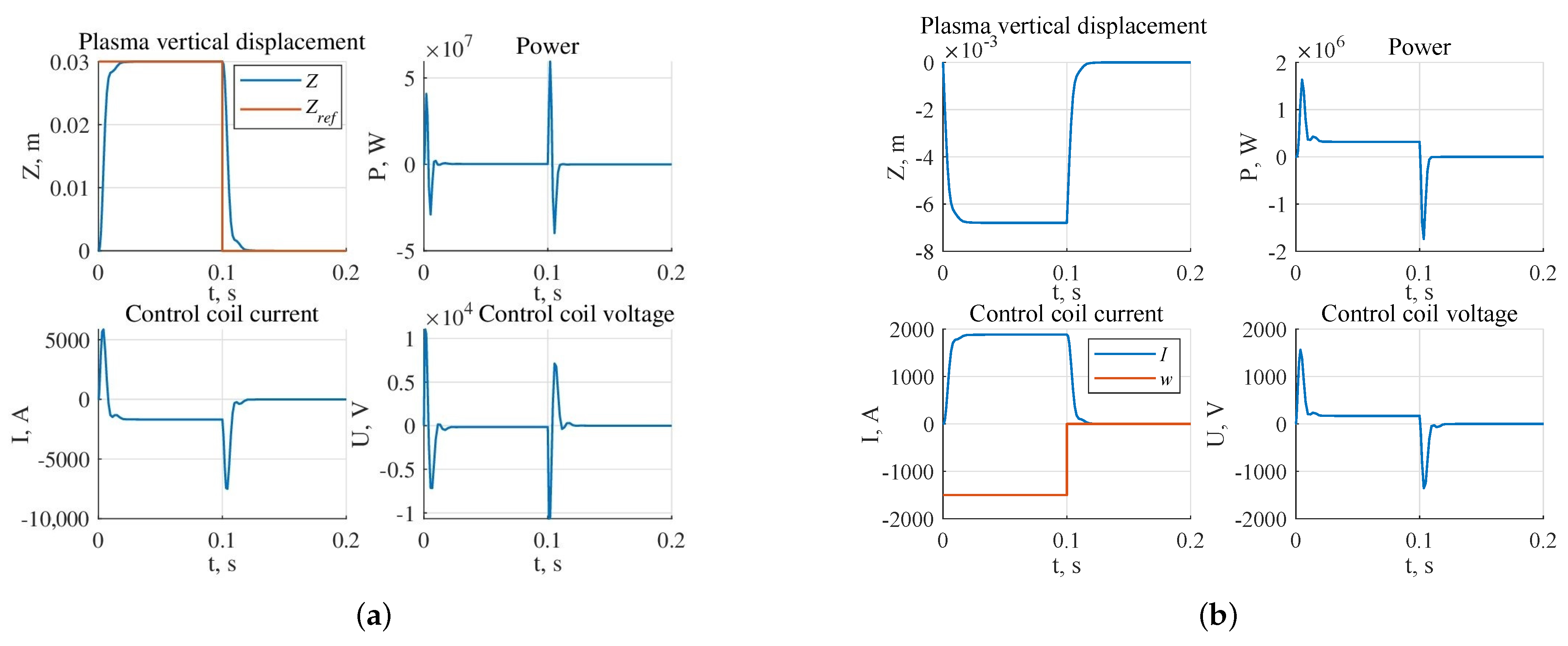
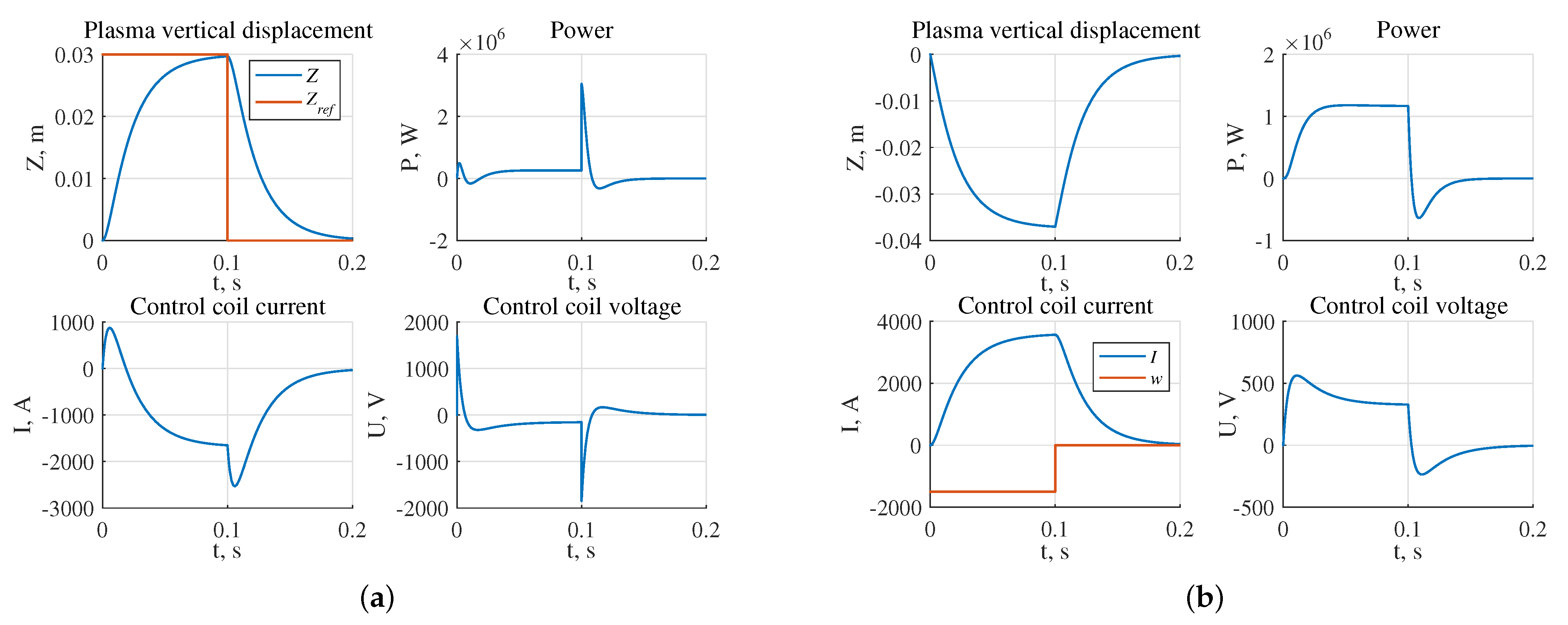
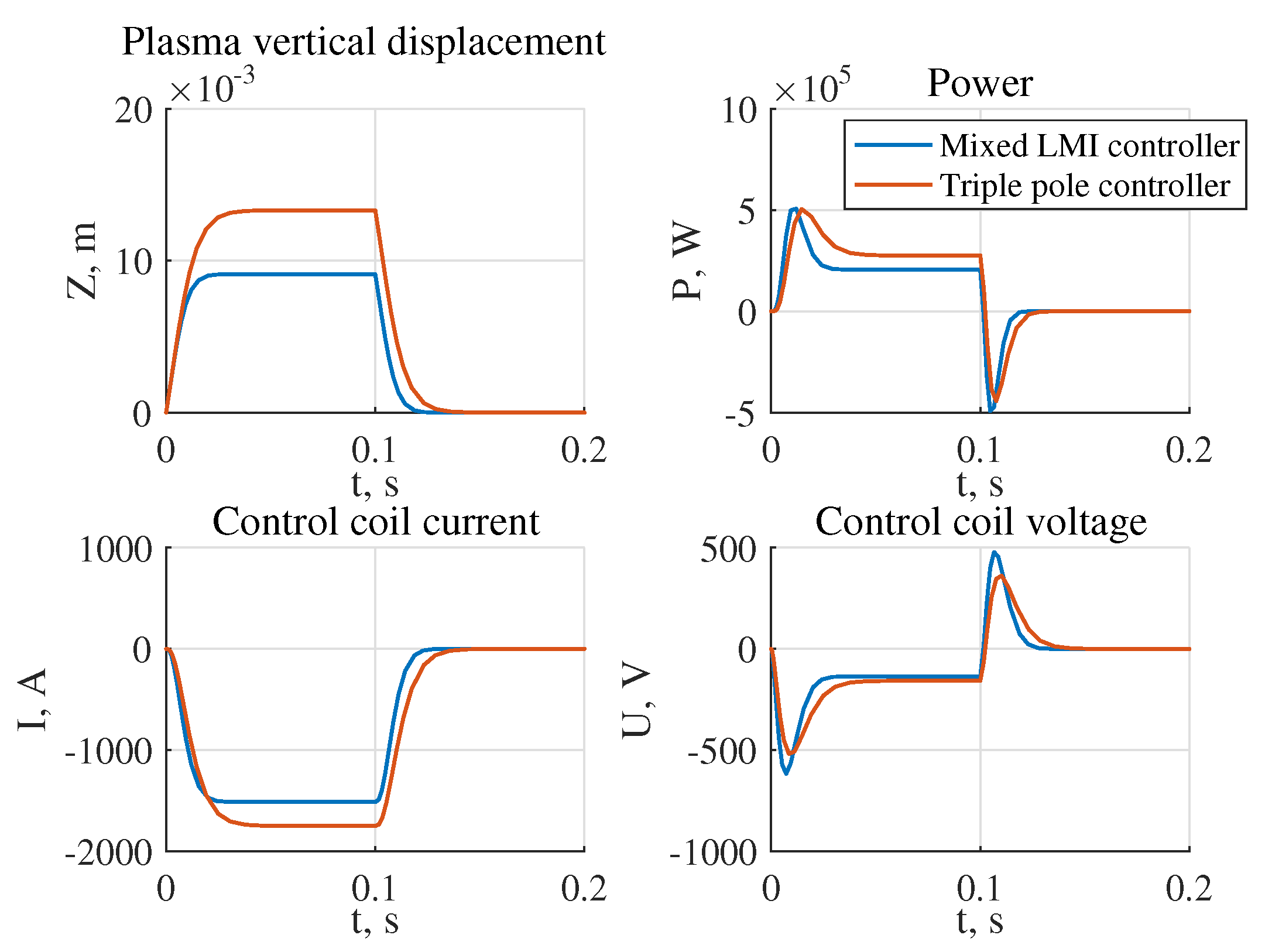
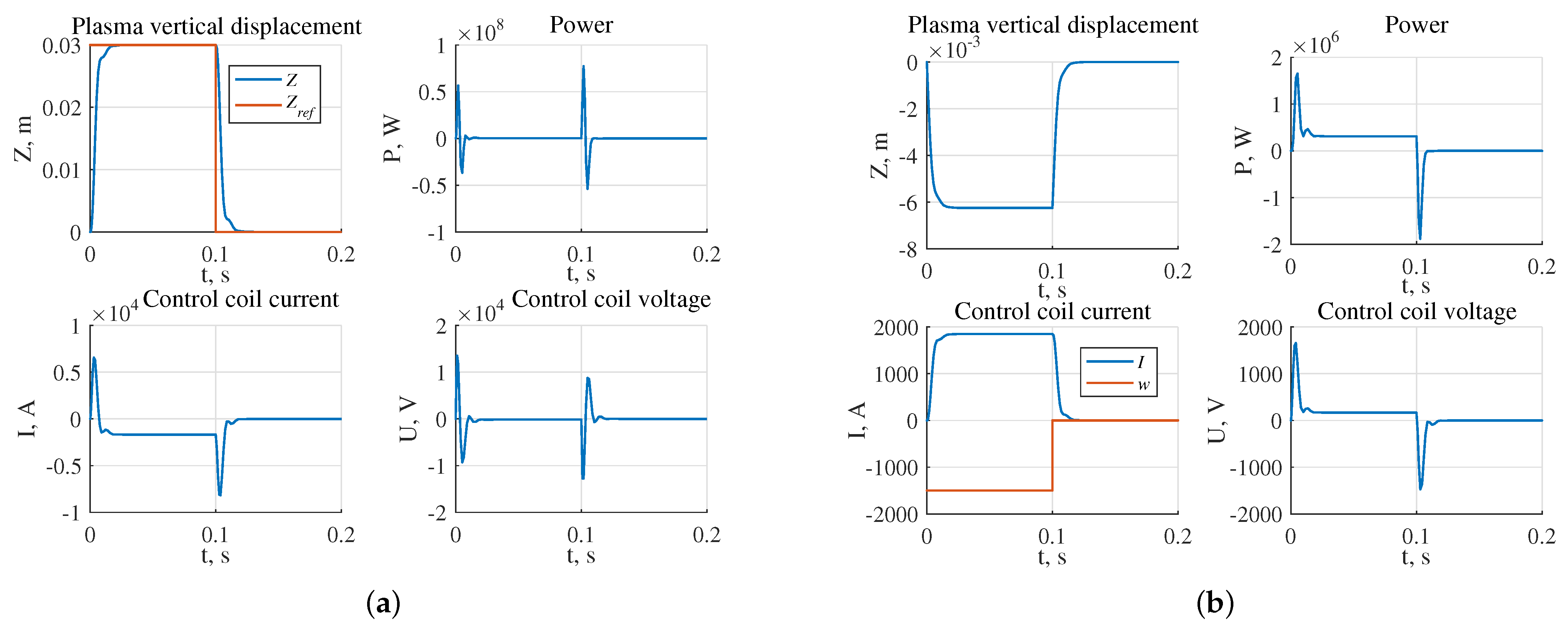
- The largest stability radius of 0.8349 was obtained for the system with the robust controller, the smallest 0.2238 is for the system with triple pole controller (Figure 17);
- The highest power of the actuator in the presence of the reference step signal is required for the system with the robust controller W, the lowest for the system with the controller W (Figure 18a);
- The highest power of the actuator in the presence of external disturbances is required for the system with robust controller and is equal to W, the lowest one for the system with the pole arrangement in the area is W (Figure 18b).
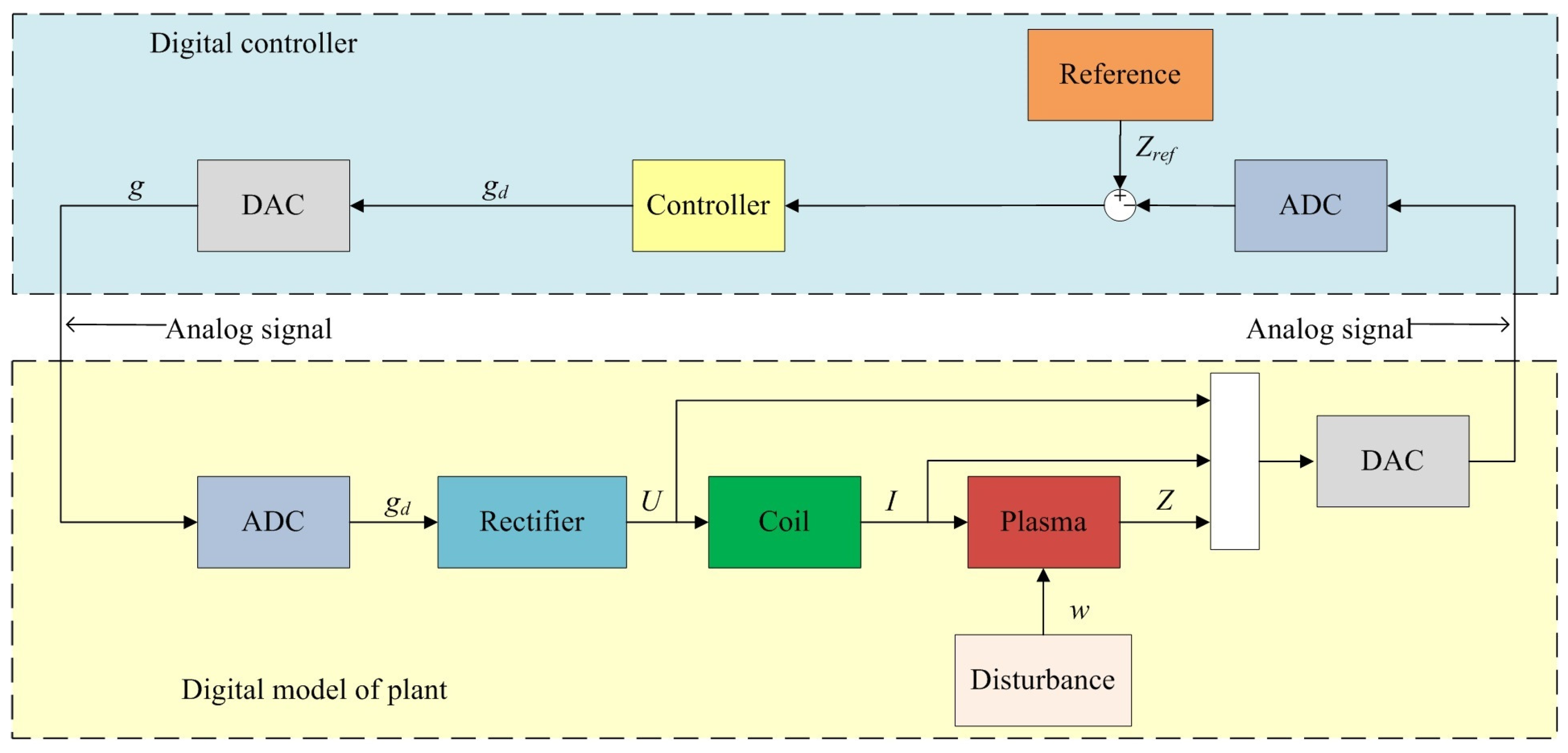
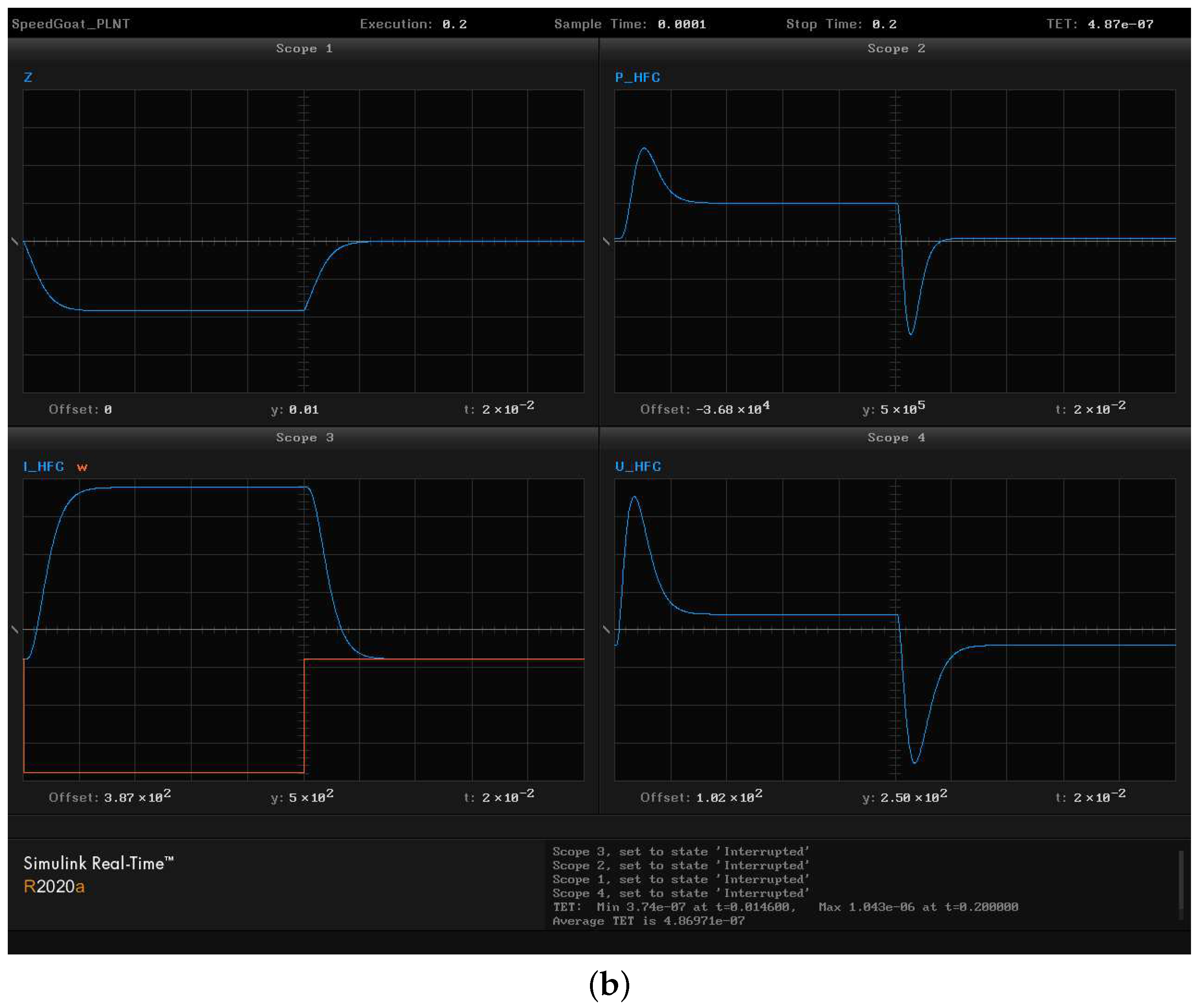
11. Modeling of the Control System on the Real-Time Digital Control Testbed
12. Discussion
13. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wesson, J. Tokamaks, 3rd ed.; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Mitrishkin, Y.V.; Korenev, P.S.; Kartsev, N.M.; Kuznetsov, E.A.; Prohorov, A.A.; Patrov, M.I. Plasma magnetic cascade multiloop control system design methodology in a tokamak. Control. Eng. Pract. 2019, 87, 7–9. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Kartsev, N.M.; Pavlova, E.A.; Prohorov, A.A.; Korenev, P.S.; Patrov, M.I. Plasma Control in Tokamaks. Part. 2. Magnetic Plasma Control Systems. Adv. Syst. Sci. Appl. 2018, 18, 39–78. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Pavlova, E.A.; Kuznetsov, E.A.; Gaydamaka, K.I. Continuous, saturation, and discontinuous tokamak plasma vertical position control systems. Fusion Eng. Des. 2016, 107, 35–47. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V. Plasma magnetic control systems in D-shaped tokamaks and imitation digital computer platform in real time for controlling plasma current and shape. Adv. Syst. Sci. Appl. 2022, 21, 1–14. [Google Scholar] [CrossRef]
- Khvostenko, P.P.; Anashkin, I.O.; Bondarchuk, E.N.; Chudnovsky, A.N.; Kavin, A.A.; Khvostenko, A.P.; Kirneva, N.A.; Kuzmin, E.G.; Levin, I.V.; Leonov, V.M.; et al. Current status of tokamak T-15MD. Fusion Eng. Des. 2021, 164, 112211. [Google Scholar] [CrossRef]
- Khvostenko, P.P.; Anashkin, I.O.; Bondarchuk, E.N.; Injutin, N.V.; Khvostenko, A.P.; Kochin, V.A.; Kuzmin, E.G.; Levin, I.V.; Lutchenko, A.V.; Modyaev, A.L.; et al. Tokamak T-15MD–Two years before the physical start-up. Fusion Eng. Des. 2019, 146, 1108–1112. [Google Scholar] [CrossRef]
- Khvostenko, P.P.; Anashkin, I.O.; Belyakov, V.A.; Bondarchuk, E.N.; Injutin, N.V. Preassembly of the tokamak T-15MD magnet system. Fusion Eng. Des. 2017, 124, 114–118. [Google Scholar] [CrossRef]
- Boyd, S.P.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Pavlova, E.A.; Mitrishkin, Y.V.; Khlebnikov, M.V. Control System Design for Plasma Unstable Vertical Position in a Tokamak by Linear Matrix Inequalities. In Proceedings of the IEEE 11th International Conference on Application of Information and Communication Technologies (AICT), Moscow, Russia, 20–22 September 2017; pp. 458–462. [Google Scholar] [CrossRef]
- Stein, G. Respect the Unstable. IEEE Control. Syst. Mag. 2003, 23, 12–25. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Kartsev, N.M.; Zenkov, S.M. Stabilization of Unstable Vertical Position of Plasma in T-15 Tokamak. Autom. Remote. Control. 2014, Part 1, 2, 281–293. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Kartsev, N.M.; Zenkov, S.M. Stabilization of Unstable Vertical Position of Plasma in T-15 Tokamak. Autom. Remote. Control. 2014, Part 2, 9, 31–44. [Google Scholar] [CrossRef]
- Lukash, V.E.; Dokuka, V.N.; Khayrutdinov, R.R. Simulation code DINA into MATLAB environment for development of tokamak plasma control design. Probl. At. Sci. Technol. Ser. Thermonucl. Fusion 2004, 1, 40–49. [Google Scholar]
- Mitrishkin, Y.V.; Prohorov, A.A.; Korenev, P.S.; Patrov, M.I. Plasma magnetic time-varying nonlinear robust control system for the Globus-M/M2 tokamak. Control. Eng. Pract. 2020, 100, 104446. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Kartsev, N.M.; Zenkov, S.M. Plasma vertical position, shape, and current control in T-15 tokamak. In Proceedings of the IFAC Conference on Manufacturing Modelling, Management and Control, Saint Petersburg, Russia, 19–21 June 2013; pp. 1820–1825. [Google Scholar]
- Khayrutdinov, R.R.; Lukash, V.E. Studies of plasma equilibrium and transport in a tokamak fusion device with the inverse-variable technique. J. Comput. Phys. 1993, 44, 193–201. [Google Scholar] [CrossRef]
- Kuznetsov, E.A.; Mitrishkin, Y.V.; Kartsev, N.M. Current Inverter as Auto-Oscillation Actuator in Applications for Plasma Position Control Systems in the Globus-M/M2 and T-11M Tokamaks. Fusion Eng. Des. 2019, 143, 247–258. [Google Scholar] [CrossRef]
- Mertens, V.; Raupp, G.; Treutterer, W. Chapter 3: Plasma Control in ASDEX Upgrade. Fusion Sci. Technol. 2003, 44, 593–604. [Google Scholar] [CrossRef]
- Ljung, L. System Identification. Theory for the User; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Systems. Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Spinosa, A.G.; Buscarino, A.; Fortuna, L.; Iafrati, M.; Mazzitelli, G. Data-driven order reduction in Hammerstein–Wiener models of plasma dynamics. Eng. Appl. Artif. Intell. 2021, 100, 104180. [Google Scholar] [CrossRef]
- Phillips, C.L.; Harbor, R.D. Feedback Control Systems, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2000. [Google Scholar]
- Duan, G.; Yu, H. LMIs in Control Systems: Analysis, Design and Applications; Taylor & Francis Group: Abingdon, UK, 2013. [Google Scholar]
- Mitrishkin, Y.V.; Savkina, I.S. A model of plasma equilibrium in a tokamak. Autom. Remote. Control. 1984, 45, 332–340. [Google Scholar]
- Gribov, Y.V.; Mitrishkin, Y.V.; Chuyanov, V.A. Study of Plasma Equilibrium Control System in Tokamak. Institute of Control Sciences of Russian Academy of Sciences (ICS RAS): Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Abedor, J.; Nagpal, K.; Poolla, K. A Linear Matrix Inequality Approach to Peak-to-Peak Gain Minimization. Int. J. Robust Nonlinear Control. 1996, 6, 899–927. [Google Scholar] [CrossRef]
- Blanchini, F.; Miani, S. Set-Theoretic Methods in Control; Birkhäuser: Boston, MA, USA, 2008. [Google Scholar]
- Polyak, B.T.; Khlebnikov, M.V.; Shcherbakov, P.S. Control of Linear Systems Subjected to Exogenous Disturbances: An LMI Approach; LENAND: Moscow, Russia, 2014. (In Russian) [Google Scholar]
- Khlebnikov, M.V.; Polyak, B.T.; Kuntsevich, V.M. Optimization of Linear Systems Subject to Bounded Exogenous Disturbances: The Invariant Ellipsoid Technique. Autom. Remote. Control 2011, 72, 2227–2275. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: New York, NY, USA, 1985. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: Hoboken, NJ, USA, 2010. [Google Scholar]
- Petersen, I. A stabilization Algorithm for a Class of Uncertain Systems. Syst. Control. Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Khlebnikov, M.V.; Shcherbakov, P.S. Petersen’s Lemma on Matrix Uncertainty and Its Generalization. Autom. Remote. Control. 2008, 69, 1932–1945. [Google Scholar] [CrossRef]
- Khlebnikov, M.V. Suppression of Bounded Exogenous Disturbances: A Linear Dynamic Output Controller. Autom. Remote. Control. 2011, 72, 699–712. [Google Scholar] [CrossRef]
- Feldbaum, A.A.; Butkovsky, A.G. Methods of Automatic Control Theory; Nauka Publishing House: Moscow, Russia, 1971. (In Russian) [Google Scholar]
- Strebulaev, S.N.; Zhorin, S.M. Computer analysis of the radius of robust stability in a single electromechanical system. Stability and oscillations of nonlinear systems. In Proceedings of the XV International Conference on Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy’s Conference) (STAB), Moscow, Russia, 3–5 June 2020; pp. 406–408. (In Russian). [Google Scholar]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Bars, R.; Colaneri, P.; Dugard, L.; Allgöwer, F.; Kleimenov, A.; Scherer, C. Trends in Theory of Control System Design Status report prepared by the IFAC Coordinating Committee on Design Methods. IFAC Proc. Vol. 2008, 41, 2144–2155. [Google Scholar] [CrossRef] [Green Version]
- Lamnabhi-Lagarrigue, F.; Annaswamy, A.; Engell, S.; Isaksson, A.; Khargonekar, P.; Murray, R.M.; Nijmeijer, H.; Samad, T.; Tilbury, D.; Van den Hof, P. Systems and Control for the future of humanity, research agenda: Current and future roles, impact and grand challenges. Annu. Rev. Control. 2017, 43, 1–64. [Google Scholar] [CrossRef]
- Baillieul, J.; Samad, T. Encyclopedia of Systems and Control; Springer: London, UK, 2015. [Google Scholar]
- Humphreys, D.A.; Casper, T.A.; Eidietis, N.; Ferrara, M.; Gates, D.A.; Hutchinson, I.H.; Jackson, G.L.; Kolemen, E.; Leuer, J.A.; Lister, J.; et al. Experimental vertical stability studies for ITER performance and design guidance. Nucl. Fusion 2009, 49, 115003. [Google Scholar] [CrossRef] [Green Version]
- Portone, A.; Albanese, R.; Ambrosino, G.; Ariola, M.; Brooks, A.; Campbell, D.J.; Casper, T.A.; Cavinato, M.; Chuyanov, V.; De Tommasi, G.; et al. ITER Plasma Vertical Stabilization. In Proceedings of the 22nd IAEA Fusion Energy Conference, Geneva, Switzerland, 13–18 October 2008. [Google Scholar]
- Yuan, Q.P.; Xiao, B.J.; Luo, Z.P.; Walker, M.L.; Welander, A.S.; Hyatt, A.; Qian, J.P.; Zhang, R.R.; Humphreys, D.A.; Leuer, J.A.; et al. Plasma current, position and shape feedback control on EAST. Nucl. Fusion 2013, 53, 043009. [Google Scholar] [CrossRef]
- Albanese, R.; Ambrosino, R.; Castaldo, A.; De Tommasi, G.; Luo, Z.P.; Mele, A.; Pironti, A.; Xiao, B.J.; Yuan, Q.P. ITER-like Vertical Stabilization system for the EAST tokamak. Nucl. Fusion 2017, 57, 086039. [Google Scholar] [CrossRef]
- Qiu, Q.; Xiao, B.; Guo, Y.; Liu, L.; Xing, Z.; Humphreys, D.A. Simulation of EAST vertical displacement events by tokamak simulation code. Nucl. Fusion 2016, 56, 106029. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V. Method of Magnetic Plasma Control in Tokamak in Real Time and Device for Its Implementation. Patent for Invention No. 2773508; Federal Institute of Industrial Property, 6 June 2022. [Google Scholar]
- Kuo, B.C. Digital Control Systems, 2nd ed.; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Minaev, V.B.; Gusev, V.K.; Sakharov, N.V.; Varfolomeev, V.I.; Bakharev, N.N.; Belyakov, V.A.; Bondarchuk, E.N.; Brunkov, P.N.; Chernyshev, F.V.; Davydenko, V.I.; et al. Spherical tokamak Globus-M2: Design, integration, construction. Nucl. Fusion 2017, 57, 066047. [Google Scholar] [CrossRef]
- Wang, J.; Li, M.; Jiang, W.; Huang, Y.; Lin, R. A Design of FPGA-Based Neural Network PID Controller for Motion Control System. Sensors 2022, 22, 889. [Google Scholar] [CrossRef]
- Suratia, P.; Patel, J.; Rajpal, R.; Kotia, S.; Govindarajan, J. FPGA based Fuzzy Logic Controller for plasma position control in ADITYA Tokamak. Fusion Eng. Des. 2012, 87, 1866–1871. [Google Scholar] [CrossRef]
- Kochetkov, S.; Krasnova, S.A.; Utkin, V.A. The New Second-Order Sliding Mode Control Algorithm. Mathematics 2022, 10, 2214. [Google Scholar] [CrossRef]



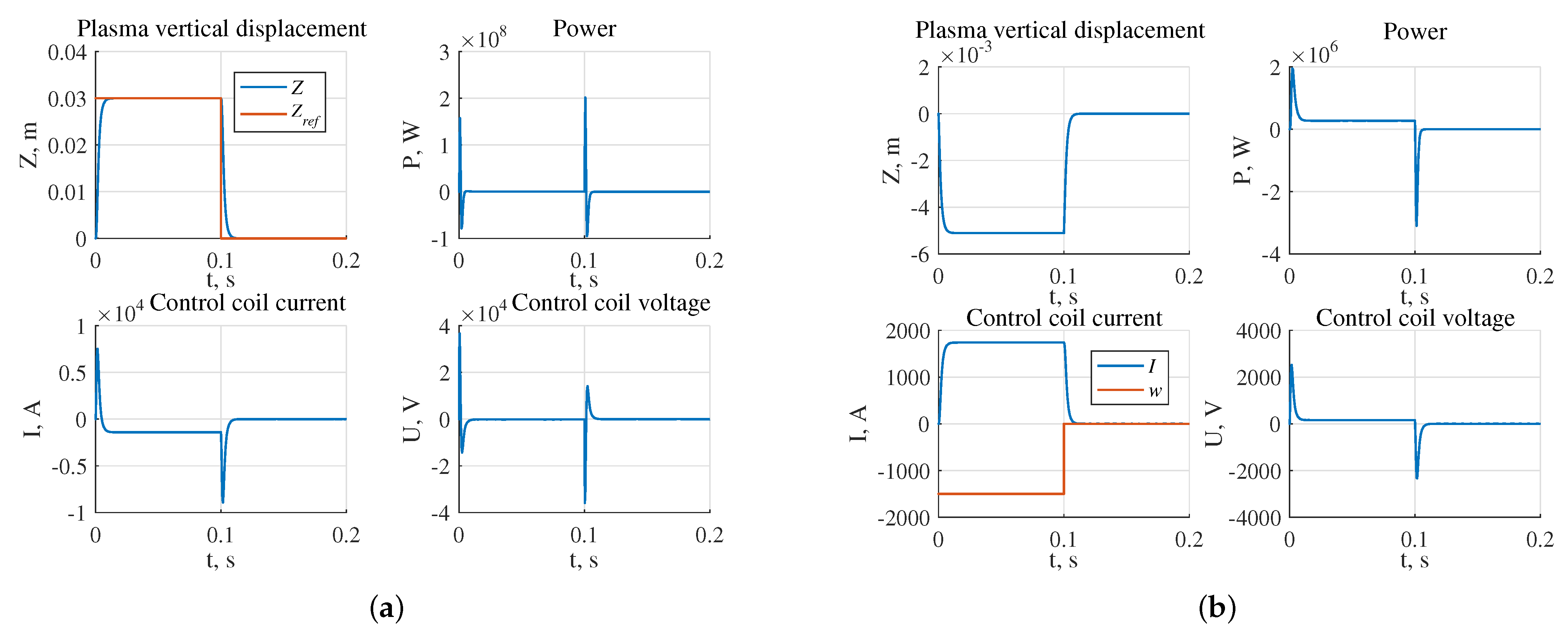
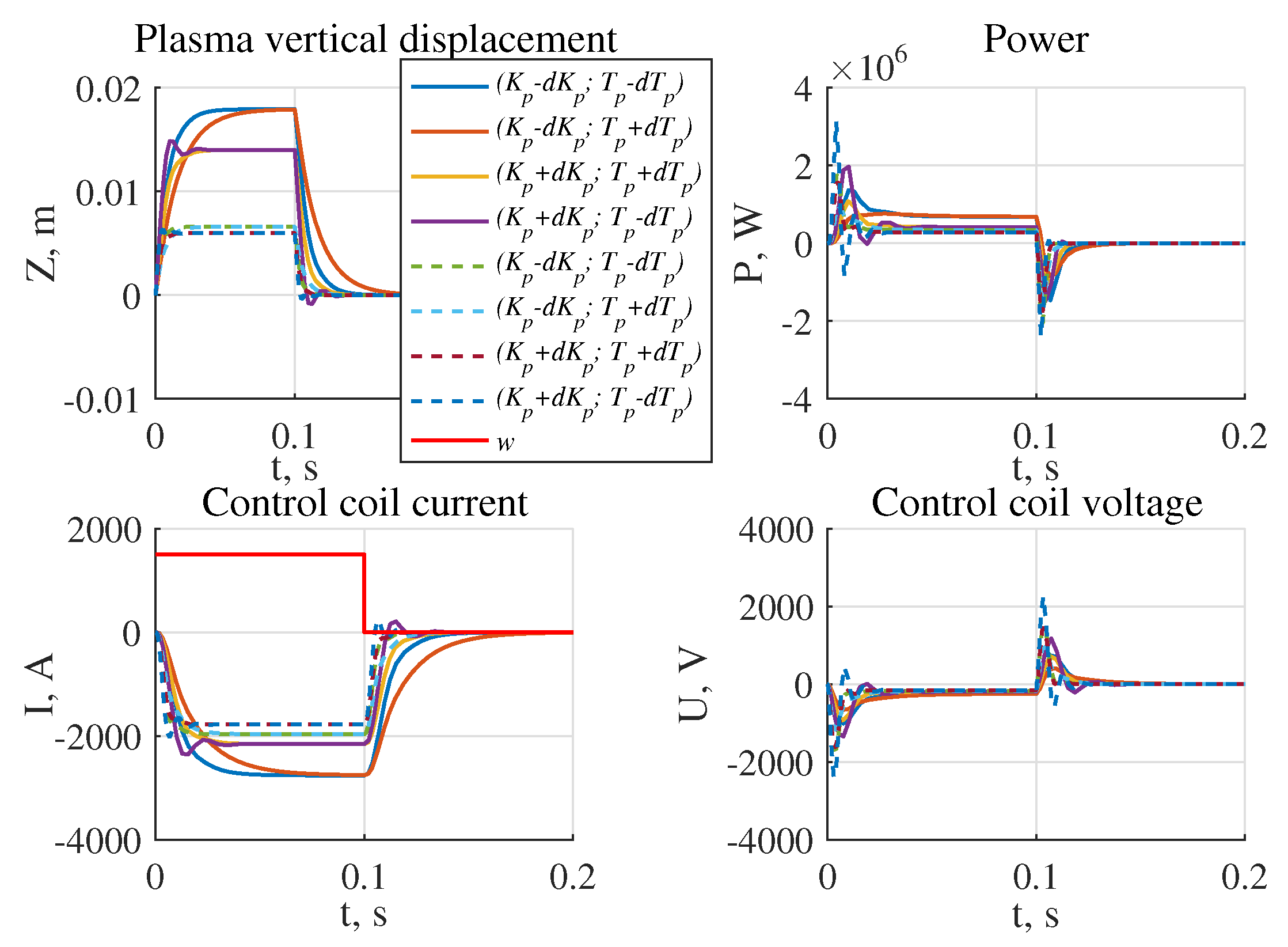
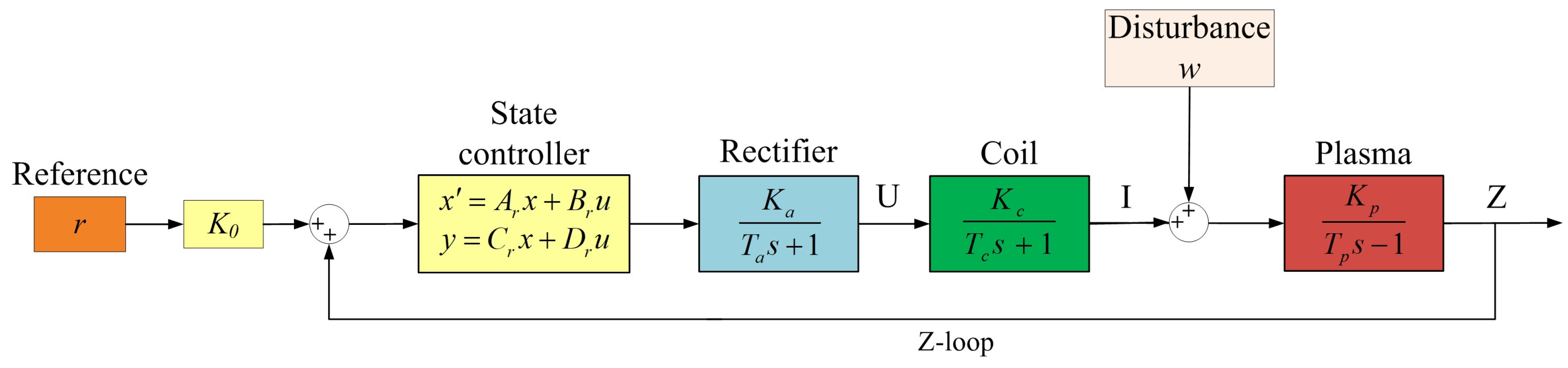

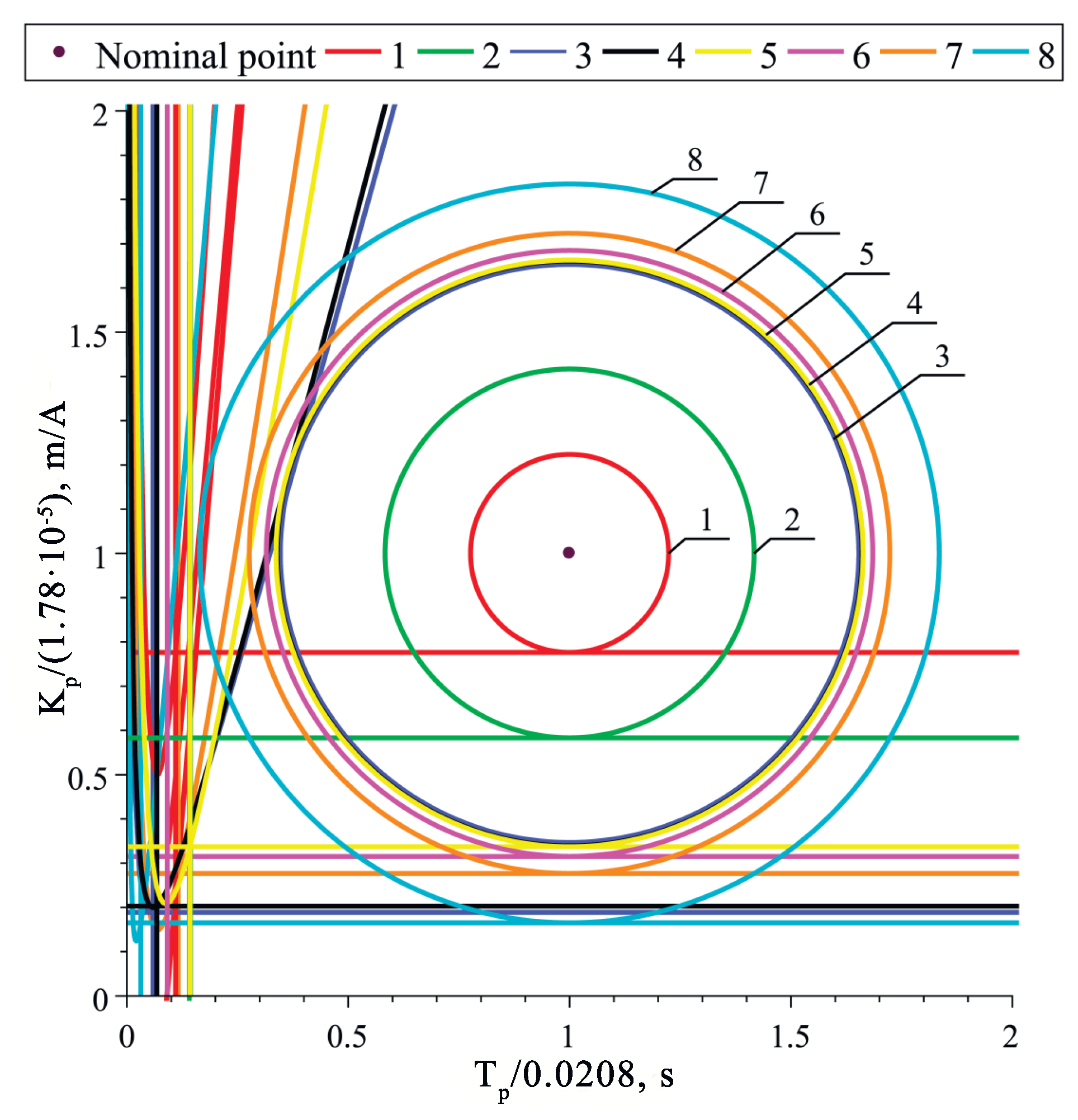
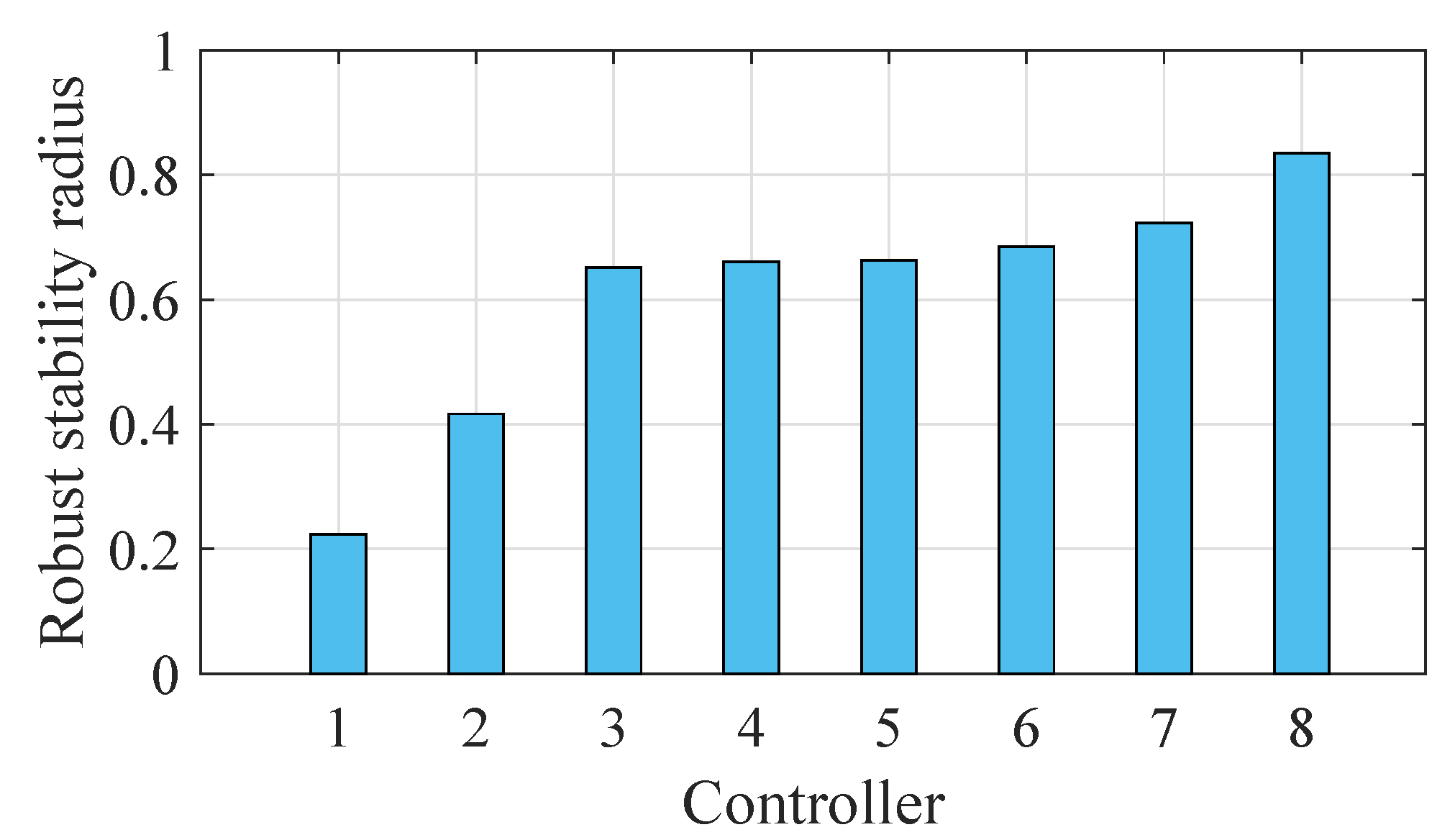




| Controller Type | Section | Radius | Peak Power (W) | ||||
|---|---|---|---|---|---|---|---|
| At the Disturbance | After Drop of the Disturbance | At the Reference Step Signal | After Drop of the Reference Step Signal | ||||
| 1. | Triple pole controller | 6 | 0.2238 | ||||
| 2. | controller | 5 | 0.4168 | ||||
| 3. | Mixed robust with pole region controller | 7.1 | 0.6515 | ||||
| 4. | pole region controller | 4.1 | 0.6609 | ||||
| 5. | Mixed with pole region controller | 6 | 0.6630 | ||||
| 6. | Output controller | 8 | 0.6848 | ||||
| 7. | pole region controller | 4.2 | 0.7234 | ||||
| 8. | robust controller | 7.2 | 0.8349 | ||||
| Controller Type | Poles | |
|---|---|---|
| 1. | Triple pole controller | {} |
| 2. | controller | {} |
| 3. | Mixed robust with pole region controller | {} |
| 4. | pole region controller | {} |
| 5. | Mixed with pole region controller | {} |
| 6. | Output controller | { } |
| 7. | pole region controller | {} |
| 8. | robust controller | {} |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitrishkin, Y.; Pavlova, E.; Khlebnikov, M. Optimization of Robust LMI-Control Systems for Unstable Vertical Plasma Position in D-Shaped Tokamak. Mathematics 2022, 10, 4531. https://doi.org/10.3390/math10234531
Mitrishkin Y, Pavlova E, Khlebnikov M. Optimization of Robust LMI-Control Systems for Unstable Vertical Plasma Position in D-Shaped Tokamak. Mathematics. 2022; 10(23):4531. https://doi.org/10.3390/math10234531
Chicago/Turabian StyleMitrishkin, Yuri, Evgeniia Pavlova, and Mikhail Khlebnikov. 2022. "Optimization of Robust LMI-Control Systems for Unstable Vertical Plasma Position in D-Shaped Tokamak" Mathematics 10, no. 23: 4531. https://doi.org/10.3390/math10234531
APA StyleMitrishkin, Y., Pavlova, E., & Khlebnikov, M. (2022). Optimization of Robust LMI-Control Systems for Unstable Vertical Plasma Position in D-Shaped Tokamak. Mathematics, 10(23), 4531. https://doi.org/10.3390/math10234531








