Chaotic Synchronization in Mobile Robots

Abstract

Chaos dynamics is an interesting nonlinear effect that can be observed in many chemical, electrical, and mechanical systems. The chaos phenomenon has many applications in various branches of engineering. On the other hand, the control of mobile robots to track unpredictable chaotic trajectories has a valuable application in many security problems and military missions. The main objective in this problem is to design a controller such that the robot tracks a desired chaotic path. In this paper, the concept of synchronization of chaotic systems is studied, and a new type-3 fuzzy system (T3FLS)-based controller is designed. The T3FLS is learned by some new adaptive rules. The new learning scheme of T3FLS helps to better stabilize and synchronize. The suggested controller has a better ability to cope with high-level uncertainties. Because, in addition to the fact that the T3FLSs have better ability in an uncertain environment, the designed compensator also improves the accuracy and robustness. Several simulations show better synchronization and control accuracy of the designed controller.

1. Introduction

In recent years, researchers from various science and engineering branches have developed chaos theory to describe complexity in nature. Today, chaos theory is considered a powerful processing tool for investigating complex systems in nature and has opened a new horizon in understanding the behavior of physical and natural systems. Many mechanical, acoustic, optical, chemical, fluid, electronic, and biological systems have been shown to exhibit chaotic behavior, and researchers are interested in researching them. Due to the chaotic system’s complex dynamics and inherent instability, controlling it to exhibit the desired behavior seems impossible. Different control goals can be imagined for these systems, which can be mentioned as bifurcation control, stabilization, and synchronization. Bifurcation is one of the phenomena that occurs before the chaos of the system. Bifurcation means that the structural characteristics (the location of the equilibrium point, stability, their number, presence or absence, as well as limit cycles with the same characteristics and conditions) are changed by changing the parameters. In bifurcation control, one of the two goals is to push back or advance bifurcation and change the type of bifurcation (stable, unstable, etc.). The relationship between bifurcation and chaos is clear because several bifurcations usually occur before the system becomes chaotic. Chaos can be delayed by delaying bifurcation. Another basic application of chaos theory is the developing of robotic systems [1,2].

Stabilizing is one of the most important and widely used methods to eliminate abnormal behavior in a chaotic system. Stabilization is divided into two categories: adjustment and pursuit. In this problem, the stabilization of the system is studied by designing a control signal to one of the equilibrium points or to one of the unstable absorbers (creating a stable limit cycle). This type of stabilization is used to control chemical reactors, oscillators, electrical circuits, lasers, long-distance telecommunications, noise removal, etc. Another category of problems in stabilizing chaotic systems is the problem of tracking [3]. In this approach, a time-varying reference is taken into account, and the control law is designed so that the system’s responses follow the reference signal. The first and second cases are clear, the system has a chaotic behavior, and this behavior is not desirable for us. For example, if there is an unacceptable chaotic oscillation in the rotor of a motor, it is necessary to remove it. The synchronization of two chaotic systems means that we want the state of two chaotic systems to be the same. On the other hand, in recent years, there have been many applications in which the optimal state of the system is described as chaotic behavior. The problem of control regarding these systems is expressed in transforming an unwanted chaotic behavior into a chaotic behavior with defined and desired characteristics. Stabilizing has been studied in some papers. For example, in [4], a cancer model is introduced by the chaotic systems, the equilibrium points are analyzed, and a fractional-order controller is developed for stabilizing. A chemical reaction is modeled by chaotic systems in [5], and proportional–integral (PI) is adjusted for stabilizing. By the use of some numerical studies, the chaotic behavior of electromagnetic machines is analyzed in [6], and the stabilization methods are reviewed. The circuit implementation is investigated in [7], and an impulsive controller is designed for stabilization. In [8], the input-to-state stability is studied for financial systems, and the effect of delay is analyzed. The chaotic behavior in earthquakes is studied in [9], and by the use of an evolutionary-based technique, the stabilization problem is analyzed.

Synchronization refers to a process between two or more identical (non-identical) chaotic systems so that a particular characteristic of their motion is the coupling or application of an external force (periodic or noise) to achieve a typical behavior. Depending on the type and intensity of the coupling established between two chaotic systems or the signal sent from one chaotic system to another, chaotic systems synchronize with each other in different ways. Various synchronization methods have been developed in recent years [10]. For example, in [11], the sliding mode controller (SMC) is developed for synchronization, and the designed approach is used in an encryption system. The SMC is a method resistant to uncertainty, whose simplicity and insensitivity to system parameters and quick response are among its advantages. This method is also used in synchronization. Despite these advantages, the sliding mode control also has disadvantages, one of the most important of which is the controller with a variable structure, which is realized with the help of high-frequency switching of the input signal. This issue leads to a kind of internal instability, causing thermal losses and the destruction of mechanical parts. Various methods have been used to reduce or eliminate the vibration, including the boundary layer, which uses the saturation function instead of the sign function. The sliding control method is based on low-pass filters, high-order sliding control, and hybrid controllers, among them. In the boundary layer method, a boundary layer is taken near the sliding surface in order to avoid noise, which smooths the dynamics of the control input and prevents control signal fluctuations. This improvement leads to increased tracking errors and reduced performance. This method is also not efficient when the noise level is high. In [12], the backstepping scheme is generalized, and it is applied for synchronization. In [13], the synchronization of Halvorsen chaotic systems is studied, and an approach is introduced for numerical implementation. The other control methods include feedback controllers [14], event-triggered [15], adaptive synchronization [16], symmetry control [17], Mittag–Leffler approach, and optimal control [18]. In [19,20,21], the chaotic behavior is studied in a dual-spin spacecraft, and some models and analysis are presented.

The other effective approach is the fuzzy system (FS)-based controllers. For example, in [22], an FS-based controller is combined with a type of neural network, and by creating some recurrent weights, the estimations capability is analyzed. In [23], a non-singleton FS is developed to design a controller and synchronization scheme for chaotic systems. In [24], a new controller is designed by the use of FSs, and the designed controller is employed for an image encryption application. In [25], an FS-based controller is developed based on the SMC systems, and it is applied for chaotic behavior in vehicle dynamics. In [26], the feedback controller is improved using FSs, and it is shown that without using a backstepping scheme, the accuracy of the designed FS controller is acceptable. In [27], the SMC is improved using type-2 (T2) FSs and the synchronization accuracy improvement is verified. In [28], the synchronization of two different systems is analyzed, and a T2FS-based controller is developed.

The control of mobile robots (MRs) to track a chaotic path and synchronized them with the chaotic systems has been studied in a few papers [29]. For example, in [30], the chaotic systems are used to design a motion controller for MRs, and the convergence is analyzed. In [31], a chaotic MR is implemented, and its chaotic behavior is studied. In [32], a chaotic oscillator is designed for MRs, and its implementation is investigated. In [33], the Lorenz chaotic system is developed to create a path for MRs, and its convergency is analyzed. The Chebyshev map is developed in [34] for planning a path for MRs, and the path convergence is analyzed. The Jerk chaotic system is developed in [35] to design a navigation system for MRs, and the movement prediction of MR is investigated. In [36], the Henon chaotic map is used to create a chaotic behavior in MRs, and by numerical analysis, the chaotic features are analyzed. In [37], an iterative algorithm based on an evolutionary algorithm is developed for the chaotic path designing of MRs.

In most studies, the dynamics of MRs are known, and the chaotic path is designed just for the special case. In addition, the stability of MR in the chaotic path is not guaranteed. In this paper, a new effective intelligent controller is designed. The main contributions are:

• An effective fuzzy controller based on novel T3-FLSs is designed for MRs.
• The chaotic synchronization is studied for MRs.
• To better enhance the robustness of MR, in addition to complicated uncertain dynamics and reference path, some external disturbances are also considered.
• An adaptive parallel compensator is designed to improve the robustness.
• The stability and robustness of MR in a chaotic path are proved.
• The designed controller is online learned to optimize itself every sample time.

2. Formulation

A class of mobile MRs is considered to track a chaotic system. The suggested controller is applied to a general class of MRs, and the dynamics of MR are considered to be entirely general and unknown as follows:

$$\begin{array}{c}\Psi \left(q\right)\ddot{q}+\upsilon \left(q,\dot{q}\right)\dot{q}+G\left(q\right)+{\tau }_d=\hfill \\ B\left(q\right)\tau -A^T\left(q\right)\lambda \hfill \end{array}$$

(1)

where, q and $\dot{q}$ are position and velocity, respectively. $\Psi \left(q\right)$, $\upsilon \left(q,\dot{q}\right)$, $G\left(q\right)$ are the inertia, Coriolis, and gravitational matrices. ${\tau }_d$ and $\tau$ are disturbances and control inputs. A and B are matrices associated with MR kinematics. In a state-space form, we can write:

$$\begin{array}{c}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2=f\left(x\right)+d+u\hfill \end{array}$$

(2)

where $x={\left[x_1,x_2\right]}^T$, the function $f\left(x\right)$ is a nonlinear function, and the control signal is denoted by u, and d represents the disturbance. Depending on the structure of MR, such as kinematic constraints, the function $f\left(x\right)$ can be different.

In this paper, the controller is designed independently of the dynamics of MR. So, the terms $f\left(x\right)+d$ is approximated by a T3FLS, as shown in Figure 1. The T3FLS is learned in the direction of stability. The parameters of T3FLS are adjusted by the laws that are extracted from a stability theorem. In other words, besides the tracking error, the candidate Lyapunov function includes the also tuning error of parameters of T3FLS. Furthermore, a compensator is designed as a supervisor controller that handles the estimation error of T3FLS and helps for more robustness.

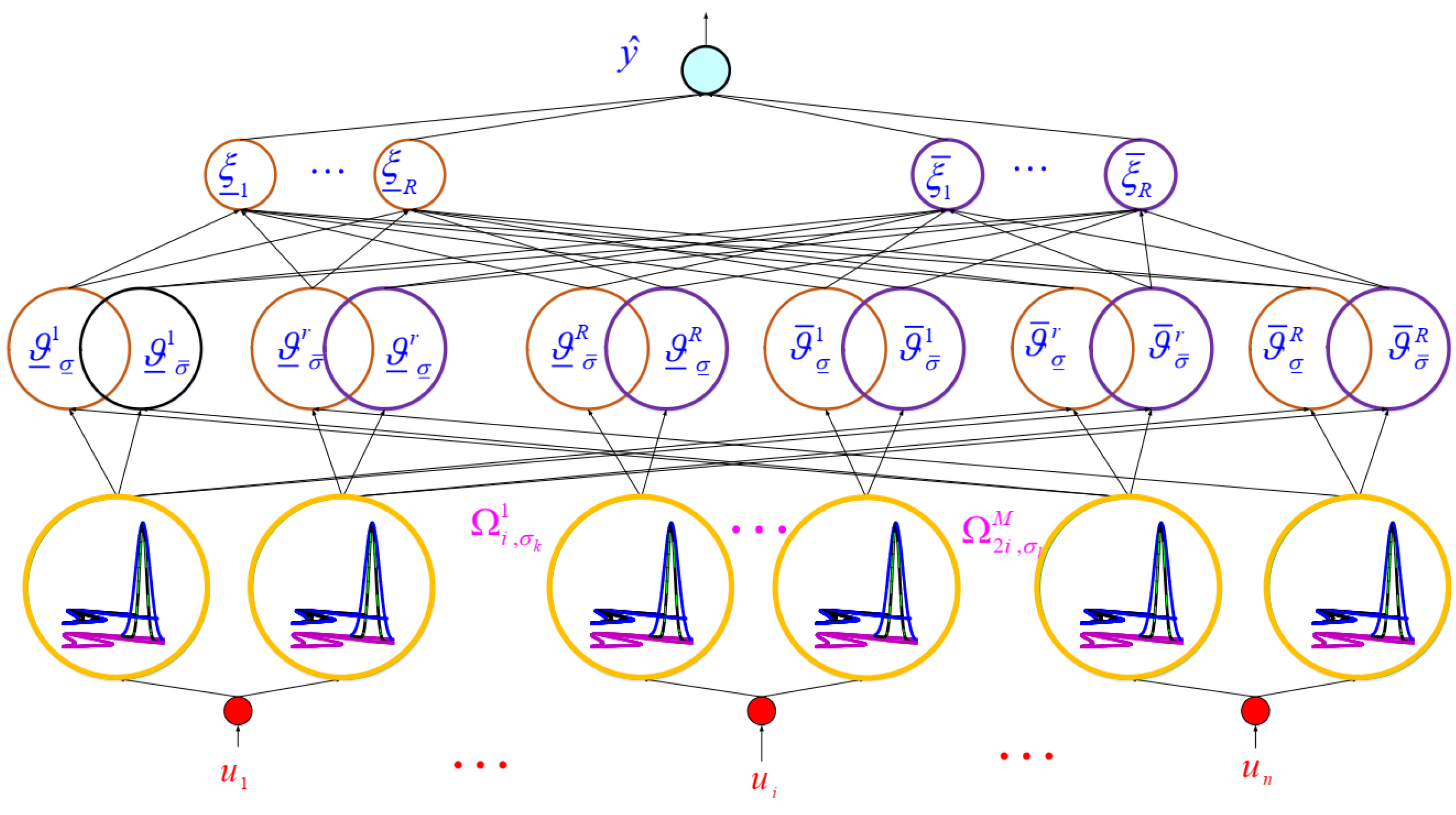
3. Type-3 FLS

As mentioned earlier, the nonlinearities $f\left(x\right)$ and disturbance d are estimated by T3FLSs. In this section, we present the basic structure of T3FLSs as is given in Figure 2.

(1)

The inputs are the states of slave system.

(2)

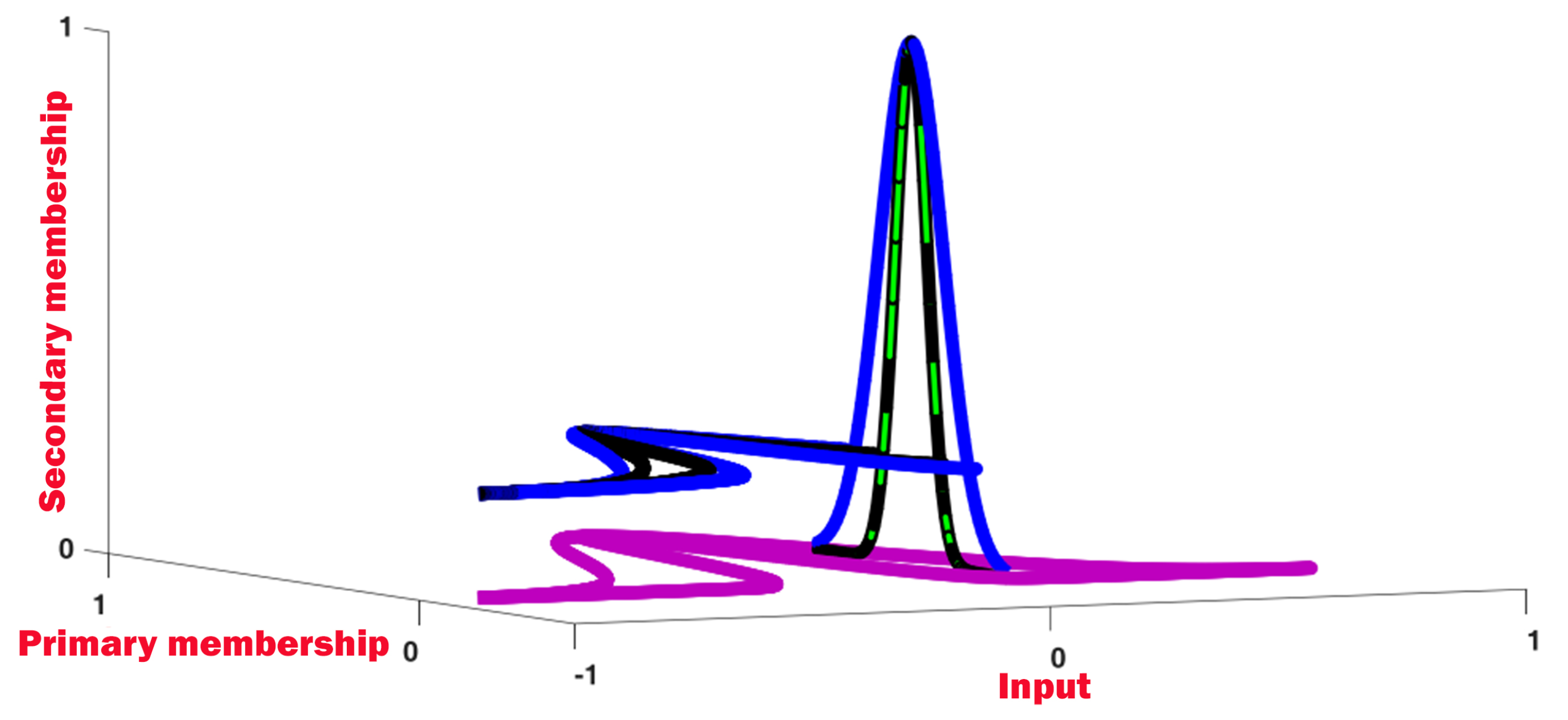
For $x_1\left(t\right)$, $x_2\left(t\right)$ and $x_n\left(t\right)$, the upper/lower memberships of M membership functions (MF) are computed as follows (see Figure 3):

$${\overline{\varsigma }}_{m_{i,{\overline{\sigma }}_k}^j}\left(x_i\right)=exp\left(-\frac{{\left(x_i-{\vartheta }_{m_{i,{\overline{\sigma }}_k}^j}\right)}^2}{{\overline{\chi }}_{m_{i,{\overline{\sigma }}_k}^j}^2}\right)$$

(3)

$${\overline{\varsigma }}_{m_{i,{\underline{\sigma }}_k}^j}\left(x_i\right)=exp\left(-\frac{{\left(x_i-{\vartheta }_{m_{i,{\underline{\sigma }}_k}^j}\right)}^2}{{\overline{\chi }}_{m_{i,{\underline{\sigma }}_k}^j}^2}\right)$$

(4)

$${\underline{\varsigma }}_{m_{i,{\overline{\sigma }}_k}^j}\left(x_i\right)=exp\left(-\frac{{\left(x_i-{\vartheta }_{m_{i,{\overline{\sigma }}_k}^j}\right)}^2}{{\underline{\chi }}_{m_{i,{\overline{\sigma }}_k}^j}^2}\right)$$

(5)

$${\underline{\varsigma }}_{m_{i,{\underline{\sigma }}_k}^j}\left(x_i\right)=exp\left(-\frac{{\left(x_i-{\vartheta }_{m_{i,{\underline{\sigma }}_k}^j}\right)}^2}{{\underline{\chi }}_{m_{i,{\underline{\sigma }}_k}^j}^2}\right)$$

(6)

(3)

The r-th rule is written as:

$$\begin{array}{c}\mathrm{Rule}\#r:\mathrm{If}{x}_1\mathrm{is}{m}_{1,{\overline{\sigma }}_k}^r\mathrm{and}{x}_2\mathrm{is}{m}_{2,{\overline{\sigma }}_k}^r\\ \mathrm{and}{x}_3\mathrm{is}{m}_{3,{\overline{\sigma }}_k}^r\mathrm{Then}\widehat{y}\in \left[{\underline{x}}_r,{\overline{x}}_r\right]\end{array}$$

(7)

where $m_{1,{\overline{\sigma }}_k}^r$, $m_{2,{\overline{\sigma }}_k}^r$ and $m_{3,{\overline{\sigma }}_k}^r$ are r-th MF for $x_1$, $x_2$ and $x_3$, respectively. The rule firings are written as:

$${\underline{\rho }}_{{\overline{\sigma }}_k}^r={\underline{\varsigma }}_{m_{1,{\overline{\sigma }}_k}^{j1}}\left(x_1\right){\underline{\varsigma }}_{m_{2,{\overline{\sigma }}_k}^{j2}}\left(x_2\right){\underline{\varsigma }}_{m_{3,{\overline{\sigma }}_k}^{j_3}}\left(x_3\right)$$

(8)

$${\underline{\rho }}_{{\underline{\sigma }}_k}^r={\underline{\varsigma }}_{m_{1,{\underline{\sigma }}_k}^{j1}}\left(x_1\right){\underline{\varsigma }}_{m_{2,{\underline{\sigma }}_k}^{j2}}\left(x_2\right){\underline{\varsigma }}_{m_{3,{\underline{\sigma }}_k}^{j_3}}\left(x_3\right)$$

(9)

$${\overline{\rho }}_{{\overline{\sigma }}_k}^r={\overline{\varsigma }}_{m_{1,{\overline{\sigma }}_k}^{j1}}\left(x_1\right){\overline{\varsigma }}_{m_{2,{\overline{\sigma }}_k}^{j2}}\left(x_2\right){\overline{\varsigma }}_{m_{3,{\overline{\sigma }}_k}^{j_3}}\left(x_3\right)$$

(10)

$${\overline{\rho }}_{{\underline{\sigma }}_k}^r={\overline{\varsigma }}_{m_{1,{\underline{\sigma }}_k}^{j1}}\left(x_1\right){\overline{\varsigma }}_{m_{2,{\underline{\sigma }}_k}^{j2}}\left(x_2\right){\overline{\varsigma }}_{m_{3,{\underline{\sigma }}_k}^{j_3}}\left(x_3\right)$$

(11)

where ${\overline{\rho }}_{{\overline{\sigma }}_k}^r$ and ${\overline{\rho }}_{{\underline{\sigma }}_k}^r$ denote the upper bound of firing degrees, and ${\underline{\rho }}_{{\overline{\sigma }}_k}^r$ and ${\underline{\rho }}_{{\underline{\sigma }}_k}^r$ represent the lower bound of firing degrees.

(4)

The output $\widehat{y}$ is written as [38]:

$$\begin{array}{c}\widehat{y}=x^T\mu \end{array}$$

(12)

where x and $\mu$ are:

$$x={\left[{\underline{x}}_1,\dots ,{\underline{x}}_M,{\overline{x}}_1,\dots ,{\overline{x}}_M\right]}^T$$

(13)

$$\mu ={\left[{\underline{\mu }}_1,\dots ,{\underline{\mu }}_M,{\overline{\mu }}_1,\dots ,{\overline{\mu }}_M\right]}^T$$

(14)

where M is rule numbers, and ${\underline{\mu }}_r$ and ${\overline{\mu }}_r$ are:

$$\begin{array}{c}{\overline{\mu }}_r=\frac{\sum _{k=1}^{n_{\sigma }}{\overline{\sigma }}_k\frac{{\overline{\rho }}_{{\overline{\sigma }}_k}^r}{\sum _{r=1}^M\left({\overline{\rho }}_{{\overline{\sigma }}_k}^r+{\underline{\rho }}_{{\overline{\sigma }}_k}^r\right)}}{\sum _{k=1}^{n_{\sigma }}\left({\overline{\sigma }}_k+{\underline{\sigma }}_k\right)}\\ +\frac{\sum _{j=1}^{n_{\sigma }}{\underline{\sigma }}_k\frac{{\overline{\rho }}_{{\underline{\sigma }}_k}^r}{\sum _{r=1}^M\left({\overline{\rho }}_{{\underline{\sigma }}_k}^r+{\underline{\rho }}_{{\underline{\sigma }}_k}^r\right)}}{\sum _{k=1}^{n_{\sigma }}\left({\overline{\sigma }}_k+{\underline{\sigma }}_k\right)},r=1,\dots ,M\end{array}$$

(15)

$$\begin{array}{c}{\underline{\mu }}_r=\frac{\sum _{k=1}^{n_{\sigma }}{\overline{\sigma }}_k\frac{{\underline{\rho }}_{{\overline{\sigma }}_k}^r}{\sum _{r=1}^M\left({\overline{\rho }}_{{\overline{\sigma }}_k}^r+{\underline{\rho }}_{{\overline{\sigma }}_k}^r\right)}}{\sum _{k=1}^{n_{\sigma }}\left({\overline{\sigma }}_k+{\underline{\sigma }}_k\right)}\\ +\frac{\sum _{j=1}^{n_{\sigma }}{\underline{\sigma }}_k\frac{{\underline{\rho }}_{{\underline{\sigma }}_k}^r}{\sum _{r=1}^M\left({\overline{\rho }}_{{\underline{\sigma }}_k}^r+{\underline{\rho }}_{{\underline{\sigma }}_k}^r\right)}}{\sum _{k=1}^{n_{\sigma }}\left({\overline{\sigma }}_k+{\underline{\sigma }}_k\right)},r=1,\dots ,M\end{array}$$

(16)

4. Control Designing and Stability Analysis

To design the controller, the sliding surface (17) is considered:

$$S=e_{}^{\left(n-1\right)}+{\lambda }_n{e}_{}^{\left(n-2\right)}+\cdots +{\lambda }_{1}e$$

(17)

where $e=y-r$, y is the output, r is the reference, and ${\lambda }_1,\dots ,{\lambda }_n$ are the fixed parameters that are chosen such that (17) to be stable. By taking the derivative of (17), we have:

$$\dot{S}=e_{}^{\left(n\right)}+{\lambda }_n{e}_{}^{\left(n-1\right)}+\cdots +{\lambda }_1\dot{e}$$

(18)

In (18), we substitute $e_{}^{\left(n\right)}$ form (2), then:

$$\dot{S}=f\left(x\right)+d+u-r^{\left(n\right)}+{\lambda }_n{e}_{}^{\left(n-1\right)}+\cdots +{\lambda }_1\dot{e}$$

(19)

where $r^{\left(n\right)}$ is the n-th derivative order r. The controller is considered as:

$$\begin{array}{c}u=\left[-\widehat{f}\left(x\right)+r^{\left(n\right)}-{\lambda }_n{e}_{}^{\left(n-1\right)}-\cdots -{\lambda }_1\dot{e}\right.\hfill \\ \left.-\left|S\right|tanh\left(S\right)+u_c\right]\hfill \end{array}$$

(20)

where tanh represents the hyperbolic tangent and acts like a sign function. By substituting (20) into the sliding surface (19), we obtain:

$$\dot{S}=f-\widehat{f}+d+\epsilon -\left|S\right|tanh\left(S\right)+u_c$$

(21)

By adding/subtracting optimal T3FLS, we have:

$$\dot{S}=f-{\widehat{f}}^{*}+f^{*}-\widehat{f}+d-\left|S\right|tanh\left(S\right)+u_c$$

(22)

In a vector form, we can write:

$$\begin{array}{c}\dot{S}=f-{\widehat{f}}^{*}+d+\epsilon +{\tilde{\theta }}^T\xi \hfill \\ -\left|S\right|tanh\left(S\right)+u_c\hfill \end{array}$$

(23)

The estimation errors entirely are shown by following relation:

$$E=f-{\widehat{f}}^{*}+d$$

(24)

Then, the sliding surface becomes:

$$\dot{S}=E+{\tilde{\theta }}^T\xi -\left|S\right|tanh\left(S\right)+u_c$$

(25)

To stability prove, we consider the Lyapunov as:

$$V=\frac{1}{2}{S}^2+\frac{1}{2\eta }{\tilde{\theta }}^T\tilde{\theta }+\frac{1}{2\eta }{\tilde{E}}^2$$

(26)

where $0<\eta \le 1$ is the adaptation rate, $\tilde{E}$ is designed as $\tilde{E}=E-\widehat{E}$, E is the upper bound of estimation error, and $\widehat{E}$ is the estimation of E. It is obvious that V is positive-definite. Because $V>0$ while we have $S>0$, $\tilde{\theta }>0$, $\tilde{E}>0$, and $V=0$ while we have $S=0$, $\tilde{\theta }=0$, $\tilde{E}=0$. The derivative of (26) yields:

$$\dot{V}=S\dot{S}-\frac{1}{\eta }{\tilde{\theta }}^T\dot{\theta }-\frac{1}{\eta }\tilde{E}\dot{\widehat{E}}$$

(27)

By substitution from (21), we obtain:

$$\begin{array}{c}\dot{V}=-\frac{1}{\eta }{\tilde{\theta }}^T\dot{\theta }-\frac{1}{\eta }\tilde{E}\dot{\widehat{E}}\hfill \\ S\left[E+{\tilde{\theta }}^T\xi -\left|S\right|tanh\left(S\right)+u_c\right]\hfill \end{array}$$

(28)

From (28), we have:

$$\begin{array}{c}\dot{V}={\tilde{\theta }}^T\left(S\xi -\frac{1}{\eta }\dot{\theta }\right)-\frac{1}{\eta }\tilde{E}\dot{\widehat{E}}\hfill \\ S\left[E-\left|S\right|tanh\left(S\right)+u_c\right]\hfill \end{array}$$

(29)

In (29), we consider:

$$\dot{\theta }=\eta S\xi$$

(30)

Then, from the fact that $\left|S\right|Stanh\left(S\right)\le S^2$, it can be concluded that:

$$\dot{V}\le -\frac{1}{\eta }\tilde{E}\dot{\widehat{E}}+SE-S^2+S{u}_c$$

(31)

Regarding $\tilde{E}=E-\widehat{E}$, it follows from expression (31):

$$\dot{V}\le -\frac{1}{\eta }\left(E-\widehat{E}\right)\dot{\widehat{E}}+E\left|S\right|-{\left|S\right|}^2+S{u}_c$$

(32)

The simplification of (32) yields:

$$\dot{V}\le -\frac{1}{\eta }E\dot{\widehat{E}}+\frac{1}{\eta }\widehat{E}\dot{\widehat{E}}+E\left|S\right|-{\left|S\right|}^2+S{u}_c$$

(33)

From (33), we have:

$$\left\{\begin{array}{c}E\left|S\right|=\frac{1}{\eta }E\dot{\widehat{E}}\hfill \\ S{u}_c=-\frac{1}{\eta }\widehat{E}\dot{\widehat{E}}\hfill \end{array}\right.$$

(34)

Then,

$$\dot{V}\le -{\left|S\right|}^2\le 0$$

(35)

From (34), the adaptation rule for E (upper bound of uncertainties) and $u_c$ (compensator signal) are derived as:

$$\left\{\begin{array}{c}\dot{\widehat{E}}=\eta \left|S\right|\hfill \\ u_c=-\widehat{E}S\left|S\right|\hfill \end{array}\right.$$

(36)

From (35), it is concluded that the system is globally stable, while the adaptations (30) and (34) are satisfied. It should be noted that from the fact that the derivative of S is bounded, then from Barbalat’s lemma, the asymptotic stability is also derived [39].

Remark 1.

In this paper, the suggested FLS is learned by Lyapunov theorem. For future studies, to improve the control accuracy, the other learning algorithms can be used such as random optimization [40,41], reinforcement learning [42], and deep learning [43].

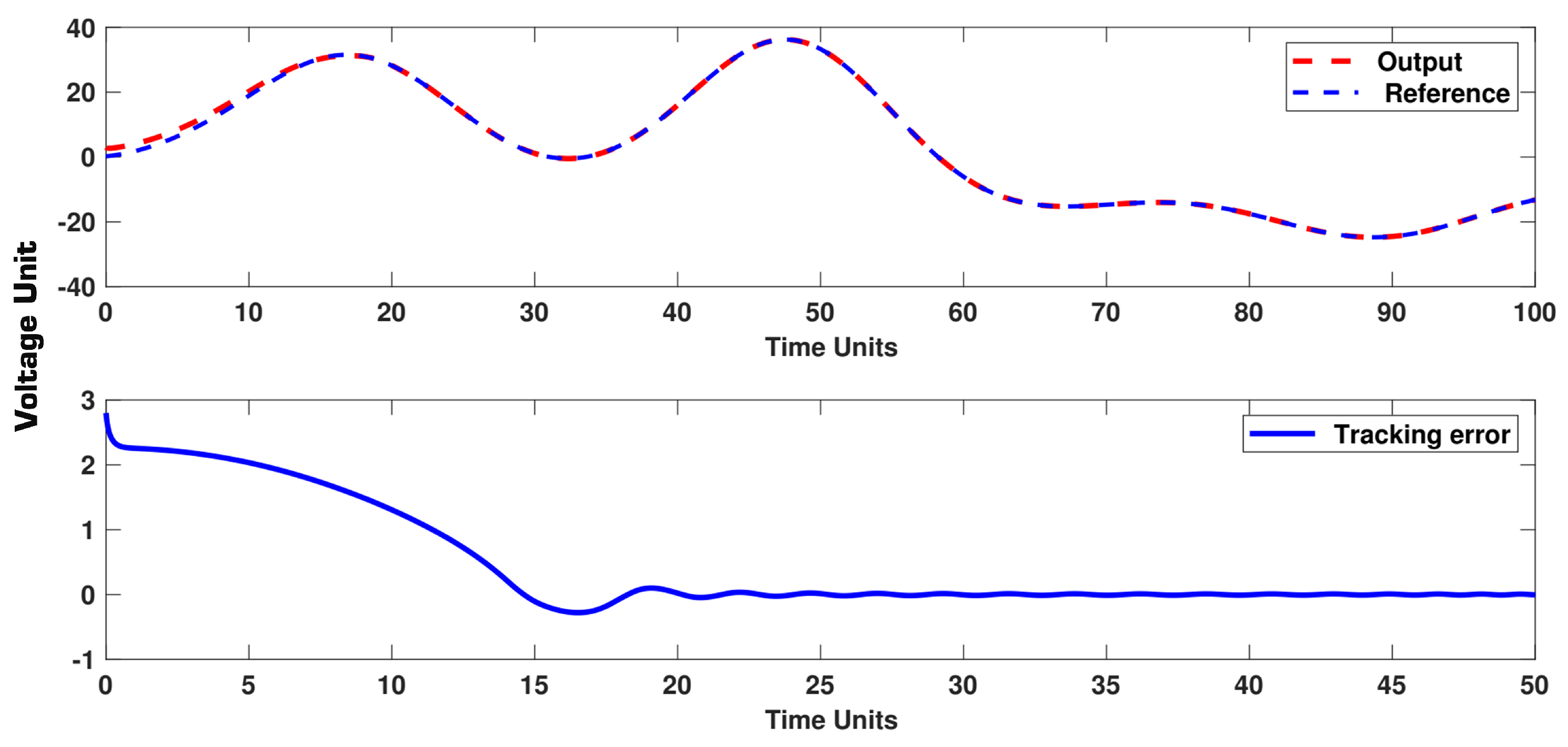
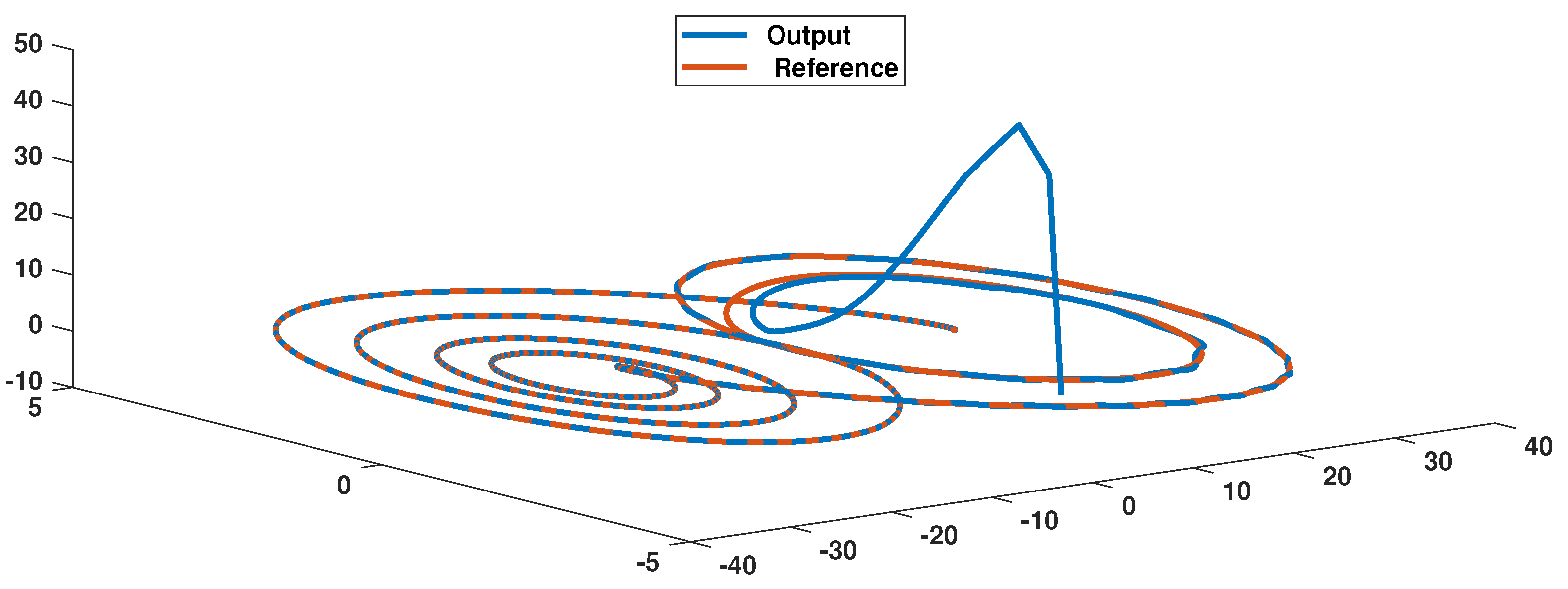
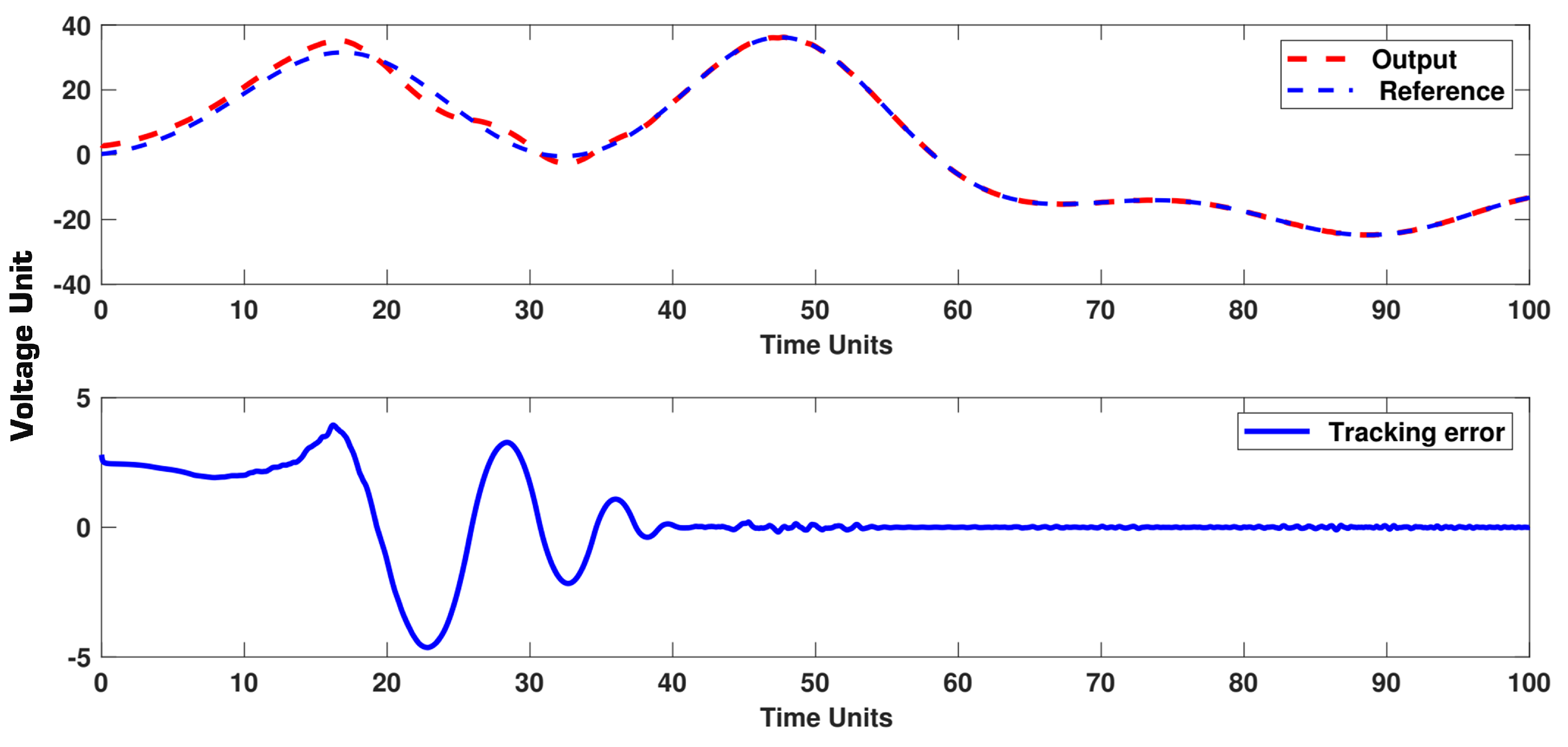
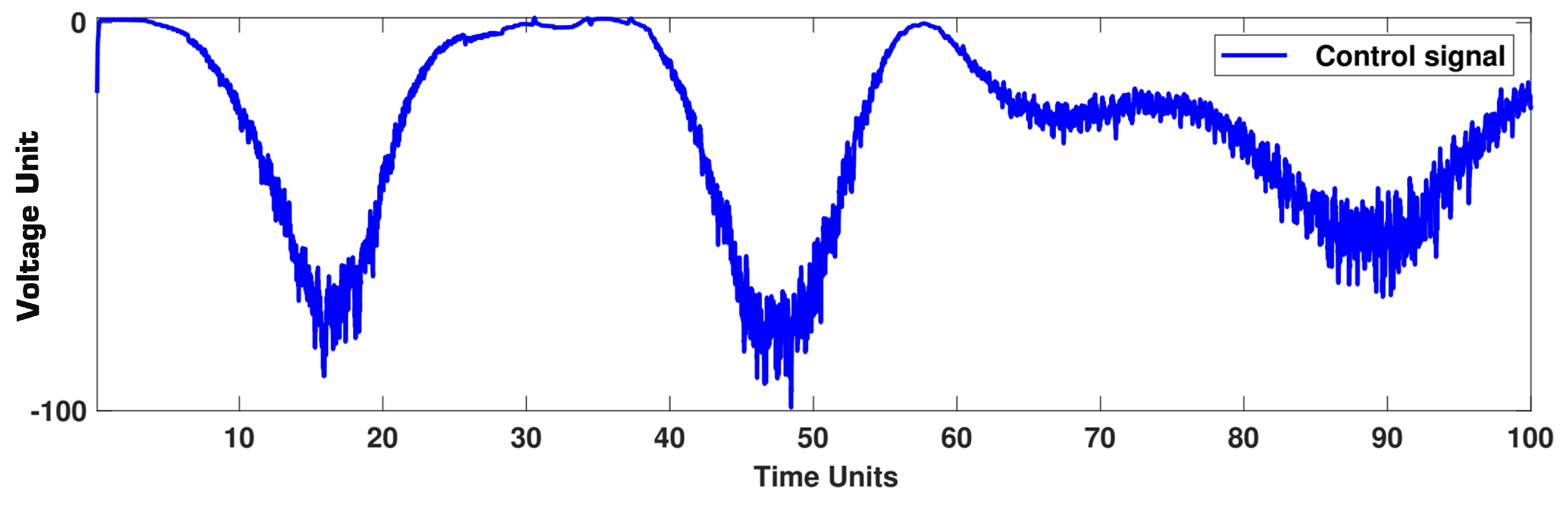
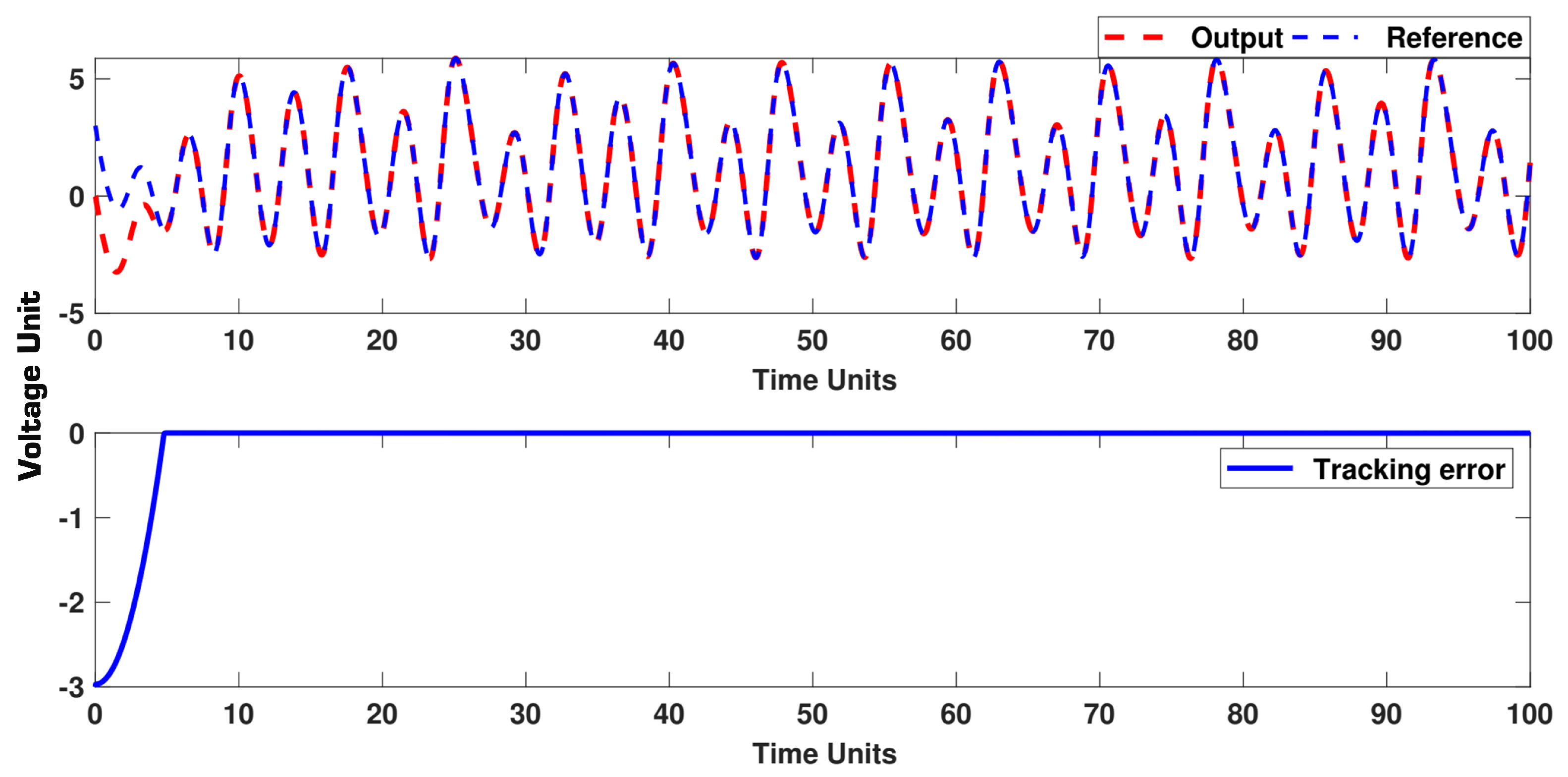
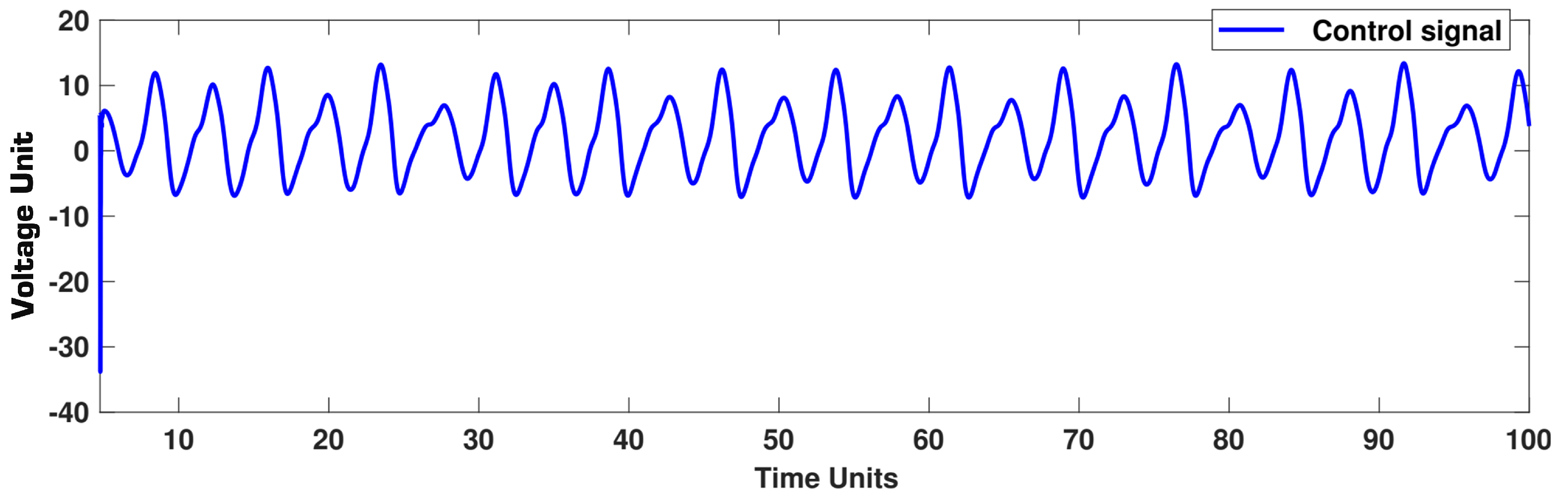
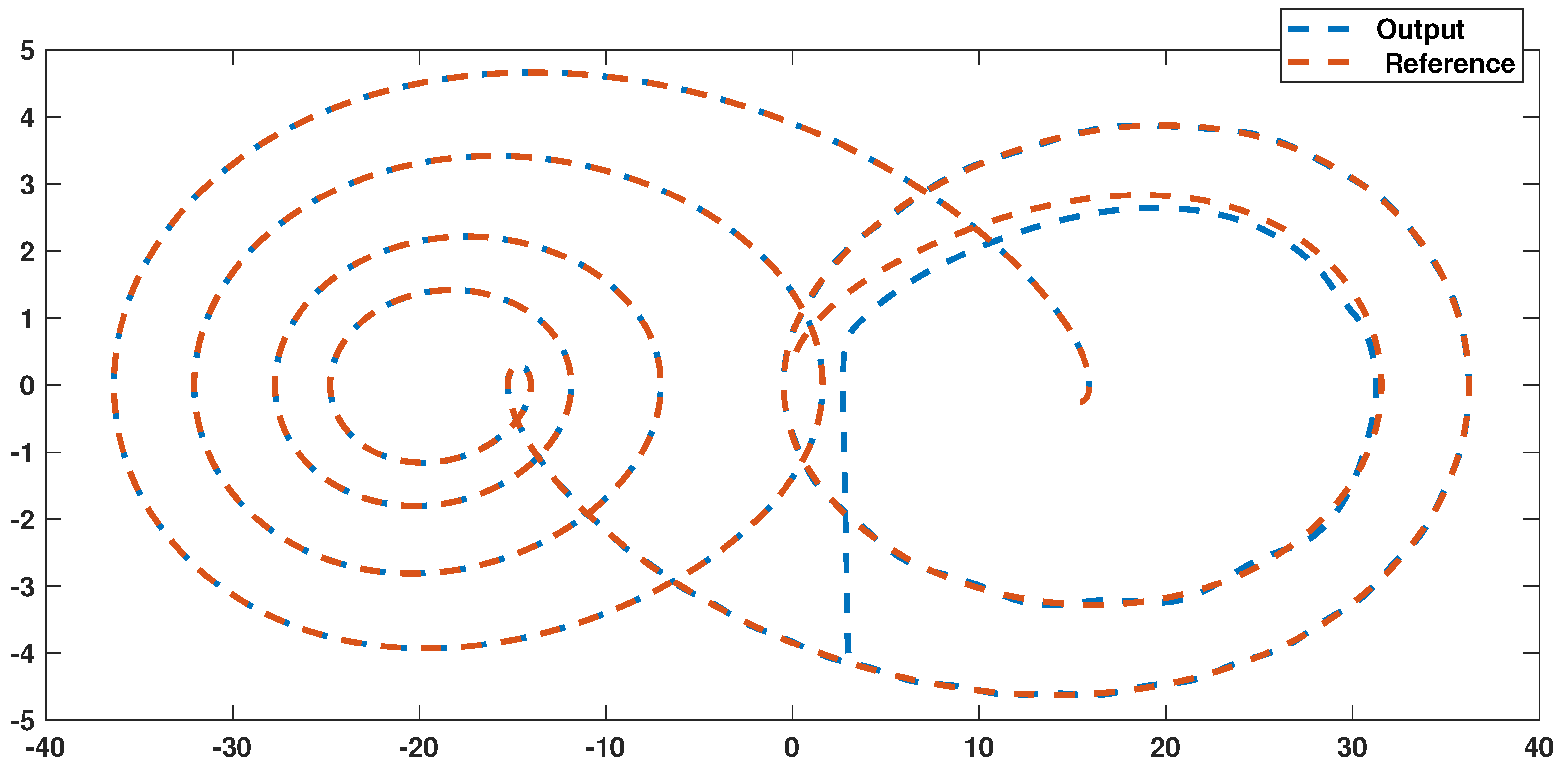
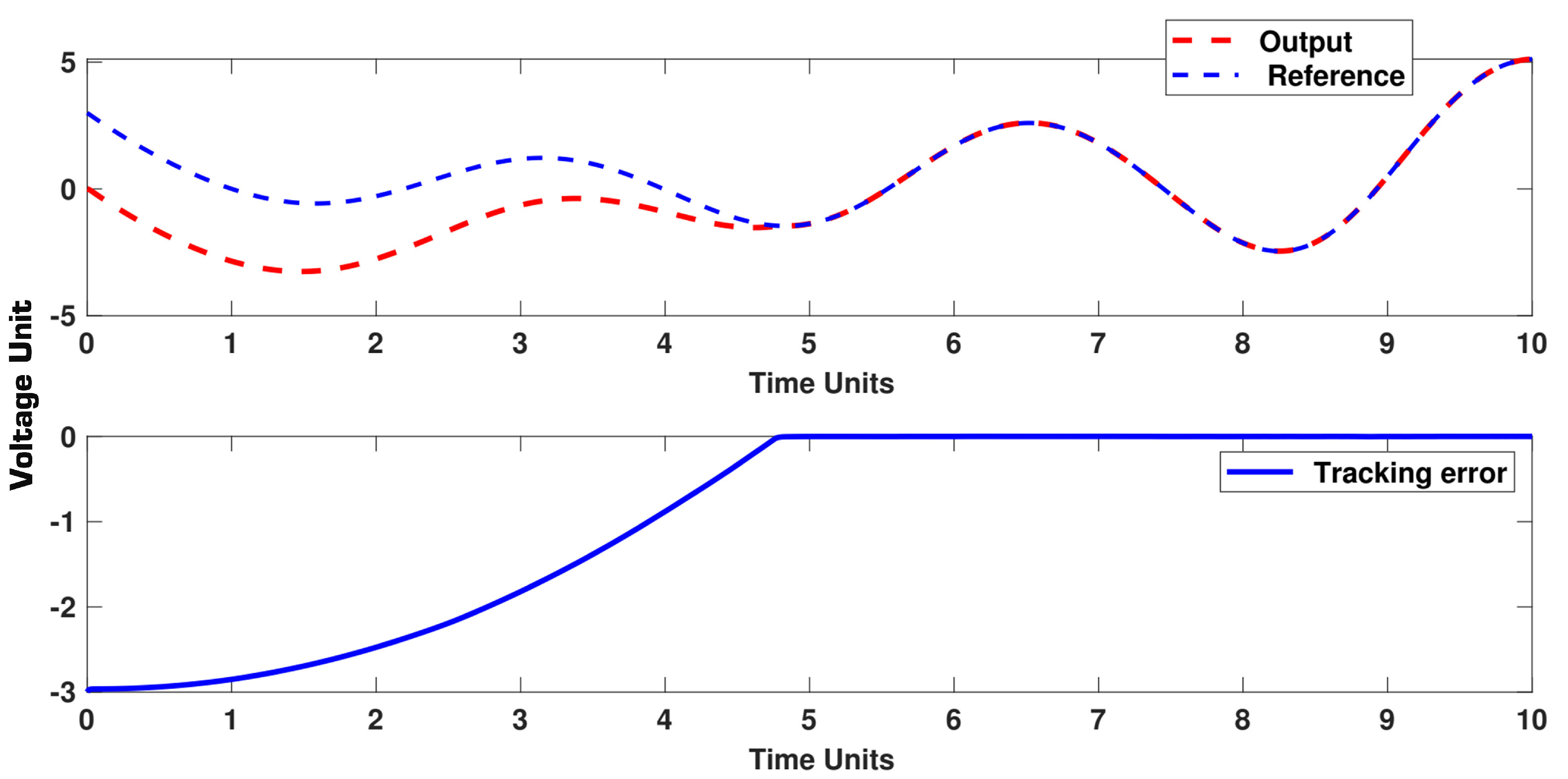
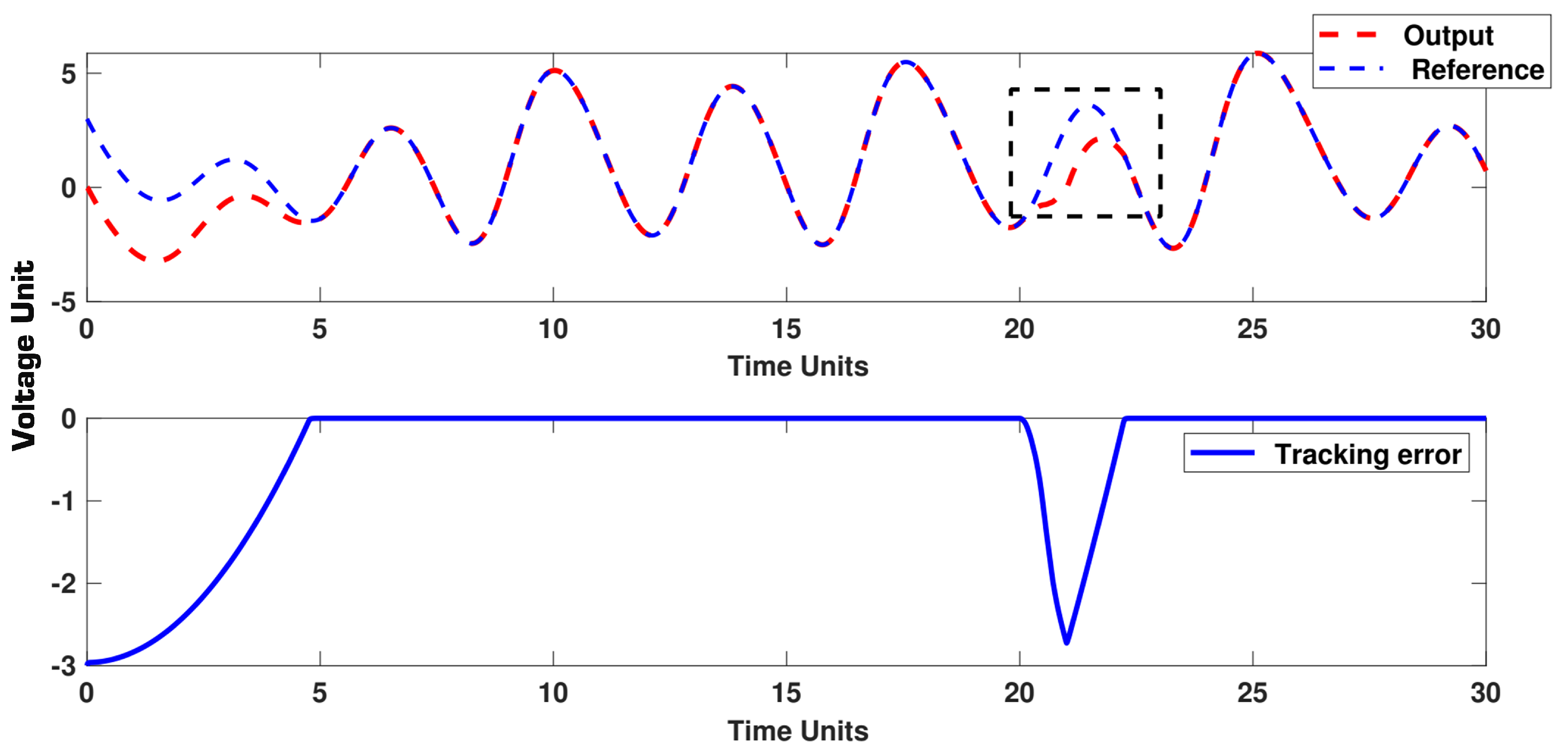
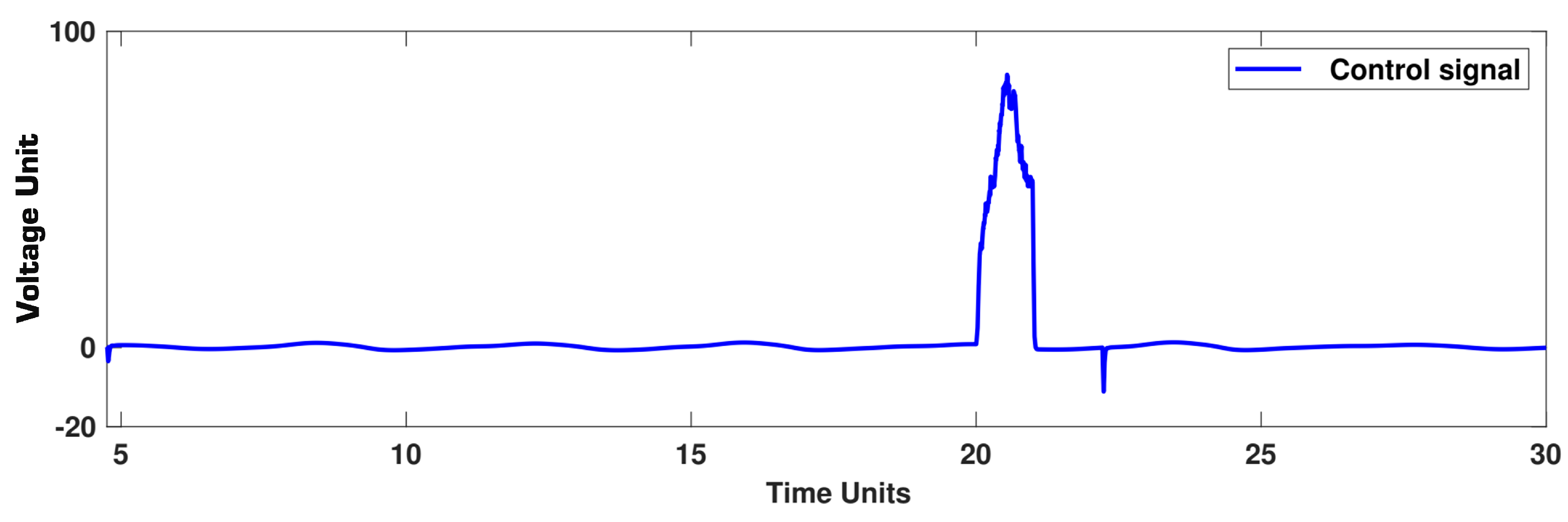
5. Simulation

Example 1.

For the first example, the Chua’s system is considered:

$$\begin{array}{c}{\dot{x}}_1=x2,{\dot{x}}_2=x3,{\dot{x}}_3=f+u\hfill \\ f=14/1805x_1+168/9025x_2+1/38x_3\hfill \\ -2/45{\left(28/361x_1+7/95x_2+x_3\right)}^3\hfill \end{array}$$

(37)

where $x_1\left(0\right)=0.2$, $x_2\left(0\right)=0.5$ and $x_3\left(0\right)=0.3$. The disturbance is $d=0.01sin\left(7t\right)+0.03cos\left(11t\right)$. The output and error signals are shown in Figure 4, and the controller is provided in Figure 5. The trajectories of Figure 4 demonstrate that the output signal is well reached to the target signal. In addition, the control trajectory has an acceptable shape. It should be noted that good tracking is achieved by the suggested controller in spite of unknown dynamics and disturbance $d\left(t\right)$.

Example 2.

For the second examination, the reference/slave systems are considered to be Chua and Genesio’s systems, respectively:

$$\begin{array}{c}{\dot{x}}_1=x2,{\dot{x}}_2=x3,{\dot{x}}_3=f\hfill \\ f=14/1805x_1+168/9025x_2+1/38x_3\hfill \\ -2/45{\left(28/361x_1+7/95x_2+x_3\right)}^3\hfill \end{array}$$

(38)

$$\begin{array}{c}{\dot{x}}_1=x2,{\dot{x}}_2=x3,{\dot{x}}_3=f+u\hfill \\ f=-6x_1-2.9x_2-1.2x_3+x_1^2\hfill \end{array}$$

(39)

where $x_1\left(0\right)=3.2$, $x_2\left(0\right)=-4.5$ and $x_3\left(0\right)=2$. The output and error signals are shown in Figure 6, and the controller is depicted in Figure 7. The phase portrait is shown in Figure 8. The convergence of the system (39) to the target system (38) is well seen in the phase portrait, as shown in Figure 8. Similar to the previous example, we see that the trajectories of Figure 6 are well reached to the target signals. Furthermore, the control trajectory has an acceptable shape. To further analyze, besides the previous perturbations, we add a dead zone on the control signal and repeat the simulation. In this case, the output and error signals are shown in Figure 9, and the controller is depicted in Figure 10. The trajectories of Figure 9 demonstrate the suggested controller has a good ability to tackle high perturbations.

Example 3.

For the third example, the reference/slave systems are considered to be Genesio and pendulum, respectively:

$$\begin{array}{c}{\dot{x}}_1=x2,{\dot{x}}_2=x3,{\dot{x}}_3=f\hfill \\ f=-6x_1-2.9x_2-1.2x_3+x_1^2\hfill \end{array}$$

(40)

$$\begin{array}{c}{\dot{x}}_1=x2,{\dot{x}}_2=f+u\hfill \\ f=-0.5x_1-0.12x_2-sin\left(x_1\right)+0.5cos0.75t\hfill \\ -0.12sin0.75t+sin(0.3cos0.75t-3)-1.5\hfill \end{array}$$

(41)

where $x_1\left(0\right)=0$, and $x_2\left(0\right)=0$. The output and error signals are shown in Figure 11, and the controller is depicted in Figure 12. The phase portrait is shown in Figure 13. The convergence of the system (41) to the target system (40) is well seen in the phase portrait, as shown in Figure 13. Similar to Example 2, we see that the trajectories of Figure 11 are well reached to the target signals. Similarly, the control trajectory has an acceptable shape. In addition, to have a better examination, similar to Example 2, we add a dead zone on the control signal and repeat the simulation. In this case, the output and error signals are shown in Figure 14, and the controller is depicted in Figure 15. The trajectories of Figure 14 demonstrate that the suggested controller has a good ability to tackle high perturbations.

Example 4.

In this example, a fault is suddenly applied to the system, and the effectiveness of the controller is evaluated. The output and error signals are shown in Figure 16, and the controller is depicted in Figure 17. We see that after a high perturbation, the output is well converged again to the references. The tracking error in the steady state has a small acceptable value. The perturbation is well tackled and the output signal has a good tracking scheme.

Remark 2.

The suggested controller uses the developed type-3 FLSs. This type of FLSs results in better robustness in high-noisy conditions. The simulation results show that by the suggested controller, the MR can track various chaotic references well. In spite of dynamic uncertainties, sudden changes in references, and complicated chaotic behavior of the reference system, the MR well follows the planned trajectory. So, the suggested approach can be used in various applications of MR. To better show the superiority of the suggested fuzzy-based controller, the root mean square of error (RMSE) is compared with a feedback controller [44] and an adaptive controller [45]. The simulation conditions are the same as shown in Example 1 for all controllers. The results are shown in

Table 1. Comparison of RMSE with different controllers.

	Proposed method	Feedback controller [44]	Adaptive controller [45]
RMSE	0.01045	0.7812	0.1357

. We see that the accuracy of the suggested approach is much better than classic controllers. However, in classic controllers, the system’s dynamic information is used in control design. In addition, to apply the traditional controllers for other MRs, we need to change a lot of settings. However, the suggested controller does not depend on the MR dynamics.

6. Conclusions

In this study, a new T3FLS-based synchronization system is introduced. The entire dynamics are unknown and also are disturbed by further perturbation. A new adaptive supervisor controller also works in parallel with the main controller to help better robustness. The schemed controller is evaluated in four illustrative examples. In the first example, the designed controller is examined on Chua’s chaotic system. The simulation results verify that the designed controller has an excellent response versus unknown dynamics. In the second examination, the designed controller is applied to a synchronization problem, and the Genesio chaotic system is synchronized with Chua’s chaotic system. The synchronization is examined in two cases. In the first one, just the Genesio dynamics are unknown, and in the second case, in addition to unknown dynamics, a high perturbation is applied to system dynamics and input signals. The results show a good robust synchronization. In the third example, a pendulum system is synchronized with the Genesio chaotic system. Similar to the second example, in two cases, the accuracy and performance are evaluated. The results demonstrate that the schemed controller shows an excellent ability to tackle high perturbations. Finally, in the last example, a fault is suddenly imposed on the system, and the good robustness/stability of the controller is evaluated. We see that after a high perturbation, the output is well converged again to the references. The tracking error in the steady state has a small acceptable value. The perturbation is tackled well and the output signal has a good tracking scheme.