Indexing Inefficacy of Efforts to Stop Escalation of COVID Mortality
Abstract
1. Introduction
2. Methods
2.1. Model Specification
2.2. Index of Inefficacy
2.3. Estimating the Efficacy Parameter
2.4. Data
3. Results
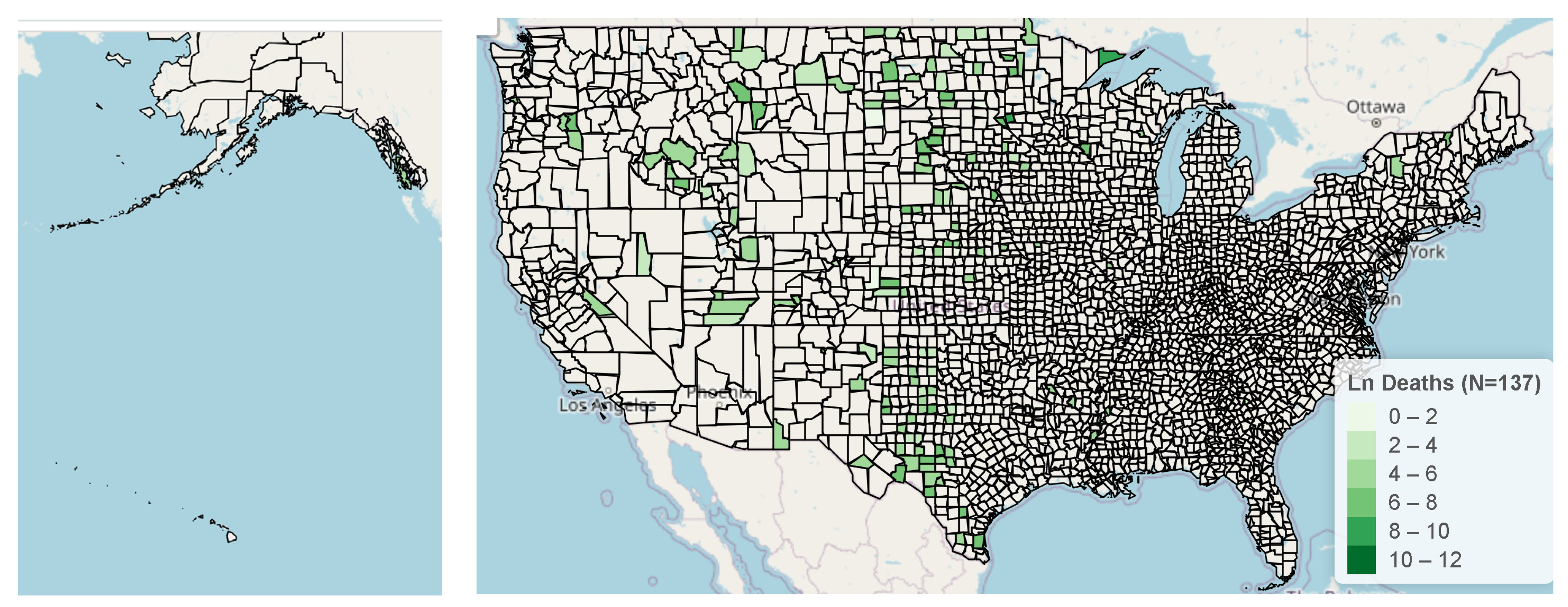
3.1. Map of Counties with Potentially Ineffective Interventions
3.2. Estimation of Parameters
3.3. Analysis of COVID Fatalities
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Le, T.T.B.; Vasanthakumaran, T.; Hien, H.N.T.; Hung, I.C.; Luu, M.N.; Khan, Z.A.; An, N.T.; Tran, V.P.; Lee, W.J.; Aziz, J.M.A. SARS-CoV-2 omicron and its current known unknowns: A narrative review. Rev. Med. Virol. 2022, e2398. [Google Scholar] [CrossRef] [PubMed]
- WHO. Who Coronavirus (COVID-19) Dashboard. 2022. Available online: https://covid19.who.int/ (accessed on 2 November 2022).
- Rajan, S.; McKee, M.; Hernández-Quevedo, C.; Karanikolos, M.; Richardson, E.; Webb, E.; Cylus, J. What have european countries done to prevent the spread of COVID-19? Lessons from the COVID-19 health system response monitor. Health Policy 2022, 126, 355–361. [Google Scholar] [CrossRef] [PubMed]
- Unruh, L.; Allin, S.; Marchildon, G.; Burke, S.; Barry, S.; Siersbaek, R.; Thomas, S.; Rajan, S.; Koval, A.; Alexander, M. A comparison of 2020 health policy responses to the COVID-19 pandemic in canada, ireland, the united kingdom and the united states of america. Health Policy 2022, 126, 427–437. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9187506/pdf/main.pdf (accessed on 2 November 2022). [CrossRef] [PubMed]
- Jiao, J.; Shi, L.; Zhang, Y.; Chen, H.; Wang, X.; Yang, M.; Yang, J.; Liu, M.; Sun, G. Core policies disparity response to COVID-19 among brics countries. Int. J. Equity Health 2022, 21, 9. [Google Scholar] [CrossRef] [PubMed]
- Brauner, J.M.; Mindermann, S.; Sharma, M.; Johnston, D.; Salvatier, J.; Gavenčiak, T.; Stephenson, A.B.; Leech, G.; Altman, G.; Mikulik, V. Inferring the effectiveness of government interventions against COVID-19. Science 2021, 371, eabd9338. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7877495/pdf/371_abd9338.pdf (accessed on 2 November 2022). [CrossRef] [PubMed]
- Feinhandler, I.; Cilento, B.; Beauvais, B.; Harrop, J.; Fulton, L. Predictors of death rate during the COVID-19 pandemic. Presented Healthc. 2020, 8, 339. [Google Scholar] [CrossRef] [PubMed]
- McAleer, M. Prevention is better than the cure: Risk management of COVID-19. J. Risk Financ. Manag. 2020, 13, 46. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Development Core Team: Vienna, Austria, 2018. [Google Scholar]
- Shanmugam, R. An intervened poisson distribution and its medical application. Biometrics 1985, 41, 1025–1029. Available online: http://www.jstor.org/stable/2530973 (accessed on 2 November 2022). [CrossRef] [PubMed]
- Shanmugam, R. An inferential procedure for the poisson intervention parameter. Biometrics 1992, 48, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Joyce, V.J.; Merlin, G.S.; Edna, K.R.J.; Fenella, S. Designing mixed sampling plan based on ipd. J. Manag. Inf. Decis. Sci. 2021, 24, 1–6. [Google Scholar]
- Shanmugam, R. Revelation of shrunken or stretched binomial dispersion and public perception of situations which might spread aids or hiv. Int. J. Res. Med. Sci. 2014, 2, 462–467. [Google Scholar] [CrossRef][Green Version]
- Shanmugam, R. Modelling web changes data recatched during a spread of internet virus. Math. Comput. Model. 2005, 42, 1175–1190. [Google Scholar] [CrossRef]
- Shanmugam, R. Predicting “successful” prevention of an epidemic. Commun. Stat.-Theory Methods 2006, 30, 93–103. [Google Scholar] [CrossRef]
- Johnson, S.G. The Nlopt Nonlinear Optimization Package. 2022. Available online: https://nlopt.readthedocs.io/en/latest/ (accessed on 2 November 2022).
- Usafacts. Us COVID-19 Cases and Deaths by State. 2022. Available online: https://usafacts.org/visualizations/coronavirus-COVID-19-spread-map (accessed on 2 November 2022).
- CDC. Trends in Number of COVID-19 Cases and Deaths in the Us Reported to CDC, by State/Territory. 2022. Available online: https://covid.cdc.gov/covid-data-tracker/#trends_weeklydeaths_select_00 (accessed on 2 November 2022).
- Cheng, J.; Karambelkar, B.; Xie, Y. Leaflet: Create Interactive Web Maps with the Javascript ‘Leaflet’ Library, 2022.
- Fulton, L. Rpubs Code. 2022. Available online: https://rpubs.com/R-Minator/Ram22 (accessed on 2 November 2022).
- Powell, M.J. A view of algorithms for optimization without derivatives. Math. Today-Bull. Inst. Math. Appl. 2007, 43, 170–174. [Google Scholar]
- Zhou, X.; Josey, K.; Kamareddine, L.; Caine, M.C.; Liu, T.; Mickley, L.J.; Cooper, M.; Dominici, F. Excess of COVID-19 cases and deaths due to fine particulate matter exposure during the 2020 wildfires in the united states. Sci. Adv. 2021, 7, eabi8789. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.; Singh, M.; Hemnani, K.; Arroyo, C. Can we abandon our masks? Deciphering cdc’s new guidelines about masking. DHR Proc. 2022, 2, 1–3. [Google Scholar] [CrossRef]
- Lake, S.; Juan, A.S. State and county population estimates for utah: 2021. Population 2021, 3, 3–4. [Google Scholar]
- Andrews, M.R.; Tamura, K.; Best, J.N.; Ceasar, J.N.; Batey, K.G.; Kearse, T.A., Jr.; Allen, L.V., III; Baumer, Y.; Collins, B.S.; Mitchell, V.M. Spatial clustering of county-level COVID-19 rates in the us. Int. J. Environ. Res. Public Health 2021, 18, 12170. Available online: https://mdpi-res.com/d_attachment/ijerph/ijerph-18-12170/article_deploy/ijerph-18-12170-v3.pdf?version=1637639494 (accessed on 2 November 2022). [CrossRef] [PubMed]
- Chin, T.; Kahn, R.; Li, R.; Chen, J.T.; Krieger, N.; Buckee, C.O.; Balsari, S.; Kiang, M.V. US county-level characteristics to inform equitable COVID-19 response. medRxiv 2020. [Google Scholar] [CrossRef]






| Variable (n = 3192 Counties) | Mean | SD | Median | Sum/Rate |
|---|---|---|---|---|
| County Population | 102,905.20 | 331,222.69 | 25,177.50 | 328,473,403 |
| Sum of Fatalities | 330.200 | 1301.39 | 102.00 | 1,054,320 |
| Fatalities per 100,000 residents | 339.32 | 337.10 | 258.71 | 320.98 per 100 K |
| State | ∑Deaths | Population | Rate/100 K | State | ∑Deaths | Population | Rate/100 K |
|---|---|---|---|---|---|---|---|
| MS | 12,992 | 2,976,149 | 436.54 | MO | 19,993 | 6,137,428 | 325.76 |
| WV | 7538 | 1,792,147 | 420.61 | IA | 10,229 | 3,155,070 | 324.21 |
| AL | 20,558 | 4,903,185 | 419.28 | DE | 3148 | 973,764 | 323.28 |
| AR | 12,523 | 3,017,804 | 414.97 | IL | 39,381 | 12,671,821 | 310.78 |
| NM | 8675 | 2,096,829 | 413.72 | CT | 11,034 | 3,565,287 | 309.48 |
| TN | 28,113 | 6,829,174 | 411.66 | TX | 89,662 | 28,995,881 | 309.22 |
| AZ | 29,852 | 7,278,717 | 410.13 | MA | 21,035 | 6,892,503 | 305.19 |
| MI | 39,574 | 9,986,857 | 396.26 | ID | 5237 | 1,787,065 | 293.05 |
| NJ | 34,940 | 8,882,190 | 393.37 | ND | 2232 | 762,062 | 292.89 |
| LA | 18,136 | 4,648,794 | 390.12 | WI | 15,516 | 5,822,434 | 266.49 |
| KY | 17,363 | 4,467,673 | 388.64 | VA | 22,231 | 8,535,519 | 260.45 |
| FL | 82,541 | 21,477,737 | 384.31 | NC | 27,264 | 10,488,084 | 259.95 |
| GA | 40,449 | 10,617,423 | 380.97 | MD | 15,578 | 6,279,560 | 248.07 |
| OK | 14,992 | 3,956,971 | 378.88 | CA | 95,990 | 39,512,223 | 242.94 |
| NV | 11,580 | 3,080,156 | 375.96 | NE | 4562 | 1,934,408 | 235.83 |
| NY | 73,097 | 19,453,561 | 375.75 | CO | 13,409 | 5,758,736 | 232.85 |
| PA | 47,994 | 12,801,989 | 374.89 | MN | 12,806 | 5,639,632 | 227.07 |
| IN | 24,950 | 6,732,219 | 370.61 | OR | 8726 | 4,217,737 | 206.89 |
| RI | 3698 | 1,059,361 | 349.08 | NH | 2761 | 1,359,711 | 203.06 |
| SD | 3078 | 884,659 | 347.93 | ME | 2711 | 1,344,212 | 201.68 |
| SC | 17,869 | 5,148,714 | 347.06 | DC | 1392 | 705,749 | 197.24 |
| OH | 40,249 | 11,689,100 | 344.33 | WA | 14,653 | 7,614,893 | 192.43 |
| MT | 3577 | 1,068,778 | 334.68 | AK | 1351 | 731,545 | 184.68 |
| WY | 1917 | 578,759 | 331.23 | UT | 5065 | 3,205,958 | 157.99 |
| KS | 9620 | 2,913,314 | 330.21 | VT | 763 | 623,989 | 122.28 |
| HI | 1716 | 1,415,872 | 121.2 |
| County | State | p-Value | ||||
|---|---|---|---|---|---|---|
| Mono | CA | 0.00681 | 0.00685 | 0.00183 | 0.03846 | 0.023 |
| Fremont | ID | 0.02852 | 0.02935 | 0.00776 | 0.08412 | 0.032 |
| Mahnomen | MN | 0.01732 | 0.01761 | 0.00468 | 0.06017 | 0.027 |
| Humphreys | MS | 0.04588 | 0.04599 | 0.01244 | 0.01312 | <0.001 |
| Meagher | MT | 0.00970 | 0.00978 | 0.00261 | 0.03624 | <0.001 |
| Brown | NE | 0.00196 | 0.00196 | 0.00052 | 0.02345 | 0.037 |
| Hooker | NE | 0.00196 | 0.00196 | 0.00052 | 0.02345 | 0.037 |
| Phelps | NE | 0.00970 | 0.00978 | 0.00261 | 0.03624 | <0.001 |
| Rock | NE | 0.00196 | 0.00196 | 0.00052 | 0.02345 | <0.001 |
| Sherman | NE | 0.00390 | 0.00391 | 0.00104 | 0.04787 | 0.043 |
| Camden | NC | 0.00970 | 0.00978 | 0.00261 | 0.03624 | 0.001 |
| Benson | ND | 0.02202 | 0.02250 | 0.00606 | 0.01428 | <0.001 |
| Cavalier | ND | 0.00681 | 0.00685 | 0.00183 | 0.03846 | 0.004 |
| Griggs | ND | 0.00196 | 0.00196 | 0.00052 | 0.02345 | <0.001 |
| Steele | ND | 0.00196 | 0.00196 | 0.00052 | 0.02345 | <0.001 |
| Armstrong | TX | 0.00970 | 0.00978 | 0.00261 | 0.03624 | <0.001 |
| Cochran | TX | 0.02202 | 0.02250 | 0.00606 | 0.01428 | <0.001 |
| Kenedy | TX | 0.00196 | 0.00196 | 0.00052 | 0.02345 | <0.001 |
| Martin | TX | 0.02482 | 0.02544 | 0.00688 | 0.00024 | <0.001 |
| Roberts | TX | 0.00196 | 0.00196 | 0.00052 | 0.02345 | 0.037 |
| Stonewall | TX | 0.00681 | 0.00685 | 0.00183 | 0.03846 | 0.023 |
| Throckmorton | TX | 0.00970 | 0.00978 | 0.00261 | 0.03624 | 0.012 |
| Upton | TX | 0.01732 | 0.01761 | 0.00468 | 0.06017 | 0.027 |
| Yoakum | TX | 0.03945 | 0.04110 | 0.01092 | 0.07399 | <0.001 |
| Garfield | UT | 0.00970 | 0.00978 | 0.00261 | 0.03624 | <0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shanmugam, R.; Fulton, L.; Betancourt, J.; Pacheco, G.J. Indexing Inefficacy of Efforts to Stop Escalation of COVID Mortality. Mathematics 2022, 10, 4646. https://doi.org/10.3390/math10244646
Shanmugam R, Fulton L, Betancourt J, Pacheco GJ. Indexing Inefficacy of Efforts to Stop Escalation of COVID Mortality. Mathematics. 2022; 10(24):4646. https://doi.org/10.3390/math10244646
Chicago/Turabian StyleShanmugam, Ramalingam, Lawrence Fulton, Jose Betancourt, and Gerardo J. Pacheco. 2022. "Indexing Inefficacy of Efforts to Stop Escalation of COVID Mortality" Mathematics 10, no. 24: 4646. https://doi.org/10.3390/math10244646
APA StyleShanmugam, R., Fulton, L., Betancourt, J., & Pacheco, G. J. (2022). Indexing Inefficacy of Efforts to Stop Escalation of COVID Mortality. Mathematics, 10(24), 4646. https://doi.org/10.3390/math10244646






