Abstract
This work focuses on presenting a novel model describing a layer of an excited microelongated semiconductor material. During the photo-excitation processes, the model is investigated in a rotational field. The model introduced the microelongation scalar function, which describes the microelement processes according to the micropolar-thermoelasticity theory. The model studies the interaction case between optical-thermo-mechanical waves under the effect of rotation parameters when the microelongation parameters are taken into consideration according to the photo-thermoelasticity theory. The main governing equations have been taken in a dimensionless form during the electronic and thermoelastic deformation and they have been studied under the harmonic wave technique. The general solutions of the basic fields of isotropic, homogeneous, and linear microelongated semiconductor medium are obtained in two dimensions (2D). Many conditions are taken at the free surface of the medium to obtain the complete solutions. The physical parameters of silicon (Si) are used to illustrate the numerical simulation of the main fields. Several comparisons were performed and illustrated graphically under the influence of different parameters of relaxation time and rotation.
Keywords:
photo-acoustics; hydroelasticity; semiconductor; microelongation; rotation; mechanical wavey MSC:
74A15
1. Introduction
With the development of materials science, the importance of semiconductors has recently emerged. Semiconductors are of great importance in the development of modern industries, especially those industries that depend on the presence of weak electric currents such as sensors and transistors. Under normal circumstances, semiconductors such as copper are not good conductors of electricity, and materials such as glass are not sufficiently insulating. However, when these materials are exposed to a gradual increase in temperature because of being affected by light falling on them or laser beams, their internal resistance begins to decrease. Therefore, in the second half of the last century, interest in studying the physical properties of semiconductors increased. As it turns out, the internal properties of these materials change with the temperature change, especially the internal composition (microelements). The so-called electronic deformation (ED) occurs as a result of the transfer of light-excited electrons to the surface and the photothermal (PT) theory appears. On the other hand, thermoelastic deformation (TD) is caused by the vibrations of the internal particles, and the thermoelasticity theory appears. As a result of the previous ED and TD deformations, there is an overlap between the PT theory and the thermoelastic theory, and a photo-thermoelasticity theory appears. During the interference processes, the effect of the microinertia process on the microelements of the semiconductor should be taken into account because they are responsible for the change in the internal resistance (changing internal structure).
As a result of the change in the internal structure of semiconductors as a result of the thermal effect, the impact of microelongation parameters is studied. A microelongated semiconductor has four degrees of freedom. Three of them depend on the change occurring during the TD deformation and the last one is a result of the rotational movement (microelongation) of the electrons during the ED deformation []. In this case, the properties of semiconductors depend on the micropolar theory based on these degrees of freedom (director) []. The directors are rigid when the microstretch and micropolar theory of the semiconductor are investigated. As a special case, the microelongational theory of material appears when the directors are orthogonal and contraction. Eringen [] took the microstructure of the elastic body into account to introduce the micropolar theory. On the other side, Eringen [] introduced a novel microstretch thermoelasticity model which describes the interaction between the microstretch parameters and thermoelasticity theory. Many applications of the generalized microstretch thermoelasticity theory are investigated for elastic bodies under the impacts of external fields [,,,,,]. Ramesh et al. [] studied stretching sheets according to the Casson fluid flow with variable thicknesses of porous media. Ezzat and Abd-Elaal [] used a viscoelastic boundary layer flow to study the hydromechanics viscoelastic porous media with one relaxation time. The microelongated elastic medium is used to obtain the wave propagations inside the medium under the effect of an internal heat source [,]. Ailawalia et al. [,,] developed thermoelastic microelongated governing equations to study the plane strain deformation of an elastic material with an internal heat source. The micropolar theory of the elastic body is used to develop the double porosity structure according to the thermoelasticity theory [].
The photothermal (PT) theory appeared when the effect of an incident beam of laser rays on a sample of a semiconductor material was studied []. The PT theory is used to determine the physical properties of semiconductors according to photoacoustic spectroscopy analysis [,,,]. Hobiny and Abbas [] studied a semiconductor medium during two-dimensional deformation according to the photothermal and thermoelastic interactions. The optical properties of semiconducting microcantilevers medium are investigated in the context of the electronic deformation mechanism by Todorovic et al. [,]. After that, many authors developed novel models to describe the interaction between the photothermal method and the thermoelasticity theory of semiconductors with various applications [,,,]. Mahdy et al. [] studied the microstretch elastic semiconductor medium under the impact of rotation field according to photothermal excitation processes. Wang et al. [] studied the front end for the 100 PW class laser facility using optical parametric based on lithium crystals. Liang et al. [] investigated the deforming atomic wave function in ultra-intense high-frequency laser pulses. On the other hand, many studies [,] used the splitting mechanism to modify the broadband optical modulator. Beams that rotate for the accurate modeling and analysis of microelongated semiconductors, which are used in various nanoscale devices, are challenging. Communications and information technology, materials characterization, chemistry, environmental monitoring, biomechanics, aerospace, and the military extensively use micro-cantilever contact-type sensors, micro gyroscopes, micro motors, biosensors, and atomic force microscopes. The rotating elements are typically the primary parts of small structures. Researchers are, therefore, intensely interested in the rotational effect. Ismail et al. [] were the first to study the thermo-mechanical waves of an excited microelongated semiconductor layer according to photothermal transport processes. On the other hand, Saeed et al. [] studied the effect of variable thermal conductivity and magnetic field for the generated photothermal waves on microelongated semiconductors.
In previous studies, the effect of the rotation field during the microelongation processes of the semiconductor-excited media was not taken into account. The main objective of posing this problem is to study the effect of microelongation parameters during the study of semiconductor materials in the context of photo-thermoelasticity theory, which has not been addressed before. In the present work, a microelongated semiconductor material is studied in a rotating field according to the photo-thermoelasticity theory. In this case, the microinertia and microelements of the semiconductor medium are taken into consideration. According to the 2D deformation, the governing main equations are introduced in a dimensionless rotational field. The introduced model is novel and can be named the generalized rotational-photo-thermo-microelongated (RPTM) model of semiconductor media. The normal mode method and numerical closed form with some boundary conditions are used to obtain the main wave propagations of physical fields inside the medium. The numerical simulation of wave propagations is presented graphically with some comparisons under the effect of the rotation field according to the microelongation parameters.
2. The Main Equations and Mathematical Model
According to the Cartesian coordinates (see Figure 1), four main quantities can be introduced. The optical function is the carrier density , which describes the plasma wave propagation. The thermal distribution can be presented by the temperature , which measures the thermal impact. The elastic wave distribution can be introduced by the displacement vector . Finally, the scalar microelongational function describes the elongation impact. A uniform rotational field is applied () to the semiconductor medium in the direction of the axis ( is in the direction of the axis ) (see the geometry of the problem, Figure 1). According to 2D deformations, the main equations for RPTM theory when the semiconductor medium is homogeneous, isotropic, and linear can be written in the following form [].
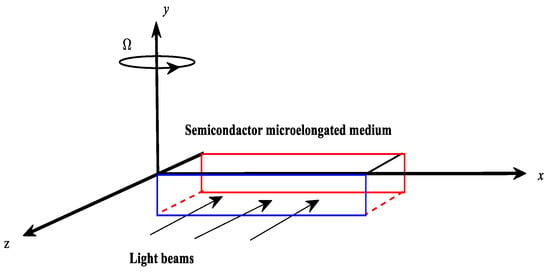
Figure 1.
The geometry of the problem.
To discuss the model, the following postulates are taken into account:
- (i)
- The electric neutrality of the semiconductor is satisfied.
- (ii)
- The magnetic field effect is ignored.
- (iii)
- The mass of charge carrier fields is negligible.
- (iv)
- The electron field within the boundary layer is very weak and can be neglected.
- (v)
- The recombination function of electrons is reduced on the basis of the fact that it takes care of defects and hence, the concentration values of the charge carrier field [].
The microelongated constitutive equations of linear, homogeneous, isotropic semiconductors in tensor form according to photo-thermoelasticity theory are [,,]:
where is the microelongational stress tensor and are components of the stress tensor.
The diffusion equation for the photogenerated plasma density, which describes the interaction between thermal and plasma waves, can be represented as []:
There are two more terms in the displacement equation of motion in the rotating frame of reference:
- (I)
- Centripetal acceleration, due to time-varying motion only;
- (II)
- Corioli’s acceleration , where is the dynamic displacement vector.
The excitation and propagation of thermal waves in a solid are accompanied by a surface expansion which may be used for the detection of thermal waves. In the context of continuum mechanics, the relation between the elastic displacement vector, plasma (under the effect of electronic (carrier) density), microelongation, and the temperature distribution can be expressed by the equation of motion which is described, under the effect of a rotation field, by [,]:
The microinertia equation of the medium is, in the case of microelongation according to the microelement processes, introduced according to [,] as:
In the elastic Equation (3), the third term describes the microelongation of the thermal wave, and the fourth and fifth terms on the left side describe the source term and influence of the thermal wave and plasma wave on the elastic wave, respectively [].
The heat conduction equation for microelongated semiconductor medium according to the general case of an elastic body theory under the effect of optical-thermal-elastic interactions can be written as []:
In Equation (5), the fourth term on the left side characterizes the effect of heat generation by the carrier volume and surface de-excitations in the sample and the third term describes the heat generated by stress waves, respectively [].
According to ED and TE deformations, the main fields can be chosen in case of 2D disturbance depending on two-space coordinates and the time . Therefore, the displacement vector and the microelongational scalar function can be formulated in the xz-plane as:
The strain relation is:
where is the coupling thermal activation parameter, is a parameter that depends on the microelongational semiconductor properties, and is the microelongation coefficient (the linear thermal expansion). In 2D disturbance, the main governing equations (Equations (2)–(5)) can be rewritten as:
The parameters are two chosen constants that determine, with thermal relaxation times, the different theories of RPTM (coupled-dynamical model (CD), Lord and Şhulman (LS) model, and Green and Lindsay (GL) model) [,,].
For further simplification, the following dimensional quantities can be taken as:
The dimensionless analysis can be obtained. For example, where using the SI units from Table 1 we have:

Table 1.
The physical input parameters of the Si medium in SI units.
In the dimensionless model, using the value of , in this case, the time can be chosen as: , using the same technique, the other quantities are obtained.
Accordingly, Equation (12) can be used to convert all main equations to the following form (by dropping the superscripts), yields:
Depending on Helmholtz’s theorem, displacements can be presented as functions in the potential scalar and vector space-time , which can be represented as:
Using Equation (18), the previous equations (Equations (14)–(17)) can be rewritten in the following form:
The 2D constitutive relations can be rewritten as:
where
3. Harmonic Wave Analysis
The normal mode analysis can be formulated in harmonic wave according to any function (main fields) in 2D as follows [,]:
where the amplitude is , , represents the wave number in the direction of the z-axis and the value refers to the complex time frequency. Using Equation (24) for Equations (13) and (19)–(22) yields:
where,
Equations (25)–(29) can be solved using the elimination technique, the following tenth-order ordinary differential equation (ODE) can be written as:
where,
To obtain the solutions to Equation (31), the factorization technique is used as follows:
where the roots of the above equation are .
The linear solutions of Equation (32) in a general form can be rewritten in terms of the roots as:
Similarly,
where and are specific (unknown) quantities which obtained in terms of and , on the other hand, the other coefficients are:
The displacement components according to Helmholtz’s theorem can be rewritten as follows:
The stresses relation in terms of can be rewritten as:
4. Boundary Conditions
The unspecific parameters in this section can be determined according to some boundary conditions which can be chosen at the boundary () of the microelongated surface []. The conditions can be formulated as:
The two mechanical conditions are:
The thermal condition can be taken in a thermally insulated case as:
The elongation can be chosen when in the free case as:
On the other side, due to the recombination processes, the plasma condition can be chosen when the concentration of the electrons is obtained, which can be rewritten in the following form:
Using the expressions of , and according to Equations (41)–(44) yields:
The complete solutions of the principle fields are obtained when the above equations (Equations (47) and (48)) are solved and when we determine the unknown parameter .
5. Validation
5.1. The Rotational Microelongation Thermoelasticity Theory
The theory of microelongation thermoelasticity under the impact of rotational field is obtained when the plasma wave effect is ignored (i.e., ). Therefore, the governing equations can be reduced to the following form [,]:
5.2. The Generalized Rotational Photo-Thermoelasticity Theory
When parameters , and are neglected, the microelongation effect has vanished and the rotational photo-thermoelasticity theory is obtained. However, the governing equations are reduced as [,]:
5.3. Rotational Photo-Thermoelasticity Models
The various models of the rotational photo-thermoelasticity in the microelongation case can be reformulated according to the different values of the parameters and and thermal memories as follows:
- (i)
- The coupled-dynamical (CD) model appears when [].
- (ii)
- The LS model appears when [].
- (iii)
- The GL model appears when [].
5.4. The Microelongation Photo-Thermoelasticity Theory
The theory of microelongation photo-thermoelasticity appears when the impact of the rotation field is ignored (the angular velocity parameters ). Therefore, the main equations can be reduced as [,]:
6. Discussion and Numerical Outcomes
To analyze the obtained numerical results, the physical field variables will be graphically illustrated under study and the comparison is made for different values of physical parameters such as rotation parameter and relaxation times (thermal memories). In this case, the numerical simulations for the input parameters of the microelongated semiconductor medium silicon (Si) are carried out. Using MATLAB, the numerical results can be shown graphically. Using the SI unit of the physical constants of Si, a graphical simulation can be made, in which the parameters of Si are given in Table 1 [,,,,,].
The non-dimensional quantities in this work are used to obtain the computations of the wave distributions of the main fields in 2D. The numerical simulation is made in the range when the wave number according to the mechanical load at and (where and ).
6.1. Impact of Thermal Memories
Figure 2a–f show the effect of different relaxation times on wave propagation of fundamental physical quantities with a change in horizontal distance . In this case, the relaxation times are chosen according to the different models in the theory of photo-thermoelasticity (three models: CD, LS, and GL). The wave propagation as a thermal wave (distributions of temperature), microelongation distributions, elastic wave (displacement), plasma wave (carrier intensity), and mechanical wave (stresses and ) for fixed values of time are shown in the six subfigures when . The physical distributions displayed in Figure 2a–f satisfy the boundary conditions at the free surface of the exciting microelongated semiconductor. The distribution of the thermal wave (Figure 2a) starts from zero at the surface and increases until reaches the maximum value in the first range due to the thermal loads of light beams. In the second range, the thermal wave decreases smoothly until reaching the minimum value with the zero line in the case of CD and LS models. However, in the case of the GL model, the thermal wave increases again and decreases until reaches the minimum at the zero line. On the other hand, the plasma wave (Figure 2d) and elastic (displacement) wave (Figure 2c) distributions take the same behavior as the thermal wave distribution for CD and LS models. However, the distribution for the GL model takes the same behavior as the CD model (exponential behavior) with the difference in the magnitude according to the difference in the values of thermal relaxation times. All computational results in the three (temperature, displacement, and carrier density) subfigures agree with the experimental results []. The second subfigure (Figure 2b) presents the vibration of microelongation distribution versus the distance for three different photo-thermoelasticity models (CD, LS, and CD). It is concluded that the wave propagation of microelongation distribution goes on increasing with an increase in the values of the relaxation times. The distribution of fine elongation at the free surface starts from zero with a gradual increase in the first range according to the thermal effect of light until the maximum value of the three models is reached. Away from the surface, and due to the decrease in the thermal effect of light, the distribution of the wave propagation begins to decrease until the minimum value, then increases and decreases periodically until it completely vanishes with the increase in the value of the distance (equilibrium state). The mechanical wave (normal stress (Figure 2e)) starts from a zero point at the surface and decreases sharply until reaching the minimum peak value due to the TE and ED deformations. As we move away a little from the surface, the distribution of the waves’ propagation begins to gradually increase until it reaches its maximum value and decreases and increases periodically before it vanishes completely with the increasing distance. On the other hand, the tangent stress distribution (Figure 2f) increases in the beginning until reaching the peak maximum value near the free surface due to the thermal effect of light. However, in the second band, the wave propagation decreases with the behavior of the exponential wave until it coincides with the zero line and it vanishes completely to reach the equilibrium state.
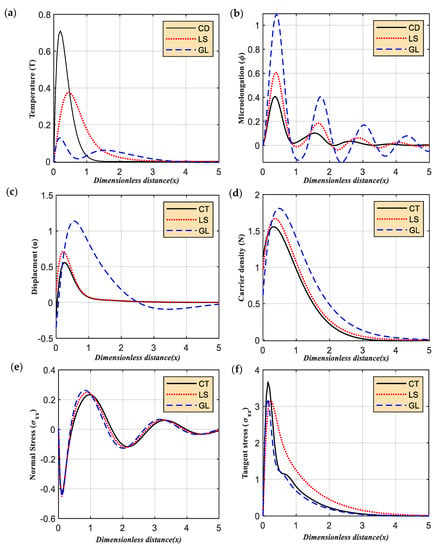
Figure 2.
(a–f) The variation of the main physical fields versus the horizontal distance according to the differences in thermal relaxation times under the effect of rotation parameters.
6.2. Impact of Rotation Parameter
Figure 3 a–f illustrate the variations of the wave propagation of the thermal, microelongation elastic, plasma, and mechanical ( and ) waves for fixed values of dimensionless time (), in the range in two cases. These two cases are when the medium is studied under the influence of a rotation effect when and without influence when according to the GL model. From this figure, the rotation field parameter has a significant impact on all the wave propagations of the considered fields.
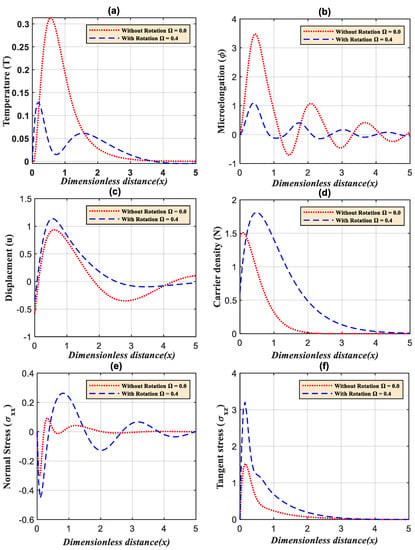
Figure 3.
(a–f) The variations of the main physical fields versus the horizontal distance in the case of the GL model with rotation field influence and without rotation field influence.
6.3. Impact of Microelongation Parameters
The investigation in Figure 4a–f compares two dimensionless cases of the primary fields with varying horizontal distances. When the microelongation parameters are disregarded, the first instance depicts the non-microelongated material (Si) under the influence of the photo-thermoelasticity theory, or PTM. However, the second case illustrates the microelongated material (Si) in the framework of photo-thermoelasticity theory, which is denoted by MPTM (when the microelongation parameters are taken into consideration). At the same time, comparisons are done using the GL model. This graphic shows that all wave propagations of the considered fields are significantly influenced by the microelongation parameters.
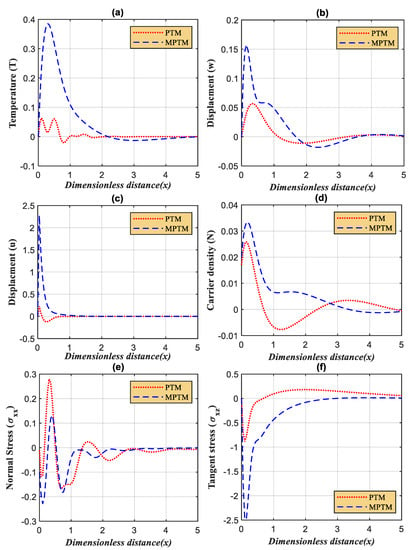
Figure 4.
(a–f) The variations of the main physical fields versus the horizontal distance according to the GL model with a rotational field under the effect of the microelongation parameters and without the microelongation parameters.
7. Conclusions
An analytical formulation for an isotropic, homogeneous microelongated semiconducting elastic medium with the influence of a rotation field is presented and illustrated graphically for fixed values of the physical input parameters. The interactions between thermal, mechanical, microelongation, and carrier intensity in the main equations in 2D are obtained according to the generalized photo-thermoelasticity theory. The microelongated semiconductor material is studied in the context of photo-excitation transport processes. Three models of the photo-thermoelasticity theory are taken into account according to the different thermal memories (CD, LS, and GL). The numerical simulations are made for the microelongated semiconducting medium silicon with some prescribed boundary conditions. It has been observed that all the physical distributions of the propagating waves tend to reach the equilibrium state. It was also found that relaxation times have a significant effect on the wave propagation of the physical quantities under study. In addition, the effect of the rotation parameter and microelongation parameters are visible in the distribution of the propagated waves. All computational findings in the three subfigures (temperature, displacement, and carrier density) are in agreement with the experimental findings in []. Silicon as a microelongated semiconductor is significant in research and can be widely used for various modern electronic devices, sensors, computer processors, diodes, accelerometers, inertial sensors, and electric circuits.
Author Contributions
Conceptualization, K.L.; methodology, K.L.; software, A.M.S. validation; investigation, M.H.A.; data curation, writing—original draft preparation, A.M.S.; visualization, K.L.; supervision, K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by Deputyship for Research & Innovation, Ministry of Education, Saudi Arabia for funding this research work through project number QU-IF-4-3-3-29655. The authors also thank Qassim University for technical support”.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education, Saudi Arabia for funding this research work through project number QU-IF-4-3-3-29655. The authors also thank Qassim University for technical support”.
Conflicts of Interest
The authors have no conflict to disclose.
Nomenclature
| Lame’s parameters | |
| Two scalar functions | |
| Deformation potential difference | |
| Coefficient of ED | |
| Reference temperature in its natural state | |
| Volume thermal expansion | |
| Microelongational elastic stress | |
| The density of the microelongated sample | |
| Linear thermal expansion | |
| Equilibrium carrier concentration | |
| Specific heat at constant strain | |
| Thermal conductivity | |
| Carrier diffusion coefficient | |
| The lifetime of photogenerated carriers | |
| Energy gap | |
| Components of the strain tensor | |
| Microinertia of microelement | |
| Microelongational material parameters | |
| Thermal relaxation times | |
| Scalar microelongational function | |
| Components of the microstretch vector | |
| Stress tensor component | |
| Kronecker delta | |
| Recombination velocities | |
| Angular velocity |
References
- Eringen, A.C. Microcontinuum Field Theories, Vol. 1, Foundations and Solids; Springer: New York, NY, USA, 1999. [Google Scholar]
- Eringen, A.C. Linear theory of micropolar elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Eringen, A.C. Theory of thermo-microstretch elastic solids. Int. J. Eng. Sci. 1990, 28, 1291–1301. [Google Scholar] [CrossRef]
- Singh, B. Reflection and refraction of plane waves at a liquid/thermo-microstretch elastic solid interface. Int. J. Eng. Sci. 2001, 39, 583–598. [Google Scholar] [CrossRef]
- Othman, M.; Lotfy, K. The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J. Comput. Theor. Nanosci. 2015, 12, 2587–2600. [Google Scholar] [CrossRef]
- Cicco, D.; Nappa, L. On the theory of thermomicrostretch elastic solids. J. Therm. Stress. 1999, 22, 565–580. [Google Scholar]
- Othman, M.; Lotfy, K. On the plane waves of generalized thermo-microstretch elastic half-space under three theories. Int. Commun. Heat Mass Transf. 2010, 37, 192–200. [Google Scholar] [CrossRef]
- Abouelregal, A.; Marin, M. The Size-Dependent Thermoelastic Vibrations of Nanobeams Subjected to Harmonic Excitation and Rectified Sine Wave Heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Othman, M.; Lotfy, K. Effect of rotating on plane waves in generalized thermo-microstretch elastic solid with one relaxation time. Multidiscip. Model. Mater. Struct. 2011, 7, 43–62. [Google Scholar] [CrossRef]
- Ramesh, G.; Prasannakumara, B.; Gireesha, B.; Rashidi, M. Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. J. Appl. Fluid Mech. 2016, 9, 1115–1122. [Google Scholar] [CrossRef]
- Ezzat, M.; Abd-Elaal, M. Free convection effects on a viscoelastic boundary layer flow with one relaxation time through a porous medium. J. Frankl. Inst. 1997, 334, 685–706. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. Periodically varying heat source response in a functionally graded microelongated medium. Appl. Math. Comput. 2012, 218, 6304–6313. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. Moving heat source response in a thermoelastic micro-elongated Solid. J. Eng. Phys. Thermophys. 2013, 86, 716–722. [Google Scholar] [CrossRef]
- Ailawalia, P.; Sachdeva, S.; Pathania, D. Plane strain deformation in a thermo-elastic microelongated solid with internal heat source. Int. J. Appl. Mech. Eng. 2015, 20, 717–731. [Google Scholar] [CrossRef]
- Sachdeva, S.; Ailawalia, P. Plane strain deformation in thermoelastic micro-elongated solid. Civ. Environ. Res. 2015, 7, 92–98. [Google Scholar]
- Ailawalia, P.; Kumar, S.; Pathania, D. Internal heat source in thermoelastic micro-elongated solid under Green Lindsay theory. J. Theor. Appl. Mech. 2016, 46, 65–82. [Google Scholar] [CrossRef]
- Marin, M.; Lupu, M. On harmonic vibrations in thermoelasticity of micropolar bodies. J. Vibrat. Control 1998, 4, 507–518. [Google Scholar] [CrossRef]
- Gordon, J.P.; Leite, R.C.C.; Moore, R.S.; Porto, S.P.S.; Whinnery, J.R. Long-transient effects in lasers with inserted liquid samples. Bull. Am. Phys. Soc. 1964, 119, 501–510. [Google Scholar] [CrossRef]
- Kreuzer, L.B. Ultralow gas concentration infrared absorption spectroscopy. J. Appl. Phys. 1971, 42, 2934. [Google Scholar] [CrossRef]
- Tam, A.C. Ultrasensitive Laser Spectroscopy; Academic Press: New York, NY, USA, 1983; pp. 1–108. [Google Scholar]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381. [Google Scholar] [CrossRef]
- Tam, A.C. Photothermal Investigations in Solids and Fluids; Academic Press: Boston, MA, USA, 1989; pp. 1–33. [Google Scholar]
- Hobinya, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Todorovic, D.M.; Nikolic, P.M.; Bojicic, A.I. Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J. Appl. Phys. 1999, 85, 7716–7726. [Google Scholar] [CrossRef]
- Song, Y.Q.; Todorovic, D.M.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871. [Google Scholar] [CrossRef]
- Lotfy, K. A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci. Rep. 2019, 9, 3319. [Google Scholar] [CrossRef] [PubMed]
- Lotfy, K. Effect of Variable Thermal Conductivity during the Photothermal Diffusion Process of Semiconductor Medium. Silicon 2019, 11, 1863–1873. [Google Scholar] [CrossRef]
- Abbas, I.; Alzahrani, F.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2019, 29, 328–343. [Google Scholar] [CrossRef]
- Khamis, A.; El-Bary, A.; Lotfy, K.; Bakali, A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex. Eng. J. 2020, 59, 1–9. [Google Scholar] [CrossRef]
- Mahdy, A.; Lotfy, K.; El-Bary, A.; Alshehri, H.; Alshehri, A.M. Thermal-microstretch elastic semiconductor medium with rotation field during photothermal transport processes. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Lu, X.; Chen, J.; Long, Y.; Li, W.; Chen, H.; Chen, X.; Bai, P.; Li, Y.; et al. 13.4 fs, 0.1 Hz OPCPA Front End for the 100 PW-Class Laser Facility. Ultrafast Sci. 2022, 2022, 9894358. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, Y.; Liao, Y.; Jiang, W.; Li, M.; Lu, P. Direct Visualization of Deforming Atomic Wavefunction in Ultraintense High-Frequency Laser Pulses. Ultrafast Sci. 2022, 2022, 9842716. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.; Li, X. The splitting mechanism of the second-order rogue wave—Interaction between two component first-order Akhmediev breathers. Chaos Solitons Fractals 2022, 161, 112334. [Google Scholar] [CrossRef]
- Han, Y.; Li, X.; Chen, E.; An, M.; Song, Z.; Huang, X.; Liu, X.; Wang, Y.; Zhao, W. Sea-Urchin-MnO2 for Broadband Optical Modulator. Adv. Opt. Mater. 2022, 10, 2201034. [Google Scholar] [CrossRef]
- Ismail, G.; Lotfy, K.; El-Bary, A.A. Response of thermo-mechanical waves of an excited microelongated semiconductor layer according to photothermal transport processes. Eur. J. Mech./A Solids 2022, 96, 104714. [Google Scholar] [CrossRef]
- Saeed, A.M.; Lotfy, K.; El-Bary, A.A. Effect of Variable Thermal Conductivity and Magnetic Field for the Generated Photo-Thermal Waves on Microelongated Semiconductor. Mathematics 2022, 10, 4270. [Google Scholar] [CrossRef]
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Biot, M. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Deresiewicz, H. Plane waves in a thermoelastic solid. J. Acoust. Soc. Am. 1957, 29, 204–209. [Google Scholar] [CrossRef]
- Chadwick, P.; Sneddon, I. Plane waves in an elastic solid conducting heat. J. Mech. Phys. Solids 1958, 6, 223–230. [Google Scholar] [CrossRef]
- Chadwick, P. Thermoelasticity: The dynamic theory. In Progress in Solid Mechanics; Sneddon, I.N., Hill, R., Eds.; North-Holland: Amsterdam, The Netherlands, 1960; Volume I, pp. 263–328. [Google Scholar]
- Todorovicć, D. Plasma, thermal, and elastic waves in semiconductors. Rev. Sci. Instrum. 2003, 74, 582–585. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W.; El-Bary, A.; Kadry, M. Response of electromagnetic and Thomson effect of semiconductor medium due to laser pulses and thermal memories during photothermal excitation. Results Phys. 2020, 16, 102877. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).