Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era
Abstract
:1. Introduction
2. Background
2.1. Neurons
2.2. Classification: Linear Separability and Nonlinear Separability
2.3. Boolean Function Approximation
2.4. Function Approximation
3. Perceptron
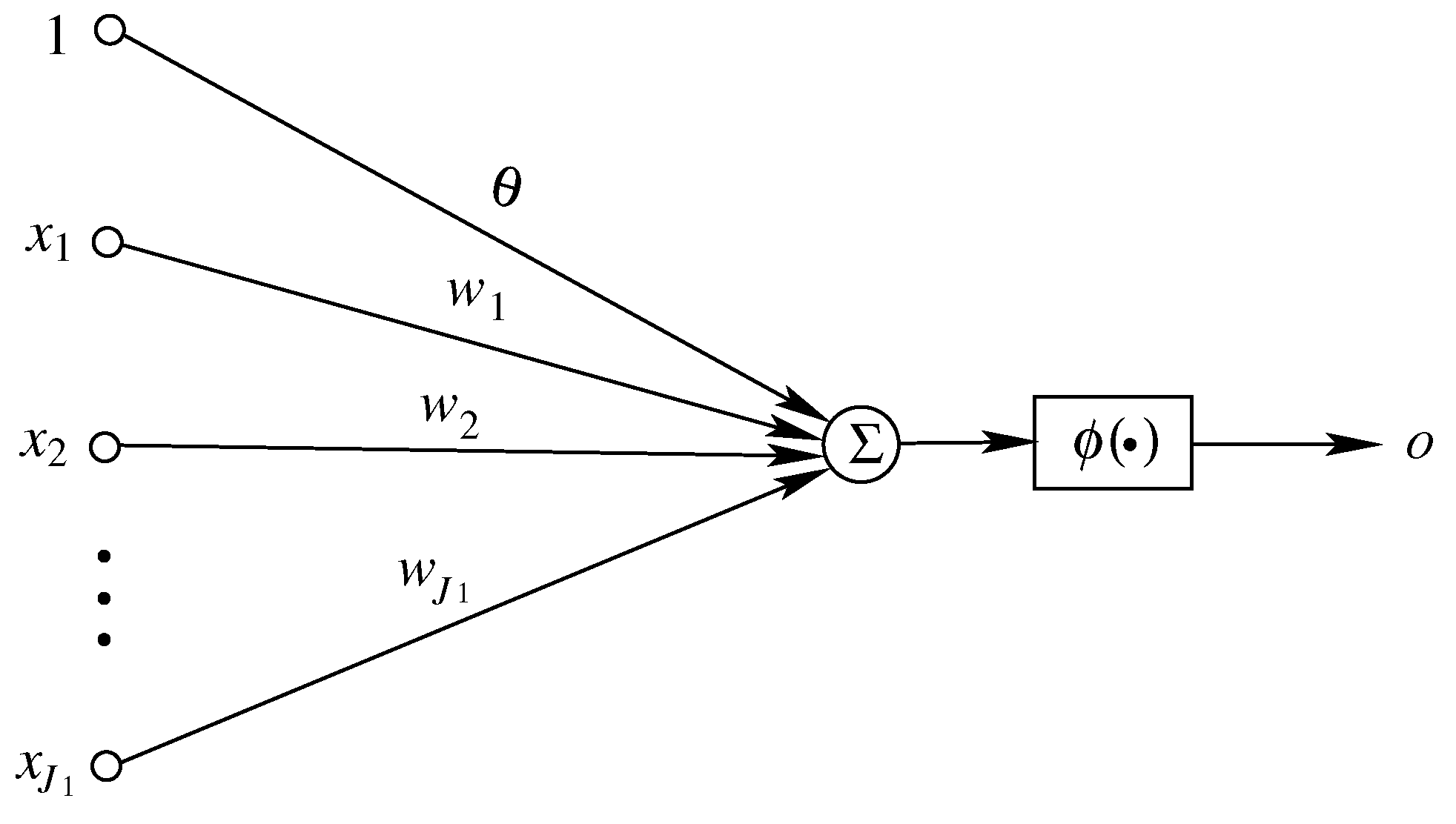
3.1. Simple Perceptron
3.2. Perceptron Learning Algorithm
3.3. Least Mean Squares Algorithm
3.4. Other Learning Algorithms
3.5. Approximation Ability of Perceptron Variants
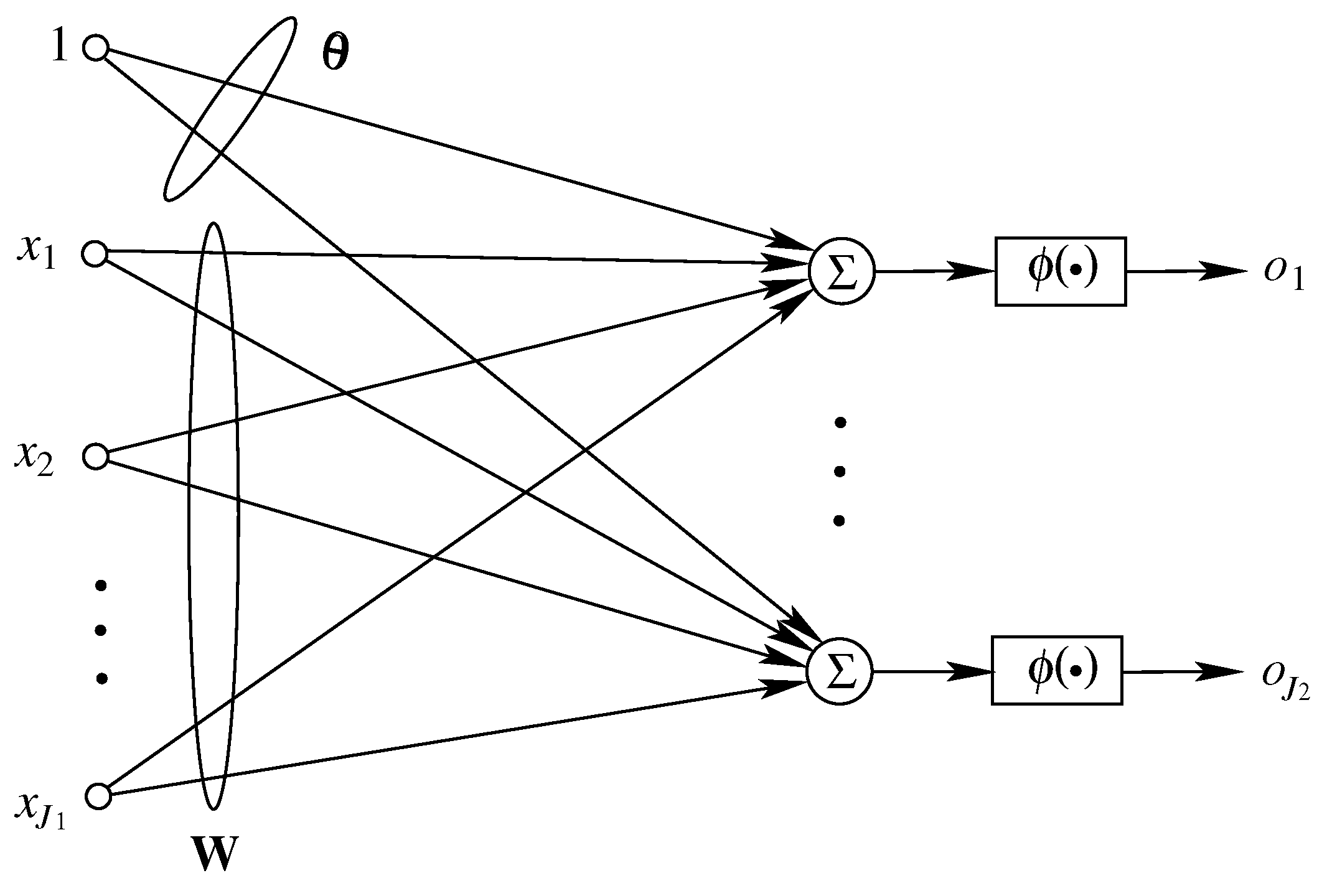
4. Multilayer Perceptrons
4.1. Structure
4.2. Approximation Ability
4.3. Backpropagation Learning Algorithm
4.4. Batch Mode and Online Mode
4.5. Momentum Term
4.6. Variance Reduction
5. Generalization
5.1. Generalization Error
5.2. Generalization by Stopping Criterion
5.3. Generalization by Regularization
5.4. Selection of Regularization Parameter
6. Optimization on Network Size
6.1. Destructive Approach: Network Pruning
6.1.1. Sensitivity-Based Network Pruning
6.1.2. Second-Order Expansion Pruning
6.1.3. Regularization-Based Methods
6.2. Constructive Approach: Network Growing
7. Acceleration on BP
7.1. Eliminating Premature Saturation
7.2. Adapting Learning Parameters
7.2.1. Globally Adapted Learning Parameters
7.2.2. Locally Adapted Learning Parameters
7.3. Initializing Weights
7.3.1. Heuristics for Weight Initialization
7.3.2. Weight Initialization Using Parametric Estimation
7.4. Adapting Activation Function
7.5. Other Acceleration Techniques
8. Second-Order Acceleration
8.1. Newton’s Methods
8.1.1. Gauss–Newton Method
8.1.2. Levenberg–Marquardt Method
8.1.3. Other Methods
8.2. Quasi-Newton Methods
8.2.1. BFGS Method
8.2.2. One-Step Secant Method
8.2.3. Other Secant Methods
8.3. Conjugate-Gradient Methods
8.4. Extended Kalman Filtering Methods
8.4.1. Extended Kalman Filtering
8.4.2. Recursive Least Squares
9. Other Learning Algorithms
10. Fault-Tolerant Learning
10.1. Open-Node Fault
10.2. Multiplicative Weight Noise
11. Perceptron in the Deep Learning Era
11.1. Solving the Difficulties
11.2. Why Deep Learning Always Achieves Good Results
11.3. Deep versus Shallow
12. Discussion and Conclusions
12.1. An Example—Iris Classification
12.2. Discussion on the Popular Learning Algorithms
12.3. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Mathm. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, R. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenblatt, R. Principles of Neurodynamics; Spartan Books: New York, NY, USA, 1962. [Google Scholar]
- Widrow, B.; Hoff, M.E. Adaptive switching circuits. In IRE Eastern Electronic Show and Convention (WESCON) Record, Part 4; IRE: New York, NY, USA, 1960; pp. 96–104. [Google Scholar]
- Minsky, M.L.; Papert, S. Perceptrons; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–368. [Google Scholar]
- Werbos, P.J. Beyond Regressions: New tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Bourlard, H.; Kamp, Y. Auto-association by multilayer perceptrons and singular value decomposition. Biol. Cybern. 1988, 59, 291–294. [Google Scholar] [CrossRef]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Wang, M.; Lu, Y.; Qin, J. A dynamic MLP-based DDoS attack detection method using feature selection and feedback. Comput. Secur. 2020, 88, 101645. [Google Scholar] [CrossRef]
- Orru, P.F.; Zoccheddu, A.; Sassu, L.; Mattia, C.; Cozza, R.; Arena, S. Machine learning approach using MLP and SVM algorithms for the fault prediction of a centrifugal pump in the oil and gas industry. Sustainability 2020, 12, 4776. [Google Scholar] [CrossRef]
- Liu, G. Data collection in MI-assisted wireless powered underground sensor networks: Directions, recent advances, and challenges. IEEE Commun. Mag. 2021, 59, 132–138. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Z.; Chen, G.; Zhang, L.; Yang, Y.; Yao, C.; Wang, J.; Yao, J. Training effective deep reinforcement learning agents for real-time life-cycle production optimization. J. Pet. Sci. Eng. 2022, 208, 109766. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Liu, Y.; Liu, S.; Yang, B.; Yin, L.; Liu, M.; Zheng, W. User OCEAN personality model construction method using a BP neural network. Electronics 2022, 11, 3022. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the em algorithm. J. R. Stat. Soc. B 1977, 39, 1–38. [Google Scholar]
- Amari, S.I. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Cover, T.M. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Trans. Electron. Comput. 1965, 14, 326–334. [Google Scholar] [CrossRef] [Green Version]
- Pao, Y.H.; Takefuji, Y. Functional-link net computing: Theory, system architecture, and functionalities. IEEE Comput. 1992, 25, 76–79. [Google Scholar] [CrossRef]
- Volper, D.; Hampson, S.E. Quadratic function nodes: Use, structure and training. Neural Netw. 1990, 3, 93–107. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Eitzinger, C.; Plach, H. A new approach to perceptron training. IEEE Trans. Neural Netw. 2003, 14, 216–221. [Google Scholar] [CrossRef]
- Gallant, S.I. Perceptron-based learning algorithms. IEEE Trans. Neural Netw. 1990, 1, 179–191. [Google Scholar] [CrossRef]
- Frean, M. A thermal perceptron learning rule. Neural Comput. 1992, 4, 946–957. [Google Scholar] [CrossRef]
- Muselli, M. On convergence properties of pocket algorithm. IEEE Trans. Neural Netw. 1997, 8, 623–629. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. Correlation matrix memories. IEEE Trans. Comput. 1972, 21, 353–359. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organization and Associative Memory, 3rd ed.; Springer: New York, NY, USA, 1989. [Google Scholar]
- Anderson, J.A. Simple neural network generating an interactive memory. Math. Biosci. 1972, 14, 197–220. [Google Scholar] [CrossRef]
- Widrow, B.; Lehr, M.A. 30 years of adaptive neural networks: Perceptron, Madaline, and backpropagation. Proc. IEEE 1990, 78, 1415–1445. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Wang, Z.Q.; Manry, M.T.; Schiano, J.L. LMS learning algorithms: Misconceptions and new results on convergence. IEEE Trans. Neural Netw. 2000, 11, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.Q. On the convergence of the LMS algorithm with adaptive learning rate for linear feedforward networks. Neural Comput. 1991, 3, 226–245. [Google Scholar] [CrossRef]
- Bouboulis, P.; Theodoridis, S. Extension of Wirtinger’s calculus to reproducing kernel Hilbert spaces and the complex kernel LMS. IEEE Trans. Signal Process. 2011, 59, 964–978. [Google Scholar] [CrossRef] [Green Version]
- Mays, C.H. Adaptive Threshold Logic. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1963. [Google Scholar]
- Ho, Y.C.; Kashyap, R.L. An algorithm for linear inequalities and its applications. IEEE Trans. Electron. Comput. 1965, 14, 683–688. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Hassoun, M.H.; Song, J. Adaptive Ho-Kashyap rules for perceptron training. IEEE Trans. Neural Netw. 1992, 3, 51–61. [Google Scholar] [CrossRef]
- Khardon, R.; Wachman, G. Noise tolerant variants of the perceptron algorithm. J. Mach. Learn. Res. 2007, 8, 227–248. [Google Scholar]
- Freund, Y.; Schapire, R. Large margin classification using the perceptron algorithm. Mach. Learn. 1999, 37, 277–296. [Google Scholar] [CrossRef]
- Krauth, W.; Mezard, M. Learning algorithms with optimal stability in neural networks. J. Phys. A 1987, 20, 745–752. [Google Scholar] [CrossRef]
- Panagiotakopoulos, C.; Tsampouka, P. The Margitron: A generalized perceptron with margin. IEEE Trans. Neural Netw. 2011, 22, 395–407. [Google Scholar] [CrossRef] [PubMed]
- Vallet, F. The Hebb rule for learning linearly separable Boolean functions: Learning and generalisation. Europhys. Lett. 1989, 8, 747–751. [Google Scholar] [CrossRef]
- Bolle, D.; Shim, G.M. Nonlinear Hebbian training of the perceptron. Network 1995, 6, 619–633. [Google Scholar] [CrossRef]
- Mansfield, A.J. Training Perceptrons by Linear Programming; NPL Report DITC 181/91; National Physical Laboratory: Teddington, UK, 1991. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Efficient perceptron learning using constrained steepest descent. Neural Netw. 2000, 13, 351–364. [Google Scholar] [CrossRef] [Green Version]
- Keller, J.M.; Hunt, D.J. Incorporating fuzzy membership functions into the perceptron algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 693–699. [Google Scholar] [CrossRef]
- Chen, J.L.; Chang, J.Y. Fuzzy perceptron neural networks for classifiers with numerical data and linguistic rules as inputs. IEEE Trans. Fuzzy Syst. 2000, 8, 730–745. [Google Scholar]
- Nagaraja, G.; Krishna, G. An algorithm for the solution of linear inequalities. IEEE Trans. Comput. 1974, 23, 421–427. [Google Scholar] [CrossRef]
- Nagaraja, G.; Chandra Bose, R.P.J. Adaptive conjugate gradient algorithm for perceptron training. Neurocomputing 2006, 69, 368–386. [Google Scholar] [CrossRef]
- Diene, O.; Bhaya, A. Perceptron training algorithms designed using discrete-time control Liapunov functions. Neurocomputing 2009, 72, 3131–3137. [Google Scholar] [CrossRef]
- Cavallanti, G.; Cesa-Bianchi, N.; Gentile, C. Tracking the best hyperplane with a simple budget perceptron. Mach. Learn. 2007, 69, 143–167. [Google Scholar] [CrossRef] [Green Version]
- Fontenla-Romero, O.; Guijarro-Berdinas, B.; Perez-Sanchez, B.; Alonso-Betanzos, A. A new convex objective function for the supervised learning of single-layer neural networks. Pattern Recognit. 2010, 43, 1984–1992. [Google Scholar] [CrossRef]
- Legenstein, R.; Maass, W. On the classification capability of sign-constrained perceptrons. Neural Comput. 2008, 20, 288–309. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.Y.-F.; Ling, B.W.-K.; Lam, H.-K.; Nasir, M.H.U. Global convergence and limit cycle behavior of weights of perceptron. IEEE Trans. Neural Netw. 2008, 19, 938–947. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.Y.-F.; Ling, B.W.-K.; Iu, H.H.-C. Invariant set of weight of perceptron trained by perceptron training algorithm. IEEE Trans. Syst. Man Cybern. Part B 2010, 40, 1521–1530. [Google Scholar] [CrossRef] [Green Version]
- Auer, P.; Burgsteiner, H.; Maass, W. A learning rule for very simple universal approximators consisting of a single layer of perceptrons. Neural Netw. 2008, 21, 786–795. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Ribeiro, J.; Cernadas, E.; Ameneiro, S.B. Direct parallel perceptrons (DPPs): Fast analytical calculation of the parallel perceptrons weights with margin control for classification tasks. IEEE Trans. Neural Netw. 2011, 22, 1837–1848. [Google Scholar] [CrossRef]
- Widrow, B. Generalization and information storage in networks of Adaline neurons. In Self-Organizing Systems 1962; Jacbi, M.Y.G., Goldstein, G., Eds.; Spartan Books: Washington, DC, USA, 1962; pp. 435–461. [Google Scholar]
- Hoff, M.E. Learning Phenomena in Networks of Adaptive Switching Circuits. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1962. [Google Scholar]
- Widrow, B.; Winter, R.G.; Baxter, R. Learning phenomena in layered neural networks. In Proceedings of the 1st IEEE International Conference Neural Networks, San Diego, CA, USA, 21–24 June 1987; Volume 2, pp. 411–429. [Google Scholar]
- Kolmogorov, A.N. On the representation of continuous functions of several variables by superposition of continuous functions of one variable and addition. Akad. Nauk. USSR 1957, 114, 953–956. [Google Scholar]
- Cybenko, G. Continuous Valued Neural Networks with Two Hidden Layers Are Sufficient; Technical Report; Dept of Computer Science, Tufts University: Medford, MA, USA, 1988. [Google Scholar]
- Tamura, S.; Tateishi, M. Capabilities of a four-layered feedforward neural network: Four layers versus three. IEEE Trans. Neural Netw. 1997, 8, 251–255. [Google Scholar] [CrossRef]
- Huang, G.B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–291. [Google Scholar] [CrossRef] [Green Version]
- Cybenko, G. Approximation by superposition of a sigmoid function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.M.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Funahashi, K. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Xiang, C.; Ding, S.Q.; Lee, T.H. Geometrical interpretation and architecture selection of MLP. IEEE Trans. Neural Netw. 2005, 16, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Llanas, B.; Lantaron, S.; Sainz, F.J. Constructive approximation of discontinuous functions by neural networks. Neural Process. Lett. 2008, 27, 209–226. [Google Scholar] [CrossRef]
- Zhang, X.M.; Chen, Y.Q.; N, N.A.; Shi, Y.Q. Mini-max initialization for function approximation. Neurocomputing 2004, 57, 389–409. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef] [Green Version]
- Du, K.-L.; Swamy, M.N.S. Neural Networks in a Softcomputing Framework; Springer: London, UK, 2006. [Google Scholar]
- Finnoff, W. Diffusion approximations for the constant learning rate backpropagation algorithm and resistance to locol minima. Neural Comput. 1994, 6, 285–295. [Google Scholar] [CrossRef]
- Fine, T.L.; Mukherjee, S. Parameter convergence and learning curves for neural networks. Neural Comput. 1999, 11, 747–769. [Google Scholar] [CrossRef]
- Oh, S.H. Improving the error backpropagation algorithm with a modified error function. IEEE Trans. Neural Netw. 1997, 8, 799–803. [Google Scholar]
- Wu, W.; Feng, G.; Li, Z.; Xu, Y. Deterministic convergence of an online gradient method for BP neural networks. IEEE Trans. Neural Netw. 2005, 16, 533–540. [Google Scholar] [CrossRef]
- Battiti, R. First- and second-order methods for learning: Between steepest sescent and newton’s method. Neural Netw. 1992, 4, 141–166. [Google Scholar] [CrossRef]
- Gori, M.; Maggini, M. Optimal convergence of on-line backpropagation. IEEE Trans. Neural Netw. 1996, 7, 251–254. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Xu, Y.S. Deterministic convergence of an on-line gradient method for neural networks. J. Computat. Appl. Math. 2002, 144, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Cochocki, A.; Unbehauen, R. Neural Networks for Optimization and Signal Processing; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Wilson, D.R.; Martinez, T.R. The general inefficiency of batch training for gradient descent learning. Neural Netw. 2003, 16, 1429–1451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.-B.; Zhang, R.; Jing, W.-F. When does online BP training converge? IEEE Trans. Neural Netw. 2009, 20, 1529–1539. [Google Scholar]
- Zhang, R.; Xu, Z.-B.; Huang, G.-B.; Wang, D. Global convergence of online BP training with dynamic learning rate. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 330–341. [Google Scholar] [CrossRef]
- Granziol, D.; Zohren, S.; Roberts, S. Learning rates as a function of batch size: A random matrix theory approach to neural network training. J. Mach. Learn. Res. 2022, 23, 1–65. [Google Scholar]
- Wang, J.; Yang, J.; Wu, W. Convergence of cyclic and almost-cyclic learning with momentum for feedforward neural networks. IEEE Trans. Neural Netw. 2011, 22, 1297–1306. [Google Scholar] [CrossRef]
- Yuan, K.; Ying, B.; Sayed, A.H. On the influence of momentum acceleration on online learning. J. Mach. Learn. Res. 2016, 17, 1–66. [Google Scholar]
- Zhang, N. A study on the optimal double parameters for steepest descent with momentum. Neural Comput. 2015, 27, 982–1004. [Google Scholar] [CrossRef] [PubMed]
- Roux, R.N.; Schmidt, M.; Bach, F. A stochastic gradient method with an exponential convergence rate for finite training sets. Adv. Neural Inf. Process. Syst. 2012, 25, 2663–2671. [Google Scholar]
- Johnson, R.; Zhang, T. Accelerating stochastic gradient descent using predictive variance reduction. Adv. Neural Inf. Process. Syst. 2013, 26, 315–323. [Google Scholar]
- Defazio, A.; Bach, F.; Lacoste-Julien, S. SAGA: A fast incremental gradient method with support for non-strongly convex composite objectives. Adv. Neural Inf. Process. Syst. 2014, 27, 1646–1654. [Google Scholar]
- Shalev-Shwartz, S.; Zhang, T. Stochastic dual coordinate ascent methods for regularized loss. J. Mach. Learn. Res. 2013, 14, 567–599. [Google Scholar]
- Mokhtari, A.; Ribeiro, A. Stochastic Quasi-Newton Methods. Proc. IEEE 2020, 108, 1906–1922. [Google Scholar] [CrossRef]
- Moody, J. Note on generalization, regularization, and architecture selection in nonlinear learning systems. In First IEEE-SP Workshop on Neural Networks for Signal Processing; Morgan Kaufmann: San Mateo, CA, USA, 1991; pp. 1–10. [Google Scholar]
- Moody, J.; Hanson, S.J.; Lippmann, R.P. The effective number of parameters: An analysis of generalization and regularization in nonlinear learning systems. Adv. Neural Inf. Process. Syst. 1992, 4, 847–854. [Google Scholar]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Niyogi, P.; Girosi, F. Generalization bounds for function approximation from scattered noisy dat. Adv. Comput. Math. 1999, 10, 51–80. [Google Scholar] [CrossRef]
- Niyogi, P.; Girosi, F. On the Relationship between Generalization Error, Hypothesis Complexity, and Sample Complexity for Radial Basis Functions; Tech. Rep.; MIT: Cambridge, MA, USA, 1994. [Google Scholar]
- Barron, A.R. Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 1993, 39, 930–945. [Google Scholar] [CrossRef] [Green Version]
- Prechelt, L. Automatic early stopping using cross validation: Quantifying the criteria. Neural Netw. 1998, 11, 761–767. [Google Scholar] [CrossRef] [Green Version]
- Amari, S.; Murata, N.; Muller, K.R.; Finke, M.; Yang, H. Statistical theory of overtraining–is cross-validation asymptotically effective. In Advances in Neural Information Processing Systems 8; Morgan Kaufmann: San Mateo, CA, USA, 1996; pp. 176–182. [Google Scholar]
- Wu, L.; Moody, J. A smoothing regularizer for feedforward and recurrent neural networks. Neural Comput. 1996, 8, 461–489. [Google Scholar] [CrossRef]
- Orr, M.J. Regularization in the selection of radial basis function centers. Neural Comput. 1995, 7, 606–623. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Guo, P. Studies of Model Selection and Regularization for Generalization in Neural Networks with Applications. Ph.D. Thesis, The Chinese University of Hong Kong, Hong Kong, China, 2002. [Google Scholar]
- Krogh, A.; Hertz, J.A. A simple weight decay can improve generalization. In Advances in Neural Information Processing Systems; Morgan Kaufmann: San Mateo, CA, USA, 1992; pp. 950–957. [Google Scholar]
- Mackay, D.J.C. A practical bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef] [Green Version]
- Reed, R.; Marks, R.J.; Oh, S. Similarities of error regularization, sigmoid gain scaling, target smoothing, and training with jitter. IEEE Trans. Neural Netw. 1995, 6, 529–538. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Training with noise is equivalent to Tikhonov regularization. Neural Comput. 1995, 7, 108–116. [Google Scholar] [CrossRef]
- Hinton, G.E.; Camp, D.V. Keeping neural networks simple by minimizing the description length of the weights. In Proceedings of the 6th Annual ACM Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993; pp. 5–13. [Google Scholar]
- Nowlan, S.J.; Hinton, G.E. Simplifying neural networks by soft weight-sharing. Neural Comput. 1992, 4, 473–493. [Google Scholar] [CrossRef]
- Tarres, P.; Yao, Y. Online learning as stochastic approximation of regularization paths: Optimality and almost-sure convergence. IEEE Trans. Inf. Theory 2014, 60, 5716–5735. [Google Scholar] [CrossRef]
- Lin, J.; Rosasco, L. Optimal rates for multi-pass stochastic gradient methods. J. Mach. Learn. Res. 2017, 18, 1–47. [Google Scholar]
- Janssen, P.; Stoica, P.; Soderstrom, T.; Eykhoff, P. Model structure selection for multivariable systems by cross-validation. Int. J. Control 1998, 47, 1737–1758. [Google Scholar] [CrossRef]
- Wang, C.; Venkatesh, S.; Stephen, J. Optimal stopping and effective machine complexity in learning. In Advances in Neural Information Processing Systems 6; Morgan Kaufmann: San Mateo, CA, USA, 1994; pp. 303–310. [Google Scholar]
- Sugiyama, M.; Ogawa, H. Optimal design of regularization term and regularization parameter by subspace information criterion. Neural Netw. 2002, 15, 349–361. [Google Scholar] [CrossRef]
- Sugiyama, M.; Müller, K.-R. The subspace information criterion for infinite dimensional hypothesis spaces. J. Mach. Learn. Res. 2003, 3, 323–359. [Google Scholar]
- Onoda, T. Neural network information criterion for the optimal number of hidden units. In Proceedings of the IEEE International Conference on Neural Networks, ICNN’95, Perth, WA, Australia, 27 November–1 December 1995; pp. 275–280. [Google Scholar]
- Murata, N.; Yoshizawa, S.; Amari, S. Network information criterion–determining the number of hidden units for an artificial neural network model. IEEE Trans. Neural Netw. 1994, 5, 865–872. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Cherkassky, V.; Shao, X.; Mulier, F.M.; Vapnik, V.N. Model complexity control for regression using vc generalization bounds. IEEE Trans. Neural Netw. 1999, 10, 1075–1089. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; Kawato, M. Estimation of generalization capability by combination of new information criterion and cross validation. IEICE Trans. 1991, 2, 955–965. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–477. [Google Scholar] [CrossRef]
- Rissanen, J. Hypothesis selection and testing by the mdl principle. Computer 1999, 42, 260–269. [Google Scholar] [CrossRef] [Green Version]
- Gallinari, P.; Cibas, T. Practical complexity control in multilayer perceptrons. Signal Process. 1999, 74, 29–46. [Google Scholar] [CrossRef]
- Chen, S. Local regularization assisted orthogonal least squares regression. Neurocomputing 2006, 69, 559–585. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Hong, X.; Harris, C.J.; Sharkey, P.M. Sparse modelling using orthogonal forward regression with press statistic and regularization. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 898–911. [Google Scholar] [CrossRef]
- Reed, R. Pruning algorithms—A survey. IEEE Trans. Neural Netw. 1993, 4, 40–747. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, H.; Chen, H.H.; Manry, M.T. Pruning of basis functions in nonlinear approximators. Neurocomputing 2000, 34, 29–53. [Google Scholar] [CrossRef]
- Mozer, M.C.; Smolensky, P. Using relevance to reduce network size automatically. Connect. Sci. 1989, 1, 3–16. [Google Scholar] [CrossRef]
- Karnin, E.D. A simple procedure for pruning back-propagation trained neural networks. IEEE Trans. Neural Netw. 1990, 1, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Goh, Y.S.; Tan, E.C. Pruning neural networks during training by backpropagation. In Proceedings of the IEEE Region 10’s Ninth Annual Int Conf (TENCON’94), Singapore, 22–26 August 1994; pp. 805–808. [Google Scholar]
- Ponnapalli, P.V.S.; Ho, K.C.; Thomson, M. A formal selection and pruning algorithm for feedforward artificial neural network optimization. IEEE Trans. Neural Netw. 1999, 10, 964–968. [Google Scholar] [CrossRef]
- Tartaglione, E.; Bragagnolo, A.; Fiandrotti, A.; Grangetto, M. LOss-Based SensiTivity rEgulaRization: Towards deep sparse neural networks. Neural Netw. 2022, 146, 230–237. [Google Scholar] [CrossRef]
- Cho, H.; Jang, J.; Lee, C.; Yang, S. Efficient architecture for deep neural networks with heterogeneous sensitivity. Neural Netw. 2021, 134, 95–106. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, M.; Manry, M.T.; Dawson, M.S.; Fung, A.K. Analysis and optimization of neural networks for remote sensing. Remote Sens. Rev. 1994, 9, 97–144. [Google Scholar] [CrossRef] [Green Version]
- Kanjilal, P.P.; Banerjee, D.N. On the application of orthogonal transformation for the design and analysis of feedforward networks. IEEE Trans. Neural Netw. 1995, 6, 1061–1070. [Google Scholar] [CrossRef]
- Teoh, E.J.; Tan, K.C.; Xiang, C. Estimating the number of hidden neurons in a feedforward network using the singular value decomposition. IEEE Trans. Neural Netw. 2006, 17, 1623–1629. [Google Scholar] [CrossRef] [PubMed]
- Levin, A.U.; Leen, T.K.; Moody, J. Fast pruning using principal components. In Advances in Neural Information Processing Systems 6; Morgan Kaufmann: San Mateo, CA, USA, 1994; pp. 847–854. [Google Scholar]
- Xing, H.-J.; Hu, B.-G. Two-phase construction of multilayer perceptrons using information theory. IEEE Trans. Neural Netw. 2009, 20, 715–721. [Google Scholar] [CrossRef] [PubMed]
- Sietsma, J.; Dow, R.J.F. Creating artificial neural networks that generalize. Neural Netw. 1991, 4, 67–79. [Google Scholar] [CrossRef]
- Castellano, G.; Fanelli, A.M.; Pelillo, M. An iterative pruning algorithm for feedforward neural networks. IEEE Trans. Neural Netw. 1997, 8, 519–531. [Google Scholar] [CrossRef]
- Cun, Y.L.; Denker, J.S.; Solla, S.A. Optimal brain damage. In Advances in Neural Information Processing Systems; Morgan Kaufmann: San Mateo, CA, USA, 1990; pp. 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G.; Wolff, G.J. Optimal brain surgeon and general network pruning. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 23–26 March 1992; pp. 293–299. [Google Scholar]
- Soulie, T.C.T.F.F.; Gallinari, P.; Raudys, S. Variable selection with neural networks. Neurocomputing 1996, 12, 223–248. [Google Scholar]
- Stahlberger, A.; Riedmiller, M. Fast network pruning and feature extraction using the unit-obs algorithm. In Advances in Neural Information Processing Systems 9; Morgan Kaufmann: San Mateo, CA, USA, 1997; pp. 655–661. [Google Scholar]
- Tresp, V.; Neuneier, R.; Zimmermann, H.G. Early brain damage. In Advances in Neural Information Processing Systems 9; Morgan Kaufmann: San Mateo, CA, USA, 1997; pp. 669–675. [Google Scholar]
- Engelbrecht, A.P. A new pruning heuristic based on variance analysis of sensitivity information. IEEE Trans. Neural Netw. 2001, 12, 1386–1399. [Google Scholar] [CrossRef]
- Bishop, C.M. Exact calculation of the hessian matrix for the multilayer perceptron. Neural Comput. 1992, 4, 494–501. [Google Scholar] [CrossRef]
- Leung, C.S.; Wong, K.W.; Sum, P.F.; Chan, L.W. A pruning method for the recursive least squared algorithm. Neural Netw. 2001, 14, 147–174. [Google Scholar] [CrossRef] [PubMed]
- Sum, J.; Chan, L.W.; Leung, C.S.; Young, G. Extended kalman filter-based pruning method for recurrent neural networks. Neural Comput. 1998, 10, 1481–1505. [Google Scholar] [CrossRef]
- Sum, J.; Leung, C.S.; Young, G.; Kan, W.K. On the kalman filtering method in neural network training and pruning. IEEE Trans. Neural Netw. 1999, 10, 161–166. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E. Connectionist learning procedure. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef] [Green Version]
- Weigend, A.S.; Rumelhart, D.E.; Huberman, B.A. Generalization by weight-elimination with application to forecasting. In Advances in Neural Information Processing Systems 3; Morgan Kaufmann: San Mateo, CA, USA, 1991; pp. 875–882. [Google Scholar]
- Ishikawa, M. Learning of modular structured networks. Artif. Intell 1995, 7, 51–62. [Google Scholar] [CrossRef] [Green Version]
- A, A.G.; Lam, S.H. Weight decay backpropagation for noisy data. Neural Netw. 1998, 11, 1127–1137. [Google Scholar]
- Aires, F.; Schmitt, M.; Chedin, A.; Scott, N. The weight smoothing regularization of mlp for jacobian stabilization. IEEE Trans. Neural Netw. 1999, 10, 1502–1510. [Google Scholar] [CrossRef] [PubMed]
- Drucker, H.; Cun, Y.L. Improving generalization performance using double backpropagation. IEEE Trans. Neural Netw. 1992, 3, 991–997. [Google Scholar] [CrossRef]
- Poggio, T.; Girosi, F. Networks for approximation and learning. Proc. IEEE 1990, 78, C1481–C1497. [Google Scholar] [CrossRef] [Green Version]
- Moody, J.; Rognvaldsson, T. Smoothness regularizers for projective basis function networks. Adv. Neural Inf. Process. Syst. 1997, 4, 585–591. [Google Scholar]
- Wang, J.; Xu, C.; Yang, X.; Zurada, J.M. A novel pruning algorithm for smoothing feedforward neural networks based on group lasso method. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2012–2024. [Google Scholar] [CrossRef]
- Ma, R.; Miao, J.; Niu, L.; Zhang, P. Transformed ℓ1 regularization for learning sparse deep neural networks. Neural Netw. 2019, 119, 286–298. [Google Scholar] [CrossRef]
- Fabisch, A.; Kassahun, Y.; Wohrle, H.; Kirchner, F. Learning in compressed space. Neural Netw. 2013, 42, 83–93. [Google Scholar] [CrossRef]
- Hirose, Y.; Yamashita, K.; Hijiya, S. Back-propagation algorithm which varies the number of hidden units. Neural New. 1991, 4, 61–66. [Google Scholar] [CrossRef]
- Fahlman, S.E.; Lebiere, C. The cascade-correlation learning architecture. In Advances in Neural Information Processing Systems 2; Morgan Kaufmann: San Mateo, CA, USA, 1990; pp. 524–532. [Google Scholar]
- Fahlman, S.E. Faster-learning variations on back-propagation: An empirical study. In Proceedings of the 1988 Connectionist Models Summer School; Morgan Kaufmann: San Mateo, CA, USA, 1989; pp. 38–51. [Google Scholar]
- Kwok, T.Y.; Yeung, D.Y. Objective functions for training new hidden units in constructive neural networks. IEEE Trans. Neural Netw. 1997, 8, 1131–1148. [Google Scholar] [CrossRef] [Green Version]
- Lehtokangas, M. Modelling with constructive backpropagation. Neural Netw. 1999, 12, 707–716. [Google Scholar] [CrossRef] [PubMed]
- Phatak, D.S.; Koren, I. Connectivity and performance tradeoffs in the cascade correlation learning architecture. IEEE Trans. Neural Netw. 1994, 5, 930–935. [Google Scholar] [CrossRef] [PubMed]
- Setiono, R.; Hui, L.C.K. Use of quasi-newton method in a feed-forward neural network construction algorithm. IEEE Trans. Neural Netw. 1995, 6, 273–277. [Google Scholar] [CrossRef]
- Moody, J.O.; Antsaklis, P.J. The dependence identification neural network construction algorithm. IEEE Trans. Neural Netw. 1996, 7, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Rathbun, T.F.; Rogers, S.K.; DeSimio, M.P.; Oxley, M.E. MLP iterative construction algorithm. Neurocomputing 1997, 17, 195–216. [Google Scholar] [CrossRef]
- Liu, D.; Chang, T.S.; Zhang, Y. A constructive algorithm for feedforward neural networks with incremental training. IEEE Trans. Circuits Syst.–I 2002, 49, 1876–1879. [Google Scholar]
- Fukuoka, Y.; Matsuki, H.; Minamitani, H.; Ishida, A. A modified back-propagation method to avoid false local minima. Neural Netw. 1998, 11, 1059–1072. [Google Scholar] [CrossRef]
- Rigler, A.K.; Irvine, J.M.; Vogl, T.P. Rescaling of variables in back propagation learning. Neural Netw. 1991, 4, 225–229. [Google Scholar] [CrossRef]
- Satoh, S.; Nakano, R. Fast and stable learning utilizing singular regions of multilayer perceptron. Neural Process. Lett. 2013, 38, 99–115. [Google Scholar] [CrossRef]
- Mezard, M.; Nadal, J.P.S. Learning in feedforward layered networks: The tiling algorithm. J. Phys. 1989, A22, 2191–2203. [Google Scholar] [CrossRef] [Green Version]
- Frean, M. The upstart algorithm: A method for constructing and training feedforward neural networks. Neural Comput. 1990, 2, 198–209. [Google Scholar] [CrossRef]
- Lee, Y.; Oh, S.H.; Kim, M.W. The effect of initial weights on premature saturation in back-propagation training. In Proceedings of the IEEE International Joint Conf Neural Networks, Seattle, WA, USA, 8–12 July 1991; pp. 765–770. [Google Scholar]
- Vitela, J.E.; Reifman, J. Premature saturation in backpropagation networks: Mechanism and necessary condition. Neural Netw. 1997, 10, 721–735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, H.M.; Chen, C.M.; Huang, T.C. Learning efficiency improvement of back-propagation algorithm by error saturation prevention method. Neurocomputing 2001, 41, 125–143. [Google Scholar] [CrossRef]
- Ng, S.C.; Leung, S.H.; Luk, A. Fast and global convergent weight evolution algorithm based on modified back-propagation. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 3004–3008. [Google Scholar]
- Wang, X.G.; Tang, Z.; Tamura, H.; Ishii, M. A modified error function for the backpropagation algorithm. Neurocomput 2004, 57, 477–484. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Cun, Y.L.; Simard, P.Y.; Pearlmutter, B. Automatic learning rate maximization by on-line estimation of the hessian’s eigenvectors. In Advances in Neural Information Processing Systems 5; Morgan Kaufmann: San Mateo, CA, USA, 1993; pp. 156–163. [Google Scholar]
- Darken, C.; Moody, J. Towards faster stochastic gradient search. In Advances in Neural Information Processing Systems 4; Morgan Kaufmann: San Mateo, CA, USA, 1992; pp. 1009–1016. [Google Scholar]
- Vogl, T.P.; Mangis, J.K.; Rigler, A.K.; Zink, W.T.; Alkon, D.L. Accelerating the convergence of the backpropagation method. Biol. Cybern. 1988, 59, 257–263. [Google Scholar] [CrossRef]
- Battiti, R. Accelerated backpropagation learning: Two optimization methods. Complex Syst. 1989, 3, 331–342. [Google Scholar]
- Parlos, A.G.; Femandez, B.; Atiya, A.F.; Muthusami, J.; Tsai, W.K. An accelerated learning algorithm for multilayer perceptron networks. IEEE Trans. Neural Netw. 1994, 5, 493–497. [Google Scholar] [CrossRef]
- Yam, Y.F.; Chow, T.W.S. Extended backpropagation algorithm. Electron. Lett. 1993, 29, 1701–1702. [Google Scholar] [CrossRef]
- Silva, F.M.; Almeida, L.B. Speeding up backpropagation. In Advanced Neural Computers; Eckmiller, R., Ed.; North-Holland: Amsterdam, The Netherlands, 1990; pp. 151–158. [Google Scholar]
- Magoulas, G.D.; Vrahatis, M.N.; Androulakis, G.S. Effective backpropagation training with variable stepsize. Neural Netw. 1997, 10, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, R.A. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988, 1, 295–307. [Google Scholar] [CrossRef]
- Choi, J.Y.; Choi, C.H. Sensitivity of multilayer perceptrons with differentiable activation functions. IEEE Trans. Neural Netw. 1992, 3, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Tesauro, G.; Janssens, B. Scaling relationships in back-propagation learning. Complex Syst. 1988, 2, 39–44. [Google Scholar]
- Tollenaere, T. Supersab: Fast adaptive backpropation with good scaling properties. Neural Netw. 1990, 3, 561–573. [Google Scholar] [CrossRef]
- Martens, J.P.; Weymaere, N. An equalized error backpropagation algorithm for the on-line training of multilayer perceptrons. IEEE Trans. Neural Netw. 2002, 13, 532–541. [Google Scholar] [CrossRef]
- Magoulas, G.D.; Vrahatis, M.N.; Plagianakos, V.P. Globally convergent algorithms with local learning rates. IEEE Trans. Neural Netw. 2002, 13, 774–779. [Google Scholar] [CrossRef]
- Cun, Y.L.; Kanter, I.; Solla, S.A. Second order properties of error surfaces: Learning time and generalization. In Advances in Neural Information Processing Systems 3; Morgan Kaufmann: San Mateo, CA, USA, 1991; pp. 918–924. [Google Scholar]
- Minai, A.A.; Williams, R.D. Backpropagation heuristics: A study of the extended delta-bar-delta algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 595–600. [Google Scholar]
- Yu, X.H.; Chen, G.A.; Cheng, S.X. Dynamic learning rate optimization of the backpropagation algorithm. IEEE Trans. Neural Netw. 1995, 6, 669–677. [Google Scholar] [PubMed]
- Yu, X.H.; Chen, G.A. Efficient backpropagation learning using optimal learning rate and momentum. Neural Netw. 1997, 10, 517–527. [Google Scholar] [CrossRef]
- Veitch, A.C.; Holmes, G. A modified quickprop algorithm. Neural Comput. 1991, 3, 310–311. [Google Scholar] [CrossRef] [PubMed]
- Kolen, J.F.; Pollack, J.B. Backpropagation is sensitive to initial conditions. Complex Syst. 1990, 4, 269–280. [Google Scholar]
- Drago, G.; Ridella, S. Statistically controlled activation weight initialization. IEEE Trans. Neural Netw. 1992, 3, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Thimm, G.; Fiesler, E. High-order and multilayer perceptron initialization. IEEE Trans. Neural Netw. 1997, 8, 349–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wessels, L.F.A.; Barnard, E. Avoiding false local minima by proper initialization of connections. IEEE Trans. Neural Netw. 1992, 3, 899–905. [Google Scholar] [CrossRef]
- McLoone, S.; Brown, M.D.; Irwin, G.; Lightbody, G. A hybrid linear/nonlinear training algorithm for feedforward neural networks. IEEE Trans. Neural Netw. 1998, 9, 669–684. [Google Scholar] [CrossRef] [PubMed]
- Yam, Y.F.; Chow, T.W.S. Feedforward networks training speed enhancement by optimal initialization of the synaptic coefficients. IEEE Trans. Neural Netw. 2001, 12, 430–434. [Google Scholar] [CrossRef]
- Denoeux, T.; Lengelle, R. Initializing backpropagation networks with prototypes. Neural Netw. 1993, 6, 351–363. [Google Scholar] [CrossRef]
- Smyth, S.G. Designing multilayer perceptrons from nearest neighbor systems. IEEE Trans. Neural Netw. 1992, 3, 323–333. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, H.; Sudjianto, A.; Zhang, A. An effective SteinGLM initialization scheme for training multi-layer feedforward sigmoidal neural networks. Neural Netw. 2021, 139, 149–157. [Google Scholar] [CrossRef]
- Nguyen, D.; Widrow, B. Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. In Proceedings of the Internatinal Joint Conference Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 21–26. [Google Scholar]
- Osowski, S. New approach to selection of initial values of weights in neural function approximation. Electron. Lett. 1993, 29, 313–315. [Google Scholar] [CrossRef]
- Yam, Y.F.; Chow, T.W.S.; Leung, C.T. A new method in determining the initial weights of feedforward neural networks. Neurocomputing 1997, 16, 23–32. [Google Scholar] [CrossRef]
- Yam, Y.F.; Chow, T.W.S. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Lehtokangas, M.; Saarinen, P.; Huuhtanen, P.; Kaski, P. Initializing weights of a multilayer perceptron network by using the orthogonal least squares algorithm. Neural Comput. 1995, 7, 982–999. [Google Scholar] [CrossRef]
- Chen, C.L.; Nutter, R.S. Improving the training speed of three-layer feedforward neural nets by optimal estimation of the initial weights. In Proceedings of the International Joint Conference Neural Networks, Seattle, WA, USA, 8–12 July 1991; pp. 2063–2068. [Google Scholar]
- Yam, Y.F.; Leung, C.T.; Tam, P.K.S.; Siu, W.C. An independent component analysis based weight initialization method for multilayer perceptrons. Neurocomputing 2002, 48, 807–818. [Google Scholar] [CrossRef]
- Chumachenko, K.; Iosifidis, A.; Gabbouj, M. Feedforward neural networks initialization based on discriminant learning. Neural Netw. 2022, 146, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Lehtokangas, M.; Korpisaari, P.; Kaski, K. Maximum covariance method for weight initialization of multilayer perceptron networks. In Proceedings of the European symp Artificial Neural Netw (ESANN’96), Bruges, Belgium, 24–26 April 1996; pp. 243–248. [Google Scholar]
- Costa, P.; Larzabal, P. Initialization of supervised training for parametric estimation. Neural Process. Lett. 1999, 9, 53–61. [Google Scholar] [CrossRef]
- Hinton, G.E. Connectionist Learning Procedures; Tech. Rep.; Carnegie-Mellon University: Pittsburgh, PA, USA, 1987. [Google Scholar]
- Yang, L.; Lu, W. Backpropagation with homotopy. Neural Comput. 1993, 5, 363–366. [Google Scholar] [CrossRef]
- Kruschke, J.K.; Movellan, J.R. Benefits of gain: Speeded learning and minimal layers in back-propagation networks. IEEE Trans. Syst. Man Cybern. 1991, 21, 273–280. [Google Scholar] [CrossRef] [Green Version]
- Sperduti, A.; Starita, A. Speed up learning and networks optimization with extended back propagation. Neural Netw. 1993, 6, 365–383. [Google Scholar] [CrossRef]
- Chandra, P.; Singh, Y. An activation function adapting training algorithm for sigmoidal feedforward networks. Neurocomputing 2004, 61, 429–437. [Google Scholar] [CrossRef]
- Eom, K.; Jung, K.; Sirisena, H. Performance improvement of backpropagation algorithm by automatic activation function gain tuning using fuzzy logic. Neurocomputing 2003, 50, 439–460. [Google Scholar] [CrossRef]
- Duch, W. Uncertainty of data, fuzzy membership functions, and multilayer perceptrons. IEEE Trans. Neural Netw. 2005, 6, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hush, D.R.; Salas, J.M. Improving the learning rate of back-propagation with the gradient reuse algorithm. In Proceedings of the IEEE International Conference Neural Networks (ICNN’88), San Diego, CA, USA, 24–27 July 1988; pp. 441–447. [Google Scholar]
- Pfister, M.; Rojas, R. Speeding-up backpropagation–a comparison of orthogonal techniques. In Proceedings of the International Joint Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; pp. 517–523. [Google Scholar]
- Kamarthi, S.V.; Pittner, S. Accelerating neural network training using weight extrapolations. Neural Netw. 1999, 12, 1285–1299. [Google Scholar] [CrossRef] [PubMed]
- Zweiri, Y.H.; Whidborne, J.F.; Seneviratne, L.D. Optimization and Stability of a Three-Term Backpropagation Algorithm; Technical Report EM-2000-01; Department of Mechanical Engineering, King’s College London: London, UK, 2000. [Google Scholar]
- Zweiri, Y.H.; Whidborne, J.F.; Seneviratne, L.D. A three-term backpropagation algorithm. Neurocomputing 2003, 50, 305–318. [Google Scholar] [CrossRef]
- Liang, Y.C.; Feng, D.P.; Lee, H.P.; Lim, S.P.; Lee, K.H. Successive approximation training algorithm for feedforward neural networks. Neurocomputing 2002, 42, 311–322. [Google Scholar] [CrossRef]
- Stich, S.U.; Karimireddy, S.P. The error-feedback framework: Better rates for SGD with delayed gradients and compressed updates. J. Mach. Learn. Res. 2020, 21, 1–36. [Google Scholar]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 25–29 October 1993; pp. 586–591. [Google Scholar]
- Hannan, J.M.; Bishop, J.M. A comparison of fast training algorithms over two real problems. In Proceedings of the IEE Conference on Artificial Neural Networks, Cambridge, UK, 21–24 July 1997; pp. 1–6. [Google Scholar]
- Du, K.-L.; Swamy, M.N.S. Neural Networks and Statistical Learning, 2nd ed.; Springer: London, UK, 2019. [Google Scholar]
- Saarinen, S.; Bramley, R.; Cybenko, G. Ill conditioning in neural network training problems. SIAM J. Sci. Comput. 1993, 14, 693–714. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, R. Practical Methods of Optimization; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Battiti, R.; Masulli, F. Bfgs optimization for faster automated supervised learning. In Proceedings of the International Neural Network Conference, Paris, France, 9–13 July 1990; pp. 757–760. [Google Scholar]
- Battiti, R.; Masulli, G.; Tecchiolli, G. Learning with first, second, and no derivatives: A case study in high energy physics. Neurocomputing 1994, 6, 181–206. [Google Scholar] [CrossRef]
- Johansson, E.M.; Dowla, F.U.; Goodman, D.M. Backpropagation learning for multilayer feedforward neural networks using the conjugate gradient method. Int. J. Neural Syst. 1991, 2, 291–301. [Google Scholar] [CrossRef]
- van der Smagt, P. Minimisation methods for training feed-forward neural networks. Neural Netw. 1994, 7, 1–11. [Google Scholar] [CrossRef]
- Moller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Haykin, S.M. Neural networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Barnard, E. Optimization for training neural nets. IEEE Trans. Neural Netw. 1992, 3, 232–240. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lin, C.T. A second-order learning algorithm for multilayer networks based on block hessian matrix. Neural Netw. 1998, 11, 1607–1622. [Google Scholar] [CrossRef] [PubMed]
- Golub, G.H.; van Loan, C.F. Matrix Computation, 2nd ed.; John Hopkins University Press: Baltimore, MD, USA, 1989. [Google Scholar]
- More, J.J. The levenberg-marquardt algorithm: Implementation and theory. In Numerical Analysis, Lecture Notes in Mathematics 630; Watson, G.A., Ed.; Springer: Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.X.; Wilamowski, B.M. TREAT: A trust-region-based error-aggregated training algorithm for neural networks. In Proceedings of the International Joint Conference Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 1463–1468. [Google Scholar]
- Wilamowski, B.M.; Iplikci, S.; Kaynak, O.; Efe, M.O. An algorithm for fast convergence in training neural networks. In Proceedings of the International Joint Conference Neural Networks, Wahington, DC, USA, 15–19 July 2001; pp. 1778–1782. [Google Scholar]
- Ngia, L.S.H.; Sjoberg, J. Efficient training of neural nets for nonlinear adaptive filtering using a recursive levenberg-marquardt algorithm. IEEE Trans. Signal Process. 2000, 48, 1915–1927. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Cotton, N.J.; Kaynak, O.; Dundar, G. Computing gradient vector and Jacobian matrix in arbitrarily connected neural networks. IEEE Trans. Ind. Electron. 2008, 55, 3784–3790. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Improved computation for Levenberg–Marquardt training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Neural network learning without backpropagation. IEEE Trans. Neural Netw. 2010, 21, 1793–1803. [Google Scholar] [CrossRef]
- Fairbank, M.; Alonso, E.; Schraudolph, N. Efficient calculation of the Gauss-Newton approximation of the Hessian matrix in neural networks. Neural Comput. 2012, 24, 607–610. [Google Scholar] [CrossRef]
- Rubio, J.d.J. Stability analysis of the modified Levenberg-Marquardt algorithm for the artificial neural network training. In IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3510–3524. [Google Scholar] [CrossRef] [PubMed]
- Ampazis, N.; Perantonis, S.J. Two highly efficient second-order algorithms for training feedforward networks. IEEE Trans. Neural Netw. 2002, 13, 1064–1074. [Google Scholar] [CrossRef] [PubMed]
- Lee, J. Attractor-based trust-region algorithm for efficient training of multilayer perceptrons. Electron. Lett. 2003, 39, 727–728. [Google Scholar] [CrossRef]
- Lee, J.; Chiang, H.D. Theory of stability regions for a class of nonhyperbolic dynamical systems and its application to constraint satisfaction problems. IEEE Trans. Circuits Syst.–I 2002, 49, 196–209. [Google Scholar]
- RoyChowdhury, P.; Singh, Y.P.; Chansarkar, R.A. Dynamic tunneling technique for efficient training of multilayer perceptrons. IEEE Trans. Neural Netw. 1999, 10, 48–55. [Google Scholar] [CrossRef]
- Ye, H.; Luo, L.; Zhang, Z. Nesterov’s acceleration for approximate Newton. J. Mach. Learn. Res. 2020, 21, 1–37. [Google Scholar]
- Beigi, H.S.M. Neural network learning through optimally conditioned quadratically convergent methods requiring no line search. In Proceedings of the IEEE 36th Midwest Symp Circuits Systems, Detroit, MI, USA, 16–18 August 1993; pp. 109–112. [Google Scholar]
- Nazareth, J.L. Differentiable Optimization and Equation Solving; Springer: New York, NY, USA, 2003. [Google Scholar]
- McLoone, S.; Irwin, G. Fast parallel off-line training of multilayer perceptrons. IEEE Trans. Neural Netw. 1997, 8, 646–653. [Google Scholar] [CrossRef]
- Phua, P.K.H.; Ming, D. Parallel nonlinear optimization techniques for training neural networks. IEEE Trans. Neural Netw. 2003, 14, 1460–1468. [Google Scholar] [CrossRef]
- Shanno, D. Conjugate gradient methods with inexact searches. Math. Oper. Res. 1978, 3, 244–256. [Google Scholar] [CrossRef]
- McLoone, S.; Irwin, G. A variable memory quasi-newton training algorithm. Neural Process. Lett. 1999, 9, 77–89. [Google Scholar] [CrossRef]
- McLoone, S.; Asirvadam, V.S.; Irwin, G. A memory optimal bfgs neural network training algorithm. In Proceedings of the 2002 International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 513–518. [Google Scholar]
- Perantonis, S.J.; Ampazis, N.; Spirou, S. Training feedforward neural networks with the dogleg method and bfgs hessian updates. In Proceedings of the International Joint Conference on Neural Networks, Como, Italy, 24–27 July 2000; pp. 138–143. [Google Scholar]
- Bortoletti, A.; Fiore, C.D.; Fanelli, S.; Zellini, P. A new class of quasi-newtonian methods for optimal learning in MLP-networks. IEEE Trans. Neural Netw. 2003, 14, 263–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1953, 49, 409–436. [Google Scholar] [CrossRef]
- Charalambous, C. Conjugate gradient algorithm for efficient training of artificial neural networks. IEE Proc. G 1992, 139, 301–310. [Google Scholar] [CrossRef]
- Dixon, L.C.W. Conjugate gradient algorithms: Quadratic termination properties without linear searches. J. Inst. Math. Appl. 1975, 15, 9–18. [Google Scholar] [CrossRef]
- Goryn, D.; Kaveh, M. Conjugate gradient learning algorithms for multilayer perceptrons. In Proceedings of the IEEE 32nd Midwest Symp Circuits Systems, Champaign, IL, USA, 14–16 August 1989; pp. 736–739. [Google Scholar]
- Fletcher, R.; Reeves, C.W. Function minimization by conjugate gradients. Comput. J. 1964, 7, 148–154. [Google Scholar]
- Polak, E. Computational Methods in Optimization: A Unified Approach; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef] [Green Version]
- A, A.B.; Kaszkurewicz, E. Steepest descent with momentum for quadratic functions is a version of the conjugate gradient method. Neural Netw. 2004, 17, 65–71. [Google Scholar]
- Towsey, M.; Alpsan, D.; Sztriha, L. Training a neural network with conjugate gradient methods. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australian, 27 November–1 December 1995; pp. 373–378. [Google Scholar]
- Liu, C.S.; Tseng, C.H. Quadratic optimization method for multilayer neural networks with local error-backpropagation. Int. J. Syst. Sci. 1999, 30, 889–898. [Google Scholar] [CrossRef]
- Kostopoulos, A.E.; Grapsa, T.N. Self-scaled conjugate gradient training algorithms. Neurocomputing 2009, 72, 3000–3019. [Google Scholar] [CrossRef]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Maybeck, P.S.; Oxley, M.E. Comparative analysis of backpropagation and the extended kalman filter for training multilayer perceptrons. IEEE Trans. Pattern. Anal. Mach. Intell. 1992, 14, 686–691. [Google Scholar] [CrossRef]
- Iguni, Y.I.; Sakai, H.; Tokumaru, H. A real-time learning algorithm for a multilayered neural network based on the extended kalman filter. IEEE Trans. Signal Process. 1992, 40, 959–967. [Google Scholar] [CrossRef]
- Leung, C.S.; Chan, L.W. Dual extended kalman filtering in recurrent neural networks. Neural Netw. 2003, 16, 223–239. [Google Scholar] [CrossRef] [PubMed]
- Singhal, S.; Wu, L. Training feedforward networks with the extended kalman algorithm. In Proceedings of the IEEE ICASSP-89, Glasgow, Scotland, 23–26 May 1989; pp. 1187–1190. [Google Scholar]
- Zhang, Y.; Li, X. A fast u-d factorization-based learning algorithm with applications to nonlinear system modeling and identification. IEEE Trans. Neural Netw. 1999, 10, 930–938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rivals, I.; Personnaz, L. A recursive algorithm based on the extended kalman filter for the training of feedforward neural models. Neurocomputing 1998, 20, 279–294. [Google Scholar] [CrossRef] [Green Version]
- Shah, S.; Palmieri, F. Meka–a fast, local algorithm for training feedforward neural networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), San Diego, CA, USA, 17–21 June 1990; pp. 41–46. [Google Scholar]
- Puskorius, G.V.; Feldkamp, L.A. Decoupled extended kalman filter training of feedforward layered networks. In Proceedings of the International Joint Conference on Neural Networks, Seattle, WA, USA, 8–12 July 1991; pp. 771–777. [Google Scholar]
- Nishiyama, K.; Suzuki, K. H∞-learning of layered neural networks. IEEE Trans. Neural Netw. 2001, 12, 1265–1277. [Google Scholar] [CrossRef]
- Azimi-Sadjadi, R.; Liou, R.J. Fast learning process of multilayer neural networks using recursive least squares method. IEEE Trans. Signal Process. 1992, 40, 446–450. [Google Scholar] [CrossRef]
- Bilski, J.; Rutkowski, L. A fast training algorithm for neural networks. IEEE Trans. Circuits Syst.–II 1998, 45, 749–753. [Google Scholar] [CrossRef]
- Leung, C.S.; Tsoi, A.C.; Chan, L.W. Two regularizers for recursive least square algorithms in feedforward multilayered neural networks. IEEE Trans. Neural Netw. 2001, 12, 1314–1332. [Google Scholar] [CrossRef]
- Xu, Y.; Wong, K.-W.; Leung, C.-S. Generalized RLS approach to the training of neural networks. IEEE Trans. Neural Netw. 2006, 17, 19–34. [Google Scholar] [CrossRef]
- Stan, O.; Kamen, E. A local linearized least squares algorithm for training feedforward neural networks. IEEE Trans. Neural Netw. 2000, 11, 487–495. [Google Scholar] [CrossRef] [PubMed]
- Parisi, R.; Claudio, E.D.D.; Orlandim, G.; Rao, B.D. A generalized learning paradigm exploiting the structure of feedforward neural networks. IEEE Trans. Neural Netw. 1996, 7, 1450–1460. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Ji, C.; Farmer, J. An efficient em-based training algorithm for feedforward neural networks. Neural Netw. 1997, 10, 243–256. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.I. Information geometry of the em and em algorithms for neural networks. Neural Netw. 1995, 8, 1379–1408. [Google Scholar] [CrossRef]
- Kosko, B.; Audhkhasi, K.; Osoba, O. Noise can speed backpropagation learning and deep bidirectional pretraining. Neural Netw. 2020, 129, 359–384. [Google Scholar] [CrossRef]
- Adigun, O.; Kosko, B. Noise-boosted bidirectional backpropagation and adversarial learning. Neural Netw. 2019, 120, 1–204. [Google Scholar] [CrossRef] [PubMed]
- Martens, J. New insights and perspectives on the natural gradient method. J. Mach. Learn. Res. 2020, 21, 1–76. [Google Scholar]
- Gonzalez, A.; Dorronsoro, J.R. Natural conjugate gradient training of multilayer perceptrons. Neurocomputing 2008, 71, 2499–2506. [Google Scholar] [CrossRef]
- Baermann, F.; Biegler-Koenig, F. On a class of efficient learning algorithms for neural networks. Neural Netw. 1992, 5, 139–144. [Google Scholar] [CrossRef]
- Scalero, R.S.; Tepedelenlioglu, N. A fast new algorithm for training feedforward neural networks. IEEE Trans. Signal Process. 1992, 40, 202–210. [Google Scholar] [CrossRef]
- Ergezinger, S.; Thomsen, E. An accelerated learning algorithm for multilayer perceptrons: Optimization layer by layer. IEEE Trans. Neural Netw. 1995, 6, 32–42. [Google Scholar] [CrossRef]
- Hunt, S.D.; Deller, J.R., Jr. Selective training of feedforward artificial neural networks using matrix perturbation theory. Neural Netw. 1995, 8, 931–944. [Google Scholar] [CrossRef]
- Rubanov, N.S. The layer-wise method and the backpropagation hybrid approach to learning a feedforward neural network. IEEE Trans. Neural Netw. 2000, 11, 295–305. [Google Scholar] [CrossRef] [PubMed]
- Manry, M.T.; Apollo, S.J.; Allen, L.S.; Lyle, W.D.; Gong, W.; Dawson, M.S.; Fung, A.K. Fast training of neural networks for remote sensing. Remote Sens. Rev. 1994, 9, 77–96. [Google Scholar] [CrossRef]
- Chen, H.H.; Manry, M.T.; Chandrasekaran, H. A neural network training algorithm utilizing multiple sets of linear equations. Neurocomputing 1999, 25, 55–72. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Manry, M.T.; Li, J.; Narasimha, P.L. An efficient hidden layer training method for the multilayer perceptron. Neurocomputing 2006, 70, 525–535. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Wang, K. Parameter by parameter algorithm for multilayer perceptrons. Neural Process. Lett. 2006, 23, 229–242. [Google Scholar] [CrossRef]
- Yu, X.; Efe, M.O.; Kaynak, O. A general backpropagation algorithm for feedforward neural networks learning. IEEE Trans. Neural Netw. 2002, 13, 251–254. [Google Scholar] [PubMed]
- Behera, L.; Kumar, S.; Patnaik, A. On adaptive learning rate that guarantees convergence in feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1116–1125. [Google Scholar] [CrossRef]
- Man, Z.; Wu, H.R.; Liu, S.; Yu, X. A new adaptive backpropagation algorithm based on Lyapunov stability theory for neural networks. IEEE Trans. Neural Netw. 2006, 17, 1580–1591. [Google Scholar]
- Brouwer, R.K. Training a feed-forward network by feeding gradients forward rather than by back-propagation of errors. Neurocomputing 1997, 16, 117–126. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.S.; Cohen, D.A. Linear programming algorithm for neural networks. Neural Netw. 1990, 3, 575–582. [Google Scholar] [CrossRef] [Green Version]
- Stoeva, S.; Nikov, A. A fuzzy backpropagation algorithm. Fuzzy Sets Syst. 2000, 112, 27–39. [Google Scholar] [CrossRef]
- Nikov, A.; Stoeva, S. Quick fuzzy backpropagation algorithm. Neural Netw. 2001, 14, 231–244. [Google Scholar] [CrossRef]
- Tao, P.; Cheng, J.; Chen, L. Brain-inspired chaotic backpropagation for MLP. Neural Netw. 2022, 155, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Delgado, M.; Mantas, C.J.; Moraga, C. A fuzzy rule based backpropagation method for training binary multilayer perceptron. Inf. Sci. 1999, 113, 1–17. [Google Scholar] [CrossRef]
- Castro, J.L.; Delgado, M.; Mantas, C.J. A fuzzy rule-based algorithm to train perceptrons. Fuzzy Sets Syst. 2001, 118, 359–367. [Google Scholar] [CrossRef]
- Wang, D.; Chaudhari, N.S. Binary neural network training algorithms based on linear sequential learning. Int. J. Neural Syst. 2003, 5, 333–351. [Google Scholar] [CrossRef] [PubMed]
- Burr, J. Digital neural network implementations. In Neural Networks, Concepts, Applications, and Implementations; Prentice Hall.: Englewood Cliffs, NJ, USA, 1991; Volume III. [Google Scholar]
- Holt, J.; Hwang, J. Finite precision error analysis of neural network hardware implementations. IEEE Trans. Comput. 1993, 42, 281–290. [Google Scholar] [CrossRef] [Green Version]
- Bolt, G.R. Fault models for artifical neural networks. In Proceedings of the IJCNN’91, Singapore, 18–21 November 1991; pp. 1373–1378. [Google Scholar]
- Bolt, G.R.; Austin, J.; Morgan, G. Fault Tolerant Multi-Layer Perceptron Networks; Tech. Rep. YCS-92-180; Department of Computer Science, University of York: York, UK, 1992. [Google Scholar]
- Chiu, C.T.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Modifying training algorithms for improved fault tolerance. In Proceedings of the ICNN’94, Orlando, FL, USA, 28 June 1994–2 July 1994; pp. 333–338. [Google Scholar]
- Murray, A.F.; Edwards, P.J. Enhanced mlp performance and fault tolerance resulting from synaptic weight noise during training. IEEE Trans. Neural Netw. 1994, 5, 792–802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phatak, D.S.; Koren, I. Complete and partial fault tolerance of feedforward neural nets. IEEE Trans. Neural Netw. 1995, 6, 446–456. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Chen, S.F.; Chen, Z.Q. Improving tolerance of neural networks against multi-node open fault. In Proceedings of the IJCNN’01, Washington, DC, USA, 15–19 July 2001; pp. 1687–1692. [Google Scholar]
- Sequin, C.H.; Clay, R.D. Fault tolerance in feedforward artificial neural networks. Neural Netw. 1990, 4, 111–141. [Google Scholar]
- Cavalieri, S.; Mirabella, O. A novel learning algorithm which improves the partial fault tolerance of multilayer neural networks. Neural Netw. 1999, 12, 91–106. [Google Scholar] [CrossRef] [PubMed]
- Hammadi, N.C.; Ito, H. A learning algorithm for fault tolerant feedforward neural networks. IEICE Trans. Inf. Syst. 1997, 80, 21–26. [Google Scholar]
- Emmerson, M.D.; Damper, R.I. Determining and improving the fault tolerance of multilayer perceptrons in a pattern-recognition application. IEEE Trans. Neural Netw. 1993, 4, 788–793. [Google Scholar] [CrossRef]
- Neti, C.; Schneider, M.H.; Young, E.D. Maximally fault tolerance neural networks. IEEE Trans. Neural Netw. 1992, 3, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Simon, D.; El-Sherief, H. Fault-tolerance training for optimal interpolative nets. IEEE Trans. Neural Netw. 1995, 6, 1531–1535. [Google Scholar] [CrossRef]
- Phatak, D.S.; Tchernev, E. Synthesis of fault tolerant neural networks. In Proceedings of the IJCNN’02, Honolulu, HI, USA, 12–17 May 2002; pp. 1475–1480. [Google Scholar]
- Zhou, Z.H.; Chen, S.F. Evolving fault-tolerant neural networks. Neural Comput. Appl. 2003, 11, 156–160. [Google Scholar] [CrossRef]
- Leung, C.S.; Sum, J. A fault-tolerant regularizer for rbf networks. IEEE Trans. Neural Netw. 2008, 19, 493–507. [Google Scholar] [CrossRef] [Green Version]
- Bernier, J.L.; Ortega, J.; Rodriguez, M.M.; Rojas, I.; Prieto, A. An accurate measure for multilayer perceptron tolerance to weight deviations. Neural Process. Lett. 1999, 10, 121–130. [Google Scholar] [CrossRef]
- Bernier, J.L.; Ortega, J.; Rojas, I.; Ros, E.; Prieto, A. Obtaining fault tolerance multilayer perceptrons using an explicit regularization. Neural Process. Lett. 2000, 12, 107–113. [Google Scholar] [CrossRef]
- Bernier, J.L.; Ortega, J.; Rojas, I.; Ros, E.; Prieto, A. A quantitative study of fault tolerance, noise immunity and generalization ability of MLPs. Neural Comput. 2000, 12, 2941–2964. [Google Scholar] [CrossRef]
- Bernier, J.L.; Ortega, J.; Rojas, I.; Ros, E.; Prieto, A. Improving the tolerance of multilayer perceptrons by minimizing the statistical sensitivity to weight deviations. Neurocomputing 2000, 31, 87–103. [Google Scholar] [CrossRef]
- Bernier, J.L.; Diaz, A.F.; Fernandez, F.J.; Canas, A.; Gonzalez, J.; Martin-Smith, P.; Ortega, J. Assessing the noise immunity and generalization of radial basis function networks. Neural Process. Lett. 2003, 18, 35–48. [Google Scholar] [CrossRef]
- Stevenson, M.; Winter, R.; Widrow, B. Sensitivity of feedfoward neural networks to weight errors. IEEE Trans. Neural Netw. 1990, 1, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Piche, S.W. The selection of weight accuracies for madalines. IEEE Trans. Neural Netw. 1995, 6, 432–445. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Wang, Y.; Zhang, K. Computation of adalines’ sensitivity to weight perturbation. IEEE Trans. Neural Netw. 2006, 17, 515–519. [Google Scholar] [CrossRef] [PubMed]
- Catala, M.A.; Parra, X.L. Fault tolerance parameter model of radial basis function networks. In Proceedings of the IEEE ICNN’96, Washington, DC, USA, 3–6 June 1996; pp. 1384–1389. [Google Scholar]
- Yang, S.H.; Ho, C.H.; Siu, S. Sensitivity analysis of the split-complex valued multilayer perceptron due to the errors of the i.i.d. inputs and weights. IEEE Trans. Neural Netw. 2007, 18, 1280–1293. [Google Scholar] [CrossRef]
- Kamiura, N.; Isokawa, T.; Hata, Y.; Matsui, N.; Yamato, K. On a weight limit approach for enhancing fault tolerance of feedforward neural networks. IEICE Trans. Inf. Syst. 2000, 83, 1931–1939. [Google Scholar]
- Simon, D. Distributed fault tolerance in optimal interpolative nets. IEEE Trans. Neural Netw. 2001, 12, 1348–1357. [Google Scholar] [CrossRef]
- Parra, X.; Catala, A. Fault tolerance in the learning algorithm of radial basis function networks. In Proceedings of the IJCNN 2000, Como, Italy, 24–27 July 2000; pp. 527–532. [Google Scholar]
- Sum, J.; Leung, C.S.; Ho, K. On objective function, regularizer and prediction error of a learning algorithm for dealing with multiplicative weight noise. IEEE Trans. Neural Netw. 2009, 20, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Le Cun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. In Advances in Neural Information Processing Systems; Touretzky, D.S., Ed.; Morgan Kaufmann: San Mateo, CA, USA, 1989; Volume 2, pp. 396–404. [Google Scholar]
- Mohamed, A.; Dahl, G.; Hinton, G. Deep belief networks for phone recognition. In Proceedings of the NIPS Workshop on Deep Learning for Speech Recognition and Related Applications, Whistler, BC, Canada, 12 December 2009. [Google Scholar]
- Larochelle, H.; Bengio, Y.; Louradour, J.; Lamblin, P. Exploring strategies for training deep neural networks. J. Mach. Learn. Res. 2009, 1, 1–40. [Google Scholar]
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.-A.; Vincent, P.; Bengio, S. Why does unsupervised pre-training help deep learning? J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Bejani, M.M.; Ghatee, M. Theory of adaptive SVD regularization for deep neural networks. Neural Netw. 2020, 128, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Cheng, Q.; Li, H.; Wu, Q.; Ma, L.; Ngan, K.N. Parametric deformable exponential linear units for deep neural networks. Neural Netw. 2020, 125, 281–289. [Google Scholar] [CrossRef]
- Mhaskar, H.N.; Poggio, T. An analysis of training and generalization errors in shallow and deep networks. Neural Netw. 2020, 121, 229–241. [Google Scholar] [CrossRef]
- Zou, D.; Cao, Y.; Zhou, D.; Gu, Q. Gradient descent optimizes over-parameterized deep ReLU networks. Mach. Learn. 2020, 109, 467–492. [Google Scholar] [CrossRef]
- Martin, C.H.; Mahoney, M.W. Implicit self-regularization in deep neural networks: Evidence from random matrix theory and implications for learning. J. Mach. Learn. Res. 2021, 22, 1–73. [Google Scholar]
- Semenova, N.; Larger, L.; Brunner, D. Understanding and mitigating noise in trained deep neural networks. Neural Netw. 2022, 146, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Liu, Z.; Zhang, T.; Yuan, T. Non-differentiable saddle points and sub-optimal local minima exist for deep ReLU networks. Neural Netw. 2021, 144, 75–89. [Google Scholar] [CrossRef] [PubMed]
- Petzka, H.; Sminchisescu, C. Non-attracting regions of local minima in deep and wide neural networks. J. Mach. Learn. Res. 2021, 22, 1–34. [Google Scholar]
- Mingard, C.; Valle-Perez, G.; Skalse, J.; Louis, A.A. Is SGD a Bayesian sampler? Well, almost. J. Mach. Learn. Res. 2021, 22, 1–64. [Google Scholar]
- Chester, D.L. Why two hidden layers are better than one. In Proceedings of the International Joint Conference on Neural Networks, Washington, DC, USA, 15–19 January 1990; pp. 265–268. [Google Scholar]
- Trenn, S. Multilayer perceptrons: Approximation order and necessary number of hidden units. IEEE Trans. Neural Netw. 2008, 19, 836–844. [Google Scholar] [CrossRef] [Green Version]
- Huang, C. ReLU networks are universal approximators via piecewise linear or constant functions. Neural Comput. 2020, 32, 2249–2278. [Google Scholar] [CrossRef]
- Yarotsky, D. Error bounds for approximations with deep ReLU networks. Neural Netw. 2017, 94, 103–114. [Google Scholar] [CrossRef] [Green Version]
- Dung, D.; Nguyen, V.K. Deep ReLU neural networks in high-dimensional approximation. Neural Netw. 2021, 142, 619–635. [Google Scholar] [CrossRef]
- Elbrachter, D.; Perekrestenko, D.; Grohs, P.; Bolcskei, H. Deep Neural Network Approximation Theory. IEEE Trans. Inf. Theory 2021, 67, 2581–2623. [Google Scholar] [CrossRef]
- Wiatowski, T.; Bolcskei, H. A Mathematical Theory of Deep Convolutional Neural Networks for Feature Extraction. IEEE Trans. Inf. Theory 2018, 64, 1845–1866. [Google Scholar] [CrossRef] [Green Version]
- Baldi, P.; Vershynin, R. The capacity of feedforward neural networks. Neural Netw. 2019, 116, 288–311. [Google Scholar] [CrossRef] [Green Version]
- Mhaskar, H.N. Dimension independent bounds for general shallow networks. Neural Netw. 2020, 123, 142–152. [Google Scholar] [CrossRef] [Green Version]
- Ryck, T.D.; Lanthaler, S.; Mishra, S. On the approximation of functions by tanh neural networks. Neural Netw. 2021, 143, 732–750. [Google Scholar] [CrossRef] [PubMed]
- Illing, B.; Gerstner, W.; Brea, J. Biologically plausible deep learning—But how far can we go with shallow networks? Neural Netw. 2019, 118, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Nemoto, I.; Kubono, M. Complex associative memory. Neural Netw. 1996, 9, 253–261. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, H.; Liu, L. Convergence analysis of three classes of split-complex gradient algorithms for complex-valued recurrent neural networks. Neural Comput. 2010, 22, 2655–2677. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, H. Adaptive complex-valued stepsize based fast learning of complex-valued neural networks. Neural Netw. 2020, 124, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Du, K.-L.; Swamy, M.N.S. Search and Optimization by Metaheuristics; Springer: New York, NY, USA, 2016. [Google Scholar]


| Algorithm | Mean Epochs | Training MSE | Classifier Accuracy (%) | Std | Mean Training Time (s) | Std (s) |
|---|---|---|---|---|---|---|
| RP | ||||||
| LM | ||||||
| BFGS | ||||||
| OSS | ||||||
| SCG | ||||||
| CGB | ||||||
| CGF | ||||||
| CGP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.-L.; Leung, C.-S.; Mow, W.H.; Swamy, M.N.S. Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics 2022, 10, 4730. https://doi.org/10.3390/math10244730
Du K-L, Leung C-S, Mow WH, Swamy MNS. Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics. 2022; 10(24):4730. https://doi.org/10.3390/math10244730
Chicago/Turabian StyleDu, Ke-Lin, Chi-Sing Leung, Wai Ho Mow, and M. N. S. Swamy. 2022. "Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era" Mathematics 10, no. 24: 4730. https://doi.org/10.3390/math10244730
APA StyleDu, K.-L., Leung, C.-S., Mow, W. H., & Swamy, M. N. S. (2022). Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics, 10(24), 4730. https://doi.org/10.3390/math10244730







