Concrelife: A Software to Solve the Chloride Penetration in Saturated and Unsaturated Reinforced Concrete
Abstract
:1. Introduction
2. The Governing Equations
2.1. Water-Saturated Concrete
2.2. Water-Unsaturated Concrete
| [42] | |
| [40] | |
| [27] |
3. The Code Concrelife
3.1. The Screens of Input Data
3.2. Simulation and Graphical Outputs
 , the model is generated by programming in the form of a text file, and NgSpice starts the simulation. This gives way to the presentation of the typical NgSpice software screen [46], where the percentage of time elapsed until complete computing is indicated. An auxiliary screen gives additional information in reference to the simulation number through which the computation progresses, Figure 11.
, the model is generated by programming in the form of a text file, and NgSpice starts the simulation. This gives way to the presentation of the typical NgSpice software screen [46], where the percentage of time elapsed until complete computing is indicated. An auxiliary screen gives additional information in reference to the simulation number through which the computation progresses, Figure 11.  accesses the graphical representation of the solutions through the screen of Figure 12. In this, the drop-down ‘Kind of representation’ allows to select between spatial representation of variables (‘Spatial’), in selected moments introduced in the drop-down ‘Time to represent’, and temporal representation of variables (‘Evolution’) at the location chosen in ‘Section to represent’ in the main screen, Figure 13a,b. The variables that can be represented for the saturated problem are (1) free chloride concentration in the solution (kg/m3), ‘Free Chloride concentration (Vol.)’; (2) free chloride concentration in concrete (kg/m3), ‘Free Chloride concentration’; (3) bounded chloride concentration in the concrete (kg/m3), ‘Bound Chloride concentration’; and (4) concrete porosity, ‘Porosity’. For the unsaturated problem, the previous variables plus (5) precipitated chloride concentration in concrete (kg/m3), ‘Precipitated Chloride concentration’; (6) volume fraction of the liquid phase in the pores, ‘Volume fraction of the liquid phase’; and (7) saturation degree, ‘Saturation degree’, Figure 14a,b.
accesses the graphical representation of the solutions through the screen of Figure 12. In this, the drop-down ‘Kind of representation’ allows to select between spatial representation of variables (‘Spatial’), in selected moments introduced in the drop-down ‘Time to represent’, and temporal representation of variables (‘Evolution’) at the location chosen in ‘Section to represent’ in the main screen, Figure 13a,b. The variables that can be represented for the saturated problem are (1) free chloride concentration in the solution (kg/m3), ‘Free Chloride concentration (Vol.)’; (2) free chloride concentration in concrete (kg/m3), ‘Free Chloride concentration’; (3) bounded chloride concentration in the concrete (kg/m3), ‘Bound Chloride concentration’; and (4) concrete porosity, ‘Porosity’. For the unsaturated problem, the previous variables plus (5) precipitated chloride concentration in concrete (kg/m3), ‘Precipitated Chloride concentration’; (6) volume fraction of the liquid phase in the pores, ‘Volume fraction of the liquid phase’; and (7) saturation degree, ‘Saturation degree’, Figure 14a,b.4. Applications
5. Final Comments and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saetta, A.V.; Scotta, R.V.; Vitaliani, R.V. Analysis of chloride diffusion into partially saturated concrete. ACI Mater. J. 1993, 90, 441–451. [Google Scholar]
- Liu, Y. Modeling the Time-to-Corrosion Cracking of the Cover Concrete in Chloride Contaminated Reinforced Concrete Structures. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1996. [Google Scholar]
- Liu, Y.; Weyers, R.E. Modeling the time to corrosion cracking in chloride contaminated reinforced concrete structures. ACI Mater. J. 1998, 95, 675–681. [Google Scholar]
- Guzman-Gutiérrez, S. Modelzación del Deterioro de Tableros de Puentes de Hormigón por Difusión de Cloruros y Corrosión de la Armadura Pasiva. Ph.D. Thesis, ETS de Ing. de Caminos Canales y Puertos, Madrid, Spain, 2010. [Google Scholar]
- Liang, M.T.; Huang, R.; Jheng, H.Y. Reconsideration for a study of the effect of the chloride binding on service life predictions. J. Mar. Sci. Technol. 2011, 19, 531–540. [Google Scholar] [CrossRef]
- Andrade, C.; Climent, M.A.; de Vera, G. Procedure for calculating the chloride diffusion coefficient and Surface concentration from a profile having a maximum beyong the concrete Surface. Mater. Struct. 2015, 48, 863–869. [Google Scholar] [CrossRef]
- Sanchez-Perez, J.F.; Hidalgo, P.; Alhama, I. Concrelife. Cementos la Cruz. Registration Requested on October 1, 2019. Nº 08/2019/743 [Software]. 2019. [Google Scholar]
- Horno, J.; García-Hernández, M.T.; González-Fernández, C.F. Digital simulation of electrochemical processes by the network approach. J. Electroanal. Chem. 1993, 352, 83–97. [Google Scholar] [CrossRef]
- González Fernández, C.F.; Alhama, F.; Horno, J.; López García, J.J. Network Simulation Method; Montijano, J.H., Ed.; Research Signpost: Trvandrum, India, 2003. [Google Scholar]
- Sánchez-Pérez, J.F.; Marín, F.; Morales, J.L.; Cánovas, M.; Alhama, F. Modeling and simulation of different and representative engineering problems using Network Simulation Method. PLoS ONE 2018, 13, e0193828. [Google Scholar] [CrossRef] [Green Version]
- Alhama, I.; Soto, A. FATSIM-A: Fluid Flow and Solute Transport Simulator. Universidad Politécnica de Cartagena. Nº Mu-1093-2010 [Software]. 2010. [Google Scholar]
- Sanchez-Perez, J.F.; Alhama, I.; García-Ros, G. SICOMED_3D (Simulación de consolidación con mechas drenantes). Universidad Politécnica de Cartagena. Registration requested on 28 November 2016. Nº 08/2017/196 [software]. 2016. [Google Scholar]
- Alhama, F.; Alhama, I.; Sanchez-Perez, J.F.; Morales-Guerrrero, J.L. CODENS_13 (Coupled Ordinary Differencial Equations by Network Simulation). Universidad Politécnica de Cartagena. Registration Requested on 16 January 2014. Nº 08/2014/56 [Software]. 2014. [Google Scholar]
- Sanchez-Perez, J.F.; Moreno, J.A.; Alhama, F. OXIPSIS_12 (Oxidation Processes Simulation Software). Universidad Politécnica de Cartagena. Registration requested on 13 July, 2013. Nº 08/2013/616 [software]. 2013. [Google Scholar]
- Alhama, I.; Soto, A.; Alhama, F. FATSIM-A: An educational tool based on electrical analogy and the code PSPICE to simulate fluid flow and solute transport processes. Comput. Appl. Eng. Educ. 2011, 16, 72–84. [Google Scholar]
- Sánchez-Pérez, J.F.; Alhama, F.; Moreno, J.A. An efficient and reliable model based on network method to simulate CO2 corrosion with protective iron carbonate films. Comput. Chem. Eng. 2012, 39, 57–64. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Moreno, J.A.; Alhama, F. Numerical Simulation of High-Temperature Oxidation of Lubricants Using the Network Method. Chem. Eng. Commun. 2015, 202, 982–991. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Conesa, M.; Alhama, I. Solving ordinary differential equations by electrical analogy: A multidisciplinary teaching tool. Eur. J. Phys. 2016, 37, 065703. [Google Scholar] [CrossRef]
- Alhama, I.; García-Ros, G.; Alhama, F. Universal solution for the characteristic time and the degree of settlement in nonlinear soil consolidation scenarios. A deduction based on nondimensionalization. Commun. Nonlinear Sci. Numer. Simular. 2018, 57, 186–201. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Alhama, F.; Moreno, J.A.; Canovas, M. Study of main parameters affecting pitting corrosion in a basic medium using the network method. Results Phys. 2019, 12, 1015–1025. [Google Scholar] [CrossRef]
- Martín-Pérez, B.; Zibara, H.; Hooton, R.D.; Thomas, M.D. A study of the effect of chloride binding on service life predictions. Cem. Concr. Res. 2000, 30, 1215–1223. [Google Scholar] [CrossRef]
- Martín-Pérez, B.; Pantazopoulou, S.J.; Thomas, M.D.A. Numerical solution of mass transport equations in concree sructures. Comput. Struct. 2001, 79, 1251–1264. [Google Scholar] [CrossRef] [Green Version]
- Meijers, S.J.H.; Bijen, J.M.; de Borst, R.; Fraaij, A.L.A. Computational results of a model for chloride ingress in concrete including convection, dry-wetting cycles and carbonatation. Mater. Struct. 2005, 38, 145–154. [Google Scholar] [CrossRef]
- Garcés, P.; Saura, P.; Mendez, A.; Zornoza, E.; Andrade, C. Effect of nitrite in corrosion of reinforcing steel in neutral and acid solutions simulating the electrolytic environments of micropores of concrete in the propagation period. Corros. Sci. 2008, 50, 498–509. [Google Scholar] [CrossRef]
- Iqbal, P.O.; Ishida, T. Modelling of chloride transport coupled with enhanced moisture coductivity in concrete exposed to marine environment. Cem. Concr. Res. 2009, 39, 329–339. [Google Scholar] [CrossRef]
- Solano-Rodríguez, S.A.; Estupiñán-Durán, H.A.; Vásquez-Quintero, C.; Peña-Ballesteros, D.Y. Simulation of ion cl- diffusion until depassivation of reinforcing steel in concrete with microsilica as additive and exposed to carbonation. Boletín Ciencias de la Tierra 2013, 34, 15–24. [Google Scholar]
- Fenaux, M. Modelling of Chloride Transport in Non-Saturated Concrete. From Microscale to Macroscale. Ph.D. Thesis, ETS de Ing. de Caminos Canales y Puertos, Madrid, Spain, 2013. [Google Scholar]
- Gálvez, J.C.; Guzmán, S.; Sancho, J.M. Cover cracking of the reinforced concrete due to rebar corrosion induced by chloride penetration. In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures (FraMCoS), Toledo, Spain, 10–14 March 2014. [Google Scholar]
- Lehner, P.; Konecny, P.; Ghosh, P.; Tran, Q. Numerical analysis of chloride diffusion considering time-dependent diffusion coefficient. Int. J. Math. Comput. Simul. 2014, 8, 102–106. [Google Scholar]
- EN 12390-11:2015. Testing Hardened Concrete. Determination of the Chloride Resistance of Concrete, Unidirectional Diffusion. Available online: https://www.une.org/ (accessed on 13 September 2019).
- Marchand, J.; Gerard, B.; Delagrave, A. Ion transport mechanisms in cement-based materials. In Material Science of Concrete; American Ceramic Society: Westerville, OH, USA, 1998; Volume 5, pp. 307–400. [Google Scholar]
- Jensen, O.M.; Hansen, P.F.; Coats, A.M.; Glasser, F.P. Chloride ingress in cement paste and mortar. Cem. Concr. Res. 1999, 29, 1497–1504. [Google Scholar] [CrossRef]
- Jooss, M.; Reinhardt, H.W. Permeability of diffusivity of concrete as function of temperature. Cem. Res. Concr. 2002, 32, 1497–1504. [Google Scholar] [CrossRef]
- Seidell, A. Solubilities of Inorganic and Metal Organic Compounds, Volume 1; D. Van Nostrand Company Inc.: New York, NY, USA, 1940. [Google Scholar]
- McCutcheon, S.C.; Martin, J.L.; Barnwell, T.O. Water Quality. In Handbook of Hydrology; Maidment, D.D., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Boufadel, M.C.; Suidan, M.T.; Venosa, A.D. A numerical model for density-and-viscosity-dependent flows in two-dimensional variably satured porous media. J. Contam. Hydrol. 1999, 37, 1–20. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Modeling the effect of temperature on ionic transport in cementittious material. Cem. Concr. Res. 2007, 37, 455–468. [Google Scholar] [CrossRef]
- Guimarăes, A.T.C.; Climent, M.A.; de Vera, G.; Vicente, F.J.; Rodrigues, F.T.; Andrade, C. Determination of chloride difussivity through partially saturated Portland cement concrete by a simplified procedure. Constr. Build. Mater. 2011, 25, 785–790. [Google Scholar] [CrossRef]
- Pradelle, S.; Thiery, M.; Véronique-Baroghel, B. Comparison of existing chloride ingress models within concretes exposed to seawater. Mater. Struct. 2016, 49, 4497–4516. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturared soils. Soil Sci. Soc. Am. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Kestin, J.; Khalifa, H.E.; Correia, R.J. figures of dynamic and kinematic viscosity of aqueous NaCl solutions in the temperature range 20–150 °C and pressure range 0.1–35 MPa. J. Phys. Chem. Ref. Data 1983, 10, 817–820. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. Irrigation and drainage division. Proc. Am. Soc. Civ. Eng. 1966, 92, 61–88. [Google Scholar]
- Matlab Software® [on line]. (Quoted 2019). Available online: https://es.mathworks.com/products/matlab.html (accessed on 4 November 2022).
- Hidalgo, P. Modelización y Simulación del Transporte de Cloruros en Estructuras de Hormigón Armado para Ambientes Marinos. Ph.D. Thesis, Universidad Politécnica de Cartagena (UPCT), Cartagena, España, 2020. [Google Scholar]
- Nagel, L.W. SPICE2: A Computer Program to Simulate Semiconductor Circuits; University of California Berkeley: Berkeley, CA, USA, 1975. [Google Scholar]
- NgSpice Software [on line]. (Quoted 2019). Available online: http://ngspice.sourceforge.net/index.html (accessed on 4 November 2022).
- Abdelkader, M. Influencia de la Composición de Distintos Hormigones en los Mecanismos de Transporte de Iones Agresivos Procedentes de Medios Marinos. Ph.D. Thesis, ETS de Ing. de Caminos Canales y Puertos, Madrid, Spain, 2010. [Google Scholar]
- Comité Euro-International d’Beton. Draft CEB Guide to Durable Concrete Structures. Bull. D'inform. 1985, 166. Available online: https://www.fib-international.org/publications/ceb-bulletins/draft-ceb-guide-to-durable-concrete-structures-detail.html (accessed on 4 November 2022).
- RILEM Committee 60-CSG, Corrosion of Steel in Concrete, State of Art Report; Schiessl, P. (Ed.) Chapman and Hall: London, UK, 1987. [Google Scholar]
- Andrade, C.; Prieto, M.; Tanner, P.; Tavares, F.; d’Andrea, R. Testing and modelling chloride penetration into concrete. Constr. Build. Mater. 2013, 39, 9–18. [Google Scholar] [CrossRef]
- CDTI. Centro para el Desarrollo Tecnológico Industrial. Ministry of Science and Competitiveness (Spain). Equipo para la determinación de la vida útil de las estructuras de hormigón armado—Concrelife. Funding Reference Number IDI-20170080. 2017. [Google Scholar]
- Cementos la Cruz [on line]. (Quoted 2019). Available online: https://www.cementoscruz.com/ (accessed on 4 November 2022).
- Universidad Politécnica de Cartagena (UPCT). Unidad de Investigación y Transferencia Tecnologica (UITT) [on line]. (Quoted 2019). Available online: https://www.upct.es/uitt/es/inicio/ (accessed on 4 November 2022).
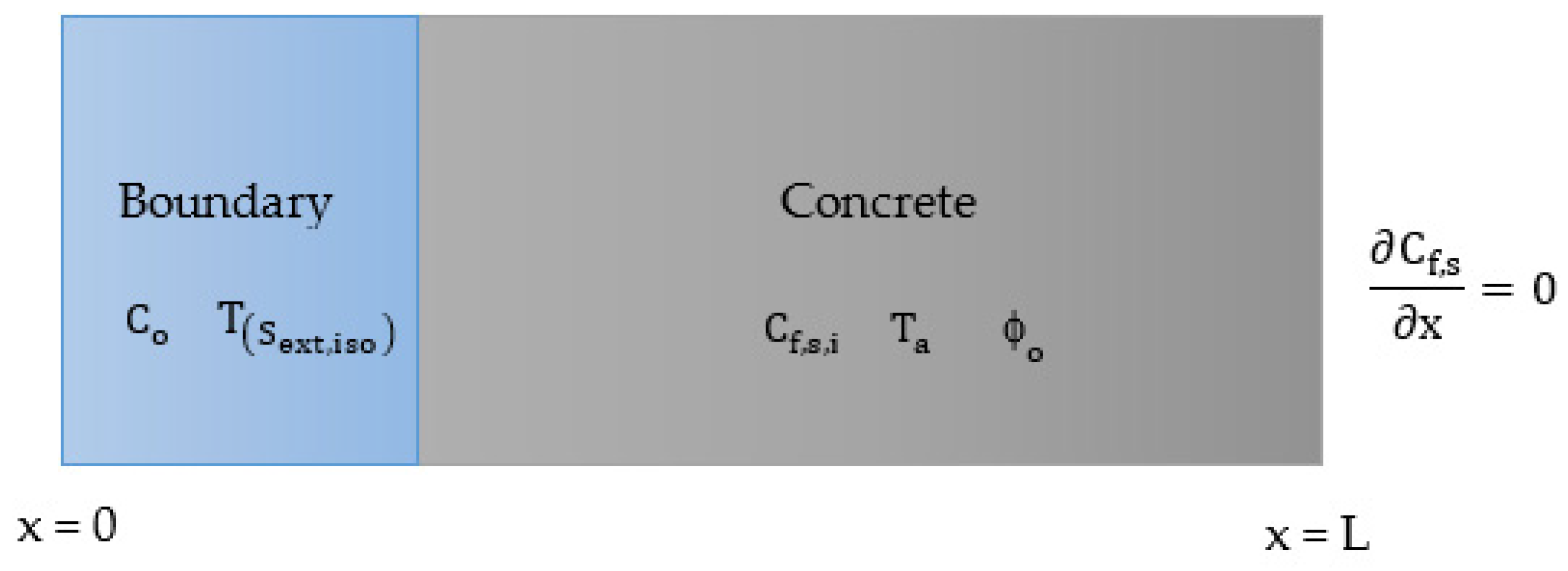
























| Heat Transport | |
|---|---|
| Governing equation: | |
| (1) | |
| Boundary conditions: | (2) |
| , at adiabatic contour | (3) |
| Initial condition: | |
| at the domain | (4) |
| Chloride transport | |
| Governing equation: | |
| (5) | |
| (6) | |
| (7) | |
| (8) | |
| (9) | |
| (10) | |
| (11) | |
| (12) | |
| (13) | |
| Isotherms: | |
| (linear) | (14a) |
| (Langmuir) | (14b) |
| (Freundlich) | (14c) |
| (Langmuir-Freundlich) | (14d) |
| Boundary conditions: | |
| (15) | |
| (16) | |
| Initial conditions: | |
| (17) | |
| (18) |
| Heat transport: | |
| Equations (1) to (4), Table 1 | |
| Chloride transport: | |
| Governing equation: | |
| (19) | |
| (20) | |
| (21) | |
| Equation (6), (7) and (9) to (12) | |
| (22) | |
| (23) | |
| (24) | |
| (25) | |
| (26) | |
| (27) | |
| Equations (14a) to (14d), Table 1 (water-saturated) | |
| Boundary conditions: | |
| Equations (15) and (16), Table 1 (saturated) | |
| (28) | |
| Initial conditions: | |
| Equation (17), Table 1 (saturated) | |
| (29) | |
| (30) |
| Common Parameters | ||||
|---|---|---|---|---|
| Rg = 8.31 J/mol K | Ea = 19,805 J | Cf,s,sat,(20 °C) = 192 kg/m3 | ρps = 2165 kg/m3 | ρps = 1892 kg/m3 |
| Co = 18.59 kg/m3 solution for 18 months | ||||
| φo = 0.134 | Dexp = 5.33 × 10−12 m2/s | L = 0.2 m | Ct,i = 0.038 kg/m3 concrete | |
| Bound chloride parameters for Langmuir–Freundlich isotherm | ||||
| Cbo = 11.895 Kg/m3 concrete | K = 1.1007 | α = 0.5639 | ||
| Temperature parameters | ||||
| Ta = 20 °C | αT = 7 × 10−7 m2/s | |||
| Experimental data [27,47] | ||||
| Distance (mm) | Free chlorides (kg/m3 concrete) | Bound chlorides (kg/m3 concrete) | Total chlorides (kg/m3 concrete) | |
| 6.430 | 1.8800 | 7.2694 | 9.1494 | |
| 9.495 | 1.6512 | 7.0625 | 8.7137 | |
| 12.160 | 1.4421 | 6.8359 | 8.2780 | |
| 14.580 | 1.2439 | 6.5984 | 7.8423 | |
| Distance (mm) | Free Chlorides (kg/m3 Concrete) | Bound Chlorides (kg/m3 Concrete) | Total Chlorides (kg/m3 Concrete) | |||
|---|---|---|---|---|---|---|
| Experimental | Simulation | Experimental | Simulation | Experimental | Simulation | |
| 6.430 | 1.8800 | 1.9140 (1.807%) | 7.2694 | 7.2508 (0.256%) | 9.1494 | 9.1648 (0.168%) |
| 9.495 | 1.6512 | 1.6638 (0.765%) | 7.0625 | 7.0423 (0.286%) | 8.7137 | 8.7062 (0.087%) |
| 12.160 | 1.4421 | 1.4571 (1.041%) | 6.8359 | 6.8296 (0.092%) | 8.2780 | 8.2867 (0.105%) |
| 14.580 | 1.2439 | 1.2804 (2.936%) | 6.5984 | 6.6072 (0.133%) | 7.8423 | 7.8876 (0.577%) |
| Common Parameters | |||||
|---|---|---|---|---|---|
| Rg = 8.31 J/mol K | Ea = 19,805 J | Cf,s,sat,(20 °C) = 192 kg/m3 | ρps = 2165 kg/m3 | ρps = 1892 kg/m3 | |
| Co = 19.455 kg/m3 solution for 0 ≤ t ≤ 5 years | Co = 1 kg/m3 solution for t > 5 years | ||||
| φo = 0.1 | Dexp = 9.35 × 10−11 m2/s | L = 0.2 m | Cf,s,i = 0 kg/m3 | ||
| Bound chloride parameters for Langmuir–Freundlich isotherm | |||||
| Cbo = 12.5366 Kg/m3 concrete | K = 0.6934 | α = 0.9451 | |||
| Temperature parameters | |||||
| Ta = 10 °C | αT = 7 × 10−7 m2/s | ||||
| External temperature | |||||
| Month | (°C) | Month | (°C) | Month | (°C) |
| 1 | 10 | 5 | 15 | 9 | 18 |
| 2 | 11 | 6 | 17 | 10 | 17 |
| 3 | 11 | 7 | 18 | 11 | 15 |
| 4 | 13 | 8 | 19 | 12 | 11 |
| Common Parameters | |||||
|---|---|---|---|---|---|
| Rg = 8.31 J/mol K | Ea = 19,805 J | Cf,s,sat,(20 °C) = 192 kg/m3 | ρps = 2165 kg/m3 | ρps= 1892 kg/m3 | |
| φo = 0.1 | Dexp = 8.30 × 10−11 m2/s | L = 0.1 m | Sat = 1 | ||
| Bound chloride parameters for Langmuir–Freundlich isotherm | |||||
| Cbo = 13.7835 Kg/m3 concrete | K = 0.8662 | α = 0.9068 | |||
| Parameters for diffusion coefficient and permeability | |||||
| e = 0.5331 (wet cycle) | e = 0.5331 (drying cycle) | ko = 2.45 × 10−21 m2 | |||
| Parameters for capillary pressure | |||||
| = 0.1 MPa (wet cycle) | = 0.1 MPa (drying cycle) | a1 = 3 (wet cycle) | a1 = 7 (drying cycle) | ||
| Concentration parameters | |||||
| Cf,s,i = 0 kg/m3 | |||||
| External concentration | |||||
| Month | Co (kg/m3 solution) | Month | Co (kg/m3 solution) | Month | Co (kg/m3 solution) |
| 1 | 19.455 | 5 | 1.822 × 10−8 | 9 | 19.455 |
| 2 | 19.455 | 6 | 1.822 × 10−8 | 10 | 1.822 × 10−8 |
| 3 | 19.455 | 7 | 19.455 | 11 | 1.822 × 10−8 |
| 4 | 1.822 × 10−8 | 8 | 19.455 | 12 | 1.822 × 10−8 |
| Temperature parameters | |||||
| Ta = 10 °C | αT = 7 × 10−7 m2/s | ||||
| External temperature | |||||
| Month | (°C) | Month | (°C) | Month | (°C) |
| 1 | 10 | 5 | 15 | 9 | 18 |
| 2 | 11 | 6 | 17 | 10 | 17 |
| 3 | 11 | 7 | 18 | 11 | 15 |
| 4 | 13 | 8 | 19 | 12 | 11 |
| Relative humidity parameters | |||||
| External relative humidity | |||||
| Month | hr | Month | hr | Month | hr |
| 1 | 1 | 5 | 0.3 | 9 | 1 |
| 2 | 1 | 6 | 0.7 | 10 | 0.5 |
| 3 | 1 | 7 | 1 | 11 | 0.4 |
| 4 | 0.4 | 8 | 1 | 12 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Pérez, J.F.; Hidalgo, P.; Alhama, F. Concrelife: A Software to Solve the Chloride Penetration in Saturated and Unsaturated Reinforced Concrete. Mathematics 2022, 10, 4810. https://doi.org/10.3390/math10244810
Sánchez-Pérez JF, Hidalgo P, Alhama F. Concrelife: A Software to Solve the Chloride Penetration in Saturated and Unsaturated Reinforced Concrete. Mathematics. 2022; 10(24):4810. https://doi.org/10.3390/math10244810
Chicago/Turabian StyleSánchez-Pérez, Juan Francisco, Pilar Hidalgo, and Francisco Alhama. 2022. "Concrelife: A Software to Solve the Chloride Penetration in Saturated and Unsaturated Reinforced Concrete" Mathematics 10, no. 24: 4810. https://doi.org/10.3390/math10244810
APA StyleSánchez-Pérez, J. F., Hidalgo, P., & Alhama, F. (2022). Concrelife: A Software to Solve the Chloride Penetration in Saturated and Unsaturated Reinforced Concrete. Mathematics, 10(24), 4810. https://doi.org/10.3390/math10244810










