Oscillation Attenuation in a Building-like Structure by Using a Flexible Vibration Absorber
Abstract
:1. Introduction
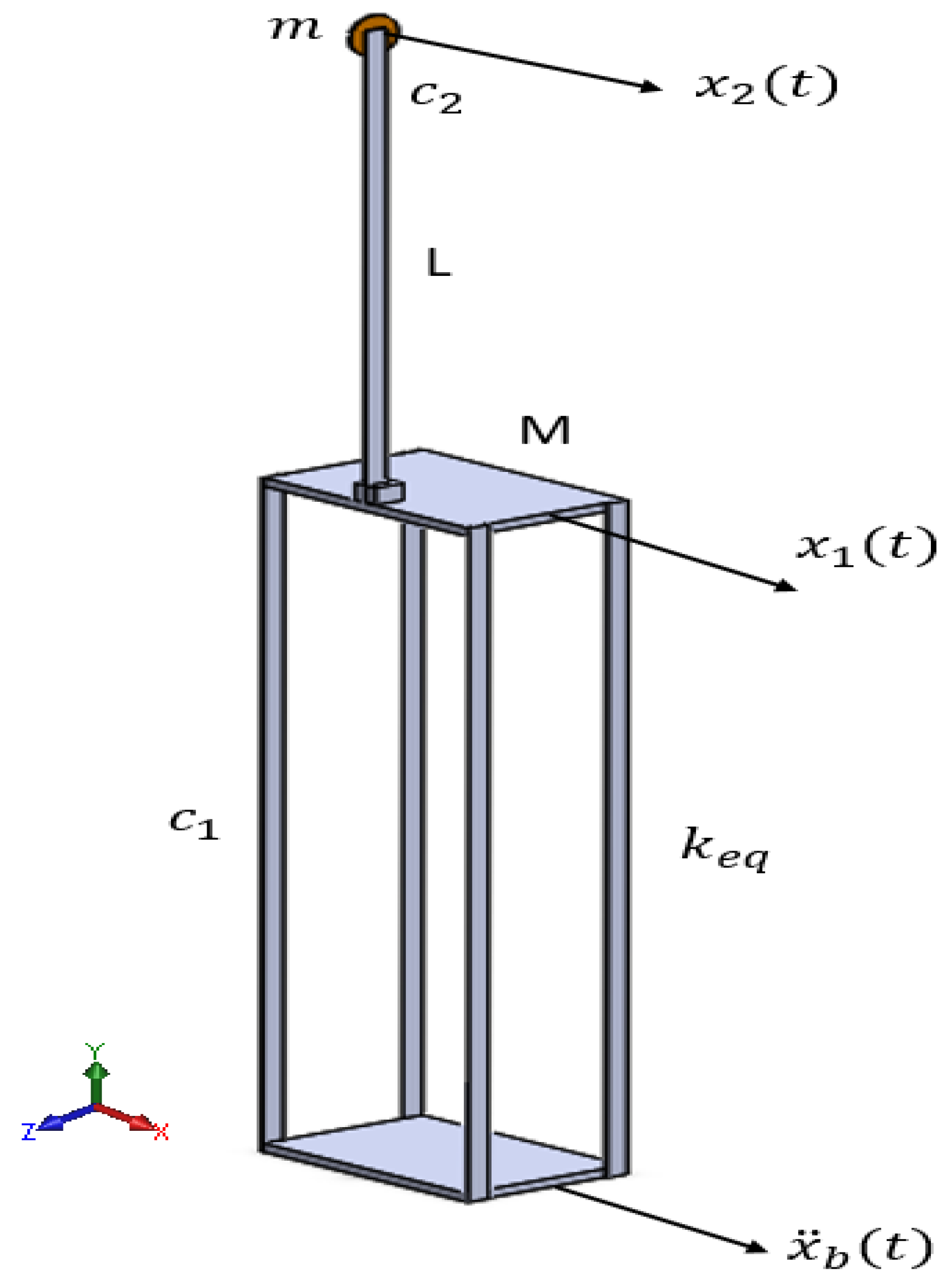
2. System Description
2.1. Equations of Motion
2.2. Tuning Condition
2.3. Other Possible Configurations of Flexible Vibration Absorber
- Configuration
- Configuration
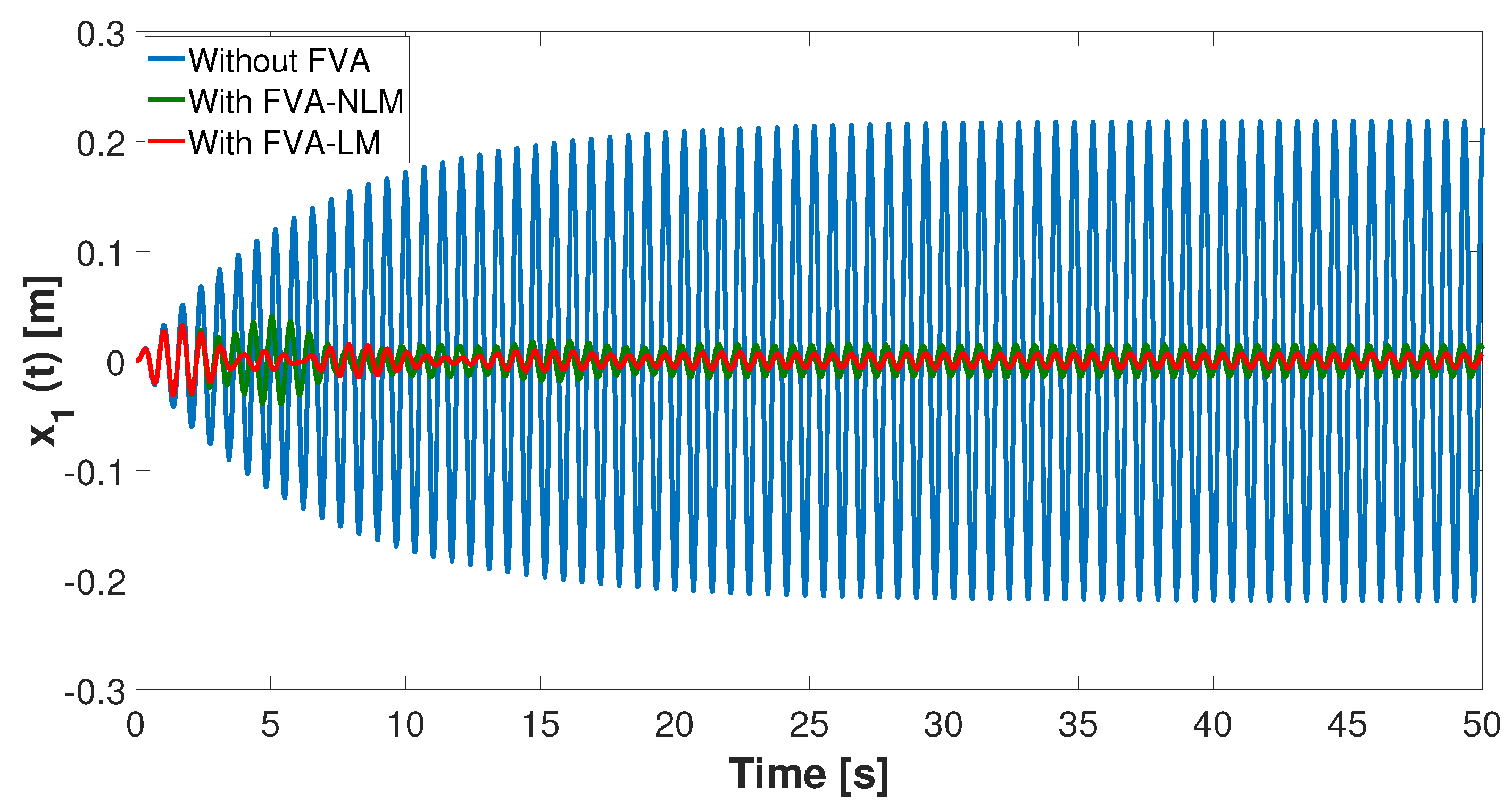
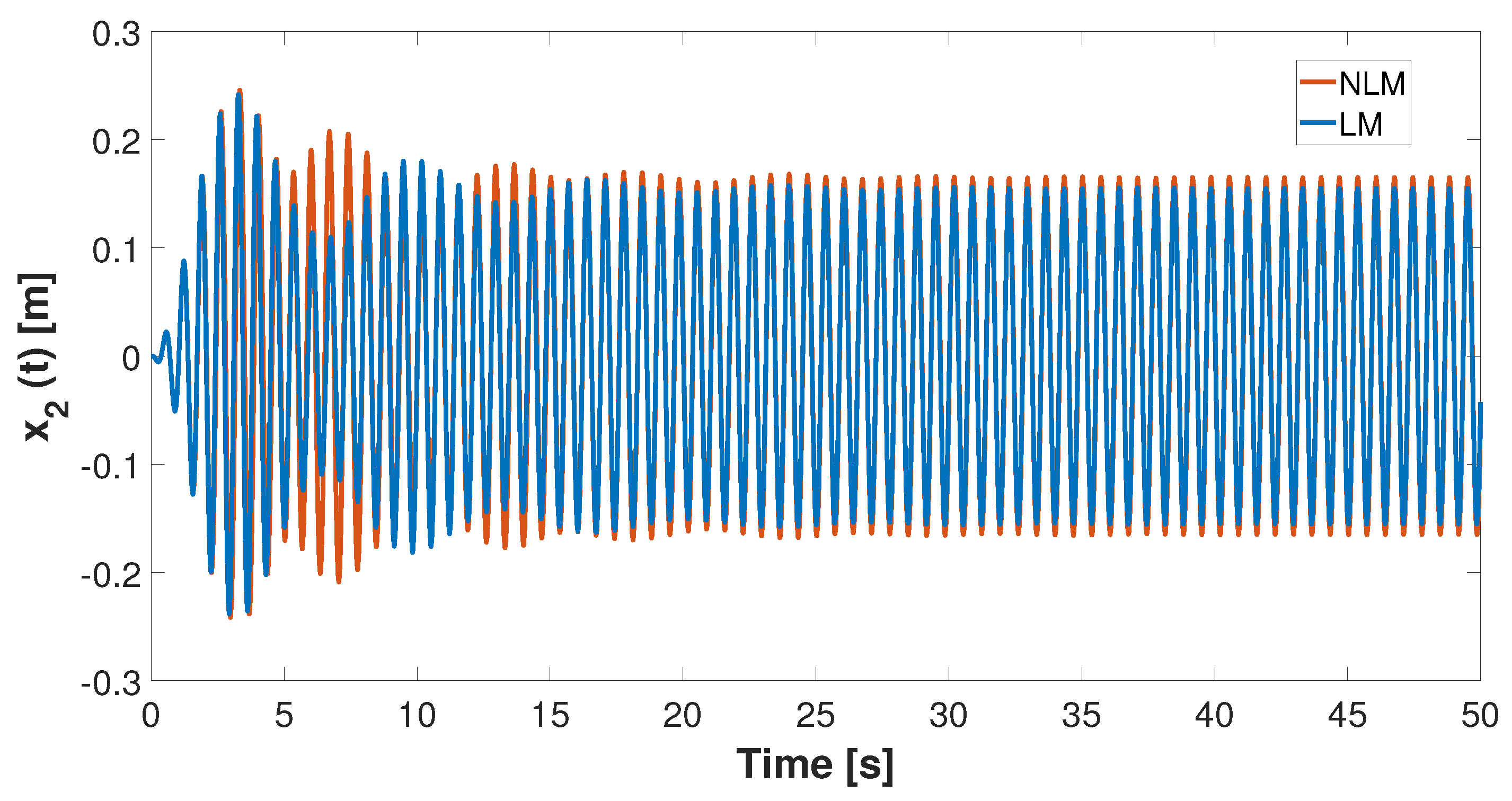
2.4. Simulation Results
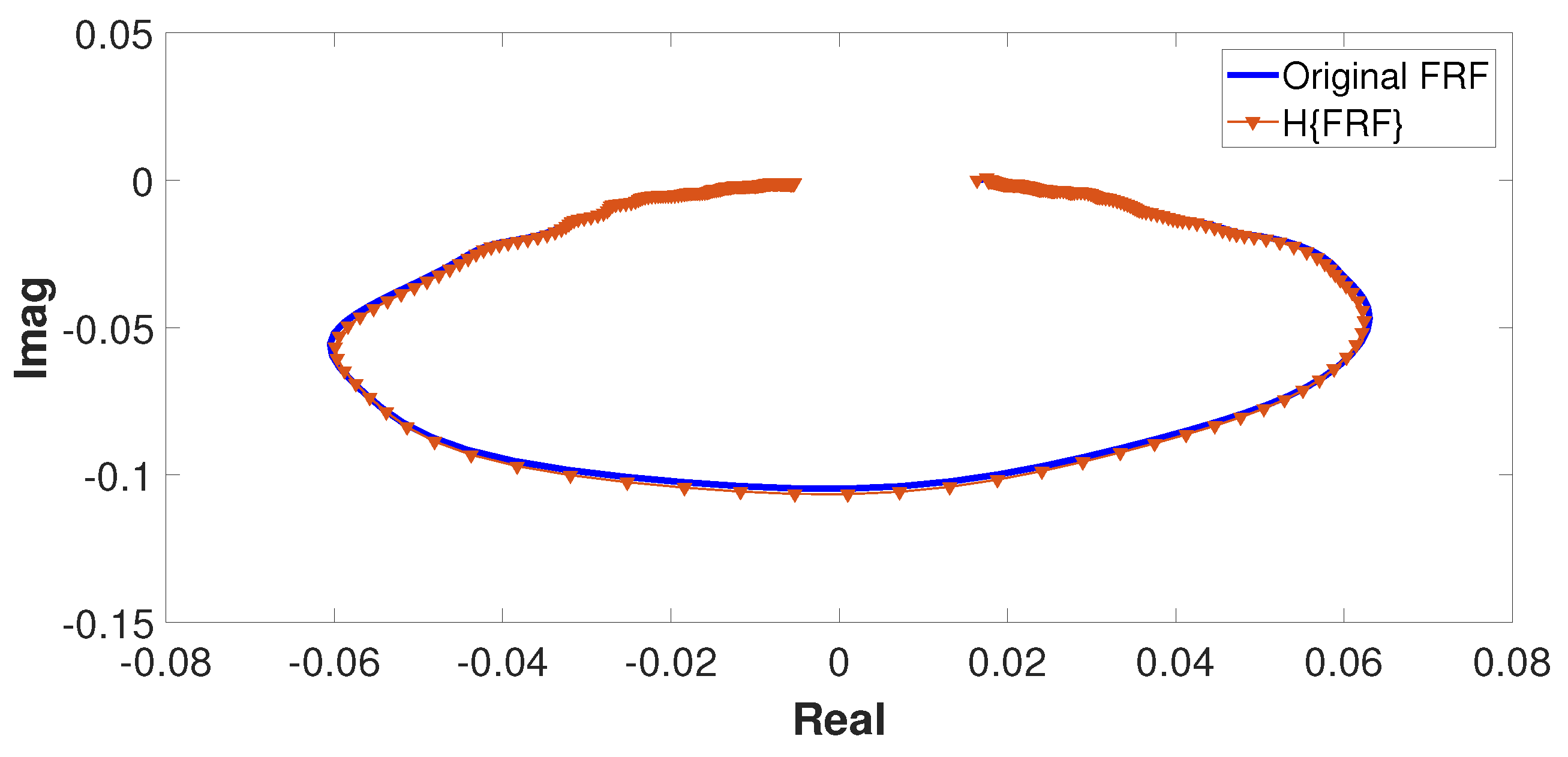
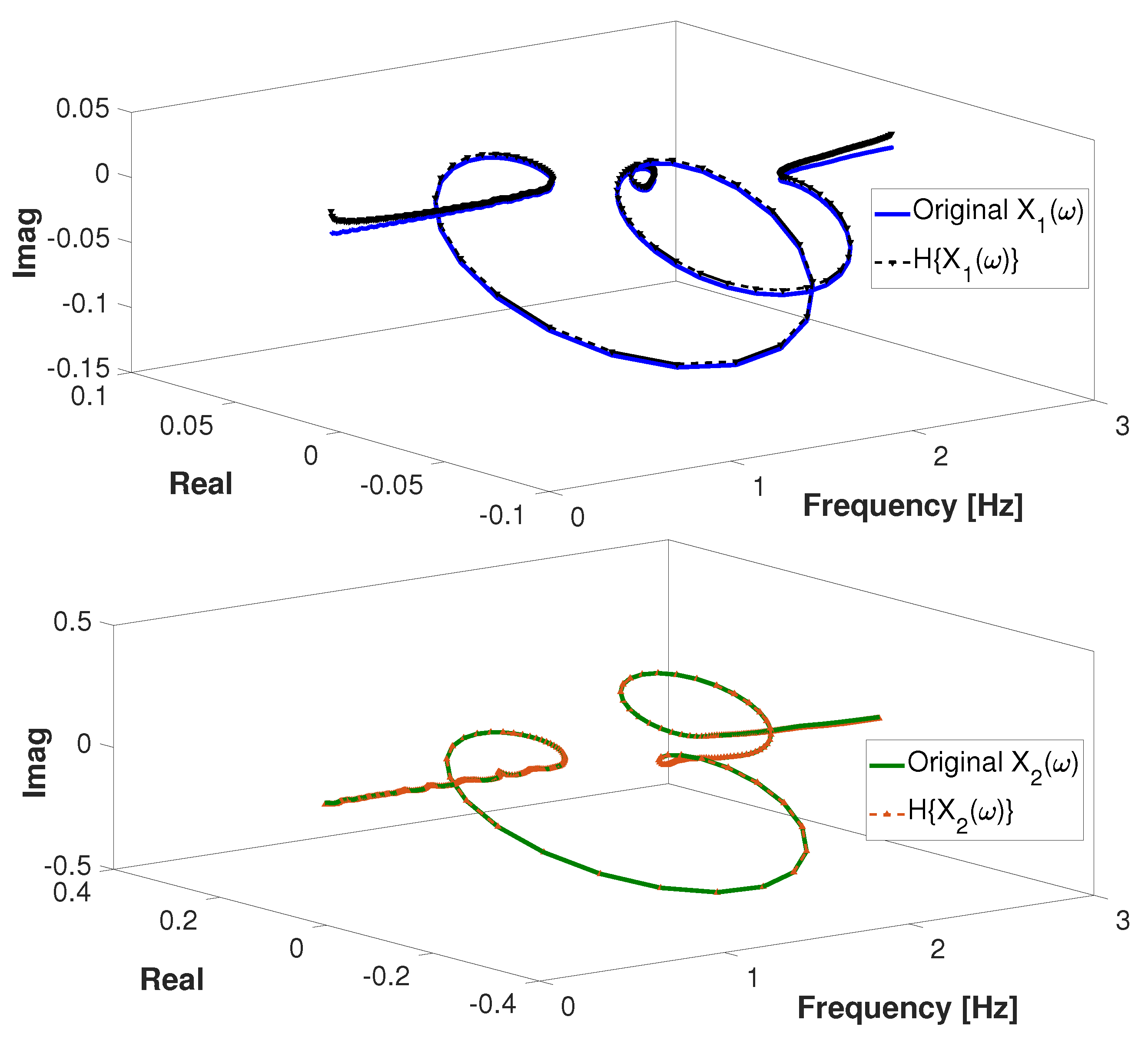
Quantification and Detection of Nonlinear Behavior
3. Experimental Results
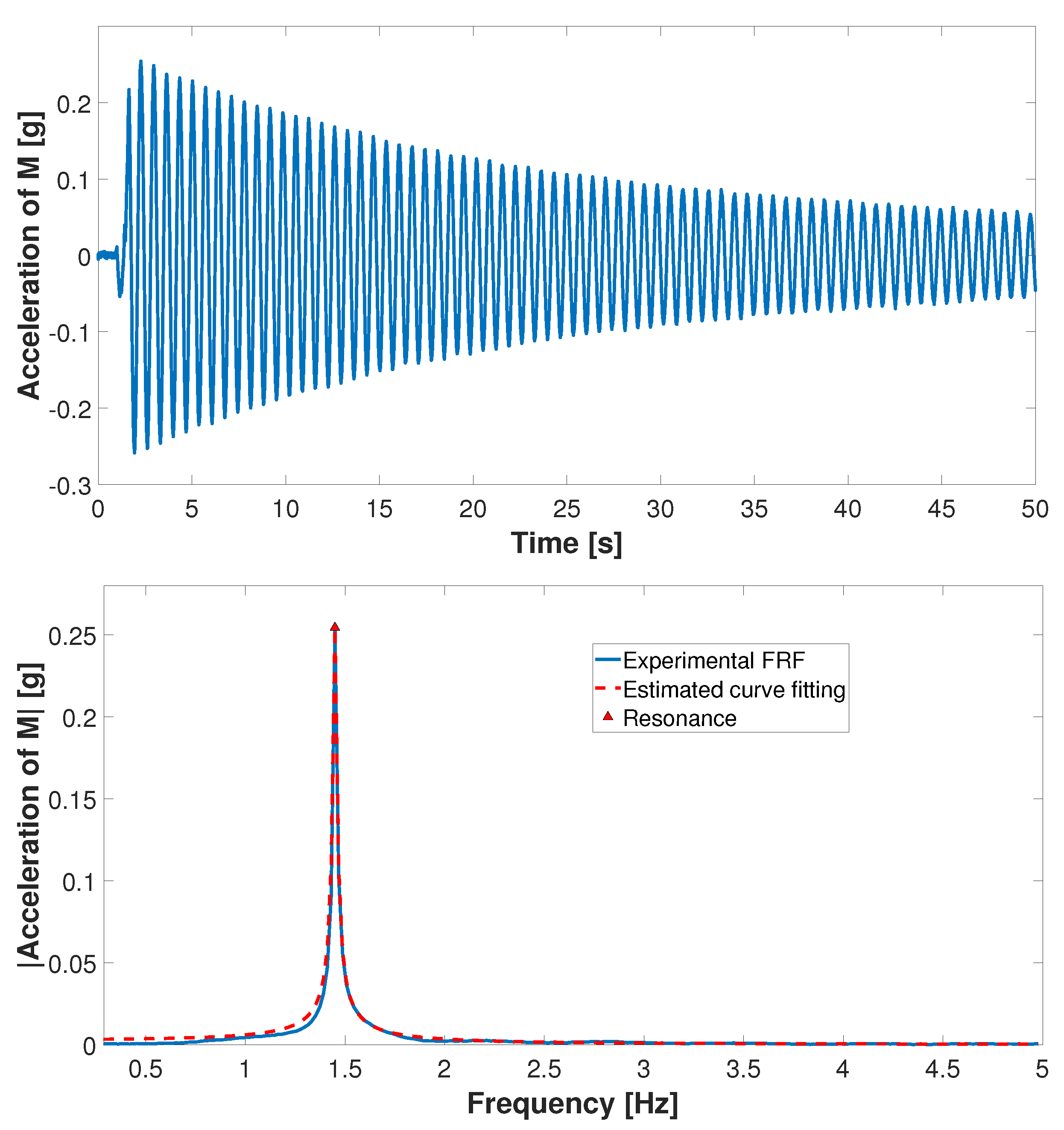
3.1. Modal Parameter Identification—Primary System
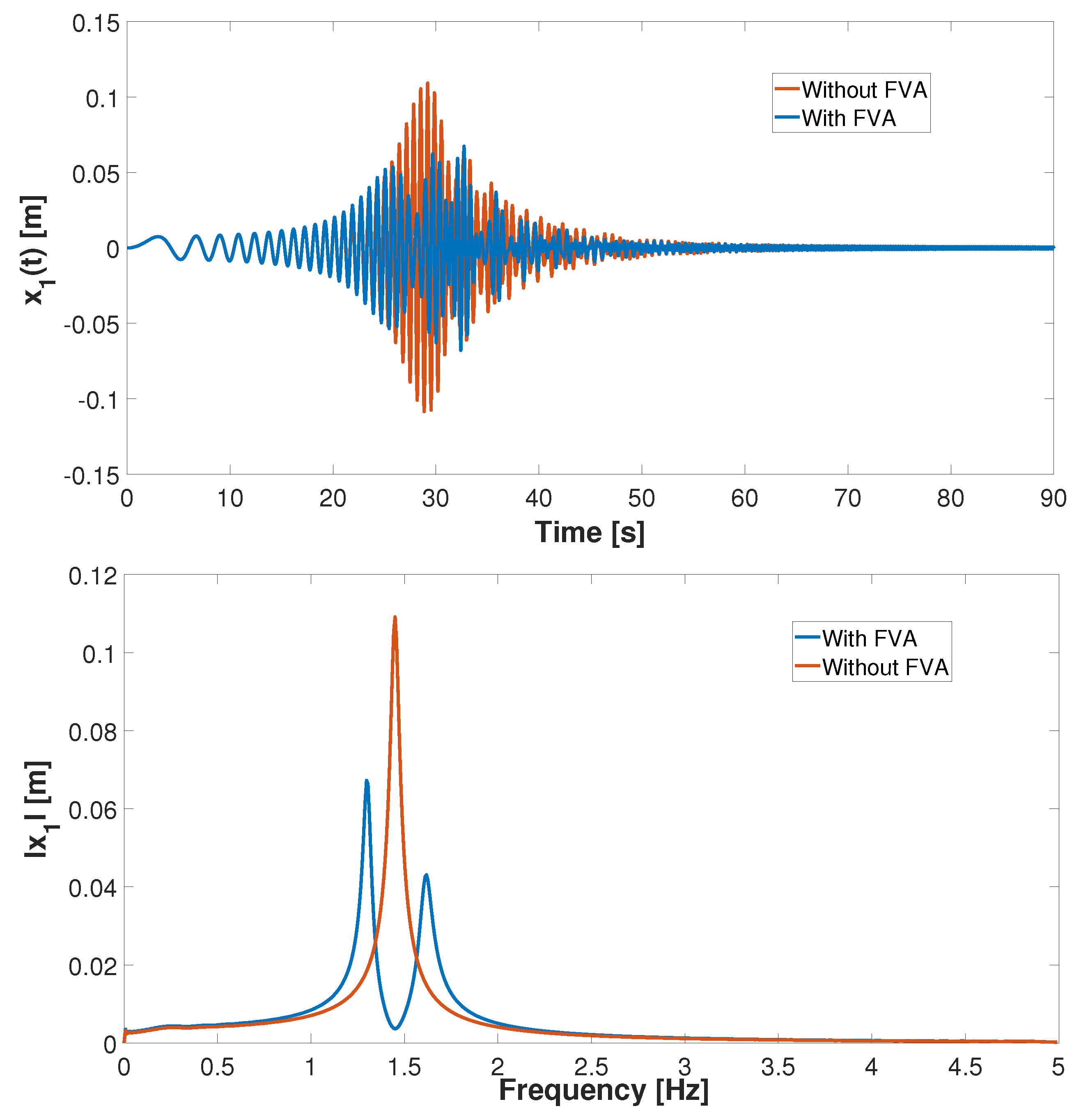
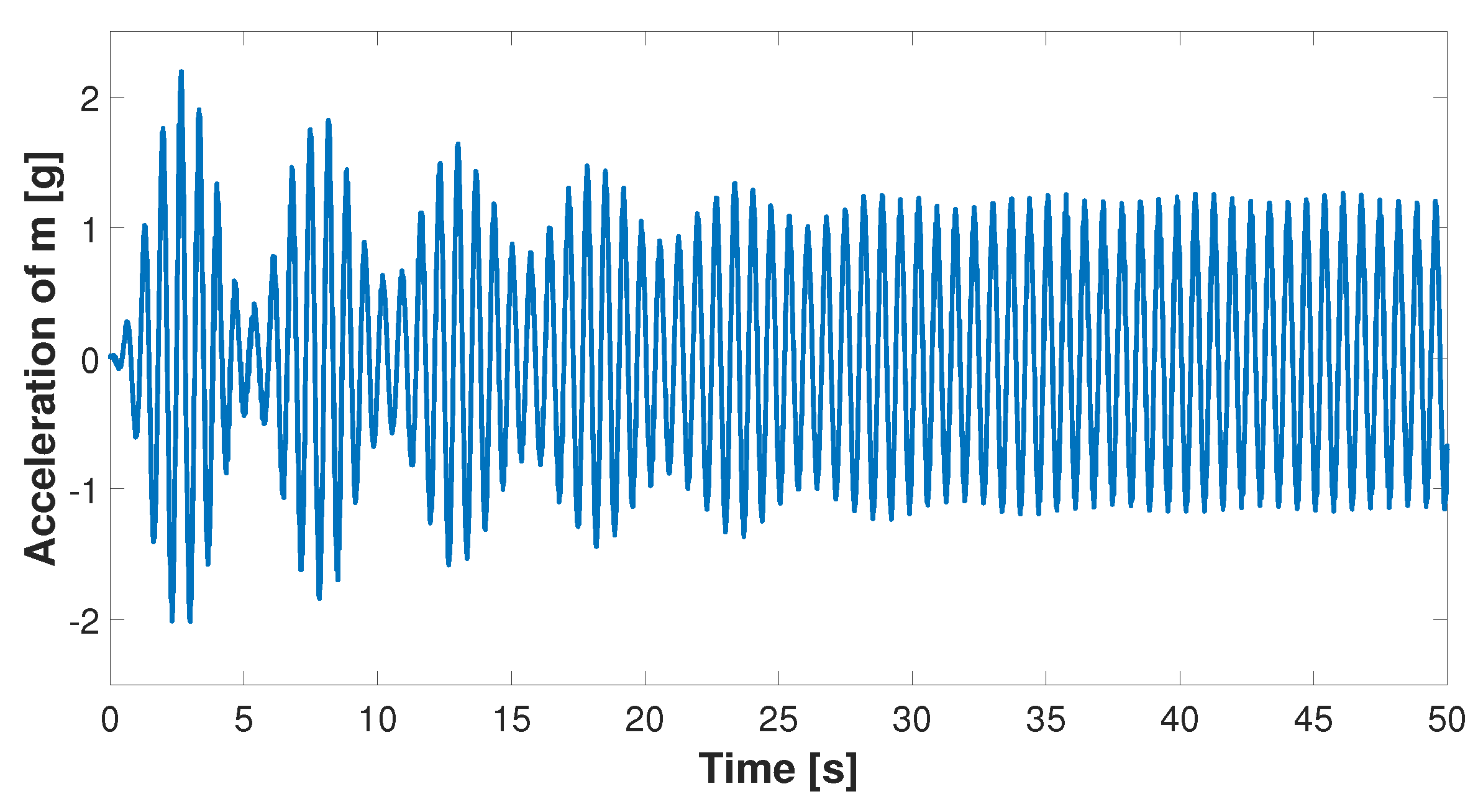
3.2. Primary System with FVA
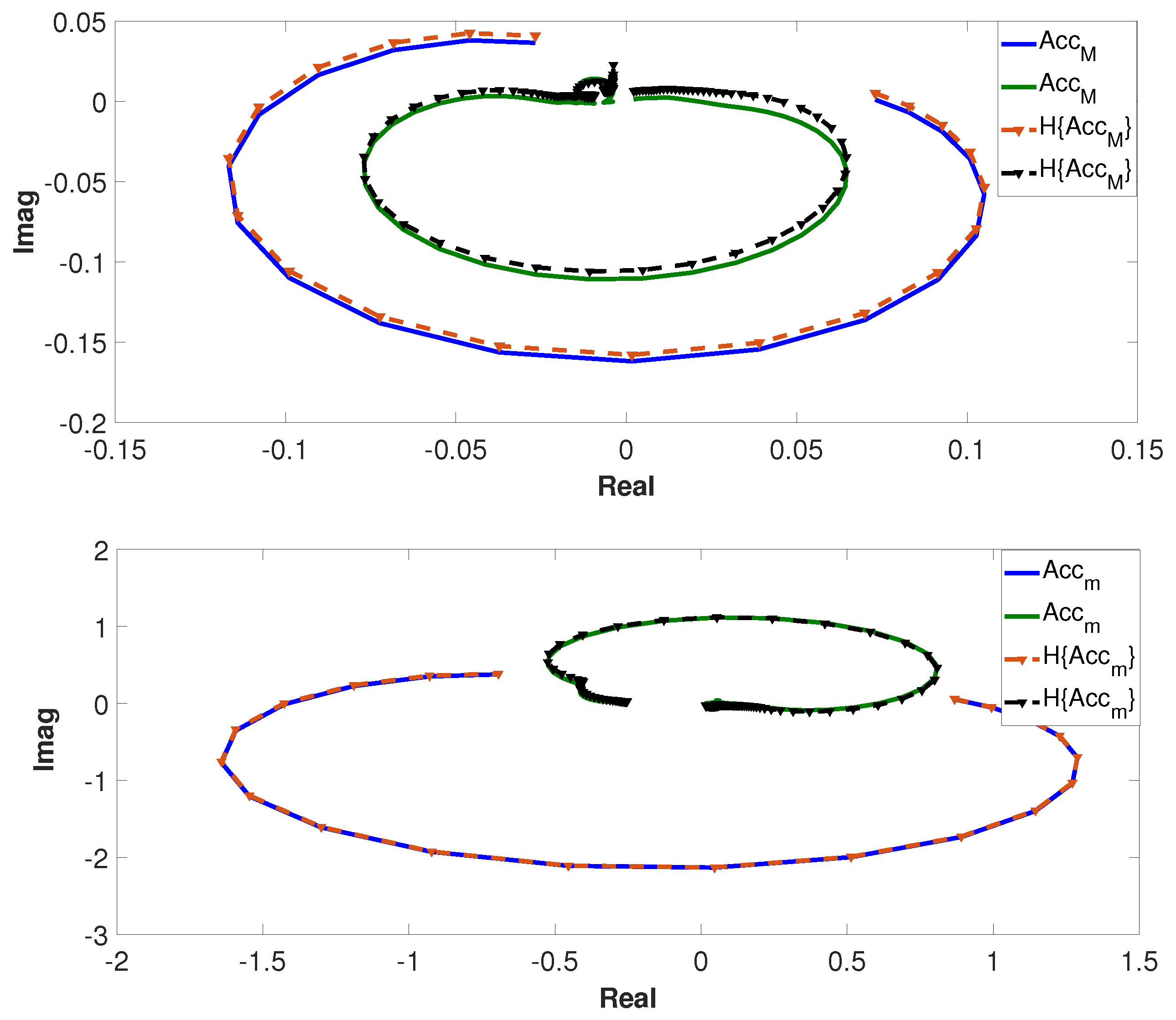
Quantification and Detection of Nonlinear Behavior
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FVA | Flexible vibration absorber |
| LM | Linear model |
| NLM | Nonlinear model |
References
- Korenev, B.G.; Reznikov, L.M. Dynamic Vibration Absorber: Theory and Technical Applications; Wiley: London, UK, 1993. [Google Scholar]
- Preumont, A.; Seto, K. Active Control of Structures; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Enríquez-Zárate, J.; Abundis-Fong, H.F.; Velazquez, R.; Gutierrez, S. Passive vibration control in a civil structure: Experimental results. Meas. Control 2019, 52, 938–946. [Google Scholar] [CrossRef]
- Sun, J.Q.; Jolly, M.R.; Norris, M.A. Passive, adaptive and active tuned vibration absorber-a survey. J. Vib. Acoust. 1995, 117, 234–242. [Google Scholar] [CrossRef]
- Frahm, H. A Device for Damping Vibrations of Bodies. U.S. Patent 989,958, 18 April 1911. [Google Scholar]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. J. Appl. Mech-T ASME 1928, 50, 9–22. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Brownjohn, J.M.W.; Carden, E.P.; Goddard, C.R.; Oudin, G. Real-time performance monitoring of tuned mass damper system for a 183 m reinforced concrete chimney. J. Wind Eng. Ind. Aerodyn. 2010, 98, 169–179. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Effectiveness of distributed tuned mass dampers for multi-mode control of chimney under earthquakes. Eng. Struct. 2016, 124, 1–16. [Google Scholar] [CrossRef]
- Belver, A.V.; Magdaleno, Á.; Brownjohn, J.M.W.; Lorenzana, A. Performance of a TMD to Mitigate Wind-Induced Interference Effects between Two Industrial Chimneys. Actuators 2021, 10, 12. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Yang, F.; Sedaghati, R.; Esmailzadeh, E. Vibration suppression of structures using tuned mass damper technology: A state-of-the-art review. Int. J. Dyn. Control 2021, 4, 1077546320984305. [Google Scholar] [CrossRef]
- Kavyashree, B.; Patil, S.; Rao, V.S. Review on vibration control in tall buildings: From the perspective of devices and applications. Int. J. Dyn. Control 2021, 9, 1316–1331. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Z.; Hua, X.; Chen, Z.; Wang, X.; Song, G. Evaluation of a pendulum pounding tuned mass damper for seismic control of structures. Eng. Struct. 2021, 228, 111554. [Google Scholar] [CrossRef]
- Pozos-Estrada, A.; Hong, H.P. Sensitivity analysis of the effectiveness of tuned mass dampers to reduce the wind-induced torsional responses. Lat. Am. J. Solids Struct. 2015, 12, 2520–2538. [Google Scholar] [CrossRef] [Green Version]
- Jin, C.; Chung, W.C.; Kwon, D.S.; Kim, M. Optimization of tuned mass damper for seismic control of submerged flotating tunnel. Eng. Struct. 2021, 241, 112460. [Google Scholar] [CrossRef]
- Wielgos, P.; Gerylo, R. Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach. Appl. Sci. 2021, 11, 1389. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Chopra, A.K. Dynamics of Structures; Prentice-Hall: Englewood Cliffs, NJ, USA, 2001. [Google Scholar]
- Esmailzadeh, E.; Nakhaie-Jazar, G. Periodic behavior of a cantilever beam with end mass subjected to harmonic base excitation. Non-Linear Mech. 1998, 33, 567–577. [Google Scholar] [CrossRef]
- Meirovitch, L. Analytical Methods in Vibrations; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Cartmell, M.O. Introduction to Linear, Parametric and Nonlinear Vibrations; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Tondl, A.; Ruijgrok, T.; Verhulst, F.; Nabergoj, R. Autoparametric Resonance in Mechanical Systems; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Haxton, R.S.; Barr, A.D.S. The Autoparametric Vibration Absorber. ASME J. Eng. Ind. 1972, 94, 119–124. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Barr, A.D.S. Autoparametric resonance in a structure containing liquid, Part 1: Two mode interaction. J. Sound Vib. 1975, 42, 159–179. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Li, W. Structural modal interaction with combination internal resonance under wide-band random excitation. J. Sound Vib. 1988, 123, 473–495. [Google Scholar] [CrossRef]
- Zhimiao, Y.; Haithem, E.T.; Ting, T. Nonlinear characteristics of an autoparametric vibration system. J. Sound Vib. 2017, 390, 1–22. [Google Scholar]
- Mahmoudkhani, S. Improving the performance of auto-parametric pendulum absorbers by means of a flexural beam. J. Sound Vib. 2008, 425, 102–123. [Google Scholar] [CrossRef]
- Silva-Navarro, G.; Abundis-Fong, H.F. Passive/active autoparametric cantilever beam absorber with piezoelectric actuator for a two-story building-like structure. J. Vib. Acoust. 2015, 2015, 011012. [Google Scholar] [CrossRef]
- Abundis-Fong, H.F.; Enríquez-Zárate, J.; Cabrera-Amado, A.; Silva-Navarro, G. Optimum Design of a Nonlinear Vibration Absorber Coupled to a Resonant Oscillator: A Case Study. Shock Vib. 2018, 137, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, R.A.; Yoon, Y.J.; Evans, M.G. Random excitation of nonlinear coupled oscillation. Nonlinear Dyn. 1990, 1, 91–116. [Google Scholar] [CrossRef]
- Enriquez-Zarate, J.; Abundis-Fong, H.F.; Silva-Navarro, G. Passive vibration control in a building-like structure using a tuned-mass-damper and an autoparametric cantilever beam absorber. In Active and Passive Smart Structures and Integrated Systems 2015; International Society for Optics and Photonics: Washington, DC, USA, 2015; Volume 9431. [Google Scholar]
- Silva-Navarro, G.; Abundis-Fong, H.F. Evaluation of Autoparametric Vibration Absorbers on N-Story Building-Like Structures. In Nonlinear Dynamics, Volume 1; Conference Proceedings of the Society for Experimental Mechanics Series; Kerschen, G., Ed.; Springer: Cham, Switzerland, 2017; pp. 177–184. [Google Scholar]
- Flores-Sanchez, D.A.; Flores-Morita, N.; Campa-Cocom, R.E.; Trujillo-Franco, L.G.; Abundis-Fong, H.F. Attenuation of Vibrations in a Mechanical Oscillator by Implementing Two Types of Vibration Absorbers: Experimental Results. In Proceedings of the International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 16–21 November 2020; pp. 104–109. [Google Scholar]
- Zhang, A.; Sorokin, V.; Li, H. Dynamic analysis of a new autoparametric pendulum absorber under the effects of magnetic forces. J. Sound Vib. 2020, 485, 115549. [Google Scholar] [CrossRef]
- Trujillo-Franco, L.G.; Silva-Navarro, G.; Beltran-Carbajal, F.; Campos-Mercado, E.; Abundis-Fong, H.F. On-Line Modal Parameter Identification Applied to Linear and Nonlinear Vibration Absorbers. Actuators 2020, 9, 119. [Google Scholar] [CrossRef]
- Zhang, A.; Sorokin, V.; Li, H. Energy harvesting using a novel autoparametric pendulum absorber-harvester. J. Sound Vib. 2021, 499, 116014. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert Transform Applications in Mechanical Vibration; John Wiley and Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Tomlinson, G.R. Developments in the use of the Hilbert transform for detecting and quantifying non-linearity associated with frequency response functions. Mech. Syst. Signal Process. 1987, 1, 151–171. [Google Scholar] [CrossRef]
- Worden, K.; Tomlinson, G.R. Nonlinearity in Structural Dynamics: Detection, Identification and Modelling; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 2001. [Google Scholar]
- Ondra, V.; Sever, I.A.; Schwingshackl, C.W. A method for detection and characterisation of structural non-linearities using the Hilbert transform and neural networks. Mech. Syst. Signal Process. 2017, 83, 210–227. [Google Scholar] [CrossRef]
- Kragh, K.A.; Thomsen, J.J.; Tcherniak, D. Experimental detection and quantification of structural nonlinearity using homogeneity and Hilbert transform methods. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 20–22 September 2010; pp. 3173–3188. [Google Scholar]
- Heylen, W.; Sas, P. Modal Analysis Theory and Testing; Departement Werktuigkunde, Katholieke Universteit Leuven: Leuven, The Netherlands, 2006. [Google Scholar]
- He, J.; Fu, Z.F. Modal Analysis; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]






| Parameter | Value | Units |
|---|---|---|
| Primary system mass (M) | 2.706 | kg |
| Equivalent stiffness () | 224.374 | N/m |
| Viscous damping () | 0.832 | Ns/m |
| Secondary system mass (m) | 0.125 | kg |
| Bending stiffness () | 0.584 | Nm2 |
| Length (L) | 0.5095 | m |
| Viscous damping () | 0.048 | Ns/m |
| Excitation frequency () | 1.4492 | Hz |
| Displacement amplitude at the base (A) | 7 | mm |
| Acceleration of gravity (g) | 9.81 | m/s2 |
| 0.98 | |
| 0.98 |
| Mode | Natural Frequency () | Damping Ratio () |
|---|---|---|
| 1 | 1.45 [Hz] | 0.0214 |
| Mode | Natural Frequency () | Damping Ratio () |
|---|---|---|
| 1 | 1.24 [Hz] | 0.0325 |
| 2 | 1.64 [Hz] | 0.0335 |
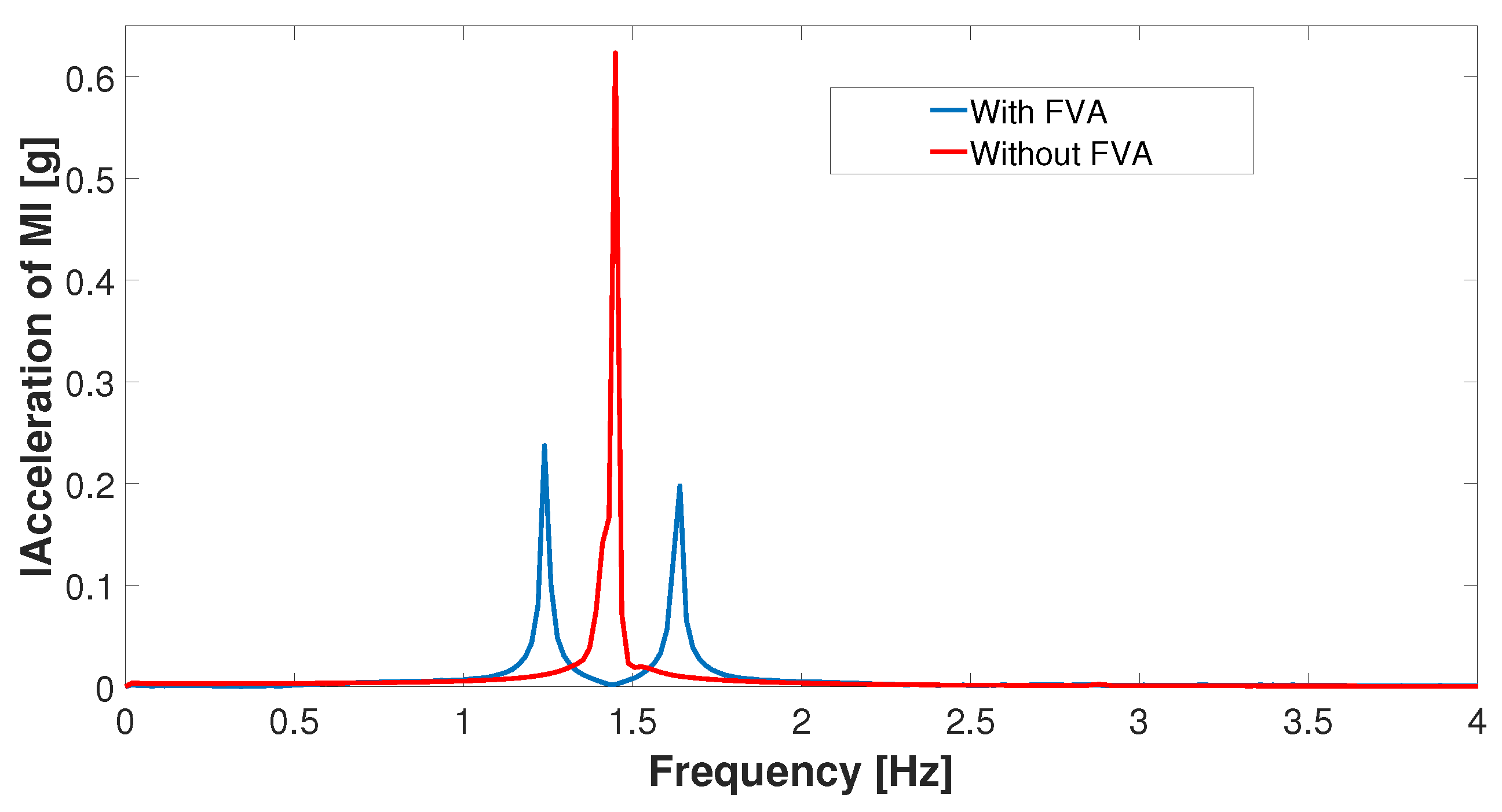
| Parameter | Without FVA | With FVA | Difference % |
|---|---|---|---|
| Damping ratio () | 0.0214 | 0.0325 | +151.86 |
| Modal amplitude |Acc| | 0.6235 | 0.2371 | −38 |
| 0.97 | |
| 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trujillo-Franco, L.G.; Flores-Morita, N.; Abundis-Fong, H.F.; Beltran-Carbajal, F.; Dzul-Lopez, A.E.; Rivera-Arreola, D.E. Oscillation Attenuation in a Building-like Structure by Using a Flexible Vibration Absorber. Mathematics 2022, 10, 289. https://doi.org/10.3390/math10030289
Trujillo-Franco LG, Flores-Morita N, Abundis-Fong HF, Beltran-Carbajal F, Dzul-Lopez AE, Rivera-Arreola DE. Oscillation Attenuation in a Building-like Structure by Using a Flexible Vibration Absorber. Mathematics. 2022; 10(3):289. https://doi.org/10.3390/math10030289
Chicago/Turabian StyleTrujillo-Franco, Luis Gerardo, Nestor Flores-Morita, Hugo Francisco Abundis-Fong, Francisco Beltran-Carbajal, Alejandro Enrique Dzul-Lopez, and Daniel Eduardo Rivera-Arreola. 2022. "Oscillation Attenuation in a Building-like Structure by Using a Flexible Vibration Absorber" Mathematics 10, no. 3: 289. https://doi.org/10.3390/math10030289
APA StyleTrujillo-Franco, L. G., Flores-Morita, N., Abundis-Fong, H. F., Beltran-Carbajal, F., Dzul-Lopez, A. E., & Rivera-Arreola, D. E. (2022). Oscillation Attenuation in a Building-like Structure by Using a Flexible Vibration Absorber. Mathematics, 10(3), 289. https://doi.org/10.3390/math10030289








