Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm
Abstract
:1. Introduction
- Applying four different algorithms as search algorithms, including artificial ecosystem-based optimization (AEO), the equilibrium optimizer (EO), the gradient-based optimizer (GBO), and turbulent flow of water-based optimization (TFWO), on IEEE 30-bus and IEEE 57-bus power systems to solve ORPD problem.
- The TFWO algorithm gives the best results for different single-objective functions, namely, the minimization of power losses and voltage deviation in both tested power systems.
- Proposing a new chaotic TFWO algorithm (CTFWO), which based on applying the chaotic approach to improve the performance of the original TFWO
- The proposed CTFWO algorithm solves the ORPD problem and gives better results than all other compared algorithms on the tested power systems, the 30-bus and the 57-bus systems, for all studied cases.
2. Materials and Methods
2.1. Objective Functions
2.1.1. Minimization of the Active Power Loss
- is the active power loss.
- is the conductance of the kth branch connected between the ith and the jth bus.
- is the admittance angle of the transmission line connected between the ith and the jth bus.
- NTL is the number of transmission lines (branches).
- are the voltage magnitudes of the ith and the jth bus, respectively.
2.1.2. Improvement of the Voltage Profile
2.2. System Constraints
2.2.1. Equality Constraint
- where:
- () and Qi () represent the real and reactive power injection at bus i.
- and are the active and reactive power generation of the ith bus.
- and are the active and reactive load demand of the ith bus.
- is the real part of the bus admittance matrix of the (i, j)th entry.
- is the imaginary part of the bus admittance matrix of the (i, j)th entry.
- is numbers of buses.
2.2.2. Inequality Constraints
3. Methodology
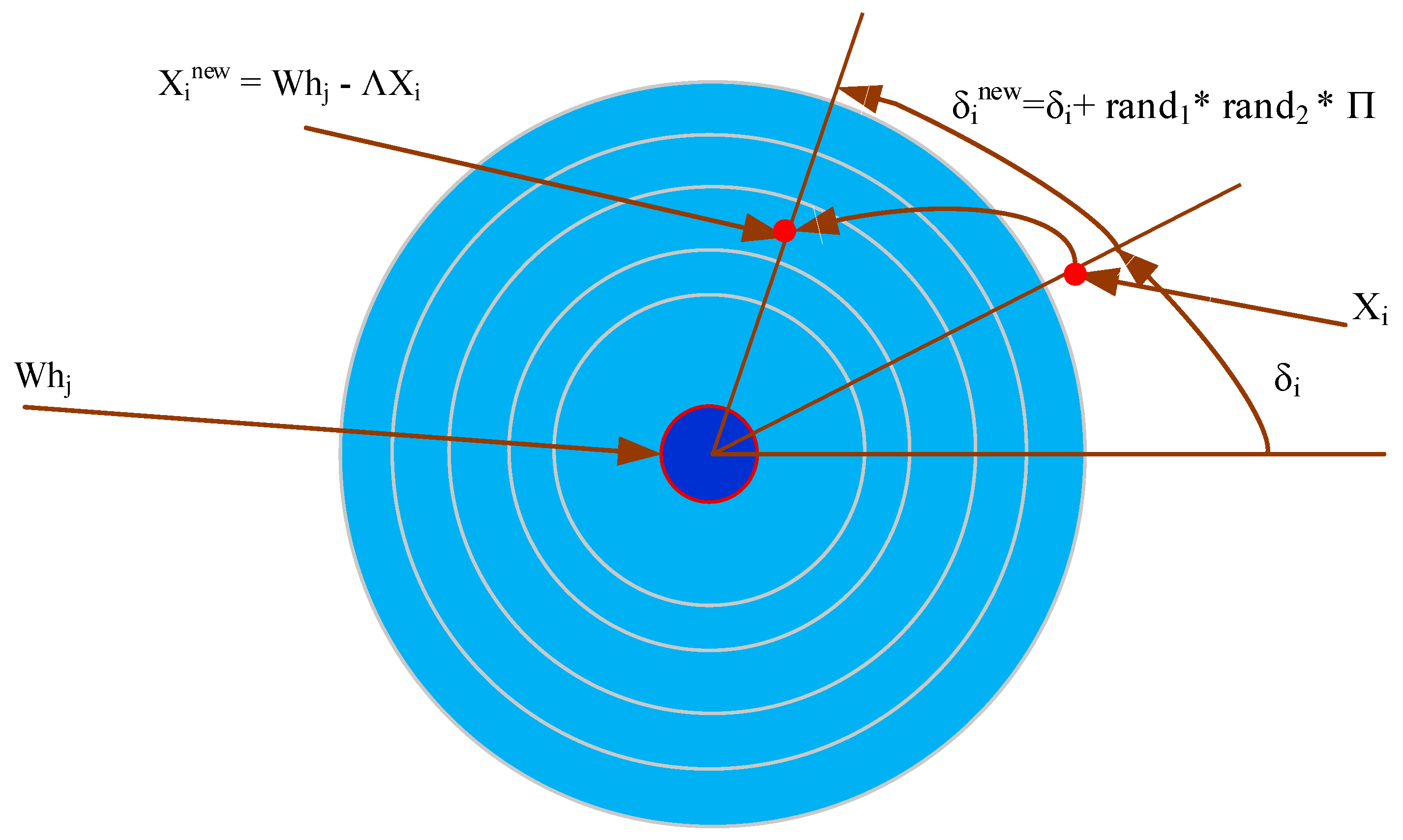
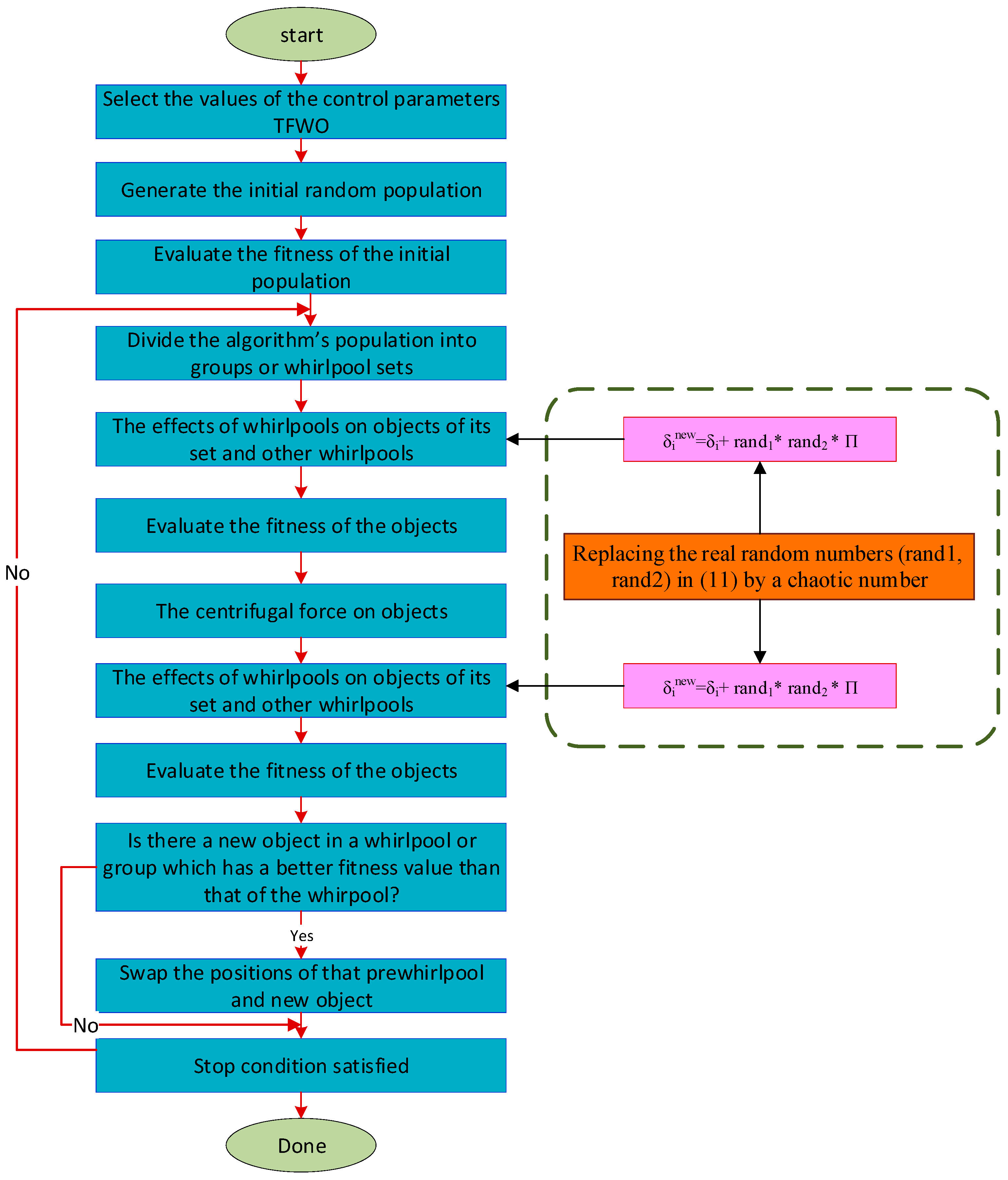
3.1. The Conventional TFWO
3.2. The Proposed CTFWO
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony algorithm | ACO | Ant colony optimization |
| AEO | Artificial ecosystem-based optimization | ALC-PSO | PSO with an aging leader and challengers |
| ABC-FF | ABC with firefly algorithm | ALO | Ant lion optimizer |
| AGA | Adaptive genetic algorithm | CKHA | Chaotic krill herd algorithm |
| CSA | Cuckoo search algorithm | CLPSO | PSO with comprehensive learning |
| CSOA | Crow search optimization algorithm | DE | Differential evolution |
| DSA | Differential search algorithm | DE-AS | Combination of DE and ant system method |
| EC | E-constraint | EO | Equilibrium optimizer algorithm |
| ECHT | Ensemble of constraint handling techniques | EMOA | Exchange market optimization algorithm |
| GA | Genetic algorithm | GBBWCA | Gaussian bare-bones water cycle algorithm |
| GBTLBO | Gaussian bare-bones-based TLBO algorithm | GBO | Gradient-based optimizer |
| GSA | Gravitational search algorithm | GWO | Gray wolf optimizer |
| HFA-NMS | Hybrid firefly algorithm-based Nelder–Mead simplex | HPSO | Hybrid PSO |
| HPSO-ICA | PSO hybrid and imperialist competitive algorithms | HPSO-TS | Hybrid PSO and tabu search method |
| HAS | Harmony search algorithm | ICA | Imperialist competitive algorithms |
| ICBO | Improved colliding bodies optimization | ICOA | Improved coyote optimization algorithm |
| ICSA | Improved CSA | JA | Jaya algorithm |
| MFO | Moth–flame optimization technique | MGBTLBO | Modified GBTLBO |
| MOGWA | Multi-objective grey wolf algorithm | MTLA-DDE | Hybrid modified teaching–learning technique and double differential evolution algorithm |
| ORPD | Optimal reactive power dispatch | OPF | Optimal power flow |
| PSO | Particle swarm optimization | PSO-GT | Combination of PSO and graph theory |
| PSO-IPG | PSO with pseudo-gradient theory and constriction factor | QODE | Quasi-oppositional differential evolution |
| QOTLBO | Quasi-oppositional teaching–learning-based optimization | RCGA | Real coded genetic algorithm |
| SARCGA | Self-adaptive real coded genetic algorithm | SGA | Specialized genetic algorithm |
| Std. dev. | Standard deviation | SF | Superiority of feasible solutions |
| SP | Self-adaptive penalty | SR | Stochastic ranking |
| TFWO | Turbulent flow of water-based optimization | TLBO | Teaching–learning-based optimization |
| Ploss | Active power losses | VD | Voltage deviation |
| WOA | Whale optimization algorithm |
References
- Nakawiro, W.; Erlich, I.; Rueda, J.L. A novel optimization algorithm for optimal reactive power dispatch: A comparative study. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization. Electr. Power Energy Syst. 2013, 53, 123–134. [Google Scholar] [CrossRef]
- Zhukov, A.; Tomin, N.; Sidorov, D.; Kurbatsky, V.; Panasetsky, D. On-line power systems security assessment using data stream random forest algorithm modification. In Innovative Computing, Optimization and Its Applications; Springer: Cham, Switzerland, 2018; pp. 183–200. [Google Scholar]
- Zhang, Y.; Song, X.; Li, Y.; Zeng, Z.; Yong, C.; Sidorov, D.; Lv, X. Two-Stage Active and Reactive Power Coordinated Optimal Dispatch for Active Distribution Network Considering Load Flexibility. Energies 2020, 13, 5922. [Google Scholar] [CrossRef]
- Voropai, N.I.; Tomin, N.V.; Sidorov, D.N.; Kurbatsky, V.G.; Panasetsky, D.A.; Zhukov, A.V.; Osak, A.B. A suite of intelligent tools for early detection and prevention of blackouts in power interconnections. Autom. Remote Control 2018, 79, 1741–1755. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; Selim, A.; Khurshaid, T.; Domínguez-García, J.L. A modified Rao-2 algorithm for optimal power flow incorporating renewable energy sources. Mathematics 2021, 9, 1532. [Google Scholar] [CrossRef]
- Hassan, M.H.; Yousri, D.; Kamel, S.; Rahmann, C. A Modified Marine Predators Algorithm for Solving Single-and Multi-Objective Combined Economic Emission Dispatch Problems. Comput. Ind. Eng. 2021, 164, 107906. [Google Scholar] [CrossRef]
- Murray, A.; Engelmann, A.; Hagenmeyer, V.; Faulwasser, T. Hierarchical distributed mixed-integer optimization for reactive power dispatch. IFAC-Pap. Line 2018, 51, 368–373. [Google Scholar] [CrossRef]
- Kien, L.C.; Hien, C.T.; Nguyen, T.T. Optimal Reactive Power Generation for Transmission Power Systems Considering Discrete Values of Capacitors and Tap Changers. Appl. Sci. 2021, 11, 5378. [Google Scholar] [CrossRef]
- Venkatesh, B.; Sasadivam, G.; Khan, M.A. Towards on-line optimal reactive power scheduling using ANN memory model based method. In Proceedings of the Power Engineering Society Winter Meeting, New York, NY, USA, 31 January–4 February 1999; Volume 2, pp. 844–848. [Google Scholar]
- Grudinin, N. Reactive power optimization using successive quadratic programming method. IEEE Trans. Power Syst. 1998, 13, 1219–1225. [Google Scholar] [CrossRef]
- Da Costa, G.R.M. Modified Newton method for reactive dispatching. Int. J. Electr. Power Energy Syst. 2002, 24, 815. [Google Scholar] [CrossRef]
- Rezania, E.; Shahidehpour, S.M. Real power loss minimization using interior point method. Int. J. Electr. Power Energy Syst. 2001, 23, 45–56. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Improving voltage stability by optimal reactive power dispatch based on genetic algorithm and linear programming technique. In Proceedings of the International Conference on IEEE: Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1357–1362. [Google Scholar]
- Villa-Acevedo, W.; López-Lezama, J.; Valencia-Velásquez, J.A. A novel constraint handling approach for the optimal reactive power dispatch problem. Energies 2018, 11, 2352. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; De, M. Optimal reactive power dispatch using hybrid loop-genetic based algorithm. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Wu, Q.H.; Cao, Y.J.; Wen, J.Y. Optimal reactive power dispatch using an adaptive genetic algorithm. In Proceedings of the Second International Conference on Genetic Algorithms in Engineering Systems, Glasgow, UK, 2–4 September 1997; pp. 117–122. [Google Scholar]
- Vaduva, A.M.; Bulac, C. New evolutionary algorithm method for solving optimal reactive power dispatch problem. In Proceedings of the International Conference on IEEE on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 6–8 October 2016; pp. 1–6. [Google Scholar]
- Mehdinejad, M.; Mohammadi-Ivatloo, B.; Dadashzadeh-Bonab, R.; Zare, K. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms. Int. J. Electr. Power Energy Syst. 2016, 83, 104–116. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Optimal reactive power dispatch by particle swarm optimization with an aging leader and challengers. Appl. Soft Comput. 2015, 29, 298–309. [Google Scholar] [CrossRef]
- Kanatip, R.; Keerati, C. Probabilistic optimal power flow considering load and solar power uncertainties using particle swarm optimization. GMSARN Int. J. 2021, 15, 37–43. [Google Scholar]
- Reddy, P.L.; Yesuratnam, G. PSO based optimal reactive power dispatch for voltage profile improvement. In Proceedings of the Conference (PCITC) on IEEE Power, Communication and Information Technology, Bhubaneswar, India, 15–17 October 2015; pp. 361–366. [Google Scholar]
- Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive power dispatch optimization with voltage profile improvement using an efficient hybrid algorithm. Energies 2018, 11, 2134. [Google Scholar] [CrossRef] [Green Version]
- Kaur, D.; Lie, T.T.; Nair, N.K.; Valles, B. An optimal reactive power dispatch (ORPD) for voltage security using particle swarm optimization (PSO) in graph theory. In Proceedings of the IEEE International Conference on Sustainable Energy Technologies (ICSET), Hanoi, Vietnam, 14–16 October 2016; pp. 25–30. [Google Scholar]
- Polprasert, J.; Ongsakul, W.; Dieu, V.N. Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr. Power Compon. Syst. 2016, 44, 518–532. [Google Scholar] [CrossRef]
- Mahadevan, K.; Kannan, P.S. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Dieu, V.N.; Nguyen, T.P.; Nguyen, K.D. Multi-objective security constrained optimal active and reactive power dispatch using hybrid particle swarm optimization and differential evolution. GMSARN Int. J. 2018, 12, 84–117. [Google Scholar]
- El Ela, A.A.; Abido, M.A.; Spea, S.R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Huang, C.M.; Huang, Y.C. Combined differential evolution algorithm and ant system for optimal reactive power dispatch. Energy Procedia 2012, 14, 1238. [Google Scholar] [CrossRef] [Green Version]
- Basu, M. Quasi-oppositional differential evolution for optimal reactive power dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 29. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Li, Z. Reactive power optimization using hybrid CABC-DE algorithm. Electr. Power Compon. Syst. 2017, 45, 980–989. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghanbarian, M.M.; Ghavidel, S.; Rahmani, S.; Moghaddam, E.M. Modified teaching learning algorithm and double differential evolution algorithm for optimal reactive power dispatch problem: A comparative study. Inf. Sci. 2014, 278, 231–249. [Google Scholar] [CrossRef]
- Chen, G.; Liu, L.; Zhang, Z.; Huang, S. Optimal reactive power dispatch by improved GSA-based algorithm with the novel strategies to handle constraints. Appl. Soft Comput. 2017, 50, 58–70. [Google Scholar] [CrossRef]
- Duman, S.; Sönmez, Y.; Güvenç, U.; Yörükeren, N. Optimal reactive power dispatch using a gravitational search algorithm. IET Gener. Transm. Distrib. 2012, 6, 563–576. [Google Scholar] [CrossRef]
- Babu, M.R.; Lakshmi, M. Gravitational search algorithm based approach for optimal reactive power dispatch. In Proceedings of the Second International Conference on IEEE on Science Technology Engineering and Management (ICONSTEM), Chennai, India, 30–31 March 2016; pp. 360–366. [Google Scholar]
- Rajan, A.; Malakar, T. Exchange market algorithm based optimum reactive power dispatch. Appl. Soft Comput. 2016, 43, 320–336. [Google Scholar] [CrossRef]
- Shareef, S.M.; Rao, R.S. Optimal reactive power dispatch under unbalanced conditions using hybrid swarm intelligence. Comput. Electr. Eng. 2018, 69, 183–193. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Salhi, A. Ant lion optimizer for solving optimal reactive power dispatch problem in power systems. Eng. Sci. Technol. Int. J. 2017, 3, 885–895. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar]
- Meddeb, A.; Amor, N.; Abbes, M.; Chebbi, S. A novel approach based on crow search algorithm for solving reactive power dispatch problem. Energies 2018, 11, 3321. [Google Scholar] [CrossRef] [Green Version]
- Abaci, K.; Yamaçli, V. Optimal reactive-power dispatch using differential search algorithm. Electr. Eng. 2017, 99, 213–225. [Google Scholar] [CrossRef]
- Nuaekaew, K.; Artrit, P.; Pholdee, N.; Bureerat, S. Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Exp. Syst. Appl. 2017, 87, 79–89. [Google Scholar] [CrossRef]
- Anbarasan, P.; Jayabarathi, T. Optimal reactive power dispatch problem solved by an improved colliding bodies optimization algorithm. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Barakat, A.F.; El-Sehiemy, R.A.; Elsaid, M.; Osman, E. Solving reactive power dispatch problem by using JAYA optimization Algorithm. Int. J. Eng. Res. Afr. Trans. Tech. Publ. 2018, 36, 12–24. [Google Scholar] [CrossRef]
- ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electric. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Ant colony optimization algorithm based optimal reactive power dispatch to improve voltage stability. In Proceedings of the International Conference on IEEE on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; p. 1. [Google Scholar]
- Khazali, A.H.; Kalantar, M. Optimal reactive power dispatch based on harmony search algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 684–692. [Google Scholar] [CrossRef]
- Ghasemi, M.; Taghizadeh, M.; Ghavidel, S.; Aghaei, J.; Abbasian, A. Solving optimal reactive power dispatch problem using a novel teaching-learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Rajan, T.M. Optimal reactive power dispatch using hybrid Nelder-Mead simplex based firefly algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef] [Green Version]
- Sulaiman, M.H.; Mustaffa, Z. Cuckoo Search Algorithm as an optimizer for Optimal Reactive Power Dispatch problems. In Proceedings of the 3rd International Conference on IEEE on Control, Automation and Robotics, Nagoya, Japan, 24–26 April 2017; pp. 735–739. [Google Scholar]
- Mukherjee, V.M. Solution of optimal reactive power dispatch by chaotic krill herd algorithm. IET Gener. Transm. Distrib. 2015, 9, 2351–2362. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Artificial Bee Colony algorithm for optimal reactive power dispatch to improve voltage stability. In Proceedings of the International Conference on IEEE on Circuit, Power and Computing Technologies (ICCPCT), Nagercoil, India, 18–19 March 2016; pp. 1–7. [Google Scholar]
- Hassan, M.H.; Kamel, S.; El-Dabah, M.A.; Khurshaid, T.; Domínguez-García, J.L. Optimal reactive power dispatch with time-varying demand and renewable energy uncertainty using Rao-3 algorithm. IEEE Access 2021, 9, 23264–23283. [Google Scholar] [CrossRef]
- An, N.H.T.; Dieu, V.N.; Nguyen, T.T.; Kien, V.T. One rank cuckoo search algorithm for optimal reactive power dispatch. GMSARN Int. J. 2015, 73, 82. [Google Scholar]
- Ghasemi, M.; Davoudkhani, I.F.; Akbari, E.; Rahimnejad, A.; Ghavidel, S.; Li, L. A novel and effective optimization algorithm for global optimization and its engineering applications: Turbulent Flow of Water-based Optimization (TFWO). Eng. Appl. Artif. Intell. 2020, 92, 103666. [Google Scholar] [CrossRef]
- Abdelminaam, D.S.; Said, M.; Houssein, E.H. Turbulent flow of water-based optimization using new objective function for parameter extraction of six photovoltaic models. IEEE Access 2021, 9, 35382–35398. [Google Scholar] [CrossRef]
- Said, M.; Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Estimating Parameters of Photovoltaic Models Using Accurate Turbulent Flow of Water Optimizer. Processes 2021, 9, 627. [Google Scholar] [CrossRef]
- Nasri, S.; Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Kalam, A.; Shahrokhi, S.; Zand, M. Maximum Power Point Tracking of Photovoltaic Renewable Energy System Using a New Method Based on Turbulent Flow of Water-Based Optimization (TFWO) Under Partial Shading Conditions. In Fundamentals and Innovations in Solar Energy; Springer: Singapore, 2021; pp. 285–310. [Google Scholar]
- Deb, S.; Houssein, E.H.; Said, M.; AbdElminaam, D.S. Performance of Turbulent Flow of Water Optimization on Economic Load Dispatch Problem. IEEE Acces 2021, 77882–77893. [Google Scholar] [CrossRef]
- Fayek, H.H.; Abdalla, O.H. Optimal Settings of BTB-VSC in Interconnected Power System Using TFWO. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Eid, A.; Kamel, S. Optimal Allocation of Shunt Compensators in Distribution Systems using Turbulent Flow of Waterbased Optimization Algorithm. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–5. [Google Scholar]
- Mallipeddi, R.; Jeyadevi, S.; Suganthan, P.N.; Baskar, S. Efficient constraint handling for optimal reactive power dispatch problems. Swarm Evol. Comput. 2012, 5, 28–36. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Improved social spider optimization algorithm for optimal reactive power dispatch problem with different objectives. Neural Comput. Appl. 2020, 32, 5919–5950. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M. Impact of chaos functions on modern swarm optimizers. PLoS ONE 2016, 11, e0158738. [Google Scholar] [CrossRef] [Green Version]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Integrated strategies of backtracking search optimizer for solving reactive power dispatch problem. IEEE Syst. J. 2018, 12, 424–433. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T. Multi-objective ant lion optimization algorithm to solve large-scale multi-objective optimal reactive power dispatch problem. Compel.-Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 304–324. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal Reactive Power Dispatch Using Chaotic Bat Algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Shaw, B.; Mukherjee, V.; Ghoshal, S.P. Solution of reactive power dispatch of power systems by an opposition-based gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Cao, Y.; Dai, L.V.; Yang, X.; Nguyen, T.T. Finding Solutions for Optimal Reactive Power Dispatch Problem by a Novel Improved Antlion Optimization Algorithm. Energies 2019, 12, 2968. [Google Scholar] [CrossRef] [Green Version]
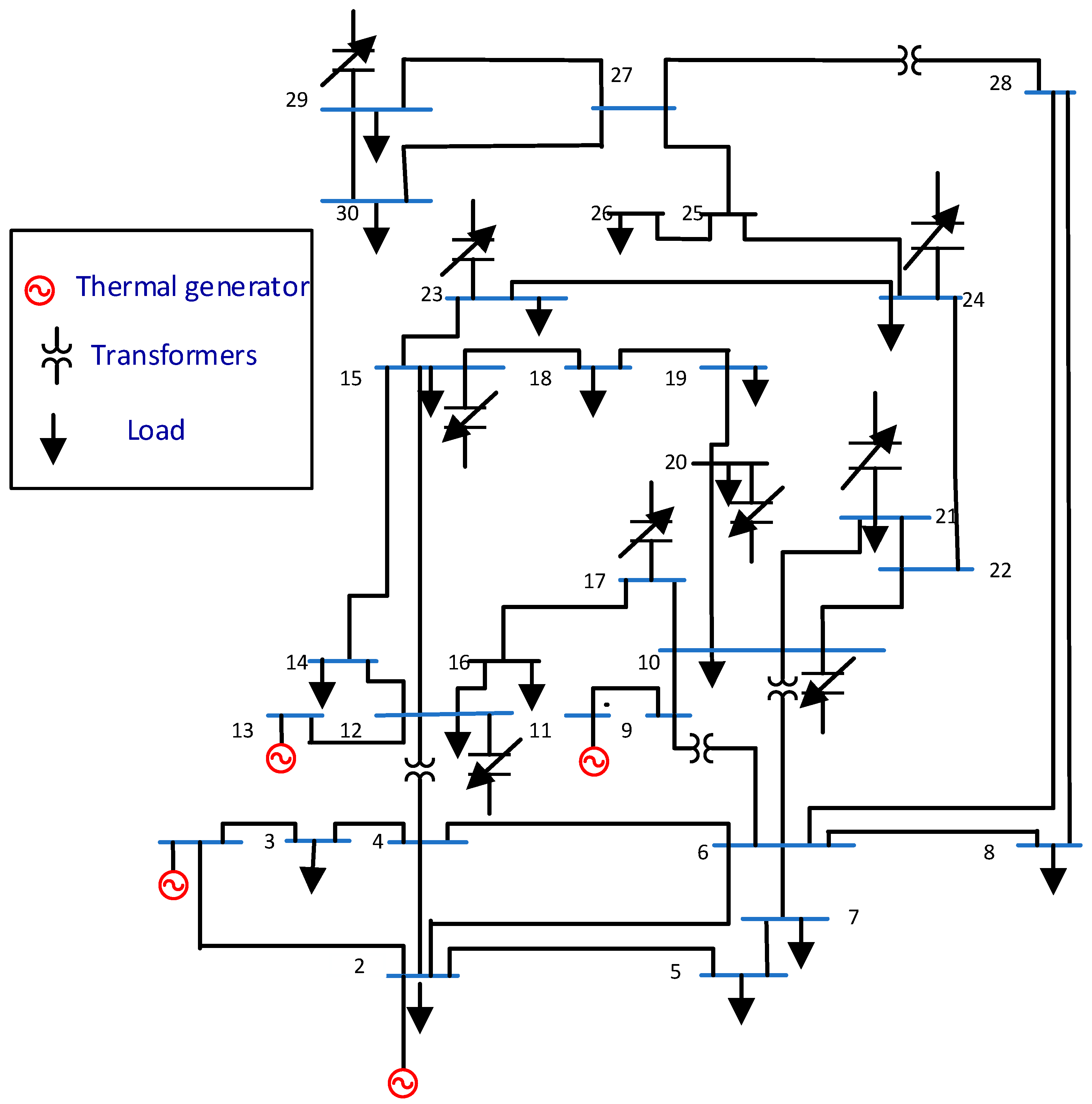


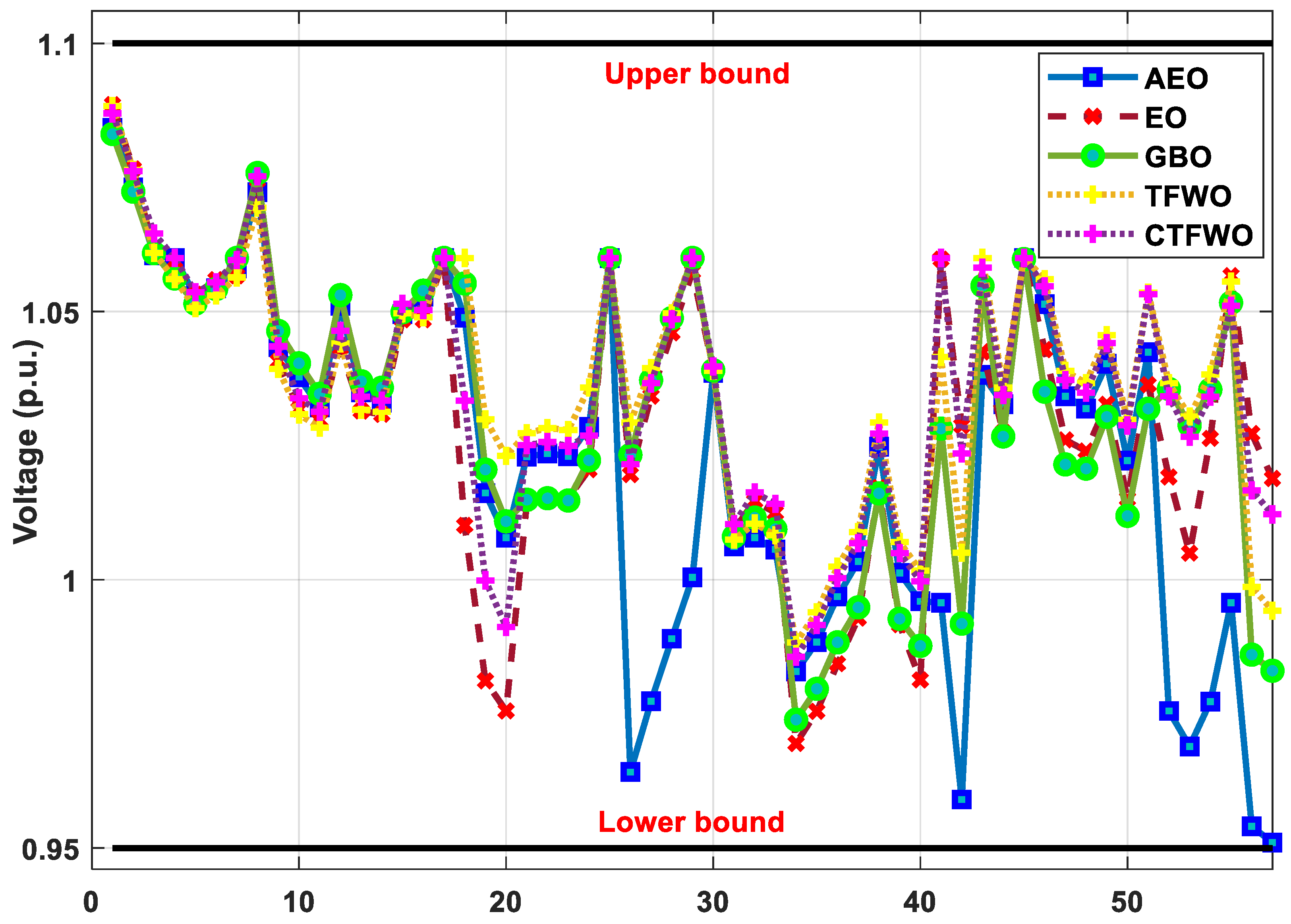
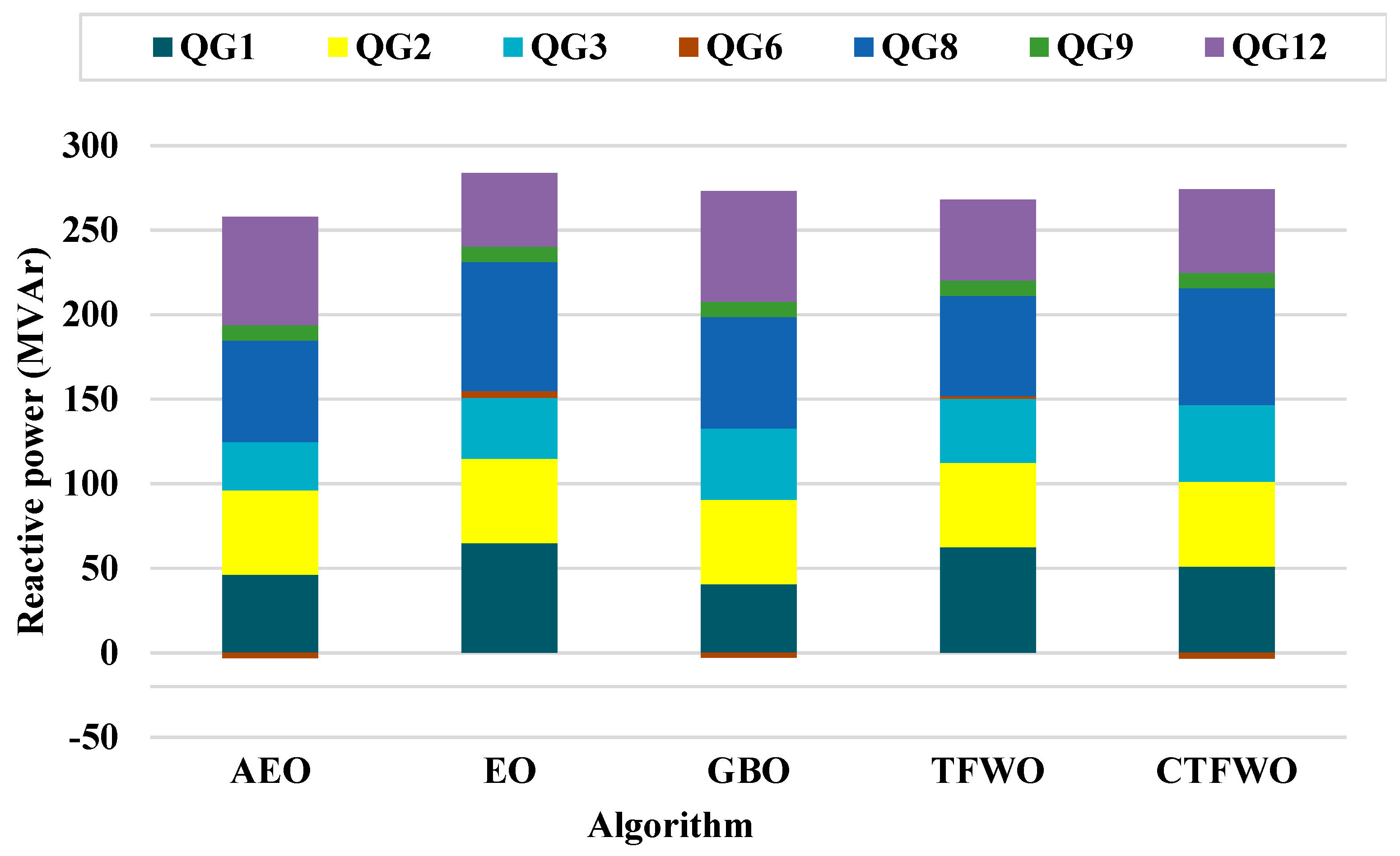

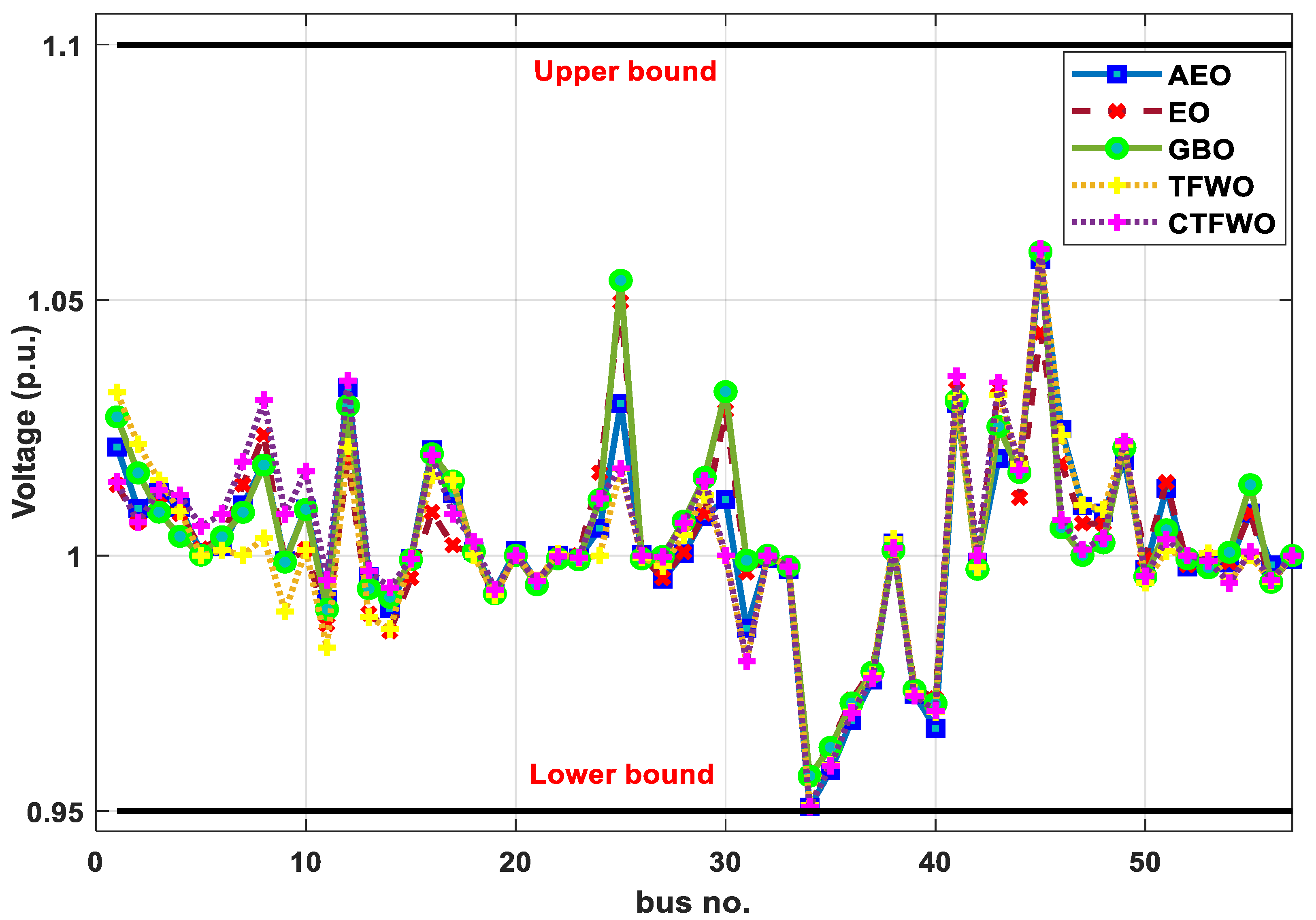
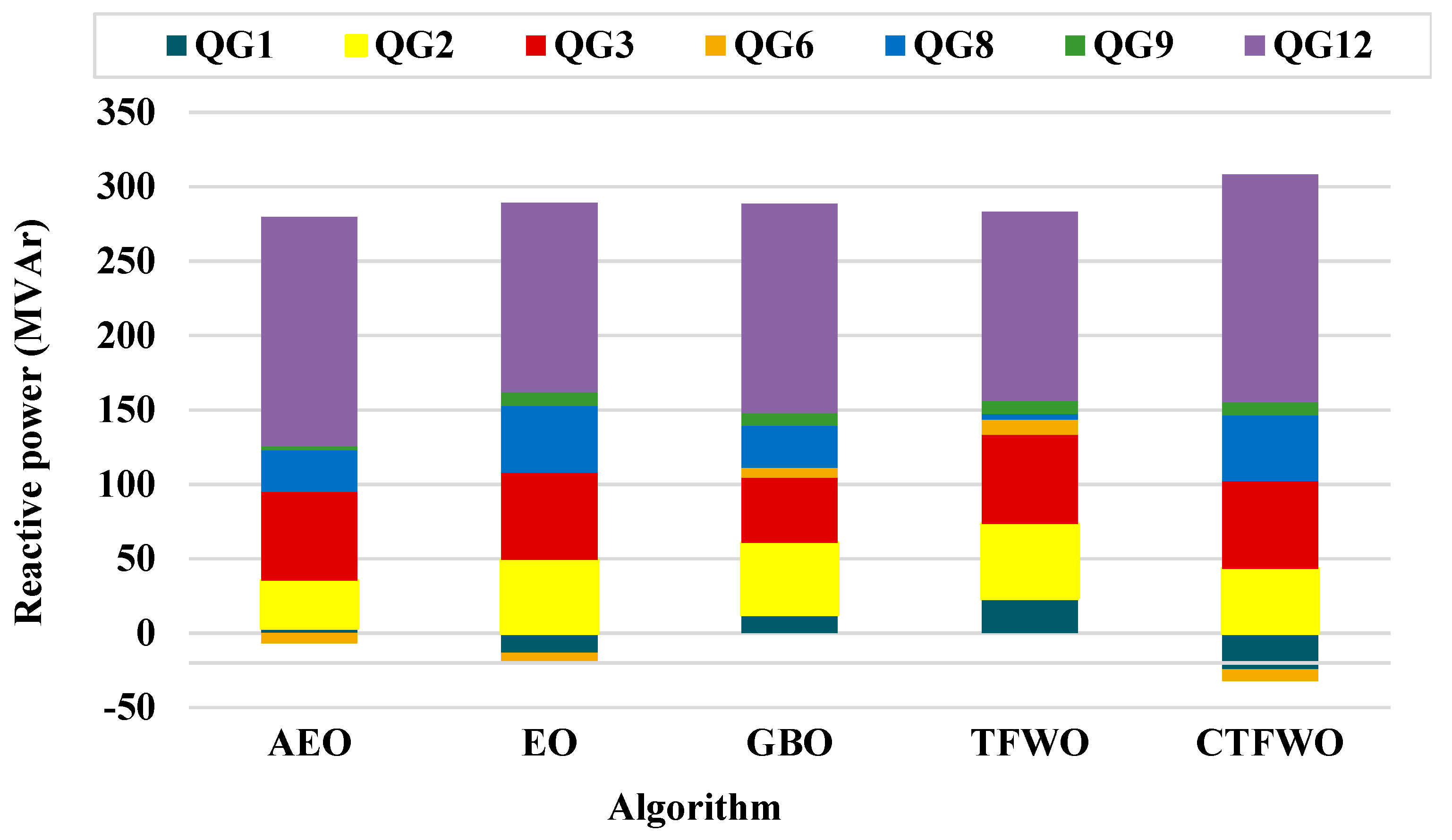
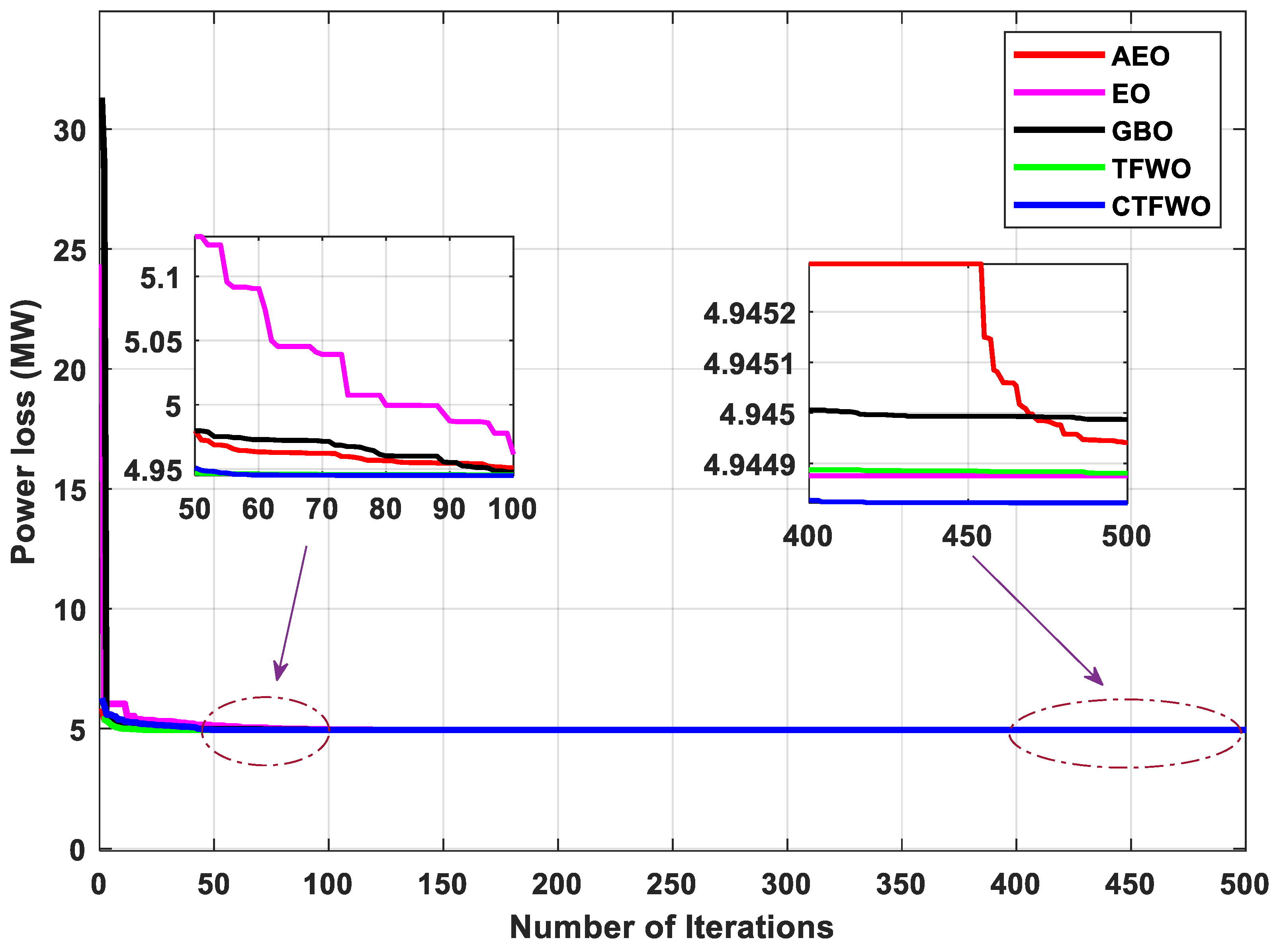
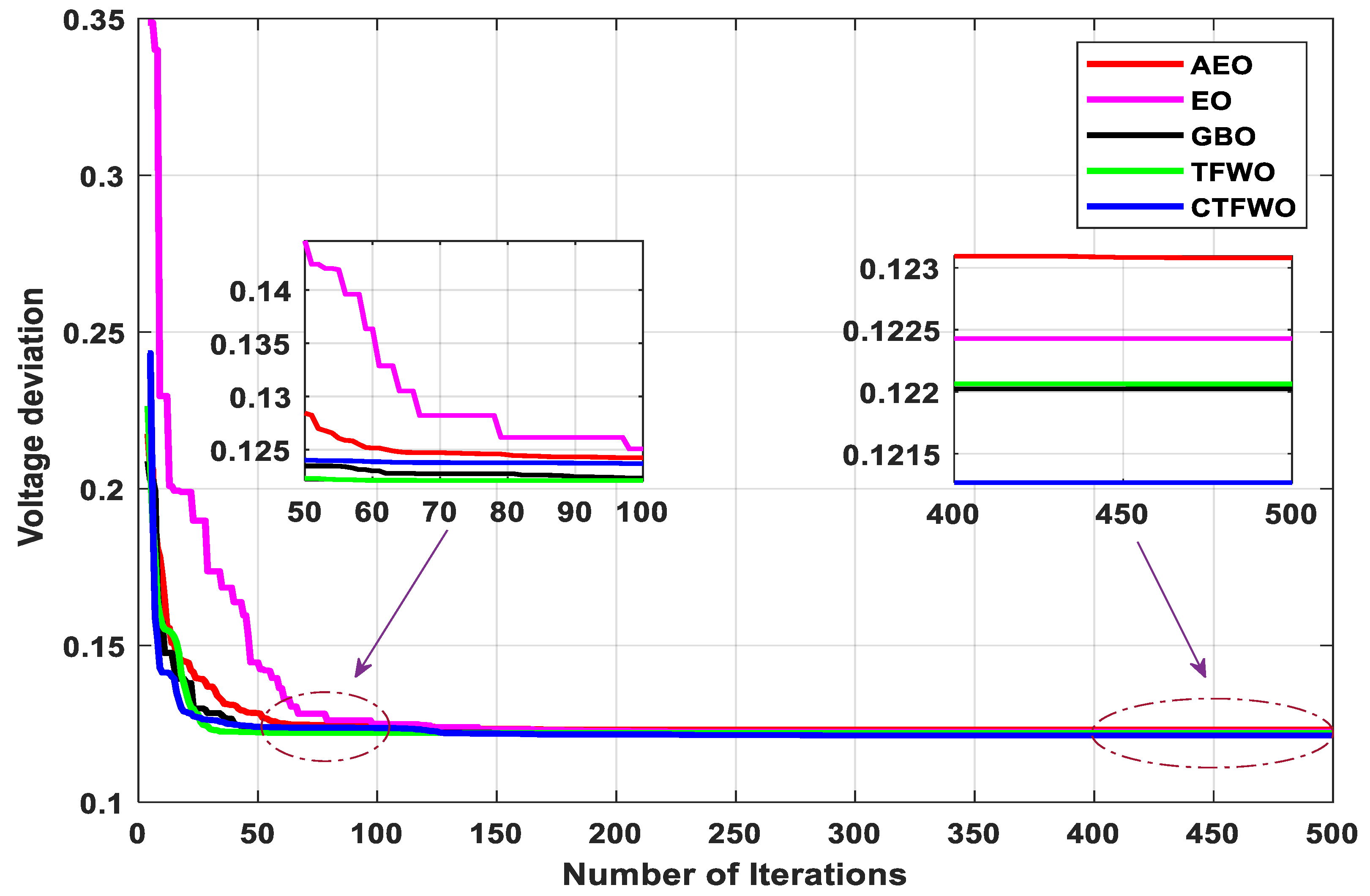


| Description | IEEE 30 Bus | IEEE 57 Bus |
|---|---|---|
| Buses, NB | 30 | 57 |
| Generators, NG | 6 | 7 |
| Transformers, NT | 4 | 15 |
| Shunts, NQ | 9 | 3 |
| Branches, NE | 41 | 80 |
| Equality constraints | 60 | 114 |
| Inequality constraints | 125 | 245 |
| Control variables | 19 | 27 |
| Discrete variables | 6 | 20 |
| Base case for Ploss, MW | 5.660 | 27.8637 |
| Base case for TVD, p.u. | 0.58217 | 1.23358 |
| Parameters | Min | Max | Case 1 (Min Ploss) | ||||
|---|---|---|---|---|---|---|---|
| AEO | EO | GBO | TFWO | CTFWO | |||
| Generator voltage | |||||||
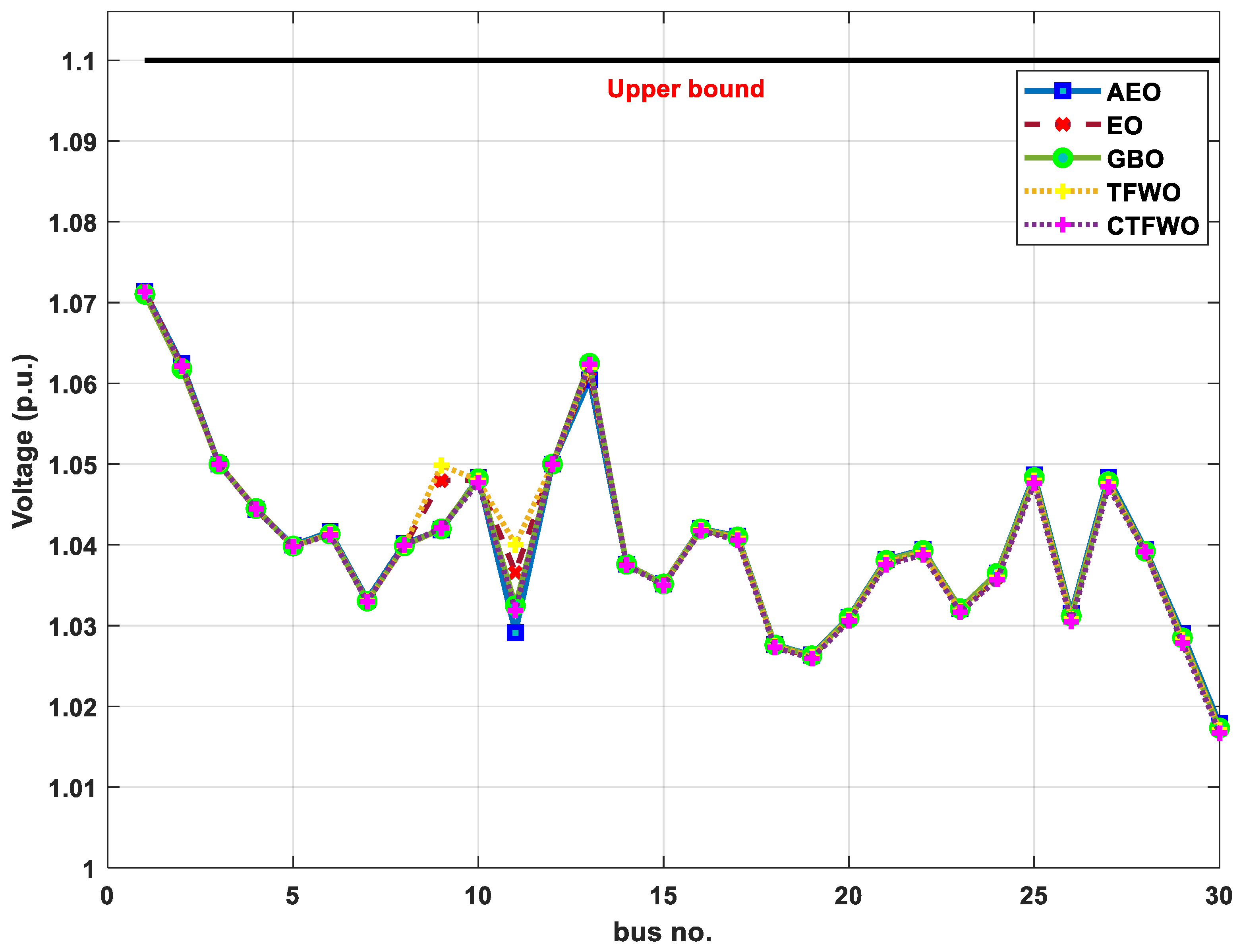
| V1 (p.u.) | 0.95 | 1.1 | 1.071383 | 1.071472 | 1.071032 | 1.071288 | 1.071342 |
| V2 (p.u.) | 0.95 | 1.1 | 1.062422 | 1.062185 | 1.061796 | 1.062056 | 1.06216 |
| V5 (p.u.) | 0.95 | 1.1 | 1.039959 | 1.039844 | 1.039846 | 1.039836 | 1.039794 |
| V8 (p.u.) | 0.95 | 1.1 | 1.040165 | 1.039817 | 1.039876 | 1.039847 | 1.039981 |
| V11 (p.u.) | 0.95 | 1.1 | 1.029138 | 1.036577 | 1.032475 | 1.040013 | 1.031899 |
| V13 (p.u.) | 0.95 | 1.1 | 1.060438 | 1.06159 | 1.062488 | 1.061949 | 1.062353 |
| Transformer tap ratio | |||||||
| T11 (p.u.) | 0.9 | 1.1 | 1.0131 | 0.996542 | 1.01535 | 0.992784 | 1.013433 |
| T12 (p.u.) | 0.9 | 1.1 | 0.908055 | 0.926149 | 0.900161 | 0.93027 | 0.900373 |
| T15 (p.u.) | 0.9 | 1.1 | 0.981065 | 0.982578 | 0.984448 | 0.983187 | 0.983546 |
| T36 (p.u.) | 0.9 | 1.1 | 0.986214 | 0.986534 | 0.986786 | 0.986749 | 0.987144 |
| Capacitor bank | |||||||
| QC10 (MVAr) | 0 | 5 | 2.578379 | 0.8186 | 0.521123 | 0 | 0.005125 |
| QC12 (MVAr) | 0 | 5 | 0.109959 | 0 | 0.260124 | 0 | 0 |
| QC15 (MVAr) | 0 | 5 | 4.465515 | 4.99961 | 4.99989 | 1.870626 | 1.870944 |
| QC17 (MVAr) | 0 | 5 | 1.942079 | 0.000254 | 0.080239 | 0.582313 | 0.792172 |
| QC20 (MVAr) | 0 | 5 | 0.672555 | 0.327968 | 1.739245 | 1.047382 | 4.978545 |
| QC21 (MVAr) | 0 | 5 | 2.894689 | 4.687609 | 0.509966 | 4.261626 | 2.360041 |
| QC23 (MVAr) | 0 | 5 | 3.222698 | 2.5062 | 4.03902 | 0 | 0.002876 |
| QC24 (MVAr) | 0 | 5 | 1.608914 | 4.962173 | 1.747189 | 4.089292 | 3.716173 |
| QC29 (MVAr) | 0 | 5 | 1.663508 | 3.687004 | 4.823309 | 0.000215 | 0 |
| Objective function | |||||||
| Ploss (MW) | NA | NA | 4.9449 | 4.944875 | 4.945 | 4.9449 | 4.9448 |
| Generator reactive power | |||||||
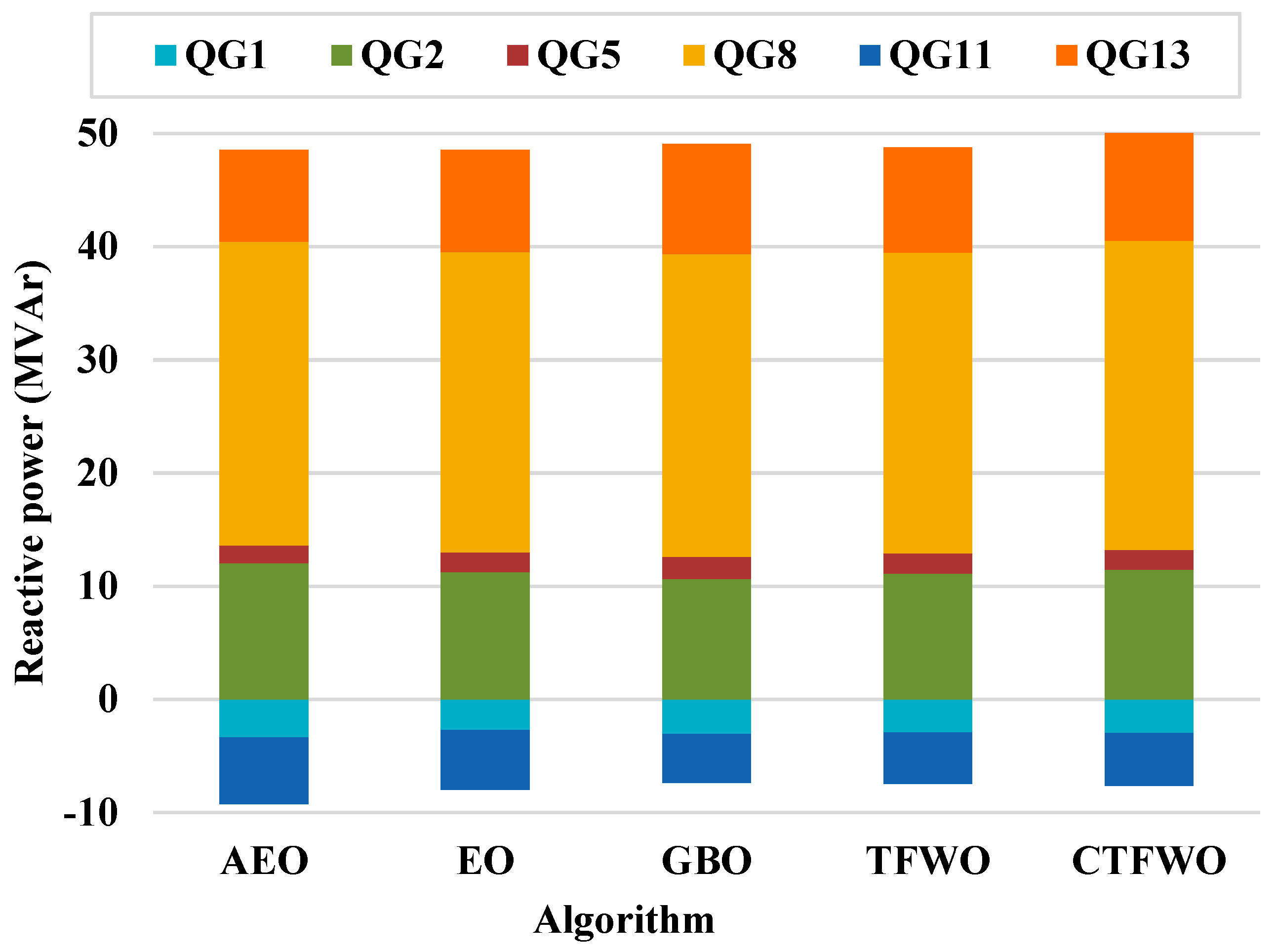
| QG1 (MVAr) | −29.8 | 59.6 | −3.37149 | −2.7178 | −3.06773 | −2.92771 | −2.98714 |
| QG2 (MVAr) | −24 | 48 | 12.04035 | 11.25537 | 10.63886 | 11.10803 | 11.47796 |
| QG5 (MVAr) | −30 | 60 | 1.583144 | 1.733564 | 1.953514 | 1.785632 | 1.750684 |
| QG8 (MVAr) | −26.5 | 53 | 26.77981 | 26.53406 | 26.73682 | 26.56385 | 27.28592 |
| QG11 (MVAr) | −7.5 | 15 | −5.89765 | −5.28439 | −4.32984 | −4.53925 | −4.66229 |
| QG13 (MVAr) | −7.8 | 15.5 | 8.15796 | 9.03965 | 9.728283 | 9.315351 | 9.62484 |
| AEO | EO | GBO | TFWO | CTFWO | |
|---|---|---|---|---|---|
| Worst | 4.9473 | 4.94658 | 4.9755 | 4.9459 | 4.9453 |
| Best | 4.9449 | 4.944875 | 4.945 | 4.9449 | 4.94480 |
| Median | 4.94555 | 4.9453745 | 4.94635 | 4.94515 | 4.9449 |
| Mean | 4.945715 | 4.9455445 | 4.949695 | 4.945205 | 4.944915 |
| Std. Deviation | 0.000640 | 0.00051849 | 0.00797776 | 0.00024381 | 0.00010399 |
| Parameters | Min | Max | Case 2 (Min VD) | ||||
|---|---|---|---|---|---|---|---|
| AEO | EO | GBO | TFWO | CTFWO | |||
| Generator voltage | |||||||
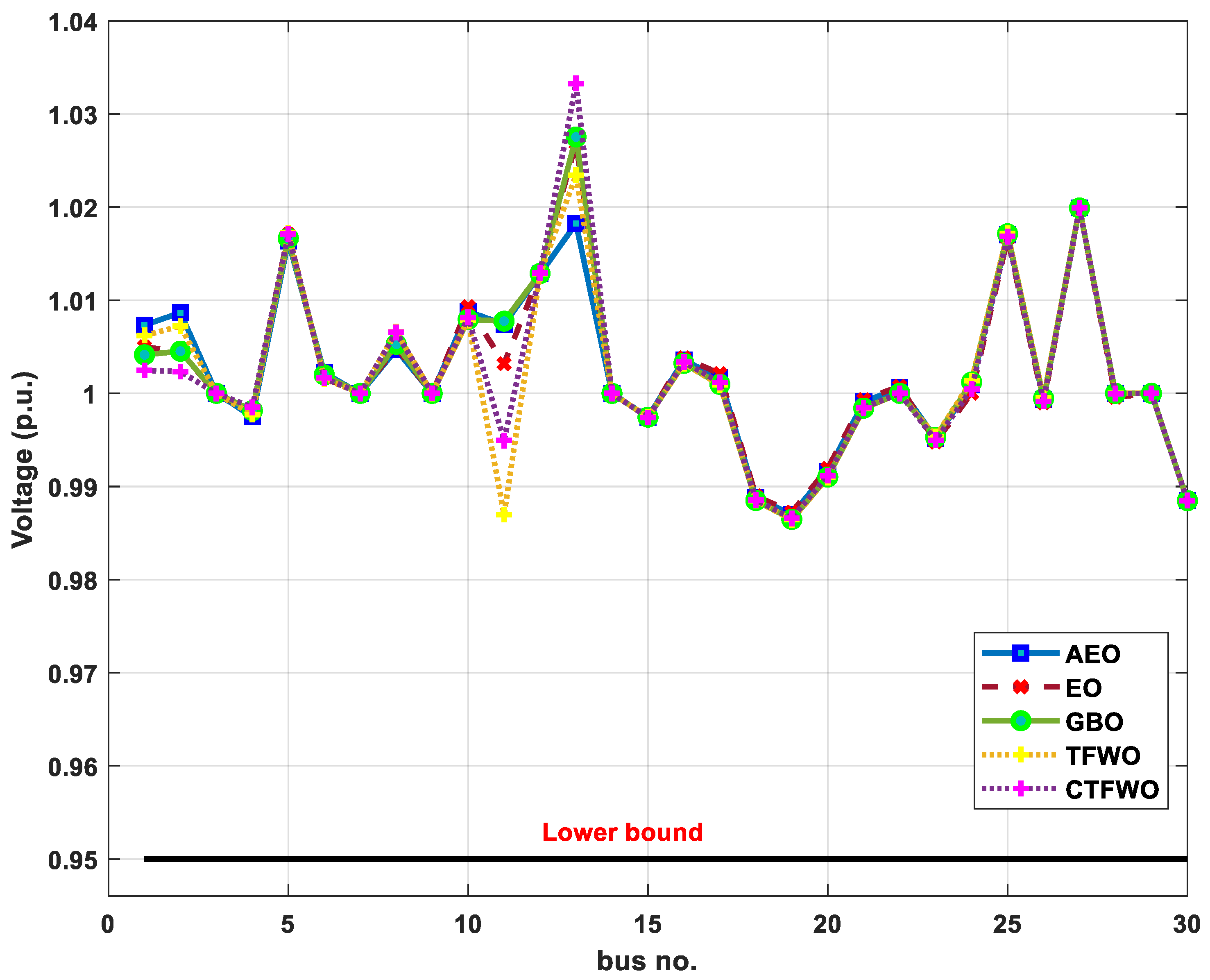
| V1 (p.u.) | 0.95 | 1.1 | 1.007321 | 1.004997 | 1.004141 | 1.006213 | 1.002472 |
| V2 (p.u.) | 0.95 | 1.1 | 1.008668 | 1.00445 | 1.004527 | 1.007222 | 1.002336 |
| V5 (p.u.) | 0.95 | 1.1 | 1.016353 | 1.017078 | 1.016646 | 1.017246 | 1.017129 |
| V8 (p.u.) | 0.95 | 1.1 | 1.004699 | 1.004935 | 1.005271 | 1.006619 | 1.006552 |
| V11 (p.u.) | 0.95 | 1.1 | 1.007415 | 1.003181 | 1.007753 | 0.986987 | 0.994936 |
| V13 (p.u.) | 0.95 | 1.1 | 1.018235 | 1.026852 | 1.027531 | 1.023421 | 1.033269 |
| Transformer tap ratio | |||||||
| T11 (p.u.) | 0.9 | 1.1 | 1.041081 | 1.037017 | 1.039456 | 1.016957 | 1.025889 |
| T12 (p.u.) | 0.9 | 1.1 | 0.906165 | 0.900177 | 0.900001 | 0.907931 | 0.9 |
| T15 (p.u.) | 0.9 | 1.1 | 0.960256 | 0.975119 | 0.975975 | 0.968549 | 0.985956 |
| T36 (p.u.) | 0.9 | 1.1 | 0.969779 | 0.968731 | 0.970034 | 0.97011 | 0.969488 |
| Capacitor bank | |||||||
| QC10 (MVAr) | 0 | 5 | 4.081875 | 4.087516 | 1.027896 | 2.676166 | 1.742964 |
| QC12 (MVAr) | 0 | 5 | 1.911945 | 0.964742 | 2.500364 | 2.653514 | 1.827241 |
| QC15 (MVAr) | 0 | 5 | 2.438076 | 0.000256 | 0.000249 | 4.026815 | 0.007227 |
| QC17 (MVAr) | 0 | 5 | 3.247676 | 4.911974 | 1.68685 | 2.796258 | 3.506281 |
| QC20 (MVAr) | 0 | 5 | 3.134319 | 1.643454 | 1.376082 | 0 | 4.730291 |
| QC21 (MVAr) | 0 | 5 | 4.002702 | 4.993874 | 4.776548 | 4.999999 | 2.19 × 10−6 |
| QC23 (MVAr) | 0 | 5 | 0.939362 | 0.04512 | 1.097063 | 0.803642 | 2.934356 |
| QC24 (MVAr) | 0 | 5 | 3.314184 | 1.963021 | 4.074833 | 1.928107 | 0.020687 |
| QC29 (MVAr) | 0 | 5 | 1.517154 | 1.885478 | 3.257629 | 0.001063 | 3.853446 |
| Objective function | |||||||
| VD (p.u.) | NA | NA | 0.12308 | 0.122428 | 0.12202 | 0.12206 | 0.12127 |
| Generator reactive power | |||||||
| QG1 (MVAr) | −29.8 | 59.6 | −29.799 | −27.7386 | −29.8 | −29.8 | −29.7778 |
| QG2 (MVAr) | −24 | 48 | 4.050136 | −6.40245 | −4.69091 | 0.917091 | −9.34062 |
| QG5 (MVAr) | −30 | 60 | 27.13882 | 30.35612 | 29.72286 | 29.12533 | 31.54037 |
| QG8 (MVAr) | −26.5 | 53 | 38.5871 | 40.69673 | 40.73791 | 45.66735 | 45.28808 |
| QG11 (MVAr) | −7.5 | 15 | 4.004549 | 1.949049 | 4.169385 | −5.75336 | −2.00473 |
| QG13 (MVAr) | −7.8 | 15.5 | 4.203959 | 10.50824 | 11.02679 | 7.990866 | 15.27388 |
| AEO | EO | GBO | TFWO | CTFWO | |
|---|---|---|---|---|---|
| Worst | 0.12811 | 0.128889 | 0.12655 | 0.12498 | 0.12365 |
| Best | 0.12308 | 0.122428 | 0.12202 | 0.12206 | 0.12127 |
| Median | 0.1244 | 0.124771 | 0.12379 | 0.12367 | 0.122195 |
| Mean | 0.124646 | 0.12517885 | 0.1238055 | 0.123365 | 0.122363 |
| Std. Deviation | 0.001245 | 0.00159252 | 0.00104612 | 0.000920 | 0.000794686 |
| Parameters | Min | Max | Case 3 (Min Ploss) | ||||
|---|---|---|---|---|---|---|---|
| AEO | EO | GBO | TFWO | CTFWO | |||
| Generator voltage | |||||||
| V1 (p.u.) | 0.95 | 1.1 | 1.084262 | 1.088584 | 1.083097 | 1.088347 | 1.086947 |
| V2 (p.u.) | 0.95 | 1.1 | 1.073155 | 1.076589 | 1.072353 | 1.076389 | 1.076199 |
| V3 (p.u.) | 0.95 | 1.1 | 1.060508 | 1.061101 | 1.060881 | 1.060936 | 1.064546 |
| V6 (p.u.) | 0.95 | 1.1 | 1.054363 | 1.05593 | 1.054203 | 1.052998 | 1.055437 |
| V8 (p.u.) | 0.95 | 1.1 | 1.072266 | 1.074526 | 1.07583 | 1.069332 | 1.075181 |
| V9 (p.u.) | 0.95 | 1.1 | 1.043366 | 1.040742 | 1.046384 | 1.03933 | 1.043497 |
| V12 (p.u.) | 0.95 | 1.1 | 1.051094 | 1.043244 | 1.053073 | 1.044047 | 1.046439 |
| Transformer tap ratio | |||||||
| T19 (p.u.) | 0.9 | 1.1 | 19.89077 | 13.69412 | 7.408436 | 9.135741 | 8.562415 |
| T20 (p.u.) | 0.9 | 1.1 | 10.16505 | 15.49922 | 10.68707 | 8.746681 | 15.89978 |
| T31 (p.u.) | 0.9 | 1.1 | 11.50229 | 13.62317 | 10.5197 | 10.15296 | 13.51124 |
| T35 (p.u.) | 0.9 | 1.1 | 19.99983 | 4.99742 | 8.079208 | 8.39333 | 9.863767 |
| T36 (p.u.) | 0.9 | 1.1 | 3.869202 | 15.18321 | 12.87629 | 18.10179 | 8.393917 |
| T37 (p.u.) | 0.9 | 1.1 | 16.57872 | 10.01611 | 9.812319 | 10.48957 | 10.46434 |
| T41 (p.u.) | 0.9 | 1.1 | 15.42004 | 9.173277 | 9.720015 | 9.478536 | 9.601751 |
| T46 (p.u.) | 0.9 | 1.1 | 5.798275 | 3.498912 | 4.356667 | 5.942918 | 4.812247 |
| T54 (p.u.) | 0.9 | 1.1 | 14.06045 | 0.000382 | 8.26881 | 5.02964 | 6.24 × 10−1 |
| T58 (p.u.) | 0.9 | 1.1 | 8.591331 | 8.13231 | 8.255977 | 8.793688 | 8.864324 |
| T59 (p.u.) | 0.9 | 1.1 | 7.440277 | 8.03943 | 9.558948 | 6.840257 | 7.132084 |
| T65 (p.u.) | 0.9 | 1.1 | 9.010086 | 8.982809 | 10.26309 | 7.232212 | 7.519419 |
| T66 (p.u.) | 0.9 | 1.1 | 4.49412 | 4.778383 | 5.390395 | 3.8371 | 4.15625 |
| T71 (p.u.) | 0.9 | 1.1 | 7.729125 | 9.197826 | 6.989455 | 6.203619 | 7.338977 |
| T73 (p.u.) | 0.9 | 1.1 | 14.15773 | 1.179605 | 10.40507 | 10.28327 | 8.63043 |
| T76 (p.u.) | 0.9 | 1.1 | 10.54353 | 5.89709 | 6.67063 | 7.707681 | 5.909717 |
| T80 (p.u.) | 0.9 | 1.1 | 14.3393 | 7.510371 | 9.155039 | 8.080104 | 8.890491 |
| Capacitor bank | |||||||
| QC18 (MVAr) | 0 | 20 | 24.44492 | 12.17391 | 8.353978 | 7.752999 | 12.36848 |
| QC25 (MVAr) | 0 | 20 | 16.00438 | 14.4781 | 14.66842 | 16.74156 | 11.78276 |
| QC53 (MVAr) | 0 | 20 | 16.51053 | 1.745298 | 15.49276 | 15.08808 | 14.34732 |
| Objective function | |||||||
| Ploss (MW) | NA | NA | 23.4554 | 23.68991 | 23.4998 | 23.3654 | 23.3235 |
| Generator reactive power | |||||||
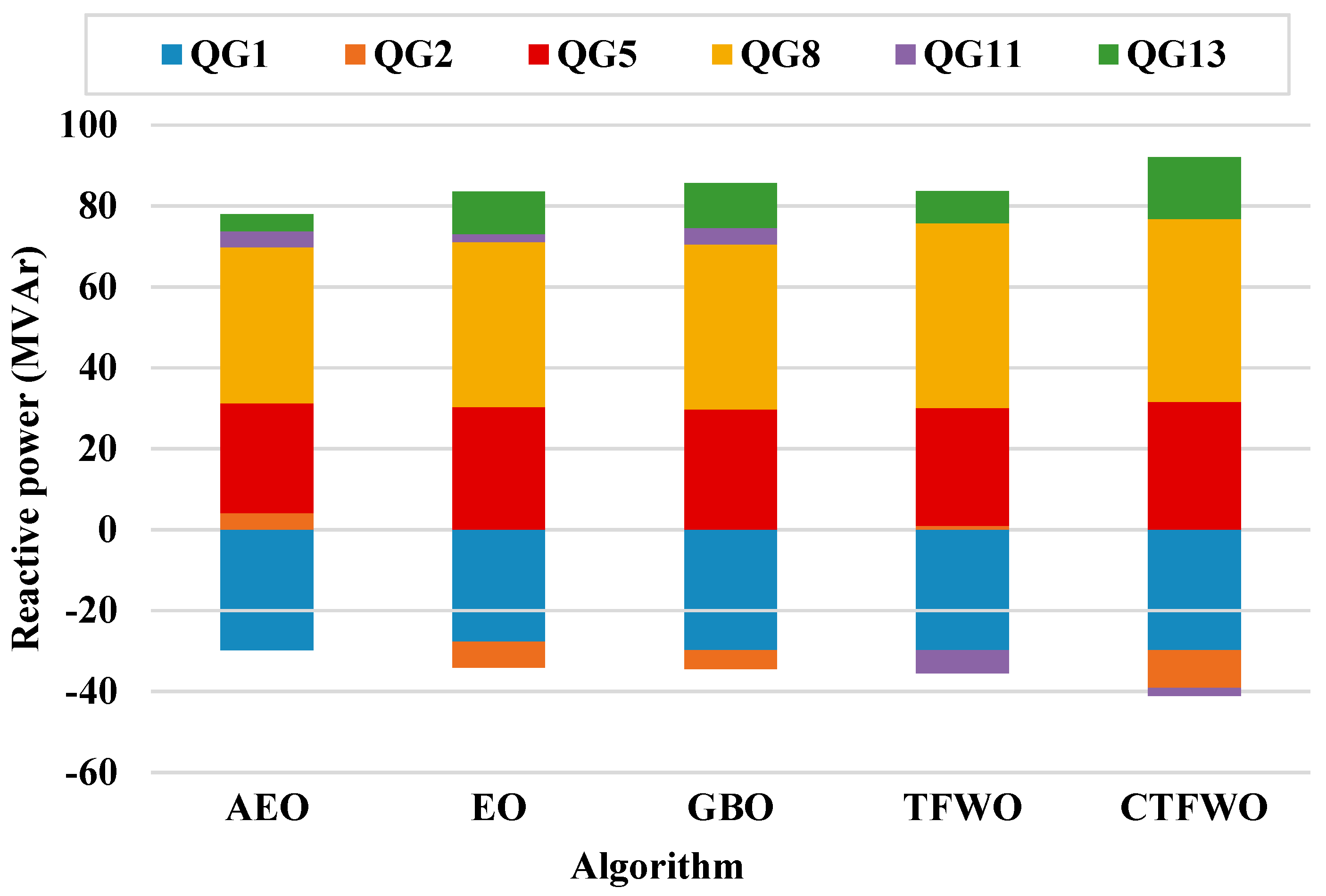
| QG1 (MVAr) | −140 | 200 | 46.0987 | 64.86378 | 40.53132 | 62.32991 | 51.02177 |
| QG2 (MVAr) | −17 | 50 | 49.99321 | 49.89506 | 49.99514 | 50 | 49.99121 |
| QG3 (MVAr) | −10 | 60 | 28.60956 | 35.96237 | 42.07875 | 38.02165 | 45.49167 |
| QG6 (MVAr) | −8 | 25 | −3.05249 | 4.164812 | −2.94065 | 1.498968 | −3.36924 |
| QG8 (MVAr) | −140 | 200 | 60.07686 | 76.3103 | 66.07949 | 59.34457 | 69.22393 |
| QG9 (MVAr) | −3 | 9 | 8.999705 | 8.943546 | 8.999614 | 8.999999 | 8.999902 |
| QG12 (MVAr) | −150 | 155 | 64.08973 | 43.69682 | 65.40404 | 47.77938 | 49.32905 |
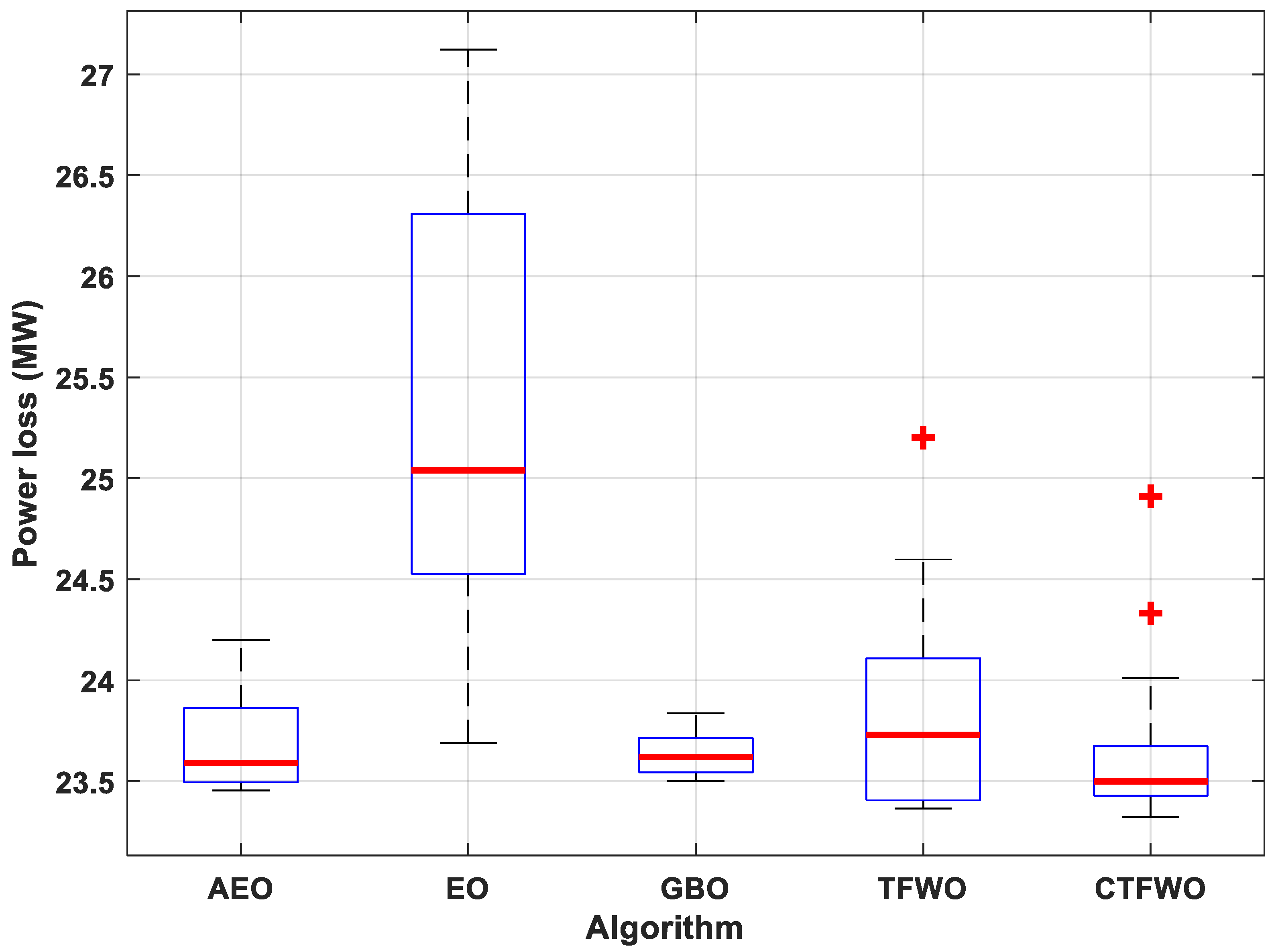
| AEO | EO | GBO | TFWO | CTFWO | |
|---|---|---|---|---|---|
| Worst | 24.1993 | 27.12346 | 23.8371 | 25.201 | 24.9111 |
| Best | 23.4554 | 23.68991 | 23.4998 | 23.3654 | 23.3235 |
| Median | 23.5902 | 25.03884 | 23.61985 | 23.7303 | 23.4988 |
| Mean | 23.683825 | 25.368013 | 23.63577 | 23.833395 | 23.639485 |
| Std. Deviation | 0.24361589 | 1.055693 | 0.10222382 | 0.4940579 | 0.38384166 |
| Parameters | Min | Max | Case 4 (Min VD) | ||||
|---|---|---|---|---|---|---|---|
| AEO | EO | GBO | TFWO | CTFWO | |||
| Generator voltage | |||||||
| V1 (p.u.) | 0.95 | 1.1 | 1.021242 | 1.013827 | 1.027151 | 1.031907 | 1.014437 |
| V2 (p.u.) | 0.95 | 1.1 | 1.009187 | 1.006551 | 1.016181 | 1.021767 | 1.006477 |
| V3 (p.u.) | 0.95 | 1.1 | 1.012401 | 1.009924 | 1.008498 | 1.014731 | 1.012832 |
| V6 (p.u.) | 0.95 | 1.1 | 1.001737 | 1.003425 | 1.003667 | 1.001059 | 1.008131 |
| V8 (p.u.) | 0.95 | 1.1 | 1.01807 | 1.023622 | 1.017704 | 1.003394 | 1.030427 |
| V9 (p.u.) | 0.95 | 1.1 | 0.998958 | 0.99855 | 0.998712 | 0.989075 | 1.008076 |
| V12 (p.u.) | 0.95 | 1.1 | 1.032864 | 1.018975 | 1.029294 | 1.021346 | 1.034201 |
| Transformer tap ratio | |||||||
| T19 (p.u.) | 0.9 | 1.1 | 15.41972 | 19.80841 | 4.345691 | 15.27412 | 10.61522 |
| T20 (p.u.) | 0.9 | 1.1 | 11.05992 | 8.455433 | 13.30462 | 7.826019 | 15.278 |
| T31 (p.u.) | 0.9 | 1.1 | 7.143219 | 7.227283 | 7.110257 | 7.249017 | 7.372825 |
| T35 (p.u.) | 0.9 | 1.1 | 19.65228 | 17.31383 | 12.17408 | 10.53058 | 17.76376 |
| T36 (p.u.) | 0.9 | 1.1 | 13.44046 | 19.99667 | 17.53505 | 19.99013 | 20 |
| T37 (p.u.) | 0.9 | 1.1 | 10.13173 | 11.21114 | 10.83356 | 9.719896 | 10.79664 |
| T41 (p.u.) | 0.9 | 1.1 | 10.82383 | 11.1787 | 9.627105 | 9.317074 | 10.74971 |
| T46 (p.u.) | 0.9 | 1.1 | 2.413594 | 3.985416 | 4.097224 | 1.68163 | 1.734963 |
| T54 (p.u.) | 0.9 | 1.1 | 0.032358 | 0.00 | 0.000183 | 2.26 × 10−6 | 0.00 |
| T58 (p.u.) | 0.9 | 1.1 | 3.247924 | 4.735199 | 2.983137 | 2.993189 | 2.95414 |
| T59 (p.u.) | 0.9 | 1.1 | 5.955591 | 6.472745 | 8.943067 | 5.794069 | 8.938434 |
| T65 (p.u.) | 0.9 | 1.1 | 9.137057 | 8.268309 | 10.09535 | 9.793917 | 11.07804 |
| T66 (p.u.) | 0.9 | 1.1 | 2.069724 | 0.419808 | 2.11 × 10−6 | 0.00 | 0.00 |
| T71 (p.u.) | 0.9 | 1.1 | 7.471875 | 5.29712 | 6.490749 | 4.988462 | 6.106468 |
| T73 (p.u.) | 0.9 | 1.1 | 5.314451 | 10.0823 | 9.159237 | 9.145331 | 10.33043 |
| T76 (p.u.) | 0.9 | 1.1 | 1.800253 | 0.00 | 4.71 × 10−5 | 0.00 | 0.00 |
| T80 (p.u.) | 0.9 | 1.1 | 9.097109 | 9.074298 | 8.345625 | 9.10713 | 10.86881 |
| Capacitor bank | |||||||
| QC18 (MVAr) | 0 | 20 | 18.26974 | 19.07913 | 4.726816 | 9.512274 | 19.13888 |
| QC25 (MVAr) | 0 | 20 | 22.14967 | 26.64133 | 23.11284 | 17.50151 | 21.75597 |
| QC53 (MVAr) | 0 | 20 | 27.88595 | 27.89456 | 22.68993 | 28.56028 | 27.37095 |
| Objective function | |||||||
| VD (p.u.) | NA | NA | 0.60495 | 0.596804 | 0.60383 | 0.58588 | 0.58553 |
| Generator reactive power | |||||||
| QG1 (MVAr) | −140 | 200 | 3.364011 | −13.2065 | 12.58937 | 23.46288 | −24.2855 |
| QG2 (MVAr) | −17 | 50 | 31.87596 | 49.2699 | 47.99061 | 49.97456 | 43.33627 |
| QG3 (MVAr) | −10 | 60 | 59.6576 | 58.89933 | 43.98599 | 59.99735 | 58.95072 |
| QG6 (MVAr) | −8 | 25 | −6.96418 | −7.98727 | 6.681949 | 10.26215 | −7.99952 |
| QG8 (MVAr) | −140 | 200 | 28.2041 | 44.74489 | 28.10331 | 3.612073 | 44.07484 |
| QG9 (MVAr) | −3 | 9 | 2.601341 | 8.979909 | 8.692275 | 8.999975 | 8.999156 |
| QG12 (MVAr) | −150 | 155 | 153.8968 | 127.2061 | 140.3891 | 126.7261 | 152.9637 |
| AEO | EO | GBO | TFWO | CTFWO | |
|---|---|---|---|---|---|
| Worst | 0.68792 | 1.067937 | 0.72276 | 0.69456 | 0.61783 |
| Best | 0.60495 | 0.596804 | 0.60383 | 0.58588 | 0.58553 |
| Median | 0.64876 | 0.718362 | 0.63507 | 0.614465 | 0.593385 |
| Mean | 0.6489715 | 0.7751617 | 0.639779 | 0.622149 | 0.596695 |
| Std. Deviation | 0.02736555 | 0.14116848 | 0.02654973 | 0.02774483 | 0.011368281 |
| Test System | Min | Mean |
|---|---|---|
| SF–DE [65] | 4.946 | 4.947 |
| SP–DE [65] | 4.947 | 4.9667 |
| EC–DE [65] | 4.946 | 4.9467 |
| SR–DE [65] | 4.946 | 4.9481 |
| ECHT–DE [65] | 4.947 | 4.9499 |
| ALC-PSO [20] | 5.1861 | - |
| EB [40] | 4.963 | - |
| QODE [33] | 5.2953 | - |
| PSOGWO [68] | 5.09037 | |
| CKHA [54] | 5.1163 | - |
| GA [68] | 5.0977 | - |
| OGSA [20] | 5.1676 | - |
| PSO [68] | 5.1041 | - |
| AEO | 4.9449 | 4.945715 |
| EO | 4.944875 | 4.945545 |
| GBO | 4.945 | 4.949695 |
| TFWO | 4.9449 | 4.945205 |
| CTFWO | 4.9448 | 4.944915 |
| Test System | Min | Mean |
|---|---|---|
| SF–DE [65] | 0.1231 | 0.1243 |
| SP–DE [65] | 0.1224 | 0.1238 |
| EC–DE [65] | 0.1217 | 0.1235 |
| SR–DE [65] | 0.123 | 0.1241 |
| ECHT–DE [65] | 0.1229 | 0.1239 |
| PGSWT-PSO [26] | 0.1539 | 0.2189 |
| PSO-TVAC [26] | 0.2064 | 0.2376 |
| GA [68] | 0.3732 | - |
| SPSO-TVAC [26] | 0.1354 | 0.1558 |
| PSO [68] | 0.2816 | - |
| SWT-PSO [26] | 0.1614 | 0.1814 |
| PSOGWO [68] | 0.278 | - |
| PSO-CF [26] | 0.1287 | 0.1557 |
| AEO | 0.12308 | 0.124646 |
| EO | 0.122428 | 0.125179 |
| GBO | 0.12202 | 0.123806 |
| TFWO | 0.12206 | 0.123365 |
| CTFWO | 0.12127 | 0.122363 |
| Test System | Min | Mean |
|---|---|---|
| SF–DE [65] | 23.363 | 23.7164 |
| SP–DE [65] | 23.35 | 23.6956 |
| EC–DE [65] | 23.34 | 23.792 |
| SR–DE [65] | 23.355 | 23.4392 |
| ECHT–DE [65] | 23.396 | 23.4963 |
| PSO [44] | 24.3826 | - |
| PGA [16] | 23.836 | 24.5448 |
| MCBOA [44] | 23.6943 | - |
| PSO-ICA [21] | 24.1386 | - |
| BA [40] | 24.9254 | - |
| BSO [69] | 24.3744 | - |
| MOGWA [43] | 23.71544 | - |
| ALC-PSO [20] | 23.39 | 23.41 |
| GSA [44] | 24.4922 | - |
| ICA [21] | 24.1607 | - |
| CSA [44] | 24.2619 | - |
| MOALO [70] | 26.593 | - |
| MFOM [40] | 24.25293 | - |
| WCA [51] | 24.82 | - |
| FPA [40] | 24.8419 | - |
| AEO | 23.4554 | 23.68383 |
| EO | 23.68991 | 25.36801 |
| GBO | 23.4998 | 23.63577 |
| TFWO | 23.3654 | 23.8334 |
| CTFWO | 23.3235 | 23.63949 |
| Test System | Min | Mean |
|---|---|---|
| SF–DE [65] | 0.586 | 0.6077 |
| SP–DE [65] | 0.589 | 0.6085 |
| EC–DE [65] | 0.59 | 0.6173 |
| SR–DE [65] | 0.59 | 0.6069 |
| ECHT-DE [65] | 0.588 | 0.6073 |
| ALC-PSO [20] | 0.6634 | 0.6689 |
| NGWCA [51] | 0.6501 | - |
| BA [71] | 0.6434 | 0.6499 |
| OGSA [72] | 0.6982 | - |
| CBA-III [71] | 0.6413 | 0.644 |
| WCA [51] | 0.6631 | - |
| ALO [73] | 0.6666 | 0.7534 |
| CBA-IV [71] | 0.6399 | 0.6424 |
| GBWCA [51] | 0.6501 | - |
| AEO | 0.60495 | 0.648972 |
| EO | 0.596804 | 0.775162 |
| GBO | 0.60383 | 0.639779 |
| TFWO | 0.58588 | 0.622149 |
| CTFWO | 0.58553 | 0.596695 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-El Wahab, A.M.; Kamel, S.; Hassan, M.H.; Mosaad, M.I.; AbdulFattah, T.A. Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm. Mathematics 2022, 10, 346. https://doi.org/10.3390/math10030346
Abd-El Wahab AM, Kamel S, Hassan MH, Mosaad MI, AbdulFattah TA. Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm. Mathematics. 2022; 10(3):346. https://doi.org/10.3390/math10030346
Chicago/Turabian StyleAbd-El Wahab, Ahmed M., Salah Kamel, Mohamed H. Hassan, Mohamed I. Mosaad, and Tarek A. AbdulFattah. 2022. "Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm" Mathematics 10, no. 3: 346. https://doi.org/10.3390/math10030346
APA StyleAbd-El Wahab, A. M., Kamel, S., Hassan, M. H., Mosaad, M. I., & AbdulFattah, T. A. (2022). Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm. Mathematics, 10(3), 346. https://doi.org/10.3390/math10030346









