Thermal Damage Constitutive Model and Brittleness Index Based on Energy Dissipation for Deep Rock
Abstract
:1. Introduction
2. Thermal Damage Constitutive Model
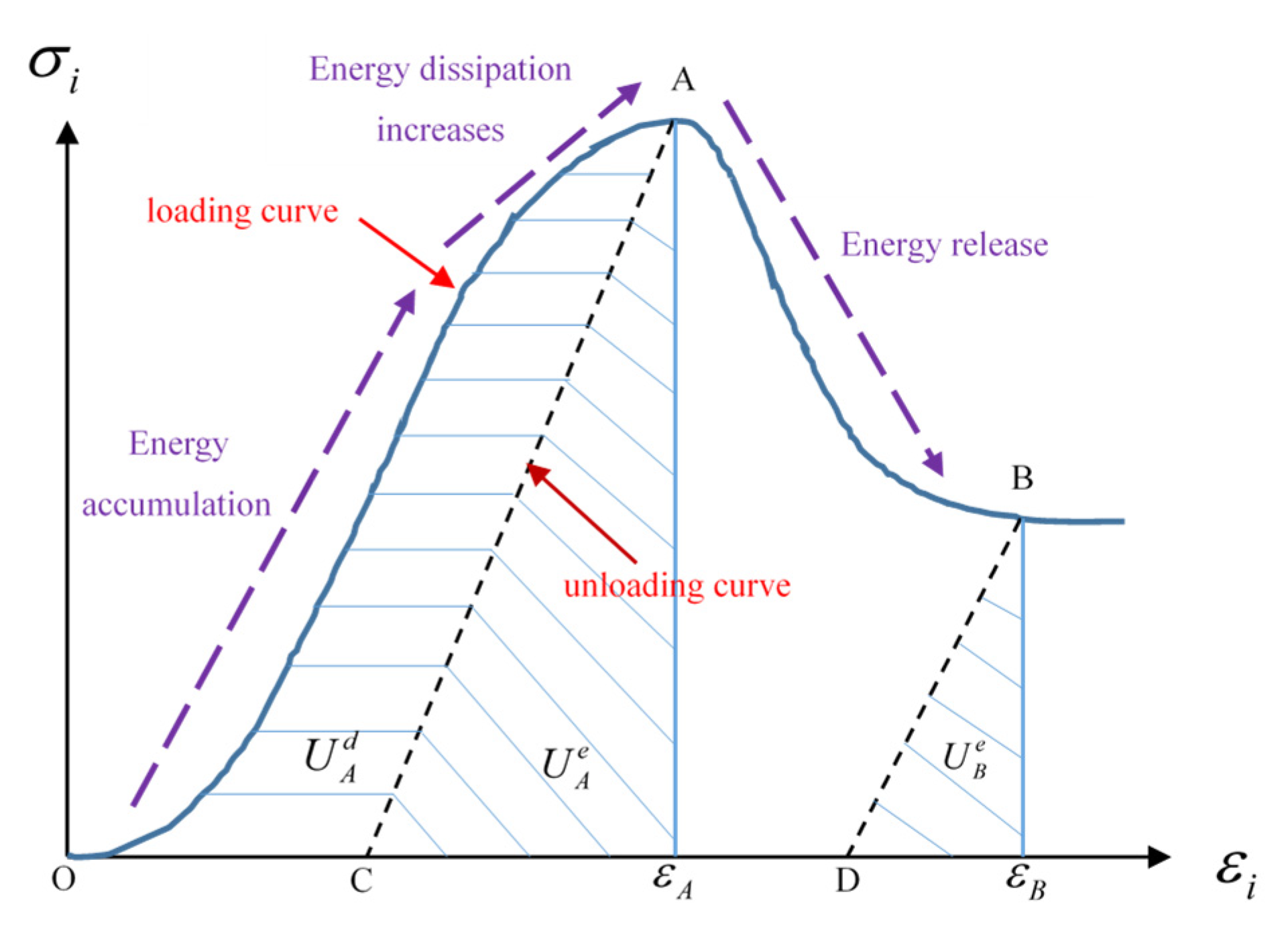
2.1. Energy Theory
2.2. Damage Variable
2.3. Energy Conversion
2.4. Damage Evolutionary
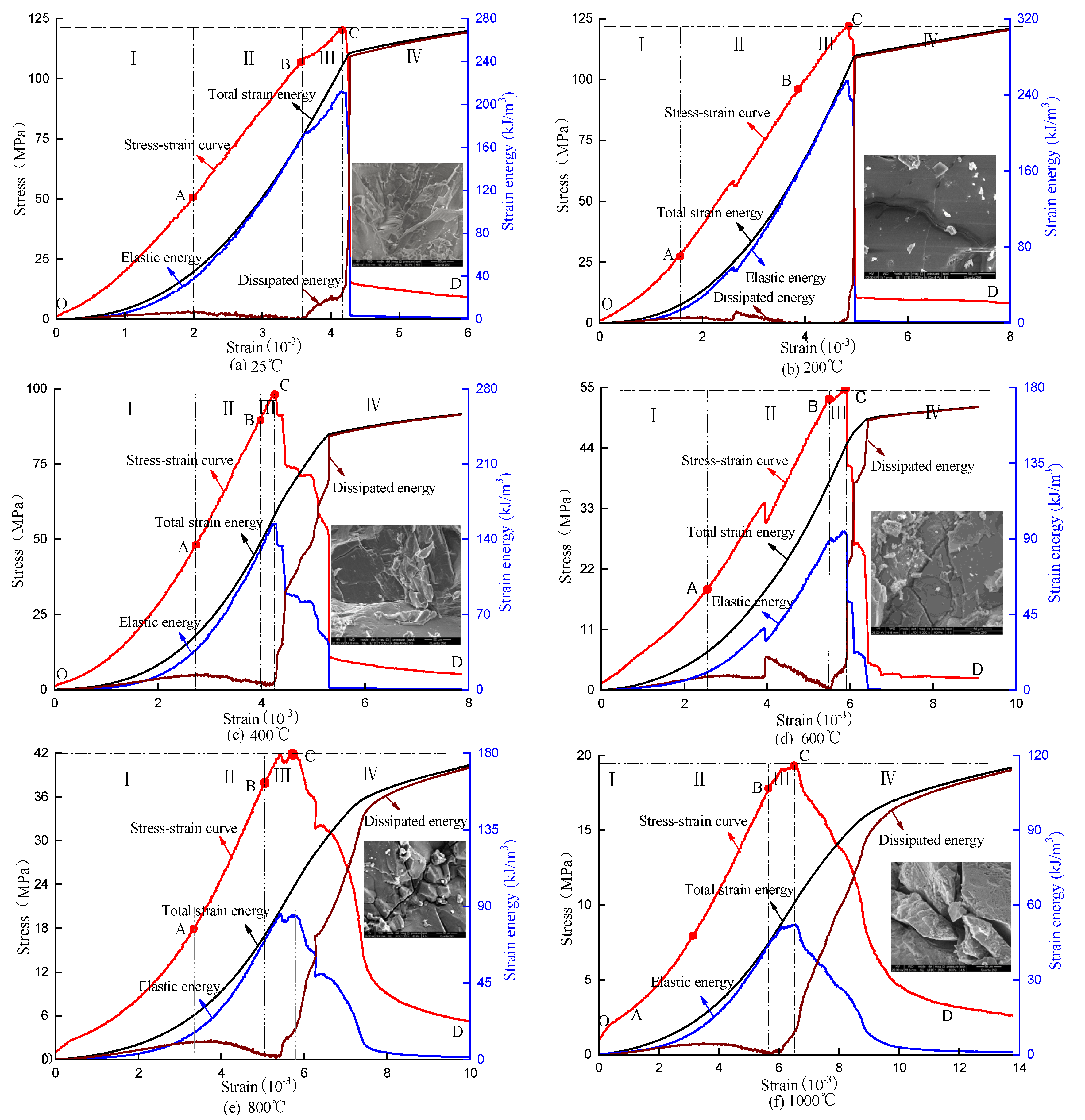
2.5. Model Validation
3. Rock Brittleness Index
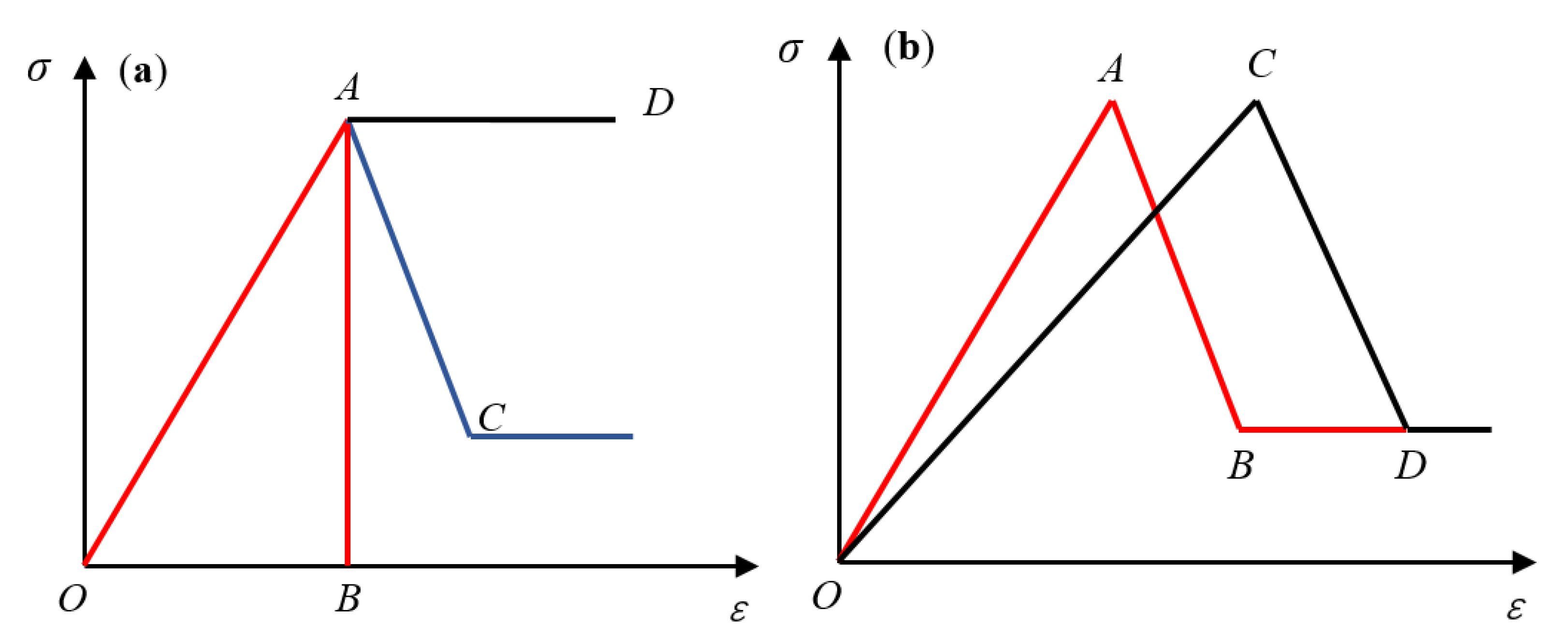
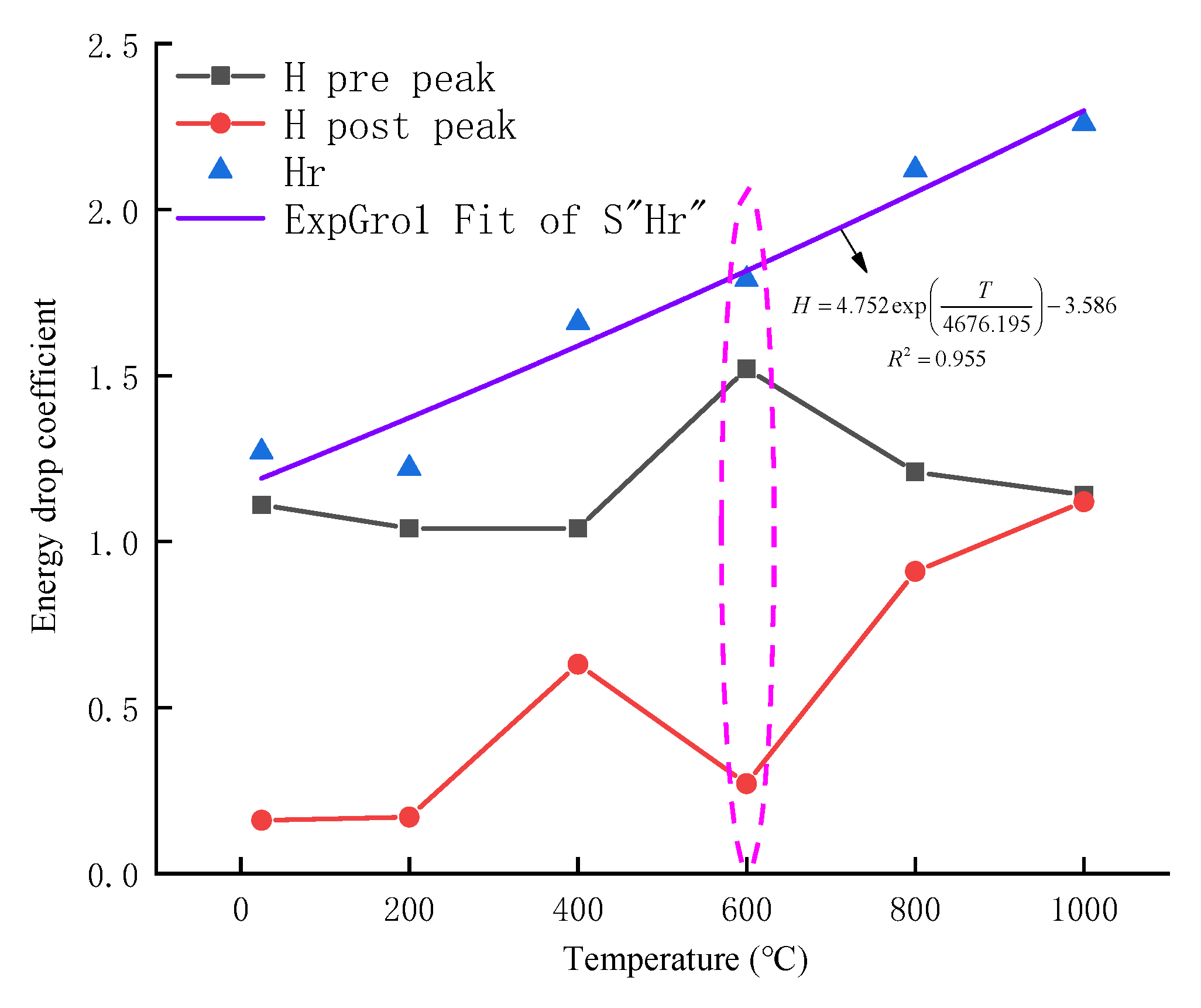
3.1. Energy Drop Coefficient Based on Stress-Strain Curve
3.2. Brittleness Index Based on Energy Drop Coefficient
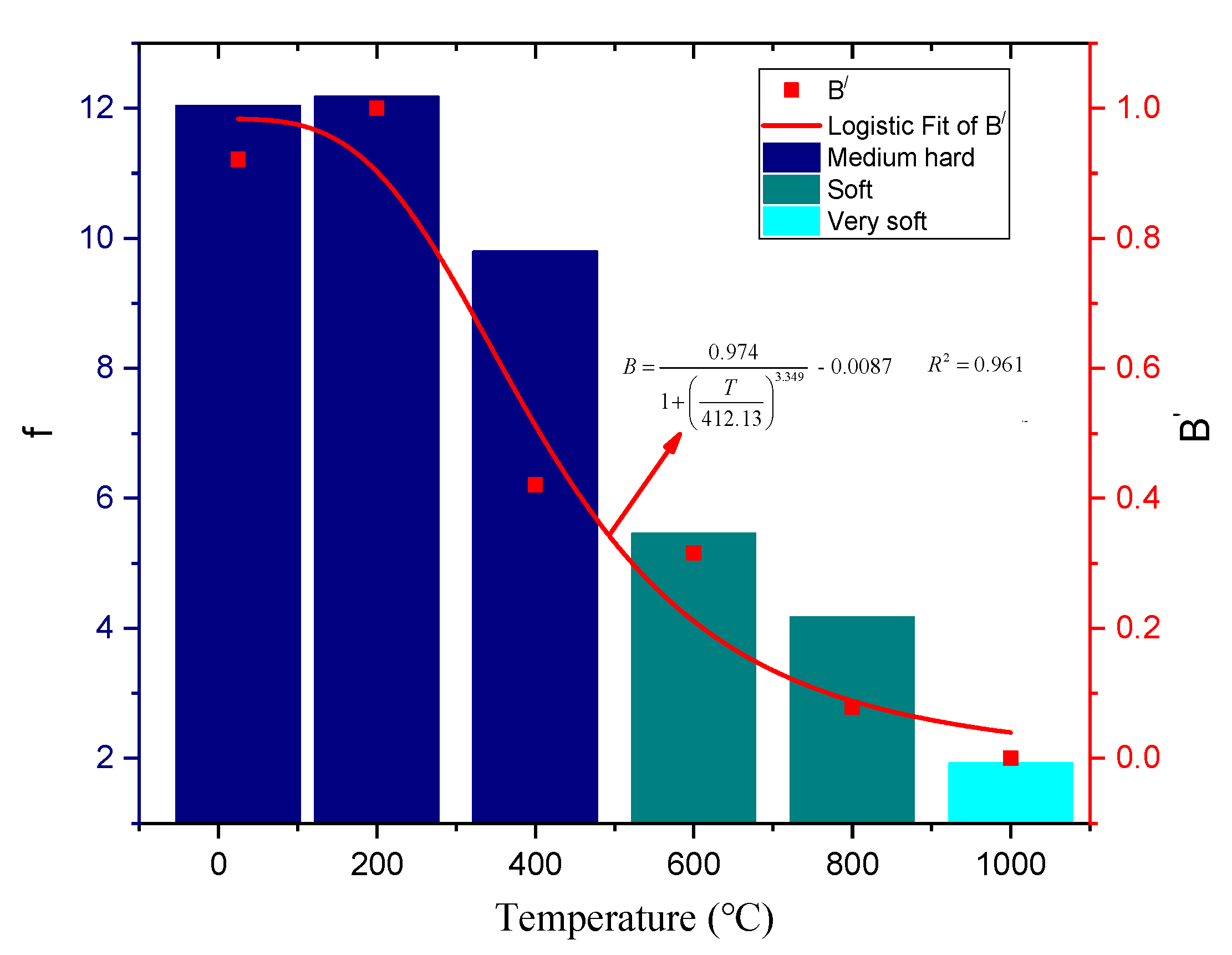
3.3. Proctor Coefficient Based on Rock Compressive Strength
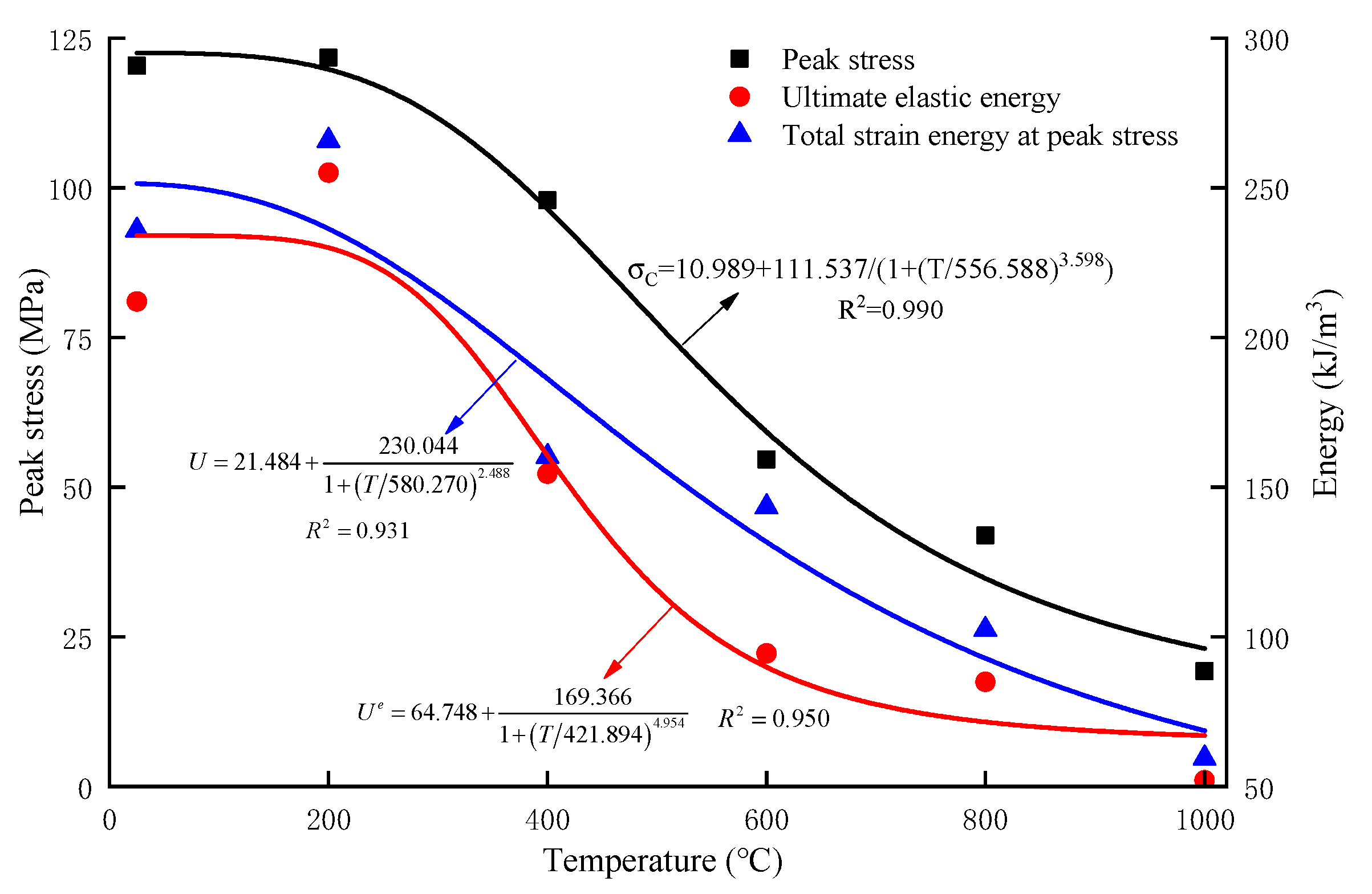
3.4. Brittleness Index and Proctor Coefficient with Temperature
4. Discussion and Conclusions
- (1)
- The peak stress, the ultimate elastic energy and the dissipated energy at the peak value of rock decrease with the increase of temperature in a logistic function, which indicates that the mechanical properties of rock deteriorate with the increase of temperature.
- (2)
- The thermal damage constitutive model established on energy dissipation can reflect stress drop phenomenon at post-peak, describe the full stress–strain curve of rock failure well, verify the rationality of the model, and reflect that the nature failure of rock is the state instability driven by energy, which provides a reference for the establishment of the rock thermal damage constitutive model.
- (3)
- The brittleness index based on the energy drop coefficient decays as a logistic function with the increase of temperature, and the brittleness evaluation results are in good agreement with the actual situation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Ji, H.; Elsworth, D.; Zhi, S.; Lv, X.; Wang, T. Dual-damage constitutive model to define thermal damage in rock. Int. J. Rock Mech. Min. Sci. 2020, 126, 104185. [Google Scholar] [CrossRef]
- Xu, X.; Gao, F.; Zhang, Z. Thermo-mechanical coupling damage constitutive model of rock based on the Hoek–Brown strength criterion. Int. J. Damage Mech. 2018, 27, 1213–1230. [Google Scholar] [CrossRef]
- Wang, Z.L.; Shi, H.; Wang, J.G. Mechanical Behavior and Damage Constitutive Model of Granite Under Coupling of Temperature and Dynamic Loading. Rock Mech. Rock Eng. 2018, 51, 3045–3059. [Google Scholar] [CrossRef]
- Kirmaci, A.; Erkayaoglu, M. Thermographic analysis of failure for different rock types under uniaxial loading. Geomech. Eng. 2020, 23, 503–512. [Google Scholar]
- Li, E.; Gao, L.; Jiang, X.; Duan, J.; Pu, S.; Wang, J. Analysis of dynamic compression property and energy dissipation of salt rock under three-dimensional pressure. Environ. Earth Sci. 2019, 78, 388. [Google Scholar] [CrossRef]
- Zhou, T.B.; Qin, Y.P.; Ma, Q.F.; Liu, J. A constitutive model for rock based on energy dissipation and transformation principles. Arab. J. Geosci. 2019, 12, 492. [Google Scholar] [CrossRef]
- Gong, F.; Yan, J.; Luo, S.; Li, X. Investigation on the Linear Energy Storage and Dissipation Laws of Rock Materials Under Uniaxial Compression. Rock Mech. Rock Eng. 2019, 52, 4237–4255. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Tang, J.; Zhang, L.; Zhou, Y.; Zhu, X.; Jia, D.; Chen, M. Rock damage evolution model of pulsating fracturing based on energy evolution theory. Energy Sci. Eng. 2019, 8, 1050–1067. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.; Ma, J.; Liu, Y. Energy Analysis of the Deformation and Failure Process of Sandstone and Damage Constitutive Model. KSCE J. Civ. Eng. 2018, 23, 513–524. [Google Scholar] [CrossRef]
- Gao, L.; Gao, F.; Zhang, Z.; Xing, Y. Research on the energy evolution characteristics and the failure intensity of rocks. Int. J. Min. Sci. Technol. 2020, 30, 705–713. [Google Scholar] [CrossRef]
- Wang, C.; He, B.; Hou, X.; Li, J.; Liu, L. Stress–Energy Mechanism for Rock Failure Evolution Based on Damage Mechanics in Hard Rock. Rock Mech. Rock Eng. 2020, 53, 1021–1037. [Google Scholar] [CrossRef]
- Miao, S.J.; Liu, Z.J.; Zhao, X.G.; Huang, Z.J. Characteristics of energy dissipation and damage of Beishan granite under cyclic loading and unloading. Chin. J. Rock Mech. Eng. 2021, 40, 928–938. [Google Scholar]
- Zhang, Y.; Zhao, G.-F.; Li, Q. Acoustic emission uncovers thermal damage evolution of rock. Int. J. Rock Mech. Min. Sci. 2020, 132, 104388. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Luo, S.; Li, J.; Huang, D. Theoretical damage characterization and damage evolution process of intact rocks based on linear energy dissipation law under uniaxial compression. Int. J. Rock. Mech. Min. 2021, 146, 104858. [Google Scholar] [CrossRef]
- Xie, H.P.; Ju, Y.; Li, L.Y.; Peng, R.D. Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 2008, 27, 1729–1740. [Google Scholar]
- Yang, S.Q.; Peng, X.; Ranjith, P.G. Damage model of coal under creep and triaxial compression. Int. J. Rock Mech. Min. 2015, 80, 337–345. [Google Scholar] [CrossRef]
- Liu, X.; Ning, J.; Tan, Y.; Gu, Q. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.J.; Zheng, Q.Q.; Ni, X.; Wang, Q.Q. Analysis of energy evolution and damage characteristics of mudstone under cyclic loading and unloading. Chin. J. Rock Mech. Eng. 2019, 38, 2084–2091. [Google Scholar]
- Gao, W.; Chen, X.; Hu, C.; Zhou, C.; Cui, S. New damage evolution model of rock material. Appl. Math. Model. 2020, 86, 207–224. [Google Scholar] [CrossRef]
- Jin, F.N.; Jiang, M.R.; Gao, X.L. Defining damage variable based on energy dissipation. Chin. J. Rock Mech. Eng. 2004, 23, 1976–1980. [Google Scholar]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Cao, R.L.; He, S.H.; Wei, J.; Wang, F. Study of modified statistical damage softening constitutive model for rock considering residual strength. Rock. Soil. Mech. 2013, 34, 1652–1660. [Google Scholar]
- Xu, X.; Karakus, M. A coupled thermo-mechanical damage model for granite. Int. J. Rock Mech. Min. Sci. 2018, 103, 195–204. [Google Scholar] [CrossRef]
- Wang, H.T.; He, M.M.; Pang, F.; Chen, Y.; Zhang, Z. Energy dissipation-based method for brittleness evolution and yield strength determination of rock. J. Petrol. Sci. Eng. 2021, 200, 108376. [Google Scholar] [CrossRef]
- Singh, S. Brittleness and the mechanical winning of coal. Min. Sci. Technol. 1986, 3, 173–180. [Google Scholar] [CrossRef]
- Xia, Y.J.; Li, L.C.; Tang, C.A.; Ma, S. Rock brittleness evaluation based on stress dropping rate after peak stress and energy ratio. Chin. J. Rock Mech. Eng. 2016, 35, 1141–1154. [Google Scholar]
- Yarali, O.; Kahraman, S. The drillability assessment of rocks using the different brittleness values. Tunn. Undergr. Space Technol. 2011, 26, 406–414. [Google Scholar] [CrossRef]
- Chen, G.Q.; Wu, J.C.; Jiang, W.Z.; Li, S.; Qiao, Z.; Yang, W.B. An evaluation method of rock brittleness based on the whole process of elastic energy evolution. Chin. J. Rock Mech. Eng. 2020, 39, 901–911. [Google Scholar]
- Zhang, J.; Ai, C.; Li, Y.W.; Zeng, J.; Qiu, D.Z. Brittleness evaluation index based on energy variation in the whole process of rock failure. Chin. J. Rock Mech. Eng. 2017, 36, 31–45. [Google Scholar]
- Zhang, Y.; Feng, X.-T.; Yang, C.; Han, Q.; Wang, Z.; Kong, R. Evaluation Method of Rock Brittleness under True Triaxial Stress States Based on Pre-peak Deformation Characteristic and Post-peak Energy Evolution. Rock Mech. Rock Eng. 2021, 54, 1277–1291. [Google Scholar] [CrossRef]
- Song, H.Q.; Zuo, J.P.; Chen, Y.; Li, L.; Hong, Z. Revised energy drop coefficient based on energy characteristics in whole process of rock failure. Rock. Soil. Mech. 2019, 40, 91–98. [Google Scholar]
- Баpaнoв, E.Г.; Xu, X.H. Application of Proctor’s firmness coefficient of rock. Min. Eng. 1985, 1, 17–18. [Google Scholar]
- Xu, L.F.; Wang, T. Stability classification of roadways based on testing of rock mechanical properties. Coal Technol. 2017, 36, 90–93. [Google Scholar]
- Zhou, H.; Meng, F.Z.; Liu, H.T.; Zhang, C.Q.; Lu, J.J.; Xu, R.C. Experimental study on characteristics and mechanism of brittle failure of granite. Chin. J. Rock Mech. Eng. 2014, 33, 1822–1827. [Google Scholar]
- Xu, X.L.; Gao, F.; Zhang, Z.Z. Influence of confining pressure on deformation and strength properties of granite after high temperatures. Chin. J. Geotech. Eng. 2014, 36, 2246–2252. [Google Scholar]


| Damage Model | Calibration Test | Researchers |
|---|---|---|
Y is the damage energy release rate; is the initial damage energy release rate; B, n are parameters. | uniaxial cyclic compression tests on sandstone | Xie et al., 2008 [15] |
, are parameters; Ud is the dissipated energy; is the dissipated energy corresponding to the initial damage. | triaxial compression tests on coal in the Xingan mine | Yang et al., 2015 [16] |
is dissipated energy; is constitutive energy. | uniaxial loading tests on sandy mudstones | Liu et al., 2016 [17] |
is the dissipated energy produced by the i-th cycle of specimen; is the total dissipated energy; is the cumulative number of cycles under each level of load (i = 1, 2, 3). | cyclic loading and unloading tests on mudstone in Hunan province of China | Xu et al., 2019 [18] |
Dc, Dt are rock damage in triaxial compression and tension tests respectively, Cc, , Ct and are parameters. | test and simulation of failure process on granite | Gao et al., 2020 [19] |
| T /°C | /GPa | H Pre Peak | H Post Peak | Hr | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 4.16 | 120.37 | 6.03 | 9.24 | 31.31 | 235.86 | 212.08 | 268.71 | 2.73 | 1.11 | 0.16 | 1.27 |
| 200 | 4.83 | 121.77 | 8.00 | 8.36 | 28.56 | 265.79 | 255.07 | 309.69 | 2.45 | 1.04 | 0.17 | 1.22 |
| 400 | 4.23 | 97.94 | 7.86 | 5.08 | 27.54 | 160.23 | 154.48 | 256.45 | 0.94 | 1.04 | 0.63 | 1.66 |
| 600 | 5.86 | 54.62 | 9.09 | 4.82 | 10.78 | 143.40 | 94.53 | 168.48 | 1.47 | 1.52 | 0.27 | 1.79 |
| 800 | 5.77 | 41.77 | 11.06 | 4.19 | 8.74 | 102.44 | 84.98 | 177.94 | 2.01 | 1.21 | 0.91 | 2.12 |
| 1000 | 6.44 | 19.30 | 13.70 | 2.92 | 3.22 | 59.57 | 52.12 | 115.08 | 2.65 | 1.14 | 1.12 | 2.26 |
| T/°C | B | f | ||
|---|---|---|---|---|
| 25 | 1.27 | 0.79 | 0.92 | 12.04 |
| 200 | 1.22 | 0.82 | 1.00 | 12.18 |
| 400 | 1.66 | 0.60 | 0.42 | 9.79 |
| 600 | 1.79 | 0.56 | 0.32 | 5.46 |
| 800 | 2.12 | 0.47 | 0.08 | 4.18 |
| 1000 | 2.26 | 0.44 | 0.00 | 1.93 |
| Hardness of Rock | Very Hard | Hard | Medium Hard | Soft | Very Soft |
|---|---|---|---|---|---|
| Proctor coefficient | >20 | 16–20 | 8–16 | 2–8 | <2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Yue, C.; Xu, L. Thermal Damage Constitutive Model and Brittleness Index Based on Energy Dissipation for Deep Rock. Mathematics 2022, 10, 410. https://doi.org/10.3390/math10030410
Xu X, Yue C, Xu L. Thermal Damage Constitutive Model and Brittleness Index Based on Energy Dissipation for Deep Rock. Mathematics. 2022; 10(3):410. https://doi.org/10.3390/math10030410
Chicago/Turabian StyleXu, Xiaoli, Changqi Yue, and Liqi Xu. 2022. "Thermal Damage Constitutive Model and Brittleness Index Based on Energy Dissipation for Deep Rock" Mathematics 10, no. 3: 410. https://doi.org/10.3390/math10030410
APA StyleXu, X., Yue, C., & Xu, L. (2022). Thermal Damage Constitutive Model and Brittleness Index Based on Energy Dissipation for Deep Rock. Mathematics, 10(3), 410. https://doi.org/10.3390/math10030410






