On Estimating the Parameters of the Beta Inverted Exponential Distribution under Type-II Censored Samples
Abstract
:1. Introduction
2. Method of Estimation
2.1. Maximum Likelihood Estimation
2.2. Bayes Estimation
2.2.1. Case 1: Bayes Estimators When Is Unknown
- SE Loss Function
- ii.
- LINEX Loss Function
- iii.
- GE Loss Function
| Algorithm 1 Importance sampling technique when is unknown based on type-II censored samples. |
|
2.2.2. Case 2: Bayes Estimators When Is Unknown
- SE Loss Function
- ii.
- LINEX Loss Function
- iii.
- GE Loss Function
| Algorithm 2 Importance sampling technique when is unknown based on type-II censored samples. |
|
2.2.3. Case 3: Bayes Estimators When Is Unknown
- SE Loss Function
- ii.
- LINEX Loss Function
- iii.
- GE Loss Function
| Algorithm 3 Importance sampling technique when is unknown based on type-II censored samples. |
|
2.2.4. Case 4: Bayes Estimators When and Are Unknown
- SE Loss Function
- ii.
- LINEX Loss Function
- iii.
- GE Loss Function
| Algorithm 4 Importance sampling technique when and are unknown based on type-II censored samples. |
|
3. Simulation Study
| Algorithm 5 ML method of the parameters , , and based on type-II censored samples. |
|
| Algorithm 6 Bayesian method of the parameters , , , and based on type-II censored samples. |
|
- For Case 1, the Bayes estimates via the standard Bayes technique of , , and perform the estimates better than the ML estimates under the different loss functions, as shown in Table 5. According to Table 6, we note that the ML estimates give better values than the Bayes estimates via the importance sampling technique;
- From Table 5, the Bayes estimates under the GE loss function () are considered the best estimates of ;
- From Table 7, the Bayes estimates of , , and via the standard Bayes technique perform the best based on MSEs and biases at . Furthermore, when , the ML estimates of , , and perform the estimates better than the Bayes estimates;
- When is unknown, the Bayes estimates of via the importance sampling technique perform the best at under the LINEX loss function . For , the ML estimates of give the best estimates. Furthermore, based on the MSEs and biases, the ML estimates of and give the best estimates (see Table 8);
- From Table 11, the ML estimates of , , and perform the best based on the smallest MSEs. Besides, the Bayes estimates of via the importance sampling technique perform the best under the LINEX loss function ().
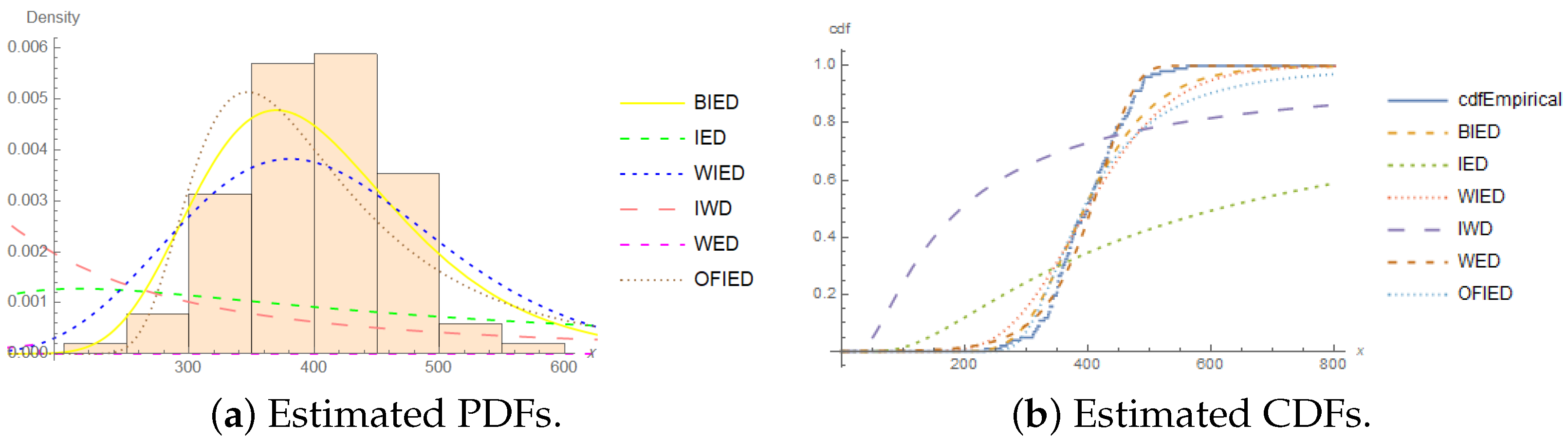
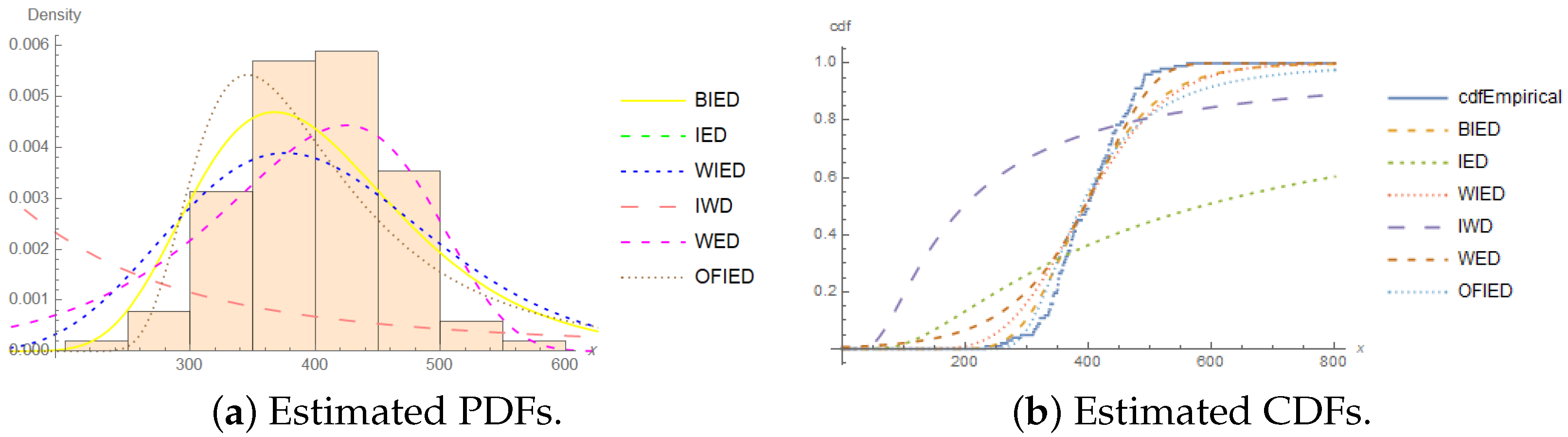
4. Application
- Aluminum coupons’ cut:
- 233, 258, 268, 276, 290, 310, 312, 315, 318, 321, 321, 329, 335, 336,338, 338, 342, 342, 342, 344, 349, 350, 350, 351, 351, 352, 352, 356,358, 358, 360, 362, 363, 366, 367, 370, 370, 372, 372, 374, 375, 376,379, 379, 380, 382, 389, 389, 395, 396, 400, 400, 400, 403, 404, 406,408, 408, 410, 412, 414, 416, 416, 416, 420, 422, 423, 426, 428, 432,432, 433, 433, 437, 438, 439, 439, 443, 445, 445, 452, 456, 456, 460,464, 466, 468, 470, 470, 473, 474, 476, 476, 486, 488, 489, 490, 491,503, 517, 540, 560.
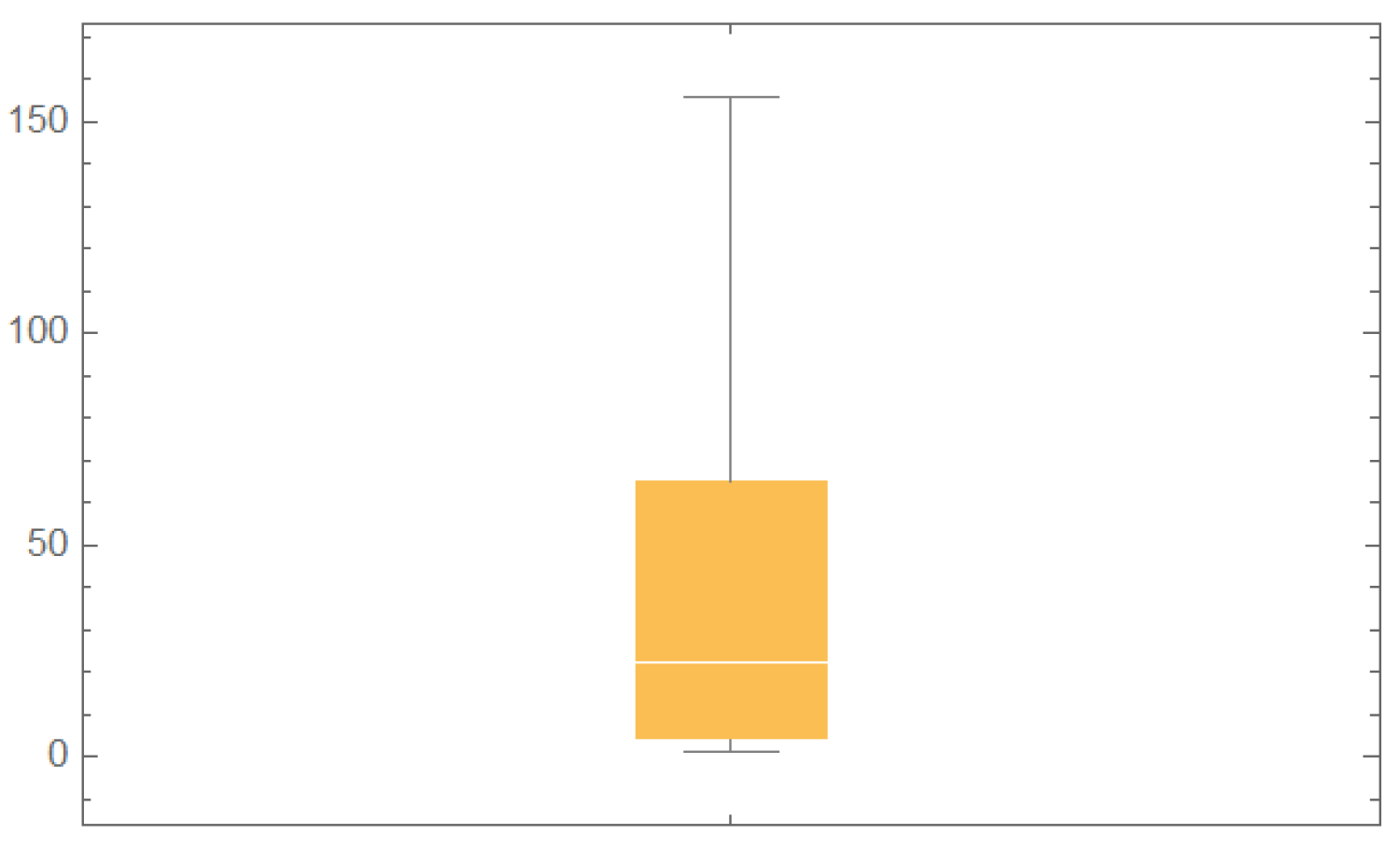
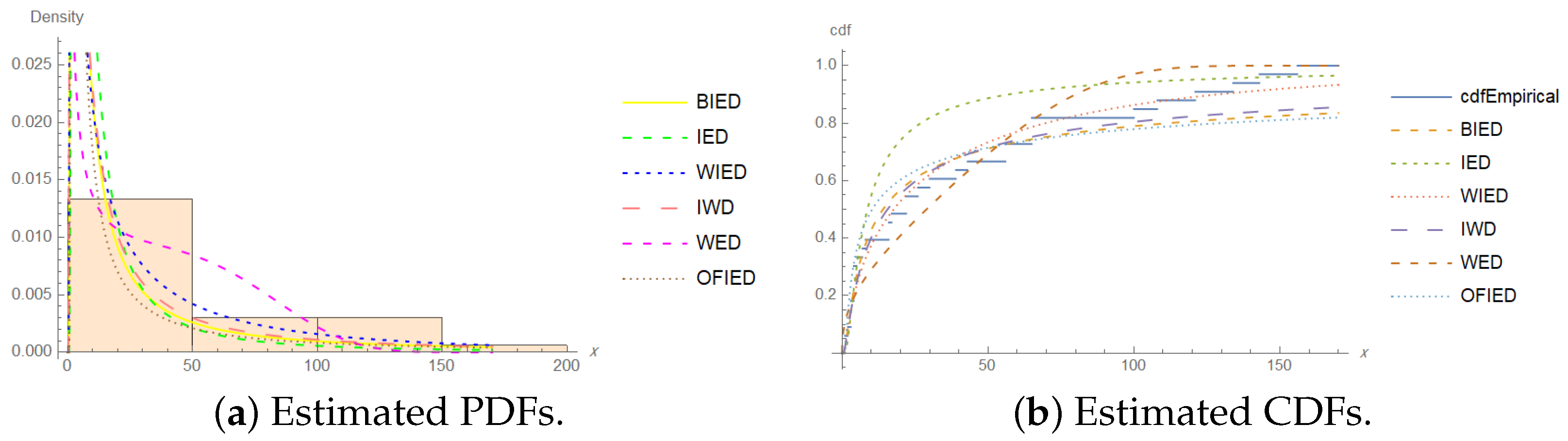
- Patients suffering from acute myelogenous leukemia:
- 1, 1, 2, 3, 3, 3, 4, 4, 4, 4, 5, 7, 8, 16, 16, 17, 22, 22, 26, 30,39, 43, 56, 56, 65, 65, 65, 100, 108, 121, 134, 143, 156
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, U.; Gupta, P.K.; Upadhyay, S.K. Estimation of parameters for exponentiated Wibull family under type-II censoring scheme. Comput. Stat. Data Anal. 2005, 48, 509–523. [Google Scholar] [CrossRef]
- Prakash, G. Some estimation procedures for the inverted exponential distribution. S. Pac. J. Nat. Appl. Sci. 2009, 27, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Dey, T. On progressively censored generalized inverted exponential distribution. J. Appl. Stat. 2014, 41, 2557–2576. [Google Scholar] [CrossRef]
- Singh, B.; Goel, R. The beta inverted exponential distribution: Properties and applications. Int. J. Appl. Sci. Math. 2015, 2, 132–141. [Google Scholar]
- Garg, R.; Dube, M.; Kumar, K.; Krishna, H. On randomly censored generalized inverted exponential distribution. Am. J. Math. Manag. Sci. 2016, 35, 361–379. [Google Scholar] [CrossRef]
- Bakoban, R.; Abu-Zinadah, H.H. The beta generalized inverted exponential distribution with real data applications. REVSTAT-Stat. J. 2017, 15, 65–88. [Google Scholar]
- Aldahlan, M.A. The inverse Weibull inverse exponential distribution with application. Int. J. Contemp. Math. Sci. 2019, 14, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. A First Course in Order Statistics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 2nd ed.; Dover Publication: New York, NY, USA, 1972. [Google Scholar]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions, 1st ed.; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Varian, H.R. A Bayesian approach to real estate assessment. Stud. Bayesian Econom. Stat. Honor. Leonard J. Savage 1975, 5, 195–208. [Google Scholar]
- Calabria, R.; Pulcini, G. An engineering approach to Bayes estimation for the Weibull distribution. Microelectron. Reliab. 1994, 34, 789–802. [Google Scholar] [CrossRef]
- Lin, C.; Duran, B.; Lewis, T. Inverted gamma as a life distribution. Microelectron. Reliab. 1989, 29, 619–626. [Google Scholar] [CrossRef]
- Keller, A.Z.; Kamath, A.R.R. Alternate reliability models for mechanical systems. In Proceedings of the 3rd International Conference on Reliability and Maintainability, Toulouse, France, 18–21 October 1982; pp. 411–415. [Google Scholar]
- Pelumi, E.O.; Adebowale, O.A.; Enahoro, A.O. The Weibull inverted exponential distribution: A generalization of the inverse exponential distribution. In Proceedings of the World Congress on Engineering, London, UK, 5–7 July 2017; Volume 1, pp. 16–19. [Google Scholar]
- Oguntunde, P.; Balogun, O.; Okagbue, H.; Bishop, S. The Weibull exponential distribution: Its properties and applications. J. Appl. Sci. 2015, 15, 1305–1311. [Google Scholar] [CrossRef]
- Alrajhi, S. The odd Fréchet inverse exponential distribution with application. J. Nonlinear Sci. Appl. 2019, 12, 535–542. [Google Scholar] [CrossRef] [Green Version]
- Christie, M.; Cliffe, A.; Dawid, P.; Senn, S.S. Simplicity, Complexity and Modelling; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
- Feigl, P.; Zelen, M. Estimation of exponential survival probabilities with concomitant information. Biometrics 1965, 21, 826–838. [Google Scholar] [CrossRef] [PubMed]

| n | r | ||||||
|---|---|---|---|---|---|---|---|
| 30 | 24 | MLE | 1.27791 | 4.05604 | 2.45134 | 0.73519 | 0.83076 |
| Bias | 0.47791 | 0.05604 | −0.54866 | 0.00615 | 0.01291 | ||
| MSE | 0.65026 | 1.07637 | 0.82283 | 0.00402 | 0.02662 | ||
| 27 | MLE | 0.89924 | 4.01143 | 2.85928 | 0.72555 | 0.82323 | |
| Bias | 0.09924 | 0.01143 | −0.14072 | −0.00349 | 0.00537 | ||
| MSE | 0.07609 | 0.92676 | 0.32039 | 0.00396 | 0.02497 | ||
| 50 | 40 | MLE | 0.88102 | 3.97067 | 2.90404 | 0.73132 | 0.81202 |
| Bias | 0.08102 | −0.02934 | −0.09596 | 0.00227 | −0.00584 | ||
| MSE | 0.05673 | 0.28639 | 0.20724 | 0.00250 | 0.01299 | ||
| 45 | MLE | 0.87403 | 3.95937 | 2.90266 | 0.73291 | 0.80861 | |
| Bias | 0.07403 | −0.04063 | −0.09734 | 0.00386 | −0.00925 | ||
| MSE | 0.03969 | 0.27514 | 0.19996 | 0.00258 | 0.01454 | ||
| 100 | 80 | MLE | 0.86352 | 3.99116 | 2.92567 | 0.73380 | 0.80855 |
| Bias | 0.06352 | −0.00884 | −0.07433 | 0.00475 | −0.00931 | ||
| MSE | 0.03542 | 0.22032 | 0.13827 | 0.00131 | 0.00643 | ||
| 90 | MLE | 0.84168 | 3.98337 | 2.96389 | 0.73189 | 0.81021 | |
| Bias | 0.04168 | −0.01664 | −0.03611 | 0.00285 | −0.00765 | ||
| MSE | 0.02752 | 0.20084 | 0.15640 | 0.00134 | 0.00786 | ||
| n | r | ||||||
|---|---|---|---|---|---|---|---|
| 30 | 24 | MLE | 3.28695 | 0.88241 | 3.08763 | 0.87765 | 0.05352 |
| Bias | 0.28695 | 0.08241 | 0.08763 | 0.00161 | −0.00000 | ||
| MSE | 0.96247 | 0.04896 | 0.18824 | 0.00214 | 0.00020 | ||
| 27 | MLE | 3.20203 | 0.87913 | 3.07017 | 0.87230 | 0.05497 | |
| Bias | 0.20203 | 0.07913 | 0.07017 | −0.00374 | 0.00144 | ||
| MSE | 0.86952 | 0.04667 | 0.15728 | 0.00203 | 0.00017 | ||
| 50 | 40 | MLE | 3.17675 | 0.86190 | 3.02640 | 0.87315 | 0.05506 |
| Bias | 0.17675 | 0.06191 | 0.02631 | −0.00288 | 0.00154 | ||
| MSE | 0.52161 | 0.02995 | 0.10801 | 0.00132 | 0.00012 | ||
| 45 | MLE | 3.09316 | 0.84395 | 3.04172 | 0.87372 | 0.05457 | |
| Bias | 0.09316 | 0.04395 | 0.04172 | −0.00232 | 0.00104 | ||
| MSE | 0.33268 | 0.02347 | 0.08888 | 0.00102 | 0.00009 | ||
| 100 | 80 | MLE | 3.09505 | 0.83487 | 3.02198 | 0.87445 | 0.05438 |
| Bias | 0.09504 | 0.03487 | 0.02198 | −0.00159 | 0.00086 | ||
| MSE | 0.25649 | 0.01383 | 0.07476 | 0.00077 | 0.00006 | ||
| 90 | MLE | 3.09843 | 0.82840 | 3.02111 | 0.87805 | 0.05333 | |
| Bias | 0.09843 | 0.02839 | 0.02111 | 0.00201 | −0.00020 | ||
| MSE | 0.14981 | 0.01212 | 0.05592 | 0.00046 | 0.00003 | ||
| n | r | ||||||
|---|---|---|---|---|---|---|---|
| 30 | 24 | MLE | 3.76231 | 8.04103 | 1.83068 | 0.22896 | 1.62124 |
| Bias | 0.76231 | 0.04103 | −0.16932 | 0.00425 | 0.01296 | ||
| MSE | 2.04744 | 0.26625 | 0.17399 | 0.00279 | 0.02465 | ||
| 27 | MLE | 3.71919 | 7.99749 | 1.84219 | 0.23080 | 1.61052 | |
| Bias | 0.71919 | −0.00251 | −0.15782 | 0.00609 | 0.00224 | ||
| MSE | 2.04687 | 0.29352 | 0.16868 | 0.00289 | 0.02392 | ||
| 50 | 40 | MLE | 3.26032 | 7.98509 | 1.93754 | 0.22686 | 1.60902 |
| Bias | 0.26032 | −0.01491 | −0.06246 | 0.00215 | 0.00074 | ||
| MSE | 0.59433 | 0.21877 | 0.07295 | 0.00142 | 0.01337 | ||
| 45 | MLE | 3.27549 | 7.95998 | 1.93706 | 0.22960 | 1.59955 | |
| Bias | 0.27549 | −0.04002 | −0.06294 | 0.00489 | −0.00873 | ||
| MSE | 0.61335 | 0.20042 | 0.07451 | 0.00132 | 0.01260 | ||
| 100 | 80 | MLE | 3.17247 | 7.97533 | 1.97010 | 0.23002 | 1.59641 |
| Bias | 0.17247 | −0.02467 | −0.02990 | 0.00531 | −0.01187 | ||
| MSE | 0.41601 | 0.17126 | 0.05337 | 0.00072 | 0.00807 | ||
| 90 | MLE | 3.18983 | 7.98382 | 1.95748 | 0.22795 | 1.60322 | |
| Bias | 0.18983 | −0.01618 | −0.04253 | 0.00324 | −0.00506 | ||
| MSE | 0.39486 | 0.16581 | 0.04962 | 0.00068 | 0.00795 | ||
| Case 1 When Is Unknown | Case 2 When Is Unknown | |
|---|---|---|
| standard Bayes technique | The Bayes estimates of under SE, LINEX, and GE are obtained by computing Equations (25), (27) and (29). | The Bayes estimates of are obtained numerically under the SE, LINEX, and GE loss functions by evaluating (38), (39) and (40), respectively. |
| importance sampling technique | According to Algorithm 1, the Bayes estimates of are obtained under the SE, LINEX, and GE loss functions by computing Equations (31), (32) and (33), respectively. | Based on Algorithm 2, the Bayes estimates of are obtained numerically by computing Equations (42)–(44) under three loss functions. |
| Case 3 When Is Unknown | Case 4 When andAre Unknown | |
| standard Bayes technique | The Bayes estimates of are obtained under the SE, LINEX, and GE loss functions by evaluating (49), (50) and (51), respectively. | — |
| importance sampling technique | Based on Algorithm 3, the Bayes estimates of are obtained numerically by computing Equations (53)–(55) under three loss functions. | The Bayes estimates of are obtained numerically according to Algorithm 4 under the SE, LINEX, and GE loss functions by computing Equations (70), (71) and (72), respectively. |
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 0.81865 | 0.78855 | 0.78855 | 0.77828 | 0.76692 | 0.78855 | 0.75448 | 0.82343 | |
| Bias | 0.01865 | −0.01148 | −0.01148 | −0.02172 | −0.03308 | −0.01148 | −0.04552 | 0.02343 | |||
| MSE | 0.01887 | 0.01353 | 0.01353 | 0.01362 | 0.01343 | 0.01353 | 0.01516 | 0.01556 | |||
| Mean | 0.73107 | 0.71139 | 0.71139 | 0.70988 | 0.70922 | 0.71139 | 0.70186 | 0.72454 | |||
| Bias | 0.00203 | −0.01766 | −0.01766 | −0.01916 | −0.01982 | −0.01766 | −0.02718 | −0.00450 | |||
| MSE | 0.00426 | 0.00362 | 0.00362 | 0.00384 | 0.00401 | 0.00362 | 0.00443 | 0.00340 | |||
| Mean | 0.80731 | 0.84351 | 0.84351 | 0.82278 | 0.78846 | 0.84351 | 0.79688 | 0.84694 | |||
| Bias | −0.01055 | 0.02566 | 0.02566 | 0.00492 | −0.02940 | 0.02566 | −0.02098 | 0.02908 | |||
| MSE | 0.01848 | 0.01440 | 0.01440 | 0.01443 | 0.01570 | 0.01440 | 0.01665 | 0.01468 | |||
| 27 | Mean | 0.81917 | 0.79216 | 0.79216 | 0.78044 | 0.76701 | 0.79216 | 0.75675 | 0.82325 | ||
| Bias | 0.01917 | −0.00784 | −0.00784 | −0.01956 | −0.03299 | −0.00784 | −0.04325 | 0.02325 | |||
| MSE | 0.01834 | 0.01359 | 0.01359 | 0.01385 | 0.01359 | 0.01359 | 0.01528 | 0.01574 | |||
| Mean | 0.73155 | 0.71345 | 0.71345 | 0.71092 | 0.70921 | 0.71345 | 0.70296 | 0.72447 | |||
| Bias | 0.00250 | −0.01559 | −0.01559 | −0.01813 | −0.01983 | −0.01559 | −0.02608 | −0.00457 | |||
| MSE | 0.00415 | 0.00355 | 0.00355 | 0.00386 | 0.00398 | 0.00355 | 0.00443 | 0.00336 | |||
| Mean | 0.80652 | 0.83954 | 0.83954 | 0.82074 | 0.78878 | 0.83954 | 0.79485 | 0.84697 | |||
| Bias | −0.01133 | 0.02168 | 0.02168 | 0.00288 | −0.02908 | 0.02168 | −0.02300 | 0.02911 | |||
| MSE | 0.01797 | 0.01425 | 0.01425 | 0.01469 | 0.01562 | 0.01425 | 0.01704 | 0.01467 | |||
| 50 | 40 | Mean | 0.81429 | 0.80057 | 0.80057 | 0.77973 | 0.78116 | 0.80057 | 0.76534 | 0.81616 | |
| Bias | 0.01429 | 0.00057 | 0.00057 | −0.02028 | −0.01884 | 0.00057 | −0.03466 | 0.01616 | |||
| MSE | 0.01037 | 0.00853 | 0.00853 | 0.00917 | 0.00878 | 0.00853 | 0.00994 | 0.00976 | |||
| Mean | 0.73215 | 0.72202 | 0.72202 | 0.71340 | 0.71759 | 0.72202 | 0.70869 | 0.72696 | |||
| Bias | 0.00311 | −0.00702 | −0.00702 | −0.01564 | −0.01146 | −0.00702 | −0.02035 | −0.00209 | |||
| MSE | 0.00241 | 0.00218 | 0.00218 | 0.00258 | 0.00246 | 0.00218 | 0.00282 | 0.00223 | |||
| Mean | 0.80789 | 0.82577 | 0.82577 | 0.82830 | 0.79768 | 0.82577 | 0.81316 | 0.83430 | |||
| Bias | −0.00997 | 0.00791 | 0.00791 | 0.01045 | −0.02017 | 0.00791 | −0.00469 | 0.01644 | |||
| MSE | 0.01043 | 0.00897 | 0.00897 | 0.00974 | 0.01006 | 0.00897 | 0.01035 | 0.00950 | |||
| 45 | Mean | 0.81224 | 0.80057 | 0.80057 | 0.78936 | 0.78158 | 0.80057 | 0.77503 | 0.81643 | ||
| Bias | 0.01224 | 0.00057 | 0.00057 | −0.01064 | −0.01842 | 0.00057 | −0.02497 | 0.01643 | |||
| MSE | 0.01046 | 0.00853 | 0.00853 | 0.00919 | 0.00860 | 0.00853 | 0.00969 | 0.00958 | |||
| Mean | 0.73105 | 0.72202 | 0.72202 | 0.71835 | 0.71788 | 0.72202 | 0.71375 | 0.72721 | |||
| Bias | 0.00201 | −0.00702 | −0.00702 | −0.01069 | −0.01116 | −0.00702 | −0.01529 | −0.00184 | |||
| MSE | 0.00249 | 0.00218 | 0.00218 | 0.00243 | 0.00238 | 0.00218 | 0.00263 | 0.00216 | |||
| Mean | 0.81007 | 0.82577 | 0.82577 | 0.81829 | 0.79734 | 0.82577 | 0.80287 | 0.83380 | |||
| Bias | −0.00779 | 0.00791 | 0.00791 | 0.00044 | −0.02052 | 0.00791 | −0.01498 | 0.01594 | |||
| MSE | 0.01066 | 0.00897 | 0.00897 | 0.00972 | 0.00982 | 0.00897 | 0.01066 | 0.00925 | |||
| 100 | 80 | Mean | 0.80413 | 0.79939 | 0.79939 | 0.79528 | 0.78855 | 0.79939 | 0.78803 | 0.80636 | |
| Bias | 0.00413 | −0.00061 | −0.00061 | −0.00472 | −0.01145 | −0.00061 | −0.01197 | 0.00636 | |||
| MSE | 0.00506 | 0.00468 | 0.00468 | 0.00454 | 0.00476 | 0.00468 | 0.00466 | 0.00496 | |||
| Mean | 0.72907 | 0.72486 | 0.72486 | 0.72400 | 0.72220 | 0.72486 | 0.72176 | 0.72698 | |||
| Bias | 0.00003 | −0.00419 | −0.00419 | −0.00504 | −0.00684 | −0.00419 | −0.00728 | −0.00207 | |||
| MSE | 0.00126 | 0.00119 | 0.00119 | 0.00118 | 0.00128 | 0.00119 | 0.00123 | 0.00121 | |||
| Mean | 0.81597 | 0.82298 | 0.82298 | 0.81716 | 0.80936 | 0.82298 | 0.80948 | 0.82824 | |||
| Bias | −0.00189 | 0.00512 | 0.00512 | −0.00079 | −0.00849 | 0.00512 | −0.00837 | 0.01038 | |||
| MSE | 0.00532 | 0.00497 | 0.00497 | 0.00485 | 0.00523 | 0.00497 | 0.00509 | 0.00514 | |||
| 90 | Mean | 0.80925 | 0.79939 | 0.79939 | 0.78986 | 0.79195 | 0.79939 | 0.78264 | 0.80978 | ||
| Bias | 0.00925 | −0.00061 | −0.00061 | −0.01014 | −0.00805 | −0.00061 | −0.01736 | 0.00981 | |||
| MSE | 0.00558 | 0.00468 | 0.00468 | 0.00443 | 0.00428 | 0.00468 | 0.00463 | 0.00458 | |||
| Mean | 0.73148 | 0.72486 | 0.72486 | 0.72129 | 0.72414 | 0.72486 | 0.71903 | 0.72887 | |||
| Bias | 0.00244 | −0.00419 | −0.00419 | −0.00775 | −0.00490 | −0.00419 | −0.01001 | −0.00017 | |||
| MSE | 0.00134 | 0.00119 | 0.00119 | 0.00117 | 0.00115 | 0.00119 | 0.00123 | 0.00110 | |||
| Mean | 0.81088 | 0.82298 | 0.82298 | 0.82279 | 0.80565 | 0.82298 | 0.81525 | 0.82449 | |||
| Bias | −0.00698 | 0.00512 | 0.00512 | 0.00494 | −0.01221 | 0.00512 | −0.00261 | 0.00663 | |||
| MSE | 0.00574 | 0.00497 | 0.00497 | 0.00468 | 0.00486 | 0.00497 | 0.00483 | 0.00464 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 0.81865 | 1.67661 | 1.67661 | 1.67045 | 1.67654 | 1.67661 | 1.67018 | 1.68018 | |
| Bias | 0.01865 | 0.87661 | 0.87661 | 0.87045 | 0.87654 | 0.87661 | 0.87018 | 0.88018 | |||
| MSE | 0.01887 | 0.80599 | 0.80599 | 0.79622 | 0.80872 | 0.80599 | 0.79580 | 0.81512 | |||
| Mean | 0.73107 | 0.95051 | 0.95051 | 0.94989 | 0.95050 | 0.95051 | 0.94988 | 0.95056 | |||
| Bias | 0.00203 | 0.22147 | 0.22147 | 0.22085 | 0.22146 | 0.22147 | 0.22083 | 0.22152 | |||
| MSE | 0.00426 | 0.04944 | 0.04944 | 0.04917 | 0.04946 | 0.04944 | 0.04917 | 0.04948 | |||
| Mean | 0.80731 | 0.23678 | 0.23678 | 0.23875 | 0.23595 | 0.23678 | 0.23778 | 0.23714 | |||
| Bias | −0.01055 | −0.58108 | −0.58108 | −0.57910 | −0.58190 | −0.58108 | −0.58008 | −0.58072 | |||
| MSE | 0.01848 | 0.34284 | 0.34284 | 0.34064 | 0.34411 | 0.34284 | 0.34175 | 0.34278 | |||
| 27 | Mean | 0.81917 | 1.59218 | 1.59218 | 1.58224 | 1.58460 | 1.59218 | 1.58198 | 1.58762 | ||
| Bias | 0.01917 | 0.79218 | 0.79218 | 0.78224 | 0.78460 | 0.79218 | 0.78198 | 0.78726 | |||
| MSE | 0.01834 | 0.66092 | 0.66092 | 0.64575 | 0.652221 | 0.66092 | 0.64539 | 0.65639 | |||
| Mean | 0.73155 | 0.94133 | 0.94133 | 0.94017 | 0.94019 | 0.94133 | 0.94015 | 0.94024 | |||
| Bias | 0.00250 | 0.21228 | 0.21228 | 0.21112 | 0.21114 | 0.21228 | 0.21110 | 0.21120 | |||
| MSE | 0.00415 | 0.04553 | 0.04553 | 0.04505 | 0.04514 | 0.04553 | 0.04504 | 0.04516 | |||
| Mean | 0.80652 | 0.26985 | 0.26985 | 0.27369 | 0.27273 | 0.26985 | 0.27290 | 0.27374 | |||
| Bias | −0.01133 | −0.54800 | −0.54800 | −0.54417 | −0.54512 | −0.54800 | −0.54496 | −0.54412 | |||
| MSE | 0.01797 | 0.30597 | 0.30597 | 0.30183 | 0.30362 | 0.30597 | 0.30268 | 0.30258 | |||
| 50 | 40 | Mean | 0.81429 | 1.02888 | 1.02888 | 1.02199 | 1.02842 | 1.02888 | 1.02189 | 1.02878 | |
| Bias | 0.01429 | 0.22888 | 0.22888 | 0.22199 | 0.22842 | 0.22888 | 0.22189 | 0.22879 | |||
| MSE | 0.01037 | 0.06184 | 0.06184 | 0.05813 | 0.06164 | 0.06184 | 0.05809 | 0.06180 | |||
| Mean | 0.73215 | 0.82255 | 0.82255 | 0.82034 | 0.82241 | 0.82255 | 0.82032 | 0.82245 | |||
| Bias | 0.00311 | 0.09350 | 0.09350 | 0.09130 | 0.09337 | 0.09350 | 0.09128 | 0.09342 | |||
| MSE | 0.00241 | 0.00982 | 0.00982 | 0.00938 | 0.00984 | 0.00982 | 0.00937 | 0.00985 | |||
| Mean | 0.80789 | 0.60854 | 0.60854 | 0.61387 | 0.60854 | 0.60854 | 0.61373 | 0.60884 | |||
| Bias | −0.00997 | −0.20932 | −0.20932 | −0.20399 | −0.20932 | −0.20932 | −0.20413 | −0.20902 | |||
| MSE | 0.01043 | 0.05011 | 0.05011 | 0.04761 | 0.05025 | 0.05011 | 0.04767 | 0.05014 | |||
| 45 | Mean | 0.81224 | 1.01755 | 1.01755 | 1.01760 | 1.01795 | 1.01755 | 1.01750 | 1.01824 | ||
| Bias | 0.01224 | 0.21755 | 0.21755 | 0.21760 | 0.21795 | 0.21755 | 0.21750 | 0.21824 | |||
| MSE | 0.01046 | 0.05601 | 0.05601 | 0.05580 | 0.05697 | 0.05601 | 0.05577 | 0.05709 | |||
| Mean | 0.73105 | 0.81880 | 0.81880 | 0.81891 | 0.81874 | 0.81880 | 0.81889 | 0.81878 | |||
| Bias | 0.00201 | 0.08976 | 0.08976 | 0.08986 | 0.08970 | 0.08976 | 0.08984 | 0.08974 | |||
| MSE | 0.00249 | 0.00909 | 0.00909 | 0.00909 | 0.00920 | 0.00909 | 0.00909 | 0.00920 | |||
| Mean | 0.81007 | 0.61768 | 0.61768 | 0.61741 | 0.61736 | 0.61768 | 0.61728 | 0.61761 | |||
| Bias | −0.00779 | −0.20017 | −0.20017 | −0.20045 | −0.20050 | −0.20017 | −0.20058 | −0.20025 | |||
| MSE | 0.01066 | 0.04604 | 0.04604 | 0.04599 | 0.04675 | 0.04604 | 0.04603 | 0.04666 | |||
| 100 | 80 | Mean | 0.80413 | 0.64656 | 0.64656 | 0.64757 | 0.64685 | 0.64656 | 0.64756 | 0.64688 | |
| Bias | 0.00413 | −0.15344 | −0.15344 | −0.15243 | −0.15315 | −0.15344 | −0.15245 | −0.15312 | |||
| MSE | 0.00506 | 0.02546 | 0.02546 | 0.02526 | 0.02531 | 0.02546 | 0.02527 | 0.02530 | |||
| Mean | 0.72907 | 0.64000 | 0.64000 | 0.64060 | 0.64022 | 0.64000 | 0.64059 | 0.64024 | |||
| Bias | 0.00003 | −0.08904 | −0.08904 | −0.08844 | −0.08882 | −0.08904 | −0.08845 | −0.08880 | |||
| MSE | 0.00126 | 0.00872 | 0.00872 | 0.00865 | 0.00865 | 0.00872 | 0.00865 | 0.00865 | |||
| Mean | 0.81597 | 0.98945 | 0.98945 | 0.98829 | 0.98903 | 0.98945 | 0.98828 | 0.98906 | |||
| Bias | −0.00189 | 0.17159 | 0.17159 | 0.17043 | 0.17117 | 0.17159 | 0.17042 | 0.17120 | |||
| MSE | 0.00532 | 0.03213 | 0.03213 | 0.03187 | 0.03189 | 0.03213 | 0.03187 | 0.03190 | |||
| 90 | Mean | 0.80925 | 0.65127 | 0.65127 | 0.65130 | 0.64958 | 0.65127 | 0.65128 | 0.64961 | ||
| Bias | 0.00925 | −0.14873 | −0.14873 | −0.14871 | −0.15042 | −0.14873 | −0.14872 | −0.15039 | |||
| MSE | 0.00558 | 0.02400 | 0.02400 | 0.02392 | 0.02447 | 0.02400 | 0.02392 | 0.02446 | |||
| Mean | 0.73148 | 0.64305 | 0.64305 | 0.64310 | 0.64198 | 0.64305 | 0.64309 | 0.64199 | |||
| Bias | 0.00244 | −0.08560 | −0.08560 | −0.08594 | −0.08706 | −0.08560 | −0.08595 | −0.08705 | |||
| MSE | 0.00134 | 0.00815 | 0.00815 | 0.00812 | 0.00834 | 0.00815 | 0.00812 | 0.00833 | |||
| Mean | 0.81088 | 0.98385 | 0.98385 | 0.98377 | 0.98579 | 0.98385 | 0.98376 | 0.98583 | |||
| Bias | −0.00698 | 0.16599 | 0.16599 | 0.16592 | 0.16794 | 0.16599 | 0.16591 | 0.16797 | |||
| MSE | 0.00574 | 0.03015 | 0.03015 | 0.03003 | 0.03078 | 0.03015 | 0.03003 | 0.03079 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 4.00137 | 3.63379 | 3.63379 | 3.21065 | 2.75023 | 3.63379 | 3.37739 | 3.84007 | |
| Bias | 0.00137 | −0.36621 | −0.36621 | −0.78935 | −1.24977 | −0.36621 | −0.62261 | −0.15993 | |||
| MSE | 0.52494 | 0.47324 | 0.47324 | 0.82890 | 1.66793 | 0.47324 | 0.68487 | 0.38669 | |||
| Mean | 0.73031 | 0.74993 | 0.74993 | 0.74633 | 0.74334 | 0.74993 | 0.74383 | 0.74885 | |||
| Bias | 0.00126 | 0.02089 | 0.02089 | 0.01729 | 0.01429 | 0.02089 | 0.01479 | 0.01981 | |||
| MSE | 0.00130 | 0.00130 | 0.00130 | 0.00121 | 0.00109 | 0.00130 | 0.00117 | 0.00121 | |||
| Mean | 0.81692 | 0.74893 | 0.74893 | 0.73874 | 0.71619 | 0.74893 | 0.70815 | 0.78359 | |||
| Bias | −0.00094 | −0.06892 | −0.06892 | −0.07911 | −0.10167 | −0.06892 | −0.10971 | −0.03426 | |||
| MSE | 0.01729 | 0.01604 | 0.01604 | 0.01690 | 0.01902 | 0.01604 | 0.02225 | 0.01299 | |||
| 27 | Mean | 3.95886 | 3.73469 | 3.73469 | 3.24211 | 2.82172 | 3.73469 | 3.39740 | 3.83642 | ||
| Bias | −0.04114 | −0.26531 | −0.26531 | −0.75789 | −1.17828 | −0.26531 | −0.60260 | −0.16358 | |||
| MSE | 0.43395 | 0.41495 | 0.41495 | 0.77379 | 1.50751 | 0.41495 | 0.64107 | 0.39905 | |||
| Mean | 0.73219 | 0.74465 | 0.74465 | 0.74681 | 0.74303 | 0.74465 | 0.74458 | 0.74802 | |||
| Bias | 0.00315 | 0.01661 | 0.01661 | 0.01777 | 0.01398 | 0.01661 | 0.01554 | 0.01897 | |||
| MSE | 0.00108 | 0.00111 | 0.00111 | 0.00116 | 0.00111 | 0.00111 | 0.00112 | 0.00121 | |||
| Mean | 0.80941 | 0.76751 | 0.76751 | 0.73881 | 0.72206 | 0.76751 | 0.71138 | 0.78332 | |||
| Bias | −0.00845 | −0.05034 | −0.05034 | −0.07904 | −0.09580 | −0.05034 | −0.10648 | −0.03453 | |||
| MSE | 0.01432 | 0.01395 | 0.01395 | 0.01616 | 0.01838 | 0.01395 | 0.02089 | 0.01338 | |||
| 50 | 40 | Mean | 3.99325 | 3.80054 | 3.80054 | 3.44623 | 3.07134 | 3.80054 | 3.58543 | 3.90027 | |
| Bias | −0.00675 | −0.19947 | −0.19947 | −0.55368 | −0.92866 | −0.19947 | −0.41457 | −0.00973 | |||
| MSE | 0.31444 | 0.34557 | 0.34557 | 0.49296 | 0.99045 | 0.34557 | 0.41568 | 0.32374 | |||
| Mean | 0.73017 | 0.74084 | 0.74084 | 0.74046 | 0.73840 | 0.74084 | 0.73876 | 074216 | |||
| Bias | 0.00113 | 0.01179 | 0.01179 | 0.01142 | 0.00935 | 0.01179 | 0.00971 | 0.01311 | |||
| MSE | 0.00077 | 0.00090 | 0.00090 | 0.00082 | 0.00085 | 0.00090 | 0.00080 | 0.00090 | |||
| Mean | 0.81593 | 0.77997 | 0.77997 | 0.76505 | 0.74927 | 0.77997 | 0.74497 | 0.79609 | |||
| Bias | −0.00193 | −0.03789 | −0.03789 | −0.05281 | −0.06858 | −0.03789 | −0.07289 | −0.02177 | |||
| MSE | 0.01034 | 0.01152 | 0.01152 | 0.01122 | 0.01302 | 0.01152 | 0.01355 | 0.01074 | |||
| 45 | Mean | 4.00362 | 3.77522 | 3.77522 | 3.47241 | 3.14740 | 3.77522 | 3.59934 | 3.91113 | ||
| Bias | 0.00362 | −0.22479 | −0.22479 | −0.52759 | −0.85260 | −0.22479 | −0.40066 | −0.08887 | |||
| MSE | 0.29272 | 0.32260 | 0.32260 | 0.54804 | 0.85118 | 0.32260 | 0.38937 | 0.29091 | |||
| Mean | 0.72960 | 0.74192 | 0.74192 | 0.74083 | 0.73739 | 0.74192 | 0.73932 | 0.74077 | |||
| Bias | 0.00056 | 0.01288 | 0.01288 | 0.01179 | 0.00084 | 0.01288 | 0.01028 | 0.01173 | |||
| MSE | 0.00072 | 0.00085 | 0.00085 | 0.00078 | 0.00076 | 0.00085 | 0.00076 | 0.00079 | |||
| Mean | 0.81786 | 0.77552 | 0.77552 | 0.76505 | 0.75623 | 0.77552 | 0.74719 | 0.79844 | |||
| Bias | 2.80599 × 10 | −0.04233 | −0.04233 | −0.05281 | −0.06163 | −0.04233 | −0.07067 | −0.01942 | |||
| MSE | 0.00961 | 0.01080 | 0.01080 | 0.01067 | 0.01145 | 0.01080 | 0.01271 | 0.00963 | |||
| 100 | 80 | Mean | 4.02104 | 3.89432 | 3.89432 | 3.68636 | 3.41183 | 3.89432 | 3.77820 | 3.92103 | |
| Bias | 0.02104 | −0.10568 | −0.10568 | −0.31364 | −0.58817 | −0.10568 | −0.22180 | −0.0790 | |||
| MSE | 0.18577 | 0.20450 | 0.20450 | 0.25076 | 0.46617 | 0.20450 | 0.22767 | 0.21109 | |||
| Mean | 0.72847 | 0.73536 | 0.73536 | 0.73507 | 0.73545 | 0.73536 | 0.73412 | 0.73752 | |||
| Bias | −0.00058 | 0.00632 | 0.00632 | 0.00602 | 0.00640 | 0.00632 | 0.00508 | 0.00847 | |||
| MSE | 0.00045 | 0.00051 | 0.00051 | 0.00051 | 0.00054 | 0.00051 | 0.00050 | 0.00056 | |||
| Mean | 0.82126 | 0.79773 | 0.79773 | 0.78971 | 0.77531 | 0.79773 | 0.77891 | 0.80144 | |||
| Bias | 0.00340 | −0.02012 | −0.02012 | −0.02814 | −0.04255 | −0.02012 | −0.03895 | −0.01641 | |||
| MSE | 0.00609 | 0.00676 | 0.00676 | 0.00681 | 0.00779 | 0.00676 | 0.00746 | 0.00699 | |||
| 90 | Mean | 4.02520 | 3.90955 | 3.90955 | 3.72222 | 3.47851 | 3.90955 | 3.80560 | 3.94136 | ||
| Bias | 0.02520 | −0.09045 | −0.09045 | −0.27778 | −0.52149 | −0.09045 | −0.19440 | −0.05864 | |||
| MSE | 0.17038 | 0.17502 | 0.17502 | 0.20935 | 0.38175 | 0.17502 | 0.19019 | 0.18087 | |||
| Mean | 0.72822 | 0.73447 | 0.73447 | 0.73424 | 0.73414 | 0.73447 | 0.73340 | 0.73599 | |||
| Bias | −0.00082 | 0.00542 | 0.00542 | 0.00520 | 0.00509 | 0.00542 | 0.00436 | 0.00695 | |||
| MSE | 0.00042 | 0.000439 | 0.000439 | 0.00042 | 0.00046 | 0.000439 | 0.00042 | 0.00047 | |||
| Mean | 0.82205 | 0.80062 | 0.80062 | 0.79333 | 0.78199 | 0.80062 | 0.78377 | 0.80538 | |||
| Bias | 0.00419 | −0.01724 | −0.01724 | −0.02453 | −0.03586 | −0.01724 | −0.03409 | −0.01248 | |||
| MSE | 0.00559 | 0.00578 | 0.00578 | 0.00571 | 0.00653 | 0.00578 | 0.00623 | 0.00597 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 4.00137 | 5.01528 | 5.01528 | 4.35481 | 3.70618 | 5.01528 | 4.68073 | 5.06025 | |
| Bias | 0.00137 | 1.01528 | 1.01528 | 0.35481 | −0.29382 | 1.01528 | 0.68073 | 1.06025 | |||
| MSE | 0.52494 | 1.73584 | 1.73584 | 0.48266 | 0.29270 | 1.73584 | 1.00883 | 1.82667 | |||
| Mean | 0.73031 | 0.68394 | 0.68394 | 0.68497 | 0.68418 | 0.68394 | 0.68241 | 0.68929 | |||
| Bias | 0.00126 | −0.04510 | −0.04510 | −0.04408 | −0.04487 | −0.04510 | −0.04663 | −0.03975 | |||
| MSE | 0.00130 | 0.00341 | 0.00341 | 0.00318 | 0.00337 | 0.00341 | 0.00346 | 0.00285 | |||
| Mean | 0.81692 | 0.99770 | 0.99770 | 0.96702 | 0.93335 | 0.99770 | 0.94390 | 1.00351 | |||
| Bias | −0.00094 | 0.17984 | 0.17984 | 0.14916 | 0.11550 | 0.17984 | 0.12605 | 0.18565 | |||
| MSE | 0.01729 | 0.05445 | 0.05445 | 0.03999 | 0.02975 | 0.05445 | 0.03339 | 0.05635 | |||
| 27 | Mean | 3.95886 | 4.88051 | 4.88051 | 4.21714 | 3.68235 | 4.88051 | 4.41388 | 4.57499 | ||
| Bias | −0.04114 | 0.88051 | 0.88051 | 0.21714 | −0.31765 | 0.88051 | 0.41388 | 0.57499 | |||
| MSE | 0.43395 | 1.42262 | 1.42262 | 0.46346 | 0.30434 | 1.42262 | 0.75868 | 0.92222 | |||
| Mean | 0.73219 | 0.68924 | 0.68924 | 0.70414 | 0.7041 8 | 0.68924 | 0.70320 | 0.70628 | |||
| Bias | 0.00315 | −0.03980 | −0.03980 | −0.02491 | −0.02486 | −0.03980 | −0.05840 | −0.02276 | |||
| MSE | 0.00108 | 0.00288 | 0.00288 | 0.00196 | 0.00187 | 0.00288 | 0.00203 | 0.00173 | |||
| Mean | 0.80941 | 0.97433 | 0.97433 | 0.90614 | 0.888818 | 0.97433 | 0.89388 | 0.91906 | |||
| Bias | −0.00845 | 0.15648 | 0.15648 | 0.08829 | 0.07033 | 0.15648 | 0.07602 | 0.10120 | |||
| MSE | 0.01432 | 0.04485 | 0.04485 | 0.02710 | 0.02106 | 0.04485 | 0.02472 | 0.02903 | |||
| 50 | 40 | Mean | 3.99325 | 4.93070 | 4.93070 | 4.29403 | 3.90463 | 4.93070 | 4.44350 | 4.63432 | |
| Bias | −0.00675 | 0.93070 | 0.93070 | 0.29403 | −0.09537 | 0.93070 | 0.44350 | 0.63432 | |||
| MSE | 0.31444 | 1.43752 | 1.43752 | 0.42635 | 0.23429 | 1.43752 | 0.63256 | 0.95327 | |||
| Mean | 0.73017 | 0.68672 | 0.68672 | 0.70382 | 0.70097 | 0.68672 | 0.70307 | 0.70263 | |||
| Bias | 0.00113 | −0.04233 | −0.04233 | −0.02522 | −0.02807 | −0.04233 | −0.02597 | −0.02642 | |||
| MSE | 0.00077 | 0.00293 | 0.00293 | 0.00164 | 0.00193 | 0.00293 | 0.00169 | 0.00182 | |||
| Mean | 0.81593 | 0.98346 | 0.98346 | 0.90816 | 0.90575 | 0.98346 | 0.89885 | 0.93003 | |||
| Bias | −0.00193 | 0.16560 | 0.16560 | 0.09031 | 0.08789 | 0.16560 | 0.08099 | 0.11218 | |||
| MSE | 0.01034 | 0.04540 | 0.04540 | 0.02248 | 0.02319 | 0.04540 | 0.02064 | 0.03003 | |||
| 45 | Mean | 4.00362 | 4.30424 | 4.30424 | 4.22921 | 3.85349 | 4.30424 | 4.27484 | 4.11707 | ||
| Bias | 0.00362 | 0.30424 | 0.30424 | 0.22921 | −0.14651 | 0.30424 | 0.27484 | 0.11707 | |||
| MSE | 0.29272 | 0.53169 | 0.53169 | 0.44464 | 0.29407 | 0.53169 | 0.49591 | 0.41340 | |||
| Mean | 0.72960 | 0.71534 | 0.71534 | 0.71516 | 0.68614 | 0.72460 | 0.71494 | 0.72503 | |||
| Bias | 0.00056 | −0.01370 | −0.01370 | −0.01388 | −0.00444 | −0.01370 | −0.01409 | −0.00402 | |||
| MSE | 0.00072 | 0.00118 | 0.00118 | 0.00116 | 0.00096 | 0.00118 | 0.00117 | 0.00096 | |||
| Mean | 0.81786 | 0.87184 | 0.87184 | 0.87012 | 0.83195 | 0.87184 | 0.86723 | 0.83792 | |||
| Bias | 2.80599 × 10 | 0.05398 | 0.05398 | 0.05226 | 0.01409 | 0.05398 | 0.04937 | 0.02006 | |||
| MSE | 0.00961 | 0.01708 | 0.01708 | 0.01636 | 0.01297 | 0.01708 | 0.01605 | 0.01342 | |||
| 100 | 80 | Mean | 4.02104 | 4.52275 | 4.52275 | 4.31180 | 3.97709 | 4.52275 | 4.33079 | 4.07013 | |
| Bias | 0.02104 | 0.52275 | 0.52275 | 0.31180 | −0.02291 | 0.52275 | 0.33079 | 0.07013 | |||
| MSE | 0.18577 | 0.61202 | 0.61202 | 0.40122 | 0.22290 | 0.61202 | 0.42078 | 0.25983 | |||
| Mean | 0.72847 | 0.70462 | 0.70462 | 0.71301 | 0.72635 | 0.70462 | 0.71291 | 0.72651 | |||
| Bias | −0.00058 | −0.02442 | −0.02442 | −0.01603 | −0.00270 | −0.02442 | −0.01613 | −0.00253 | |||
| MSE | 0.00045 | 0.00133 | 0.00133 | 0.00095 | 0.00061 | 0.00133 | 0.00095 | 0.00061 | |||
| Mean | 0.82126 | 0.91137 | 0.91137 | 0.87845 | 0.82762 | 0.91137 | 0.87722 | 0.82990 | |||
| Bias | 0.00340 | 0.09352 | 0.09352 | 0.06059 | 0.00976 | 0.09352 | 0.05936 | 0.01204 | |||
| MSE | 0.00609 | 0.01957 | 0.01957 | 0.01368 | 0.00837 | 0.01957 | 0.01354 | 0.00845 | |||
| 90 | Mean | 4.02520 | 3.71260 | 3.71260 | 3.72549 | 3.85324 | 3.71260 | 3.72811 | 3.87665 | ||
| Bias | 0.02520 | −0.28740 | −0.28740 | −0.27451 | −0.14676 | −0.28740 | −0.27189 | −0.12335 | |||
| MSE | 0.17038 | 0.26820 | 0.26820 | 0.29151 | 0.23423 | 0.26820 | 0.29072 | 0.23222 | |||
| Mean | 0.72822 | 0.74401 | 0.74401 | 0.74315 | 0.73580 | 0.74401 | 0.74313 | 0.73586 | |||
| Bias | −0.00082 | 0.01497 | 0.01497 | 0.01410 | 0.00676 | 0.01497 | 0.01408 | 0.00681 | |||
| MSE | 0.00042 | 0.00070 | 0.00070 | 0.00075 | 0.00058 | 0.00070 | 0.00075 | 0.00058 | |||
| Mean | 0.82205 | 0.76509 | 0.76509 | 0.76820 | 0.79421 | 0.76509 | 0.76792 | 0.79492 | |||
| Bias | 0.00419 | −0.05276 | −0.05276 | −0.04966 | −0.02365 | −0.05276 | −0.04994 | −0.02294 | |||
| MSE | 0.00559 | 0.00896 | 0.00896 | 0.00966 | 0.00771 | 0.00896 | 0.00969 | 0.00768 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 3.02350 | 2.88990 | 2.88990 | 2.80094 | 2.68837 | 2.88990 | 2.82593 | 2.92667 | |
| Bias | 0.02350 | −0.11010 | −0.11010 | −0.19906 | −0.31163 | −0.11010 | −0.17407 | −0.07333 | |||
| MSE | 0.10261 | 0.12187 | 0.12187 | 0.13665 | 0.18271 | 0.12187 | 0.13498 | 0.11895 | |||
| Mean | 0.72733 | 0.69350 | 0.69350 | 0.68927 | 0.68403 | 0.69350 | 0.68035 | 0.70038 | |||
| Bias | −0.00171 | −0.03554 | −0.03554 | −0.03977 | −0.04501 | −0.03554 | −0.04870 | −0.02867 | |||
| MSE | 0.00387 | 0.00605 | 0.00605 | 0.00639 | 0.00700 | 0.00605 | 0.00759 | 0.00534 | |||
| Mean | 0.89150 | 0.89845 | 0.89845 | 0.87606 | 0.84129 | 0.89845 | 0.84459 | 0.92167 | |||
| Bias | 0.00164 | 0.08059 | 0.08059 | 0.05820 | 0.02349 | 0.08059 | 0.02673 | 0.10381 | |||
| MSE | 0.02237 | 0.03386 | 0.03386 | 0.02930 | 0.02509 | 0.03386 | 0.02845 | 0.03753 | |||
| 27 | Mean | 3.03297 | 2.77639 | 2.77639 | 2.68512 | 2.58070 | 2.77639 | 2.70513 | 2.79645 | ||
| Bias | 0.03297 | −0.22361 | −0.22361 | −0.31488 | −0.41930 | −0.22361 | −0.29487 | −0.20355 | |||
| MSE | 0.10538 | 0.12345 | 0.12345 | 0.16758 | 0.23514 | 0.12345 | 0.16040 | 0.11978 | |||
| Mean | 0.81531 | 0.95272 | 0.95272 | 0.93646 | 0.90221 | 0.95272 | 0.90794 | 0.98287 | |||
| Bias | −0.00255 | 0.13486 | 0.13486 | 0.11861 | 0.08435 | 0.13486 | 0.09009 | 0.16501 | |||
| MSE | 0.02285 | 0.03888 | 0.03888 | 0.03525 | 0.02713 | 0.03888 | 0.03085 | 0.04856 | |||
| Mean | 0.72906 | 0.67094 | 0.67094 | 0.66374 | 0.65772 | 0.67094 | 0.65409 | 0.67485 | |||
| Bias | 0.000016 | −0.05811 | −0.05811 | −0.06530 | −0.07132 | −0.05811 | −0.07495 | −0.05420 | |||
| MSE | 0.00395 | 0.00706 | 0.00706 | 0.00822 | 0.00911 | 0.00706 | 0.00989 | 0.00664 | |||
| 50 | 40 | Mean | 3.00595 | 3.04594 | 3.04594 | 2.97749 | 2.90249 | 3.04594 | 2.99763 | 3.07076 | |
| Bias | 0.00595 | 0.04594 | 0.04594 | −0.02251 | −0.09751 | 0.04594 | −0.00237 | 0.07076 | |||
| MSE | 0.05281 | 0.09092 | 0.09092 | 0.08649 | 0.08430 | 0.09092 | 0.09053 | 0.09503 | |||
| Mean | 0.72688 | 0.72875 | 0.72875 | 0.72480 | 0.72355 | 0.72875 | 0.72022 | 0.73277 | |||
| Bias | −0.00217 | −0.00029 | −0.00029 | −0.00424 | −0.00550 | −0.00029 | −0.00882 | 0.00373 | |||
| MSE | 0.00211 | 0.00325 | 0.00325 | 0.00347 | 0.00334 | 0.00325 | 0.00370 | 0.00309 | |||
| Mean | 0.82174 | 0.81501 | 0.81501 | 0.80523 | 0.78035 | 0.81501 | 0.78425 | 0.82975 | |||
| Bias | 0.00389 | −0.00284 | −0.00284 | −0.01262 | −0.03751 | −0.00284 | −0.03361 | 0.01189 | |||
| MSE | 0.01209 | 0.01898 | 0.01898 | 0.01940 | 0.01872 | 0.01898 | 0.02117 | 0.01862 | |||
| 45 | Mean | 3.00590 | 2.90753 | 2.90753 | 2.84820 | 2.78888 | 2.90753 | 2.86444 | 2.94098 | ||
| Bias | 0.00590 | −0.09247 | −0.09247 | −0.15180 | −0.21112 | −0.09247 | −0.13556 | −0.05902 | |||
| MSE | 0.05150 | 0.06803 | 0.06803 | 0.07886 | 0.09791 | 0.06803 | 0.07695 | 0.06776 | |||
| Mean | 0.72696 | 0.70264 | 0.70264 | 0.69916 | 0.69909 | 0.70264 | 0.69415 | 0.70881 | |||
| Bias | −0.00208 | −0.02641 | −0.02641 | −0.02989 | −0.02995 | −0.02641 | −0.03490 | −0.02023 | |||
| MSE | 0.00202 | 0.00329 | 0.00329 | 0.00353 | 0.00370 | 0.00329 | 0.00398 | 0.00304 | |||
| Mean | 0.82158 | 0.87826 | 0.87826 | 0.86676 | 0.83816 | 0.87826 | 0.84777 | 0.88764 | |||
| Bias | 0.00372 | 0.06040 | 0.06040 | 0.04891 | 0.02031 | 0.06040 | 0.02992 | 0.06979 | |||
| MSE | 0.01161 | 0.01839 | 0.01839 | 0.01686 | 0.01500 | 0.01839 | 0.01602 | 0.02017 | |||
| 100 | 80 | Mean | 2.99586 | 3.14547 | 3.14547 | 3.11569 | 3.06687 | 3.14547 | 3.12795 | 3.16113 | |
| Bias | −0.00414 | 0.14547 | 0.14547 | 0.11569 | 0.06687 | 0.14547 | 0.12795 | 0.16113 | |||
| MSE | 0.01098 | 0.09093 | 0.09093 | 0.08384 | 0.06509 | 0.09093 | 0.08881 | 0.09265 | |||
| Mean | 0.72752 | 0.75051 | 0.75051 | 0.74998 | 0.74866 | 0.75051 | 0.74797 | 0.75305 | |||
| Bias | −0.00152 | 0.02147 | 0.02147 | 0.02093 | 0.01962 | 0.02147 | 0.01892 | 0.02400 | |||
| MSE | 0.00044 | 0.00261 | 0.00261 | 0.00273 | 0.00254 | 0.00261 | 0.00271 | 0.00264 | |||
| Mean | 0.82123 | 0.76348 | 0.76348 | 0.75526 | 0.74468 | 0.76348 | 0.74405 | 0.76983 | |||
| Bias | 0.00337 | −0.05438 | −0.05438 | −0.06560 | −0.07318 | −0.05438 | −0.07380 | −0.04803 | |||
| MSE | 0.00250 | 0.01584 | 0.01584 | 0.01727 | 0.01738 | 0.01584 | 0.01905 | 0.01483 | |||
| 90 | Mean | 2.99828 | 2.98179 | 2.98179 | 2.95965 | 2.92042 | 2.98179 | 2.96936 | 3.00405 | ||
| Bias | −0.00172 | −0.01821 | −0.01821 | −0.04035 | −0.07958 | −0.01821 | −0.03064 | 0.00405 | |||
| MSE | 0.01196 | 0.03735 | 0.03735 | 0.03685 | 0.03998 | 0.03735 | 0.03708 | 0.03716 | |||
| Mean | 0.72794 | 0.72114 | 0.72114 | 0.72153 | 0.72051 | 0.72114 | 0.71928 | 0.72524 | |||
| Bias | −0.00111 | −0.00791 | −0.00791 | −0.00752 | −0.00853 | −0.00791 | −0.00977 | −0.00380 | |||
| MSE | 0.00048 | 0.00152 | 0.00152 | 0.00150 | 0.00154 | 0.00152 | 0.00158 | 0.00143 | |||
| Mean | 0.82020 | 0.83515 | 0.83515 | 0.82441 | 0.81232 | 0.83515 | 0.81433 | 0.83768 | |||
| Bias | 0.00235 | 0.01730 | 0.01730 | 0.00656 | −0.00554 | 0.01730 | −0.00353 | 0.01982 | |||
| MSE | 0.00273 | 0.00870 | 0.00870 | 0.00819 | 0.00805 | 0.00870 | 0.00835 | 0.00864 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 3.02350 | 4.10736 | 4.10736 | 4.03328 | 3.81324 | 4.10736 | 4.10185 | 4.16576 | |
| Bias | 0.02350 | 1.10736 | 1.10736 | 1.03328 | 0.81324 | 1.10736 | 1.10185 | 1.16576 | |||
| MSE | 0.10261 | 1.49058 | 1.49058 | 1.34756 | 0.86803 | 1.49058 | 1.53082 | 1.65682 | |||
| Mean | 0.72733 | 0.87067 | 0.87067 | 0.87277 | 0.86982 | 0.87067 | 0.87101 | 0.87427 | |||
| Bias | −0.00171 | 0.14163 | 0.14163 | 0.14373 | 0.14077 | 0.14163 | 0.14196 | 0.14523 | |||
| MSE | 0.00387 | 0.02235 | 0.02235 | 0.02328 | 0.02232 | 0.02235 | 0.02288 | 0.02339 | |||
| Mean | 0.89150 | 0.44980 | 0.44980 | 0.43213 | 0.42517 | 0.44980 | 0.41085 | 0.46252 | |||
| Bias | 0.00164 | −0.36805 | −0.36805 | −0.38573 | −0.39268 | −0.36805 | −0.40701 | −0.35534 | |||
| MSE | 0.02237 | 0.15292 | 0.15292 | 0.16807 | 0.17119 | 0.15292 | 0.18540 | 0.14449 | |||
| 27 | Mean | 3.03297 | 3.89131 | 3.89131 | 3.78047 | 3.60496 | 3.89131 | 3.83332 | 3.90260 | ||
| Bias | 0.03297 | 0.89131 | 0.89131 | 0.78047 | 0.60496 | 0.89131 | 0.83332 | 0.90260 | |||
| MSE | 0.10538 | 1.02343 | 1.02343 | 0.81888 | 0.50581 | 1.02343 | 0.92742 | 1.02966 | |||
| Mean | 0.72906 | 0.84946 | 0.84946 | 0.84693 | 0.84566 | 0.84946 | 0.84481 | 0.85056 | |||
| Bias | 0.000016 | 0.12042 | 0.12042 | 0.11789 | 0.11662 | 0.12042 | 0.11577 | 0.12151 | |||
| MSE | 0.00395 | 0.01709 | 0.01709 | 0.01681 | 0.01616 | 0.01709 | 0.01641 | 0.01718 | |||
| Mean | 0.81531 | 0.50806 | 0.50806 | 0.50268 | 0.49126 | 0.50806 | 0.48351 | 0.52755 | |||
| Bias | −0.00255 | −0.30980 | −0.30980 | −0.31518 | −0.32660 | −0.30980 | −0.33434 | −0.29030 | |||
| MSE | 0.02285 | 0.11475 | 0.11475 | 0.11952 | 0.12364 | 0.11475 | 0.13273 | 0.10155 | |||
| 50 | 40 | Mean | 3.00595 | 3.35995 | 3.35995 | 3.35887 | 3.34464 | 3.35995 | 3.36414 | 3.38831 | |
| Bias | 0.00595 | 0.35995 | 0.35995 | 0.35887 | 0.34464 | 0.35995 | 0.36414 | 0.38831 | |||
| MSE | 0.05281 | 0.25250 | 0.25250 | 0.25440 | 0.23530 | 0.25250 | 0.25959 | 0.27492 | |||
| Mean | 0.72688 | 0.78564 | 0.78564 | 0.78693 | 0.78888 | 0.78564 | 0.78639 | 0.79005 | |||
| Bias | −0.00217 | 0.05660 | 0.05660 | 0.05789 | 0.05983 | 0.05660 | 0.05734 | 0.06100 | |||
| MSE | 0.00211 | 0.00618 | 0.00618 | 0.00632 | 0.00637 | 0.00618 | 0.00628 | 0.00649 | |||
| Mean | 0.82174 | 0.06763 | 0.06763 | 0.67058 | 0.66243 | 0.06763 | 0.66794 | 0.66911 | |||
| Bias | 0.00389 | −0.14155 | −0.14155 | −0.14728 | −0.15543 | −0.14155 | −0.14991 | −0.14874 | |||
| MSE | 0.01209 | 0.03864 | 0.03864 | 0.04022 | 0.04160 | 0.03864 | 0.04106 | 0.03969 | |||
| 45 | Mean | 3.00590 | 3.26007 | 3.26007 | 3.28537 | 3.25634 | 3.26007 | 3.29045 | 3.29795 | ||
| Bias | 0.00590 | 0.26007 | 0.26007 | 0.28537 | 0.25634 | 0.26007 | 0.29045 | 0.29795 | |||
| MSE | 0.05150 | 0.16148 | 0.16148 | 0.18213 | 0.16170 | 0.16148 | 0.18621 | 0.19122 | |||
| Mean | 0.72696 | 0.77077 | 0.77077 | 0.77626 | 0.77529 | 0.77077 | 0.77567 | 0.77656 | |||
| Bias | −0.00208 | 0.04173 | 0.04173 | 0.04722 | 0.04624 | 0.04173 | 0.04662 | 0.04751 | |||
| MSE | 0.00202 | 0.00427 | 0.00427 | 0.00487 | 0.00484 | 0.00427 | 0.00484 | 0.00493 | |||
| Mean | 0.82158 | 0.71391 | 0.71391 | 0.69751 | 0.69632 | 0.71391 | 0.69481 | 0.70328 | |||
| Bias | 0.00372 | −0.10395 | −0.10395 | −0.12035 | −0.12153 | −0.10395 | −0.12305 | −0.11458 | |||
| MSE | 0.01161 | 0.02630 | 0.02630 | 0.03071 | 0.03116 | 0.02630 | 0.03143 | 0.02963 | |||
| 100 | 80 | Mean | 2.99586 | 2.88566 | 2.88566 | 2.88583 | 2.88962 | 2.88566 | 2.88604 | 2.89182 | |
| Bias | −0.00414 | −0.11434 | −0.11434 | −0.11417 | −0.11038 | −0.11434 | −0.11396 | −0.10818 | |||
| MSE | 0.01098 | 0.05951 | 0.05951 | 0.05756 | 0.05676 | 0.05951 | 0.05753 | 0.05624 | |||
| Mean | 0.72752 | 0.70238 | 0.70238 | 0.70264 | 0.70369 | 0.70238 | 0.70258 | 0.70382 | |||
| Bias | −0.00152 | −0.02666 | −0.02666 | −0.02640 | −0.02535 | −0.02666 | −0.02646 | −0.02522 | |||
| MSE | 0.00044 | 0.00277 | 0.00277 | 0.00272 | 0.00260 | 0.00277 | 0.00273 | 0.00259 | |||
| Mean | 0.82123 | 0.88026 | 0.88026 | 0.87943 | 0.87657 | 0.88026 | 0.87924 | 0.87720 | |||
| Bias | 0.00337 | 0.06240 | 0.06240 | 0.06158 | 0.05871 | 0.06240 | 0.06138 | 0.05934 | |||
| MSE | 0.00250 | 0.01551 | 0.01551 | 0.01519 | 0.01449 | 0.01551 | 0.01516 | 0.01460 | |||
| 90 | Mean | 2.99828 | 2.80776 | 2.80776 | 2.81487 | 2.80215 | 2.80776 | 2.81506 | 2.80426 | ||
| Bias | −0.00172 | −0.19224 | −0.19224 | −0.18513 | −0.19785 | −0.19224 | −0.18494 | −0.19574 | |||
| MSE | 0.01196 | 0.07459 | 0.07459 | 0.07104 | 0.07827 | 0.07459 | 0.07098 | 0.07743 | |||
| Mean | 0.72794 | 0.68584 | 0.68584 | 0.68761 | 0.68481 | 0.68584 | 0.68754 | 0.68495 | |||
| Bias | −0.00111 | −0.04320 | −0.04320 | −0.04143 | −0.04424 | −0.04320 | −0.04151 | −0.04409 | |||
| MSE | 0.00048 | 0.00373 | 0.00373 | 0.00352 | 0.00392 | 0.00373 | 0.00353 | 0.00390 | |||
| Mean | 0.82020 | 0.91954 | 0.91954 | 0.91512 | 0.92128 | 0.91954 | 0.91493 | 0.92194 | |||
| Bias | 0.00235 | 0.10168 | 0.10168 | 0.09726 | 0.10342 | 0.10168 | 0.09707 | 0.10408 | |||
| MSE | 0.00273 | 0.02070 | 0.02070 | 0.01947 | 0.02156 | 0.02070 | 0.01943 | 0.02172 | |||
| n | r | Parameters | ML Estimates | Bayes Estimates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | |||||||||
| 30 | 24 | Mean | 4.16607 | 5.28285 | 5.28285 | 5.06967 | 4.52576 | 5.28285 | 5.20078 | 5.04745 | |
| Bias | 0.16607 | 1.28285 | 1.28285 | 1.06967 | 0.52576 | 1.28285 | 1.20078 | 1.04745 | |||
| MSE | 1.67464 | 1.72315 | 1.72315 | 1.19408 | 0.29629 | 1.72315 | 1.50711 | 1.15652 | |||
| Mean | 3.03499 | 4.26197 | 4.26197 | 4.17048 | 3.95053 | 4.26197 | 4.21649 | 4.20813 | |||
| Bias | 0.03499 | 1.26197 | 1.26197 | 1.17048 | 0.95053 | 1.26197 | 1.21649 | 1.20813 | |||
| MSE | 0.25231 | 1.75037 | 1.75037 | 1.52003 | 1.01733 | 1.75037 | 1.64189 | 1.61824 | |||
| Mean | 0.73095 | 0.86271 | 0.86271 | 0.86064 | 0.85785 | 0.86271 | 0.85912 | 0.86186 | |||
| Bias | 0.00191 | 0.13367 | 0.13367 | 0.13160 | 0.12881 | 0.13367 | 0.13008 | 0.13281 | |||
| MSE | 0.00381 | 0.01949 | 0.01949 | 0.01909 | 0.01831 | 0.01949 | 0.01876 | 0.01924 | |||
| Mean | 0.80548 | 0.50812 | 0.50812 | 0.50185 | 0.48638 | 0.50812 | 0.47848 | 0.52651 | |||
| Bias | −0.01238 | −0.30973 | −0.30973 | −0.31601 | −0.33147 | −0.30973 | −0.33937 | −0.29135 | |||
| MSE | 0.02586 | 0.11072 | 0.11072 | 0.11496 | 0.12278 | 0.11072 | 0.13028 | 0.09937 | |||
| 27 | Mean | 3.93086 | 5.20625 | 5.20625 | 5.02841 | 4.50613 | 5.20625 | 5.13947 | 4.96516 | ||
| Bias | −0.06914 | 1.20625 | 1.20625 | 1.02841 | 0.50613 | 1.20625 | 1.13947 | 0.96516 | |||
| MSE | 0.99679 | 1.54481 | 1.54481 | 1.12231 | 0.28407 | 1.54481 | 1.37923 | 1.00406 | |||
| Mean | 2.96485 | 4.21493 | 4.21493 | 4.12865 | 3.96655 | 4.21493 | 4.16967 | 4.20868 | |||
| Bias | −0.03516 | 1.21493 | 1.21493 | 1.12865 | 0.96656 | 1.21493 | 1.16967 | 1.20868 | |||
| MSE | 0.22540 | 1.65026 | 1.65026 | 1.41292 | 1.04495 | 1.65026 | 1.51704 | 1.61560 | |||
| Mean | 0.72508 | 0.85882 | 0.85882 | 0.85756 | 0.86006 | 0.85882 | 0.85608 | 0.86378 | |||
| Bias | −0.00396 | 0.12978 | 0.12978 | 0.12852 | 0.13101 | 0.12978 | 0.12704 | 0.13473 | |||
| MSE | 0.00415 | 0.01867 | 0.01867 | 0.01820 | 0.01877 | 0.01867 | 0.01787 | 0.01966 | |||
| Mean | 0.80782 | 0.51779 | 0.51779 | 0.51001 | 0.48025 | 0.51779 | 0.48721 | 0.51821 | |||
| Bias | −0.01003 | −0.30007 | −0.30007 | −0.30785 | −0.33761 | −0.30007 | −0.29964 | −0.28406 | |||
| MSE | 0.02341 | 0.10651 | 0.10651 | 0.10894 | 0.12634 | 0.10651 | 0.12354 | 0.10339 | |||
| 50 | 40 | Mean | 4.05159 | 4.66134 | 4.66134 | 4.58093 | 4.3328 | 4.66134 | 4.63320 | 4.69727 | |
| Bias | 0.05159 | 0.66134 | 0.66134 | 0.58093 | 0.43329 | 0.66134 | 0.63320 | 0.69727 | |||
| MSE | 0.93907 | 0.54113 | 0.54113 | 0.43373 | 0.26693 | 0.54113 | 0.50220 | 0.59661 | |||
| Mean | 2.9930 | 3.44872 | 3.44872 | 3.43808 | 3.42955 | 3.44872 | 3.44368 | 3.47011 | |||
| Bias | −0.00699 | 0.44872 | 0.44872 | 0.43808 | 0.42955 | 0.44872 | 0.44368 | 0.47011 | |||
| MSE | 0.15451 | 0.28342 | 0.28342 | 0.27496 | 0.26221 | 0.28342 | 0.28092 | 0.30397 | |||
| Mean | 0.72659 | 0.77715 | 0.77715 | 0.77642 | 0.77788 | 0.77715 | 0.77535 | 0.78020 | |||
| Bias | −0.00328 | 0.04811 | 0.04811 | 0.04738 | 0.04883 | 0.04811 | 0.04630 | 0.05115 | |||
| MSE | 0.00259 | 0.00461 | 0.00461 | 0.00459 | 0.00466 | 0.00461 | 0.00453 | 0.00484 | |||
| Mean | 0.81581 | 0.73021 | 0.73021 | 0.72526 | 0.71216 | 0.73021 | 0.71607 | 0.73270 | |||
| Bias | −0.00205 | −0.08764 | −0.08764 | −0.09259 | −0.10570 | −0.08764 | −0.10178 | −0.08516 | |||
| MSE | 0.01664 | 0.02475 | 0.02475 | 0.02555 | 0.02724 | 0.02475 | 0.02738 | 0.02423 | |||
| 45 | Mean | 4.09112 | 4.45987 | 4.45987 | 4.39046 | 4.29615 | 4.45987 | 4.42271 | 4.47300 | ||
| Bias | 0.09112 | 0.45987 | 0.45987 | 0.39046 | 0.29615 | 0.45987 | 0.42271 | 0.47300 | |||
| MSE | 0.85313 | 0.30271 | 0.30271 | 0.24252 | 0.16649 | 0.30271 | 0.27075 | 0.31575 | |||
| Mean | 3.01325 | 3.43271 | 3.43271 | 3.40664 | 3.37651 | 3.43271 | 3.41345 | 3.42173 | |||
| Bias | 0.01532 | 0.43271 | 0.43271 | 0.40664 | 0.37651 | 0.43271 | 0.41345 | 0.42173 | |||
| MSE | 0.15142 | 0.27312 | 0.27312 | 0.25098 | 0.22452 | 0.27312 | 0.25766 | 0.26411 | |||
| Mean | 0.72828 | 0.78136 | 0.78136 | 0.77934 | 0.77736 | 0.78136 | 0.77816 | 0.77985 | |||
| Bias | −0.00076 | 0.05231 | 0.05231 | 0.05030 | 0.04832 | 0.05231 | 0.04911 | 0.05081 | |||
| MSE | 0.00263 | 0.00503 | 0.00503 | 0.00489 | 0.00463 | 0.00503 | 0.00481 | 0.00481 | |||
| Mean | 0.81454 | 0.71017 | 0.71017 | 0.70742 | 0.70328 | 0.71017 | 0.69774 | 0.72367 | |||
| Bias | −0.00332 | −0.10768 | −0.10768 | −0.11044 | −0.11458 | −0.10768 | −0.12011 | −0.09419 | |||
| MSE | 0.01549 | 0.02820 | 0.02820 | 0.02879 | 0.02832 | 0.02820 | 0.03108 | 0.02514 | |||
| 100 | 80 | Mean | 4.05071 | 4.59825 | 4.59825 | 4.56338 | 3.78855 | 4.59825 | 4.58227 | 3.86137 | |
| Bias | 0.05070 | 0.59825 | 0.59825 | 0.56338 | −0.21145 | 0.59825 | 0.58227 | −0.13863 | |||
| MSE | 0.72617 | 0.47415 | 0.47415 | 0.42489 | 0.12062 | 0.47415 | 0.44698 | 0.09656 | |||
| Mean | 2.99159 | 3.15642 | 3.15642 | 3.13728 | 3.10475 | 3.15642 | 3.13801 | 3.11545 | |||
| Bias | −0.00841 | 0.15642 | 0.15642 | 0.13728 | 0.10475 | 0.15642 | 0.13801 | 0.11545 | |||
| MSE | 0.09857 | 0.06558 | 0.06558 | 0.05925 | 0.05418 | 0.06558 | 0.05947 | 0.05666 | |||
| Mean | 0.72703 | 0.72996 | 0.72996 | 0.72630 | 0.75405 | 0.72996 | 0.72584 | 0.75520 | |||
| Bias | −0.00201 | 0.00092 | 0.00092 | −0.00274 | 0.02501 | 0.00092 | −0.00320 | 0.026153 | |||
| MSE | 0.00134 | 0.00169 | 0.00169 | 0.00181 | 0.00225 | 0.00169 | 0.00182 | 0.00228 | |||
| Mean | 0.81773 | 0.85016 | 0.85016 | 0.85649 | 0.74084 | 0.85016 | 0.85334 | 0.75007 | |||
| Bias | −0.00012 | 0.03231 | 0.03231 | 0.03864 | −0.07702 | 0.03231 | 0.03549 | −0.06778 | |||
| MSE | 0.00853 | 0.01369 | 0.01369 | 0.01488 | 0.01634 | 0.01369 | 0.01459 | 0.01537 | |||
| 90 | Mean | 4.13316 | 4.12649 | 4.12649 | 4.11049 | 4.10047 | 4.12649 | 4.11853 | 4.14749 | ||
| Bias | 0.13316 | 0.12649 | 0.12649 | 0.11049 | 0.10047 | 0.12649 | 0.11853 | 0.14749 | |||
| MSE | 0.63163 | 0.09053 | 0.09053 | 0.08638 | 0.08943 | 0.09053 | 0.08811 | 0.10049 | |||
| Mean | 3.03671 | 3.14705 | 3.14705 | 3.13727 | 3.12428 | 3.14705 | 3.13863 | 3.13364 | |||
| Bias | 0.03671 | 0.14705 | 0.14705 | 0.13727 | 0.12428 | 0.14705 | 0.13863 | 0.13364 | |||
| MSE | 0.08624 | 0.06907 | 0.06907 | 0.06479 | 0.05953 | 0.06907 | 0.06532 | 0.06197 | |||
| Mean | 0.73130 | 0.74822 | 0.74822 | 0.74685 | 0.74436 | 0.74822 | 0.74640 | 0.74528 | |||
| Bias | 0.00225 | 0.01918 | 0.01918 | 0.01781 | 0.01532 | 0.01918 | 0.01735 | 0.01624 | |||
| MSE | 0.00123 | 0.00207 | 0.00207 | 0.00204 | 0.00188 | 0.00207 | 0.00203 | 0.00189 | |||
| Mean | 0.81449 | 0.77804 | 0.77804 | 0.77874 | 0.78228 | 0.77804 | 0.77556 | 0.78958 | |||
| Bias | −0.00398 | −0.03982 | −0.03982 | −0.03911 | −0.03558 | −0.03982 | −0.04230 | −0.02828 | |||
| MSE | 0.00769 | 0.01314 | 0.01314 | 0.01315 | 0.01228 | 0.01314 | 0.01342 | 0.01209 | |||
| Measure | Value | Measure | Value |
|---|---|---|---|
| n | 102 | Minimum | 223 |
| Maximum | 560 | Mean | 397.88 |
| Q1 | 352 | Q3 | 439 |
| Median | 400 | Skewness | −0.003 |
| Kurtosis | 2.85 | Variance | 3884.30 |
| Standard deviation | 62.32 |
| Model | r | Parameters | ML Estimates | Bayes Estimates | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | ||||||||
| BIED | 82 | 411.2780 | 3.8423 | 3.8423 | 3.1272 | 2.4938 | 3.8423 | 3.3474 | 4.0774 | |
| 1.5256 | 0.1721 | 0.1721 | 0.1717 | 0.1710 | 0.1721 | 0.1672 | 0.1745 | |||
| 92 | 432.7910 | 4.3285 | 4.3285 | 3.5184 | 2.8021 | 4.3285 | 3.8318 | 4.5658 | ||
| 1.83122 | 0.1968 | 0.1968 | 0.1963 | 0.1955 | 0.1968 | 0.1917 | 0.1993 | |||
| Models | r | ML Estimates | ℓ | AIC | BIC | CAIC | HQIC | ||
|---|---|---|---|---|---|---|---|---|---|
| BIED | 82 | 44.7839 | 20.9497 | 150.0270 | −151.342 | 308.684 | 316.559 | 308.929 | 311.873 |
| 92 | 43.2797 | 20.0114 | 148.1150 | −172.933 | 351.867 | 359.742 | 352.112 | 355.056 | |
| IED | 82 | — | — | 424.3190 | −248.584 | 499.168 | 501.793 | 499.208 | 500.231 |
| 92 | — | — | 404.397 | −288.006 | 578.013 | 580.638 | 578.053 | 579.076 | |
| WIED | 82 | 52.3513 | 0.6796 | 2540.0300 | −159.233 | 324.467 | 332.342 | 324.712 | 327.655 |
| 92 | 53.5041 | 0.6438 | 2660.4100 | −180.559 | 367.117 | 374.992 | 367.362 | 370.306 | |
| IWD | 82 | 138.1880 | 1.0897 | — | −293.464 | 590.927 | 596.177 | 591.049 | 593.053 |
| 92 | 148.2970 | 1.2775 | — | −321.958 | 647.916 | 653.166 | 648.037 | 650.042 | |
| WED | 82 | 0.0004 | 0.0047 | 3.9449 | −151.652 | 309.303 | 317.178 | 309.548 | 312.492 |
| 92 | 0.0064 | 0.0106 | 1.1240 | −179.223 | 364.447 | 372.321 | 364.691 | 367.635 | |
| OFIED | 82 | 3.5426 | — | 252.0410 | −157.345 | 318.689 | 323.939 | 318.810 | 320.815 |
| 92 | 3.7253 | — | 250.2300 | −180.356 | 364.713 | 369.963 | 364.834 | 366.839 | |
| Measure | Value | Measure | Value |
|---|---|---|---|
| n | 33 | Minimum | 1 |
| Maximum | 156 | Mean | 40.88 |
| Q1 | 4 | Q3 | 65 |
| Median | 22 | Skewness | 1.16 |
| Kurtosis | 3.12 | Variance | 2181.17 |
| Standard deviation | 46.70 |
| Model | r | Parameters | ML Estimates | Bayes Estimates | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | GE | ||||||||
| BIED | 26 | 4.4313 | 1.7585 | 1.7585 | 1.5146 | 1.2642 | 1.7585 | 1.4025 | 1.9172 | |
| 0.4524 | 0.3622 | 0.3622 | 0.3563 | 0.3481 | 0.3622 | 0.3298 | 0.3786 | |||
| 30 | 4.8218 | 1.9092 | 1.9092 | 1.6483 | 1.3788 | 1.9092 | 1.5626 | 2.0654 | ||
| 0.5142 | 0.4058 | 0.4058 | 0.3993 | 0.3902 | 0.4058 | 0.3737 | 0.4220 | |||
| Models | r | ML Estimates | ℓ | AIC | BIC | CAIC | HQIC | ||
|---|---|---|---|---|---|---|---|---|---|
| BIED | 26 | 2.5699 | 0.4672 | 1.2091 | −40.404 | 84.808 | 87.801 | 85.208 | 85.815 |
| 30 | 5.5948 | 0.5282 | 0.5915 | −56.103 | 116.205 | 119.198 | 116.605 | 117.212 | |
| IED | 26 | — | — | 6.0189 | −46.888 | 95.777 | 97.273 | 95.906 | 96.280 |
| 30 | — | — | 6.0164 | −61.848 | 125.695 | 127.191 | 125.824 | 126.198 | |
| WIED | 26 | 0.3738 | 0.5673 | 5.1250 | −41.701 | 89.402 | 93.892 | 90.230 | 90.913 |
| 30 | 0.3535 | 0.5788 | 4.9131 | −57.983 | 121.965 | 126.455 | 122.793 | 123.476 | |
| IWD | 26 | 8.6392 | 0.6227 | — | −40.672 | 87.344 | 91.834 | 88.172 | 88.855 |
| 30 | 8.2490 | 0.6557 | — | −56.731 | 119.462 | 123.952 | 120.29 | 120.973 | |
| WED | 26 | 0.4269 | 0.4431 | 0.0478 | −44.422 | 94.844 | 99.333 | 95.671 | 96.354 |
| 30 | 0.4985 | 0.3479 | 0.0390 | −61.213 | 128.426 | 132.916 | 129.254 | 129.937 | |
| OFIED | 26 | 0.4202 | — | 3.6035 | −42.007 | 88.014 | 91.007 | 88.414 | 89.021 |
| 30 | 0.4600 | — | 3.3522 | −58.573 | 121.146 | 124.139 | 121.546 | 122.153 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldahlan, M.A.; Bakoban, R.A.; Alzahrani, L.S. On Estimating the Parameters of the Beta Inverted Exponential Distribution under Type-II Censored Samples. Mathematics 2022, 10, 506. https://doi.org/10.3390/math10030506
Aldahlan MA, Bakoban RA, Alzahrani LS. On Estimating the Parameters of the Beta Inverted Exponential Distribution under Type-II Censored Samples. Mathematics. 2022; 10(3):506. https://doi.org/10.3390/math10030506
Chicago/Turabian StyleAldahlan, Maha A., Rana A. Bakoban, and Leena S. Alzahrani. 2022. "On Estimating the Parameters of the Beta Inverted Exponential Distribution under Type-II Censored Samples" Mathematics 10, no. 3: 506. https://doi.org/10.3390/math10030506
APA StyleAldahlan, M. A., Bakoban, R. A., & Alzahrani, L. S. (2022). On Estimating the Parameters of the Beta Inverted Exponential Distribution under Type-II Censored Samples. Mathematics, 10(3), 506. https://doi.org/10.3390/math10030506





