Multi-Objective Feeder Reconfiguration Using Discrete Particle Swarm Optimization
Abstract
:1. Introduction
Description of the Feeder Reconfiguration
2. Feeder Reconfiguration in a Distribution Network
- -
- a set of optimal solutions (non-dominated set) and
- -
- a set of non-optimal solutions (dominated set).
- -
- is no worse than for all objectives, i.e., , and
- -
- is strictly better than for at least one objective, i.e., for at least one.
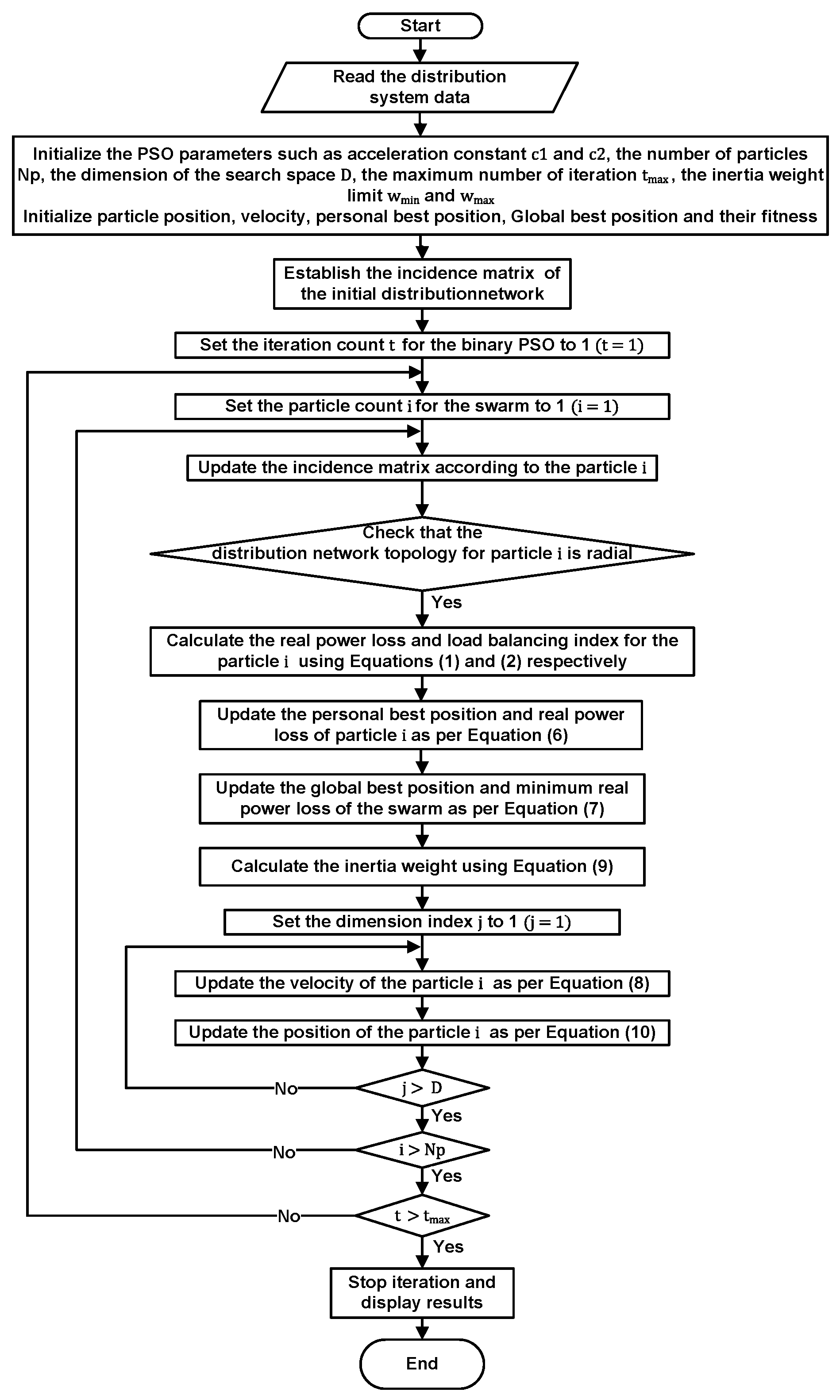
3. Development of the Discrete Particle Swarm Optimization Method
4. The BPSO Solution Algorithm’s Results for the Multi-Objective Distribution Network Feeder Reconfiguration Problem
- -
- IEEE 16 bus distribution system;
- -
- IEEE 33 bus distribution system; and
- -
- IEEE 69-bus distribution system.
4.1. Case Study 1: The IEEE 16-Bus Distribution System
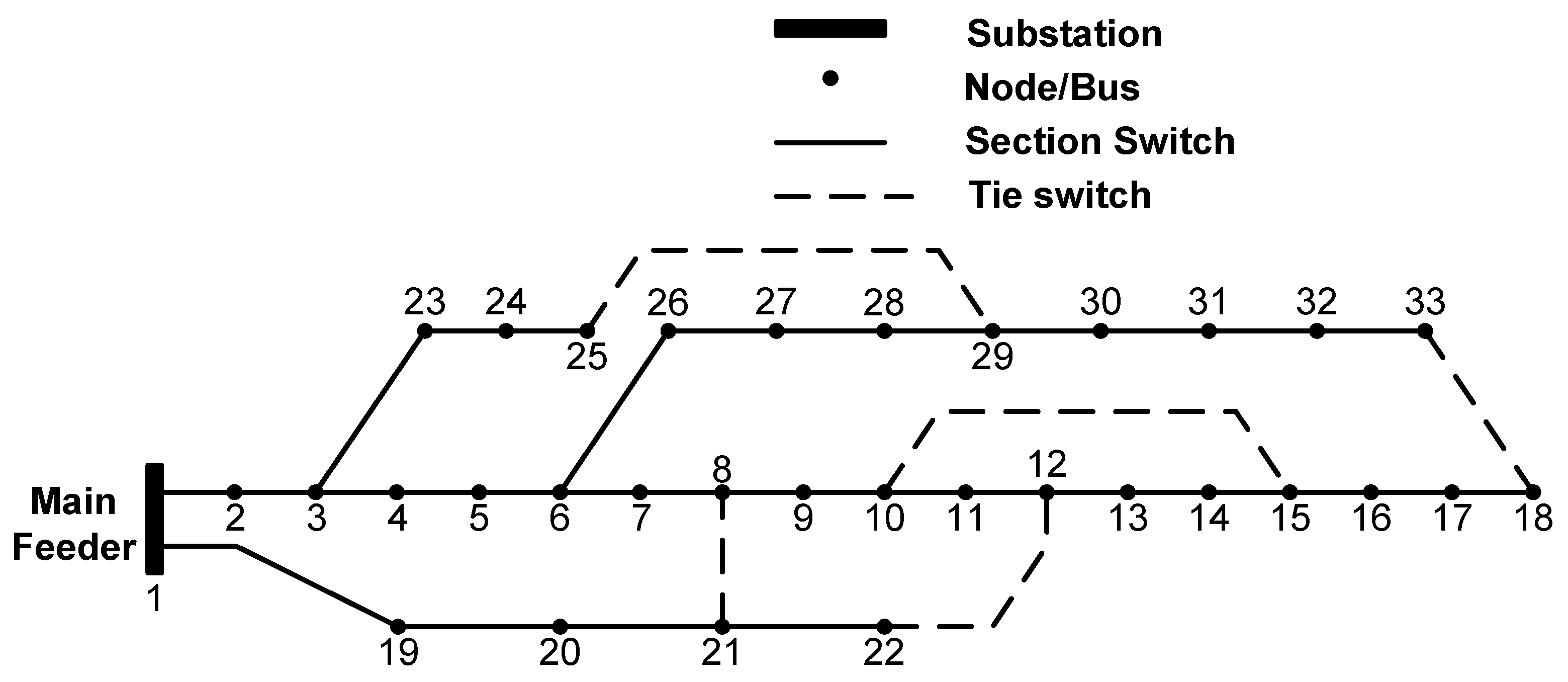
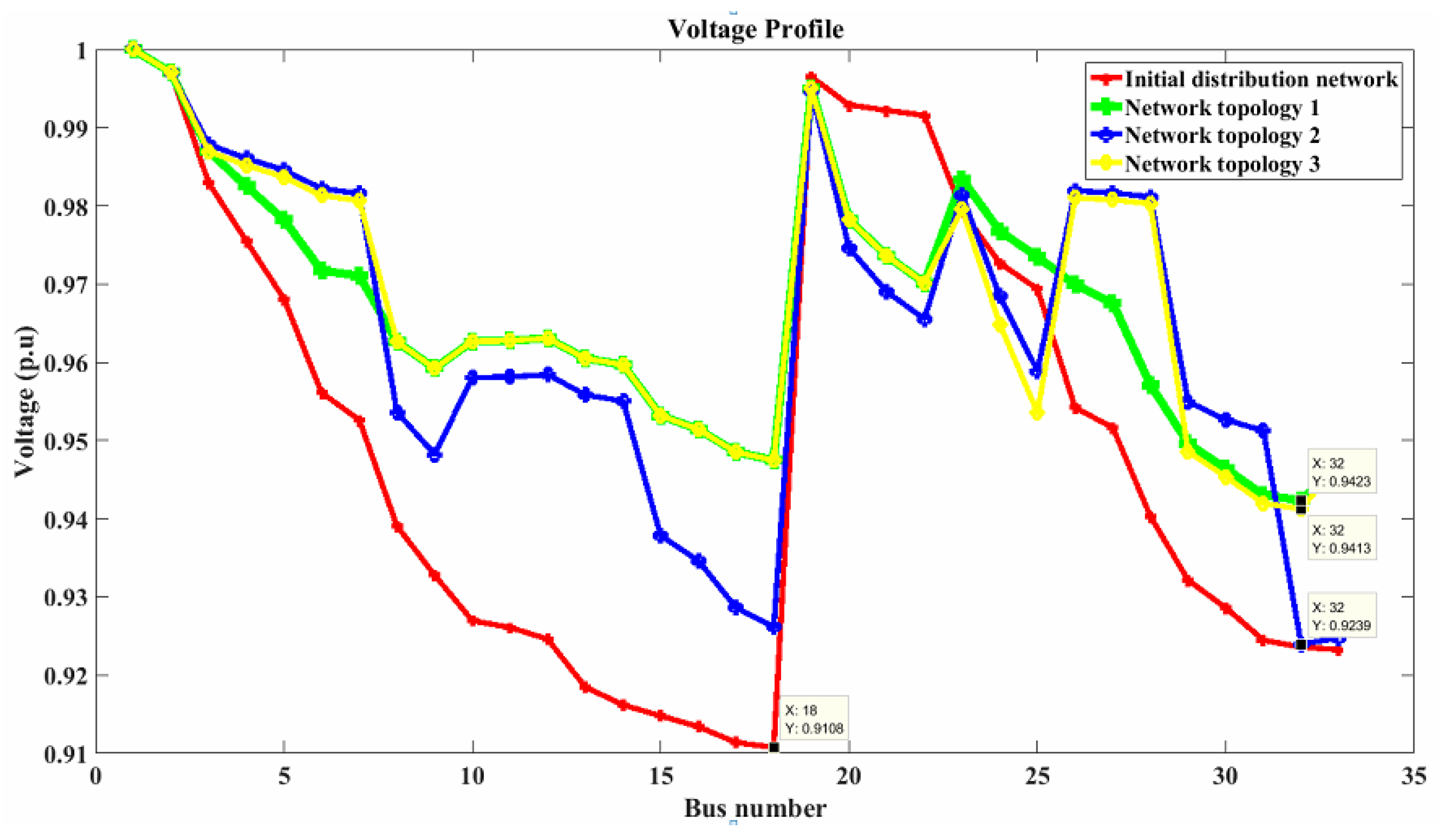
4.2. Case Study 2: The IEEE 33-Bus Distribution System
- -
- Network topology 1: The tie switches for the 33-bus distribution system may be found at branches 7 (branch 7-8), 9 (branch 9–10), 14 (branch 14–15), 32 (branch 32–33), and 37 (branch 25–29). The real power loss for this network design is 138.9105 kW, and the load balancing index is . Compared to the baseline distribution system, this optimization method results in a real power loss reduction of roughly 33.3546 percent and an LBI improvement of 29.2125 percent. In the search space, network topology 1 has the lowest real power loss. As a result, network topology 1 outperforms all other proposed network topologies in terms of real power loss.
- -
- Network topology 2: The tie switches of the 33-bus distribution system are branches 7 (branch 7–8), 9 (branch 9–10), 14 (branch 14–15), 28 (branch 28–29), and 31 (branch 31–32). The real power loss for this network design is 144.1694 kW and the load balancing index is . Compared to the original distribution system, this optimization method results in an actual power loss reduction of roughly 30.8315 percent and an LBI improvement of 34.1697 percent. Network topology 2 has the lowest load balancing index in the search space. As a result, network topology 2 is non-dominant in the search space in terms of load balancing index.
- -
- Network topology 3: The tie switches of the 33-bus distribution system are branches 7 (branch 7–8), 9 (branch 9–10), 14 (branch 14–15), 28 (branch 28–29), and 32 (branch 32–33). The real power loss for this network design is 139.9645 kW and the load balancing index is . Compared to the baseline distribution system, this optimization method results in a real power loss reduction of roughly 32.8489 percent and an LBI improvement of 32.88251 percent.
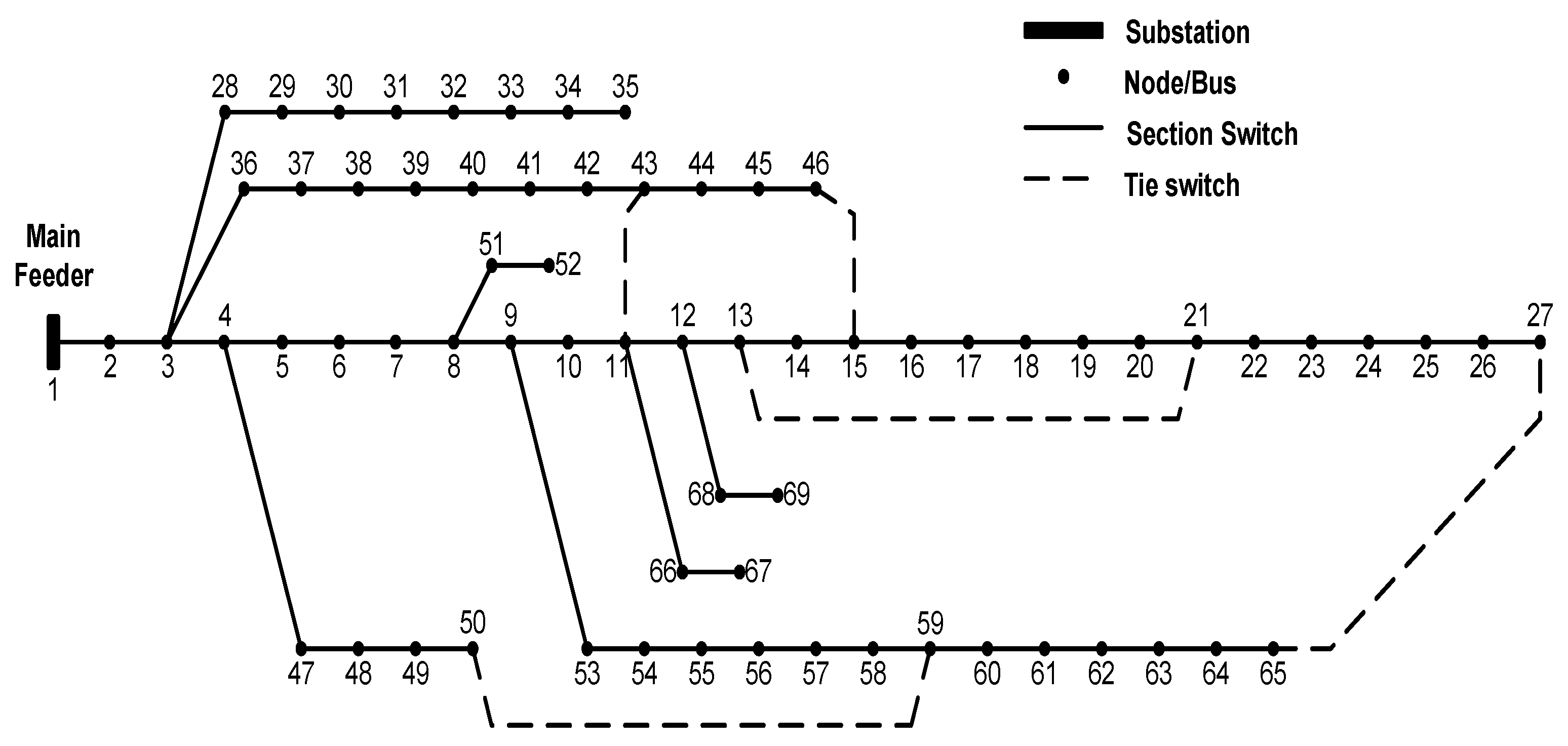
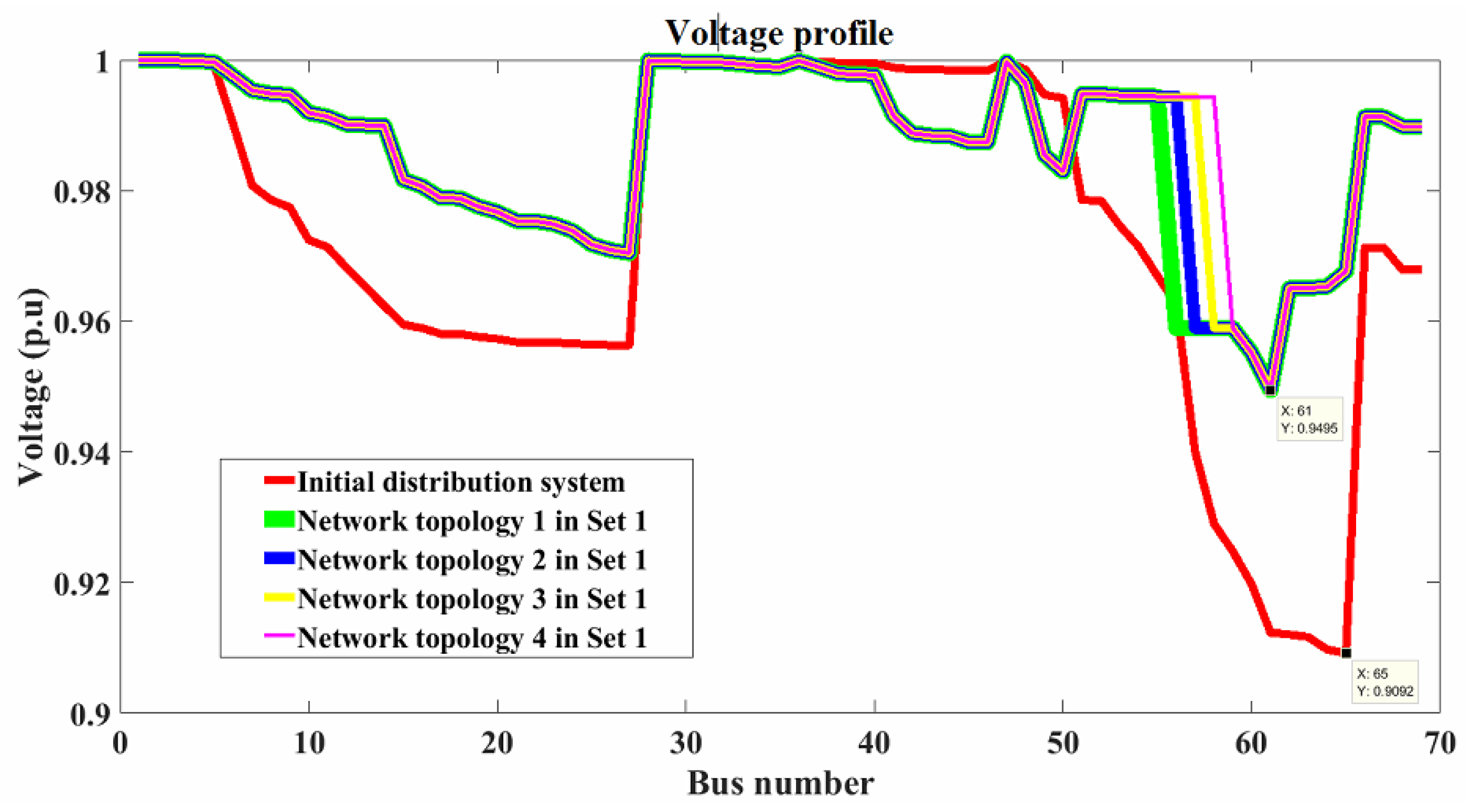
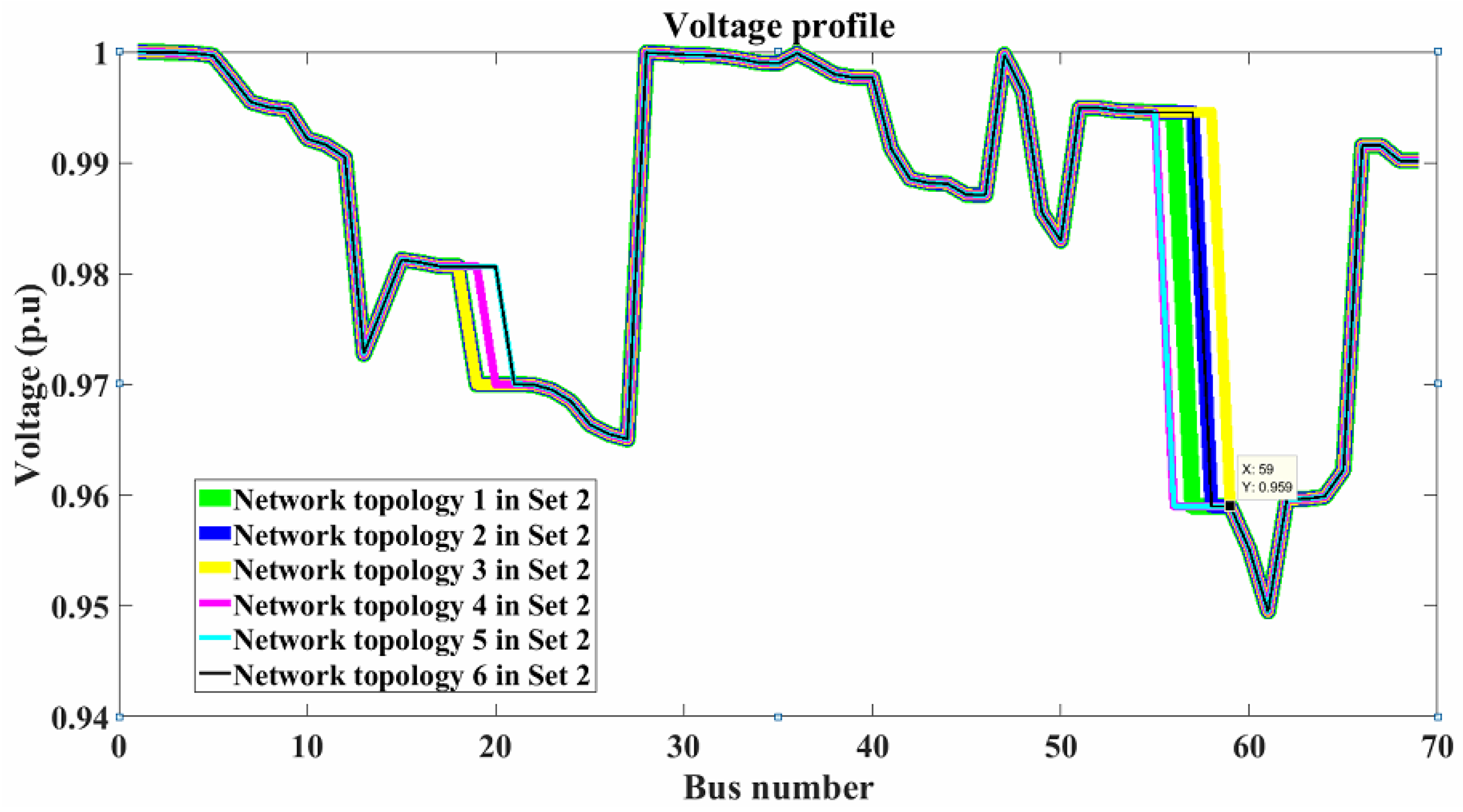
4.3. Case Study 3: The IEEE 69-Bus Distribution System
| Algorithm | Developed BPSO Algorithm | Harmony Search [25] | Selective PSO [26] | ||
|---|---|---|---|---|---|
| Before reconfiguration | Tie switches | ||||
| Real power loss | |||||
| Load Balancing Index (LBI) | − | − | |||
| After reconfiguration | Tie switches | ||||
| Real power loss | |||||
| Real power loss reduction | |||||
| Load Balancing Index (LBI) | − | − | |||
| Load balancing improvement | − | − | |||
| Minimum voltage | − | ||||
| CPU Time | − | − | |||
- -
- Set 1 is a collection of solution network topologies with a total power loss of 98.5952 kW and a load balancing index of . Compared to the initial distribution system, these optimization techniques result in an actual power loss reduction of roughly 56.1761 percent and an LBI improvement of 35.6355 percent.
- -
- Set 2 is a collection of solution network topologies with a real power loss of 101.2961 kW and a load balancing index of . Compared to the initial distribution system, these optimization techniques result in an actual power loss reduction of roughly 54.9756 percent and an LBI improvement of 36.4006 percent.
5. Discussion on the Comparison of the Developed BPSO Results with the Literature
6. Conclusions
- -
- For the analyzed 16-bus, 33-bus, and 69-bus distribution systems, the developed BPSO algorithm provides an optimal solution network topology to the multi-objective feeder reconfiguration problem.
- -
- The aims of real power loss minimization and load balancing are diametrically opposed. They may appear to be non-conflicting, depending on the loads, parameters, and distribution system design, as seen with the 16-bus distribution system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Mathematical Notations and Acronyms | |
| real power loss of at iteration | |
| load balancing index of at iteration | |
| personal best position of particle at iteration | |
| real power loss of at iteration | |
| load balancing index of at iteration | |
| real power loss of particle at iteration | |
| load balancing index of particle at iteration | |
| conjugate of the current flow in line | |
| position of particle at iteration | |
| global best solution of the swarm at iteration | |
| load balance index of the network | |
| total real power loss in the distribution system | |
| power rating of branch | |
| apparent power loss in the branch | |
| are the sending and receiving end voltage of the line , respectively | |
| fitness of particle | |
| and | are the inequality and equality constraints, respectively |
| maximum number of iterations | |
| maximum velocity | |
| minimum velocity | |
| maximum inertia weight | |
| minimum inertia weight | |
| ACO | Ant Colony Optimization |
| D | dimension of search space |
| DPSO | Discrete Particle Swarm Optimization |
| GA | Genetic Algorithm |
| HBMO | Honey Bee Mating Optimization |
| Np | number of particles |
| PSO | Particle Swarm Optimization |
| number of buses in the network | |
| number of branches in the distribution system | |
| real power loss for the particle’s position | |
| load balancing index for the particle’s position | |
| sending bus of line | |
| receiving bus of line | |
| branch number of the line | |
| number of objective functions | |
| uniformly distributed random number in the interval [0,1] | |
| random number in the range . | |
| sigmoid function defined by | |
| iteration number | |
| inertia weight | |
References
- Liu, C.; Lee, S.; Vu, K. Loss minimization of distribution feeders: Optimality and algorithms. IEEE Trans. Power Deliv. 1989, 4, 1281–1289. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Tzoneva, R.; Apostolov, A. Method for a Parallel Solution of a Combined Economic Emission Dispatch Problem. Electr. Power Compon. Syst. 2017, 45, 393–409. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T. An improved cuckoo search algorithm for the problem of electric distribution network reconfiguration. Appl. Soft Comput. 2019, 84, 105720. [Google Scholar] [CrossRef]
- Enacheanu, B.; Bienia, W.; Devaux, O.; Caire, R.; Raison, B.; HadjSaid, N. Radial network reconfiguration using Genetic Algorithm based on the Matroid theory. IEEE Trans. Power Syst. 2008, 23, 186–195. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, J.; Sun, Y.; Li, K.; Zhang, B. Distribution network reconfiguration for load balancing using binary particle swarm optimization. In Proceedings of the 2004 International Conference on Power System Technology (PowerCon 2004), Singapore, 21–24 November 2004; IEEE: Singapore, 2004; pp. 507–510. [Google Scholar]
- Hu, Z.; He, X.; Gao, Y.; Liu, D. Distribution network reconfiguration based on ant colony system algorithm. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 2470–2474. [Google Scholar]
- Niknam, T. An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration. Expert Syst. Appl. 2011, 38, 2878–2887. [Google Scholar] [CrossRef]
- Gebru, Y.; Bitew, D.; Aberie, H.; Gizaw, K. Performance enhancement of radial distribution system using simultaneous network reconfiguration and switched capacitor bank placement. Cogent Eng. 2021, 8, 1897929. [Google Scholar] [CrossRef]
- ElDesouky, A.; Reyad, E.; Mahmoud, G. Implementation of boolean PSO for service restoration using distribution network reconfiguration simultaneously with distributed energy resources and capacitor banks. Int. J. Renew. Energy Res. 2020, 10, 354–365. [Google Scholar]
- Wu, W.; Tsai, M. Feeder Reconfiguration Using Binary Coding Particle Swarm Optimization. Int. J. Control Autom. Syst. 2008, 6, 488–494. [Google Scholar]
- Muhammad, M.A.; Mokhlis, H.; Naidu, K.; Amin, A.; Franco, J.F.; Othman, M. Distribution Network Planning Enhancement via Network Reconfiguration and DG Integration Using Dataset Approach and Water Cycle Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 86–93. [Google Scholar] [CrossRef]
- Helmi, A.M.; Carli, R.; Dotoli, M.; Ramadan, H.S. Efficient and Sustainable Reconfiguration of Distribution Networks via Metaheuristic Optimization. IEEE Trans. Autom. Sci. Eng. 2021, 19, 82–98. [Google Scholar] [CrossRef]
- Djiepkop, N. Feeder Reconfiguration Scheme with Integration of Renewable Energy Sources Using a Particle Swarm Optimisation Method. Master’s Thesis, Electrical, Cape Peninsula University of Technology, Cape Town, South Africa, 2018. [Google Scholar]
- Caramia, M.; Dell’Olmo, P. Multi-Objective Management in Freight Logistics: Increasing Capacity, Service Level and Safety with Optimization Algorithms; Springer: London, UK, 2014. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the Computational Cybernetics and Simulation 1997 IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Civanlar, S.; Grainger, J.; Yin, H.; Lee, S. Distribution feeder reconfiguration for loss reduction. IEEE Trans. Power Deliv. 1988, 3, 1217–1223. [Google Scholar] [CrossRef]
- Su, C.-T.; Chang, C.-F.; Chiou, J.-P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electr. Power Syst. Res. 2005, 75, 190–199. [Google Scholar] [CrossRef]
- de Oliveira, L.W.; de Oliveira, E.J.; Gomes, F.V.; Silva, I.C.; Marcato, A.L.; Resende, P.V. Artificial Immune Systems applied to the reconfiguration of electrical power distribution networks for energy loss minimization. Int. J. Electr. Power Energy Syst. 2014, 56, 64–74. [Google Scholar] [CrossRef]
- Zhu, J. Optimal reconfiguration of electrical distribution network using the refined genetic algorithm. Electr. Power Syst. Res. 2002, 62, 37–42. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Mohamed, F.M.; Mekhamer, S.F.; Badr, M.A.L. Distribution system reconfiguration using a modified Tabu Search algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- Singh, S.P.; Raju, G.S.; Rao, G.K.; Afsari, M. A heuristic method for feeder reconfiguration and service restoration in distribution networks. Int. J. Electr. Power Energy Syst. 2009, 31, 309–314. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Mohammed, F.M.; Mekhamer, S.F.; Badr, M.A.L. Distribution Systems Reconfiguration using a modified particle swarm optimization algorithm. Electr. Power Syst. Res. 2009, 79, 1521–1530. [Google Scholar] [CrossRef]
- Savier, J.S.; Das, D. Impact of Network Reconfiguration on Loss Allocation of Radial Distribution Systems. IEEE Trans. Power Deliv. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Khalil, T.; Gorpinich, A. Reconfiguration for Loss Reduction of Distribution Systems Using Selective Particle Swarm Optimization. Int. J. Multidiscip. Sci. Eng. 2012, 3, 16–21. [Google Scholar]
- Baloch, Z. A new nonlinear constructive method for loss reduction and load balancing in radial distribution network reconfiguration. Eur. Sci. J. 2013, 9, 93–98. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]


| Line No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sending Bus | 1 | 4 | 4 | 6 | 2 | 8 | 8 | 9 | 9 | 3 | 13 | 13 | 15 | 5 | 10 | 7 |
| Receivingbus | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 11 | 14 | 16 |
| Status | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Algorithm | Developed BPSO Algorithm | ACO [18] | MINLP [19] | Refined GA [20] | Modified Tabu-Search [21] | |
|---|---|---|---|---|---|---|
| Before reconfiguration | Tie switches | |||||
| Real power loss | ||||||
| Load Balancing index (LBI) | − | − | − | − | ||
| Minimum voltage | ||||||
| After reconfiguration | Tie switches | |||||
| Real power loss | ||||||
| Real power loss reduction | ||||||
| Load Balancing index (LBI) | − | − | − | − | ||
| Load balance improvement | − | − | − | − | ||
| Minimum voltage | ||||||
| CPU Time | − | − | − | − | ||
| Algorithm | Developed BPSO Algorithm | Sequential Switch Opening Method [22] | Modified PSO [23] | HBMO [7] | |
|---|---|---|---|---|---|
| Before reconfiguration | Tie switches | ||||
| Real power loss | |||||
| Load Balancing Index (LBI) | − | − | − | ||
| After reconfiguration | Tie switches | ||||
| Real power loss | |||||
| Real power loss reduction | |||||
| Load Balancing Index (LBI) | − | − | − | ||
| Load balancing improvement | − | − | − | ||
| Minimum voltage | |||||
| CPU Time | ~1.9 s | − | − | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noudjiep Djiepkop, G.F.; Krishnamurthy, S. Multi-Objective Feeder Reconfiguration Using Discrete Particle Swarm Optimization. Mathematics 2022, 10, 531. https://doi.org/10.3390/math10030531
Noudjiep Djiepkop GF, Krishnamurthy S. Multi-Objective Feeder Reconfiguration Using Discrete Particle Swarm Optimization. Mathematics. 2022; 10(3):531. https://doi.org/10.3390/math10030531
Chicago/Turabian StyleNoudjiep Djiepkop, Giresse Franck, and Senthil Krishnamurthy. 2022. "Multi-Objective Feeder Reconfiguration Using Discrete Particle Swarm Optimization" Mathematics 10, no. 3: 531. https://doi.org/10.3390/math10030531
APA StyleNoudjiep Djiepkop, G. F., & Krishnamurthy, S. (2022). Multi-Objective Feeder Reconfiguration Using Discrete Particle Swarm Optimization. Mathematics, 10(3), 531. https://doi.org/10.3390/math10030531






