Event-Triggered Asynchronous Filter of Nonlinear Switched Positive Systems with Output Quantization
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
3.1. Positivity
3.2. Static Event-Triggering Case
3.3. Dynamic Event-Triggering Case
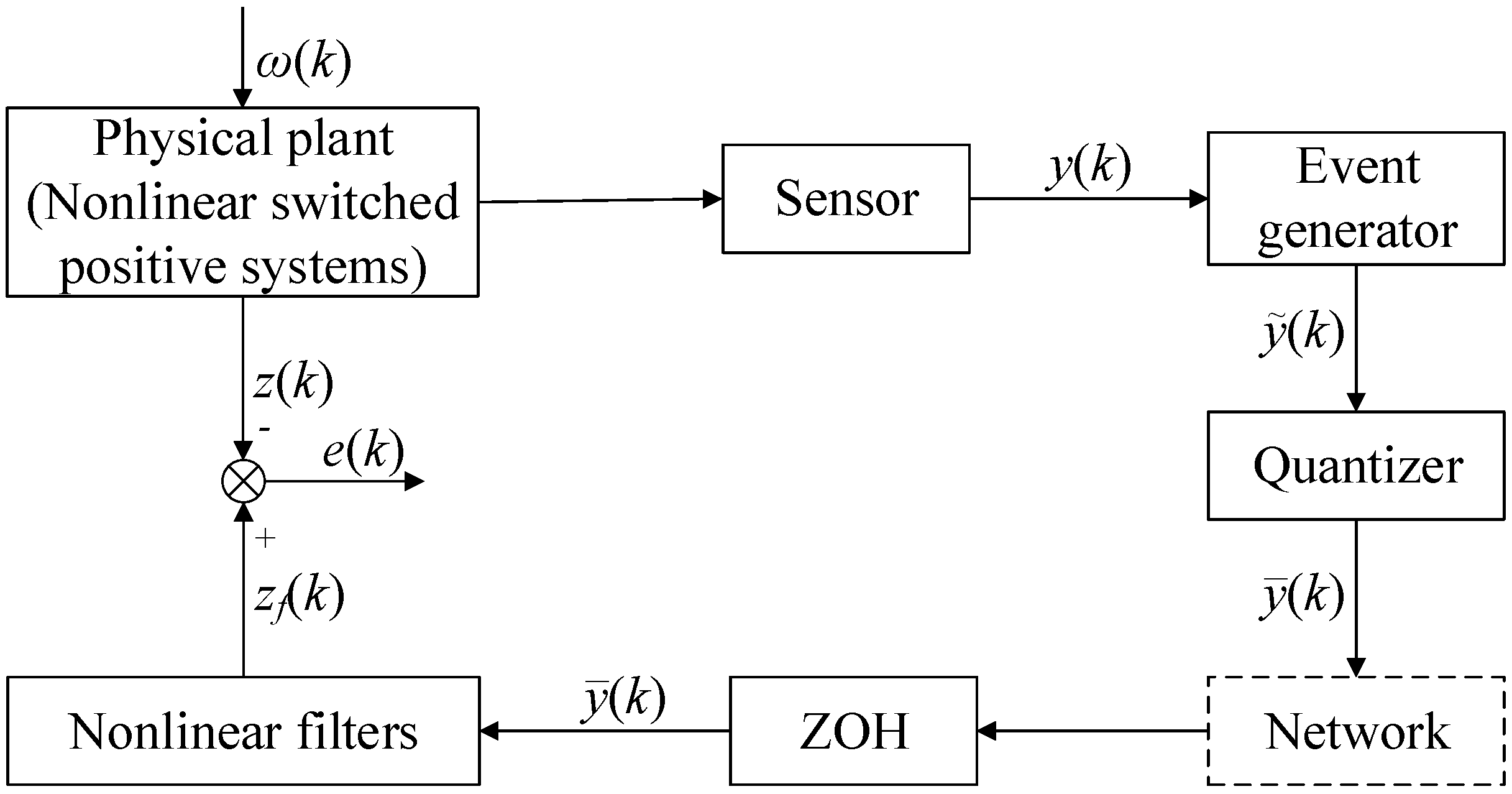
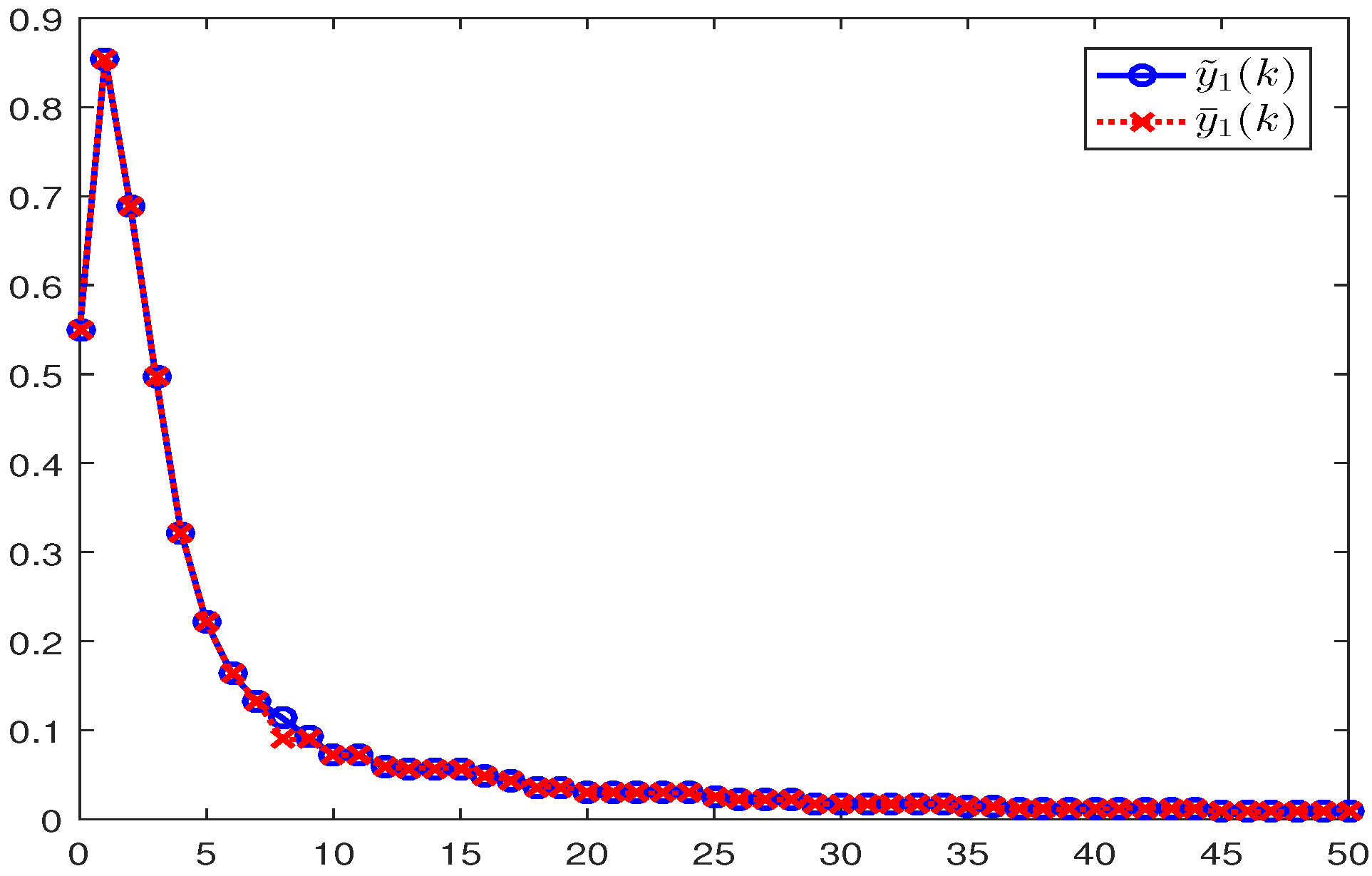
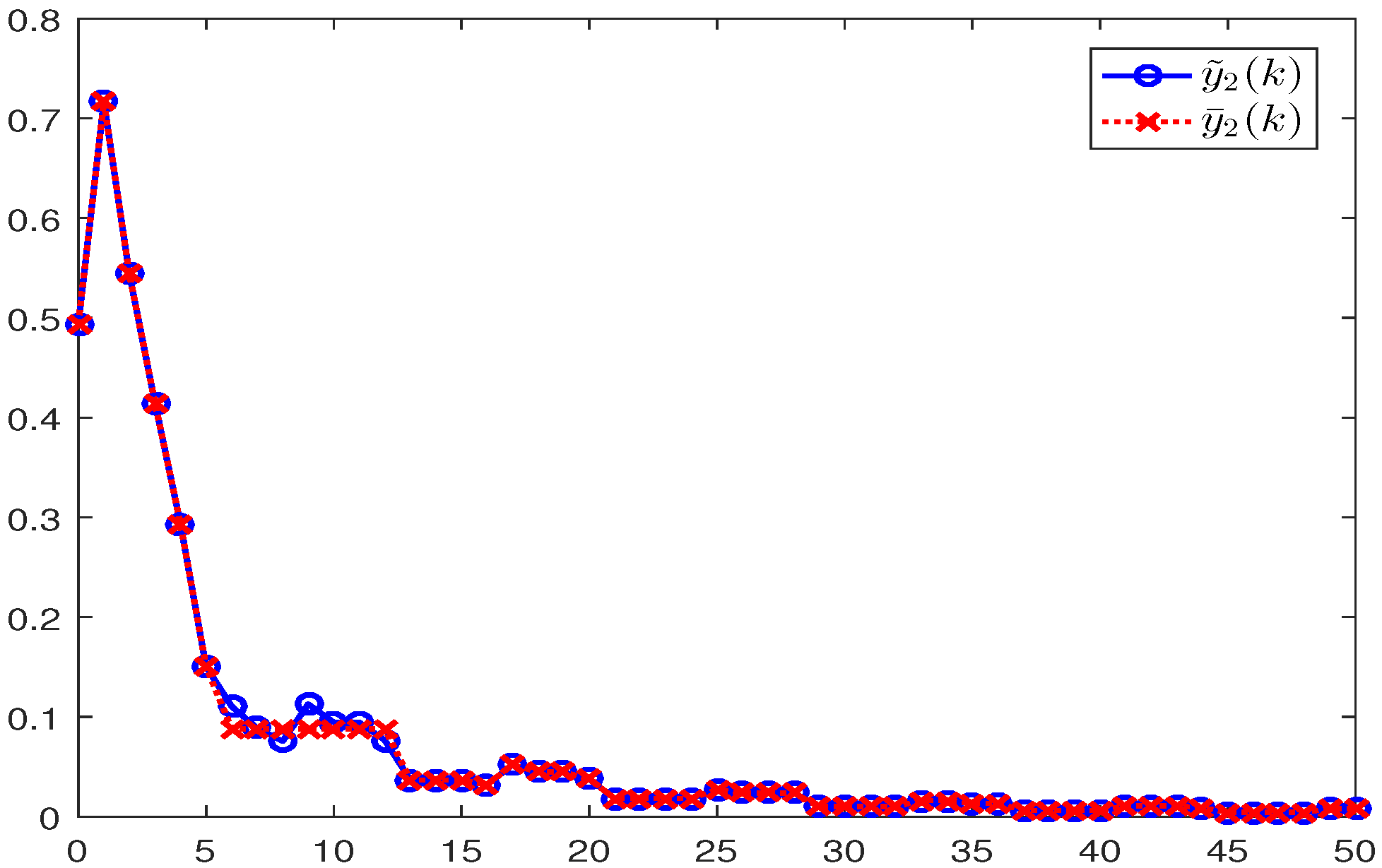
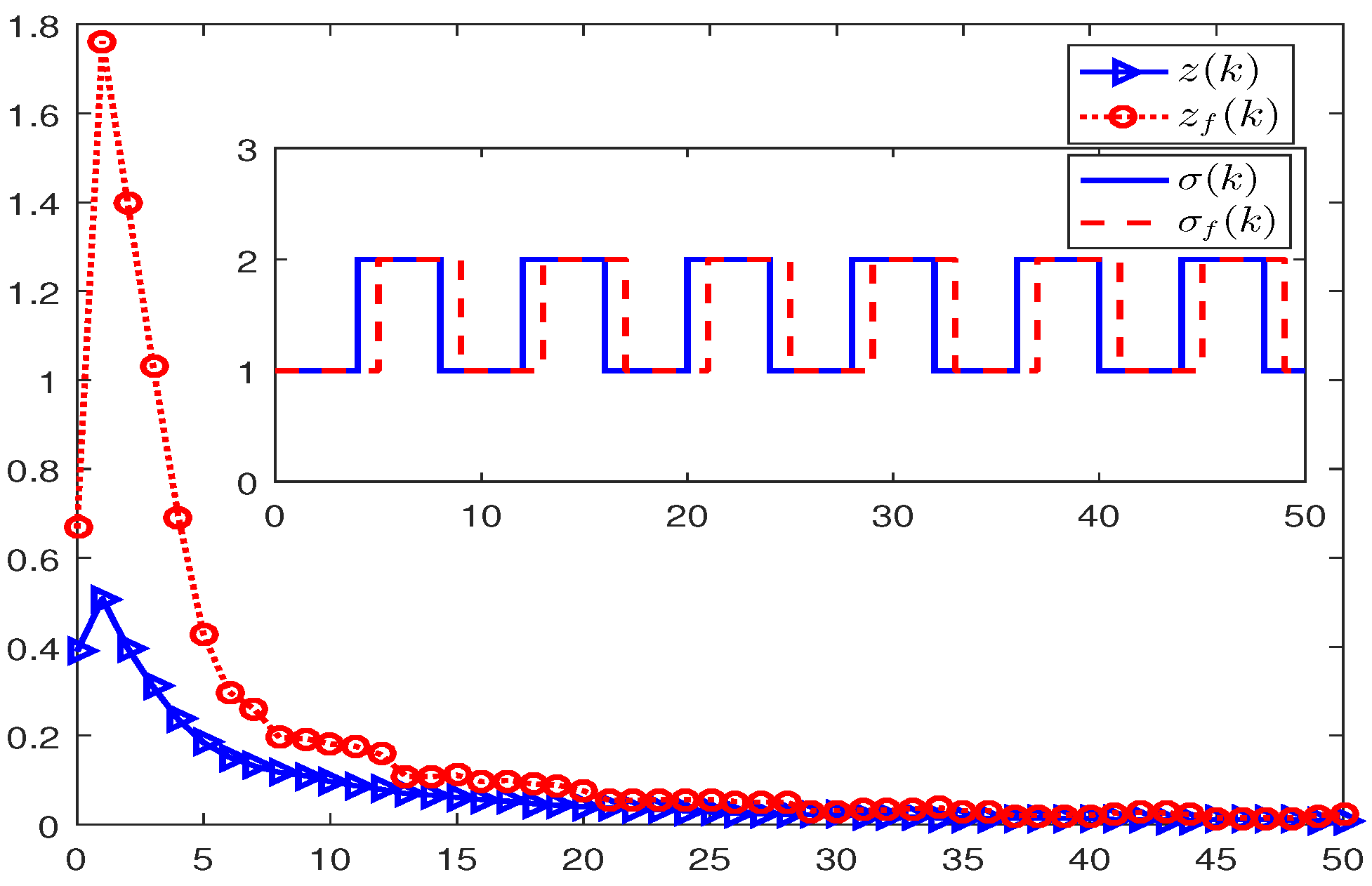
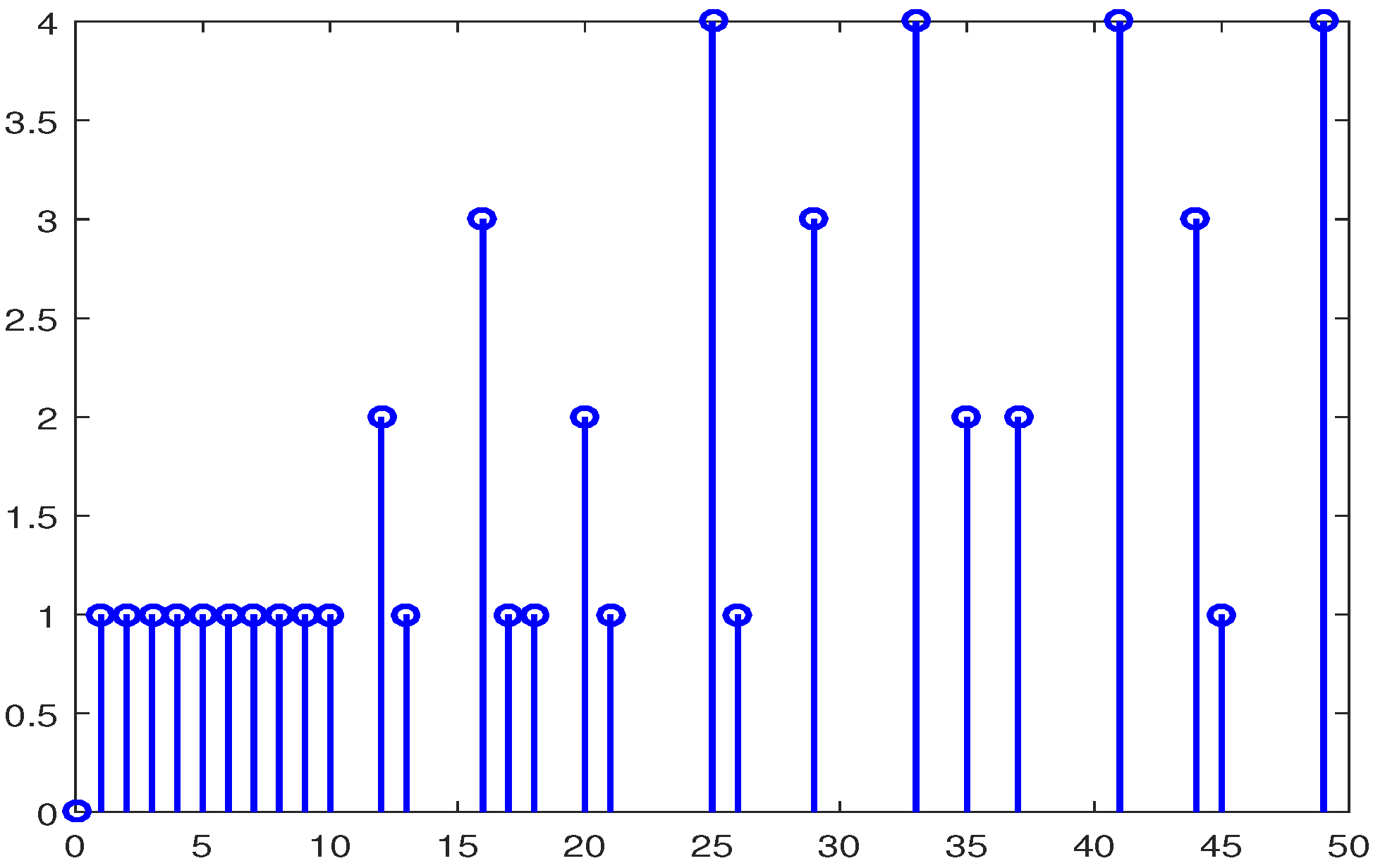
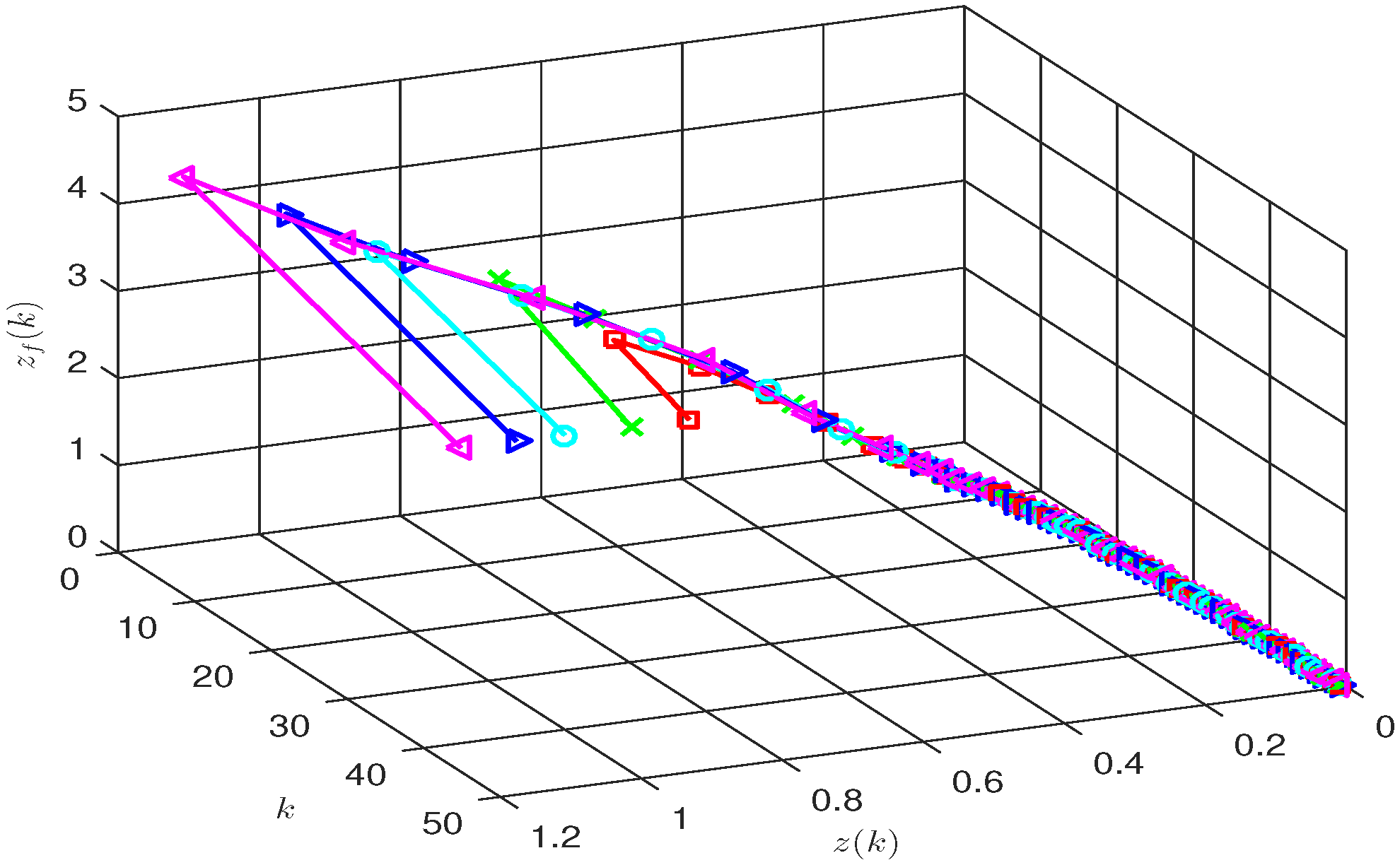
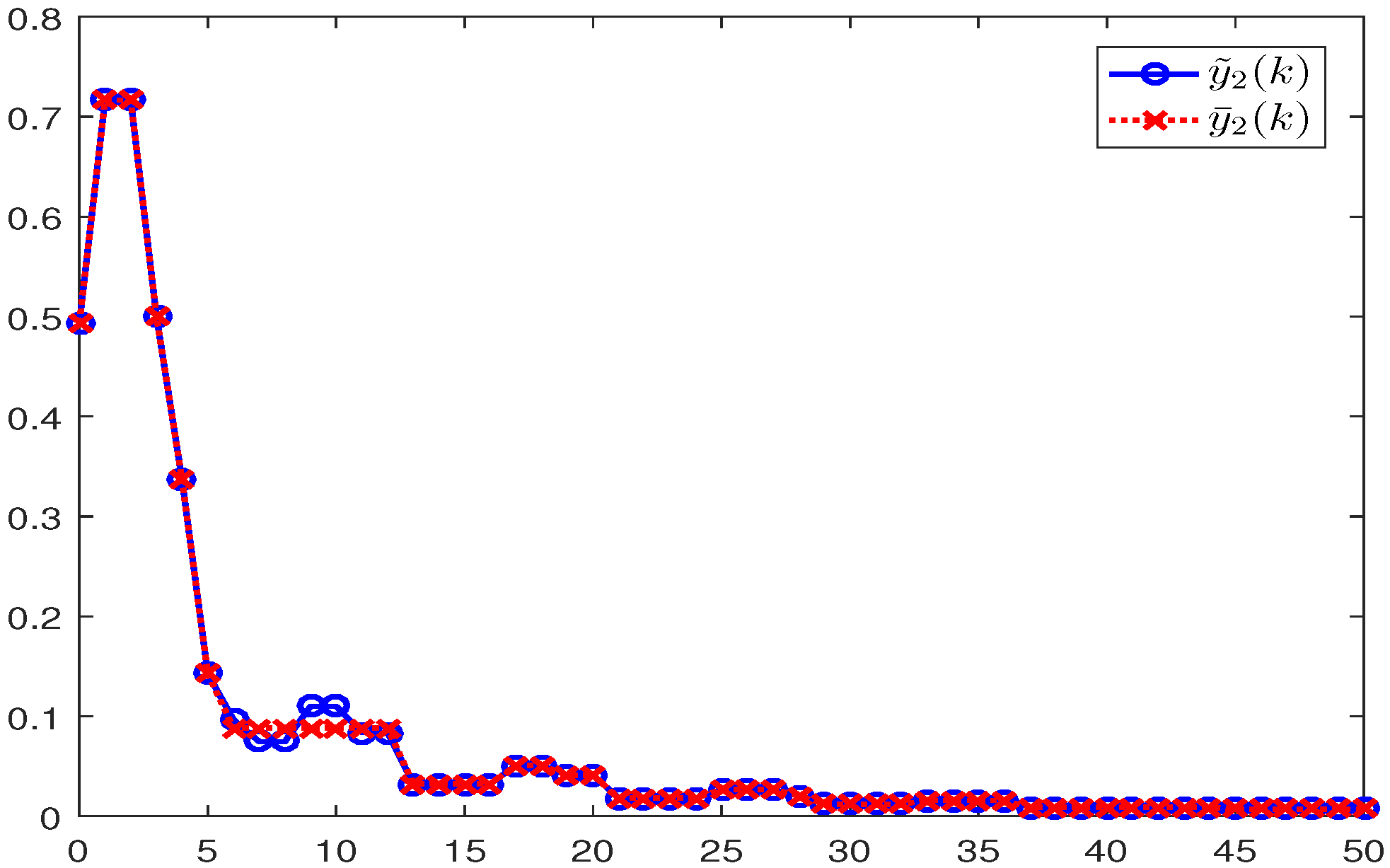
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Kaczorek, T. Positive 1D and 2D Systems; Springer: London, UK, 2001. [Google Scholar]
- Hespanha, J.P.; Morse, A.S. Stability of switched systems with average dwell-time. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999; Volume 3, pp. 2655–2660. [Google Scholar]
- Dinh, T.N.; Marouani, G.; Raïssi, T.; Wang, Z.; Messaoud, H. Optimal interval observers for discrete-time linear switched systems. Int. J. Control 2020, 93, 2613–2621. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef] [Green Version]
- Liberzon, D. Switching in Systems and Control; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Silva-Navarro, G.; Alvarez-Gallegos, J. On the property sign-stability of equilibria in quasimonotone positive nonlinear systems. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 4, pp. 4043–4048. [Google Scholar]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of predictive control strategies to the management of complex networks in the urban water cycle. IEEE Control. Syst. Mag. 2013, 33, 15–41. [Google Scholar]
- Fornasini, E.; Valcher, M.E. Stability and stabilizability criteria for discrete-time positive switched systems. IEEE Trans. Autom. Control 2011, 57, 1208–1221. [Google Scholar] [CrossRef]
- Pastravanu, O.C.; Matcovschi, M.H. Max-type copositive Lyapunov functions for switching positive linear systems. Automatica 2014, 50, 3323–3327. [Google Scholar] [CrossRef]
- Xiang, W.; Lam, J.; Shen, J. Stability analysis and L1-gain characterization for switched positive systems under dwell-time constraint. Automatica 2017, 85, 1–8. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Z.; Zhu, F. L1-gain analysis and control synthesis of positive switched systems. Int. J. Syst. Sci. 2015, 46, 2111–2121. [Google Scholar] [CrossRef]
- Fainshil, L.; Margaliot, M.; Chigansky, P. On the stability of positive linear switched systems under arbitrary switching laws. IEEE Trans. Autom. Control 2009, 54, 897–899. [Google Scholar] [CrossRef] [Green Version]
- Blanchini, F.; Colaneri, P.; Valcher, M.E. Co-positive Lyapunov functions for the stabilization of positive switched systems. IEEE Trans. Autom. Control 2012, 57, 3038–3050. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z.; Karimi, H.R. Stabilization of positive switched systems with time-varying delays under asynchronous switching. Int. J. Control. Autom. Syst. 2014, 512, 939–947. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wang, Z.; Li, G.; Wang, W. Distributed filtering for switched nonlinear positive systems with missing measurements over sensor networks. IEEE Sens. J. 2016, 16, 4940–4948. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhao, X.; Cai, X. Absolute exponential L1-gain analysis and synthesis of switched nonlinear positive systems with time-varying delay. Appl. Math. Comput. 2016, 284, 24–36. [Google Scholar]
- Zhang, J.; Raïssi, T. Saturation control of switched nonlinear systems. Nonlinear Anal. Hybrid Syst. 2019, 32, 320–336. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, S. Reduced-order fault detection filter design for switched nonlinear systems with time delay. Nonlinear Dyn. 2012, 67, 601–617. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, H. H∞ filtering for a class of nonlinear switched systems with stable and unstable subsystems. Signal Process. 2017, 141, 240–248. [Google Scholar] [CrossRef]
- Aleksandrov, A.; Aleksandrova, E.; Zhabko, A. Stability analysis of some classes of nonlinear switched systems with time delay. Int. J. Syst. Sci. 2017, 48, 2111–2119. [Google Scholar] [CrossRef]
- Baleghi, N.A.; Shafiei, M.H. Stability analysis and stabilization of a class of discrete-time nonlinear switched systems with time-delay and affine parametric uncertainty. J. Vib. Control 2019, 25, 1326–1340. [Google Scholar] [CrossRef]
- Huo, X.; Ma, L.; Zhao, X.; Zong, G. Observer-based fuzzy adaptive stabilization of uncertain switched stochastic nonlinear systems with input quantization. J. Frankl. Inst. 2019, 356, 1789–1809. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Zheng, Z.; Qian, W. Robust adaptive state estimation for uncertain nonlinear switched systems with unknown inputs. Trans. Inst. Meas. Control. 2018, 40, 1082–1091. [Google Scholar] [CrossRef]
- Niu, B.; Zhao, P.; Liu, J.D.; Ma, H.J.; Liu, Y.J. Global adaptive control of switched uncertain nonlinear systems: An improved MDADT method. Automatica 2020, 115, 108872. [Google Scholar] [CrossRef]
- Xiang, W.; Xiao, J. H∞ filtering for switched nonlinear systems under asynchronous switching. Int. J. Syst. Sci. 2011, 42, 751–765. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S.; Zhang, Z. Asynchronous nonfragile H∞ filtering for discrete-time nonlinear switched systems with quantization. Nonlinear Anal. Hybrid Syst. 2020, 37, 100911. [Google Scholar] [CrossRef]
- Ren, Y.; Er, M.J.; Sun, G. Asynchronous ℓ1 positive filter design for switched positive systems with overlapped detection delay. IET Control Theory Appl. 2017, 11, 319–328. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Wang, G.; Dang, C. Asynchronous H∞ filtering for linear switched systems with average dwell time. Int. J. Syst. Sci. 2016, 47, 2783–2791. [Google Scholar] [CrossRef]
- Li, Y.; Du, W.; Xu, X.; Zhang, H.; Xia, J. A novel approach to L1 filter design for asynchronously switched positive linear systems with dwell time. Int. J. Robust Nonlinear Control 2019, 29, 5957–5978. [Google Scholar] [CrossRef]
- Brockett, R.W.; Liberzon, D. Quantized feedback stabilization of linear systems. IEEE Trans. Autom. Control 2000, 45, 1279–1289. [Google Scholar] [CrossRef] [Green Version]
- Wakaiki, M.; Yamamoto, Y. Stabilization of switched linear systems with quantized output and switching delays. IEEE Trans. Autom. Control 2016, 62, 2958–2964. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Cao, J.; Zhang, D. Quantized H∞ filtering for switched linear parameter-varying systems with sojourn probabilities and unreliable communication channels. Inf. Sci. 2018, 466, 289–302. [Google Scholar] [CrossRef]
- Yang, L.; Guan, C.; Fei, Z. Finite-time asynchronous filtering for switched linear systems with an event-triggered mechanism. J. Frankl. Inst. 2019, 356, 5503–5520. [Google Scholar] [CrossRef]
- Zong, G.; Ren, H.; Karimi, H.R. Event-triggered communication and annular finite-time H∞ filtering for networked switched systems. IEEE Trans. Cybern. 2020, 51, 309–317. [Google Scholar] [CrossRef]
- Liu, X.; Su, X.; Shi, P.; Nguang, S.K.; Shen, C. Fault detection filtering for nonlinear switched systems via event-triggered communication approach. Automatica 2019, 101, 365–376. [Google Scholar] [CrossRef]
- Wang, Y.L.; Shi, P.; Lim, C.C.; Liu, Y. Event-triggered fault detection filter design for a continuous-time networked control system. IEEE Trans. Cybern. 2016, 46, 3414–3426. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, G.; Feng, Y.; Chen, Y. Event-triggered state-feedback and dynamic output-feedback control of positive Markovian jump systems with intermittent faults. IEEE Trans. Autom. Control 2022. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, Y.; Xu, Q.; Zhang, B. Event-triggered network-based L1-gain filtering for positive linear systems. Int. J. Syst. Sci. 2017, 48, 1281–1290. [Google Scholar] [CrossRef]
- Zhang, J.; Raïssi, T.; Shao, Y.; Cai, X. Event-triggered filter design of positive systems with state saturation. IEEE Syst. J. 2020, 15, 4281–4285. [Google Scholar] [CrossRef]
- Shao, Y.; Jiao, C.; Zhang, S.; Zhang, J. Event-triggered filter of switched positive systems with state saturation. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems, Guangzhou, China, 13–15 November 2020; pp. 1–6. [Google Scholar]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2014, 60, 1992–1997. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.; Tian, E.; Liu, J. Adaptive event-triggered control of a class of nonlinear networked systems. J. Frankl. Inst. 2017, 354, 3854–3871. [Google Scholar] [CrossRef]
- Li, Q.; Shen, B.; Wang, Z.; Sheng, W. Recursive distributed filtering over sensor networks on Gilbert-Elliott channels: A dynamic event-triggered approach. Automatica 2020, 113, 108681. [Google Scholar] [CrossRef]
- Liu, D.; Yang, G.H. Dynamic event-triggered control for linear time-invariant systems with-gain performance. Int. J. Robust Nonlinear Control 2019, 29, 507–518. [Google Scholar] [CrossRef]
- Luo, S.; Deng, F.; Chen, W.H. Dynamic event-triggered control for linear stochastic systems with sporadic measurements and communication delays. Automatica 2019, 107, 86–94. [Google Scholar] [CrossRef]
- Lu, R.; Wu, F.; Xue, A. Networked control with reset quantized state based on Bernoulli processing. IEEE Trans. Ind. Electron. 2013, 61, 4838–4846. [Google Scholar] [CrossRef]
- Dong, S.; Su, H.; Shi, P.; Lu, R.; Wu, Z.G. Filtering for discrete-time switched fuzzy systems with quantization. IEEE Trans. Fuzzy Syst. 2016, 25, 1616–1628. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Q. Network-based modelling and dynamic output feedback control for unmanned marine vehicles in network environments. Automatica 2018, 91, 43–53. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Lin, P.; Zhang, J. Event-Triggered Asynchronous Filter of Nonlinear Switched Positive Systems with Output Quantization. Mathematics 2022, 10, 599. https://doi.org/10.3390/math10040599
Zhang S, Lin P, Zhang J. Event-Triggered Asynchronous Filter of Nonlinear Switched Positive Systems with Output Quantization. Mathematics. 2022; 10(4):599. https://doi.org/10.3390/math10040599
Chicago/Turabian StyleZhang, Shitao, Peng Lin, and Junfeng Zhang. 2022. "Event-Triggered Asynchronous Filter of Nonlinear Switched Positive Systems with Output Quantization" Mathematics 10, no. 4: 599. https://doi.org/10.3390/math10040599





