Balancing the Electromagnetic Field Exposure in Wireless Multi-Hop Networks: An EMF-Aware Routing Scheme
Abstract
:1. Introduction
- Definition of a general exposure model for wireless multi-hop networks;
- Introduction of an optimization problem to include the EMF exposure in routing schemes;
- Proposal of a novel EMF-aware routing protocol based on AODV, coined EA-AODV, that practically solves the aforementioned optimization problem;
- Implementation of EA-AODV protocol in the NS-3 framework;
- Evaluation of the EA-AODV operation in comparison with legacy solutions.
2. Related Work
3. EMF-Aware Routing Framework for WMNs
3.1. Theoretical Approach of EMF Exposure on WMNs
3.1.1. General Description of the Exposure Model
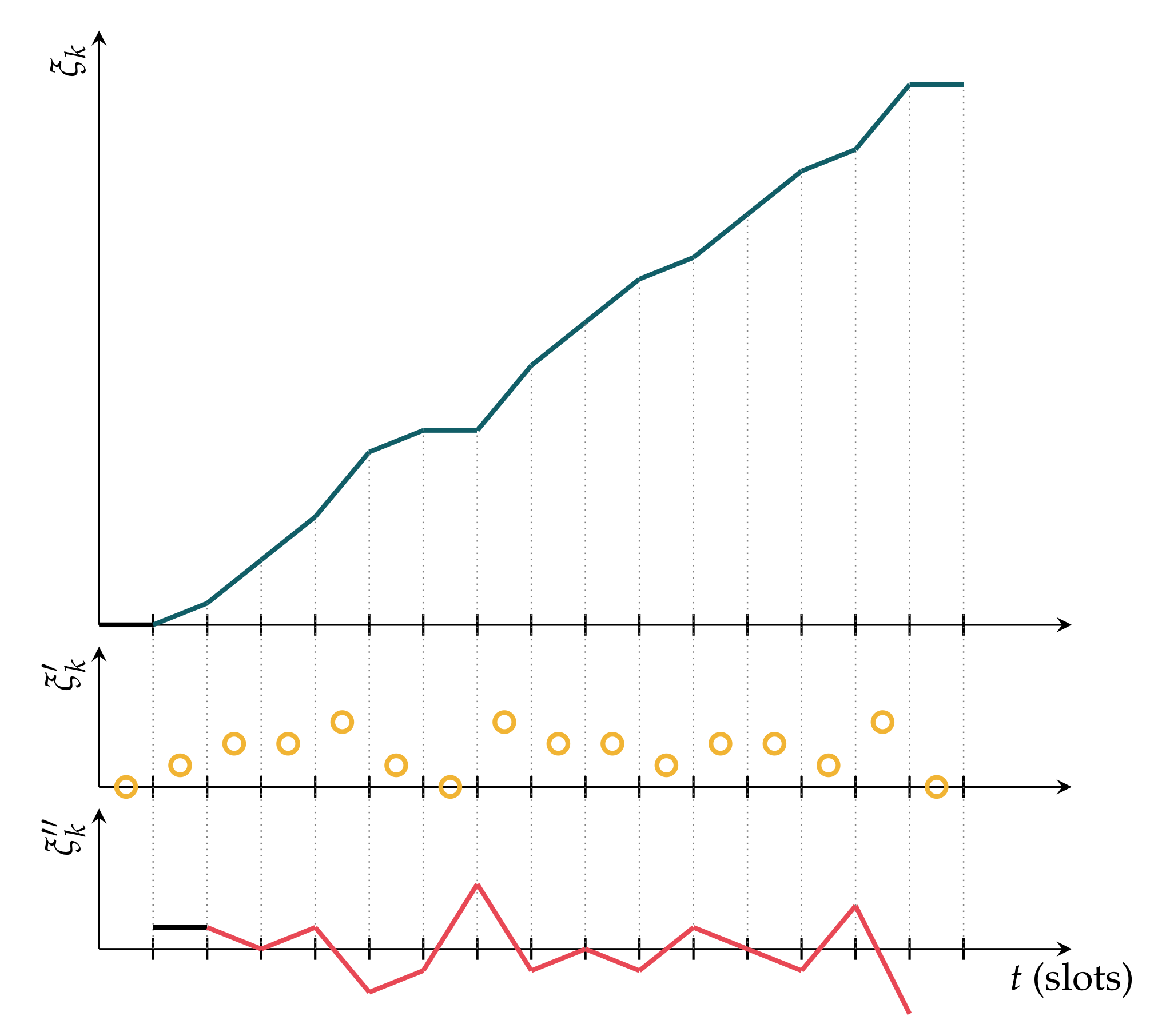
3.1.2. Computing the Exposure on WMNs
- 1.
- Since the exposure is accumulative, ;
- 2.
- Consequently, , corresponding to this growing function over t;
- 3.
- Depending on the value of , we can establish various circumstances, as can be seen below:
- If , the rhythm of accumulating exposure on node k is increasing;
- If , the pace of accumulating exposure on node k is constant;
- If , the rhythm of accumulating exposure on node k is decreasing.
3.1.3. Integrating the EMF Exposure into Routing
3.2. EMF-Aware Routing Algorithm
3.2.1. Network Model
- Node accumulated exposure : this cost represents the accumulated exposure that has been induced by a node i up to a certain time. In this sense, it does not depend on the amount of traffic traversing a node at a particular time, since we are interested in just considering its transmission history. It is worth noting that the proposed routing framework would allow using different definitions of this cost, provided it remains independent of the traffic currently traversing the node. Since the EMF exposure grows with the transmission power, we will later consider to be proportional to the power transmitted by the node until a particular moment. Nevertheless, more accurate models could be used, for instance considering advanced antenna patterns, or user density around the node;
- Edge power exposure : this reflects the transmission power that the node requires to send a packet to the next hop through an edge e. It is therefore attributed to each of the edges. should be proportional to the traffic load over every link, since the more a node is traversed by traffic, the more packets it will need to forward. This way, we can define the cost of an edge e connecting two nodes as ; where is the required transmission power, and represents the traffic load in that edge.
3.2.2. An Optimization Problem to Minimize the EMF Exposure
3.2.3. The Algorithm That Addresses the Minimization Problem
| Algorithm 1:Cycle Canceling Algorithm. |
| Require: |
| 1: Establish possible one flow |
| 2: while contains a negative cycle do |
| 3: Identify one negative cycle |
| 4: |
| 5: Increment flow units in the flow and update |
| 6: end while |
3.3. EMF-Aware AODV Protocol
3.3.1. Signaling in EA-AODV
- HELLO: this message is periodically broadcasted with a twofold purpose. First, it allows neighbor discovery. Furthermore, we also use it to notify about a change in the node’s cost, due to an accumulated exposure modification. Figure 3 depicts the fields of this message. As can be seen, it includes two flags to indicate the role of the message: M determines whether the packet is used for neighbor discovery purposes (M = 0) or for notifying a change in the corresponding cost (M = 1). In the latter case, the S flag indicates the sign of such modification (0 or 1 for positive or negative change, respectively). Finally, the COST field carries the corresponding value;
- ROUTE_DISC: a broadcast message initiated by a source to find the route to a particular destination. Each node receiving this packet forwards it, until the packet reaches its destination. It carries the route accumulated costs, so as to populate it during the route discovery process. Each node increments the cost, proportionally to the transmission power that would have been required by the previous node to reach it. The fields of this type of message can be observed in Figure 4;
- DISC_ACK: this message follows a ROUTE_DISC, and it is sent by the destination as a unicast transmission towards the corresponding source. Its format corresponds to the one presented for the ROUTE_DISC message, the only difference being in the corresponding TYPE field. Since the nodes follow the same procedure as the one depicted for the management of the ROUTE_DISC message, the protocol is able to handle asymmetric links, in which the power required to send a packet depends on the particular direction. The fields of this type of message can be observed in Figure 4;
- REPORT: used to disseminate a cost change, either an increase or a decrease of the accumulated exposure. Although the accumulated exposure does not physically decrease, the protocol considers this option to include aging functions. For instance, if a node is not used for a while, the cost related to the accumulated exposure can be reduced to foster the use of such a node. It thus follows a HELLO with M = 1, and it is propagated to ensure that all affected nodes receive the information. Figure 5 illustrates the format of this message.
- InUse: the route is being used to send locally generated data. This means that the node is the actual source of such an entry;
- Active: the route is being used to forward data. This is used when the node acts as a forwarding entity;
- Active_InUse: this state applies when the two previous conditions apply;
- Valid: the entry is not currently being used, but it has not yet expired.
3.3.2. Updating the Cost of a Node in EA-AODV
4. Results
4.1. Network Model Analysis
4.2. Dynamic Traffic Flows
4.3. Protocol Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NS-3 | Network Simulator 3 |
| D2D | device-to-device |
| QoS | Quality of Service |
| AODV | Ad hoc On-Demand Distance Vector Routing |
| EA-AODV | EMF Aware AODV |
| CCA | Cycle Canceling Algorithm |
| CCDF | Complementary Cumulative Distribution Function |
| ICNIRP | International Commission on Non-ionizing Radiation Protection |
| mmWave | Millimeter Waves |
| NRR | Nearest Neighbor Routing |
| MANET | Mobile Ad-hoc Networks |
| VANET | Vehicular Ad-hoc Network |
| MCF | Minimum Cost Flow Problem |
| EMF | Electromagnetic Fields |
| LEXNET | Low EMF Exposure Networks |
| EI | Exposure Index |
| WMN | Wireless Mesh Networks |
| WSN | Wireless Sensor Networks |
| Probability Density Function | |
| ETX | Expected Transmission Count |
| ETT | Expected Transmission Time |
| WCETT | Weighted Commutative Expected Transmission Time |
| MIC | Metric for Interference and Channel Switching |
| iAWARE | Interference Aware |
| EETT | Exclusive Expected Transmission Time |
| SAR | Specific Absorption Rate |
| IoT | Internet of Things |
Appendix A. Proof of the Continuous Individual Exposure
Appendix B. Proof of the Discrete Individual Exposure
References
- Cisco and/or Its Affiliated. Cisco Annual Internet Report (2018–2023). 2018. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 13 January 2022).
- Internation Commission on Non-Ionizing Radiation Protection (ICNIRP). ICNIRP Guidelines For Limiting Exposure To Electromagnetic Fields (100 kHz to 300 GHz). 2020. Available online: https://www.icnirp.org/cms/upload/publications/ICNIRPrfgdl2020.pdf (accessed on 13 January 2022).
- Low Electromagnetic Field Exposure Networks. 2012. Available online: https://cordis.europa.eu/project/id/318273 (accessed on 13 January 2022).
- Wu, T.; Rappaport, T.S.; Collins, C.M. The human body and millimeter-wave wireless communication systems: Interactions and implications. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2423–2429. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, L.; Azam, M.A.; Amin, Y.; Al-Ghamdi, M.A.; Chai, K.K.; Khan, M.F.N.; Khan, M.A. Integration of D2D, Network Slicing, and MEC in 5G Cellular Networks: Survey and Challenges. IEEE Access 2021, 9, 37590–37612. [Google Scholar] [CrossRef]
- Tesanovic, M.; Conil, E.; De Domenico, A.; Aguero, R.; Freudenstein, F.; Correia, L.; Bories, S.; Martens, L.; Wiedemann, P.; Wiart, J. The LEXNET Project: Wireless Networks and EMF: Paving the Way for Low-EMF Networks of the Future. Veh. Technol. Mag. IEEE 2014, 9, 20–28. [Google Scholar] [CrossRef] [Green Version]
- Perkins, C.; Belding-Royer, E.; Das, S. Ad Hoc On-Demand Distance Vector (AODV) Routing. 2003. Available online: https://www.rfc-editor.org/info/rfc3561 (accessed on 13 January 2022).
- Abolhasan, M.; Abdollahi, M.; Ni, W.; Jamalipour, A.; Shariati, N.; Lipman, J. A Routing Framework for Offloading Traffic From Cellular Networks to SDN-Based Multi-Hop Device-to-Device Networks. IEEE Trans. Netw. Serv. Manag. 2018, 15, 1516–1531. [Google Scholar] [CrossRef]
- Pattnaik, P.K.; Panda, B.K.; Sain, M. Design of Novel Mobility and Obstacle-Aware Algorithm for Optimal MANET Routing. IEEE Access 2021, 9, 110648–110657. [Google Scholar] [CrossRef]
- Kacem, I.; Sait, B.; Mekhilef, S.; Sabeur, N. A New Routing Approach for Mobile Ad Hoc Systems Based on Fuzzy Petri Nets and Ant System. IEEE Access 2018, 6, 65705–65720. [Google Scholar] [CrossRef]
- Mohamed, E.M.; Elhalawany, B.M.; Khallaf, H.S.; Zareei, M.; Zeb, A.; Abdelghany, M.A. Relay Probing for Millimeter Wave Multi-Hop D2D Networks. IEEE Access 2020, 8, 30560–30574. [Google Scholar] [CrossRef]
- Feng, G.; Li, X.; Gao, Z.; Wang, C.; Lv, H.; Zhao, Q. Multi-Path and Multi-Hop Task Offloading in Mobile Ad Hoc Networks. IEEE Trans. Veh. Technol. 2021, 70, 5347–5361. [Google Scholar] [CrossRef]
- Wang, X.; Weng, Y.; Gao, H. A Low-Latency and Energy-Efficient Multimetric Routing Protocol Based on Network Connectivity in VANET Communication. IEEE Trans. Green Commun. Netw. 2021, 5, 1761–1776. [Google Scholar] [CrossRef]
- Youssef, M.; Ibrahim, M.; Abdelatif, M.; Chen, L.; Vasilakos, A. Routing Metrics of Cognitive Radio Networks: A Survey. Commun. Surv. Tutor. IEEE 2014, 16, 92–109. [Google Scholar] [CrossRef]
- Guerin, J.; Portmann, M.; Pirzada, A. Routing metrics for multi-radio wireless mesh networks. In Proceedings of the Telecommunication Networks and Applications Conference, ATNAC, Christchurch, New Zealand, 2–5 December 2007; pp. 343–348. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, F.; Javed, M.; Iqbal, M. Diversity based review of Multipath Routing Metrics of Wireless Mesh Networks. In Proceedings of the Multi-Topic Conference (INMIC), 2014 IEEE 17th International, Karachi, Pakistan, 8–10 December 2014; pp. 320–325. [Google Scholar] [CrossRef]
- De Couto, D.S.J.; Aguayo, D.; Bicket, J.; Morris, R. A High-throughput Path Metric for Multi-hop Wireless Routing. Wirel. Netw. 2005, 11, 419–434. [Google Scholar] [CrossRef]
- Draves, R.; Padhye, J.; Zill, B. Routing in Multi-radio, Multi-hop Wireless Mesh Networks. In Proceedings of the 10th Annual International Conference on Mobile Computing and Networking, Philadelphia, PA, USA, 26 September–1 October 2004; ACM: New York, NY, USA, 2004; pp. 114–128. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, S.; Zhu, Y.; Zhang, Z. Optimizing Routing Metrics for Large-Scale Multi-Radio Mesh Networks. In Proceedings of the Wireless Communications, Networking and Mobile Computing, WiCom, Shanghai, China, 21–25 September 2007; pp. 1550–1553. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Kravets, R. Interference-Aware Load Balancing for Multihop Wireless Networks; Tech. Rep. UIUCDCS-R-2005-2526; Department of Computer Science, University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2005. [Google Scholar]
- Subramanian, A.; Buddhikot, M.; Miller, S. Interference aware routing in multi-radio wireless mesh networks. In Proceedings of the Wireless Mesh Networks, Reston, VA, USA, 25–28 September 2006; pp. 55–63. [Google Scholar] [CrossRef]
- Auer, G.; Giannini, V.; Desset, C.; Godor, I.; Skillermark, P.; Olsson, M.; Imran, M.; Sabella, D.; Gonzalez, M.; Blume, O.; et al. How much energy is needed to run a wireless network? Wirel. Commun. IEEE 2011, 18, 40–49. [Google Scholar] [CrossRef]
- Correia, L.; Zeller, D.; Blume, O.; Ferling, D.; Jading, Y.; Godor, I.; Auer, G.; Van der Perre, L. Challenges and enabling technologies for energy aware mobile radio networks. Commun. Mag. IEEE 2010, 48, 66–72. [Google Scholar] [CrossRef]
- Veeraiah, N.; Ibrahim Khalaf, O.; Prasad, C.V.P.R.; Alotaibi, Y.; Alsufyani, A.; Alghamdi, S.A.; Alsufyani, N. Trust Aware Secure Energy Efficient Hybrid Protocol for MANET. IEEE Access 2021, 9, 120996–121005. [Google Scholar] [CrossRef]
- Ibrahim, A.; Ngatched, T.M.N.; Dobre, O.A. Using Bender’s Decomposition for Optimal Power Control and Routing in Multihop D2D Cellular Systems. IEEE Trans. Wirel. Commun. 2019, 18, 5050–5064. [Google Scholar] [CrossRef]
- Lee, S.W.; Ali, S.; Yousefpoor, M.S.; Yousefpoor, E.; Lalbakhsh, P.; Javaheri, D.; Rahmani, A.M.; Hosseinzadeh, M. An Energy-Aware and Predictive Fuzzy Logic-Based Routing Scheme in Flying Ad Hoc Networks (FANETs). IEEE Access 2021, 9, 129977–130005. [Google Scholar] [CrossRef]
- Das, A.; Das, N. Multihop D2D Communication to Minimize and Balance SAR in 5G. In Proceedings of the 2020 International Conference on COMmunication Systems NETworkS (COMSNETS), Bengaluru, India, 7–11 January 2020; pp. 590–593. [Google Scholar] [CrossRef]
- Iancu, V.; Diez, L.; Rodriguez de Lope, L.; Slusanschi, E.; Aguero, R. A reward-based routing protocol to reduce the EMF exposure over wireless mesh networks. In Proceedings of the Wireless Days (WD), 2014 IFIP, Rio de Janeiro, Brazil, 12–14 November 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Diez, L.; Igareda, J.; Iancu, V.; Slusanschi, E.; Aguero, R. Routing algorithm to fairly distribute the exposure to electromagnetic fields over wireless mesh networks. In Proceedings of the 2015 IEEE 11th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Abu Dhabi, United Arab Emirates, 19–21 October 2015; pp. 468–473. [Google Scholar] [CrossRef]
- Rathan, K.; Roslin, S.E. A survey on routing protocols and load balancing techniques in Wireless Mesh Networks. In Proceedings of the 2017 International Conference on Intelligent Computing and Control (I2C2), Coimbatore, India, 23–24 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Riley, G.F.; Henderson, T.R. The ns-3 Network Simulator. In Modeling and Tools for Network Simulation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 15–34. [Google Scholar] [CrossRef]














| Topology | ||||
|---|---|---|---|---|
| TP1 | TP2 | TP3 | TP4 | |
| Sources | ||||
| Area m2 | ||||
| PDF of reachable gateways |  | |||
| Cost Parameter | Value |
|---|---|
| P | distance (m) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iancu, V.; Diez, L.; Sluşanschi, E.; Agüero, R. Balancing the Electromagnetic Field Exposure in Wireless Multi-Hop Networks: An EMF-Aware Routing Scheme. Mathematics 2022, 10, 668. https://doi.org/10.3390/math10040668
Iancu V, Diez L, Sluşanschi E, Agüero R. Balancing the Electromagnetic Field Exposure in Wireless Multi-Hop Networks: An EMF-Aware Routing Scheme. Mathematics. 2022; 10(4):668. https://doi.org/10.3390/math10040668
Chicago/Turabian StyleIancu, Voichiţa, Luis Diez, Emil Sluşanschi, and Ramón Agüero. 2022. "Balancing the Electromagnetic Field Exposure in Wireless Multi-Hop Networks: An EMF-Aware Routing Scheme" Mathematics 10, no. 4: 668. https://doi.org/10.3390/math10040668
APA StyleIancu, V., Diez, L., Sluşanschi, E., & Agüero, R. (2022). Balancing the Electromagnetic Field Exposure in Wireless Multi-Hop Networks: An EMF-Aware Routing Scheme. Mathematics, 10(4), 668. https://doi.org/10.3390/math10040668







