Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method
Abstract
:1. Introduction
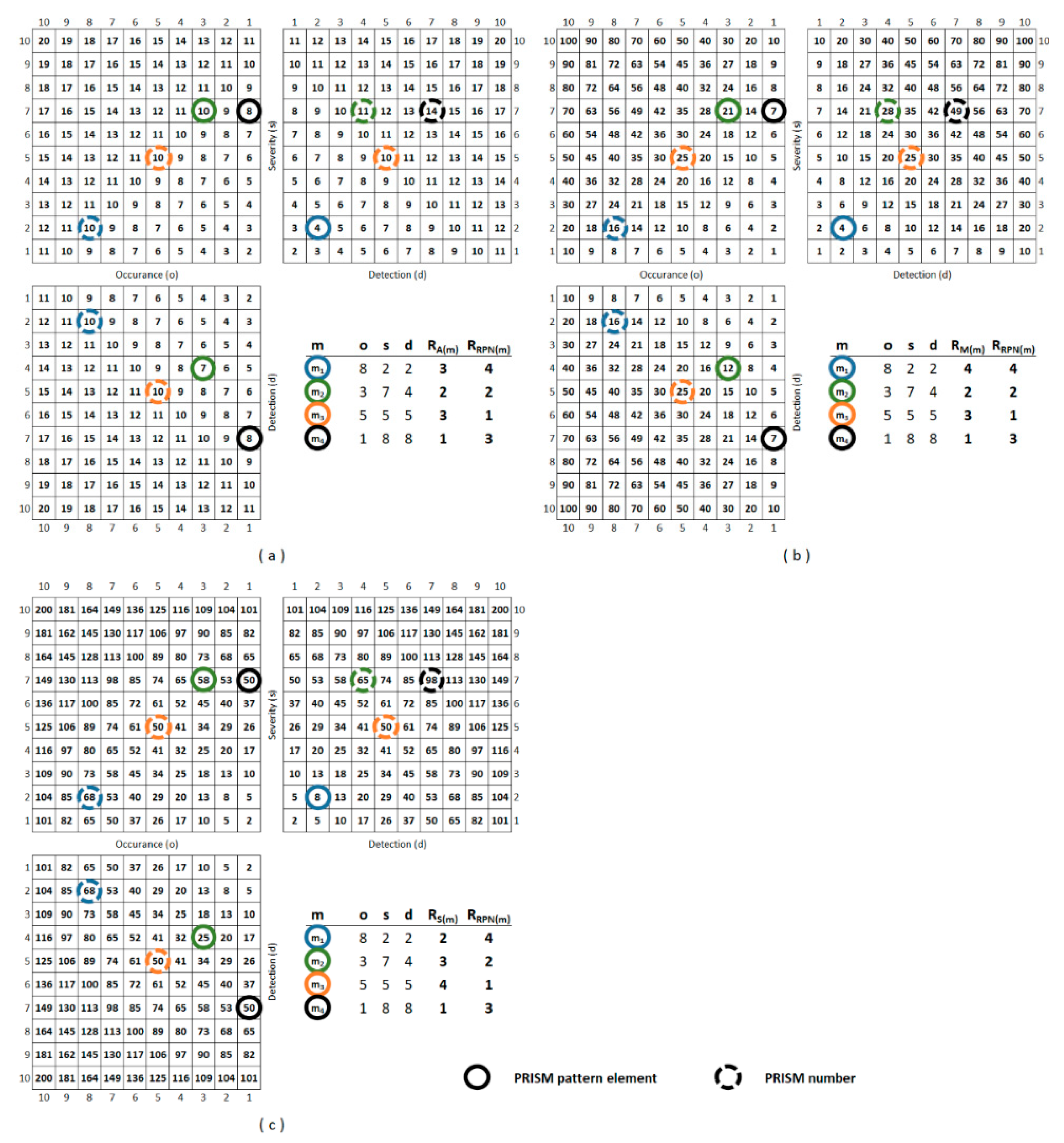
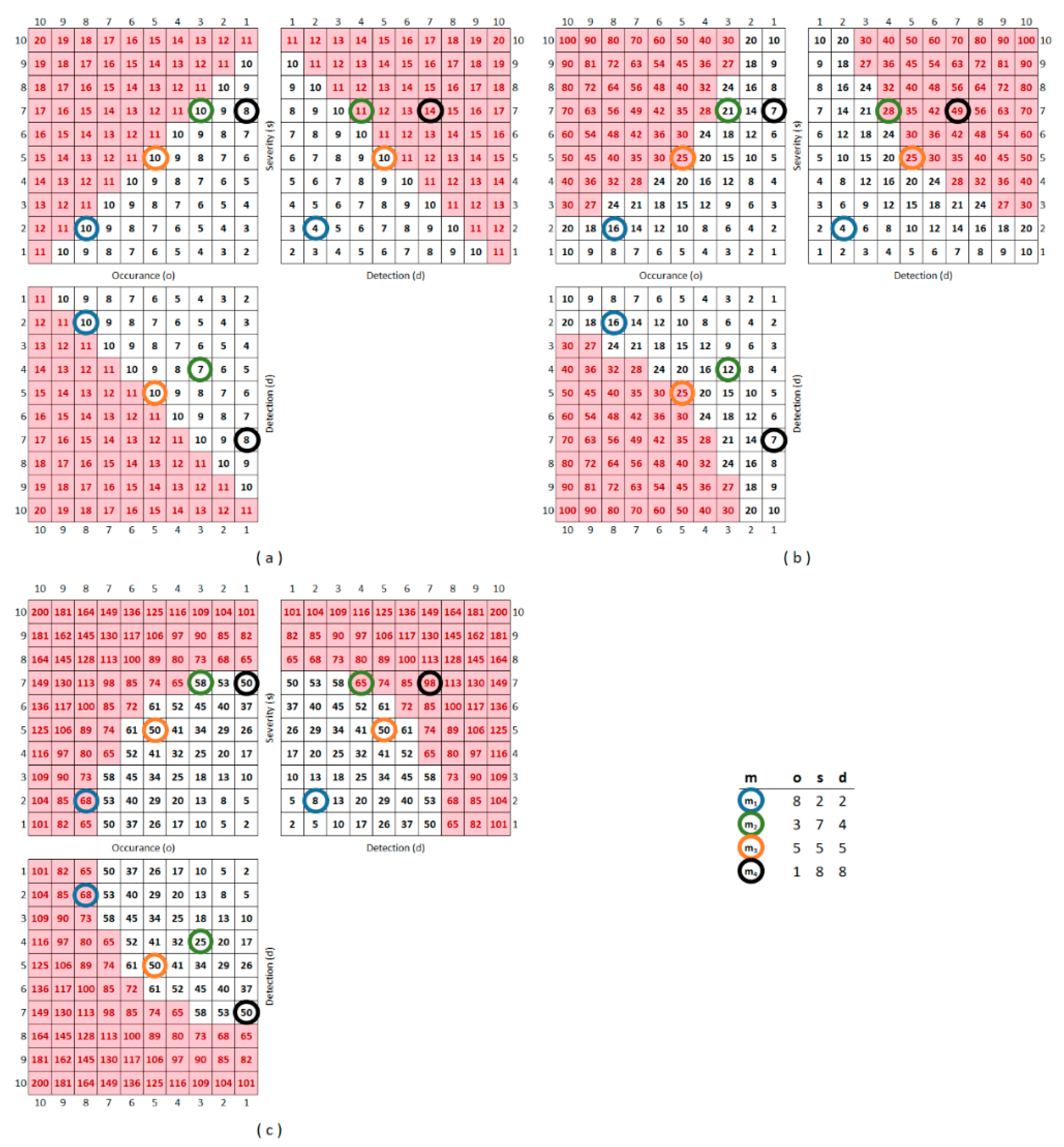
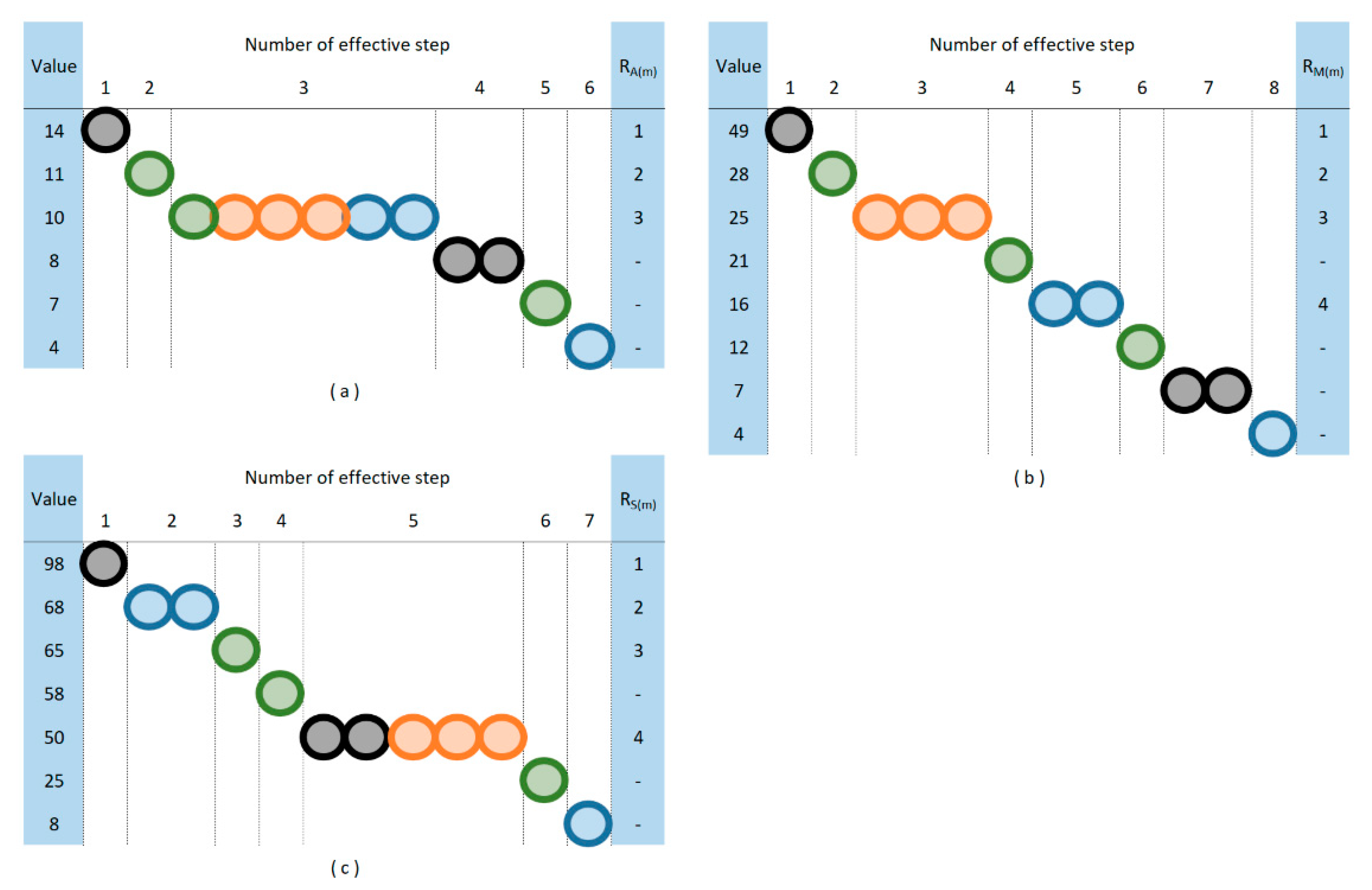
- Three functions are developed for assessing partial risks (one algorithm is sensitive for incidents, having a high risk level at one rating factor, one algorithm is sensitive for middle risk levels at all the rating factors, one is a balanced algorithm). Applying the new functions, proactive assessment can be executed, and predictions can be given related to the incidents based on the nature of their hidden risk.
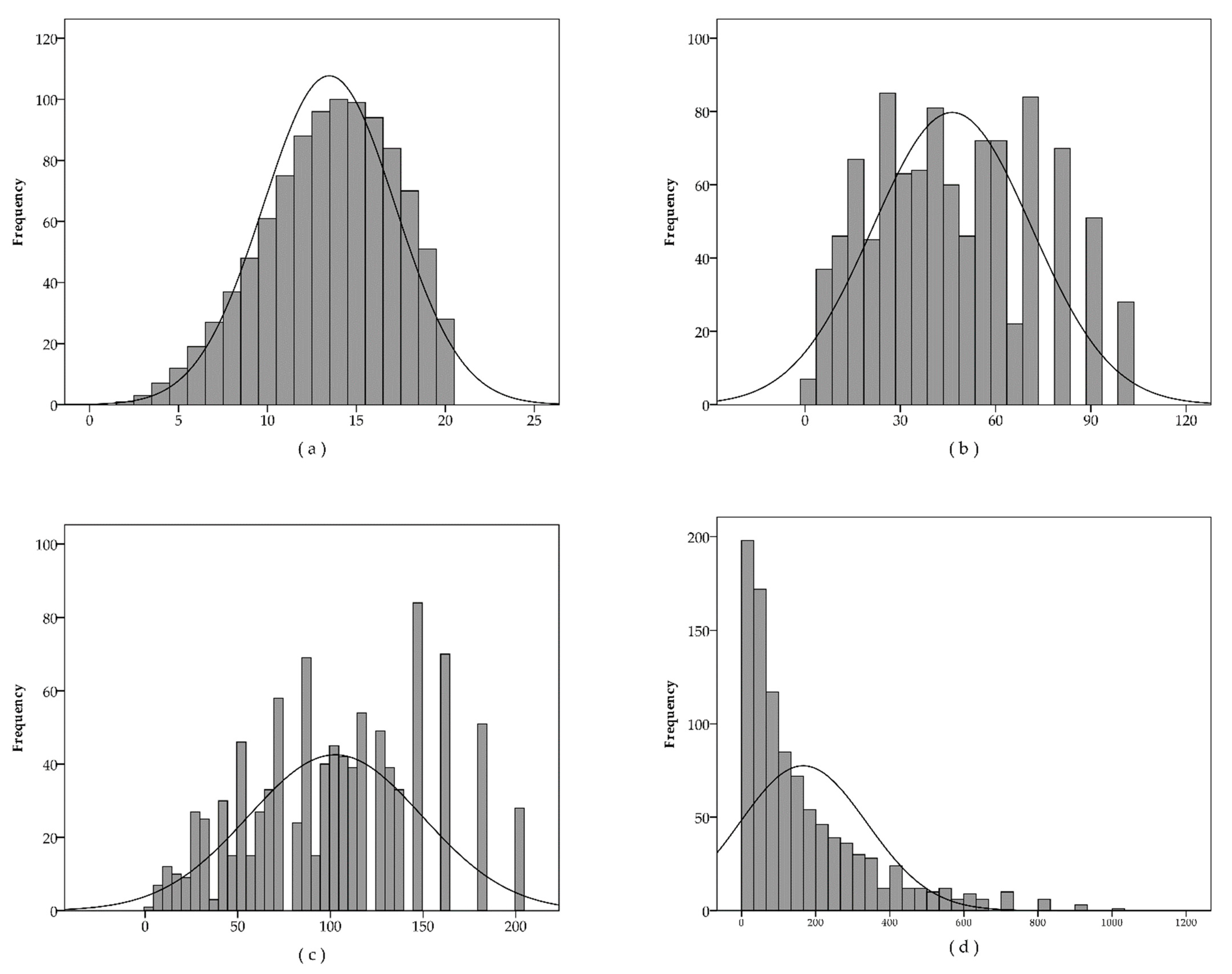
- The developed functions have an exact description based on the distribution of their possible values and these are compared to the distribution of RPN number.
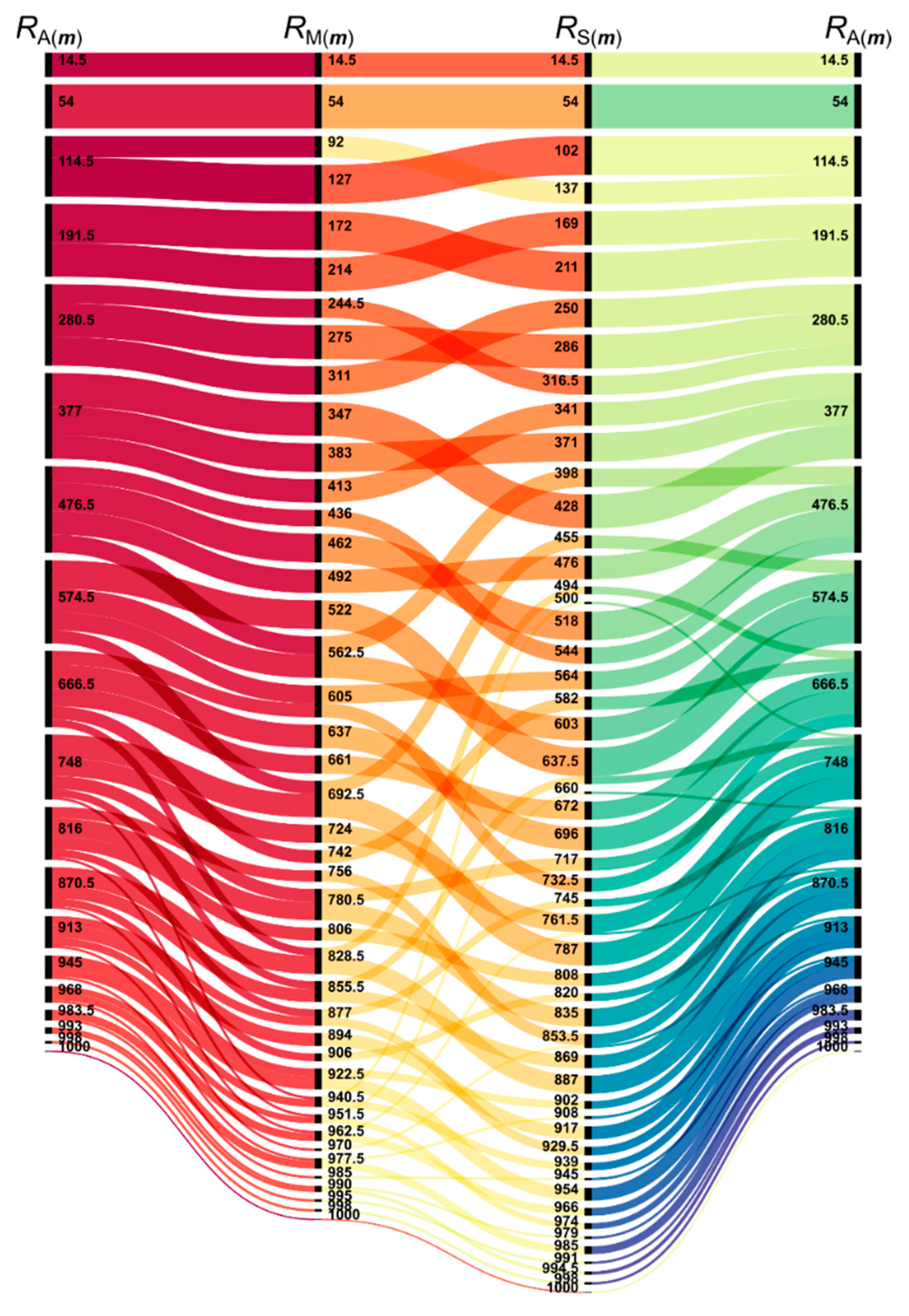
- The rankings of the functions are compared to each other by applying different analyses, and detailed discussion of the theoretical differences is given based on the comparison.
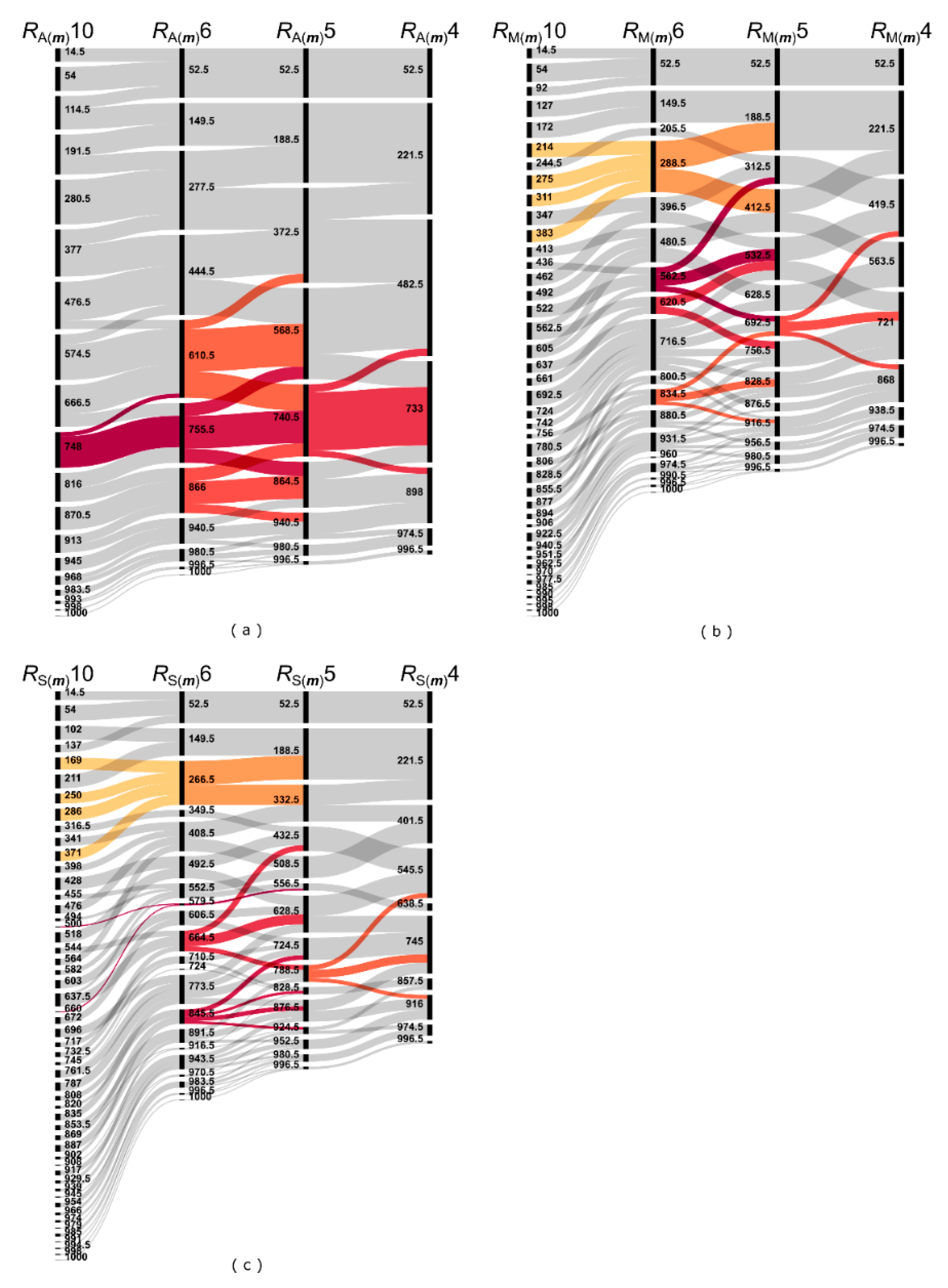
- The rankings are robust related to the change of evaluation factor scales. This test is important, since, in the practical field, the evaluation scale lengths can be different.
1.1. Brief Description of the RM and FMEA
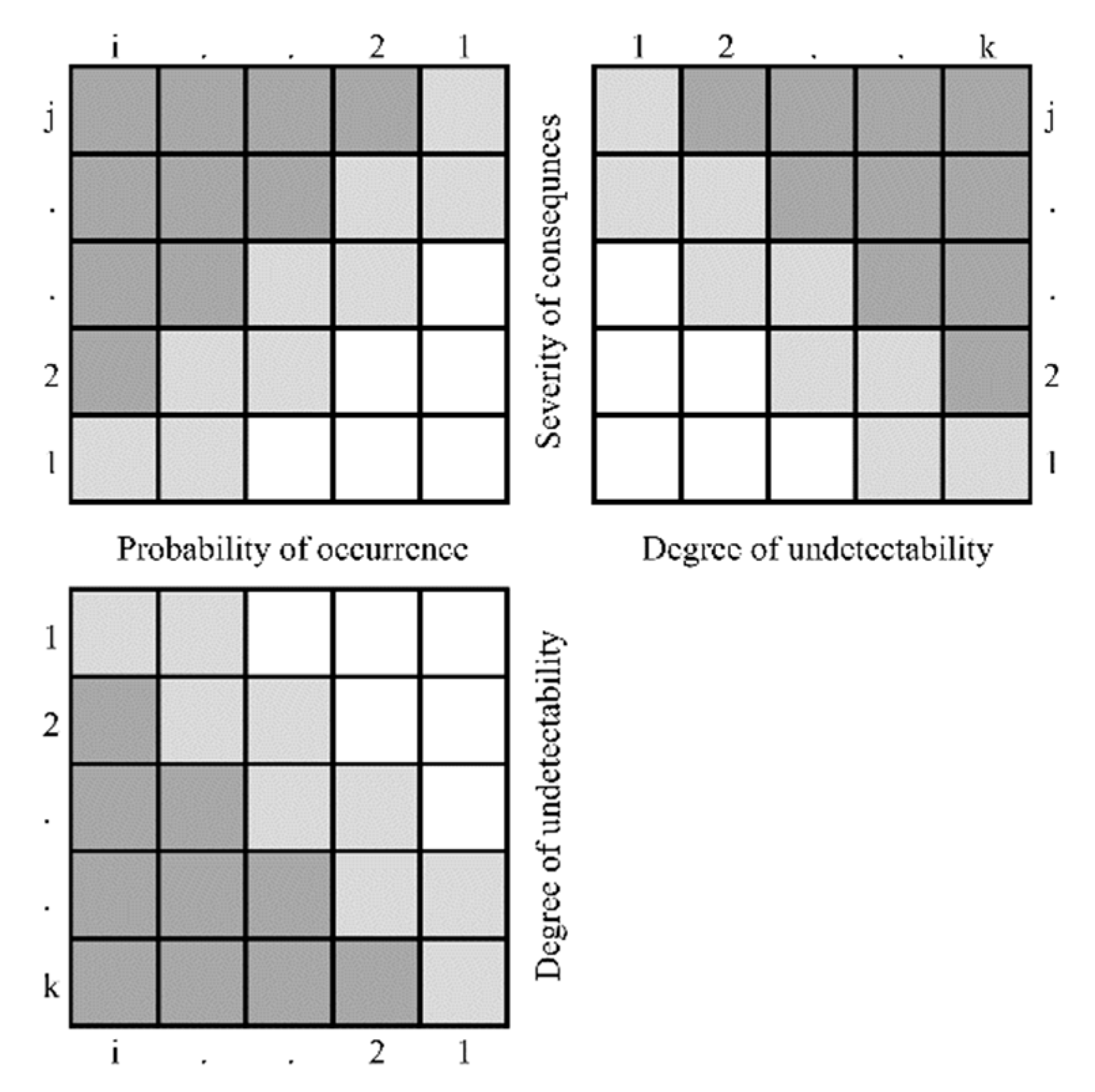
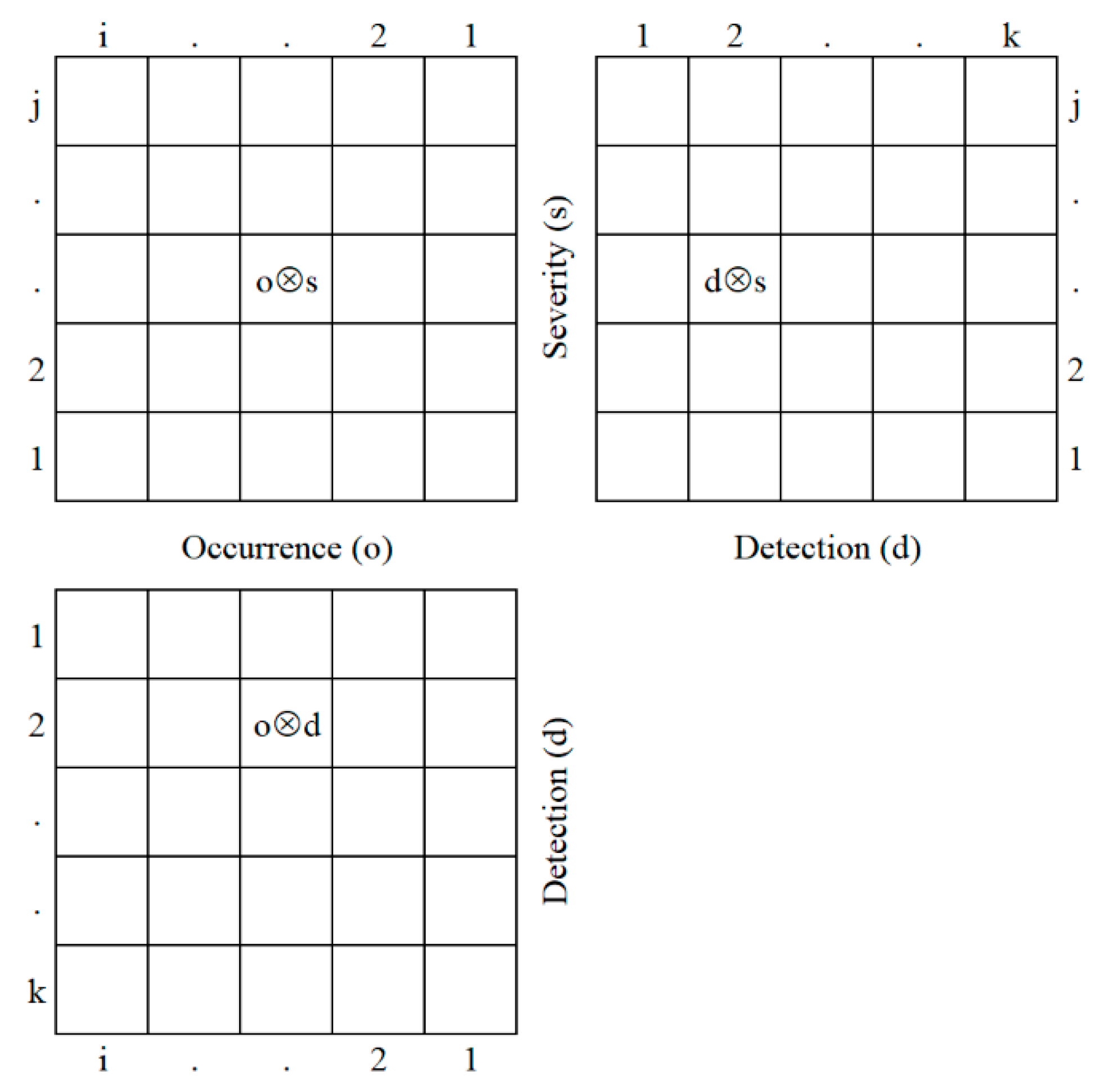
1.2. Brief Description of the Partial Risk Map (PRISM) Methodology
2. Materials and Methods
3. Results
3.1. Descriptive Statistics
3.2. Comparison of the Methods
3.3. Effect of the Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Braglia, M. MAFMA: Multi-attribute failure mode analysis. Int. J. Qual. Reliab. Manag. 2000, 17, 1017–1033. [Google Scholar] [CrossRef] [Green Version]
- Shan, H.; Tong, Q.; Shi, J.; Zhang, Q. Risk Assessment of Express Delivery Service Failures in China: An Improved Failure Mode and Effects Analysis Approach. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2490–2514. [Google Scholar] [CrossRef]
- Somi, S.; Seresht, N.G.; Fayek, A.R. Developing a risk breakdown matrix for onshore wind farm projects using fuzzy case-based reasoning. J. Clean. Prod. 2021, 311, 127572. [Google Scholar] [CrossRef]
- Marhavilas, P.K.; Filippidis, M.; Koulinas, G.K.; Koulouriotis, D.E. Safety-assessment by hybridizing the MCDM/AHP & HAZOP-DMRA techniques through safety’s level colored maps: Implementation in a petrochemical industry. Alex. Eng. J. 2022, 61, 6959–6977. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, J.; Sun, L.; Bai, X. Risk assessment of floating offshore wind turbines based on fuzzy fault tree analysis. Ocean Eng. 2021, 239, 109859. [Google Scholar] [CrossRef]
- Shafiee, M.; Enjema, E.; Kolios, A. An Integrated FTA-FMEA Model for Risk Analysis of Engineering Systems: A Case Study of Subsea Blowout Preventers. Appl. Sci. 2019, 9, 1192. [Google Scholar] [CrossRef] [Green Version]
- Schafer, H.L.; Beier, N.A.; Macciotta, R. A Failure Modes and Effects Analysis Framework for Assessing Geotechnical Risks of Tailings Dam Closure. Minerals 2021, 11, 1234. [Google Scholar] [CrossRef]
- Bradley, J.R.; Guerrero, H.H. An Alternative FMEA Method for Simple and Accurate Ranking of Failure Modes. Decis. Sci. 2011, 42, 743–771. [Google Scholar] [CrossRef]
- Kang, J.; Sun, L.; Sun, H.; Wu, C. Risk assessment of floating offshore wind turbine based on correlation-FMEA. Ocean Eng. 2017, 129, 382–388. [Google Scholar] [CrossRef]
- Ivančan, J.; Lisjak, D. New FMEA Risks Ranking Approach Utilizing Four Fuzzy Logic Systems. Machines 2021, 9, 292. [Google Scholar] [CrossRef]
- Fabis-Domagala, J.; Domagala, M.; Momeni, H. A Concept of Risk Prioritization in FMEA Analysis for Fluid Power Systems. Energies 2021, 14, 6482. [Google Scholar] [CrossRef]
- Carnero, M.C. Waste Segregation FMEA Model Integrating Intuitionistic Fuzzy Set and the PAPRIKA Method. Mathematics 2020, 8, 1375. [Google Scholar] [CrossRef]
- Bognár, F.; Benedek, P. A Novel Risk Assessment Methodology—A Case Study of the PRISM Methodology in a Compliance Management Sensitive Sector. Acta Polytech. Hung. 2021, 18, 89–108. [Google Scholar] [CrossRef]
- Bognár, F.; Benedek, P. Case Study on a Potential Application of Failure Mode and Effects Analysis in Assessing Compliance Risks. Risks 2021, 9, 164. [Google Scholar] [CrossRef]
- Qazi, A.; Shamayleh, A.; El-Sayegh, S.; Formaneck, S. Prioritizing risks in sustainable construction projects using a risk matrix-based Monte Carlo Simulation approach. Sustain. Cities Soc. 2021, 65, 102576. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Risk Analysis of Out-drum Mixing Cement Solidification by HAZOP and Risk Matrix. Ann. Nucl. Energy 2020, 147, 107679. [Google Scholar] [CrossRef]
- Losiewicz-Dniestrzanska, E. Monitoring of compliance risk in the bank. Procedia Econ. Financ. 2015, 26, 800–805. [Google Scholar] [CrossRef] [Green Version]
- Jeon, H.; Park, K.; Kim, J. Comparison and Verification of Reliability Assessment Techniques for Fuel Cell-Based Hybrid Power System for Ships. J. Mar. Sci. Eng. 2020, 8, 74. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Tang, Y. Deng Entropy Weighted Risk Priority Number Model for Failure Mode and Effects Analysis. Entropy 2020, 22, 280. [Google Scholar] [CrossRef] [Green Version]
- Lv, Y.; Liu, Y.; Jing, W.; Woźniak, M.; Damaševičius, R.; Scherer, R.; Wei, W. Quality Control of the Continuous Hot Pressing Process of Medium Density Fiberboard Using Fuzzy Failure Mode and Effects Analysis. Appl. Sci. 2020, 10, 4627. [Google Scholar] [CrossRef]
- Lo, H.W.; Liou, J.J.H.; Huang, C.N.; Chuang, Y.C. A novel failure mode and effect analysis model for machine tool risk analysis. Reliab. Eng. Syst. Saf. 2019, 183, 173–183. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Liu, P.C.Y.; Lo, H.W. A Failure Mode Assessment Model Based on Neutrosophic Logic for Switched-Mode Power Supply Risk Analysis. Mathematics 2020, 8, 2145. [Google Scholar] [CrossRef]
- Chang, T.W.; Lo, H.W.; Chen, K.Y.; Liou, J.J.H. A Novel FMEA Model Based on Rough BWM and Rough TOPSIS-AL for Risk Assessment. Mathematics 2019, 7, 874. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.W.; Liou, J.J.H. A novel multiple-criteria decision-making-based FMEA model for risk assessment. Appl. Soft Comput. 2018, 73, 684–696. [Google Scholar] [CrossRef]
- Ghoushchi, S.J.; Yousefi, S.; Khazaeili, M. An extended FMEA approach based on the Z-MOORA and fuzzy BWM for prioritization of failures. Appl. Soft Comput. 2019, 81, 105505. [Google Scholar] [CrossRef]
- Chanamool, N.; Naenna, T. Fuzzy FMEA application to improve decision-making process in an emergency department. Appl. Soft Comput. 2016, 43, 441–453. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N.; Mao, X.L. Risk evaluation in failure mode and effects analysis with extended VIKOR method under fuzzy environment. Expert Syst. Appl. 2012, 39, 12926–12934. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioğlu, M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Zúñiga, A.A.; Baleia, A.; Fernandes, J.; Branco, P.J.D.C. Classical Failure Modes and Effects Analysis in the Context of Smart Grid Cyber-Physical Systems. Energies 2020, 13, 1215. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.K.; Kumar, D.; Kumar, P. Modeling and analysing system failure behaviour using RCA, FMEA and NHPPP models. Int. J. Qual. Reliab. Manag. 2007, 24, 525–546. [Google Scholar] [CrossRef]
- Zammori, F.; Gabbrielli, R. ANP/RPN: A multi criteria evaluation of the risk priority number. Qual. Reliab. Eng. Int. 2011, 28, 85–104. [Google Scholar] [CrossRef]
- Gargama, H.; Chaturvedi, S.K. Criticality assessment models for failure mode effects and criticality analysis using fuzzy logic. IEEE Trans. Reliab. 2011, 60, 102–110. [Google Scholar] [CrossRef]
- Braglia, M.; Frosolini, M.; Montanari, R. Fuzzy criticality assessment model for failure modes and effects analysis. Int. J. Qual. Reliab. Manag. 2003, 20, 503–524. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Abdelgawad, M.; Fayek, A.R. Risk management in the construction industry using combined fuzzy FMEA and fuzzy AHP. J. Constr. Eng. Manag. 2010, 136, 1028–1036. [Google Scholar] [CrossRef]
- Forgács, A.; Lukács, J.; Horváth, R. The Investigation of the Applicability of Fuzzy Rule-based Systems to Predict Economic Decision-Making. Acta Polytech. Hung. 2021, 18, 97–115. [Google Scholar] [CrossRef]
- Rosenberger, P.; Tick, J. Multivariate Optimization of PMBOK, Version 6 Project Process Relevance. Acta Polytech. Hung. 2021, 18, 9–28. [Google Scholar] [CrossRef]
- Kollár-Hunek, K.; Héberger, K. Method and model comparison by sum of ranking differences in cases of repeated observations (ties). Chemom. Intell. Lab. Syst. 2013, 127, 139–146. [Google Scholar] [CrossRef]
- Héberger, K.; Kollár-Hunek, K. Sum of ranking differences for method discrimination and its validation: Comparison of ranks with random numbers. J. Chemom. 2011, 25, 151–158. [Google Scholar] [CrossRef]
- Ipkovich, Á.; Héberger, K.; Abonyi, J. Comprehensible Visualization of Multidimensional Data: Sum of Ranking Differences-Based Parallel Coordinates. Mathematics 2021, 9, 3203. [Google Scholar] [CrossRef]
- Mizik, T.; Gál, P.; Török, Á. Does Agricultural Trade Competitiveness Matter? The Case of the CIS Countries. AGRIS On-Line Pap. Econ. Inform. 2020, 12, 61–72. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Jia, G.; Jia, Y.; Song, W. A new approach for risk assessment of failure modes considering risk interaction and propagation effects. Reliab. Eng. Syst. Saf. 2021, 216, 108044. [Google Scholar] [CrossRef]
- AIAG; VDA. FMEA Handbook, 1st ed.; Automotive Industry Action Group: Southfield, MI, USA, 2019. [Google Scholar]
- Koval, K.; Torabi, M. Failure mode and reliability study for Electrical Facility of the High Temperature Engineering Test Reactor. Reliab. Eng. Syst. Saf. 2021, 210, 107529. [Google Scholar] [CrossRef]
- Abrahamsen, A.B.; Abrahamsen, E.B.; Høyland, S. On the need for revising healthcare failure mode and effect analysis for assessing potential for patient harm in healthcare processes. Reliab. Eng. Syst. Saf. 2016, 155, 160–168. [Google Scholar] [CrossRef]
- Benedek, P. Compliance management—A new response to legal and business challenges. Acta Polytech. Hung. 2012, 9, 135–148. [Google Scholar]
- Liu, H.C.; Chen, X.Q.; Duan, C.Q.; Wang, Y.M. Failure mode and effect analysis using multi-criteria decision making methods: A systematic literature review. Comput. Ind. Eng. 2019, 135, 881–897. [Google Scholar] [CrossRef]
- Huang, J.; You, J.X.; Liu, H.C.; Song, M.S. Failure mode and effect analysis improvement: A systematic literature review and future research agenda. Reliab. Eng. Syst. Saf. 2020, 199, 106885. [Google Scholar] [CrossRef]
- Tay, K.M.; Lim, C.P. Enhancing the failure mode and effect analysis methodology with fuzzy inference techniques. J. Intell. Fuzzy Syst. 2010, 21, 135–146. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Chu, X.N. Risk prioritization in failure mode and effects analysis under uncertainty. Expert Syst. Appl. 2011, 38, 206–214. [Google Scholar] [CrossRef]
- Ilangkumaran, M.; Shanmugam, P.; Sakthivel, G.; Visagavel, K. Failure mode and effect analysis using fuzzy analytic hierarchy process. Int. J. Product. Qual. Manag. 2014, 14, 296–313. [Google Scholar] [CrossRef]
- Kosztyán, Z.T.; Csizmadia, T.; Kovács, Z.; Mihálcz, I. Total Risk Evaluation Framework. Int. J. Qual. Reliab. Manag. 2020, 37, 575–608. [Google Scholar] [CrossRef]

| A(m) | M(m) | S(m) | RPN(m) | ||
|---|---|---|---|---|---|
| Number of incidents (M) | 1000 | 1000 | 1000 | 1000 | |
| Mean | 13.48 | 46.32 | 102.64 | 166.38 | |
| Std. error of mean | 0.117 | 0.791 | 1.483 | 5.424 | |
| Mode | 14 | 90 | 181 | 60 | |
| Std. deviation | 3.704 | 25.012 | 46.901 | 171.509 | |
| Variance | 13.721 | 625.594 | 2199.668 | 29,415.400 | |
| Coefficient of variation | 0.275 | 0.540 | 0.457 | 1.031 | |
| Skewness | −0.383 | 0.274 | 0.044 | 1.672 | |
| Kurtosis | −0.398 | −0.838 | −0.727 | 2.828 | |
| Number of different ranks (N) | 19 | 42 | 52 | 120 | |
| Range | 18 | 99 | 198 | 999 | |
| Minimum | 2 | 1 | 2 | 1 | |
| Maximum | 20 | 100 | 200 | 1000 | |
| Percentiles | 25 | 11.00 | 25.00 | 65.00 | 42.00 |
| 50 | 14.00 | 45.00 | 101.00 | 105.00 | |
| 75 | 16.00 | 64.00 | 136.00 | 240.00 | |
| Method | Formula | SRD |
|---|---|---|
| RPN(m) | 0.2074 | |
| A(m) | 0.0653 | |
| M(m) | 0.0897 | |
| S(m) | 0.0967 |
| A(m) Ranking | M(m) Ranking | S(m) Ranking | |
|---|---|---|---|
| A(m) ranking | SRDA = 0.0170 | SRDAM = 0.0594 | SRDAS = 0.0596 |
| M(m) ranking | ρMA = 0.990 | SRDM = 0.0606 | SRDMS = 0.1182 |
| S(m) ranking | ρSA = 0.988 | ρSM = 0.957 | SRDS = 0.0624 |
| RA(m)6 | RA(m)5 | RA(m)4 | RM(m)10 | RM(m)6 | RM(m)5 | RM(m)4 | RS(m)10 | RS(m)6 | RS(m)5 | RS(m)4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| RA(m)10 | 0.982 | 0.981 | 0.958 | 0.990 | 0.980 | 0.970 | 0.951 | 0.988 | 0.969 | 0.969 | 0.943 |
| RA(m)6 | 0.955 | 0.965 | 0.966 | 0.990 | 0.932 | 0.947 | 0.977 | 0.993 | 0.958 | 0.959 | |
| RA(m)5 | 0.950 | 0.974 | 0.949 | 0.990 | 0.939 | 0.966 | 0.946 | 0.987 | 0.939 | ||
| RA(m)4 | 0.945 | 0.954 | 0.929 | 0.987 | 0.951 | 0.959 | 0.951 | 0.989 | |||
| RM(m)10 | 0.982 | 0.981 | 0.957 | 0.957 | 0.939 | 0.942 | 0.913 | ||||
| RM(m)6 | 0.944 | 0.956 | 0.956 | 0.968 | 0.932 | 0.930 | |||||
| RM(m)5 | 0.938 | 0.936 | 0.909 | 0.954 | 0.900 | ||||||
| RM(m)4 | 0.923 | 0.924 | 0.917 | 0.953 | |||||||
| RS(m)10 | 0.980 | 0.976 | 0.954 | ||||||||
| RS(m)6 | 0.965 | 0.968 | |||||||||
| RS(m)5 | 0.960 | ||||||||||
| SRD | 0.106 | 0.107 | 0.143 | 0.090 | 0.109 | 0.124 | 0.153 | 0.097 | 0.129 | 0.128 | 0.162 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bognár, F.; Hegedűs, C. Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics 2022, 10, 676. https://doi.org/10.3390/math10050676
Bognár F, Hegedűs C. Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics. 2022; 10(5):676. https://doi.org/10.3390/math10050676
Chicago/Turabian StyleBognár, Ferenc, and Csaba Hegedűs. 2022. "Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method" Mathematics 10, no. 5: 676. https://doi.org/10.3390/math10050676
APA StyleBognár, F., & Hegedűs, C. (2022). Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics, 10(5), 676. https://doi.org/10.3390/math10050676







