Modeling Uranium Transport in Rough-Walled Fractures with Stress-Dependent Non-Darcy Fluid Flow
Abstract
:1. Introduction
2. Mathematical Model for Uranium Transport in Rough-Walled Fractures
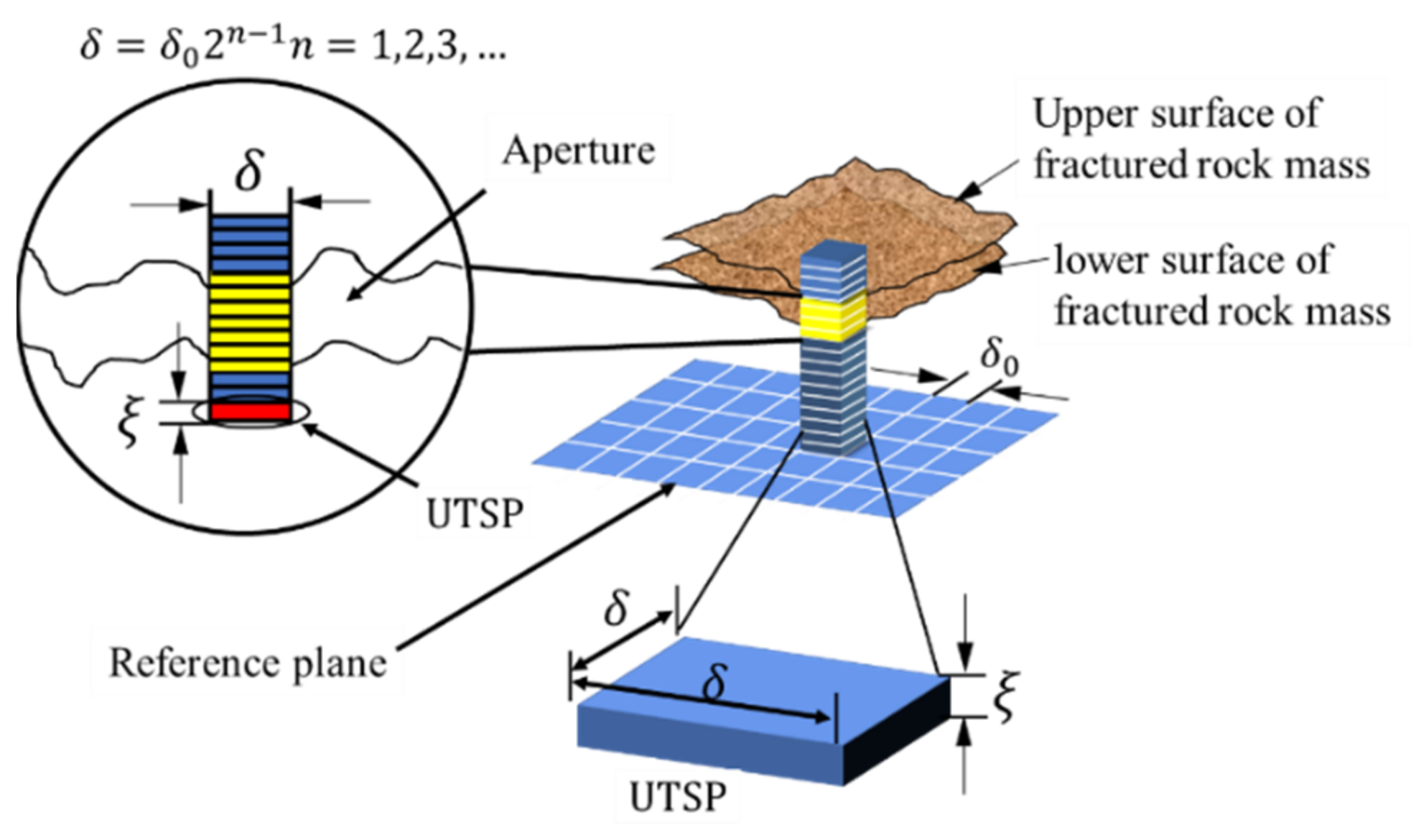
2.1. Equivalent Hydromechanical Coupling Description
2.2. Flow Regime in Fractured Structures
2.3. Reactive Transport in Fractured Rock Mass
2.4. Transport Kinetic Equation
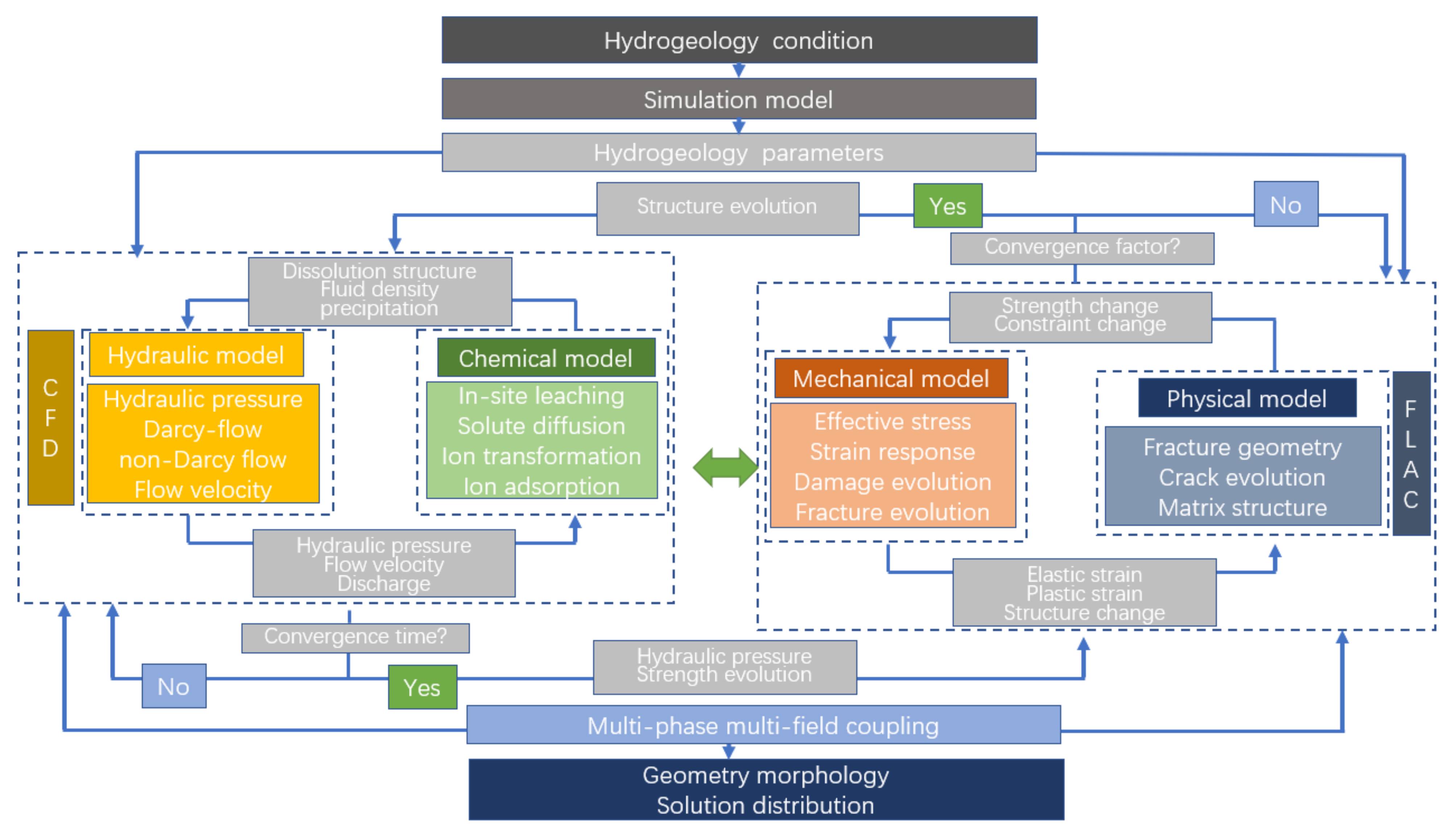
2.5. Integrated Reactive Transport Model
2.6. Simulation Scheme
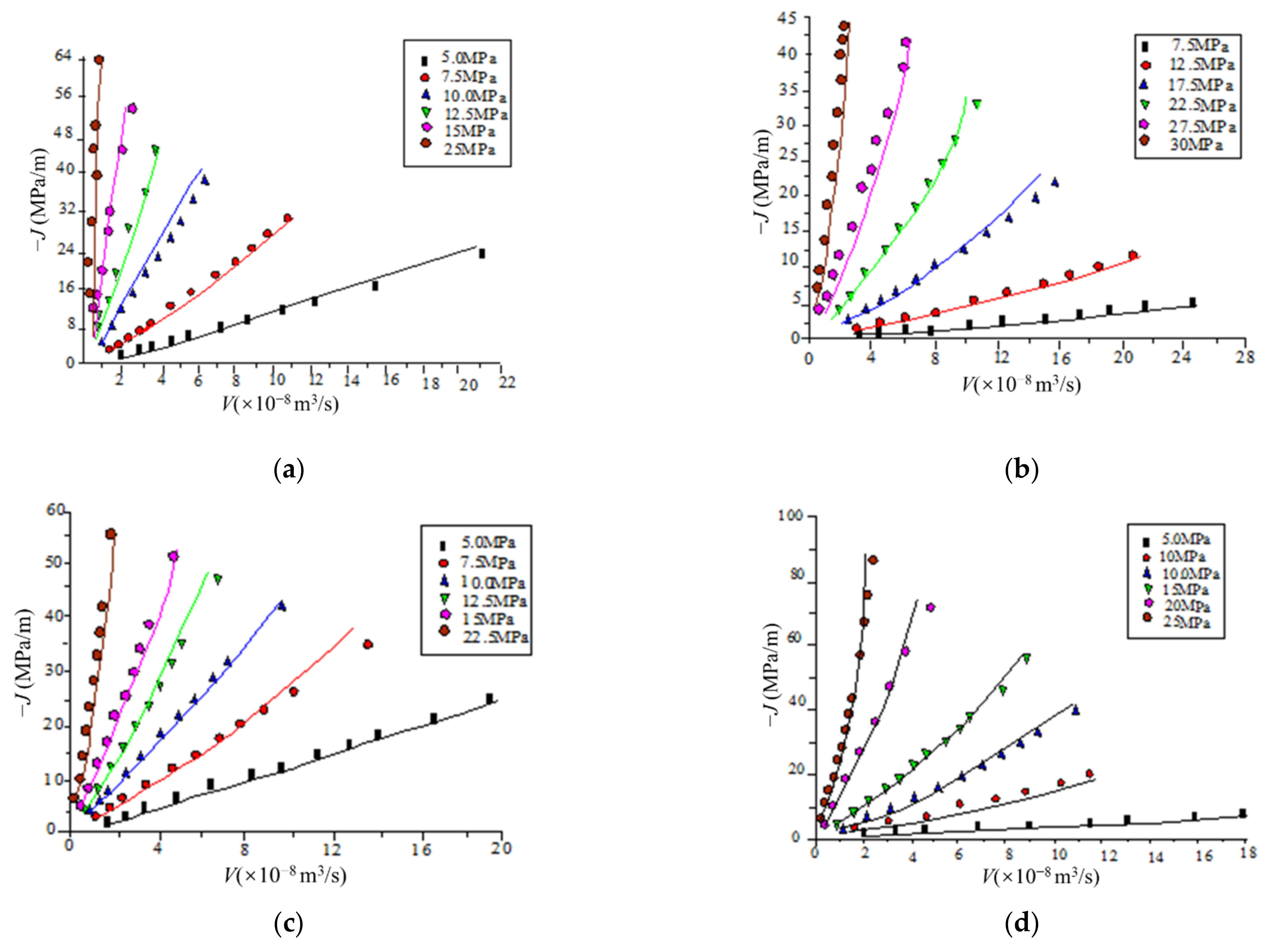
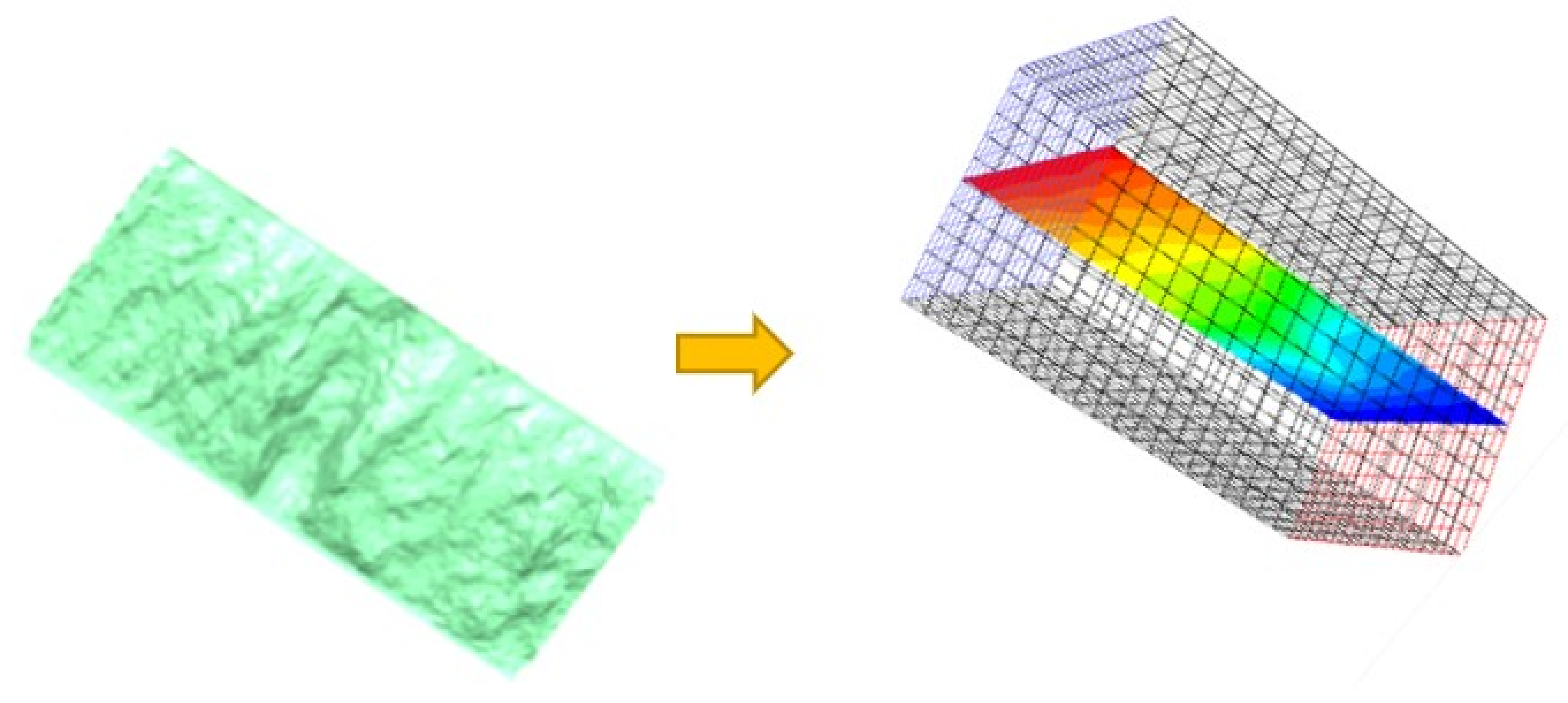
2.7. Model Verification
3. Case Study
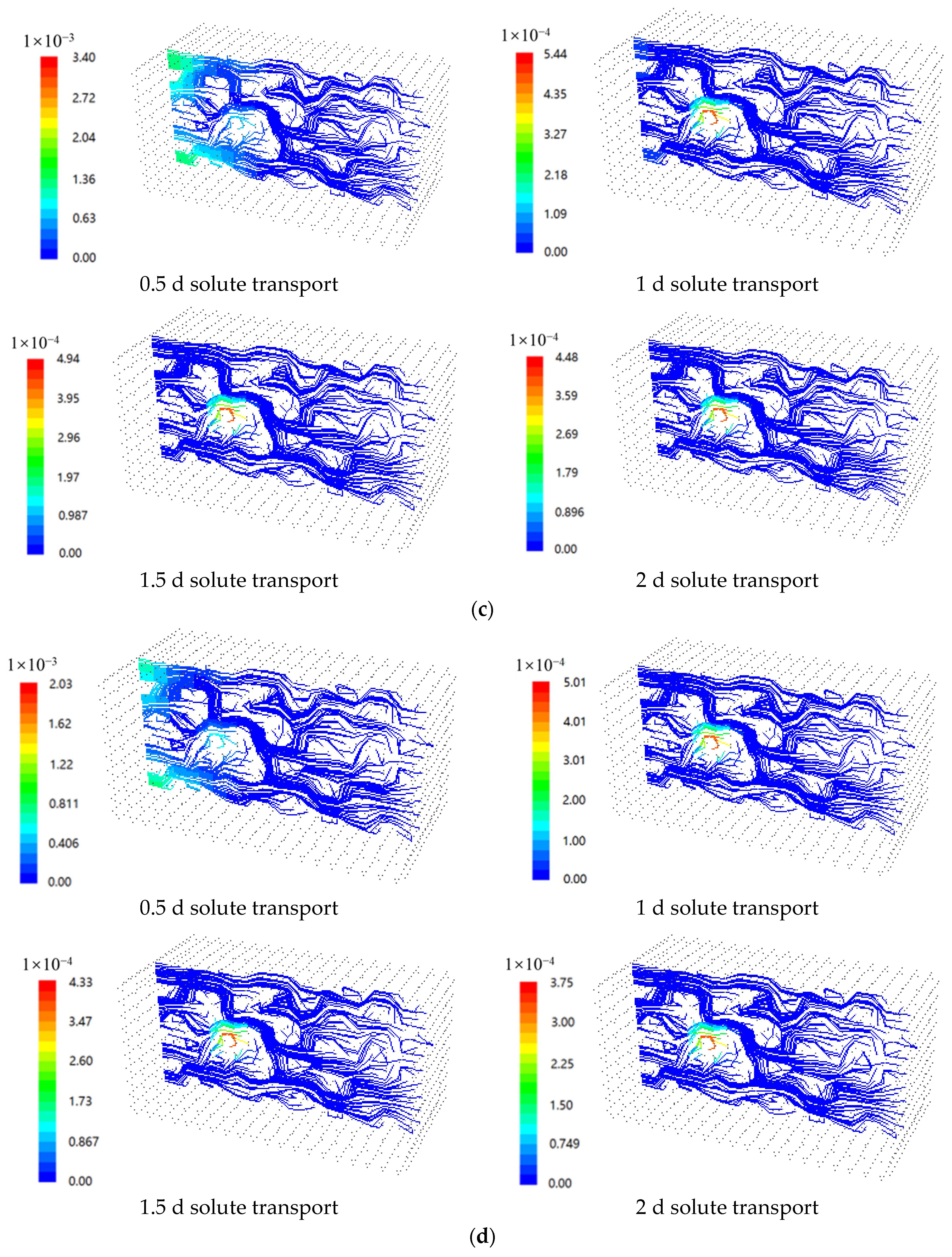
Transport and Distribution
4. Sensitivity Analysis
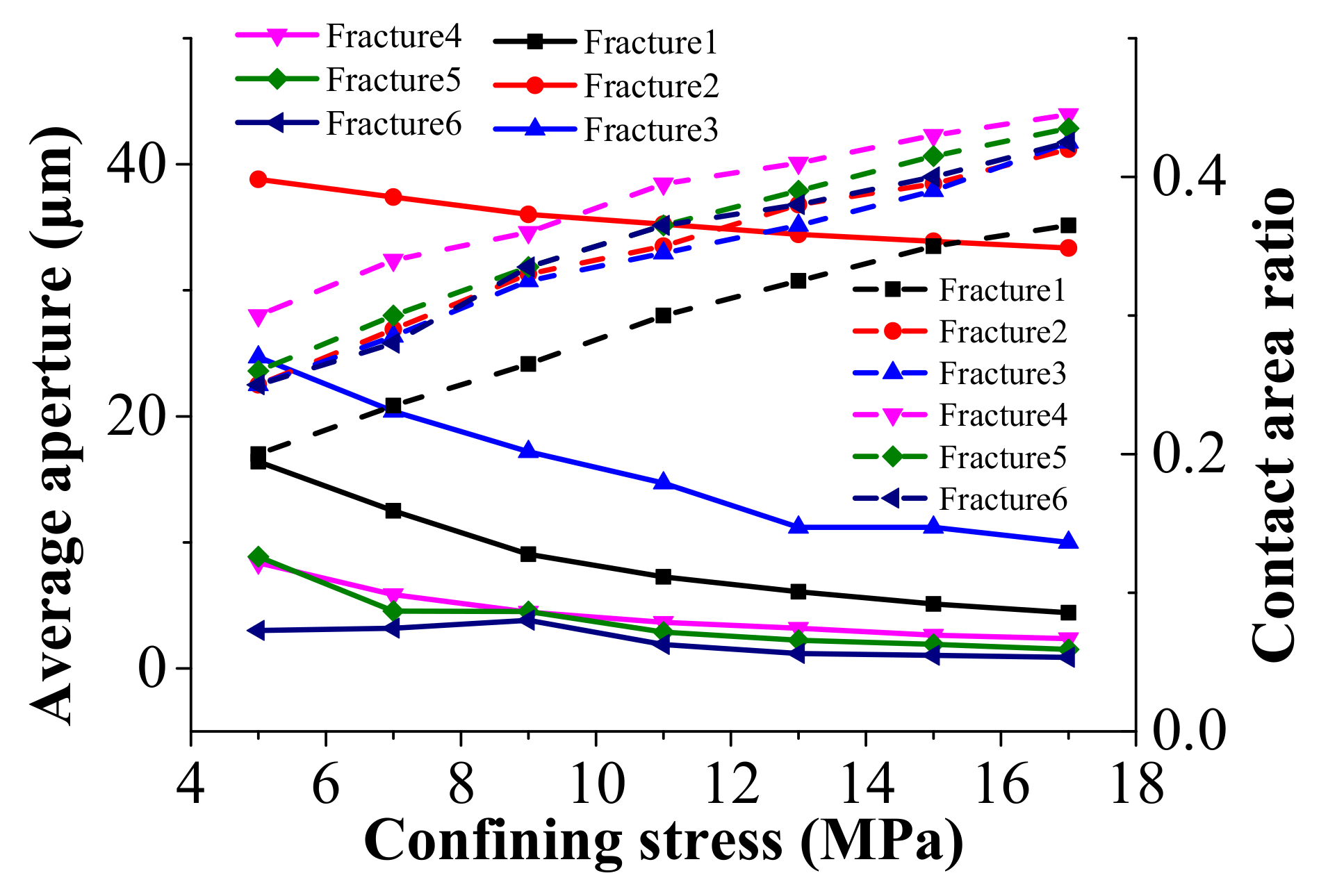
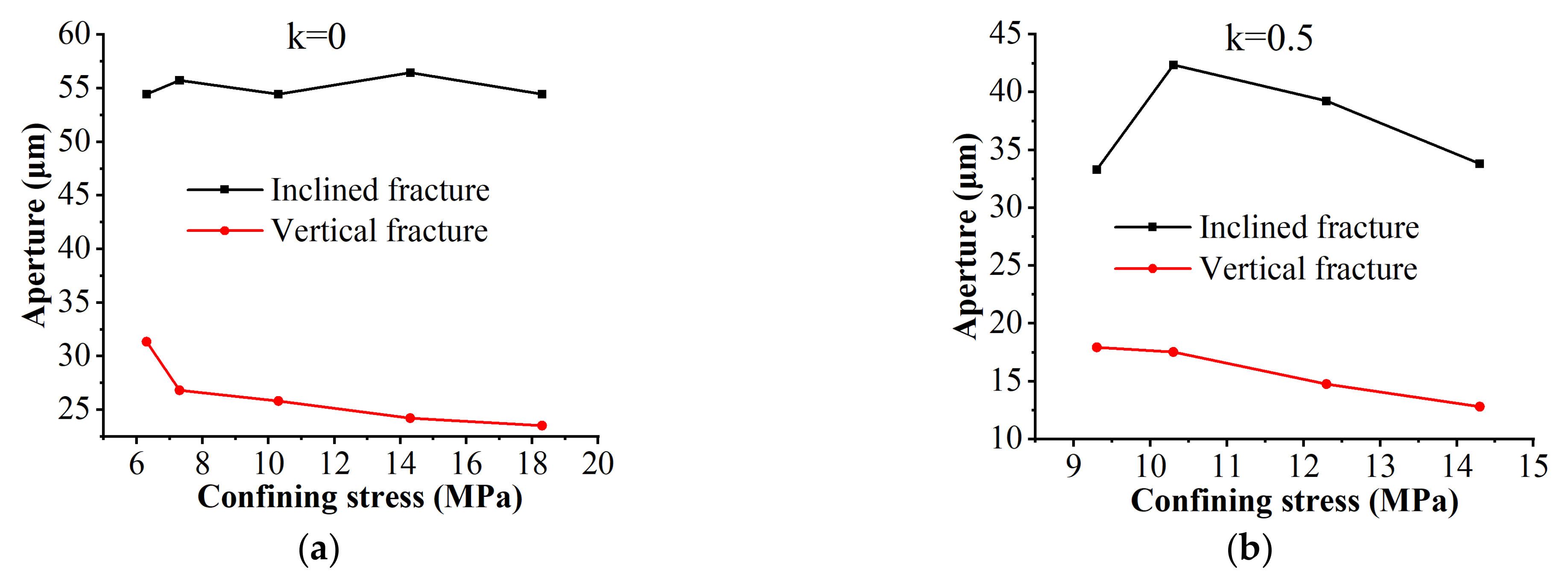
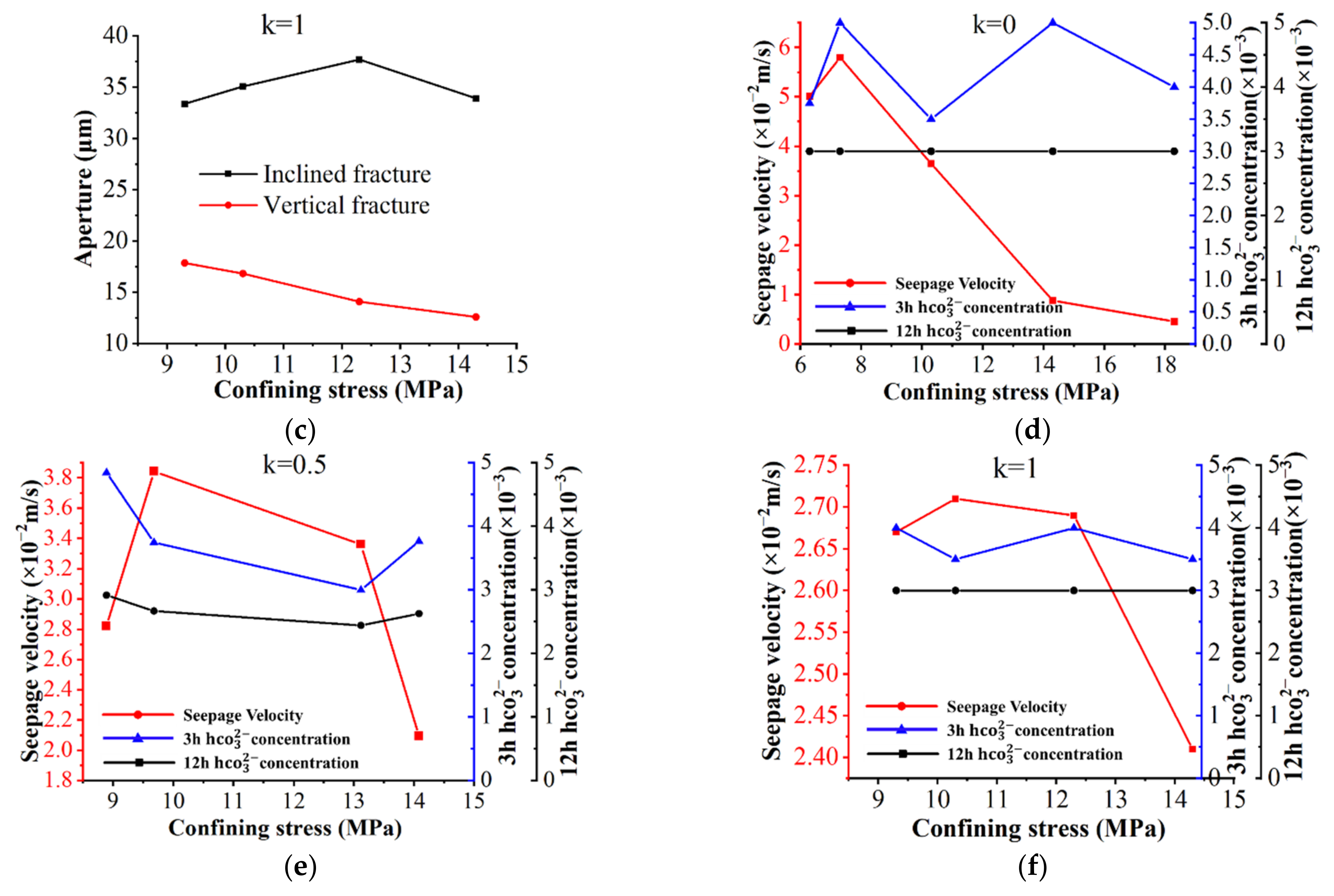
4.1. Confining Stress
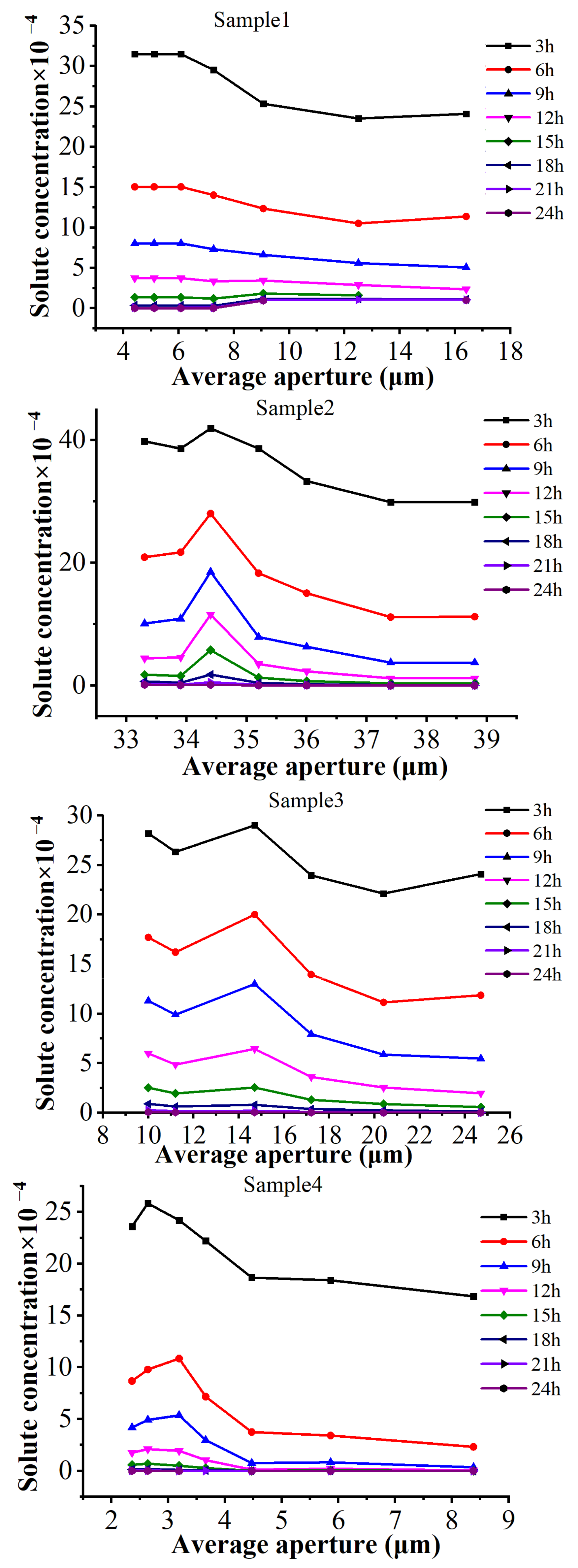
4.2. Fracture Aperture
4.3. Cross Channel of the Fracture
4.4. Loading Path
5. Conclusions
- (1)
- A mathematical model describing the stress-dependent fracture structure and uranium-containing solute transport was established. The evolution of a connected channel in fracture aperture is influenced by the increase of confining stress, and a dynamic and slight decrease zone was confirmed for confining stress of 5–13 MPa and 13–17 MPa. The concentration of uranium-containing solution is directly influenced by the fracture aperture and hydraulic pressure, and a 2–5 μm fracture aperture was identified as a width threshold from a lower to higher uranium-containing solute concentration.
- (2)
- The number and size of a connected channel decreased with the increase of confining stress in double-fractures. The turbulent flow was presented in a high fluid velocity and confining stress condition, and retention of uranium-containing solution characterized by block and ribbon-shaped solute concentration areas was observed in both inclined and vertical fractures, and dynamic decrease of uranium-containing solution was presented at the fracture intersections region. The dynamic decrease presented in the initial 12 h, and a slight decrease presented in the following period.
- (3)
- The loading and unloading direction and rate significantly influence the fracture geometry and uranium-containing solute transportation. As the ration of vertical stress loading and horizontal stress loading k increases, the decrease in fracture aperture, seepage velocity, and uranium-containing solute concentration was observed. In addition, high seepage velocity and strong solute transport capacity for k = 1, and the laminar flow for k = 0 were observed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Zhou, J.; Hu, S.; Hu, R.; Zhou, C.-B. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures. J. Hydrol. 2015, 529, 993–1006. [Google Scholar] [CrossRef]
- Dangelmayr, M.A.; Reimus, P.W.; Wasserman, N.L.; Punsal, J.J.; Johnson, R.H.; Clay, J.T.; Stone, J.J. Laboratory column experiments and transport modeling to evaluate retardation of uranium in an aquifer downgradient of a uranium in-situ recovery site. Appl. Geochem. 2017, 80, 1–13. [Google Scholar] [CrossRef]
- Zhang, T.; Gan, Q.; Zhao, Y.; Zhu, G.; Nie, X.; Yang, K.; Li, J. Investigations into Mining-Induced Stress–Fracture–Seepage Field Coupling Effect Considering the Response of Key Stratum and Composite Aquifer. Rock Mech. Rock Eng. 2019, 52, 4017–4031. [Google Scholar] [CrossRef]
- Sims, R.; Lawless, T.A.; Alexander, J.L.; Bennett, D.G.; Read, D. Uranium migration through intact sandstone: Effect of pollutant concentration and the reversibility of uptake. J. Contam. Hydrol. 1996, 21, 215–228. [Google Scholar] [CrossRef]
- Dittrich, T.M.; Reimus, P.W. Uranium transport in a crushed granodiorite: Experiments and reactive transport modeling. J. Contam. Hydrol. 2015, 175–176, 44–59. [Google Scholar] [CrossRef] [Green Version]
- Dittrich, T.M.; Reimus, P.W. Reactive transport of uranium in fractured crystalline rock: Upscaling in time and distance. J. Environ. Manag. 2016, 165, 124. [Google Scholar] [CrossRef] [Green Version]
- Panfilov, M.; Uralbekov, B.; Burkitbayev, M. Reactive transport in the underground leaching of uranium: Asymptotic analytical solution for multi-reaction model. Hydrometallurgy 2016, 160, 60–72. [Google Scholar] [CrossRef]
- Read, D.; Ross, D.; Sims, R.J. The migration of uranium through Clashach Sandstone: The role of low molecular weight organics in enhancing radionuclide transport. J. Contam. Hydrol. 1998, 35, 235–248. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, T.; Yu, Q.; Xu, T.; Zhu, W.; Liu, H.; Zhou, J.; Zhao, Y. Microseismicity Induced by Fault Activation during the Fracture Process of a Crown Pillar. Rock Mech. Rock Eng. 2015, 48, 1673–1682. [Google Scholar] [CrossRef]
- Cui, G.; Wei, J.; Feng, X.T.; Liu, J.; Elsworth, D.; Chen, T.; Xiong, W. Preliminary study on the feasibility of co-exploitation of coal and uranium-ScienceDirect. Int. J. Rock Mech. Min. Sci. 2019, 123, 104098. [Google Scholar] [CrossRef]
- Du, L.; Li, S.; Li, X.; Wang, P.; Huang, Z.; Tan, Z.; Liu, C.; Liao, J.; Liu, N. Effect of humic acid on uranium(VI) retention and transport through quartz columns with varying pH and anion type. J. Environ. Radioact. 2017, 177, 142–150. [Google Scholar] [CrossRef]
- Wang, G.; Wu, M.; Wang, R.; Xu, H.; Song, X. Height of the mining-induced fractured zone above a coal face. Eng. Geol. 2017, 216, 140–152. [Google Scholar] [CrossRef]
- Ahn, H.; Oh, Y.; Ryu, J.H.; Jo, H.Y. Uranium sequestration in fracture filling materials from fractured granite aquifers. J. Environ. Radioact. 2020, 225, 106440. [Google Scholar] [CrossRef]
- Tan, K.; Li, C.; Liu, J.; Qu, H.; Xia, L.; Hu, Y.; Li, Y. A novel method using a complex surfactant for in-situ leaching of low permeable sandstone uranium deposits. Hydrometallurgy 2014, 150, 99–106. [Google Scholar] [CrossRef]
- Zeng, F.; Zhao, G. The optimal hydraulic fracture geometry under non-Darcy flow effects. J. Pet. Sci. Eng. 2010, 72, 143–157. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, C.; Sheng, Y. Formulation of strain-dependent hydraulic conductivity for a fractured rock mass. Int. J. Rock Mech. Min. Sci. 2007, 44, 981–996. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Shovkun, I.; Makni, O.; Lenoir, N. Natural and induced fractures in coal cores imaged through X-ray computed microtomograph—Impact on desorption time. Int. J. Coal Geol. 2016, 154, 165–175. [Google Scholar] [CrossRef]
- Lai, P.; Samson, C.; Bose, P. Visual enhancement of 3D images of rock faces for fracture mapping. Int. J. Rock Mech. Min. Sci. 2014, 72, 325–335. [Google Scholar] [CrossRef]
- He, R.; Yang, Z.; Li, X.; Li, Z.; Liu, Z.; Chen, F. A comprehensive approach for fracability evaluation in naturally fractured sandstone reservoirs based on analytical hierarchy process method. Energy Sci. Eng. 2019, 7, 529–545. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, G.; Xu, L.; Liu, J.; Sun, Z.; Shi, W. Uranium recovery from sandstone-type uranium deposit by acid in-situ leaching—An example from the Kujieertai. Hydrometallurgy 2019, 191, 105209. [Google Scholar] [CrossRef]
- Devaraj, N.; Panda, B.; Chidambaram, S.; Prasanna, M.V.; Singh, D.K.; Ramanathan, A.L.; Sahoo, S.K. Spatio-temporal variations of Uranium in groundwater: Implication to the environment and human health. Sci. Total Environ. 2021, 775, 145787. [Google Scholar]
- Liu, H.; Wei, M.; Rutqvist, J. Normal-stress dependence of fracture hydraulic properties including two-phase flow properties. Hydrogeol. J. 2013, 21, 371–382. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Zhou, C. Hydraulic properties of partially saturated rock fractures subjected to mechanical loading. Eng. Geol. 2014, 179, 24–31. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Y.; Konietzky, H.; Cai, X. Mechanical behavior of marble exposed to freeze-thaw-fatigue loading. Int. J. Rock Mech. Min. Sci. 2021, 138, 104648. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Wang, S.; Sun, L.; Li, X.; Wang, S.; Du, K.; Li, X.; Feng, F. Experimental investigation of cuttability improvement for hard rock fragmentation using conical cutter. Int. J. Geomech. 2021, 21, 06020039. [Google Scholar] [CrossRef]
- Kim, J.W.; Baik, M.H.; Jung, H.; Jeong, J.T. Reactive transport of uranium with bacteria in fractured rock: Model development and sensitivity analysis. J. Contam. Hydrol. 2013, 152, 82–96. [Google Scholar] [CrossRef]
- De Boissezon, H.; Levy, L.; Jakymiw, C.; Distinguin, M.; Guerin, F.; Descostes, M. Modeling uranium and 226Ra mobility during and after an acidic in situ recovery test (Dulaan Uul, Mongolia). J. Contam. Hydrol. 2020, 235, 103711. [Google Scholar] [CrossRef]
- Feng, S.; Wang, H.; Cui, Y.; Ye, Y.; Liu, Y.; Li, X.; Wang, H.; Yang, R. Fractal discrete fracture network model for the analysis of radon migration in fractured media. Comput. Geotech. 2020, 128, 103810. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Lei, H.; Wang, Y.; Liu, H.; Li, X.; Su, X. Potential for uranium release under geologic CO2 storage conditions: The impact of Fe (III). Int. J. Greenh. Gas Control 2021, 107, 103266. [Google Scholar] [CrossRef]
- Wang, Q.; Miao, X.; Wang, Y.; Gan, M.; Aftab, S.M.; Li, X.; Zhang, L.; Wang, Z. Simulation of uranium mobilization potential in a deep aquifer under geological carbon storage conditions. Appl. Geochem. 2020, 118, 104620. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Rong, G.; Hou, D.; Yang, J.; Cheng, L.; Zhou, C. Experimental study of flow characteristics in non-mated rock fractures considering 3D definition of fracture surfaces. Eng. Geol. 2017, 220, 152–163. [Google Scholar] [CrossRef]
- Zhang, Z.; Nemcik, J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures. J. Hydrol. 2013, 477, 139–151. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H. A two-dimensional coupled hydro-mechanical finite-discrete model considering porous media flow for simulating hydraulic fracturing. Int. J. Rock Mech. Min. Sci. 2016, 88, 115–128. [Google Scholar] [CrossRef]
- Koyama, T.; Fardin, N.; Jing, L.; Stephansson, O. Numerical simulation of shear-induced flow anisotropy and scale-dependent aperture and transmissivity evolution of rock fracture replicas. Int. J. Rock Mech. Min. Sci. 2006, 43, 89–106. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, L.; Neretnieks, I.; Moreno, L. Numerical modeling of stress effects on solute transport in fractured rocks. Comput. Geotech. 2011, 38, 113–126. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Herbst, M. Bonded-particle model-based simulation of artificial rock subjected to cyclic loading. Acta Geotech. 2019, 14, 955–971. [Google Scholar] [CrossRef]
- Rutqvist, J.; Leung, C.; Hoch, A.; Wang, Y.; Wang, Z. Linked multicontinuum and crack tensor approach for modeling of coupled geomechanics, fluid flow and transport in fractured rock. Rock Mech. Geotech. Eng. 2013, 5, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Lei, Q.; Latham, J.-P.; Xiang, J.; Tsang, C.-F. Polyaxial stress-induced variable aperture model for persistent 3D fracture networks. Geomech. Energy Environ. 2015, 1, 34–47. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Jing, L.; Neretnieks, I.; Moreno, L. Analytical solution of coupled stress-flow-transport processes in a single rock fracture. Comput. Geosci. 2011, 37, 1437–1449. [Google Scholar] [CrossRef]
- Crandall, D.; Bromhal, G.; Karpyn, Z.T. Numerical simulations examining the relationship between wall-roughness and fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2010, 47, 784–796. [Google Scholar] [CrossRef]
- Akhavan, A.; Shafaatian, S.; Rajabipour, F. Quantifying the effects of crack width, tortuosity, and roughness on water permeability of cracked mortars. Cem. Concr. Res. 2012, 42, 313–320. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, W.; Lian, H.; Yang, J.; Nguyen, V.P. Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures. Int. J. Rock Mech. Min. Sci. 2017, 98, 121–140. [Google Scholar] [CrossRef]
- Bandis, S.; Lumsden, A.; Barton, N. Fundamentals of rock joints deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Gan, Q.; Elsworth, D. A continuum model for coupled stress and fluid flow in discrete fracture networks. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 43–61. [Google Scholar] [CrossRef] [Green Version]

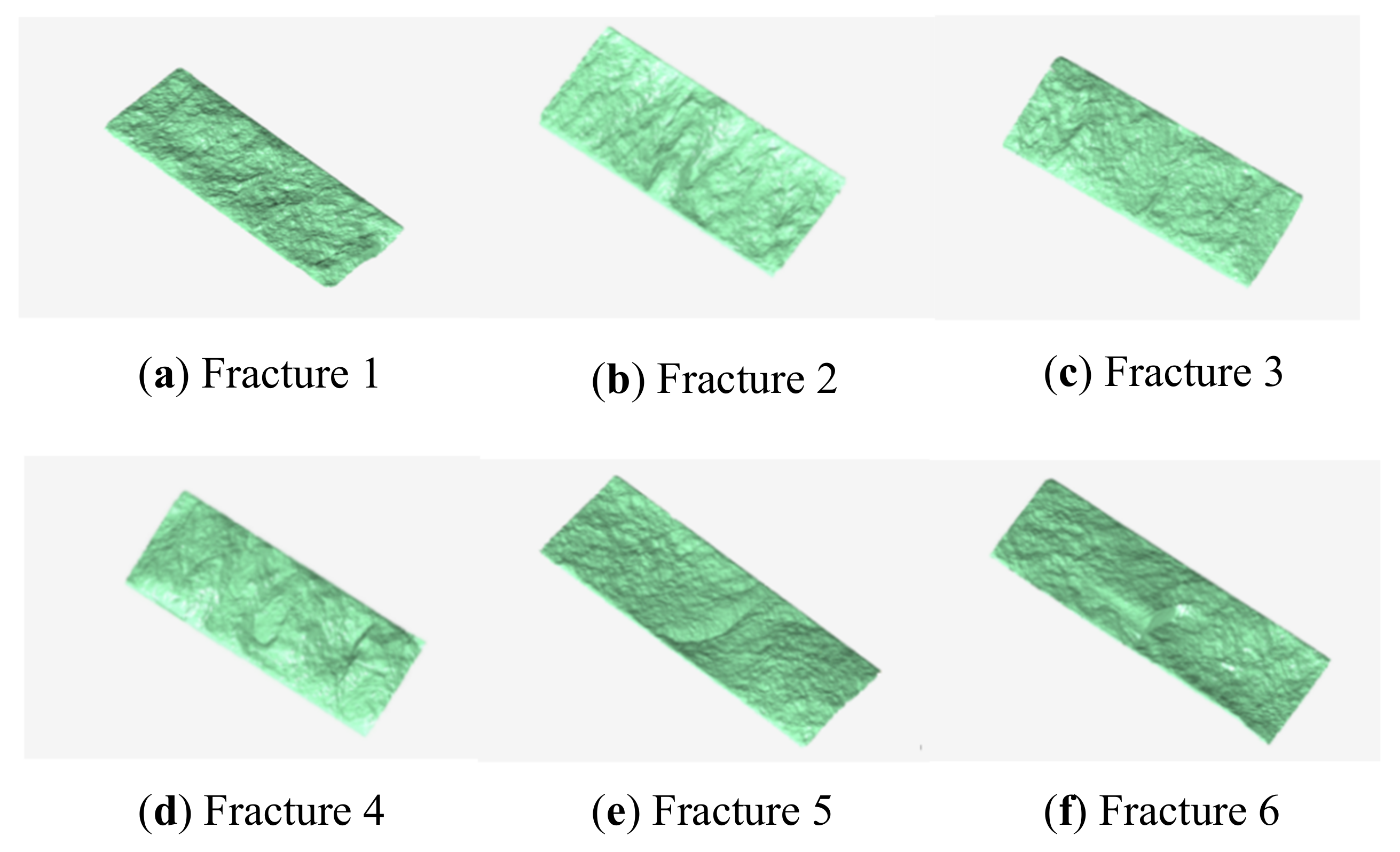




| No. | Fracture Length L (mm) | Fracture Width w (mm) | Contact Ratio (5 MPa) | Fracture Aperture (μm) (5 MPa) |
|---|---|---|---|---|
| 1 | 100 | 49 | 0.20 | 1.64 × 10−5 |
| 2 | 100 | 49 | 0.25 | 3.88 × 10−5 |
| 3 | 100 | 49 | 0.25 | 2.47 × 10−5 |
| 4 | 100 | 49 | 0.30 | 8.38 × 10−6 |
| 5 | 100 | 49 | 0.26 | 8.86 × 10−6 |
| 6 | 100 | 49 | 0.25 | 3.00 × 10−6 |
| Stress Field | Density d (kg/m3) | Bulk Modulus B (GPa) | Shear Modulus S (GPa) | Cohesion C (MPa) | Tensile Strength t (MPa) | Internal Friction Angle ψ (°) | Initial Permeability K (m2) |
| 2660 | 33.94 | 22.4 | 4.0 | 22.52 | 35 | ||
| Chemical field | UO2(CO3)34− | reaction rate (kg/m3s) | Dispersion coefficient (m2/s) | ||||
| 5.0 × 10−4 | 10.5 | 0 | |||||
| Fracture field | Initial mean fracture width (μm) | Initial permeability (m2) | Initial non-darcy flow factor β (m−1) | ||||
| 30 | 7.0 × 10−12 | 1.0 × 108 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Nie, X.; Song, S.; Hao, X.; Yang, X. Modeling Uranium Transport in Rough-Walled Fractures with Stress-Dependent Non-Darcy Fluid Flow. Mathematics 2022, 10, 702. https://doi.org/10.3390/math10050702
Zhang T, Nie X, Song S, Hao X, Yang X. Modeling Uranium Transport in Rough-Walled Fractures with Stress-Dependent Non-Darcy Fluid Flow. Mathematics. 2022; 10(5):702. https://doi.org/10.3390/math10050702
Chicago/Turabian StyleZhang, Tong, Xiaodong Nie, Shuaibing Song, Xianjie Hao, and Xin Yang. 2022. "Modeling Uranium Transport in Rough-Walled Fractures with Stress-Dependent Non-Darcy Fluid Flow" Mathematics 10, no. 5: 702. https://doi.org/10.3390/math10050702
APA StyleZhang, T., Nie, X., Song, S., Hao, X., & Yang, X. (2022). Modeling Uranium Transport in Rough-Walled Fractures with Stress-Dependent Non-Darcy Fluid Flow. Mathematics, 10(5), 702. https://doi.org/10.3390/math10050702






