Improving User’s Experience in Exploring Knowledge Structures: A Gamifying Approach

Abstract

Gamifying user experience while navigating knowledge structures is the new paradigm in online learning and improving human–computer interaction. Learning by playing and learning by doing lie at the core of this approach. Rooted in the paradigm of Conceptual Knowledge Processing and conceptual landscapes of knowledge, this research proposes an immersive experience in 3D knowledge structures, the VR FCA project. We exemplify this experience, at least the amount possible in a journal paper, by using data sets about topological spaces, a mathematical field which is notoriously hard to grasp by beginners or sometimes even at an intermediate level. We present the stages of this project, the technologies we have used in the implementation and also some basics of Formal Concept Analysis (FCA), the mathematical theory which lies at heart of Conceptual Knowledge Processing.

1. Introduction

From the very beginning of the Information Age, investigating the structure of knowledge was a central approach. Cognitive sciences, psychology and Artificial Intelligence were equally concerned about defining and understanding the structure of knowledge.

The term knowledge structure was established in the 1970s in Cognitive Sciences, a discipline that emerged at the intersection of Psychology and Computer Science [1]. Jonassen [2] defines knowledge structures in education as the knowledge of how concepts in a domain are interrelated. According to this author, these structures are utilised in intelligent educational systems to adapt navigation, to provide knowledge tracing, or learner guidance. The role of knowledge structure in learning was investigated by Ley in [3]. Here, he analyses the experience of more than 10 years of research intending to offer intelligent services through capturing and leveraging knowledge structures in workplace learning.

Formal Concept Analysis (FCA) is a prominent field of applied mathematics providing an elegant, intuitive yet powerful knowledge representation as order diagrams. Using the conceptual landscapes of knowledge paradigm of R. Wille [4], knowledge is activated by using the landscape metaphor and FCA and its algorithmic machinery plays an important role in mining knowledge, identifying patterns, processing concepts and representing them. The basic data set of FCA is the formal context, i.e., a collection of objects and attributes linked by a binary relation, called incidence relation. This data set is usually represented as a two-dimensional data table, encoding in 2D the entire information contained in the data set. Formal concepts are the mathematisation of the traditional understanding of a concept, i.e., a maximal collection of objects and commonly shared attributes. In his seminal paper, R. Wille [5] proposes an order theoretical approach to the problem of concept mining. More precisely, using a Galois connection between the power sets of the sets of objects and that of attributes, concept forming operators are defined. The Basic Theorem on Concept Lattices [6] proves that, for each formal context, the correspondent concept set carries a complete lattice structure and each complete lattice can be obtained as a concept lattice of some formal context.

This was the starting point of the development of a brand new research field, with major applications in Artificial Intelligence, Knowledge Processing and Representation. The concept lattice or concept hierarchy represents the concepts, i.e., knowledge units and their hierarchy, and builds the basis for further communication, navigation and investigation of the data set. Conceptual structures gained more and more importance and they became the counterpart of knowledge structures from the cognitive sciences in FCA. Reference  [7] provides an overview on how FCA and Conceptual Graphs (CGs) can be used in many areas, serving as a benchmark of research on conceptual structures.

This research starts from the definition of Jonassen  [2] and uses a new approach to visualisation and navigation of concept sets in knowledge structure based on FCA and virtual reality (VR) following the outlines of Conceptual Knowledge Processing defined by R. Wille in [8]. According to R. Wille, “Conceptual Knowledge Processing is understood as the general scientific discipline which activates acts of thinking such as representing, reasoning, acquiring, and communicating conceptual knowledge”. We prove that moving from a two-dimensional representation of conceptual structures into a three-dimensional virtual reality representation of these structure not only enhances understanding of these knowledge structures but also opens new possibilities to navigate, explore and communicate over the knowledge represented herein.

From our own experience in undertaking research projects and from the experience we gathered over the last decades from the main FCA community, there is a gap between the results, projects, algorithms and software tools developed within the FCA community and their usage outside the scientific community. While other related fields, such as, for instance, learning space theory, have software implementations which are heavily used by millions of users (https://www.aleks.com (accessed on 15 December 2021)), the usage of FCA tools and algorithms remains modest. It is not the aim of this research to discuss the reasons for this situation but to propose an approach which has the potential to close the gap between the powerful machinery and elegant knowledge representation of FCA and regular users.

We propose a gamifying approach towards exploring knowledge structures not in the sense that we transform navigation in concept lattice in a computer game but we offer users the possibility to explore 3D concept lattices in a VR environment, to rotate these structures, to fly around, to teleport from one node to another, to laser point to a certain node and to interact with these FCA based conceptual landscapes in a more lively way than on a regular 2D computer screen. This approach has been extensively tested by the FCA community in 2019 at the last prepandemic International Conference on Formal Concept Analysis. The feedback gathered from senior and junior researchers helped us to further improve the system to a multiuser VR based FCA navigation tool fulfilling R. Wille’s dream of navigating conceptual landscapes of knowledge in a similar way we navigate and explore natural landscapes.

The present research presents a new use case of some previous results [9], which deepens [10] focusing on a proof of concept of how FCA enhanced with VR has the potential both to improve user’s experience in exploring knowledge structures and also to gamify this approach. The multiuser modus also makes it possible to communicate in this VR environment, to analyse the structure of knowledge and to highlight interesting parts beyond the classical knowledge representation of knowledge.

2. Formal Concept Analysis

In the following, we briefly sketch some basic notions about FCA. For more, please refer to [6].

The fundamental data structure in FCA is a so-called formal context which consists of two sets of objects and attributes, respectively. These sets are denoted in the literature by G and M, respectively, from the German word Gegenstände for objects and Merkmale for attributes. The fact that an object $g\in G$ has an attribute $m\in M$ is formalised by a binary relation $I\subseteq G\times M$. Hence, a formal context can be represented as a triple $𝕂=(G,M,I)$. Starting from this very basic data structure, there are many other enhancements, such as many-valued context, i.e., objects have attributes with a certain value, or triadic FCA, i.e., objects have attributes under certain conditions, etc.

For finite formal contexts, a very natural and at hand representation is by using a cross-table. Cross-tables can be easily understood by humans; the rows are labelled by object names, the columns are labelled by attribute names. The incidence relation is represented by crosses in that table (see Figure 1).

The whole point in FCA that makes the difference between other search or representation methods in data sets (SQL, rough sets, clustering, etc.) is the focus on concepts, which are understood as maximal clusters of information, bearing a clear meaning. While in philosophy the notion of a concept has been extensively discussed, FCA gives an elegant formalisation of a concept based on a Galois connection between the power sets of the object and attributes sets, respectively. This Galois connection is defined via the so-called derivation operator. More precisely, for a subset $A\subseteq G$ of objects, the derivation of A is defined as the set of all commonly shared attributes of all objects $g\in A$, $A^I:=\{m\mid \mathit{gIm}\mathrm{for}\mathrm{all}g\in A\}$. Dually, the derivation of a subset $B\subseteq M$ of attributes is defined as the set of all objects sharing exactly the attributes in B, $B^I=\{g\mid \mathit{gIm}\mathrm{for}\mathrm{all}m\in B\}$.

The derivation operators and the subsequent closure systems that this Galois connection gives rise can be seen as concept forming operators. By this, we can define a formal concept as being a pair $(A,B)$, where $A\subseteq G$ and $B\subseteq M$ are satisfying $A^I=B$ and $B^I=A$. This is similar to a clustering process, with the condition that the clusters are maximal with respect to the incidence relation. In the cross-table representation, formal concepts are maximal rectangles of crosses obtained by permuting rows and columns.

If $(A,B)$ is a formal concept, the set A is called extent and B is called intent. The set of all concepts of a formal context $𝕂=(G,M,I)$ is denoted by $\mathfrak{B}\left(𝕂\right)$.

The set $\mathfrak{B}\left(𝕂\right)$ is naturally ordered by the subconcept–superconcept relationship. We say that $(A,B)$ is a subconcept of $(C,D)$ (or equivalently, $(C,D)$ is a superconcept of $(A,B)$), and we write $(A,B)\le (C,D)$ if and only if $A\subseteq C$ ($\iff D\subseteq B$). The fundamental theorem of FCA states that $\left(\mathfrak{B}\right(𝕂),\le )$ is a complete lattice and every complete lattice is obtained as the concept lattice of a suitable chosen formal context. The graphical representation of this conceptual hierarchy can be achieved in an elegant way by using order diagrams.

Figure 2 shows the concept system of the context in Figure 1. In this figure, we considered the reduced labelling representation generally used in FCA to improve readability: Each node is a concept but only the object concepts and attribute concepts are labelled. These concepts are particular concepts of the form $(g^{″},g^{\prime })$ and $(m^{\prime },m^{″})$ for $g\in G$ and $m\in M$. Since some of these object or attribute concepts can overlap, i.e., some objects and attributes can generate the same object concept or attribute concept, respectively, it might happen that some of these concepts bear more than one object or attribute label. Due to the above mentioned Fundamental Theorem of FCA, every other concept is obtained as the infimum or supremum of object concepts or attribute concepts.

This also explains how a concept lattice should be read, respectively how navigation in concept lattices takes place: Each node is a concept. The extent is obtained by collecting all object names which we find as labels for concepts which are reachable by downward going paths. Dually, the intent is obtained by collecting all attribute names which are reachable by upward going paths. The upmost node contains all attributes which are commonly shared by all objects in the formal context, i.e., full columns in the cross-table representation. Dually, the bottommost concept contains all objects which have all attributes of the context, i.e., full rows in the cross-table representation.

3. Setting the Stage: The VR FCA Project

From its very beginnings in the late ’80s of the previous century, FCA offered a very elegant way to represent knowledge structures as order diagrams and the aesthetics of these diagrams were always valued in R. Wille’s group. Over the decades, many FCA graphical representation tools have appeared. A very early project was ConImp [11] which was devoted to the computation of implications and implementation of some early algorithms. A meanwhile classic tool for dyadic FCA is Concept Explorer (conexp.sourceforge.net). ConExp-FX (https://github.com/francesco-kriegel/conexp-fx (accessed on 15 December 2021)), and ConExp-NG (https://github.com/fcatools/conexp-ng (accessed on 15 December 2021)) are reimplementations of the former. The latter one is part of FCA Tools, a collection of FCA related software tools (https://github.com/fcatools (accessed on 15 December 2021)). An overview of attribute exploration with domain knowledge was given in [12]. FCA Tools Bundle [13] is an ambitious project aiming to gather all FCA Tools in a single software over a web interface. Besides the classical dyadic approach, FCA Tools Bundle handles tricontexts, navigation tools in triadic data sets, contains an implementation of a local navigation paradigm in triadic data sets as well as a like–dislike Answer Set Programming based method to narrow down the set of concepts we would like to investigate, and many more. LatViz [14] is a joint effort of another FCA research community to improve existing tools, implementing new functionalities such as visualisation of Pattern Structures, concept annotations, intuitive visualisation of implications, etc.

The VR FCA project [9,10] is an attempt to include modern graphic capabilities, new technologies and game engines in FCA software tools. The aim is gamifying the FCA experience in order to activate the Conceptual Knowledge Processing features necessary for a good learning experience. For this, we need an intuitive and captivating technological environment which triggers a new kind of navigating conceptual structures experience. Once you enter a VR room, a 3D concept lattice unfolds in front of you, allowing you to interact with it, to fly around, to rotate, to teleport or to narrow the perspective to a certain group of nodes. The multiuser experience allows users to simultaneously enter the same VR room and to discuss and interact all together. This research is based on [9]. Here, we focus on improvements and applications in particular fields, such as Topology, in order to highlight that gamifying the FCA experience is a major step forward in designing new intelligent systems aiming for a better human–computer interaction.

One of the major challenges was how to represent a concept lattice in three dimensions. Diagrams, and particularly order diagrams, are used in Knowledge Representation in order to reduce the cognitive load for the user. In this research, we focus on a particular representation of conceptual hierarchy as an order diagram. Nevertheless, there is no canonical representation of an order diagram in 2D, which makes it even more difficult to represent if in 3D. Following the school of R. Wille, the founder of FCA, which emphasises the need of nice order diagrams to support the user in his knowledge structure navigation, 2D order diagrams as many parallelograms as possible and avoids overlapping of the nodes and unnecessary edge intersections. However, this still does not solve the problem of 3D representation of a conceptual hierarchy.

A visualisation method which proved to be very effective was described in [15] and is called 3D Cone Tree. A cone tree is a hierarchical knowledge representation laid out uniformly in three dimensions, also using the depth of the monitor not only the height or width of the monitor. In this seminal paper, cone trees rotate whenever a node is selected, and each node in the path from the selected node up to the top are brought to the front and highlighted. The rotations follow the shortest path, and they are animated. By this, the user can see the transformation and is able to better understand the underlying structure of the represented knowledge system. Paper [15] proposes interactive animation is used to shift some of the user’s cognitive load to the human perceptual system. Instead of this, our approach is using Unity and SteamVR technologies to enable interactivity with the graphical representation of knowledge structures.

This research is proposing a particular approach to the exploration of knowledge structures by moving the entire experience into a 3D VR environment and gamifying this experience by using the capabilities of state-of-the-art VR technologies. By this, the idea of [15] of using 3D representations of knowledge structures is realised at a completely other level the authors thought might be possible in their paper. Even more, it also brings into life the paradigm of R. Wille of considering concept hierarchies of knowledge structures as conceptual landscapes of knowledge and to explore and navigate them according to the paradigm of landscape.

Upgrading the navigation experience to 3D and using modern VR technologies allows us to shift the perception and also the cognitive experience of navigating knowledge structures to another level. As experiments showed, this might be quite an overwhelming experience, but the gaming experience the user has by rotating, flying around, teleport or laser pointing concepts does the trick.

As mentioned in [9], the FCA VR tool is designed specifically for people that had no connection to FCA before. In order to underline the gamifying experience of navigating 3D knowledge structures, we propose in this research a use case related to concept hierarchies built over some abstract topological notions. From our own teaching experience, they are notoriously hard to grasp for beginners or even mathematicians with less background in Topology.

This idea is by itself a real challenge and this challenge is doubled by the fact that every user is different and has another understanding of how a graphical representation should look in order to match their expectations of a working system. To overcome this problem, we gathered feedback from various sources, from students, junior researchers, professors teaching at the University and active researchers in the FCA community. Because feedback came from such many places, it gave us a good overview over the overall aspect of the application, the common ground of these people, and what could be improved in the future.

Without entering into details which can be found in [9], the VR FCA project is using Unity as the engine on which we run the applications. Because it offers a scripting API over the engine, and you can build a virtual environment that can be later rendered to the user, it has been proved to be of a huge value since we did not have to use low-level graphics rendering libraries such as OpenGL.

SteamVR is a plugin for Unity which allows virtual reality application developers to target one single API that all the popular virtual reality headsets can connect to. HoverUI Kit is a tool that allows the developer to create virtual reality interfaces, based on the mechanism of hovering.

The use of Unity technologies with the SteamVR plugin had very many deciding factors:

• Unity with the SteamVR plugin took the responsibility of presenting the objects in the VR world, allowing us to focus on functionality of the application rather than writing our own.
• The SteamVR API is simply to use, while learning Unity is also simple since everything is based on C#.
• At the time of writing the application, the SteamVR was the best well-maintained VR Abstraction framework we could find.
• SteamVR provided better Input Controls Configuration than other plugins.

4. Describing the Stage: App Description

The core of the presentation layer is the MVC model, where we synchronise the user and multiplayer input to actual models and views that can be shown to the user. Figure 3 gives an overview of the VR FCA Application. For details about various VR related functionalities, we refer to https://github.com/zraul123/FCAVR and [9,10] (accessed on 15 December 2021).

This presentation module has the role of abstracting all inputs and data into a form presentable to the user. Additionally, here we have wrappers over Unity objects and UI elements—the UnityObjectFactory and Menus modules.

The UnityObjectFactory wrapper takes simply a View and creates its 3D Lattice representation with the data it is given.

The Menus wrapper contains all the Menus available (Main Menu, Tutorials).

The Scenario module serves as an abstraction layer over the various lattices we support—regular concept lattices, conceptual scales and Lifetrack lattices (for Temporal Concept Analysis, see [10]). The Scenario module uses the FileSystem Repository to extract the lattices definitions (we have a predetermined path for the lattice locations), which are then presented to the user as available lattices. If a user selects a lattice, it will load in the SQLite Repository its metadata, and depending on the Lattice type, it may also store the objects there (for conceptual scales and Lifetrack lattices) for quicker reference. The lattice definition is loaded from the filesystem, and the file is parsed using the LatticeService, which is actually a business wrapper over Formal Concept Analysis algorithms. The FCALib is simply a module in which we keep the Formal Concept Analysis algorithms we need (currently, only the parsing of the file format).

The MultiplayerSync modules serves as a facade for all network operations transmitted. This may be saving of nodes or additional metadata. It opens an internal WebSocket port, which is used for bi-directional communication with the server. This also contains code for Voice communication.

The Multiplayer Server external application serves as a router and broadcaster for websockets. It registers sessions/rooms and makes sure everyone in a particular session receives the network packages. This application should, obviously, live on an open port (using port-forwarding rules, for example) that is able to listen/send data to the external network.

The Multiplayer Configuration external application is an internal application to the user. It is used as a sidecar for the VR application to allow the user to configure externally to which server he wishes to connect to. The reason this was not performed inside the VR application is that it is challenging and tedious to type in VR.

The lattice format is parsed, providing a list of nodes with their subconcept-superconcept relations. Then, we calculate the longest node-chain we can find, which gives us the depth of the lattice. Having the depth of the lattice, we can create at each increment ($1,2,3,\dots ,n$) a circle around the Y axis. This circle will serve as a reference for position calculation later.

After all circles are created, we assign each node to its corresponding circle, based on its depth.

In this last step, depending on how many nodes we have on a circle, we have a step parameter that distributes nodes uniformly around its 360 angle. After this is achieved, we can simply calculate the nodes position relative to the circle centre (which, in this case, is the lattice centre on that plane) using sin and cos.

The module responsible for calculating the node position and move is the Move module, by using the following Algorithm 1:

Algorithm 1 Node position calculation.

1: max_chain_length = the maximum length of a chain 2: for current_length in max_chain_length do 3:     depth_nodes = find the nodes with depth current_length 4:     angle_deg = 20 5:     width_scale_factor = Math.clamp(length(depth_nodes), 1, 10) / 4 + 1 6:     for node in depth_nodes do 7:         node.position.x = sin(angle) + circle_base_with * width_scale_factor 8:         node.position.y = cos(angle) + circle_base_with * width_scale_factor 9:     end for 10:     angle += (360 / length(depth_nodes)) 11: end for

5. VR Enhanced Navigation at Work

We exemplify the capabilities of the VR FCA project in navigating complex data sets, using a more unusual data set, namely various properties of topological spaces. The data have been gathered from [16], and we refer to that work for a complete list of topologies and properties. From our experience, both as university staff and students, teaching mathematical notions can be sometimes difficult because of their abstractness and lack of visualisation. Moreover, the connections between various notions and concepts described in mathematics textbooks are hard to grasp for a beginner or even at an intermediate level and there is a constant need for study and practice in order to achieve mastery. Following the idea of gamifying the human–computer interaction and enhance it with new capabilities offered by VR technologies (such as fly, teleport, laser pinpoint, rotate, etc.), we have selected three different data sets from [16].

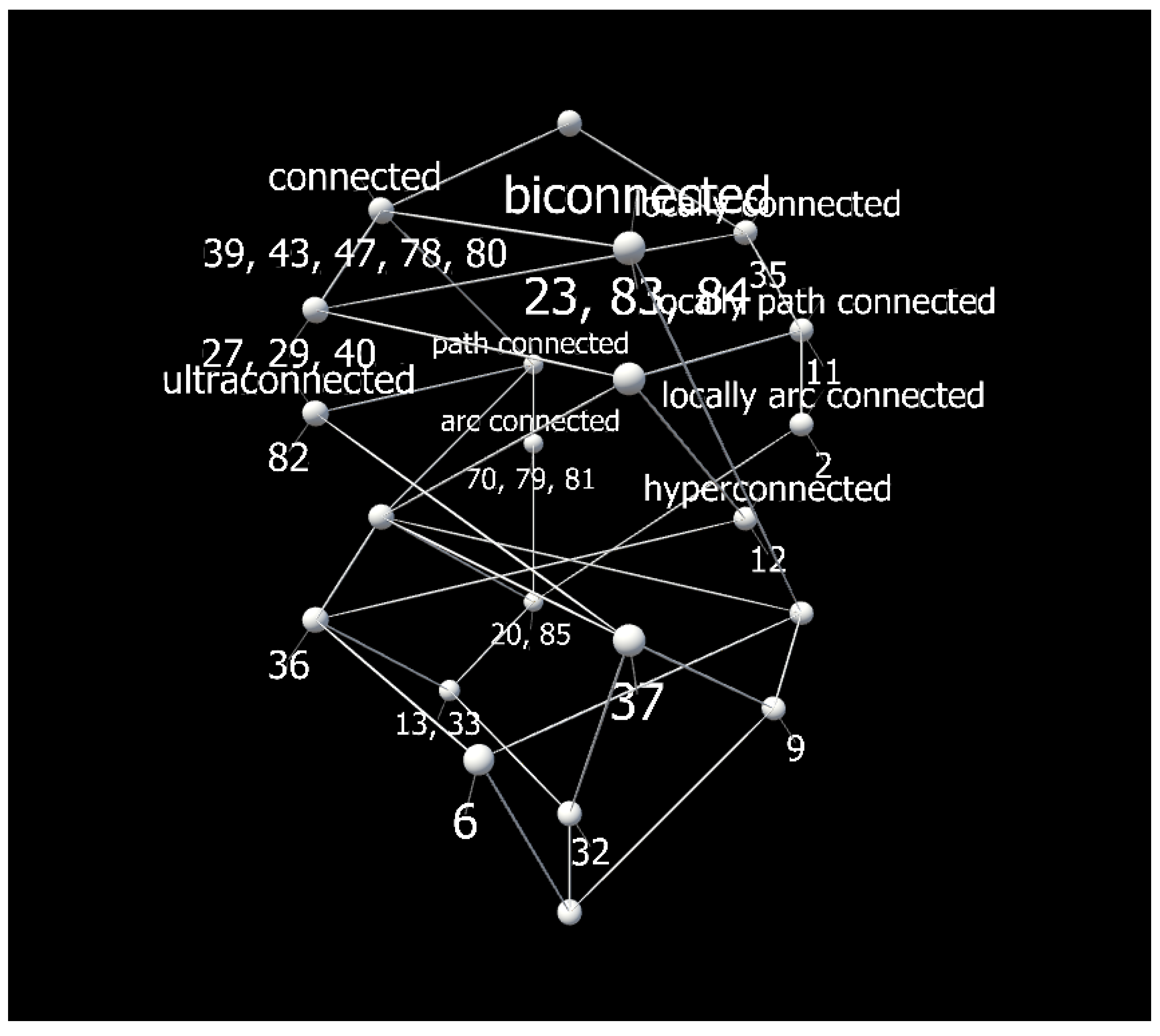
The first data set is the so-called Connectedness Chart, exemplifying various connectedness properties in topological spaces. The attributes are various connectedness properties, while the objects are topologies.

$C_1$: connected	$C_2$: path connected	$C_3$: arc connected
$C_4$: hyperconnected	$C_5$: ultraconnected	$C_6$: locally connected
$C_7$: locally path connected		$C_8$: locally arc connected
$C_9$: biconnected.

The 3D visualisation of the knowledge structure of

Table 1. Formal context of Connectedness Properties.

	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{C}}_6$	${\mathit{C}}_7$	${\mathit{C}}_8$	${\mathit{C}}_9$
$G_2$						x	x	x
$G_6$	x	x		x		x	x		x
$G_9$	x	x			x	x	x		x
$G_{11}$						x	x
$G_{12}$	x			x		x	x
$G_{13}$	x	x	x	x		x	x	x
$G_{20}$	x	x	x			x	x	x
$G_{23}$	x								x
$G_{27}$	x					x
$G_{29}$	x					x
$G_{32}$	x	x	x	x	x	x	x	x
$G_{33}$	x	x	x	x		x	x	x
$G_{35}$						x
$G_{36}$	x	x		x		x	x
$G_{37}$	x	x			x	x	x
$G_{39}$	x
$G_{40}$	x					x
$G_{43}$	x
$G_{47}$	x
$G_{70}$	x	x	x
$G_{78}$	x
$G_{79}$	x	x	x
$G_{80}$	x
$G_{81}$	x	x	x
$G_{82}$	x	x			x
$G_{83}$	x								x
$G_{84}$	x								x
$G_{85}$	x	x	x			x	x	x

is given in Figure 4.

While representing these 3D diagrams in 2D is somehow misleading for the entire immersive VR experience, short movies showing only rotations of these structures can be seen at https://www.cs.ubbcluj.ro/~fca/paper/ (accessed on 15 December 2021).

Teleporting, laser pointing, floating and flying through these structures, together with many-players experience, contribute to the deeper understanding of these structures and of the topic under study.

Let us explain briefly how all these features work. A user may be able to connect to a remote or local virtual room. When a virtual room is first launched up, the creator of the virtual room needs to select a conceptual structure that they want to inspect. After this is performed, any user can connect to this virtual room. All actions that can be performed, such as lattice rotating, node moving, scale are mapped to the controller. In the following, we have included an example for the controller from the HTC Vive headset, which we used for testing and experimenting (see Figure 5, where the footnote refers to the browsing capabilities of the system through the conceptual scales of lifetrack lattices).

All actions are handled on the client side. This means that, if you rotate or move the nodes around, this will be visible only for yourself. This has been conducted for multiple reasons:

• Performance wise, we have far less data to send/receive and handle.
• The user is free to explore without any distraction or constraint (such as being in the same stage of conceptual scale lattices).
• Solves most concurrency issues that we may run into.

For the multiplayer version, the question is what is shared between the players so that we can really call it multiplayer?

• Users have a voice chat that allows them to speak directly from the VR environment.
• Users can save nodes and map them to different colours, for easier identification. Saving a node also puts it into a shared menu, where other users can select a saved node and the node will be highlighted and focused.

We briefly include two more examples of topological properties and knowledge structures. The next one is the separation axioms chart. These properties play a major role in Topology, since they clarify, for instance, whether a net is convergent or not. For details about separation axioms and their definitions, see [16] or [17].

The 3D concept lattice of the formal context considered in

Table 2. Formal context of separation properties.

	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$	${\mathit{A}}_6$	${\mathit{A}}_7$	${\mathit{A}}_8$	${\mathit{A}}_9$	${\mathit{A}}_{10}$	${\mathit{A}}_{11}$	${\mathit{A}}_{12}$	${\mathit{A}}_{13}$	${\mathit{A}}_{14}$	${\mathit{A}}_{15}$
$O_1$					x	x	x	x
$O_2$	x
$O_3$	x						x	x
$O_4$	x	x
$O_5$	x	x	x	x	x	x	x	x	x	x	x	x	x	x
$O_6$	x	x	x	x	x	x	x	x	x	x	x	x	x	x	x
$O_7$							x	x
$O_8$
$O_9$	x						x
$O_{10}$	x	x	x						x
$O_{11}$	x	x	x	x							x
$O_{12}$	x	x	x
$O_{13}$	x	x	x	x					x
$O_{14}$	x	x	x	x	x	x			x	x	x	x
$O_{15}$	x	x	x	x	x	x	x		x	x	x	x	x
$O_{16}$	x	x	x	x					x		x
$O_{17}$	x	x	x	x	x				x	x
$O_{18}$	x	x	x	x	x				x	x	x
$O_{19}$	x	x	x	x

is given in Figure 6.

Compact sets play a central role in various fields of Mathematics. Different compactness properties are mentioned in [16].

The corresponding compactness properties chart is given by

Table 3. Formal context of compactness properties.

	${\mathit{A}}_{16}$	${\mathit{A}}_{17}$	${\mathit{A}}_{18}$	${\mathit{A}}_{19}$	${\mathit{A}}_{20}$	${\mathit{A}}_{21}$	${\mathit{A}}_{22}$	${\mathit{A}}_{23}$	${\mathit{A}}_{24}$	${\mathit{A}}_{25}$	${\mathit{A}}_{26}$	${\mathit{A}}_{27}$	${\mathit{A}}_{28}$
$O_{20}$		x	x				x	x	x	x	x	x	x
$O_{21}$							x	x				x	x
$O_{22}$		x	x			x	x	x	x	x	x	x
$O_{23}$		x	x				x		x	x	x	x
$O_{24}$							x			x		x
$O_{25}$	x	x	x	x	x	x	x	x	x	x	x	x
$O_{26}$	x	x	x	x	x	x	x	x	x			x
$O_{27}$	x	x	x	x	x	x	x	x	x	x
$O_{28}$			x
$O_{29}$			x			x
$O_{30}$		x	x							x
$O_{31}$		x	x							x	x	x	x
$O_{32}$			x							x	x	x	x
$O_{33}$				x	x	x	x	x				x
$O_{34}$	x	x	x	x	x	x	x	x	x
$O_{35}$				x	x	x
$O_{36}$		x	x			x	x		x	x	x	x
$O_{37}$			x							x		x
$O_{38}$		x	x							x	x	x
$O_{39}$							x	x		x		x
$O_{40}$			x							x	x	x
$O_{41}$										x		x
$O_{42}$												x
$O_{43}$							x	x
$O_{44}$
$O_{45}$	x	x	x	x		x	x	x	x	x
$O_{46}$				x		x	x	x
$O_{47}$	x	x	x	x	x	x	x	x	x	x		x
$O_{48}$												x	x

.

The compactness 3D chart in Figure 7 is quite complex and, with a bit of imagination, an immersive 3D VR experience of teleporting and flying through this structure can be imagined. For more, we refer to the above mentioned link.

6. Conclusions

In this paper, we have shown a design and implementation plan of a virtual reality tool that makes possible a VR immersive experience of 3D representation of knowledge structure, aiming a gamification of this experience.

As future work, we intend to extend the application in various ways, but the most important extensions are:

• Include attribute and concept exploration strategies.
• Visualisation Algorithms: Using genetic algorithms, the visualisation of the lattice can be greatly improved.
• Navigation Assistant: Defining what the user is looking for, an AI assistant could be helping the user find the desired node.