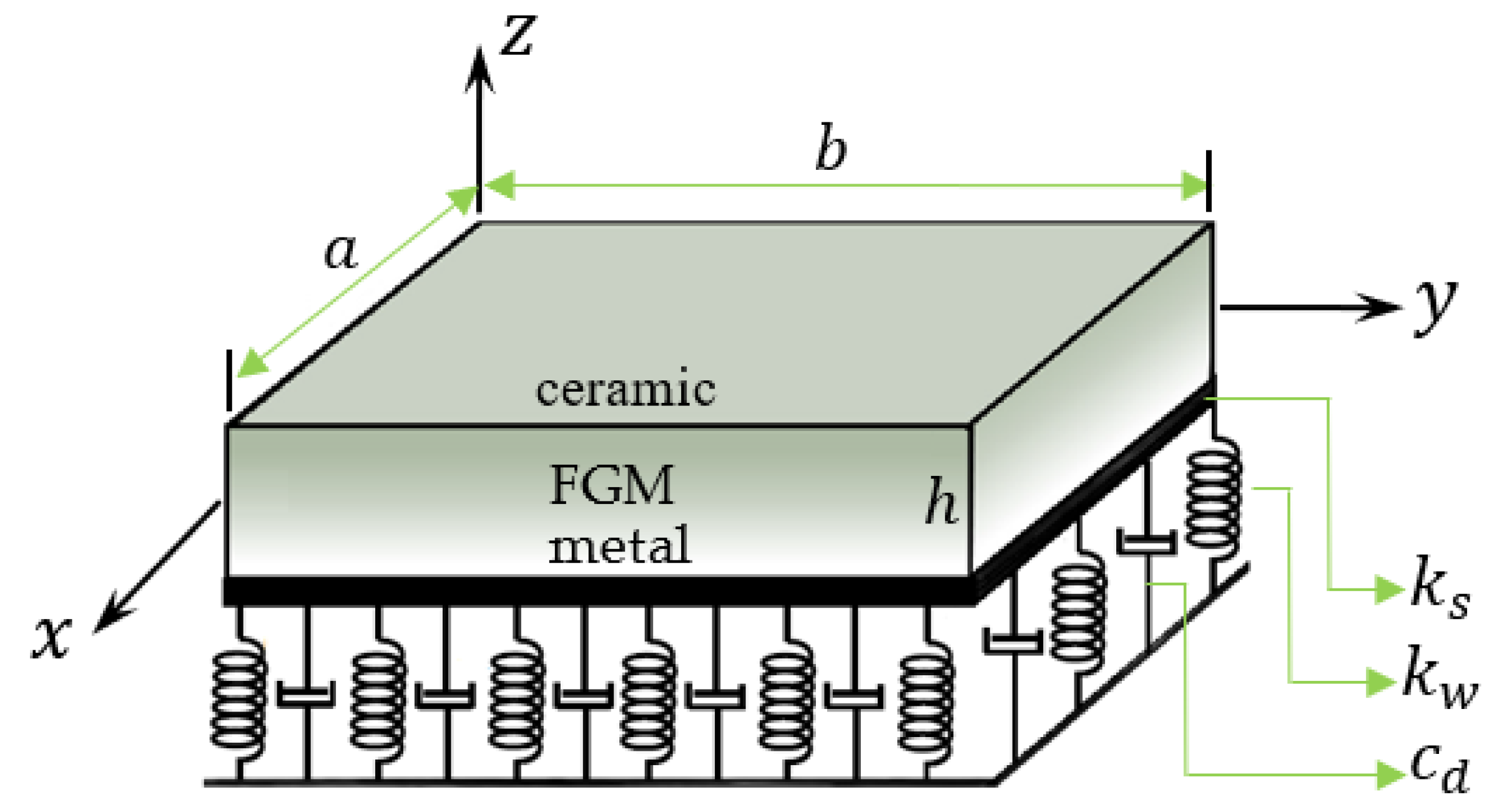
This section presents some numerical examples for vibration frequencies of isotropic and FG rectangular plates. The accuracy and efficiency of the present quasi-3D refined theory in predicting fundamental and natural frequencies of simply-supported plates are discussed. The results due to the present theory are compared with those found in the literature using various theories. Different material properties are assumed as follows:
3.3. Analysis of Isotropic Plates
In this section, the special case of homogeneous isotropic plates is analyzed.
Table 1,
Table 2,
Table 3 and
Table 4 present the results of the non-dimensional natural frequency obtained by the present quasi-3D theory for square plates. In
Table 1,
Table 2,
Table 3 and
Table 4, the non-dimensional natural frequencies and nondimensional coefficients of foundations are utilized as
in which
,
,
denote Young’s modulus, Poisson’s ratio, and density of the isotropic material.
Table 1 presents the natural frequencies of isotropic square plates due to the first eight modes. These frequencies are compared with the solutions of different authors: the 3D exact solutions by Leissa [
29], Zhou et al. [
30], Nagino et al. [
31]; the FSDT using differential quadrature element method (DQM) by Liu and Liew [
32]; and HDTs by Hosseini-Hashemi et al. [
33], Shufrin et al. [
34], Akavci [
35], and a quasi-3D hybrid type HSDT by Mantari et al. [
36].
Table 1.
Non-dimensional natural frequencies for isotropic square plates.
Table 1.
Non-dimensional natural frequencies for isotropic square plates.
| Theory | Mode |
|---|
| (1,1) | (1,2) | (2,1) | (2,2) | (1,3) | (3,1) | (2,3) | (3,2) |
|---|
| 1000 | Leissa [29] | 19.7392 | 49.3480 | 49.3480 | 78.9568 | 98.6960 | 98.6960 | 128.3021 | 128.3021 |
| Zhou et al. [30] | 19.7115 | 49.3470 | 49.3470 | 78.9528 | 98.6911 | 98.6911 | 128.3048 | 128.3048 |
| Akavci [35] | 19.7391 | 49.3476 | 49.3476 | 78.9557 | 98.6943 | 98.6943 | 128.3020 | 128.3020 |
| Mantari et al. [36] | 19.7396 | 49.3482 | 49.3482 | 78.9568 | 98.6956 | 98.6956 | 128.3036 | 128.3036 |
| Present | 19.73914 | 49.34760 | 49.34760 | 78.95574 | 98.69434 | 98.69434 | 128.30197 | 128.30197 |
| 100 | Leissa [29] | 19.7319 | 49.3027 | 49.3027 | 78.8410 | 98.5150 | 98.5150 | 127.9993 | 127.9993 |
| Nagino et al. [31] | 19.7320 | 49.3050 | 49.3050 | 78.8460 | 98.5250 | 98.5250 | 128.0100 | 128.0100 |
| Akavci [35] | 19.7322 | 49.3045 | 49.3045 | 78.8456 | 98.5223 | 98.5223 | 128.0120 | 128.0120 |
| Mantari et al. [36] | 19.7326 | 49.3055 | 49.3055 | 78.8475 | 98.5250 | 98.5250 | 128.0156 | 128.0156 |
| Present | 19.73231 | 49.30491 | 49.30491 | 78.84657 | 98.52386 | 98.52386 | 128.01415 | 128.01415 |
| 10 | Liu et al. [32] | 19.0584 | 45.4478 | 45.4478 | 69.7167 | 84.9264 | 84.9264 | 106.5154 | 106.5154 |
| Hosseini et al. [33] | 19.0653 | 45.4869 | 45.4869 | 69.8093 | 85.0646 | 85.0646 | 106.7350 | 106.7350 |
| Akavci [35] | 19.0850 | 45.5957 | 45.5957 | 70.0595 | 85.4315 | 85.4315 | 107.3040 | 107.3040 |
| Mantari et al. [36] | 19.0901 | 45.6200 | 45.6200 | 70.1083 | 85.4964 | 85.4964 | 107.3896 | 107.3896 |
| Present | 19.09028 | 45.62185 | 45.62185 | 70.11284 | 85.50305 | 85.50305 | 107.39973 | 107.39973 |
| 5 | Shufrin et al. [34] | 17.4524 | 38.1884 | 38.1884 | 55.2539 | 65.3130 | 65.3130 | 78.9864 | 78.9864 |
| Hosseini et al. [33] | 17.4523 | 38.1883 | 38.1883 | 55.2543 | 65.3135 | 65.3135 | 78.9865 | 78.9865 |
| Akavci [35] | 17.5149 | 38.4722 | 38.4722 | 55.8358 | 66.1207 | 66.1207 | 80.1637 | 80.1637 |
| Mantari et al. [36] | 17.5271 | 38.4991 | 38.4991 | 55.8410 | 66.0874 | 66.0874 | 80.0364 | 80.0364 |
| Present | 17.52821 | 38.50383 | 38.50383 | 55.84950 | 66.09809 | 66.09809 | 80.04976 | 80.04976 |
It is clear from
Table 1 that for the value of the side-to-thickness ratio (
), the first mode of the present frequency is identical to those given by Leissa [
29] and Akavci [
35] and has proximity with the one obtained by Mantari et al. [
36]. Additionally, the high modes of the present natural frequencies are identical to those given by Akavci [
35] and are very close to the ones obtained by Zhou et al. [
30], Leissa [
29], and Mantari et al. [
36] For the side-to-thickness ratio (
), it is noted that the results are slightly less than those predicted by Mantari et al. [
36] and slightly greater than those predicted by Leissa [
29], Nagino et al. [
31], and Akavci [
35]. For moderately thick plates (
), the present natural frequencies are very close to those obtained by Mantari et al. [
36] and slightly greater than those predicted by Liu et al. [
32], Hosseini et al. [
33], and Akavci [
35]. For thin plates (
), the present natural frequencies are close to those obtained by Akavci [
35] and Mantari et al. [
36]
In
Table 2,
Table 3 and
Table 4, the outcomes of the non-dimensional natural frequency
represented in Equation (34) for isotropic square plates resting on visco–Pasternak foundations are reported. The nondimensional coefficients of the three-parameter foundations are utilized as
The most important case is considered for isotropic square plates resting on the two-parameter Pasternak foundation. However, additional results for plates resting on three-parameter visco–Pasternak foundations are also included for future comparisons. Different values for the three-parameter coefficients
,
, and
are discussed.
Table 2.
Non-dimensional fundamental frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 2.
Non-dimensional fundamental frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, ).
| | Matsunaga [37] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| | | |
|---|
| 0 | 0 | 17.5260 | 17.4523 | 17.5271 | 17.52821 | --- | --- | --- |
| 10 | 17.7847 | 17.7248 | 17.7858 | 17.78691 | 17.80266 | 17.85029 | 17.93085 |
| 102 | 19.9528 | 20.0076 | 19.9613 | 19.96234 | 19.98001 | 20.03340 | 20.12372 |
| 103 | 34.3395 | 35.5039 | 34.7796 | 34.78009 | 34.81060 | 34.90277 | 35.05861 |
| 104 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 |
| 105 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 |
| 0 | 10 | 22.0429 | 22.2145 | 22.0707 | 22.07157 | 22.09109 | 22.15007 | 22.24983 |
| 10 | 22.2453 | 22.4286 | 22.2757 | 22.27657 | 22.29627 | 22.35578 | 22.45646 |
| 102 | 23.9830 | 24.2723 | 24.0401 | 24.04090 | 24.06214 | 24.12631 | 24.23485 |
| 103 | 36.6276 | 38.0650 | 37.2169 | 37.21732 | 37.24990 | 37.34833 | 37.51475 |
| 104 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 |
| 105 | 45.5260 | 45.5255 | 45.5260 | 45.52600 | 45.52600 | 45.52600 | 45.52600 |
Table 3.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
Table 3.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
| | Matsunaga [37] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| | | |
|---|
| 0 | 0 | 38.4827 | 38.1883 | 38.4991 | 38.50383 | --- | --- | --- |
| 10 | 38.5929 | 38.3098 | 38.6093 | 38.61403 | 38.75920 | 39.21005 | 40.01800 |
| 102 | 39.5669 | 39.3895 | 39.5860 | 39.59068 | 39.73930 | 40.20086 | 41.02792 |
| 103 | 47.8667 | 48.8772 | 48.1688 | 48.17300 | 48.35118 | 48.90436 | 49.89463 |
| 104 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 |
| 105 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 |
| 0 | 10 | 43.4816 | 43.7943 | 43.5741 | 43.57850 | 43.74104 | 44.24576 | 45.14976 |
| 10 | 43.5747 | 43.9009 | 43.6701 | 43.67455 | 43.83742 | 44.34317 | 45.24900 |
| 102 | 44.3994 | 44.8445 | 44.5241 | 44.52853 | 44.69434 | 45.20920 | 46.13126 |
| 103 | 51.6029 | 53.3580 | 52.2029 | 52.20676 | 52.39828 | 52.99275 | 54.05639 |
| 104 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 |
| 105 | 71.9829 | 71.9829 | 71.9829 | 71.98293 | 71.98293 | 71.98293 | 71.98293 |
The first three non-dimensional natural frequencies of a thicker square plate (
) resting on the elastic foundation are presented in
Table 2,
Table 3 and
Table 4. The first mode (
) fundamental frequencies
are represented in
Table 2 while natural frequencies
and
are presented in
Table 3 and
Table 4, respectively. In such tables, the frequencies are compared with the refined shear deformation theory given by Thai and Choi [
38], the HSDT proposed by Matsunaga [
37], and a quasi-3D hybrid type HSDT by Mantari et al. [
36]
Table 4.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
Table 4.
Non-dimensional natural frequencies for isotropic square plates resting on Visco-Winkler-Pasternak foundations (, , ).
| | Matsunaga [37] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| | | |
|---|
| 0 | 0 | 65.9961 | 65.3135 | 66.0874 | 66.09809 | --- | --- | --- |
| 10 | 66.0569 | 65.3841 | 66.1481 | 66.15875 | 66.40586 | 67.17631 | 68.56834 |
| 102 | 66.5995 | 66.0138 | 66.6907 | 66.70143 | 66.95005 | 67.72517 | 69.12547 |
| 103 | 71.5577 | 72.0036 | 71.8192 | 71.83050 | 72.09271 | 72.90970 | 74.38380 |
| 104 | 97.4964 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 |
| 105 | 101.7992 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 |
| 0 | 10 | 71.4914 | 71.9198 | 71.7485 | 71.75974 | 72.02177 | 72.83822 | 74.31135 |
| 10 | 71.5423 | 71.9839 | 71.8028 | 71.81402 | 72.07618 | 72.89304 | 74.36692 |
| 102 | 71.9964 | 72.5554 | 72.2886 | 72.29990 | 72.56328 | 73.38389 | 74.86433 |
| 103 | 76.1848 | 78.0290 | 76.9124 | 76.92383 | 77.19813 | 78.05223 | 79.59112 |
| 104 | 99.0187 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 |
| 105 | 101.7992 | 101.7990 | 101.7992 | 101.79924 | 101.79924 | 101.79924 | 101.79924 |
The fundamental frequencies in
Table 2 are close to those obtained by Matsunaga [
37] and Mantari et al. [
36] and slightly greater than those of Thai and Choi [
38]. It is clear that the frequencies increase as the two-parameter coefficients increase. For higher values of the first parameter coefficient
, the frequencies still have the same values. The inclusion of the third-parameter coefficient
is also discussed here. It is interesting to see that the frequencies increase with the increase in the value of
.
The natural frequencies in
Table 3 and
Table 4 are also closer to those obtained by Matsunaga [
37] and Mantari et al. [
36] and slightly greater than those of Thai and Choi [
38]. Once again, the frequencies increase as the three-parameter coefficients increase. For higher values of the first parameter coefficient
the frequencies still have the same values. It is to be noted that in
Table 2,
Table 3 and
Table 4, as the mode
increases, the frequency increases irrespective of the values of the three-parameter coefficients.
3.4. Analysis of FG Plates
Here, the non-dimensional fundamental frequencies of FG square plates are discussed in
Table 5 and
Table 6. The FG plates are fabricated of different materials. The mechanical properties of such materials are given in Equations (31)–(33). The non-dimensional frequency is utilized as
The non-dimensional fundamental frequencies
for thicker (
) Aluminum-Zirconia (Al/ZrO
2) FG square plates without elastic foundations are compared with the corresponding results in
Table 5. Additional results for plates resting on Visco-Winkler-Pasternak foundations are also presented. The nondimensional coefficients of the three-parameter foundations are utilized as
In
Table 5, the fundamental frequencies for three values of the FG power-law index
are computed and compared with the 3D exact solution by Vel et al. [
39], quasi-3D sinusoidal and hyperbolic HSDTs by Neves et al. [
40,
41], a quasi-3D hybrid type HSDT by Mantari et al. [
36], and HSDTs by Akavci [
35], Hosseini-Hashemi et al. [
32], and Matsunaga [
42]. The frequencies increase with the increase in the FG power-law index
. Neglecting the three-parameter foundation coefficients shows that the present frequencies are identical to those of Mantari et al. [
36]. In addition, the present frequencies agree well with the HSDTs’ frequencies. For the sake of future comparison, dome frequencies for plates on the Visco-Winkler-Pasternak foundation are also included in the same table. Once again, the frequencies increase with the increase in the three-parameter foundation coefficients.
Table 5.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates resting on Visco-Winkler-Pasternak foundations ().
Table 5.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates resting on Visco-Winkler-Pasternak foundations ().
| Theory | |
|---|
| 2 | 3 | 5 |
|---|
| Vel and Batra [39] | 0.2197 | 0.2211 | 0.2225 |
| Neves et al. () [40] | 0.2189 | 0.2202 | 0.2215 |
| Neves et al. () [40] | 0.2198 | 0.2212 | 0.2225 |
| Neves et al. () [41] | 0.2191 | 0.2205 | 0.2220 |
| Neves et al. () [41] | 0.2201 | 0.2216 | 0.2230 |
| Hosseini-Hashemi et al. [33] | 0.2264 | 0.2276 | 0.2291 |
| Akavci [35] | 0.2263 | 0.2268 | 0.2277 |
| Matsunaga [42] | 0.2264 | 0.2270 | 0.2280 |
| Mantari et al. [36] | 0.2285 | 0.2290 | 0.2295 |
| Present | | 0.22848 | 0.22901 | 0.22952 |
| , , | 0.23062 | 0.23130 | 0.23199 |
| , , | 0.26937 | 0.27256 | 0.27610 |
| , , | 0.26976 | 0.27301 | 0.27664 |
| , , | 0.27095 | 0.27438 | 0.27825 |
| , , | 0.28694 | 0.29132 | 0.29627 |
The non-dimensional fundamental frequencies
for Aluminum-Alumina (Al/Al
2O
3) FG rectangular plates are presented in
Table 6. The frequencies are computed for four different values of the FG power-law index
and compared with a quasi-3D hybrid type HSDT by Mantari et al. [
36] and a 3D exact solution proposed by Jin et al. [
43]. Generally, the frequencies decrease with the increase in the FG power-law index
. Additionally, the frequencies increase as both
and
decrease. Neglecting the three-parameter foundation coefficients shows that the present frequencies give good accuracy with those in [
36] and [
43] for square plates (
). However, for rectangular plates (
), the present frequencies are very close to those of Mantari et al. [
36] and slightly greater than those of Jin et al. [
43] For the sake of future comparison, some frequencies for plates on the Visco-Winkler-Pasternak foundation are also included in
Table 6. The non-dimensional coefficients of the three-parameter foundations are given in Equation (37). For all cases studied, the frequencies increase with the increase in the three-parameter foundation coefficients.
Table 6.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations.
Table 6.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations.
| | Theory | |
|---|
| 0 | 1 | 2 | 5 |
|---|
| 1 | 10 | Jin et al. [43] | 0.1135 | 0.0870 | 0.0789 | 0.0741 |
| Mantari et al. [36] | 0.1135 | 0.0882 | 0.0806 | 0.0755 |
| Present | | 0.11350 | 0.08818 | 0.08057 | 0.07553 |
| , , | 0.11627 | 0.09230 | 0.08533 | 0.08090 |
| , , | 0.11889 | 0.09613 | 0.08969 | 0.08578 |
| , , | 0.12152 | 0.09991 | 0.09397 | 0.09051 |
| 5 | Jin et al. [43] | 0.4169 | 0.3222 | 0.2905 | 0.2676 |
| Mantari et al. [36] | 0.4168 | 0.3260 | 0.2961 | 0.2722 |
| Present | | 0.41685 | 0.32605 | 0.29613 | 0.27221 |
| , , | 0.42816 | 0.34278 | 0.31556 | 0.29463 |
| , , | 0.43885 | 0.35824 | 0.33329 | 0.31481 |
| , , | 0.44956 | 0.37344 | 0.35056 | 0.33425 |
| 2 | Jin et al. [43] | 1.8470 | 1.4687 | 1.3095 | 1.1450 |
| Mantari et al. [36] | 1.8505 | 1.4774 | 1.3219 | 1.1551 |
| Present | | 1.85081 | 1.47762 | 1.32213 | 1.15544 |
| , , | 1.93506 | 1.59673 | 1.46375 | 1.33166 |
| , , | 2.01192 | 1.70066 | 1.58405 | 1.47548 |
| , , | 2.08633 | 1.79759 | 1.69386 | 1.60293 |
| 2 | 10 | Jin et al. [43] | 0.0719 | 0.0550 | 0.0499 | 0.0471 |
| Mantari et al. [36] | 0.0718 | 0.0557 | 0.0510 | 0.0479 |
| Present | | 0.07181 | 0.05573 | 0.05097 | 0.04794 |
| , , | 0.07614 | 0.06209 | 0.05824 | 0.05605 |
| , , | 0.07711 | 0.06348 | 0.05981 | 0.05778 |
| , , | 0.08115 | 0.06912 | 0.06611 | 0.06466 |
| 5 | Jin et al. [43] | 0.2713 | 0.2088 | 0.1888 | 0.1754 |
| Mantari et al. [36] | 0.2712 | 0.2115 | 0.1926 | 0.1786 |
| Present | | 0.27124 | 0.21151 | 0.19262 | 0.17861 |
| , , | 0.28875 | 0.23709 | 0.22197 | 0.21183 |
| , , | 0.29268 | 0.24266 | 0.22828 | 0.21885 |
| , , | 0.30894 | 0.26520 | 0.25347 | 0.24662 |
| 2 | Jin et al. [43] | 0.9570 | 0.7937 | 0.7149 | 0.6168 |
| Mantari et al. [36] | 1.3040 | 1.0346 | 0.9293 | 0.8236 |
| Present | | 1.30422 | 1.03469 | 0.92945 | 0.82385 |
| , , | 1.42513 | 1.20475 | 1.12760 | 1.06040 |
| , , | 1.45155 | 1.24029 | 1.16792 | 1.10679 |
| , , | 1.55824 | 1.37906 | 1.32259 | 1.28071 |
The non-dimensional fundamental frequencies
for Aluminum-Zirconia (Al/ZrO
2) FG square plates resting on Visco-Winkler-Pasternak foundations are reported in
Table 7. When
, the frequency parameter tends to
. The frequencies, without the three-parameter foundation coefficients, are compared with the 3D exact solutions proposed by Vel and Batra [
39], HSDTs proposed by Akavci [
35], a quasi-3D hybrid type HSDT by Mantari et al. [
36], and Matsunaga [
42]. In general, the frequencies increase as both
and
increase. The present frequencies are compared well with those reported in [
36]. Additionally, the frequencies approach to the corresponding solutions obtained in [
35,
39,
42]. If the Visco-Winkler-Pasternak foundations are taken into account, the frequencies increase. Once again, the non-dimensional coefficients of the three-parameter foundations are given in Equation (37).
Table 7.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates on Visco-Winkler-Pasternak foundations.
Table 7.
Non-dimensional fundamental frequencies for Al/ZrO2 FG square plates on Visco-Winkler-Pasternak foundations.
| | Vel and Batra [39] | Akavci [35] | Matsunaga [42] | Mantari et al. [36] | |
|---|
| (0,0,0) | (10,0,0.1) | (0,10,0.1) | (10,10,0.1) |
|---|
| 0 * | | 4.6582 | 4.6569 | 4.6582 | 4.6601 | 4.66072 | 4.68987 | 5.20264 | 5.22844 |
| 10 | 5.7769 | 5.7754 | 5.7769 | 5.7769 | 5.77698 | 5.80392 | 6.28692 | 6.31166 |
| 1 | 5 | 5.4806 | 5.7110 | 5.7123 | 5.7501 | 5.75043 | 5.79726 | 6.61170 | 6.65231 |
| 10 | 5.9609 | 6.1924 | 6.1932 | 6.2365 | 6.23656 | 6.28244 | 7.08625 | 7.12659 |
| 20 | 6.1076 | 6.3388 | 6.3390 | 6.3842 | 6.38419 | 6.42989 | 7.23208 | 7.27240 |
| 2 | 5 | 5.4923 | 5.6593 | 5.6599 | 5.7115 | 5.71197 | 5.76558 | 6.68866 | 6.73430 |
| 3 | 5 | 5.5285 | 5.6718 | 5.6757 | 5.7246 | 5.72519 | 5.78258 | 6.76582 | 6.81423 |
| 5 | 5 | 5.5632 | 5.6941 | 5.7020 | 5.7376 | 5.73811 | 5.79984 | 6.85123 | 6.90276 |
In
Table 8,
Table 9 and
Table 10, the non-dimensional natural frequencies
for Aluminum-Alumina (Al/Al
2O
3) FG rectangular plates (
) resting on Visco-Winkler-Pasternak foundations are reported. Three values of the side-to-thickness ratio
,
,
are considered. The non-dimensional frequency and the non-dimensional coefficients of the three-parameter foundations are utilized as
Table 8,
Table 9 and
Table 10 present the first four non-dimensional natural frequencies
,
,
and
of FG plates for various values of the FG power-law index
. Firstly, the frequencies increase as both the mode number and side-to-thickness ratio
increase and as the FG power-law index
decreases. For
, the present frequencies are compared with the corresponding ones due to the HSDTs proposed by Akavci [
35], Thai et al. [
44], a quasi-3D hybrid type HSDT by Mantari et al. [
36], and the FSDT utilized by Hosseini-Hashemi et al. [
3] The present frequencies are very close to those in [
35,
36] and slightly greater than those in [
3,
44]. Furthermore, it is shown that for different values of
the present frequencies get good agreements with the other theories. The frequencies, with the inclusion of the three-parameter foundation coefficients, are presented for future comparisons. The results represent benchmarks to help other investigators to assure their results for plates resting on three-parameter viscoelastic foundations. It is obvious that the frequency slightly increases when adding the three parameters of viscoelastic foundations one by one. The maximum frequencies occurred when all foundation coefficients are included.
Table 8.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
Table 8.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |
|---|
| 0 | 1 | 2 | 5 | 8 | 10 |
|---|
| (1,1) | Akavci [35] | 3.4495 | 2.6529 | 2.3989 | 2.2275 | 2.1724 | 2.1455 |
| Thai et al. [44] | 3.4412 | 2.6475 | 2.3949 | 2.2272 | 2.1697 | 2.1407 |
| Hosseini et al. [3] | 3.4409 | 2.6473 | 2.4017 | 2.2528 | 2.1985 | 2.1677 |
| Mantari et al. [36] | 3.4513 | 2.6913 | 2.4508 | 2.2725 | 2.2032 | 2.1689 |
| Present | | 3.45145 | 2.69138 | 2.45102 | 2.27273 | 2.20328 | 2.16887 |
| , , | 3.57401 | 2.87249 | 2.66011 | 2.51080 | 2.45332 | 2.42438 |
| , , | 4.74470 | 4.43132 | 4.37556 | 4.37628 | 4.37573 | 4.37110 |
| , , | 4.83425 | 4.54296 | 4.49522 | 4.50341 | 4.50555 | 4.50200 |
| (1,2) | Akavci [35] | 5.3003 | 4.0906 | 3.6900 | 3.3952 | 3.3031 | 3.2626 |
| Thai et al. [44] | 5.2813 | 4.0781 | 3.6805 | 3.3938 | 3.2964 | 3.2514 |
| Hosseini et al. [3] | 5.2802 | 4.0773 | 3.6953 | 3.4492 | 3.3587 | 3.3094 |
| Mantari et al. [36] | 5.3039 | 4.1487 | 3.7677 | 3.4633 | 3.3484 | 3.2955 |
| Present | | 5.30428 | 4.14891 | 3.76818 | 3.46376 | 3.34863 | 3.29565 |
| , , | 5.38275 | 4.26554 | 3.90401 | 3.62103 | 3.51478 | 3.46565 |
| , , | 6.67940 | 6.03846 | 5.88419 | 5.81358 | 5.78825 | 5.77233 |
| , , | 6.74143 | 6.11832 | 5.97100 | 5.90714 | 5.88422 | 5.86923 |
| (1,3) | Akavci [35] | 8.1179 | 6.2950 | 5.6614 | 5.1479 | 4.9921 | 4.9313 |
| Thai et al. [44] | 8.0749 | 6.2663 | 5.6390 | 5.1425 | 4.9758 | 4.9055 |
| Hosseini et al. [3] | 8.0710 | 6.2636 | 5.6695 | 5.2579 | 5.1045 | 5.0253 |
| Mantari et al. [36] | 8.1244 | 6.3814 | 5.7751 | 5.2484 | 5.0560 | 4.9747 |
| Present | | 8.12516 | 6.38194 | 5.77596 | 5.24934 | 5.05661 | 4.97515 |
| , , | 8.17497 | 6.45589 | 5.86279 | 5.35193 | 5.16569 | 5.08687 |
| , , | 9.58143 | 8.41316 | 8.08122 | 7.86334 | 7.78824 | 7.75204 |
| , , | 9.62310 | 8.46823 | 8.14203 | 7.93018 | 7.85721 | 7.82177 |
| (2,1) | Akavci [35] | 10.1828 | 7.9209 | 7.1105 | 6.4181 | 6.2111 | 6.1355 |
| Thai et al. [44] | 10.1164 | 7.8762 | 7.0751 | 6.4074 | 6.1846 | 6.0954 |
| Hosseini et al. [3] | 9.7416 | 7.8711 | 7.1189 | 6.5749 | 5.9062 | 5.7518 |
| Mantari et al. [36] | 10.1907 | 8.0264 | 7.2479 | 6.5397 | 6.2856 | 6.1833 |
| Present | | 10.19182 | 8.02721 | 7.24906 | 6.54102 | 6.28651 | 6.18403 |
| , , | 10.23084 | 8.08500 | 7.31724 | 6.62262 | 6.37363 | 6.27329 |
| , , | 11.69616 | 10.13547 | 9.65993 | 9.31233 | 9.19418 | 9.14170 |
| , , | 11.72947 | 10.17994 | 9.70947 | 9.36749 | 9.25130 | 9.19949 |
Table 9.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
Table 9.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |
|---|
| 0 | 1 | 2 | 5 | 8 | 10 |
|---|
| (1,1) | Akavci [35] | 3.6542 | 2.7952 | 2.5376 | 2.3915 | 2.3418 | 2.3124 |
| Thai et al. [44] | 3.6518 | 2.7937 | 2.5364 | 2.3916 | 2.3411 | 2.3110 |
| Hosseini et al. [3] | 3.6518 | 2.7937 | 2.5386 | 2.3998 | 2.3504 | 2.3197 |
| Mantari et al. [36] | 3.6549 | 2.8365 | 2.5943 | 2.4398 | 2.3761 | 2.3398 |
| Present | | 3.65486 | 2.83651 | 2.59442 | 2.43983 | 2.37599 | 2.33961 |
| , , | 3.77600 | 3.01640 | 2.80120 | 2.67192 | 2.61867 | 2.58757 |
| , , | 4.94508 | 4.58507 | 4.52571 | 4.53573 | 4.53665 | 4.53077 |
| , , | 5.03519 | 4.69835 | 4.64720 | 4.66450 | 4.66813 | 4.66344 |
| (1,2) | Akavci [35] | 5.7754 | 4.4231 | 4.0118 | 3.7682 | 3.6864 | 3.6403 |
| Thai et al. [44] | 5.7694 | 4.4192 | 4.0090 | 3.7682 | 3.6846 | 3.6368 |
| Hosseini et al. [3] | 5.7693 | 4.4192 | 4.0142 | 3.7881 | 3.7072 | 3.6580 |
| Mantari et al. [36] | 5.7769 | 4.4881 | 4.1008 | 3.8443 | 3.7401 | 3.6827 |
| Present | | 5.77698 | 4.48818 | 4.10112 | 3.84448 | 3.74004 | 3.68252 |
| , , | 5.85372 | 4.60305 | 4.23389 | 3.99463 | 3.89754 | 3.84363 |
| , , | 7.13799 | 6.38008 | 6.21360 | 6.16032 | 6.13672 | 6.11716 |
| , , | 7.20008 | 6.46117 | 6.30177 | 6.25482 | 6.23361 | 6.21512 |
| (1,3) | Akavci [35] | 9.2029 | 7.0612 | 6.3959 | 5.9766 | 5.8388 | 5.7662 |
| Thai et al. [44] | 9.1880 | 7.0515 | 6.3886 | 5.9765 | 5.8341 | 5.7575 |
| Hosseini et al. [3] | 9.1876 | 7.0512 | 6.4015 | 6.0247 | 5.8887 | 5.8086 |
| Mantari et al. [36] | 9.2066 | 7.1643 | 6.5363 | 6.0976 | 5.9231 | 5.8315 |
| Present | | 9.20678 | 7.16448 | 6.53682 | 6.09800 | 5.92308 | 5.83137 |
| , , | 9.25458 | 7.23620 | 6.62003 | 6.19285 | 6.02286 | 5.93351 |
| , , | 10.62513 | 9.17828 | 8.80991 | 8.61977 | 8.54454 | 8.49887 |
| , , | 10.66630 | 9.23397 | 8.87138 | 8.68657 | 8.61339 | 8.56863 |
| (2,1) | Akavci [35] | 11.8560 | 9.1093 | 8.2428 | 7.6738 | 7.4892 | 7.3965 |
| Thai et al. [44] | 11.8315 | 9.0933 | 8.2309 | 7.6731 | 7.4813 | 7.3821 |
| Hosseini et al. [3] | 11.8310 | 9.0928 | 8.2515 | 7.7505 | 7.5688 | 7.4639 |
| Mantari et al. [36] | 11.8616 | 9.2416 | 8.4222 | 7.8291 | 7.5963 | 7.4783 |
| Present | | 11.86203 | 9.24189 | 8.42299 | 7.82973 | 7.59651 | 7.47829 |
| , , | 11.89892 | 9.29724 | 8.48733 | 7.90347 | 7.67423 | 7.55787 |
| , , | 13.30715 | 11.31242 | 10.77355 | 10.45683 | 10.33484 | 10.26714 |
| , , | 13.33967 | 11.35714 | 10.82331 | 10.51139 | 10.39125 | 10.32437 |
Table 10.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 10.
Non-dimensional natural frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
| Mode | Theory | |
|---|
| 0 | 1 | 2 | 5 | 8 | 10 |
|---|
| (1,1) | Akavci [35] | 3.7129 | 2.8357 | 2.5774 | 2.4402 | 2.3924 | 2.3623 |
| Thai et al. [44] | 3.7123 | 2.8352 | 2.5771 | 2.4403 | 2.3923 | 2.3619 |
| Hosseini et al. [3] | 3.7123 | 2.8352 | 2.5777 | 2.4425 | 2.3948 | 2.3642 |
| Mantari et al. [36] | 3.7132 | 2.8777 | 2.6354 | 2.4892 | 2.4277 | 2.3908 |
| Present | | 3.71313 | 2.87770 | 2.63557 | 2.48923 | 2.42750 | 2.39055 |
| , , | 3.83394 | 3.05727 | 2.84172 | 2.71973 | 2.66821 | 2.63648 |
| , , | 5.00322 | 4.62897 | 4.56905 | 4.58347 | 4.58523 | 4.57888 |
| , , | 5.09349 | 4.74266 | 4.69098 | 4.71261 | 4.71708 | 4.71193 |
| (1,2) | Akavci [35] | 5.9215 | 4.5238 | 4.1108 | 3.8883 | 3.8112 | 3.7632 |
| Thai et al. [44] | 5.9199 | 4.5228 | 4.1100 | 3.8884 | 3.8107 | 3.7622 |
| Hosseini et al. [3] | 5.9198 | 4.5228 | 4.1115 | 3.8939 | 3.8170 | 3.7681 |
| Mantari et al. [36] | 5.9220 | 4.5909 | 4.2032 | 3.9665 | 3.8672 | 3.8084 |
| Present | | 5.92192 | 4.59085 | 4.20342 | 3.96649 | 3.86700 | 3.80806 |
| , , | 5.99822 | 4.70524 | 4.33538 | 4.11474 | 4.02212 | 3.96672 |
| , , | 7.28089 | 6.48489 | 6.31643 | 6.27436 | 6.25285 | 6.23193 |
| , , | 7.34305 | 6.56631 | 6.40495 | 6.36905 | 6.34989 | 6.33007 |
| (1,3) | Akavci [35] | 9.5711 | 7.3159 | 6.6453 | 6.2759 | 6.1488 | 6.0715 |
| Thai et al. [44] | 9.5669 | 7.3132 | 6.6433 | 6.2760 | 6.1476 | 6.0690 |
| Hosseini et al. [3] | 9.5668 | 7.3132 | 6.6471 | 6.2903 | 6.1639 | 6.0843 |
| Mantari et al. [36] | 9.5723 | 7.4242 | 6.7942 | 6.4023 | 6.2391 | 6.1440 |
| Present | | 9.57223 | 7.42418 | 6.79463 | 6.40232 | 6.23878 | 6.14351 |
| , , | 9.61945 | 7.49521 | 6.87676 | 6.49490 | 6.33580 | 6.24279 |
| , , | 10.98422 | 9.43713 | 9.06263 | 8.90094 | 8.83088 | 8.78146 |
| , , | 11.02533 | 9.49302 | 9.124280 | 8.96765 | 8.89955 | 8.85106 |
| (2,1) | Akavci [35] | 12.4633 | 9.5307 | 8.6542 | 8.1634 | 7.9954 | 7.8950 |
| Thai et al. [44] | 12.4562 | 9.5261 | 8.6509 | 8.1636 | 7.9934 | 7.8909 |
| Hosseini et al. [3] | 12.4560 | 9.5261 | 8.6572 | 8.1875 | 8.0207 | 7.9166 |
| Mantari et al. [36] | 12.4652 | 9.6715 | 8.8478 | 8.3279 | 8.1127 | 7.9888 |
| Present | | 12.46522 | 9.67154 | 8.84835 | 8.32803 | 8.11232 | 7.98825 |
| , , | 12.50143 | 9.72605 | 8.91143 | 8.39926 | 8.18701 | 8.06469 |
| , , | 13.89984 | 11.73763 | 11.18768 | 10.91733 | 10.80357 | 10.72952 |
| , , | 13.93224 | 11.78246 | 11.23750 | 10.97160 | 10.85959 | 10.78637 |
Table 11,
Table 12,
Table 13 and
Table 14 present the non-dimensional fundamental frequencies for Aluminum-Alumina (Al/Al
2O
3) FG rectangular plates resting on visco–Pasternak foundations (
,
). Several values of the FG power-law index
, aspect ratio
, and side-to-thickness ratio
are considered. In fact, there is no foundation in
Table 11, and the inclusion of one-by-one elastic foundation is made in
Table 12,
Table 13 and
Table 14. In such tables, the inclusion of the third-parameter coefficient
is also discussed. The non-dimensional frequency and the non-dimensional third coefficient of the viscoelastic foundations are utilized as
and the other non-dimensional coefficients of the two-parameter foundations are given in Equation (37). In the absence of the third coefficient of the viscoelastic foundations
, the present frequencies are compared with the HSDTs proposed by Thai and Choi [
38], Akavci [
35], and a quasi-3D hybrid type HSDT by Mantari et al. [
36]
Table 11.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
Table 11.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
| | | Akavci [35] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| 0.5 | 5 | 1 | 5.2122 | 5.2016 | 5.2875 | 5.28772 |
| 5 | 4.3763 | 4.3757 | 4.4648 | 4.46520 |
| 10 | 4.2153 | 4.2058 | 4.2611 | 4.26116 |
| 10 | 1 | 5.4918 | 5.4887 | 5.5728 | 5.57286 |
| 5 | 4.6986 | 4.6987 | 4.7934 | 4.79350 |
| 10 | 4.5432 | 4.5404 | 4.5969 | 4.59661 |
| 20 | 1 | 5.5712 | 5.5704 | 5.6538 | 5.65379 |
| 5 | 4.7943 | 4.7943 | 4.8906 | 4.89057 |
| 10 | 4.6411 | 4.6404 | 4.6971 | 4.69669 |
| 1 | 5 | 1 | 8.0368 | 8.0122 | 8.1509 | 8.15131 |
| 5 | 6.6705 | 6.6678 | 6.8043 | 6.80521 |
| 10 | 6.4099 | 6.3879 | 6.4746 | 6.47492 |
| 10 | 1 | 8.6899 | 8.6824 | 8.8178 | 8.81788 |
| 5 | 7.4033 | 7.4034 | 7.5529 | 7.55319 |
| 10 | 7.1521 | 7.1453 | 7.2353 | 7.23501 |
| 20 | 1 | 8.8879 | 8.8859 | 9.0196 | 9.01959 |
| 5 | 7.6393 | 7.6394 | 7.7929 | 7.79291 |
| 10 | 7.3934 | 7.3916 | 7.4823 | 7.48166 |
| 2 | 5 | 1 | 17.8289 | 17.7148 | 18.0607 | 18.06273 |
| 5 | 14.3625 | 14.3312 | 14.6274 | 14.63068 |
| 10 | 13.7120 | 13.6095 | 13.8083 | 13.81014 |
| 10 | 1 | 20.8487 | 20.8063 | 21.1501 | 21.15090 |
| 5 | 17.5051 | 17.5028 | 17.8593 | 17.86082 |
| 10 | 16.8613 | 16.8232 | 17.0445 | 17.04463 |
| 20 | 1 | 21.9670 | 21.9548 | 22.2914 | 22.29144 |
| 5 | 18.7946 | 18.7950 | 19.1737 | 19.17401 |
| 10 | 18.1727 | 18.1616 | 18.3877 | 18.38645 |
Table 12.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco-Winkler foundations (, ).
Table 12.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco-Winkler foundations (, ).
| | | Akavci [35] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| |
|---|
| 0.5 | 5 | 1 | 5.8746 | 5.8654 | 5.9257 | 5.92588 | 5.92620 |
| 5 | 5.2360 | 5.2355 | 5.2934 | 5.29366 | 5.29417 |
| 10 | 5.1288 | 5.1212 | 5.1467 | 5.14660 | 5.14722 |
| 10 | 1 | 6.1393 | 6.1366 | 6.2077 | 6.20770 | 6.20801 |
| 5 | 5.5276 | 5.5277 | 5.6038 | 5.60384 | 5.60430 |
| 10 | 5.4199 | 5.4176 | 5.4596 | 5.45931 | 5.45987 |
| 20 | 1 | 6.2152 | 6.2144 | 6.2883 | 6.28824 | 6.28829 |
| 5 | 5.6156 | 5.6157 | 5.6969 | 5.69685 | 5.69692 |
| 10 | 5.5087 | 5.5080 | 5.5545 | 5.55415 | 5.55422 |
| 1 | 5 | 1 | 8.4748 | 8.4517 | 8.5671 | 8.56752 | 8.56801 |
| 5 | 7.2560 | 7.2534 | 7.3618 | 7.36260 | 7.36336 |
| 10 | 7.0373 | 7.0175 | 7.0758 | 7.07594 | 7.07683 |
| 10 | 1 | 9.1107 | 9.1035 | 9.2282 | 9.22829 | 9.22876 |
| 5 | 7.9520 | 7.9521 | 8.0866 | 8.08681 | 8.08751 |
| 10 | 7.7356 | 7.7293 | 7.8067 | 7.80636 | 7.80720 |
| 20 | 1 | 9.3044 | 9.3025 | 9.4292 | 9.42918 | 9.42925 |
| 5 | 8.1789 | 8.1790 | 8.3212 | 8.32122 | 8.32132 |
| 10 | 7.9658 | 7.9640 | 8.0468 | 8.04617 | 8.04629 |
| 2 | 5 | 1 | 18.0231 | 17.9108 | 18.2385 | 18.24050 | 18.24161 |
| 5 | 14.6363 | 14.6057 | 14.8810 | 14.88418 | 14.88578 |
| 10 | 14.0098 | 13.9101 | 14.0861 | 14.08780 | 14.08965 |
| 10 | 1 | 21.0241 | 20.9821 | 21.3187 | 21.31945 | 21.32062 |
| 5 | 17.7396 | 17.7373 | 18.0843 | 18.08585 | 18.08761 |
| 10 | 17.1126 | 17.0751 | 17.2873 | 17.28741 | 17.28949 |
| 20 | 1 | 22.1378 | 22.1257 | 22.4585 | 22.45857 | 22.45967 |
| 5 | 19.0187 | 19.0192 | 19.3921 | 19.39248 | 19.39408 |
| 10 | 18.4115 | 18.4005 | 18.6222 | 18.62087 | 18.62278 |
It can be seen from
Table 11,
Table 12,
Table 13 and
Table 14 that the present frequencies are in excellent agreement with the corresponding results of Mantari et al. [
36] and slightly more than those of Thai and Choi [
38] and Akavci [
35]. The frequencies increase as both
and
increase and as
decreases in case of neglecting the foundation medium. The frequency when
is more than twice of this when
.
Table 13.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco–Pasternak foundations (, ).
Table 13.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on visco–Pasternak foundations (, ).
| | | Akavci [35] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| |
|---|
| 0.5 | 5 | 1 | 10.8489 | 10.8450 | 10.7649 | 10.76493 | 10.76552 |
| 5 | 10.9925 | 10.9919 | 10.9106 | 10.91023 | 10.91134 |
| 10 | 11.0818 | 11.0793 | 10.9611 | 10.96027 | 10.96164 |
| 10 | 1 | 11.0940 | 11.0926 | 11.1042 | 11.10417 | 11.10472 |
| 5 | 11.2538 | 11.2538 | 11.2645 | 11.26443 | 11.26537 |
| 10 | 11.3313 | 11.3302 | 11.3190 | 11.31873 | 11.31989 |
| 20 | 1 | 11.1660 | 11.1656 | 11.1999 | 11.19984 | 11.20017 |
| 5 | 11.3343 | 11.3343 | 11.3680 | 11.36794 | 11.36849 |
| 10 | 11.4093 | 11.4090 | 11.4236 | 11.42342 | 11.42390 |
| 1 | 5 | 1 | 14.3923 | 14.3818 | 14.2406 | 14.24088 | 14.24170 |
| 5 | 14.3071 | 14.3052 | 14.1562 | 14.15569 | 14.15721 |
| 10 | 14.3829 | 14.3759 | 14.1600 | 14.15860 | 14.16046 |
| 10 | 1 | 14.9443 | 14.9401 | 14.9631 | 14.96319 | 14.96395 |
| 5 | 14.8693 | 14.8692 | 14.8895 | 14.88945 | 14.89075 |
| 10 | 14.9193 | 14.9162 | 14.8957 | 14.89520 | 14.89681 |
| 20 | 1 | 15.1189 | 15.1177 | 15.1825 | 15.18244 | 15.18316 |
| 5 | 15.0607 | 15.0607 | 15.1251 | 15.12506 | 15.12623 |
| 10 | 15.1056 | 15.1047 | 15.1330 | 15.13257 | 15.13403 |
| 2 | 5 | 1 | 25.6912 | 25.6294 | 25.2563 | 25.25781 | 25.25932 |
| 5 | 24.3625 | 24.3453 | 23.8994 | 23.89854 | 23.90119 |
| 10 | 24.3109 | 24.2696 | 23.6297 | 23.62625 | 23.62944 |
| 10 | 1 | 28.2316 | 28.2023 | 28.2878 | 28.28833 | 28.28988 |
| 5 | 26.7223 | 26.7201 | 26.7859 | 26.78627 | 26.78890 |
| 10 | 26.5586 | 26.5362 | 26.4775 | 26.47653 | 26.47974 |
| 20 | 1 | 29.2272 | 29.2181 | 29.4271 | 29.42715 | 29.42860 |
| 5 | 27.7770 | 27.7772 | 27.9891 | 27.98915 | 27.99147 |
| 10 | 27.5919 | 27.5847 | 27.6803 | 27.67920 | 27.68203 |
In each table, in addition to the examination of the aspect ratios
, thickness ratios
, and the FG power-law index
, we discussed several combinations of the foundation parameters
and
. Furthermore, different values of the third damping coefficient
are considered. The results show that the three Visco-Winkler-Pasternak foundation parameters have effects of increasing the non-dimensional frequencies. The Pasternak parameter
has more of an effect on increasing the frequencies than the Winkler parameter
. However, the damping parameter
has a little and sensitive effect on increasing the frequencies. It is interesting to discuss the effect of the FG power-law index
on the non-dimensional frequencies. As shown in
Table 11, the frequency parameter
decreases with the increase in
and this is irrespective of the values of
and
. Additionally, it is observed in
Table 12 that if a plate is just rested on Winkler’s foundation or visco-Winkler foundations, the increase of the FG power-law index decreases the non-dimensional frequency. However, this situation is inversed if the plate is rested on Pasternak’s foundation regardless of the absence (
Table 13) or presence (
Table 14) of Winkler’s foundation or visco-Winkler foundations.
Table 14.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
Table 14.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates resting on Visco-Winkler-Pasternak foundations (, ).
| | | Akavci [35] | Thai and Choi [38] | Mantari et al. [36] | Present |
|---|
| |
|---|
| 0.5 | 5 | 1 | 11.1817 | 11.1780 | 11.0894 | 11.08946 | 11.09007 |
| 5 | 11.3598 | 11.3593 | 11.2700 | 11.26956 | 11.27071 |
| 10 | 11.4581 | 11.4558 | 11.3285 | 11.32767 | 11.32909 |
| 10 | 1 | 11.4284 | 11.4270 | 11.4358 | 11.43582 | 11.43638 |
| 5 | 11.6243 | 11.6243 | 11.6322 | 11.63214 | 11.63311 |
| 10 | 11.7103 | 11.7093 | 11.6957 | 11.69536 | 11.69657 |
| 20 | 1 | 11.5008 | 11.5005 | 11.5331 | 11.53311 | 11.53346 |
| 5 | 11.7054 | 11.7054 | 11.7374 | 11.73738 | 11.73796 |
| 10 | 11.7888 | 11.7886 | 11.8021 | 11.80186 | 11.80257 |
| 1 | 5 | 1 | 14.6407 | 14.6305 | 14.4792 | 14.47947 | 14.48030 |
| 5 | 14.5862 | 14.5843 | 14.4258 | 14.42519 | 14.42675 |
| 10 | 14.6702 | 14.6636 | 14.4366 | 14.43508 | 14.43698 |
| 10 | 1 | 15.1927 | 15.1887 | 15.2084 | 15.20848 | 15.20924 |
| 5 | 15.1498 | 15.1497 | 15.1669 | 15.16678 | 15.16811 |
| 10 | 15.2075 | 15.2045 | 15.1810 | 15.18053 | 15.18217 |
| 20 | 1 | 15.3674 | 15.3663 | 15.4293 | 15.42927 | 15.43000 |
| 5 | 15.3414 | 15.3414 | 15.4039 | 15.40390 | 15.40509 |
| 10 | 15.3938 | 15.3929 | 15.4198 | 15.41946 | 15.42094 |
| 2 | 5 | 1 | 25.8251 | 25.7640 | 25.3782 | 25.37974 | 25.38125 |
| 5 | 24.5206 | 24.5036 | 24.0450 | 24.04408 | 24.04674 |
| 10 | 24.4759 | 24.4352 | 23.7803 | 23.77672 | 23.77992 |
| 10 | 1 | 28.3613 | 28.3322 | 28.4137 | 28.41429 | 28.41586 |
| 5 | 26.8763 | 26.8741 | 26.9360 | 26.93632 | 26.93896 |
| 10 | 26.7186 | 26.6964 | 26.6338 | 26.63282 | 26.63605 |
| 20 | 1 | 29.3557 | 29.3467 | 29.5539 | 29.55394 | 29.55539 |
| 5 | 27.9292 | 27.9294 | 28.1392 | 28.13924 | 28.14156 |
| 10 | 27.7497 | 27.7426 | 27.8366 | 27.83544 | 27.83829 |
Table 15 presents the non-dimensional fundamental frequencies for Al/Al
2O
3 FG rectangular plates resting on viscoelastic foundations with
and several values of
. The non-dimensional frequency and the non-dimensional viscoelastic foundation coefficients are utilized as
Table 15.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
Table 15.
Non-dimensional fundamental frequencies for Al/Al2O3 FG rectangular plates ().
| | Theory | |
|---|
| 0 | 1 | 5 | |
|---|
| (0,0) | 0.5 | Akavci [35] | 0.08018 | 0.06148 | 0.05215 | 0.04081 |
| Hosseini et al. [3] | 0.08006 | 0.06335 | 0.05379 | 0.04100 |
| Mantari et al. [36] | 0.08021 | 0.06238 | 0.05321 | 0.04083 |
| Present | | 0.080209 | 0.062382 | 0.053210 | 0.040825 |
| 1 | Akavci [35] | 0.12508 | 0.09613 | 0.08089 | 0.06366 |
| Hosseini et al. [3] | 0.12480 | 0.09644 | 0.08027 | 0.06335 |
| Mantari et al. [36] | 0.12514 | 0.09753 | 0.08253 | 0.06370 |
| Present | | 0.12514 | 0.09753 | 0.08253 | 0.063696 |
| 2 | Akavci [35] | 0.28659 | 0.22189 | 0.18232 | 0.14587 |
| Hosseini et al. [3] | 0.28513 | 0.20592 | 0.16315 | 0.14591 |
| Mantari et al. [36] | 0.28682 | 0.22498 | 0.18592 | 0.14600 |
| Present | | 0.286844 | 0.224999 | 0.185947 | 0.146000 |
| (100,10) | 0.5 | Baferani et al. [45] | 0.12869 | 0.10498 | 0.09227 | --- |
| Akavci [35] | 0.12876 | 0.10388 | 0.09098 | 0.06554 |
| Hosseini et al. [3] | 0.12870 | 0.10519 | 0.09223 | 0.06591 |
| Mantari et al. [36] | 0.12804 | 0.10388 | 0.09118 | 0.06517 |
| Present | | 0.128037 | 0.103883 | 0.091179 | 0.065169 |
| 0.128140 | 0.103981 | 0.091284 | 0.065243 |
| 1 | Baferani et al. [45] | 0.17020 | 0.13854 | 0.12077 | --- |
| Akavci [35] | 0.17039 | 0.13592 | 0.11774 | 0.08673 |
| Hosseini et al. [3] | 0.17020 | 0.13652 | 0.11786 | 0.08663 |
| Mantari et al. [36] | 0.16931 | 0.13610 | 0.11825 | 0.08618 |
| Present | | 0.169312 | 0.136102 | 0.118253 | 0.086178 |
| 0.169454 | 0.136236 | 0.118398 | 0.086279 |
| 2 | Baferani et al. [45] | 0.31449 | 0.26966 | 0.22932 | --- |
| Akavci [35] | 0.32889 | 0.25901 | 0.21785 | 0.16741 |
| Hosseini et al. [3] | 0.32768 | 0.24674 | 0.20359 | 0.16773 |
| Mantari et al. [36] | 0.32670 | 0.25992 | 0.21953 | 0.16630 |
| Present | | 0.326723 | 0.259934 | 0.219551 | 0.166298 |
| 0.327020 | 0.260213 | 0.219848 | 0.166511 |
It is to be noted that when (ceramic plate), will tends to while when (metal plate) will tends to .
The present frequencies are compared with the corresponding ones of the FSDT of Hosseini-Hashemi et al. [
3], the HSDTs proposed by Akavci [
35] and Baferani et al. [
45], and a quasi-3D hybrid type HSDT by Mantari et al. [
36] It can be seen from this table that the present results are identical to those proposed by Mantari et al. [
36], close to the ones of Akavci [
38] and Mantari et al. [
36], and slightly more than those of Baferani et al. [
45] Once again, the frequencies increase with the inclusion of the damping coefficient
.
Table 16 presents the non-dimensional fundamental frequencies for Aluminum-Zirconia (Al/ZrO
2) FG rectangular plates (
) resting on viscoelastic foundations with several values of the side-to-thickness ratio
. The non-dimensional frequency and the non-dimensional viscoelastic foundation coefficients are utilized as given in Equation (40). The present solution is compared with the corresponding ones of the theories presented in
Table 15. In general, the frequencies are slightly decreasing as the FG power-law index
increases while they rapidly increase as the side-to-thickness ratio
increases. Furthermore, the inclusion of the viscoelastic foundations increases the values of the frequency parameter. Once again, the present results are identical to those proposed by Mantari et al. [
36] for free pleats or plates resting on elastic foundations. In the case of
, the present frequencies are slightly greater than those proposed by Akavci [
38] and Hosseini et al. [
3]. However, in the case of
,
, the present frequencies are slightly smaller than those proposed by Akavci [
38] and Hosseini et al. [
3], especially when
. In the case of the viscoelastic coefficients, the frequencies increase with the inclusion of the damping coefficient
.
Table 16.
Non-dimensional fundamental frequencies for Al/ZrO2 FG rectangular plates ().
Table 16.
Non-dimensional fundamental frequencies for Al/ZrO2 FG rectangular plates ().
| | Theory | |
|---|
| 0 | 1 | 5 | |
|---|
| (0,0) | 20 | Akavci [35] | 0.02393 | 0.02202 | 0.02244 | 0.02056 |
| Hosseini et al. [3] | 0.02392 | 0.02156 | 0.02180 | 0.02046 |
| Mantari et al. [36] | 0.02393 | 0.02217 | 0.02260 | 0.02057 |
| Present | | 0.023931 | 0.022174 | 0.022597 | 0.02056 |
| 10 | Akavci [35] | 0.09203 | 0.08489 | 0.08576 | 0.07908 |
| Hosseini et al. [3] | 0.09188 | 0.08155 | 0.08171 | 0.07895 |
| Mantari et al. [36] | 0.09207 | 0.08549 | 0.08638 | 0.07911 |
| Present | | 0.092068 | 0.085493 | 0.086386 | 0.079111 |
| 5 | Akavci [35] | 0.32471 | 0.30152 | 0.31860 | 0.27902 |
| Hosseini et al. [3] | 0.32284 | 0.29399 | 0.29099 | 0.27788 |
| Mantari et al. [36] | 0.32498 | 0.30349 | 0.29990 | 0.27925 |
| Present | | 0.325006 | 0.303514 | 0.299939 | 0.279268 |
| (250,25) | 20 | Baferani et al. [45] | 0.03421 | 0.03249 | 0.03314 | --- |
| Akavci [35] | 0.03422 | 0.03213 | 0.03277 | 0.02940 |
| Hosseini et al. [3] | 0.03421 | 0.03184 | 0.03235 | 0.02937 |
| Mantari et al. [36] | 0.03417 | 0.03220 | 0.03283 | 0.02936 |
| Present | | 0.034169 | 0.032200 | 0.032834 | 0.029361 |
| 0.034272 | 0.032213 | 0.032848 | 0.029395 |
| 10 | Baferani et al. [45] | 0.13365 | 0.12749 | 0.12950 | --- |
| Akavci [35] | 0.13375 | 0.12585 | 0.12778 | 0.11492 |
| Hosseini et al. [3] | 0.13365 | 0.12381 | 0.12533 | 0.11484 |
| Mantari et al. [36] | 0.13302 | 0.12557 | 0.12755 | 0.11430 |
| Present | | 0.133019 | 0.125569 | 0.127554 | 0.114299 |
| 0.133127 | 0.125707 | 0.127731 | 0.114495 |
| 5 | Baferani et al. [45] | 0.43246 | 0.46406 | 0.44824 | --- |
| Akavci [35] | 0.50044 | 0.47298 | 0.47637 | 0.43000 |
| Hosseini et al. [3] | 0.49945 | 0.46997 | 0.47400 | 0.43001 |
| Mantari et al. [36] | 0.48945 | 0.46401 | 0.46838 | 0.42057 |
| Present | | 0.489466 | 0.464028 | 0.468392 | 0.420583 |
| 0.489910 | 0.464595 | 0.469153 | 0.421389 |