Stochastic Robustness of Delayed Discrete Noises for Delay Differential Equations
Abstract
1. Introduction
2. Problem Statement
3. Robust Stability
4. Robust Boundedness
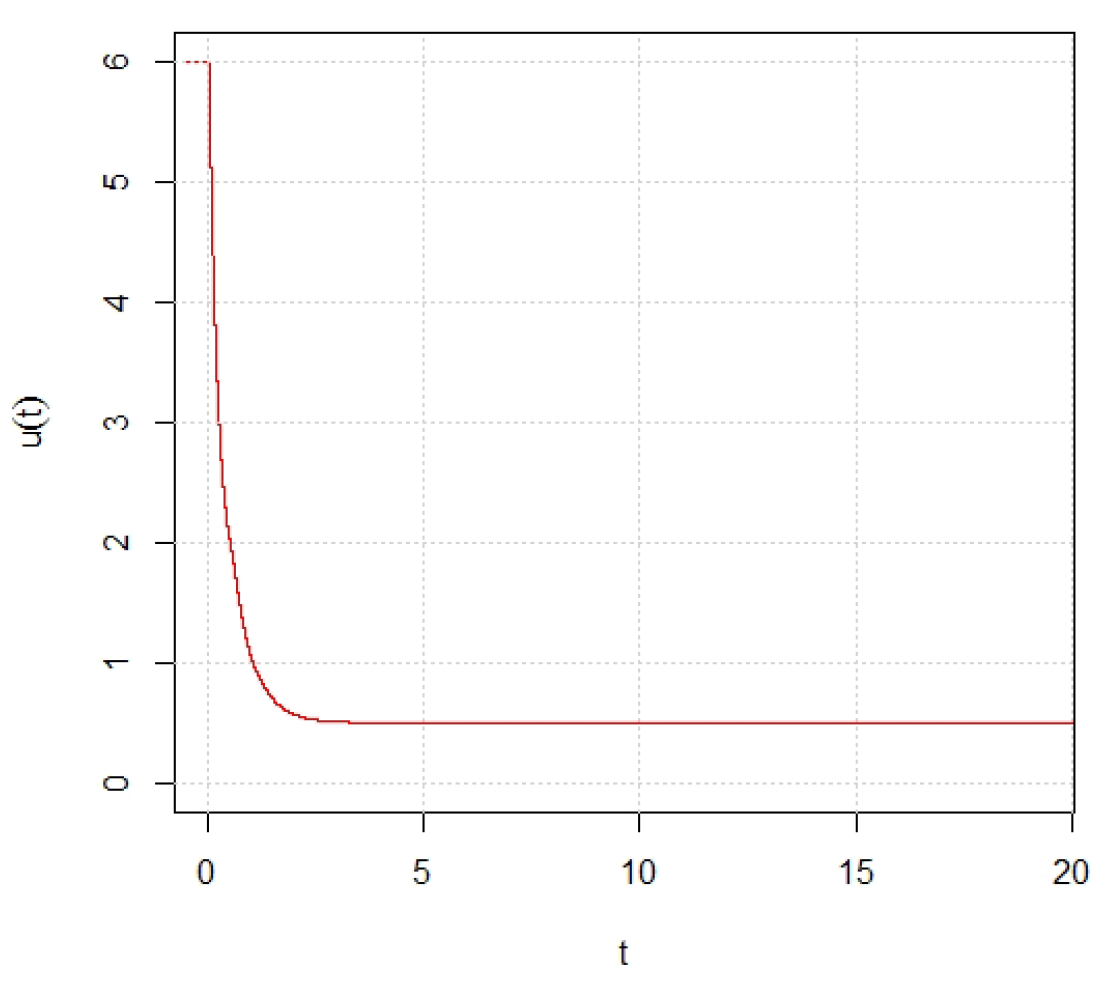
5. An Example
Example
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
References
- Arnold, L. Stochastic Differential Equations: Theory and Applications; John Wily and Sons: New York, NY, USA, 1974. [Google Scholar]
- Khasminskii, R. Stochastic Stability of Differential Equations; Sijthoff & Noordhoff: San Francisco, CA, USA, 1980. [Google Scholar]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus; Springer: New York, NY, USA, 1988. [Google Scholar]
- Oksendal, B. Stochastic Diffrential Equations, 6th ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Horwood Publishing: Chichester, UK, 2007. [Google Scholar]
- Appleby, J.A.D.; Riedle, M. Almost sure asymptotic stability of stochastic Volterra integro-differential equations with fading perturbations. Stoch. Anal. Appl. 2006, 24, 813–826. [Google Scholar] [CrossRef]
- Shaikhet, L. Stability of equilibrium states of a nonlinear delay differential equation with stochastic perturbations. Int. J. Robust Nonlinear Control 2017, 27, 915–924. [Google Scholar] [CrossRef]
- Song, R.; Zhu, Q. Stability of linear stochastic delay differential equations with infinite Markovian switchings. Int. J. Robust Nonlinear Control 2018, 28, 825–837. [Google Scholar] [CrossRef]
- Feng, L.; Li, S.; Song, R.; Li, Y. Suppression of explosion by polynomial noise for nonlinear differential systems. Sci. China Inf. Sci. 2018, 61, 070215. [Google Scholar] [CrossRef]
- Feng, L.; Liu, L.; Cao, J.; Rutkowski, L.; Lu, G. General decay stability for nonautonomous neutral stochastic systems with time-varying delays and Markovian switching. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Shen, Y.; Jiang, F. The almost sure asymptotic stability and pth moment asymptotic stability of nonlinear stochastic differential systems with polynomial growth. IEEE Trans. Autom. Control 2011, 56, 1985–1990. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Su, H.; Wang, K. Asymptotic boundedness for stochastic coupled systems on networks with Markovian switching. Neurocomputing 2014, 136, 180–189. [Google Scholar] [CrossRef]
- Peng, S.; Yang, L. The pth moment boundedness of stochastic functional differential equations with Markovian switching. J. Frankl. Inst. 2017, 354, 345–359. [Google Scholar] [CrossRef]
- Xu, L.; Hu, H. Boundedness analysis of stochastic pantograph differential systems. Appl. Math. Lett. 2021, 111, 106630. [Google Scholar] [CrossRef]
- Hu, L.; Mao, X.; Zhang, L. Robust stability and boundedness of nonlinear hybrid stochastic differential delay equations. IEEE Trans. Autom. Control 2013, 58, 2319–2332. [Google Scholar] [CrossRef]
- Feng, L.; Li, S.; Liu, Z.; Zheng, S. Robust stability of a class of stochastic functional differential equations with Markovian switching. Adv. Differ. Equ. 2016, 2016, 205. [Google Scholar] [CrossRef][Green Version]
- Haussmann, U.G. Asymptotic stability of the linear Itô equation in infinite dimensions. J. Math. Anal. Appl. 1978, 65, 219–235. [Google Scholar] [CrossRef]
- Ichikawa, A. Stability of semilinear stochastic evolution equations. J. Math. Anal. Appl. 1982, 90, 12–44. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, F.; Huang, C. Robustness of exponential stability of a class of stochastic functional differential equations with infinite delay. Automatica 2009, 45, 2577–2584. [Google Scholar] [CrossRef]
- Wu, F.; Hu, S. Attraction, stability and boundedness for stochastic functional differential equations with infinite delay. Automatica 2011, 47, 2224–2232. [Google Scholar] [CrossRef]
- Zhu, F.; Han, Z.; Zhang, J. Robust stability and stabilization of linear stochastic systems with Markovian switching and uncertain transition rates. J. Math. Anal. Appl. 2014, 415, 677–685. [Google Scholar] [CrossRef]
- Fei, C.; Shen, M.; Fei, W.; Mao, X.; Yan, L. Stability of highly nonlinear hybrid stochastic integro-differential delay equations. Nonlinear Anal. Hybrid Syst. 2019, 415, 180–199. [Google Scholar] [CrossRef]
- Mao, X. Almost sure exponential stabilization by discrete-time stochastic feedback control. IEEE Trans. Autom. Control 2016, 61, 1619–1624. [Google Scholar] [CrossRef]
- Feng, L.; Cao, J.; Liu, L. Robust analysis of discrete time noises for stochastic systems and application in neural networks. Int. J. Control 2020, 93, 2908–2921. [Google Scholar] [CrossRef]
- Briat, C. Linear Parameter-Varying and Time-Delay Systems; Springer: Heidelberg, Germany, 2015. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaadi, F.E.; Feng, L.; Alassafi, M.O.; Alotaibi, R.M.; Ahmad, A.M.; Cao, J. Stochastic Robustness of Delayed Discrete Noises for Delay Differential Equations. Mathematics 2022, 10, 743. https://doi.org/10.3390/math10050743
Alsaadi FE, Feng L, Alassafi MO, Alotaibi RM, Ahmad AM, Cao J. Stochastic Robustness of Delayed Discrete Noises for Delay Differential Equations. Mathematics. 2022; 10(5):743. https://doi.org/10.3390/math10050743
Chicago/Turabian StyleAlsaadi, Fawaz E., Lichao Feng, Madini O. Alassafi, Reem M. Alotaibi, Adil M. Ahmad, and Jinde Cao. 2022. "Stochastic Robustness of Delayed Discrete Noises for Delay Differential Equations" Mathematics 10, no. 5: 743. https://doi.org/10.3390/math10050743
APA StyleAlsaadi, F. E., Feng, L., Alassafi, M. O., Alotaibi, R. M., Ahmad, A. M., & Cao, J. (2022). Stochastic Robustness of Delayed Discrete Noises for Delay Differential Equations. Mathematics, 10(5), 743. https://doi.org/10.3390/math10050743







