A Localized Method of Fundamental Solution for Numerical Simulation of Nonlinear Heat Conduction
Abstract
1. Introduction
2. Problem Description
3. Introduction of the LMFS
4. Fictitious Time Integration Method
5. Numerical Results and Discussions
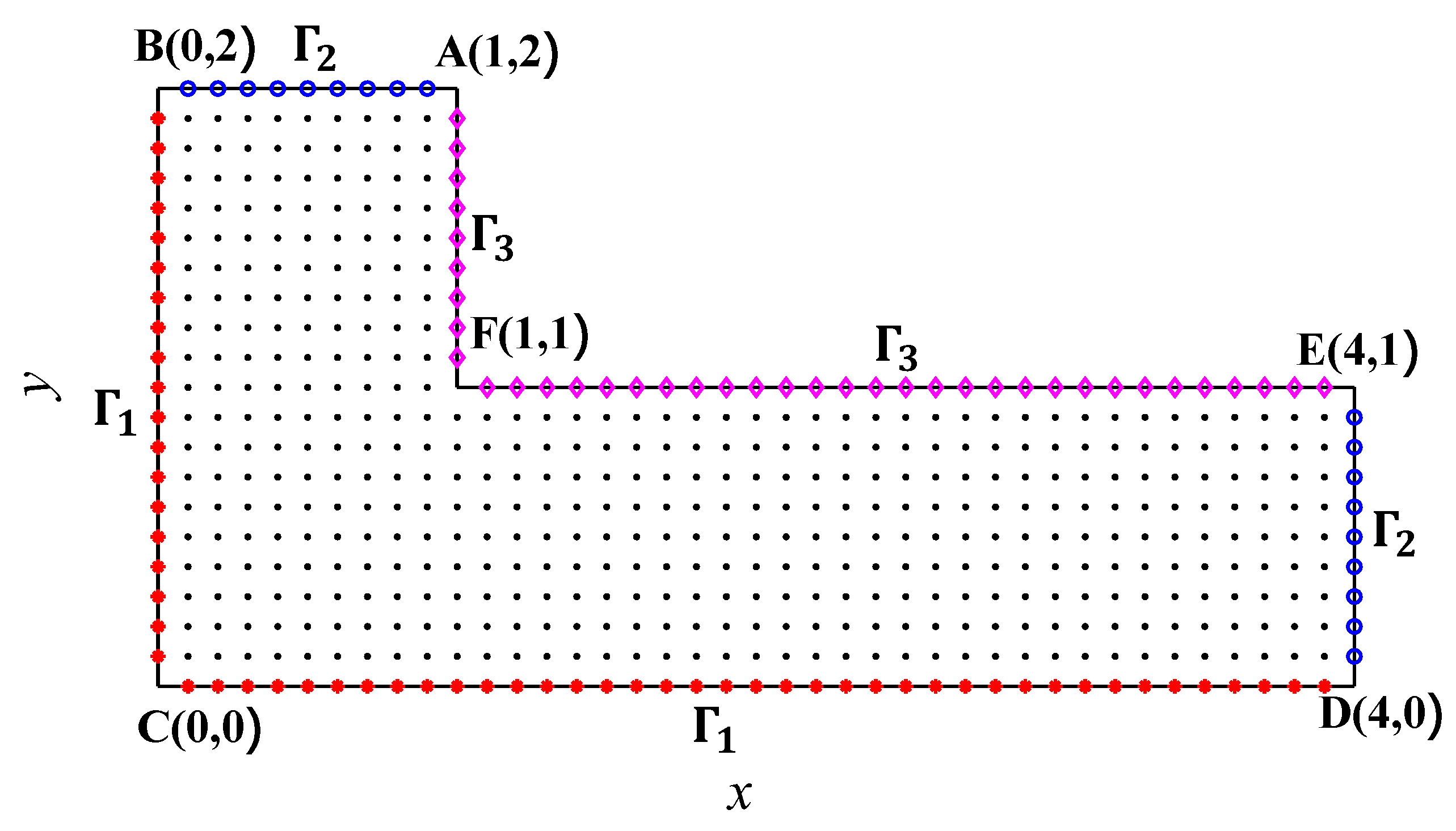
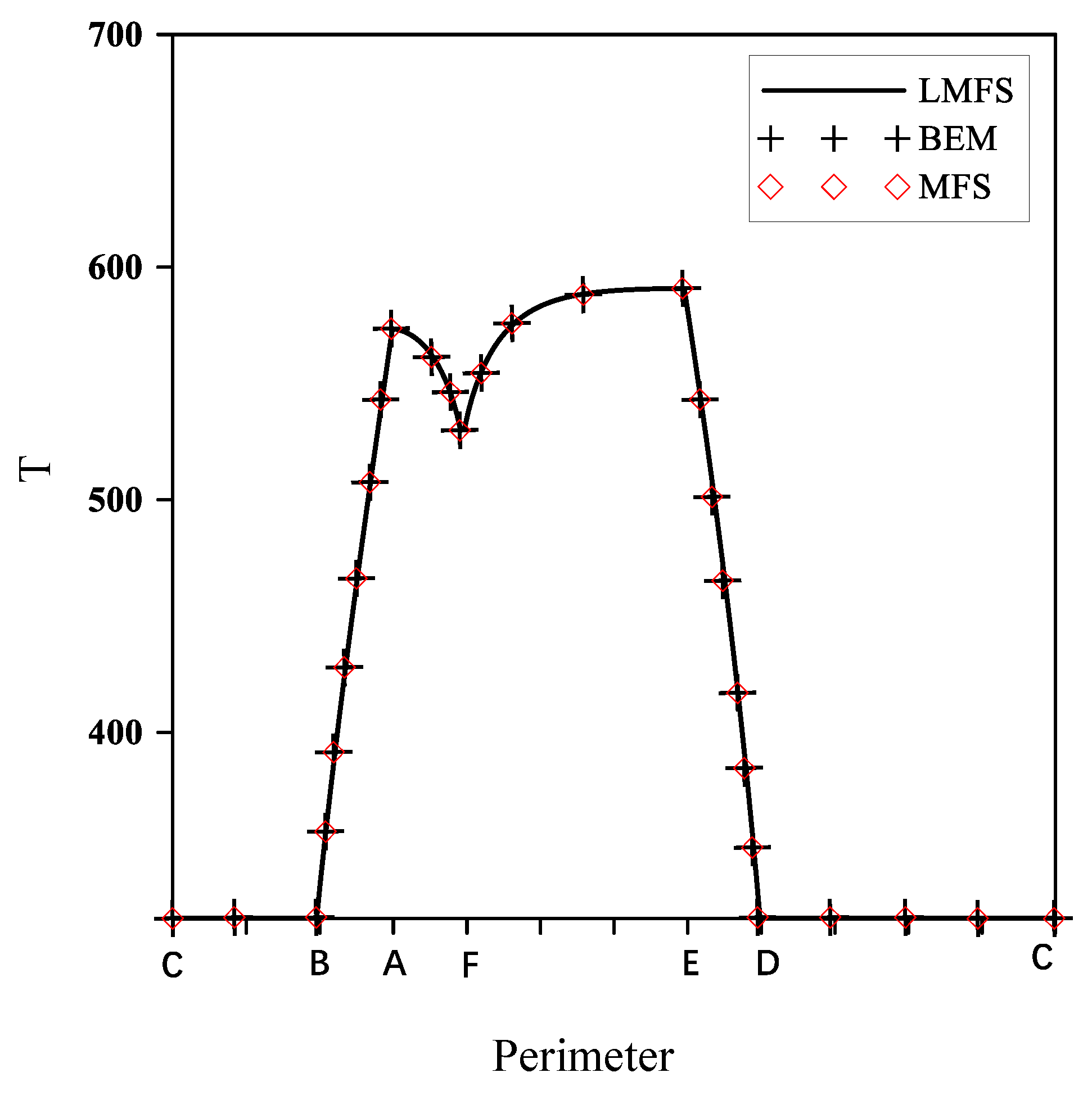
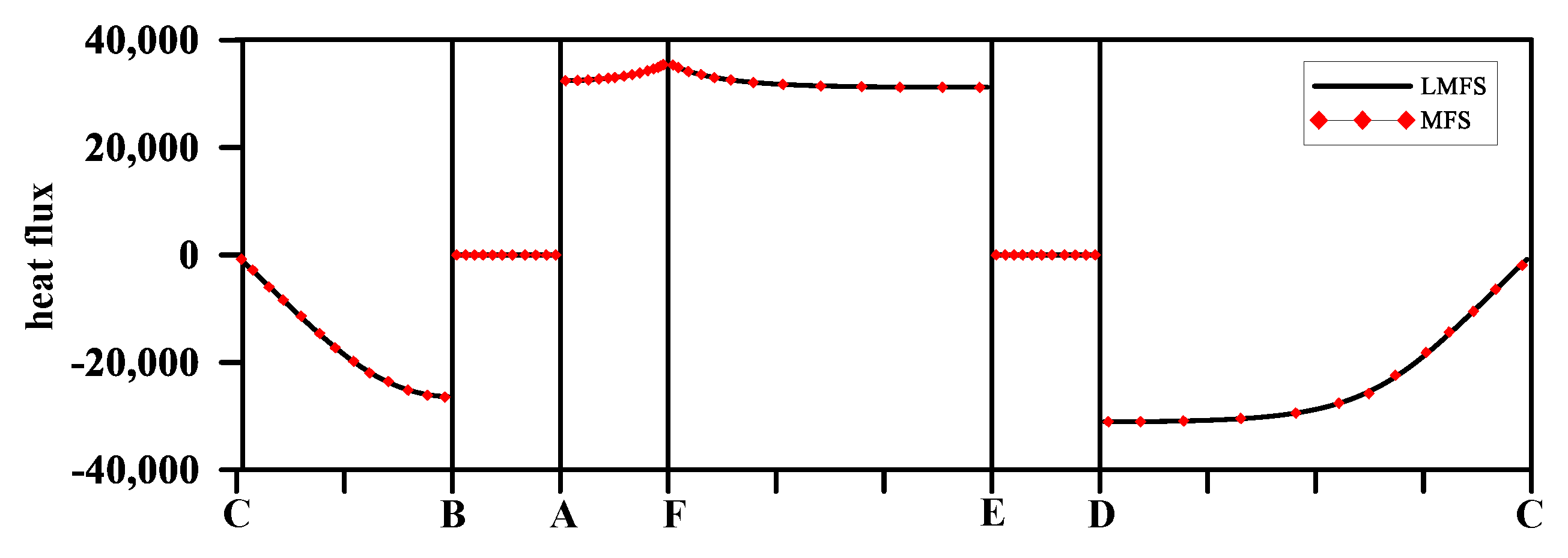
5.1. Example 1
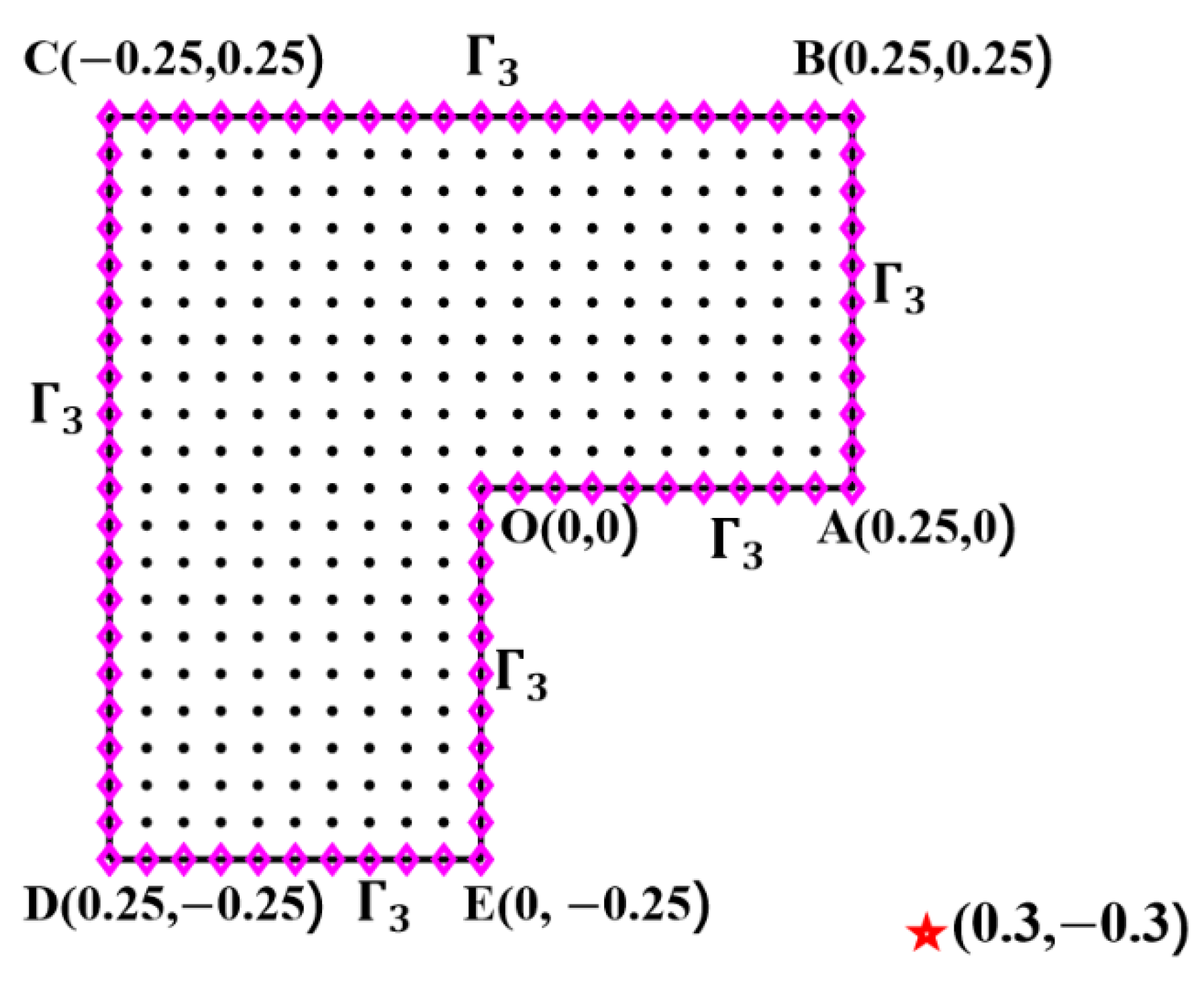
5.2. Example 2
5.3. Example 3
5.4. Example 4
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bagnall, K.R.; Muzychka, Y.S.; Wang, E.N. Application of the Kirchhoff transform to thermal spreading problems with convection boundary conditions. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 408–420. [Google Scholar] [CrossRef]
- Mosayebidorcheh, S.; Ganji, D.D.; Farzinpoor, M. Approximate solution of the nonlinear heat transfer equation of a fin with the power-law temperature-dependent thermal conductivity and heat transfer coefficient. Propuls. Power Res. 2014, 3, 41–47. [Google Scholar] [CrossRef]
- Moradi, A.; Ahmadikia, H. Analytical solution for different profiles of fin with temperature-dependent thermal conductivity. Math. Probl. Eng. 2010, 15, 568263. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Hatami, M.; Ganji, D.D. Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation. Case Stud. Therm. Eng. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Chang, J.Y.; Tsai, C.C.; Young, D.L. Homotopy method of fundamental solutions for solving nonlinear heat conduction problems. Eng. Anal. Bound. Elem. 2019, 108, 179–191. [Google Scholar] [CrossRef]
- Mitchell, A.R.; Griffiths, D.F. The Finite Difference Method in Partial Differential Equations; John Wiley: New York, NY, USA, 1980. [Google Scholar]
- Warming, R.F.; Hyett, B.J. The Modified Equation Approach to the Stability and Accuracy of Finite Difference Method. J. Comput. Phys. 1974, 14, 159–179. [Google Scholar] [CrossRef]
- Strang, G.; Fix, G.J.; Griffin, D.S. An Analysis of the Finite Element Method; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Qiang, C.; Wang, G.; Jerzy, P.M. Homogenization and localization of nanoporous composites-A critical review and new developments. Compos. Part B Eng. 2018, 155, 329–368. [Google Scholar]
- Uwe, M.; Georgios, P. Mechanism based diffusion-reaction modelling for predicting the influence of SARA composition and ageing stage on spurt completion time and diffusivity in bitumen. Constr. Build. Mater. 2021, 267, 120592. [Google Scholar]
- Bialecki, R.; Kuhn, G. Boundary element solution of heat conduction problems in multizone bodies of non-linear material. Int. J. Numer. Methods Eng. 1993, 36, 799–809. [Google Scholar] [CrossRef]
- Cavalcante, M.; Marques, S.; Pindera, M.J. Parametric Formulation of the Finite-Volume Theory for Functionally Graded Materials—Part I: Analysis. J. Appl. Mech. 2007, 74, 935. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Pearson education: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Oliveira, P.J.; Pinho, F.T.; Pinto, G.A. Numerical simulation of non-linear elastic flows with a general collocated finite-volume method. J. Non-Newton. Fluid Mech. 1998, 79, 1–43. [Google Scholar] [CrossRef]
- Zheng, H.; Sladek, J.; Sladek, V.; Wen, P.H. Fracture analysis of functionally graded material by hybrid meshless displacement discontinuity method. Eng. Fract. Mech. 2021, 247, 107591. [Google Scholar] [CrossRef]
- Zheng, H.; Zhou, C.B.; Yan, D.J.; Wang, Y.S.; Zhang, C.Z. A meshless collocation method for band structure simulation of nanoscale phononic crystals based on nonlocal elasticity theory. J. Comput. Phys. 2020, 408, 109268. [Google Scholar] [CrossRef]
- Zheng, H.; Sladek, J.; Sladek, V.; Wen, P.H. Hybrid meshless/displacement discontinuity method for FGM Reissner’s plate with cracks. Appl. Math. Model. 2021, 90, 1226–1244. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, F.; Chen, C.S.; Lei, M.; Wang, Y. Improved 3D surface reconstruction via the method of fundamental solutions. Numer. Math. Theory Methods Appl. 2020, 13, 973–985. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Touzé, D.L.; Zhang, A.M. Extension of SPH model for simulating Vortex-Induced-Vibration problems. J. Fluids Struct. 2019, 90, 19–42. [Google Scholar] [CrossRef]
- Li, Q.H.; Chen, S.S.; Kou, G.X. Transient heat conduction analysis using the MLPG method and modified precise time step integration method. J. Comput. Phys. 2011, 230, 2736–2750. [Google Scholar] [CrossRef]
- Tsai, C.C. Homotopy method of fundamental solutions for solving certain nonlinear partial differential equations. Eng. Anal. Bound. Elem. 2012, 36, 1226–1234. [Google Scholar] [CrossRef]
- Chati, M. The boundary node method for three-dimensional linear elasticity. Int. J. Numer. Methods Eng. 2015, 46, 1163–1184. [Google Scholar] [CrossRef]
- Tan, G.; Wang, H.; Song, C. 2-D simulation of electrostatic properties of piezoelectric composites using the boundary node method. J. Tsinghua Univ. 2007, 5, 734–737. [Google Scholar]
- Fan, C.M.; Chan, H.F.; Kuo, C.L. Numerical solutions of boundary detection problems using modified collocation Trefftz method and exponentially convergent scalar homotopy algorithm. Eng. Anal. Bound. Elem. 2012, 36, 2–8. [Google Scholar] [CrossRef]
- Fan, C.M.; Young, D.L.; Chiu, C.L. Method of Fundamental Solutions with External Source for the Eigenfrequencies of Waveguides. J. Mar. Sci. Technol. 2009, 17, 164–172. [Google Scholar] [CrossRef]
- Gu, Y.; Wen, C.; Zhang, C.Z. Singular boundary method for solving plane strain elastostatic problems. Int. J. Solids Struct. 2011, 48, 2549–2556. [Google Scholar] [CrossRef]
- Fu, Z.J.; Wen, C.; Lin, J. Singular Boundary Method for Various Exterior Wave Applications. Int. J. Comput. Methods 2015, 12, 1550011. [Google Scholar] [CrossRef]
- Chen, C.S.; Golberg, M.A.; Hon, Y.C. The method of fundamental solutions and quasi-Monte-Carlo method for diffusion equations. Int. J. Numer. Methods Eng. 2015, 43, 1421–1435. [Google Scholar] [CrossRef]
- Young, D.L.; Wu, J.T.; Chiu, C.L. Method of Fundamental Solutions for Stokes Problems by the Pressure-Stream Function Formulation. J. Mech. 2008, 24, 137–144. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, Z.J.; Zhang, C.Z.; Tyrer, M. A local radial basis function collocation method for band structure computation of phononic crystals with scatterers of arbitrary geometry. Appl. Math. Model. 2018, 60, 447–459. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, C.Z.; Wang, Y.S.; Chen, W.; Sladek, J.; Sladek, V. A local RBF collocation method for band structure computations of 2D solid/fluid and fluid/solid phononic crystals. Int. J. Numer. Methods Eng. 2017, 110, 467–500. [Google Scholar] [CrossRef]
- Kupradze, V.D.; Aleksidze, M.A. The method of functional equations for the approximate solution of certain boundary value problems. Ussr Comput. Math. Math. Phys. 1964, 4, 82–126. [Google Scholar] [CrossRef]
- Fan, C.M.; Chen, C.S.; Monroe, J. The Method of Fundamental Solutions for Solving Convection-Diffusion Equations with Variable Coefficients. Adv. Appl. Math. Mech. 2009, 1, 215–230. [Google Scholar]
- Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 1996, 9, 23–28. [Google Scholar] [CrossRef]
- Yan, L.; Fu, C.; Yang, F. The method of fundamental solutions for the inverse heat source problem. Eng. Anal. Bound. Elem. 2008, 32, 216–222. [Google Scholar] [CrossRef]
- Fan, C.M.; Huang, Y.K.; Chen, C.S. Localized method of fundamental solutions for solving two-dimensional Laplace and biharmonic equations. Eng. Anal. Bound. Elem. 2019, 101, 188–197. [Google Scholar] [CrossRef]
- Qu, W.; Fan, C.M.; Gu, Y. Analysis of three-dimensional interior acoustic fields by using the localized method of fundamental solutions. Appl. Math. Model. 2019, 76, 122–132. [Google Scholar] [CrossRef]
- Li, W. Localized method of fundamental solutions for 2D harmonic elastic wave problems. Appl. Math. Lett. 2021, 112, 106759. [Google Scholar] [CrossRef]
- Reutskiy, S. The method of fundamental solutions for Helmholtz eigenvalue problems in simply and multiply connected domains. Eng. Anal. Bound. Elem. 2006, 30, 150–159. [Google Scholar] [CrossRef]
- Wang, X.; Gu, Y.; Golub, M.V. Analysis of bimaterial interface cracks using the localized method of fundamental solutions. Results Math. 2022, 13, 100231. [Google Scholar] [CrossRef]
- Alves, C.; Antunes, P. The Method of Fundamental Solutions applied to the calculation of eigensolutions for simply connected plates. Int. J. Numer. Methods Eng. 2006, 77, 177–194. [Google Scholar] [CrossRef]
- Tsai, C.C. The method of fundamental solutions with dual reciprocity for three-dimensional thermoelasticity under arbitrary body forces. Eng. Comput. 2009, 26, 229–244. [Google Scholar] [CrossRef]
- Carslaw, H.; Jaeger, J. Conduction of Heat in Solids; Oxford Science Publications: Oxford, UK, 1959. [Google Scholar]
- Barnett, T.L. Application of a Nonlinear Least-Squares Method to Atmospheric Temperature Sounding. J. Atmos. Sci. 1969, 26, 457–461. [Google Scholar] [CrossRef][Green Version]
- Blaha, G.; Bessette, R.P. Nonlinear least-squares method via an isomorphic geometrical setup. Bull. Geod. 1989, 63, 115–137. [Google Scholar] [CrossRef]
- Fernandez, M.A.; Moubachir, M. A Newton method using exact jacobians for solving fluid-structure coupling. Comput. Struct. 2005, 83, 127–142. [Google Scholar] [CrossRef]
- Liu, C.S. A fictitious time integration method for two-dimensional quasi-linear elliptic boundary value problems. Comput. Modeling Eng. Sci. 2008, 33, 179–198. [Google Scholar]
- Liu, C.S. A fictitious time integration method for a quasilinear elliptic boundary value problem, defined in an arbitrary plane domain. Comput. Mater. Contin. 2009, 11, 15–32. [Google Scholar]
- Karageorghis, A.; Lesnic, D. The Method of Fundamental Solutions for Steady-State Heat Conduction in Nonlinear Materials. Commun. Comput. Phys. 2008, 4, 911–928. [Google Scholar] [CrossRef]
- Bialecki, R.; Nowak, A.J. Boundary value problems in heat conduction with nonlinear material and nonlinear boundary conditions. Appl. Math. Model. 1981, 5, 417–421. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liu, Y.-C.; Zheng, H. A Localized Method of Fundamental Solution for Numerical Simulation of Nonlinear Heat Conduction. Mathematics 2022, 10, 773. https://doi.org/10.3390/math10050773
Wang F, Liu Y-C, Zheng H. A Localized Method of Fundamental Solution for Numerical Simulation of Nonlinear Heat Conduction. Mathematics. 2022; 10(5):773. https://doi.org/10.3390/math10050773
Chicago/Turabian StyleWang, Feng, Yan-Cheng Liu, and Hui Zheng. 2022. "A Localized Method of Fundamental Solution for Numerical Simulation of Nonlinear Heat Conduction" Mathematics 10, no. 5: 773. https://doi.org/10.3390/math10050773
APA StyleWang, F., Liu, Y.-C., & Zheng, H. (2022). A Localized Method of Fundamental Solution for Numerical Simulation of Nonlinear Heat Conduction. Mathematics, 10(5), 773. https://doi.org/10.3390/math10050773





