Stability Analysis and Synthesis for 2-D Switched Systems with Random Disturbance
Abstract
:1. Introduction
- 1.
- System stability without being restricted by switching signals:The switching signal does not restrict the 2-D switched systems. Even if every subsystem in the system is in a stable state, the entire 2-D switched system may be unstable under a specific switching signal.
- 2.
- System stability under restricted switching laws:The switched system may not be stable under arbitrary switching, but the system may be stable under restricted switching signals, such as a closed-loop multi-controller system. Dwell time and average dwell time switching are typical restricted switching signals. They were proposed and developed by Hespanha and Morse [20,21,22], respectively. Applying it to a restricted switching signal can effectively solve the stability problem in restricted switching.
2. Problem Formulation
- 1.
- 2.
- and
- 3.
- and
3. Stability Analysis with Random Disturbance
3.1. Under Arbitrary Switching
3.2. Under Restricted Switching
4. Controller Design
4.1. Under Arbitrary Switching
4.2. Under Restricted Switching
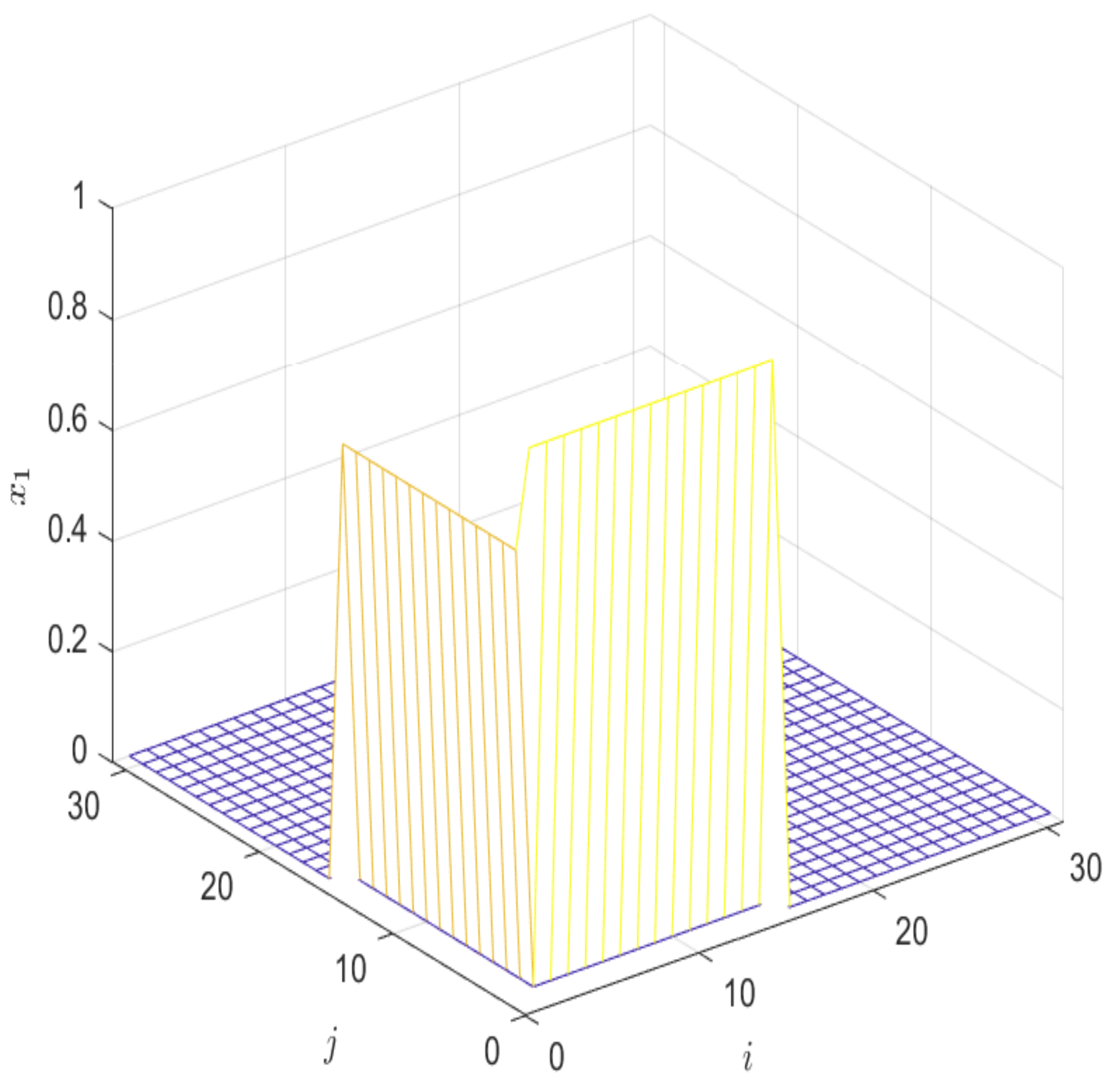
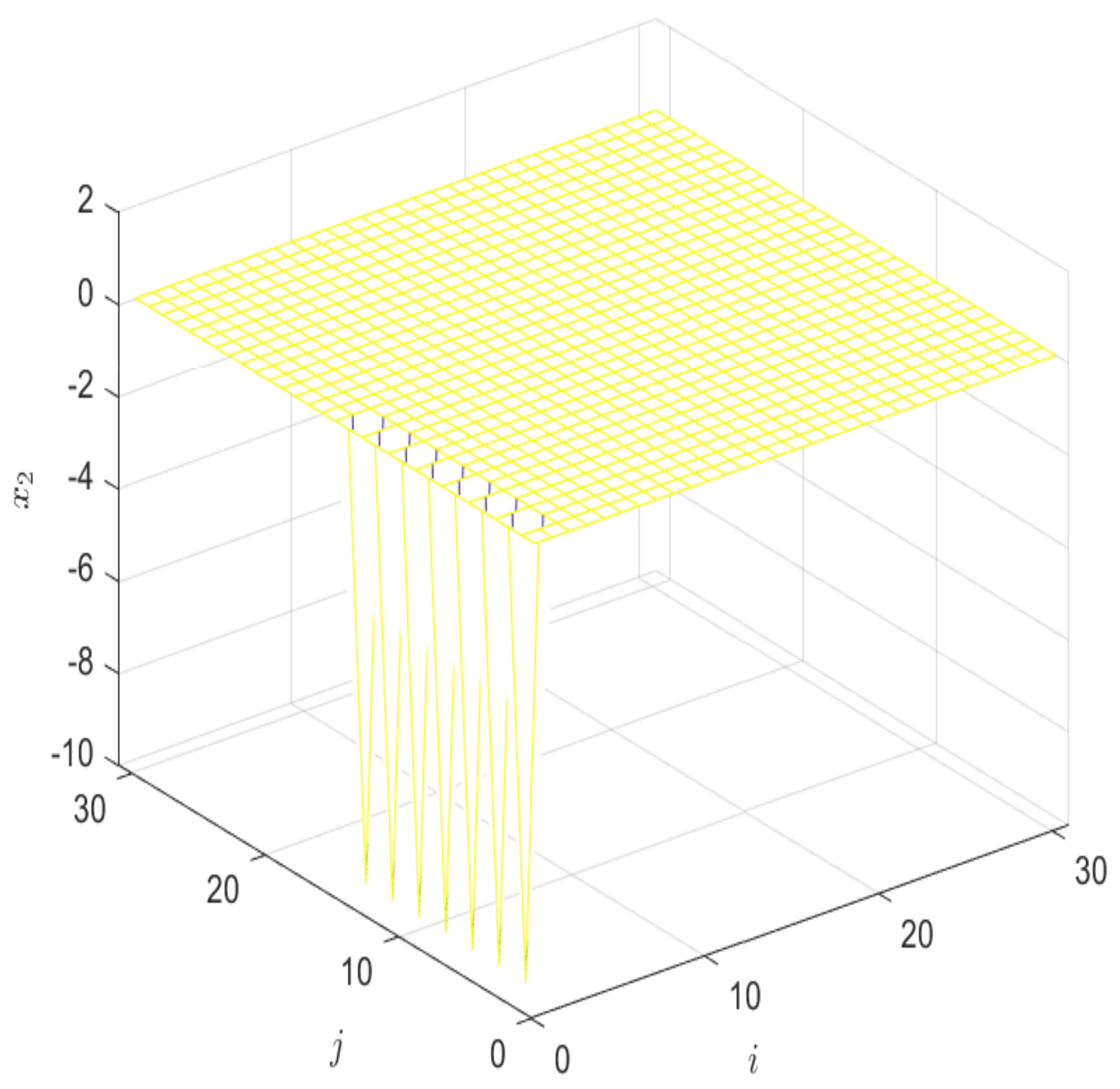
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marszalek, W. Two-dimensional state-space discrete models for hyperbolic partial differential equations. Appl. Math. Model. 1984, 8, 11–14. [Google Scholar] [CrossRef]
- Bouagada, D.; Dooren, P. On the stability of 2D state-space models. Numer. Linear Algebra Appl. 2013, 20, 198–207. [Google Scholar] [CrossRef]
- Fornasini, E.; Marchesini, G. Stability analysis of 2-D systems. IEEE Trans. Circuits Syst. 1980, 27, 1210–1217. [Google Scholar] [CrossRef]
- Paszke, W.; Lam, J.; Gałkowski, K.; Xu, S.; Lin, Z. Robust stability and stabilisation of 2D discrete state-delayed systems. Syst. Control Lett. 2004, 51, 277–291. [Google Scholar] [CrossRef]
- Gao, H.; Lam, J.; Wang, C.; Xu, S. Robust H∞ filtering for 2D stochastic systems. Circuits Syst. Signal Process. 2004, 23, 479–505. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Ding, S.X.; Karimi, H.R.; Li, Y. Robust H∞ Filtering for T wo-Dimensional Uncertain Linear Discrete Time-Varying Systems: A Krein Space-Based Method. IEEE Trans. Autom. Control 2019, 64, 5124–5131. [Google Scholar] [CrossRef]
- Rongni, Y.; Yaru, Y. Event-triggered control of discrete-time 2-D switched Fornasini–Marchesini systems. Eur. J. Control 2019, 48, 42–52. [Google Scholar]
- Ligang, W.; Rongni, Y.; Peng, S.; Xiaojie, S. Stability analysis and stabilization of 2-D switched systems under arbitrary and restricted switchings. Automatica 2015, 59, 206–215. [Google Scholar]
- Xiang, W.; Xiao, J. Stabilization of switched continuous-time systems with all modes unstable via dwell time switching. Automatica 2014, 50, 940–945. [Google Scholar] [CrossRef]
- Zhu, L.; Qiu, J.; Karimi, H. Region Stabilization of Switched Neural Networks With Multiple Modes and Multiple Equilibria: A Pole Assignment Method. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3280–3293. [Google Scholar] [CrossRef]
- Wang, Y.E.; Sun, X.M.; Mazenc, F. Stability of switched nonlinear systems with delay and disturbance. Automatica 2016, 69, 78–86. [Google Scholar] [CrossRef] [Green Version]
- Benzaouia, A.; Abdelaziz Hmamed, F.T.; Hajjaji, A.E. Stabilisation of discrete 2D time switching systems by state feedback control. Int. J. Syst. Sci. 2011, 42, 479–487. [Google Scholar] [CrossRef]
- Xiang, Z.; Huang, S. Stability analysis and stabilization of discrete-time 2D switched systems. Circuits Syst. Signal Process. 2013, 32, 401–414. [Google Scholar] [CrossRef]
- Shuang, S.; Zhongyang, F.; Weichao, S.; Yang, X. Stabilization of 2-D Switched Systems With All Modes Unstable via Switching Signal Regulation. IEEE Trans. Autom. Control 2018, 63, 857–863. [Google Scholar]
- Fan, Y.; Wang, M.; Fu, H.; Zhang, B.; Bian, Y.; Sun, G. Quasi-Time-Dependent H∞ Filtering of Discrete-Time 2-D Switched Systems with Mode-Dependent Persistent Dwell-Time. Circuits Syst. Signal Process. 2021, 40, 5886–5912. [Google Scholar] [CrossRef]
- Gao, W.; Yang, Y.; Duan, H.; Li, M.; Ma, J.; Jin, S. Output Feedback Robust H∞ Control for Discrete 2D Switched Systems. Comput. Syst. Sci. Eng. 2021, 39, 69–85. [Google Scholar] [CrossRef]
- Ren, W.; Xiong, J. Robust Filtering for 2-D Discrete-Time Switched Systems. IEEE Trans. Autom. Control 2021, 66, 4747–4760. [Google Scholar] [CrossRef]
- Badie, K.; Alfidi, M.; Chalh, Z. Exponential stability analysis for 2D discrete switched systems with state delays. Optim. Control Appl. Methods 2019, 40, 1088–1103. [Google Scholar] [CrossRef]
- Kaiqun, Z.; Jun, H.; Yurong, L.; Naif, D.A.; Fuad, E.A. On l2–l∞ output-feedback control scheduled by stochastic communication protocol for two-dimensional switched systems. Int. J. Syst. Sci. 2021, 52, 2961–2976. [Google Scholar]
- Branicky, M.S. Multiple Lyapunov Functions and Other Analysis Tools for Switched and Hybrid Systems. IEEE Trans. Autom. Control 1998, 43, 475–782. [Google Scholar] [CrossRef] [Green Version]
- Liberzon, D.; Morse, A.S. Basic Problems in Stability and Design of Switched Systems. IEEE Control Syst. Mag. 1999, 19, 59–70. [Google Scholar]
- Morse, A.S. Supervisory Control of Families of Linear Set-point Controllers-Part 11: Exact Matching. IEEE Trans. Autom. Control 1996, 41, 1413–1431. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, W.; Hou, T. Infinite horizon H2/H∞ control for discrete-time time-varying Markov jump systems with multiplicative noise. Automatica 2012, 48, 1447–1454. [Google Scholar] [CrossRef]
- Qi, Q.; Zhang, H. Output Feedback Control and Stabilization for Multiplicative Noise Systems With Intermittent Observations. IEEE Trans. Cybern. 2018, 48, 2128–2138. [Google Scholar] [CrossRef]
- Ghous, I.; Xiang, Z.; Karimi, H.R. H∞ control of 2-D continuous Markovian jump delayed systems with partially unknown transition probabilities. Inf. Sci. 2017, 382–383, 274–291. [Google Scholar] [CrossRef]
- Jiang, B.; Karimi, H. Further criterion for stochastic stability analysis of semi-Markovian jump linear systems. Int. J. Robust Nonlinear Control 2020, 30, 2689–2700. [Google Scholar] [CrossRef]
- Gao, H.; Lam, J.; Xu, S.; Wang, C. Stabilization and Stabilization of uncertain 2-D discrete systems with stochastic perturbation. Multidimens. Syst. Signal Process. 2014, 16, 85–106. [Google Scholar] [CrossRef]
- Yao, J.; Ye, S.; Wang, W. Robust stabilization of 2D state-delayed systems with stochastic perturbation. In Proceedings of the 11th International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2010; Volume 16, pp. 1951–1956. [Google Scholar]
- Cui, J.; Hu, G. Stability for 2-D linear discrete systems with stochastic parameters. In Proceedings of the International Conference on Logistics Systems and Intelligent Management, Harbin, China, 9–10 January 2010; pp. 1243–1446. [Google Scholar]
- Cui, J.; Hu, G. State estimation of 2-D stochastic systems represented by FM-II model. Acta Autom. Sin. 2011, 35, 755–761. [Google Scholar]
- Yeganefar, N.; Yeganefar, N.; Ghamgui, M.; Moulay, E. Lyapunov theory for 2-D nonlinear Roesser models: Application to asymptotic and exponential stability. IEEE Trans. Autom. Control 2013, 58, 1299–1304. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Shen, X.; Li, X. Stability Analysis and Synthesis for 2-D Switched Systems with Random Disturbance. Mathematics 2022, 10, 810. https://doi.org/10.3390/math10050810
Meng F, Shen X, Li X. Stability Analysis and Synthesis for 2-D Switched Systems with Random Disturbance. Mathematics. 2022; 10(5):810. https://doi.org/10.3390/math10050810
Chicago/Turabian StyleMeng, Fei, Xuyu Shen, and Xiaofeng Li. 2022. "Stability Analysis and Synthesis for 2-D Switched Systems with Random Disturbance" Mathematics 10, no. 5: 810. https://doi.org/10.3390/math10050810
APA StyleMeng, F., Shen, X., & Li, X. (2022). Stability Analysis and Synthesis for 2-D Switched Systems with Random Disturbance. Mathematics, 10(5), 810. https://doi.org/10.3390/math10050810





