Modified Exp-Function Method to Find Exact Solutions of Ionic Currents along Microtubules
Abstract
:1. Introduction
2. The Description of the Method
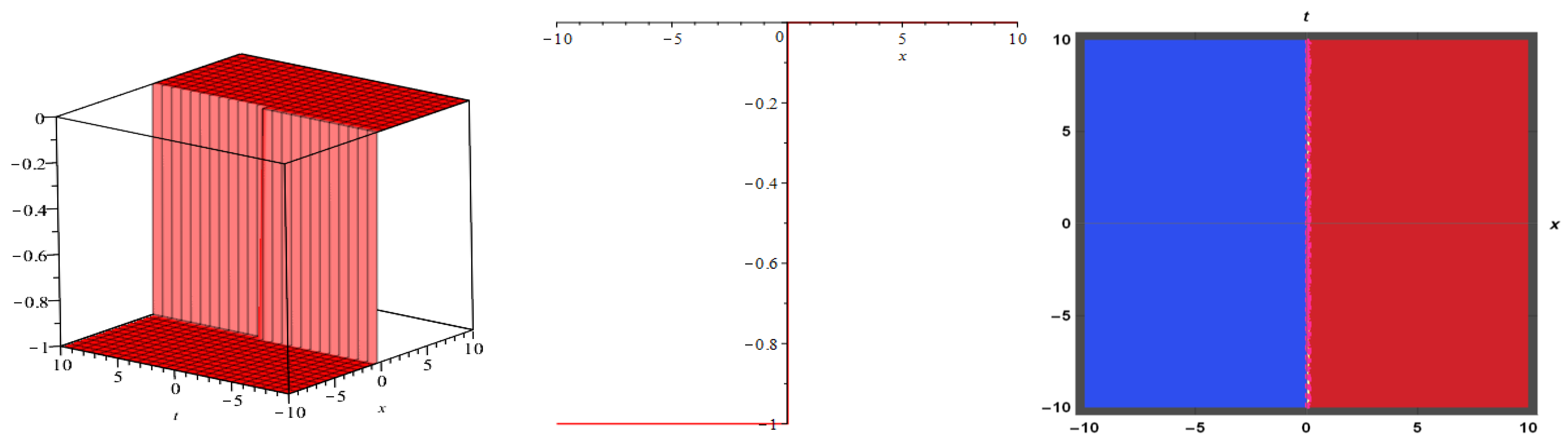
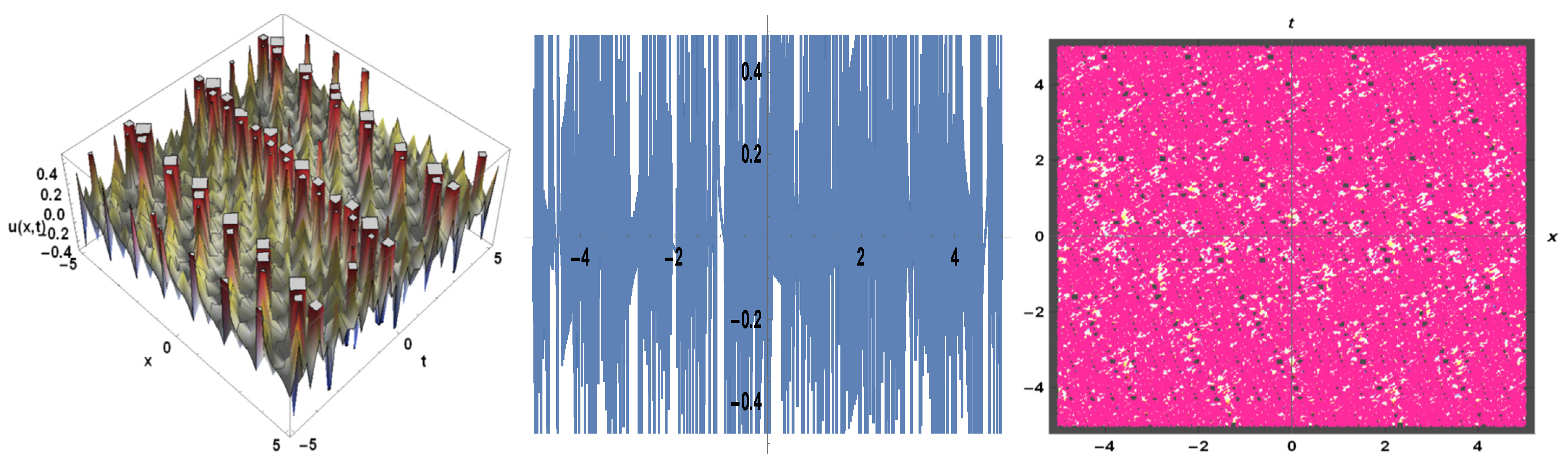
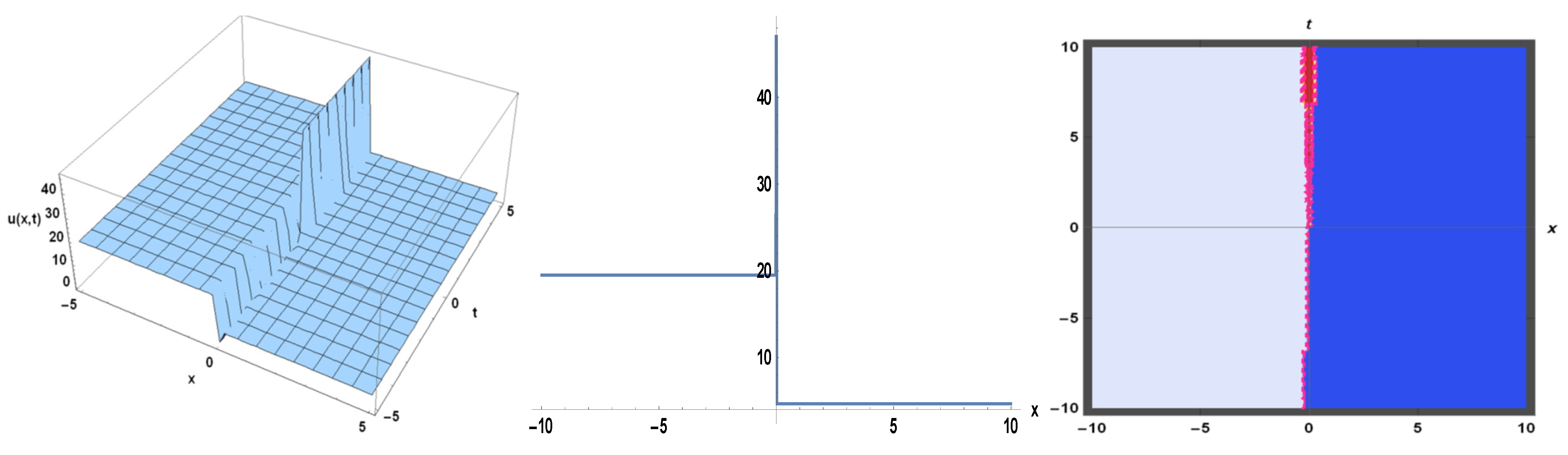
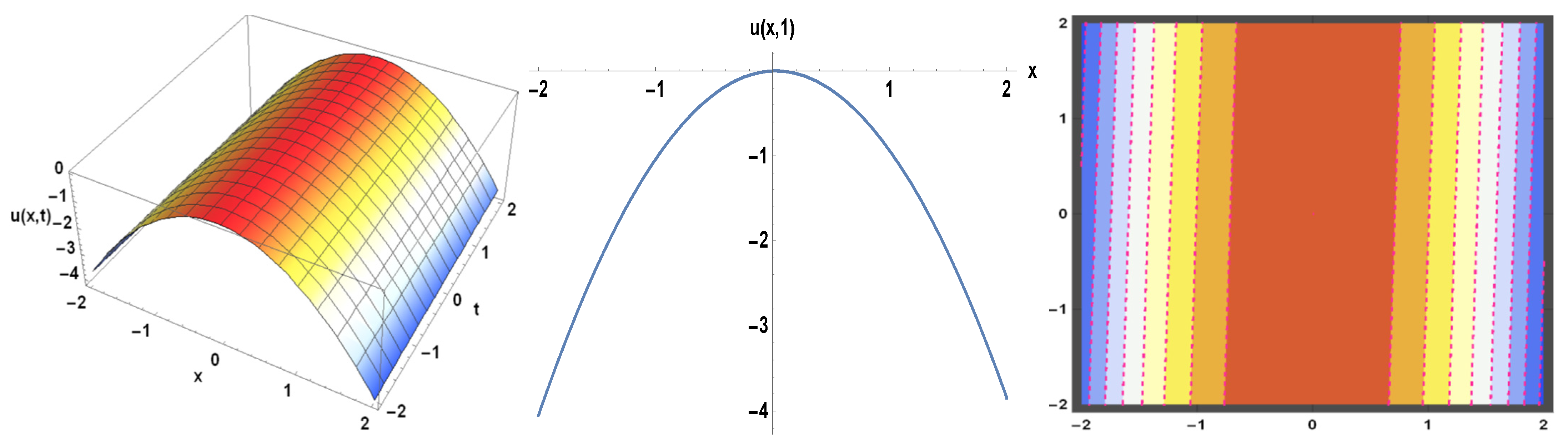
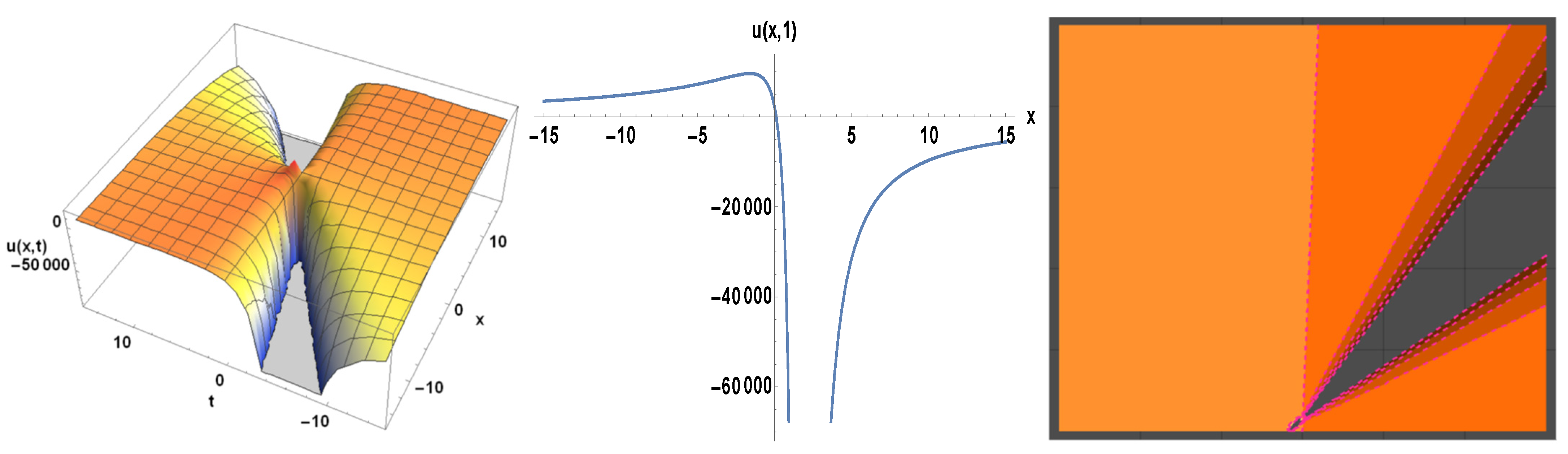
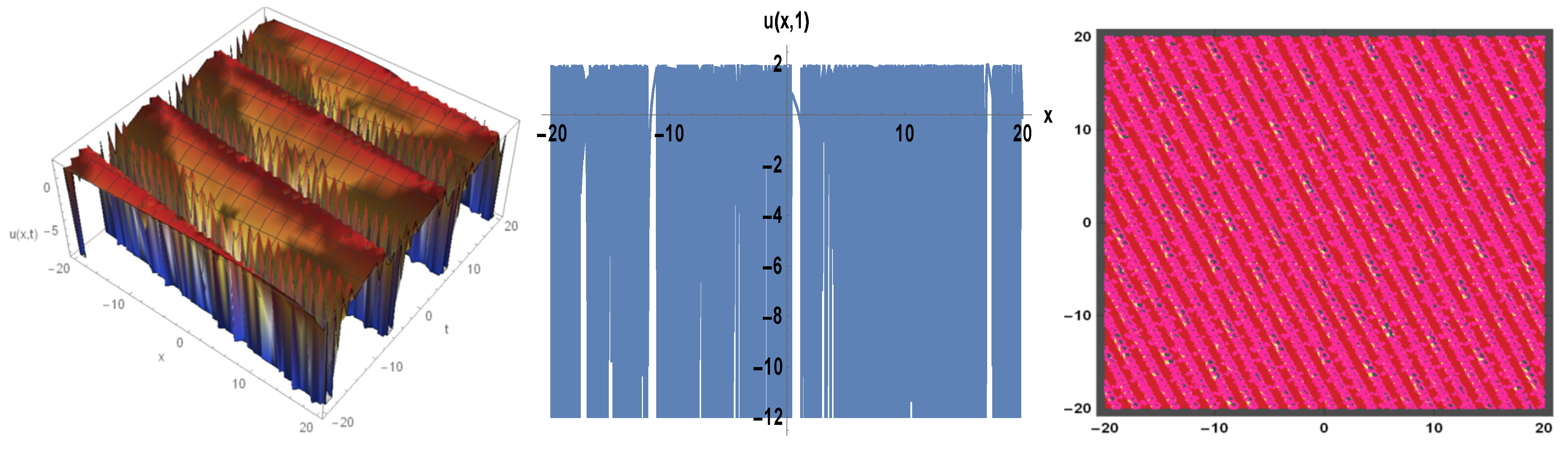
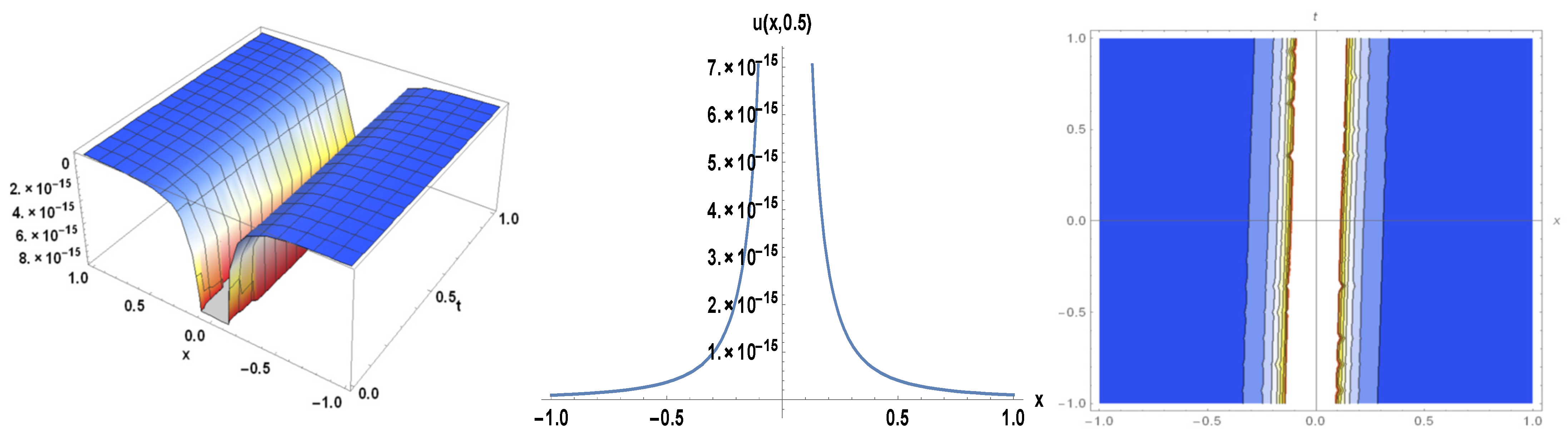
3. Applications
4. Physical Expression of the Problem
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jawad, J.M.; Petković, M.D.; Biswas, A. Soliton solutions of a few nonlinear wave equations. Appl. Math. Comput. 2010, 216, 2649–2658. [Google Scholar]
- Jafar, B.; Asadi, M.A.; Salehi, F. Rational Homotopy Perturbation Method for solving stiff systems of ordinary differential equations. Appl. Math. Model. 2015, 39, 1291–1299. [Google Scholar]
- Cariello, F.; Tabor, M. Painlevé expansions for nonintegrable evolution equations. Phys. D Nonlinear Phenom. 1989, 39, 77–94. [Google Scholar] [CrossRef]
- Philip, D.G.; Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press: Cambridge, UK, 1989; Volume 2. [Google Scholar]
- Aslam, M.N.; Akbar, M.A.; Mohyud-Din, S.T. General traveling wave solutions of the strain wave equation in microstructured solids via the new approach of generalized (G′/G)-expansion method. Alex. Eng. J. 2014, 53, 233–241. [Google Scholar] [CrossRef] [Green Version]
- Shakeel, M.; Ul-Hassan, Q.M.; Ahmad, J.; Naqvi, T. Exact solutions of the time fractional BBM-Burger equation by novel (G′/G)-expansion method. Adv. Math. Phys. 2014, 2014, 181594. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, M.; Wang, Y. Periodic wave solutions to a coupled KdV equations with variable coefficients. Phys. Lett. A 2003, 308, 31–36. [Google Scholar] [CrossRef]
- Ali, A.T. New generalized Jacobi elliptic function rational expansion method. J. Comput. Appl. Math. 2011, 235, 4117–4127. [Google Scholar] [CrossRef] [Green Version]
- Lü, D. Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos Solitons Fractals 2005, 24, 1373–1385. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Fan, E. Two new applications of the homogeneous balance method. Phys. Lett. A 2000, 265, 353–357. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Sekulić, D.L.; Satarić, M.V.; Živanov, M.B. Symbolic computation of some new nonlinear partial differential equations of nanobiosciences using modified extended tanh-function method. Appl. Math. Comput. 2011, 218, 3499–3506. [Google Scholar] [CrossRef]
- Soliman, A.A. The modified extended tanh-function method for solving Burgers-type equations. Phys. A Stat. Mech. Its Appl. 2006, 361, 394–404. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y. RATH: A Maple package for finding travelling solitary wave solutions to nonlinear evolution equations. Comput. Phys. Commun. 2002, 148, 256–266. [Google Scholar] [CrossRef]
- Peng, Y.Z. A mapping method for obtaining exact travelling wave solutions to nonlinear evolution equations. Chin. J. Phys. 2003, 41, 103–110. [Google Scholar]
- Yomba, E. Construction of new soliton-like solutions of the (2 + 1) dimensional dispersive long wave equation. Chaos Solitons Fractals 2004, 20, 1135–1139. [Google Scholar] [CrossRef]
- Alam, N.; Alam, M.M. An analytical method for solving exact solutions of a nonlinear evolution equation describing the dynamics of ionic currents along microtubules. J. Taibah Univ. Sci. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Jeffrey, A.; Mohamad, M.N.B. Exact solutions to the KdV-Burgers’ equation. Wave Motion 1991, 14, 369–375. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Petković, M.D.; Biswas, A. Soliton solutions of Burgers equations and perturbed Burgers equation. Appl. Math. Comput. 2010, 216, 3370–3377. [Google Scholar]
- Satarić, M.V.; Ilić, D.I.; Ralević, N.; Tuszynski, J.A. A nonlinear model of ionic wave propagation along microtubules. Eur. Biophys. J. 2009, 38, 637–647. [Google Scholar] [CrossRef]
- Satarić, M.V.; Sekulić, D.; Živanov, M. Solitonic ionic currents along microtubules. J. Comput. Theor. Nanosci. 2010, 7, 2281–2290. [Google Scholar] [CrossRef]
- Sekulić, D.L.; Satarić, B.M.; Tuszynski, J.A.; Satarić, M.V. Nonlinear ionic pulses along microtubules. Eur. Phys. J. E 2011, 34, 49. [Google Scholar] [CrossRef] [PubMed]
- Zayed, E.M.E.; Amer, Y.A.; Shohib, R.M.A. The improved generalized Riccati equation mapping method and its application for solving a nonlinear partial differential equation (PDE) describing the dynamics of ionic currents along microtubules. Sci. Res. Essays 2014, 9, 238–248. [Google Scholar]
- Shakeel, M.; Iqbal, M.A.; Din, Q.; Hassan, Q.M.; Ayub, K. New exact solutions for coupled nonlinear system of ion sound and Langmuir waves. Indian J. Phys. 2020, 94, 885–894. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attaullah; Shakeel, M.; Shah, N.A.; Chung, J.D. Modified Exp-Function Method to Find Exact Solutions of Ionic Currents along Microtubules. Mathematics 2022, 10, 851. https://doi.org/10.3390/math10060851
Attaullah, Shakeel M, Shah NA, Chung JD. Modified Exp-Function Method to Find Exact Solutions of Ionic Currents along Microtubules. Mathematics. 2022; 10(6):851. https://doi.org/10.3390/math10060851
Chicago/Turabian StyleAttaullah, Muhammad Shakeel, Nehad Ali Shah, and Jae Dong Chung. 2022. "Modified Exp-Function Method to Find Exact Solutions of Ionic Currents along Microtubules" Mathematics 10, no. 6: 851. https://doi.org/10.3390/math10060851
APA StyleAttaullah, Shakeel, M., Shah, N. A., & Chung, J. D. (2022). Modified Exp-Function Method to Find Exact Solutions of Ionic Currents along Microtubules. Mathematics, 10(6), 851. https://doi.org/10.3390/math10060851






