Knowledge of Fractions of Learners in Slovakia

Abstract

In this research, we set two main goals: to provide empirical data that point to the knowledge of fractions among fifth-grade primary school pupils on a national scale; and to determine the level of knowledge about fractions among university students, including future primary school teachers. We used two tests—the national-wide test T5 for the fifth-graders (a research sample of approximately 45,000 pupils), and the modified fraction test based on Sfard’s theory of reification, for the university students (162 students). At the end of the study, we focused on a content analysis of the university students’ solutions. We identified persistent difficulties with concepts of fractions not only by fifth graders but also by future primary school teachers.

1. Introduction

The processing of fractions is part of our everyday life and is used in situations such as the estimation of rebates, following recipes, or reading maps. Moreover, fractions play a key role in mathematics, since they are involved in probabilistic, proportional, and algebraic reasoning [1]. Fractions involve a qualitative leap for students learning mathematics. Pupils cannot use meanings, models, and symbols for addition, subtraction, multiplication, and division that are valid for integers. For natural and integer units, the unit “one” always represents one object. However, in the case of fractions, a unit, one whole, may consist of several objects (such as three pizzas, or four chocolates), or it may be a composite unit consisting of several objects that form a whole (such as a package including three frozen pizzas, or a box of chocolates containing four chocolate bars) [2].

Fractions belong to one of the most problematic thematic units in the teaching of mathematics. This was proven by many Slovak, Czech, and foreign studies [3,4,5,6]. These studies show that students have difficulty in understanding the concept of fractions. However, what causes students’ low understanding of fractions remains questionable. The authors of [7] state that students tend to be satisfied with mastering numerical operations. They focus on how a rule works and not why a rule works. Pupils learn the rules for counting fractions relatively quickly, only to forget them after a while. In practice, we often find that, even though students control the rules for counting fractions, they remain clueless in a task that involves unusual situations. This means that knowledge is stored only as memory traces, regardless of the previously created knowledge structure.

1.1. Aims of Research

The main goal of this research was to provide empirical data that point to the knowledge of fractions in fifth-grade primary school students on a national scale. Our first goal was to analyze thematic units about fractions in the curriculum in Slovakia. The second aim was to determine the level of knowledge about fractions among university students—future primary school teachers. In this part of the research, we also focused on the content analysis of solutions.

The research was divided into two parts. In the first, we focused on the knowledge of fractions (especially parts of the whole) among fifth-year students on a national scale. In this part of the research, we collaborated with the National Institute for Certified Educational Measurements (NUCEM). This is a state organization founded by the Ministry of Education of Slovakia. It has legal authority. NUCEM provides:

• the external part and the written form of the internal part of the school-leaving examination assigned by the Ministry of Education;
• external testing of fifth and ninth graders;
• preparation of international measurements with the participation of Slovakia.

One of the reasons for the national T5 testing was the lower long-term results of Slovak pupils in international TIMSS testing. In 2019, in mathematics, the students of the Slovak Republic (510 points) achieved a result statistically significantly lower than the average results of EU (527 points) and OECD countries (529 points). In mathematics, our 10-year-old students are comparable in performance to students from Australia, Bulgaria, Italy, Canada, Croatia, Malta, and Spain. Pupils from three EU/OECD countries achieved a lower performance than Slovak students. By contrast, students from 22 EU/OECD countries achieved significantly better results [8].

1.2. Research at the Elementary School

Primary school students only see fractions at an introductory level. With the cooperation of NUCEM, we examined tasks with fractions in Testing 5 (T5). The goal of T5 is to obtain objective information about the performance of pupils from the entrance to the second level of elementary school, to verify the level of their knowledge and skills, and their ability to apply knowledge from the primary level in practical tasks.

The authors of the tasks prepared pilot tests. A sample of 300–400 pupils was given pilot tests. Tasks with 50–60% success progressed to nationwide Testing 5 (cca 45,000 fifth-grade pupils). Pupils solve tests in form A and in form B. These forms were different only in order of tasks or order of distractors. Form A was statistically evaluated.

Research Question

What is the level of knowledge about fractions at the propaedeutic level in primary school pupils?

The second part of the research took place at the university and the sample consisted of students—future primary school teachers. For them, we focused on the level of knowledge according to Sfard’s theory of reification. We also evaluated the tasks that were focused on a part of the whole.

1.3. Research at the University

The T5 results motivated us to verify the fractions knowledge of university students. The research sample consisted of 162 participants, students at Constantine the Philosopher University, in Nitra. These students are future primary level teachers and have an important role in building pupils’ mathematical concepts and knowledge. Primary school students become acquainted with fractions at the propaedeutic level. Therefore, they work mainly with models. We studied how students—future teachers—can work with models, based on Sfard’s theory of reification. The test based on this theory consists of tasks in which different models of fractions appear. In this part of the research, we looked for answers to the questions:

What is the level of Sfard’s theory of reification among future teachers? Can they use fraction models correctly? We also focused on content analysis. Our goal was to point out the most common misconceptions.

2. Theoretical Framework

Pupils acquire knowledge in different ways. The process of forming mathematical knowledge is mainly procedural or conceptual [9,10,11]. Mathematical knowledge is defined as the tendency of an individual in each social context to react and perceive problem situations and to construct, reconstruct, and organize in his mind mathematical processes and objects by which the situation can be solved [11,12].

Procedural knowledge is focused on processes—it requires knowledge of algorithms, techniques, and methods [13]. Conceptual knowledge expresses the interrelationships between the basic elements within a larger structure that allow them to function together. Sfard describes conceptual knowledge as structural concepts that treat mathematical concepts as abstract objects (a static structure). Procedural knowledge of fractions contains various operations and algorithms: addition/subtraction with or without common denominators, multiplication, simplification, etc. Conceptual knowledge of fractions contains various subconstructs—part–whole, operator, proportion, etc., and the various representations of fractions (relation between figural, numeral, verbal representations, etc.) [1].

According to [11], any mathematical concept is usually defined conceptually and procedurally (e.g., when defining rational numbers procedurally, we speak of a rational number as the result of dividing two integers; in the conceptual definition of a rational number, we mean a pair of integers as a member of a specially defined set of pairs).

These two different types of knowledge affect students’ mathematical performance. The conceptual definition of mathematical concepts seems to be more abstract. Based on this, we can consider it as a more advanced stage in the process of developing the concept. In other words, we can say that in the cognitive process, procedural ideas precede structural ideas [12].

Sfard’s theory is of significant interest to us. She defines three levels. They correspond to three degrees of structuralization: interiorization, condensation, and reification.

• In the first stage—interiorization—learners interiorize the process. This means thinking about the process without needing its actual realization.
• In the second stage—condensation—learners can think about a complicated process as a condensed set. They do not need to go into details; rather, they use alternative forms and representations of the concept, combine more processes, and make comparisons and generalizations.
• In the last stage—reification—learners can imagine a concept as a “fully-fledged object” [12]; more representations of the concept are integrated into the student’s reified construct which doesn’t depend upon any process. The learners understand the conceptual category in which it belongs, know its main properties, and use relations between its representatives. Therefore, the created concept is used as an input in higher processes, through which new mathematical objects can be constructed.

2.1. Structure of School System in Slovakia

The school system in Slovakia is divided into:

• Pre-school education (3–6-aged children);
• Basic education—elementary school (6–15-aged learners);
• Basic first stage—primary education (6–10-aged learners);
• Basic second stage—lower secondary education (10–15-aged learners);
• Secondary education: Gymnasia, secondary vocational school, Conservatories (15–19 aged);
• Higher education—universities, higher education institutions.

The network of primary schools also includes multi-grade schools. They do not provide education across grades 1–9, but only within the primary level, as 1-, 2-, 3-, or 4-grade schools. Apart from four-class schools, such schools do not have a separate class for each year. They are located mainly in small villages or in ethnically mixed areas and constitute about one-third of Slovak primary schools. The Hungarian minority has a large representation in Slovakia. There are also schools in which instruction takes place in Hungarian.

2.2. Fractions in the Mathematics Curriculum in Elementary School

Pupils in Slovakia have encountered fractions since the primary stage of primary school (third and fourth year). We were interested in determining the concepts and knowledge about fractions of pupils and students at different levels of education in Slovakia. We focused on primary and tertiary education, first- and second- degree.

Mathematical education in Slovakia is governed by the state’s educational program. Using fractions at the propaedeutic level is one of the goals of teaching mathematics at the primary level of education. Within the thematic unit focused on multiplication and division in the field of multiplication, pupils should know to divide the whole into groups of a given size (division according to content); divide the whole into a given number of equal parts (division into equal parts); name one part of the whole (half, third, quarter); and determine which part of the whole is marked (two thirds, three quarters). Later, pupils should be able to represent a given part of the whole (half, third, quarter, etc.) on a suitable geometric model. They should use different geometric models of fractions (line, circle, rectangular model). Examples of tasks from the textbook are in Figure 1 and Figure 2.

The propaedeutics of fractions (as a part of the whole and as a ratio) continue at the lower secondary level of education. As part of working with natural numbers, problem-solving, and problems developing specific thinking using numerical operations, students should be able to analyze simple problems for the propaedeutics of decimal numbers, fractions, and direct proportionality. Furthermore, when working with decimal numbers, they encounter the propaedeutics of fractions in different contexts (whole, part of the whole, fraction as a part of the whole, representation of the fractional part of the whole).

Compared to abroad (Finland, Sweden, UK), students in Slovakia become acquainted with fractions later. In the United Kingdom, pupils are introduced to fractions in their first year of school. Children learn to identify, find, and name:

• a half as one of two equal parts of an object, shape, or quantity;
• a quarter as one of four equal parts of an object, shape, or quantity.

In the second year, children learn to: recognize, locate, read, and write fractions: $\frac{1}{3 }, \frac{1}{4 },\frac{2}{4 }, \mathrm{and} \frac{3}{4}$ of a length, shape, set of objects, or quantity, write simple fractions, such as half of six is three, and discover the equivalence between two quarters and one half [16]. In Sweden, core content in grades, 1–3 is:

• recognizing parts of a whole and parts of a number;
• learning to name parts and express them as simple fractions;
• discover the relation between simple fractions and natural numbers, and their use in real life.

Knowledge requirements for acceptable knowledge at the end of year 3: Pupils have basic knowledge of fractions by dividing natural numbers into equal parts, and they can compare and name these parts as simple fractions [17].

3. Materials and Methods

We used T5 testing tasks to find out the knowledge of fractions in primary school pupils. For university students, the research tool was a specially designed test focused on fractions by [12]. We adapted the test to the conditions of Slovak schools.

From the T5 tests, we evaluated three fractional tasks from the years 2015, 2018, 2019 (Figure 3).

Problem 1: The problems with fractions first appeared in T5 in 2015. Pupils were to recognize one-third of the picture.

Problem 2: The first task was a task with a mathematical context. The second fractions task (T5-2018) was a task with a real context. The task was focused on determining a part of the whole. We included it in the category of conceptual knowledge and understanding. One half, one quarter, one third and two thirds should be identifiable for the pupils. In options C and D, thirds of the round bed are marked, but the third with tulips is in option D.

Problem 3: This task was only on the pilot test in 2019. Pupils were to identify two-thirds of twelve. The fraction appeared as an operator.

Each task from the T5 test was evaluated separately in the statistical system SPSS 13.0. We used the methods of statistical description, inference, and significant difference. In the descriptive parts, absolute and relative frequencies, mean, standard deviation, standard error of the mean, confidence intervals, pedagogical indicators, and standard error of measurement were used. Statistical inference consists of the application of t-tests and ANOVA. The material significance of the differences was verified by appropriate correlation rates. The formula KR-20 was used to calculate the reliability of the tests because all the tasks were evaluated in binary (0–1) [18].

In the fraction test for university students, we focused on the percentage of success of students in each task. We also focused on a content analysis of students’ solutions.

According to Sfard’s theory of reification, the authors of [11] set up a test for the determination of the level of learners’ conception of fractions. The test contain 21 tasks. They are divided into seven groups (1–7) and three columns (A, B, C). The stages of Sfards´ theory of reification are presented by the columns.

The first three triples of the tasks are focused on part–whole subconstructs of fractions. The fourth triple of the tasks is focused on measuring the subconstruct of fractions. Learners should be able to find a number on a number line and to recognize a number shown by a point on the number line. The fifth, sixth, and seven triples of tasks are related to the notion of equivalence, comparison, and addition of fractions. Some fraction problems are easy, with only a step-by-step procedure required to obtain the solution. Other problems expected include the application of conceptual and procedural understanding [19]. In this article, we take a closer look at only the first three tasks—A1, A2, A3, B1, B2, B3, C1, C2, C3—because they are focused on understanding the fraction as a part in relation to the whole (Figure 4).

Task A1: This problem is concentrated on the part–whole subconstruct. Students need to know that this fraction represents equal shares of a quantity. Its solution contains a step-by-step procedure necessary for interiorization [20].

Task A2: This problem also belongs to the stage of interiorization. To obtain the correct solution, it is necessary to perform a certain process, i.e., to determine the number of triangles, to determine the number of rectangles and triangles together, and to write the fraction.

Task A3: Correct solution depends on a certain procedure: to determine a specific number of objects, divide it by the denominator, and finally multiply by the numerator.

Task B1: Learners can combine various procedures to create the whole, so this task belongs to the second stage—condensation [21].

Task B2: The condensation stage. The correct solution needs alternation between various representations and the combination of procedures with other processes.

Task B3: The solution needs a degree of interiorization of the concept of fractions and the subsequent coupling of different processes.

Task C1: Reification. The square is divided into parts of different sizes and shapes; learners should reconnect the whole. This process presents a final step in understanding the part–whole subconstruct [20]. Reification means an ability to understand the fraction as an object and imagine the representations of the units.

Task C2: This problem assumes the independence of the concept from the process. This is one of the definitions of reification: the different representations of the concept are unified.

Task C3: The last problem requires a combination of the different relations of fractions categories (unit fraction, fraction, whole, improper fraction).

4. Results

This section describes the results of both parts of the research. We present evaluations of tasks with fractions that appeared in T5 in 2015 and 2019. The next section describes the results of the research with the university students and future teachers at the primary level. Pupils’ knowledge depends on the knowledge of teachers. Therefore, we chose these samples.

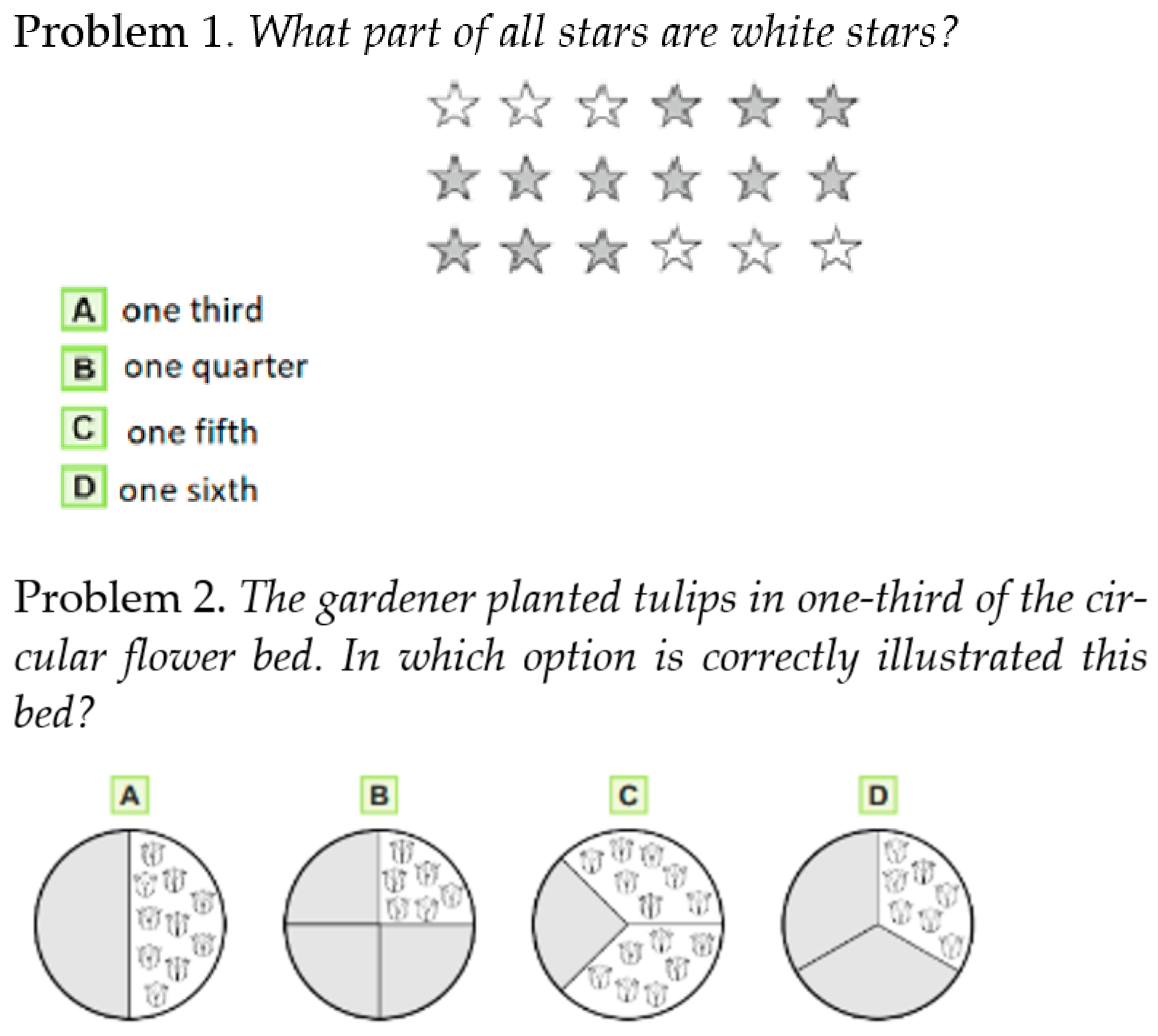
4.1. T5 Results—Pupils’ Solving of Fractions Tasks

Below, we evaluate problems with fractions focused on a part of the whole and we also focus on the analysis of incorrect solutions.

Statistical evaluation of the first task from T5:

The individual distractors are statistically processed (form A) in

Table 1. Item analysis of the first task.

		A	B	C	D	X
1	P.Bis	0.29	−0.04	−0.12	−0.17	−0.24
2	P	0.55	0.08	0.03	0.33	0.02
3	N	11,449	1747	538	6868	403

. The first row of the table shows the values of the interpolation correlation (P.Bis.). In the second row of the table, P means the proportion of students who chose the option. In the third row of the table, N means the number of students who chose the option. The correct answer is marked in yellow.

In the given year, 43,134 fifth-grade pupils took part in the T5 testing; 21,005 of them solved form A. IN total, 11,449 pupils solved the task correctly and 403 pupils did not try to solve the task.

The all-Slovak success rate was 55%. Boys had a higher success rate than girls (66% vs. 59%), and single-grade schools had a higher success rate than multi-grade schools (63% vs. 50%). Pupils with Slovak as the language of instruction were more successful than pupils with Hungarian as the language of instruction (65% vs. 49%). These differences were not statistically significant.

Statistical evaluation of the second task from T5:

The individual distractors are statistically processed in

Table 2. Item analysis of the second task.

		A	B	C	D	X
1	P.Bis	−0.29	−0.18	−0.26	0.51	−0.19
2	P	0.05	0.16	0.15	0.62	0.02
3	N	1360	4191	4.035	16,474	468

. The first row of the table shows the values of the interpolation correlation (P.Bis.). In the second row of the table, P means the proportion of students who chose the option. In the third row of the table, N means the number of students who chose the option. The correct answer is marked in yellow.

In the given year, 48,570 fifth-grade pupils took part in the T5 testing; 26,528 of them solved form A. In form A, 16,474 pupils solved the task correctly and 468 pupils did not try to solve the task.

In total, 62.1% of the tested pupils marked the correct option, D. Pupils from socially disadvantaged backgrounds more often chose option C, where the whole was divided into thirds, but two thirds with planted tulips were marked. Girls had a higher success rate than boys (62.8% vs. 61.5%). The task was easy for pupils from single-grade schools, as well as for schools with Slovak as the language of instruction. The task was moderately difficult for pupils with Hungarian as the language of instruction. The differences were not statistically significant (given the number of pupils in the general population).

The fractions were a part of a whole in these tasks. These problems were of medium difficulty for the pupils.

The third task from the T5 evaluation:

The tasks with fractions as operators were very difficult for pupils.

We tested such a task in a pilot test in 2019. Two-hundred-and-ninety-six pupils took the pilot test and solved the task.

The success rate was only 18.6%. Option B (six pitchers) was chosen by 48.6% of pupils. This task could not be in the national test.

The results show that students have fewer problems with the representation of the unit fractions $\frac{1}{2}$ and $\frac{1}{3}$. Problems occur with the representation of other fractions, e.g., $\frac{2}{3}$. The first introduction to fractions in school is as a part–whole comparison. Pupils start with the unit fractions (one part of a whole), such as a half, a quarter, or a third. For example, if a shape is partitioned equally into five parts, then each unit part is called one-fifth and is written as $\frac{1}{5}$. Pupils who are shown only unit fractions may use a strategy for solving/understanding focused only on the bottom number [22]. Primary school pupils have better results on tasks with familiar fractions ($\frac{1}{2},\frac{1}{4},\frac{3}{4}$) than on tasks with less-familiar fractions. This fact may be due to the more frequent use of the term $\frac{1}{2}$ than other fractional terms. It is shown that the concept of the half could be the first step in creating concepts of fractions [23]. As stated earlier, four subconstructs of fractions are defined. One can understand from some of these subconstructs that a fraction also represents a single number—a rational number with a given magnitude. The complexity of these subconstructs can be a reason why pupils experience difficulty in understanding them. Pupils cannot correctly capture the fraction and determine a part of the whole. These conclusions also correspond to the results obtained by the authors of [24], who state that learners use the division of a continuous whole into an expected number of equal parts; they use the decomposition of any number of those parts as both a separate collection and as parts of the whole. It is not clear when pupils begin quantifying continuous quantities in informal contexts. For pupils’ understanding, part/part relations are easier as an understanding of part/whole relations [1]. Before primary school, most preschool children have a basic understanding of fractions. Young preschoolers can correctly solve non-symbolic calculations with fractions and have a sense of fractions through equal division; an early sense of proportionality and partitioning is also evident. Despite these early foundational abilities, children also develop misconceptions about fractions that can last for many years [25].

When we compared our results with the tasks with fractions that appeared in TIMSS 2011 for Grade 4, we found that Slovak students also had problems with them. In 2011, TIMSS tested five tasks with fractions for: comparison (task 1), determination of a part (task 2), addition of 1/2 and 1/4 (task 3), equivalent fractions (task 4), and inequivalent fractions (5). Figure 5 shows Slovak pupils’ results in comparison with the international average.

Slovak pupils achieved a lower average score in four tasks from five than the international average. They were only more successful on the task in which pupils had to shade one half. The biggest difference to the detriment of Slovak students was in task 4, where it was necessary to choose from the fractions the one that is equivalent to one half. Slovakia achieved a success rate of 32% in this task; the international average was 46% [26].

The fractions tasks were in TIMSS in 2015 and 2019. In comparison with the EU and OECD countries, Slovak pupils achieved a success rate of only 16% in 2015 and 23% in 2019. The international average was 42% in 2015 and 47% in 2019 [8].

As stated in the book from the published TIMMS Level 4 Mathematics assessment items, quantities often do not appear only in natural numbers. Therefore, it is important that pupils understand the concept of fractions. Knowledge should contain the determination of subconstructs as parts of wholes or sets; naming fractions using words, numbers, or models; comparing and arranging simple fractions; and adding and subtracting simple fractions [27].

Our results show that fraction concepts continue to be a problem for primary school students. Fractions tasks generally appear to be problematic. Teachers play an important role in obtaining pupils’ mathematical knowledge.

4.2. Evaluation of the Test and Content Analysis—University Students

We estimated the internal consistency of the test items (reliability) with Cronbach’s alpha, and its value for the whole test is 0.79. The internal consistency of the items can therefore be considered acceptable [28].

Based on statistical data processing, we found that the given test focused on fractions is sufficiently reliable in the conditions of Slovak schools (Cronbach’s alpha for the whole test is 0.79) and is used as a unidimensional tool. The latent variable for us was knowledge of fractions.

Regarding the estimates of the parameters of the test items, using the discriminant parameter $a_i$, we found that out of 21 items, 17 had very strong discrimination, and 4 had moderate discrimination. Based on this, we can argue that the individual items of the test are useful for distinguishing between different levels of knowledge about fractions. About difficulty $b_i$, the items cover a wide range of the latent variable range, from −2.99 to 0.63. The average complexity of the items reached the value of −0.28. We can consider the test less demanding for university students (

Table 3. The percentage success rate for the resolution of the tasks on the fractions test.

Item	%	Factor Loading	Discrimination		Difficulty
			${\mathit{a}}_{\mathit{i}}$	SE	${\mathit{b}}_{\mathit{i}}$	SE
A1	75.3%	0.22	0.38	0.22	−2.99	1.67
A2	84.6%	0.82	2.42	0.65	−1.24	0.20
A3	80.3%	0.74	1.86	0.45	−1.15	0.21
A4	70.4%	0.76	2.02	0.47	−0.70	0.15
A5	90.7%	0.56	1.15	0.40	−2.39	0.65
A6	71.6%	0.31	0.56	0.22	−1.75	0.69
A7	85.8%	0.47	0.92	0.32	−2.24	0.65
B1	63.6%	0.80	2.32	0.55	−0.44	0.13
B2	74.1%	0.41	0.76	0.25	−1.53	0.48
B3	77.2%	0.72	1.77	0.43	−1.03	0.20
B4	61.1%	0.74	1.91	0.42	−0.38	0.14
B5	79.6%	0.23	0.41	0.23	−3.47	1.94
B6	0.6%	0.53	1.07	1.07	5.30	4.26
B7	74.7%	0.47	0.91	0.27	−1.37	0.38
C1	68.5%	0.64	1.43	0.33	−0.75	0.19
C2	37.0%	0.66	1.49	0.33	0.49	0.17
C3	32.1%	0.72	1.75	0.39	0.63	0.16
C4	25.3%	0.67	1.52	0.36	0.99	0.21
C5	5.6%	0.71	1.71	0.57	2.34	0.48
C6	8.0%	0.54	1.10	0.37	2.66	0.70
C7	1.9%	0.73	1.84	0.90	3.03	0.82

Fraction test parameter estimates using a Rasch model (percentage success rate for resolution, factor loading, difficulty—item difficulty, SE—standard error) [28].

).

Items A1, A2, A3, B1, B2, B3, C1, C2, and C3 were of most interest to us in terms of pupils solutions.

When evaluating the tasks, we used only code 0 for an incorrect answer, code 1 for the correct answer, and code N/A if the student did not solve the task. In the case of multiple choices, the student received 1 if he marked all the options correctly.

Figure 6 shows the overall success of solving tasks A1–C3 by university students. The correct answer is coded as 1, the incorrect answer is coded as 0, and if the student did not solve the problem, he was assigned the code N/A.

As we can see, the least demanding were tasks A1, A2, and A3, which were solved correctly by approximately 80% of the students. These tasks are at a level at which the student needs to master basic procedures and algorithms to solve them. Tasks B2, B3 were moderately demanding, and they were solved correctly by approximately 71% of students. Here, however, we also observed a gradual increase in incorrect answers and in the number of students who did not solve the tasks. These tasks were at a level where the student can already combine and connect individual procedures, compare them, and generalize.

The most difficult tasks for students were B1, C1, C2, and C3. Task C2 was solved correctly by approximately 37% of students and task C3 by only 32% of students. The highest percentage of incorrect answers was for task C2 (approximately 50%) and the most frequently unresolved task was task C3 (20%).

Task B1 is from the interiorization stage, but only 63% of students solved it correctly. We were interested in the mistakes of the students made in solving it.

In this example, the student did not distinguish the size of the unit parts. He did not realize that the whole is not divided into equal parts and focused only on the number of parts. This led to incorrect results: one-fifth and one-seventh (Figure 7).

A different student incorrectly determined the whole, from which he wrote the part in the shape of a fraction. The student incorrectly expressed a part of the already redistributed part of the whole (one quarter of the whole square). Thus, 1/2 and 1/3 expressed the marked parts of the smaller square (Figure 8).

Another student identified a quantity and one eighth of a whole, but it was not precisely determined. Furthermore, there is a numerical quantity expressed in the form of a fraction of the relationship between a part and a whole, where the numerator can express the number of marked parts and the denominator the number of all parts into which the whole is divided. The student tried to express numerically that the whole (square) is divided into four parts and the marked part in the problem after Figure 9a represents the one-half of the four parts and in the problem after Figure 9b, again, one eighth. One eighth was incorrect based on the division of the whole into four parts and then again into four smaller parts, which is a sum of eight parts (Figure 9).

The next student determined half and a quarter of some whole, which, however, he incorrectly identified, and he could not correctly express his idea numerically in the form of a fraction. According to the entries in the form of a mixed number, 4 and 1/2 and 4 and 1/4, the student considered one smaller square. Consequently, the student wrote four units and a half as a part of this unit, and, in the case of Figure 10b as a quarter of this unit (Figure 10).

Of the other solutions, we would like to point out some correct numerical expressions of the relationship between the marked part and the whole, which were not in the basic form of a fraction. These entries express the process of dividing the whole into parts. We can say that these students had acquired more procedural knowledge of fractions than conceptual (Figure 11).

The most common misconceptions when interpreting a fraction as part of a whole were as follows:

Failure to realize the need to divide the whole into equal parts when working with continuous and discrete models.

Incorrect identification of the whole and treatment of a part of the whole as a whole.

Poor understanding of the meaning of numbers in the notation of a fraction, along with the perception of these numbers as isolated natural numbers without a mutual relation.

Not realizing that the number in the denominator expresses the number of parts into which the whole is divided, and that the numerator expressing the number of these parts manifests itself in problems in the equivalence and comparison of fractions, especially in the addition of fractions.

Expressing a part of the whole on the principle of interpreting the fraction as a ratio, indicating a complete misunderstanding of the fraction as a part of the whole.

Knowledge of fractions in university students is at the level of the transition stage between interiorization and condensation. We consider this result to be below average for future teachers.

5. Discussion and Conclusions

Fractions have a significant place in mathematics. They provide a different understanding of the world of numbers than natural/whole numbers [29].

This research dealt with the knowledge of fractions held by pupils in the fifth year of primary school on a national scale. In finding an answer to the research question, ‘What is the level of knowledge about fractions at the propaedeutic level in primary school students?’, we concluded that fifth-grade pupils control stem fractions but have a problem with fractions in which the numerator does not equal 1.

Children experience fractions in everyday life (half an hour, a quarter of a cake). These experiences are classified and together form an organized whole, the so-called condensed experience. Based on this, students can divide wholes into equal parts, which is the concept of stem fractions. The unit fraction is 1/n, one part of the whole, and represents the developmental stage of understanding fractions. This should not be a transitional concept before the introduction of the concept of fractions [6]. The unit fraction is a very important concept, and its understanding creates a base for fraction operations [30]. In the practice, we can see that teachers do not pay enough attention to this concept [31].

We agree with the statements in [1] that most learners probably do not understand the equivalent fraction. This can be related to the differences between the concept of fractions and the concept of natural numbers. It is very important to perform a conceptual reorganization for a deeper understanding of the properties and subconstructs of fractions. The fraction lesson should include exercises with specific models to improve pupils’ grasp of the concept. The conclusions of previous research showed that primary-level pupils work with fractions as natural numbers. Equivalent and improper fractions present a very difficult concept for understanding, so learners use misunderstood processes. This phenomenon can be related to educational practice—learners spend most of their time practicing basic algorithms [1].

Concrete activities and their teaching can help primary school pupils develop the necessary abstract concepts [32].

In the second part of this research, we focused on university students, who are future teachers in primary education. We were interested in the level of their knowledge about fractions and how they can work with fraction models.

The results showed that future teachers know about fractions at the level of the transition stage between interiorization and condensation. This means that they are beginning to combine, process, compare, and generalize processes.

Fractions are a very complex mathematical area, and it is necessary that primary-level teachers understand the. Fractional concepts create the base for understanding other advanced mathematical concepts [33]. The analysis of students’ solutions enabled us to identify several students’ difficulties with understanding fractions on an informal level. The most substantial misconceptions occurred in various areas of the manipulation of fractions, such as determining a part of a whole in a geometrical model of a fraction, expressing a part of a whole in the form of a fraction, the notation of a fraction as a number in the form of a numerator, fraction bar, or denominator, the meaning of the numerator and the denominator of a fraction in expressing the number of given parts and the number of all parts into which the whole is divided, positioning a number on the number line; and arranging and comparing fractions with a tendency to derive it from the natural arrangement of natural numbers.

Many students perceive fractions only as objects of arithmetic operations and as ordered pairs of numbers. The rules for working with fractions are kept in students’ memories, but they use the language of fractions when modeling real situations, derive other rules from known rules, reconstruct forgotten rules, and justify the rules of argumentation. Understanding fractions is often very demanding for students, who create a correct idea of the fraction within their thinking. Thus, we can say that many students manage fractions only at the level of interiorization. Over time, they remember only fragments of work [6].

Our results correspond with [34], where it was found that teachers have an inadequate understanding of fractions. Teachers need to be better prepared and may need more comprehensive mathematical education to be more effective in the classroom. This is one of the reasons for improving the knowledge of fractions in primary school students. Teachers’ knowledge of mathematics is very important for their success. This success also depends on the mathematical knowledge of the teacher [35]. This statement corresponds with Shin’s argument that senior learners are sensitive to the professional mathematical competence of teachers. This competence may affect the mathematical results of learners, and their other interests in mathematics [36].

Brown’s research has confirmed that students are at risk of failing to study mathematics in college, not because of a lack of understanding of high school concepts, but rather because of a lack of understanding of the concepts most explicitly addressed in the fifth, sixth, and seventh grades. The misunderstanding of fractions was common among these students [37].

The learning and teaching of fractions present a difficult and complex process. It is necessary to use multiple fraction models for their conceptual understanding. Learners who understand fractions deeply can recognize all the subconstructs of fractions. They know that various representations do not represent different fractions [38]. According to studies by [39,40], an incorrect conceptual understanding can be one of the reasons for the different success levels of learners when using fraction operations in various contexts.

Developing meaningful learning and creating correct concepts of fractions and their subconstructs in schools depends upon how teachers present these fraction concepts to their learners [23]. According to [41], if teachers use incorrect or confusing language to explain fraction concepts, students can learn to describe fractions using the misconceptions in the teacher’s language, and not understand the concepts correctly enough. Teachers, in their pedagogy, must use different subconstructs of fraction concepts. This is a way to correct learners’ understanding of fraction concepts.

Although manipulative models are necessary in mathematics teaching in general, they are irreplaceable in the development of learners’ conceptual understanding of fractions. Circular and rectangular models, colored chips, and Cruisenaire rods should become components of fractions teaching. In addition to various models of fractions representation, fractions lessons should consist of various activities, including discourse among learners [39].

Our research has shown that not only fifth graders but also university students, who are future primary level teachers, have shortcomings in their understanding of fractions. Among university students, we observed significant misconceptions in the understanding of fractions, as well as the subconstruct of the relationship between parts and wholes. This fact may be reflected in their pedagogical practice. Therefore, it is necessary to focus our attention on the training of future teachers. Didactic mathematics courses should focus on working with different models of fractions, their creation, and their discussion.