Exact Analytical H-BER for Ad Hoc XOR H-Map Detector for Two Differentially Modulated BPSK Sources in H-MAC Channel

Abstract

In the article, we present an ad hoc (AH) detector for two differentially encoded BPSK sources in the Hierarchical MAC (H-MAC), i.e., for the case when the receiver sees the superposition of non-orthogonal signals from individual sources. (Prefix “H-” means Hierarchical, it emphasizes that the entity is related to the many-to-one principle.) The AH detector decodes the XOR H-map of the two BPSK streams—in other words, it decides whether the transmitted symbols from the two sources are the same or opposite. The BER of the detection in H-MAC is denoted as H-BER. The H-BER is compared with the other two differential detectors, with the coherent (Coh) detector, and with an approximate coherent (ApC) detector. The exact analytical H-BER formula is derived for the ad hoc and coherent detectors. The proposed ad hoc detector is very simple for evaluation, does not require the estimation of subchannel phases, does not depend on noise variance, and it is uniformly only roughly 3.5 dB worse than the coherent one.

1. Introduction

The two-way relay channel (TWRC) with one relay and two BPSK/PSK sources is a well-studied network. In the standard four-phase communication protocol, the first source transmits to the relay, then the relay resends the data to the second source. The same occurs in the opposite direction—the second source sends its data to the relay, and the relay again retransmits its data to the first source. The four-phase protocol can be reduced to the three-phase protocol by the application of network coding [1]—the relay collects data from both sources, computes a network function, and broadcasts the output back to the sources. Each source can then compute the data of the other source. In the most simple case, the relay computes the XOR of the source messages. Wireless networks allow further reduction of the number of phases—a two-phase protocol can be established. Both sources can transmit simultaneously to the relay. There are two main relay strategies: (1) Amplify and Forward (AF)—the relay simply retransmits the signal it receives without decoding anything; (2) Hierarchical Decode and Forward (HDF)—the relay decodes the XOR of the source symbols directly from the non-orthogonal superposition of source signals, and forwards this “XOR frame”. HDF is also called Denoise and Forward by some authors. Network coding applied in wireless networks, specifically on their physical layer, is often called Physical Layer Network Coding (PLNC) or Wireless Physical Layer Network Coding (WPNC). Details on WPNC can be found in the book [2]. The key idea is to let sources transmit at the same frequency and time, and so save communication resources. Even though the relay cannot separate the interfering signals (by linear methods), it can decode the network function—the XOR of source symbols. The critical phase, when sources transmit at the same frequency and time to the relay, is called Hierarchical MAC (H-MAC). Our work focuses on the transmission and detection in H-MAC. The performance of coherent PLNC schemes is critically dependent on precise channel estimation. We use the differential modulation to compensate for the need to know subchannel phases, i.e., to know complete channel state information (CSI) at the relay node. We consider the detector at the relay to be “differential” to emphasize the fact that the sources are differentially encoded, i.e., that it uses two subsequent channel observations.

2. Related Works

The AF relay strategy is mainly analyzed in other works. In [3], Song et al. analyze differential BPSK in TWRC with the AF relay strategy in Rayleigh fading channels. The differential method is only 3 dB worse than the coherent method. The same scenario, but with multiple relays, is analyzed by Song et al. in [4]—again, the differential method is 3 dB worse than the coherent case. In [5], Xu et al. investigate both AF and HDF with differential modulation for TWRC with multiple relays and MIMO systems. Kanthimatchi and Amutha in [6] introduce generalized differential amplitude-phase modulation for TWRC, and the AF relay strategy is assumed.

In [7], Ju and Kim derived tight upper and lower bounds for H-BER, Huang and Yuan in [8] studied the TWRC with multiple antennas, both papers studied coherent detection with the HDF relay strategy. The HDF relay strategy with differential BPSK/PSK is studied in [9] by Guan and Liu. They derived the covariance matrix of the two-point observation where the mean is over subchannel phases and noise. Subsequently, they approximated the joint distribution of the two-point observation by the joint complex normal (JCN) distribution with this covariance matrix. The detector is used with energy harvesting schemes in [10]. The work of Guan and Liu is extended by Fan et al. in [11] to 4 and 8PSK alphabets, a bitwise-XOR H-map, but the error performance is poor. Another approach is used in [12], where the authors used the product of subsequent observations, as an analogy with one-to-one transmission and reception. In [13], Hron and Sykora derived a closed-form detector that does not need the knowledge of subchannel phases. The joint pdf of observation is marginalized by the maximum over subchannel phases (joint maximum likelihood, JML). The performance is only approximately 3 dB worse than the coherent case.

The paper is organized as follows. In Section 3, the system model for both coherent detection and differential detection in H-MAC is given. The ad hoc detector is presented. Moreover, the coherent detector and its high SNR approximation are given. In Section 4, we present analytical formulae for H-BER of the AH detector and coherent detectors, and we compare our differential AH detector with JML from [13] and JCN from [9]. Further, we present other numerical results such as decision regions and H-BER figures. In Section 5, we conclude the paper.

The key contribution of the paper is the proposition of the differential ad hoc (AH) detector of the XOR of source symbols. Sources use differential BPSK (DBPSK) modulation. The AH detector uses two subsequent observations together with the knowledge of the magnitudes of subchannel attenuations, i.e., the minimum of them. The loss of the proposed ad hoc (AH) detector in the error rate is 0.5 dB with regard to the JML and 3.5 dB with regard to the coherent detector. AH is slightly worse than JCN for low SNRs, where H-BER of both detectors is approximately ${10}^{-2}$, but AH substantially outperforms JCN for higher SNRs.

3. Materials and Methods

The section starts with stating system models of reception in H-MAC. System models for both uncoded BPSK sources and differentially modulated/encoded BPSK sources are given. For H-MAC with uncoded BPSK sources, we recall the coherent detector (Coh) of the XOR H-map. Additionally, a very good approximation of the Coh detector is given—it is denoted as the approximate coherent (ApC) detector. Further, for H-MAC with differentially modulated BPSK sources, an ad hoc detector of the XOR H-map is derived. It uses two subsequent observations. Finally, a general expression for H-BER is shown.

The system model with uncoded BPSK sources is given as

$$y_n={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{d}_n^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{d}_n^{\left(2\right)}+w_n.$$

(1)

It is depicted in Figure 1.

In Equation (1), $d_n^{\left(1\right)},d_n^{\left(2\right)}$ are uncoded n-th BPSK symbols. ${\eta }_1,{\eta }_2$ and ${\phi }_1,{\phi }_2$ are magnitudes and phases of subchannel attenuations, respectively. Index 1 and 2 indicate the source. $w_n\sim CN(0,{\sigma }_w^2)$ is the complex Gaussian noise with mean 0 and variance ${\sigma }_w^2$.

The H-MAC system model for the differentially encoded BPSK (DBPSK) sources is given as

$$y_n={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{q}_n^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{q}_n^{\left(2\right)}+w_n.$$

(2)

The communication system is illustrated in Figure 2.

Differential BPSK modulation is given as

$$q_n^{\left(i\right)}=q_{n-1}^{\left(i\right)}{d}_n^{\left(i\right)},q_0^{\left(i\right)}=1,i\in 1,2.$$

(3)

$d_n^{\left(1\right)},d_n^{\left(2\right)}$ are uncoded BPSK symbols; $q_n^{\left(1\right)},q_n^{\left(2\right)}$ are differentially encoded BPSK symbols. Other variables in (2) are the same as in (1).

The ad hoc detector will use two subsequent observations of the H-MAC channel with DBPSK sources. The two-point observation is

$$y_0={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{q}_0^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{q}_0^{\left(2\right)}+w_0,$$

(4)

$$y_1={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{q}_0^{\left(1\right)}{d}_1^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{q}_0^{\left(2\right)}{d}_1^{\left(2\right)}+w_1.$$

(5)

In the Equations (4) and (5), we will use the following substitutions:

$$\begin{array}{cc}\hfill u_A& ={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{q}_0^{\left(1\right)}={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1},{\alpha }_1={\phi }_1+arg\left(q_0^{\left(1\right)}\right).\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill u_B& ={\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{q}_0^{\left(2\right)}={\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2},{\alpha }_2={\phi }_2+arg\left(q_0^{\left(2\right)}\right).\hfill \end{array}$$

(7)

However, for simplicity of notation, we will omit ${}_1$ index in $d_1^{\left(1\right)},d_1^{\left(2\right)}$, and obtain

$$\begin{array}{cc}\hfill y_0& =u_A+u_B+w_0,\hfill \\ \hfill y_1& =u_A{d}^{\left(1\right)}+u_B{d}^{\left(2\right)}+w_1.\hfill \end{array}$$

(8)

Now, we recall the coherent detector. It uses one observation from H-MAC with uncoded BPSK (1). The channel likelihood function conditioned by the source BPSK symbols and the one conditioned by the H-symbol b is given as

$$\begin{array}{c}\hfill p\left(y\right|d^{\left(1\right)},d^{\left(2\right)})=exp\left(\frac{-1}{{\sigma }_w^2}{|y-u(d^{\left(1\right)},d^{\left(2\right)})|}^2\right),\end{array}$$

(9)

$$\begin{array}{c}\hfill p\left(y\right|b)=\frac{1}{2}\sum _{[d^{\left(1\right)},d^{\left(2\right)}]:b=\mathrm{xor}(d^{\left(1\right)},d^{\left(2\right)})}p\left(y\right|d^{\left(1\right)},d^{\left(2\right)}),\end{array}$$

(10)

where (for notation simplicity, we have omitted lower time-index n) the useful signal u is

$$\begin{array}{cc}\hfill u(d^{\left(1\right)},d^{\left(2\right)})& ={\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{d}^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{d}^{\left(2\right)}.\hfill \end{array}$$

(11)

We recall that the H-symbol b is the output of the H-map. In our case, $b=\mathrm{xor}(b^{\left(1\right)},b^{\left(2\right)})\equiv \mathrm{xor}(d^{\left(1\right)},d^{\left(2\right)})$. The coherent detector of the XOR H-map is derived from the likelihood test

$$\begin{array}{cc}\hfill p\left(y\right|b=0)& \underset{\widehat{b}=0}{\overset{\stackrel{\wedge }{b}=1}{\lessgtr }}p\left(y\right|b=1),\hfill \end{array}$$

(12)

$$e^{\frac{-1}{{\sigma }_w^2}{|y-u(1,1)|}^2}+e^{\frac{-1}{{\sigma }_w^2}{|y-u(-1,-1)|}^2}\underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}{e}^{\frac{-1}{{\sigma }_w^2}{|y-u(-1,1)|}^2}+e^{\frac{-1}{{\sigma }_w^2}{|y-u(1,-1)|}^2}.$$

(13)

We obtain the coherent detector of the form

$$\begin{array}{cc}\hfill M_{\mathrm{Coh}}& =\frac{cosh\left(\frac{2}{{\sigma }_w^2}\Re \left\{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\right\}\right)}{cosh\left(\frac{2}{{\sigma }_w^2}\Re \left\{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}-{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\right\}\right)},\hfill \end{array}$$

(14)

$$M_{\mathrm{Coh}}\underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}exp\left(\frac{4{\eta }_1{\eta }_2}{{\sigma }_w^2}cos\left(\phi \right)\right).$$

(15)

In the Equation (15), $\phi ={\phi }_1-{\phi }_2$. In addition, $\widehat{b}$ is the estimated H-symbol.

For the derivation of the approximate coherent detector, we use the following substitutions:

$$\begin{array}{cc}\hfill a& =\Re \left\{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\right\},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill b& =\Re \left\{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}-{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\right\}.\hfill \end{array}$$

(17)

The derivation follows.

$$\frac{cosh\left(\frac{2}{{\sigma }_w^2}a\right)}{cosh\left(\frac{2}{{\sigma }_w^2}b\right)}=\frac{e^{\frac{2}{{\sigma }_w^2}\left|a\right|}+e^{\frac{-2}{{\sigma }_w^2}\left|a\right|}}{e^{\frac{2}{{\sigma }_w^2}\left|b\right|}+e^{\frac{-2}{{\sigma }_w^2}\left|b\right|}}=e^{\frac{2}{{\sigma }_w^2}\left(\right|a|-\left|b\right|)}\underset{Q}{\underbrace{\frac{1+e^{\frac{-4}{{\sigma }_w^2}\left|a\right|}}{1+e^{\frac{-4}{{\sigma }_w^2}\left|b\right|}}}}\underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}{e}^{\frac{4}{{\sigma }_w^2}{\eta }_1{\eta }_{2}cos\left(\phi \right)},$$

(18)

$$\begin{array}{cc}\hfill \left|a\right|-\left|b\right|+\frac{{\sigma }_w^2}{2}ln\left(Q\right)& \underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}2{\eta }_1{\eta }_{2}cos(\phi ).\hfill \end{array}$$

(19)

We obtain criterion (19) from (18) by applying $\frac{{}^2}{2}ln(.)$ to both sides of (18). In the expressions (18) and (19),

$$\begin{array}{cc}\hfill Q& \in \left(\frac{1}{2},2\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill ln\left(Q\right)& \in (-ln(2),ln(2\left)\right)\approx (-0.7,0.7).\hfill \end{array}$$

(21)

Finally, after resubstitution (16) and (17) to the (19), we obtain the approximate detector of the form

$$\begin{array}{cc}\hfill M_{\mathrm{ApC}}& =|\Re \{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\left\}\right|\hfill \\ \hfill & -|\Re \{y^{*}({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}-{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})\left\}\right|,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill M_{\mathrm{ApC}}& \underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}2{\eta }_1{\eta }_{2}cos(\phi ).\hfill \end{array}$$

(23)

The approximation is based on the omission of the expression $\frac{{\sigma }_w^2}{2}ln\left(Q\right)$ from (19). It is close to zero for higher SNR.

Now, we derive an ad hoc differential detector. Assume the H-MAC channel with DBPSK sources, given by the channel model (2). In the derivation of the ad hoc detector, we take the two-point observation (8), and assume a no-noise case. Thus, $y_0=u_A+u_B$, $y_1=u_A{d}^{\left(1\right)}+u_B{d}^{\left(2\right)}$. We define two auxiliary sets, $B_0=\{u_A+u_B,-u_A-u_B\}$ and $B_1=\{u_A-u_B,-u_A+u_B\}$. The sets are composed to correspond to H-symbols $b=0$ and $b=1$, respectively. The detector has to decide whether $y_1\in B_0$ or $y_1\in B_1$. It will choose the set ($B_0$ or $B_1$, i.e., the H-symbol $b=0$ or $b=1$) to which $y_1$ is closer. We use the Euclidean distance. The distance to the $B_0$ can be computed directly, because $B_0=\{y_0,-y_0\}$, and $y_0$ is known. Thus, the detector metric is

$$\begin{array}{c}\hfill M_{\mathrm{AdH}}=min\left\{\right|y_1-y_0|,|y_1+y_0\left|\right\}.\end{array}$$

(24)

The decision threshold is selected to be the mid-value between the case $y_1\in B_0$, i.e., $M_{\mathrm{AdH}}=0$, and the case $y_1\in B_1$, i.e., $M_{\mathrm{AdH}}=2min\left\{\right|u_A|,|u_B\left|\right\}=2min\{{\eta }_1,{\eta }_2\}$, as can be seen from

Table 1. Values of $y_0+y_1$ and $y_0-y_1$ for all tuples of $[d^{\left(1\right)},d^{\left(2\right)}]$.

Event Name	$d^{\left(1\right)}$	$d^{\left(2\right)}$	${\mathit{y}}_0+{\mathit{y}}_1$	${\mathit{y}}_0-{\mathit{y}}_1$	b
$A_1$	1	1	$2(u_A+u_B)$	0	0
$A_2$	1	−1	$2u_A$	$2u_B$	1
$A_3$	−1	1	$2u_B$	$2u_A$	1
$A_4$	−1	−1	0	$2(u_A+u_B)$	0

.

Thus,

$$\begin{array}{cc}\hfill M_{\mathrm{AdH}}& \underset{\widehat{b}=1}{\overset{\widehat{b}=0}{\lessgtr }}min\{{\eta }_1,{\eta }_2\}.\hfill \end{array}$$

(25)

In the criterion (25), we will use the shortcut ${\eta }_{\min }=min\{{\eta }_1,{\eta }_2\}$.

To gain insight into what other differential detectors look like, we will proceed as in [13]. The parts of two-point observation $y_0,y_1$ are independent complex Gaussian distributed given ${\eta }_1$, ${\eta }_2$, ${\phi }_1$, ${\phi }_2$, $d^{\left(1\right)}$, $d^{\left(1\right)}$. We assign $\mathit{\eta }=[{\eta }_1,{\eta }_2]$, $\mathit{\phi }=[{\phi }_1,{\phi }_2]$. Single and joint likelihood of observations is, respectively,

$$\begin{array}{cc}\hfill p(y_0& |\mathit{\eta },\mathit{\phi })=\frac{1}{\pi {\sigma }_w^2}exp\left(\frac{-1}{{\sigma }_w^2}|y_0-({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_2}){|}^2\right),\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill p(y_1& |d^{\left(1\right)},d^{\left(2\right)},\mathit{\eta },\mathit{\phi })=\frac{1}{\pi {\sigma }_w^2}exp\left(\frac{-1}{{\sigma }_w^2}|y_1-({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{d}^{\left(1\right)}+{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_2}{d}^{\left(2\right)}){|}^2\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill p(y_0,y_1& |d^{\left(1\right)},d^{\left(2\right)},\mathit{\eta },\mathit{\phi })=p\left(y_0\right|\mathit{\eta },\mathit{\phi })p\left(y_1\right|d^{\left(1\right)},d^{\left(2\right)},\mathit{\eta },\mathit{\phi }).\hfill \end{array}$$

(28)

The joint pdf (Probability Density Function) of the two-point observation given H-symbol (Hierarchical symbol) b is

$$\begin{array}{cc}\hfill p(y_0,y_1|b=0,\mathit{\eta },\mathit{\phi })& =\frac{1}{2}\left[p(y_0,y_1|-1,-1,\mathit{\eta },\mathit{\phi })+p(y_0,y_1|1,1,\mathit{\eta },\mathit{\phi })\right].\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill p(y_0,y_1|b=1,\mathit{\eta },\mathit{\phi })& =\frac{1}{2}\left[p(y_0,y_1|-1,1,\mathit{\eta },\mathit{\phi })+p(y_0,y_1|1,-1,\mathit{\eta },\mathit{\phi })\right].\hfill \end{array}$$

(30)

The detector decides according to the ML (maximum likelihood) criterion

$$\begin{array}{c}\hfill p(y_0,y_1|b=0,\mathit{\eta },\mathit{\phi })\underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}p(y_0,y_1|b=1,\mathit{\eta },\mathit{\phi }).\end{array}$$

(31)

The criterion (31) can be simplified to the form

$$\begin{array}{cc}\hfill & \left[exp\left(\frac{2}{{\sigma }_w^2}\Re \left\{({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})y_{+}^{*}\right\}\right)+exp\left(\frac{2}{{\sigma }_w^2}\Re \left\{({\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2})y_{-}^{*}\right\}\right)\right]\hfill \\ \hfill & ·exp\left(\frac{-4}{{\sigma }_w^2}{\eta }_1{\eta }_{2}cos({\phi }_1-{\phi }_2)\right)-[exp\left(\frac{2}{{\sigma }_w^2}\Re \{{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{y}_{+}^{*}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{y}_{-}^{*}\}\right)\hfill \\ \hfill & +exp\left(\frac{2}{{\sigma }_w^2}\Re \{{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}{y}_{-}^{*}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}{y}_{+}^{*}\}\right)]\underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}0,\hfill \end{array}$$

(32)

where $=y_0+y_1$ and $=y_0-y_1$. Upper index ${}^{*}$ means a complex conjugate. We can marginalize the (32) criterion by taking the maximum over $[{\phi }_1,{\phi }_2]\in {(0,2\pi )}^2$, as was done in [13], or by integration. However, in all types of marginalization over phases $[{\phi }_1,{\phi }_2]$, the resulting detector should be a function of the sum and the difference of subsequent observations. This is also true of our ad hoc case.

H-BER Formula Derivation

In this subsection, we derive a general expression for the H-BER of a detector of the XOR H-map of two BPSK sources. The detector metric will be called M—it is a function of observation(s). Denote by a the decision threshold. We assume the detector to be of the form

$$\begin{array}{cc}\hfill M& \underset{\widehat{b}=0}{\overset{\widehat{b}=1}{\lessgtr }}a.\hfill \end{array}$$

(33)

Next, the probability of the symbol error P_e = H-BER is derived.

$$\begin{array}{cc}\hfill P_e& =Pr\{\widehat{b}\ne b\}=Pr\{\widehat{b}=0,b=1\}+Pr\{\widehat{b}=1,b=0\},\hfill \\ \hfill & =\frac{1}{2}[Pr\{\widehat{b}=0|b=1\}+Pr\{\widehat{b}=1|b=0\}],\hfill \\ \hfill & =\frac{1}{4}[Pr\{\widehat{b}=0|A_2\}+Pr\{\widehat{b}=0|A_3\}+Pr\{\widehat{b}=1|A_1\}+Pr\{\widehat{b}=1|A_4\}],\hfill \\ \hfill & =\frac{1}{4}\left[2+{\int }_{x\le a}[p_M\left(x\right|A_1)+p_M\left(x\right|A_4)-(p_M\left(x\right|A_2)+p_M\left(x\right|A_3))]\mathrm{d}x\right],\hfill \end{array}$$

(34)

where $p_M\left(x\right|A_i)$ is the pdf (Probability Density Function) of M, given event $A_i$. The events are defined in Table 1.

4. Results

In this section, we first show the derived H-BER formulae. The key is to derive the pdf of the detector metric, which is then submitted to Equation (34). Channel observations are taken as random variables (RVs) and detector metrics are functions of observations—functions of RVs. We use standard procedures from the book [14] to derive the pdf of the transformed RVs. Subsequently, we show H-BER of detectors in figures. Details of the derivation can be found in Appendix B. Gaussian RVs (random variables) are recalled in Appendix A. Other supplementary operations with RVs are in Appendix C.

4.1. Analytical H-BER Formula for Ad Hoc (AH) Differential Detector

$p_{M_{\mathrm{AdH}}}$ can be derived to be

$$\begin{array}{cc}\hfill p_M\left(x\right|A_i)& =p_{|Y_0+Y_1|}\left(x\right|A_i)(1-F_{|Y_0-Y_1|}\left(x\right|A_i))\hfill \\ \hfill & +p_{|Y_0-Y_1|}\left(x\right|A_i)(1-F_{|Y_0+Y_1|}\left(x\right|A_i)),\hfill \end{array}$$

(35)

where $p_{|Y_0\pm Y_1|}$ and $F_{|Y_0\pm Y_1|}\left(x\right|A_i)$ is the pdf and cdf (Cumulative Density Function) of Rice distribution, respectively,

$$\begin{array}{cc}\hfill p_{|Y_0\pm Y_1|}\left(x\right|A_i)& \equiv p\left(x\right|\nu ,\sigma ),\hfill \\ \hfill & =\frac{x}{{\sigma }^2}exp\left(\frac{-(x^2+{\nu }^2)}{2{\sigma }^2}\right)I_0\left(\frac{x\nu }{{\sigma }^2}\right).\hfill \end{array}$$

(36)

In the expression (36), $\nu =|u_A(1\pm d^{\left(1\right)})+u_B(1\pm d^{\left(2\right)})|$, $\sigma ={\sigma }_w$. Then,

$$\begin{array}{c}{P}_e=\frac{1}{2}+\frac{1}{4}{\int }_0^{{\eta }_{\min }}[p_{M_{\mathrm{AdH}}}\left(x\right|A_2)+p_{M_{\mathrm{AdH}}}\left(x\right|A_3)-p_{M_{\mathrm{AdH}}}\left(x\right|A_1)-p_{M_{\mathrm{AdH}}}\left(x\right|A_4)]\mathrm{d}x,\hfill \\ \hfill & =\frac{1}{2}+\frac{1}{2}{\int }_0^{{\eta }_{\min }}[p\left(x\right|2{\eta }_1,{\sigma }_w)Q_1\left(\frac{2{\eta }_2}{{\sigma }_w},\frac{x}{{\sigma }_w}\right)+p\left(x\right|2{\eta }_2,{\sigma }_w)Q_1\left(\frac{2{\eta }_1}{{\sigma }_w},\frac{x}{{\sigma }_w}\right)\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & -\left[p\right(x\left|2\right|u_A+u_B|,{\sigma }_w)Q_1\left(0,\frac{x}{{\sigma }_w}\right)+p\left(x\right|0,{\sigma }_w)Q_1\left(\frac{2|u_A+u_B|}{{\sigma }_w},\frac{x}{{\sigma }_w}\right)\left]\right]\mathrm{d}x,\hfill \end{array}$$

(38)

where $Q_1$ is the Marcum Q-function and

$$\begin{array}{cc}\hfill p\left(x\right|2|u_A+u_B|,{\sigma }_w)& =\frac{1}{2}\left(p\left(x\right|2|{\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|{\sigma }_w,)+p(x||{\eta }_1-{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|,{\sigma }_w)\right).\hfill \\ \hfill Q_1(\frac{2|u_A+u_B|}{{\sigma }_w},& \frac{x}{{\sigma }_w})=\frac{1}{2}(Q_1\left(\frac{2|{\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|}{{\sigma }_w},\frac{x}{{\sigma }_w}\right)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & +Q_1\left(\frac{2|{\eta }_1-{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|}{{\sigma }_w},\frac{x}{{\sigma }_w}\right)).\hfill \end{array}$$

(40)

Again, we have used $\phi ={\phi }_2-{\phi }_1$.

4.2. Analytical H-BER Formula for Coherent Detector (Coh)

To express $p_{M_{\mathrm{Coh}}}$ (pdf of M given in (14)) it is useful to define some auxiliary variables. The detector’s decision-threshold is

$$\begin{array}{cc}\hfill a_{\mathrm{Coh}}& =exp\left(\frac{4{\eta }_1{\eta }_{2}cos\left(\phi \right)}{{\sigma }_w^2}\right).\hfill \end{array}$$

(41)

Define (complex valued constant)

$$c=\frac{{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}-{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}}{{\eta }_1{\mathrm{e}}^{\mathrm{j}{\phi }_1}+{\eta }_2{\mathrm{e}}^{\mathrm{j}{\phi }_2}},c_{\mathrm{re}}=\Re \left\{c\right\},c_{\mathrm{im}}=\Im \left\{c\right\}.$$

(42)

Let a joint probability $p_{U,V}(x_{\mathrm{re}},y_{\mathrm{re}})$, $x_{\mathrm{re}},y_{\mathrm{re}}\in ℝ$ be

$$\begin{array}{c}{p}_{U,V}(x_{\mathrm{re}},y_{\mathrm{re}})=\frac{1}{\pi {\sigma }_1^2\left|c_{\mathrm{im}}\right|}exp\left(\frac{-1}{{\sigma }_1^2}\left({(x_{\mathrm{re}}-y_{\mathrm{re}})}^2+{\left(\frac{x_{\mathrm{re}}{c}_{\mathrm{re}}-y_{\mathrm{re}}}{c_{\mathrm{im}}}-{\mu }_{\mathrm{im}}\right)}^2\right)\right),\hfill \\ \mathrm{for}{c}_{\mathrm{im}}\ne 0.\hfill \end{array}$$

(43)

$$\begin{array}{c}{p}_{U,V}(x_{\mathrm{re}},y_{\mathrm{re}})=\frac{1}{\sqrt{\pi {\sigma }_1^2}}exp\left(\frac{-1}{{\sigma }_1^2}{(x_{\mathrm{re}}-{\mu }_{\mathrm{re}})}^2\right)\delta (y_{\mathrm{re}}-x_{\mathrm{re}}{c}_{\mathrm{re}}),\mathrm{for}{c}_{\mathrm{im}}=0.\hfill \end{array}$$

(44)

In Equations (43) and (44),

$$\begin{array}{cc}\hfill {\sigma }_1^2& =\frac{4}{{\sigma }_w^2}{|{\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|}^2,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill \mu & =({\eta }_1{d}^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{-\mathrm{j}\phi }{d}^{\left(2\right)})\frac{2}{{\sigma }_w^2}({\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }),\hfill \end{array}$$

(46)

and $\delta$ is the Dirac-delta function. Let the joint probability $p_{W,X}(s,t)$, $s,t\ge 1$ be

$$\begin{array}{cc}\hfill p& {}_{W,X}(s,t)=\frac{1}{\sqrt{s^2-1}\sqrt{t^2-1}}[\hfill \\ & p_{U,V}(+ln(s+\sqrt{s^2-1}),+ln(t+\sqrt{t^2-1}))+\hfill \\ \hfill & +p_{U,V}(+ln(s+\sqrt{s^2-1}),-ln(t+\sqrt{t^2-1}))\hfill \\ \hfill & +p_{U,V}(-ln(s+\sqrt{s^2-1}),+ln(t+\sqrt{t^2-1}))\hfill \\ \hfill & +p_{U,V}(-ln(s+\sqrt{s^2-1}),-ln(t+\sqrt{t^2-1}))].\hfill \end{array}$$

(47)

Finally,

$$\begin{array}{cc}& p_{M_{\mathrm{Coh}}}\left(z\right)={\int }_{max\{1/z,1\}}^{\infty }q{p}_{W,X}(zq,q)\mathrm{d}q.\hfill \end{array}$$

(48)

$$\begin{array}{c}{P}_{\mathrm{e}}=\frac{1}{2}+\frac{1}{4}{\int }_0^{a_{\mathrm{Coh}}}[p_{M_{\mathrm{Coh}}}\left(z\right|A_1)+p_{M_{\mathrm{Coh}}}\left(z\right|A_4)-p_{M_{\mathrm{Coh}}}\left(z\right|A_2)-p_{M_{\mathrm{Coh}}}\left(z\right|A_3)]\mathrm{d}z.\hfill \end{array}$$

(49)

In (48), we can use the substitution (50). The 2D integral is then more numerically stable.

$$\begin{array}{cc}\hfill \Theta \left({}_y^x\right)& =\left({}_{cosh\left(y\right)}^{\frac{cosh\left(x\right)}{cosh\left(y\right)}}\right)=\left({}_q^z\right).\hfill \end{array}$$

(50)

4.3. Analytical H-BER Formula for Approximate Coherent (ApC) Detector

Again, it is practical to define a few auxiliary definitions. The detector’s decision threshold is

$$\begin{array}{cc}\hfill a_{\mathrm{ApC}}& =2{\eta }_1{\eta }_{2}cos\left(\phi \right).\hfill \end{array}$$

(51)

The constant c is defined in the same way as in (42). $p_{U^{\prime },V^{\prime }}$ is formally the same as $p_{U,V}$ in (43) and (44), but

$$\begin{array}{cc}\hfill {\sigma }_1^2& ={|{\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }|}^2{\sigma }_w^2,\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \mu & =({\eta }_1{d}^{\left(1\right)}+{\eta }_2{\mathrm{e}}^{-\mathrm{j}\phi }{d}^{\left(2\right)})({\eta }_1+{\eta }_2{\mathrm{e}}^{\mathrm{j}\phi }).\hfill \end{array}$$

(53)

We define the joint pdf $p_{W^{\prime },X^{\prime }}$ as

$$\begin{array}{cc}\hfill & p_{W^{\prime },X^{\prime }}(x,y)=p_{U^{\prime },V^{\prime }}(x,y)+p_{U^{\prime },V^{\prime }}(x,-y)\hfill \\ \hfill & +p_{U^{\prime },V^{\prime }}(-x,y)+p_{U^{\prime },V^{\prime }}(-x,-y),x,y\ge 0.\hfill \end{array}$$

(54)

Finally, $p_{M_{\mathrm{ApC}}}\left(z\right)$ and P_e are

$$\begin{array}{cc}\hfill & p_{M_{\mathrm{ApC}}}\left(z\right)={\int }_{max\{0,-z\}}^{\infty }{p}_{W^{\prime },X^{\prime }}(z+x,x)\mathrm{d}x,\hfill \end{array}$$

(55)

$$\begin{array}{cc}& P_e=\frac{1}{2}+\frac{1}{4}{\int }_{-\infty }^{a_{\mathrm{ApC}}}[p_{M_{\mathrm{ApC}}}\left(y\right|A_1)+p_{M_{\mathrm{ApC}}}\left(y\right|A_4)-p_{M_{\mathrm{ApC}}}\left(y\right|A_2)-p_{M_{\mathrm{ApC}}}\left(y\right|A_3)]\mathrm{d}y.\hfill \end{array}$$

(56)

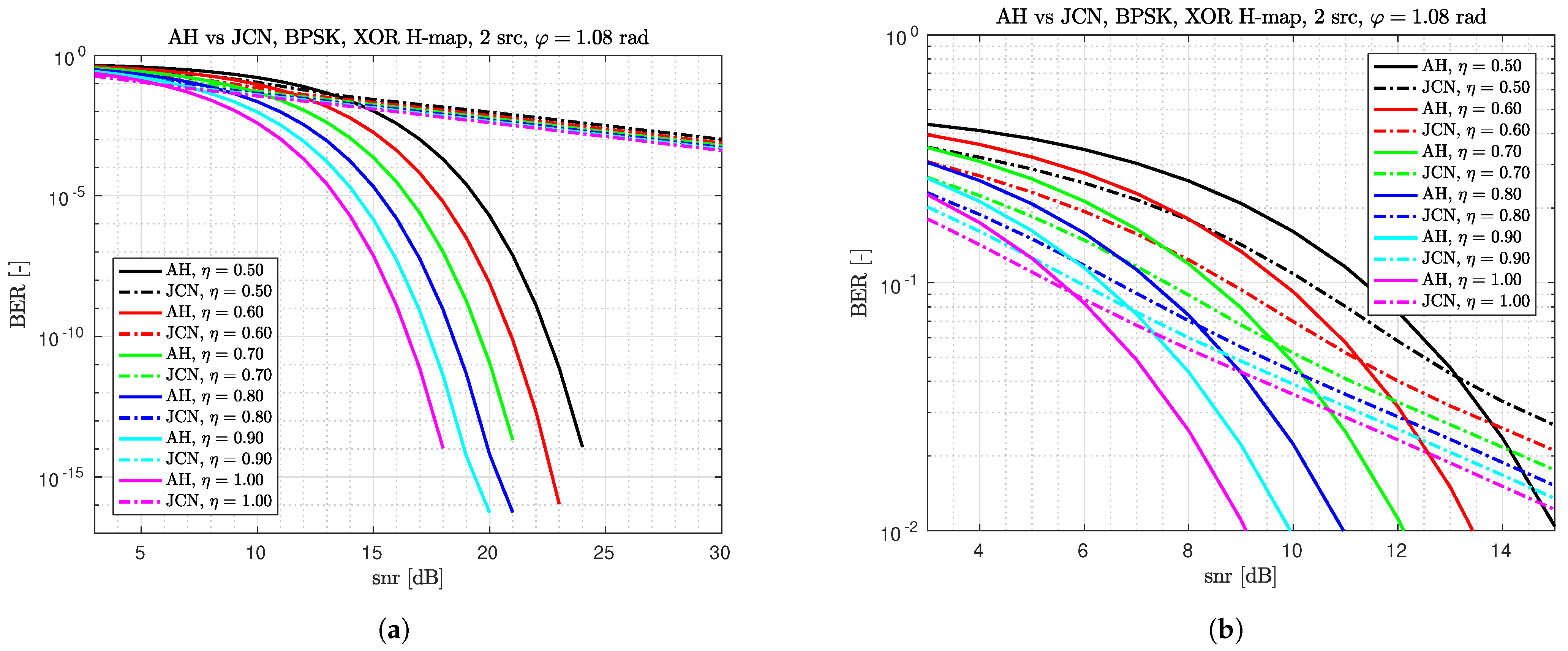
4.4. Comparison of AH Differential Detector with Other Two Differential Detectors

In this subsection, we compare the H-BER performance of the ad hoc (AH) detector with the joint complex normal (JCN) detector from [9] and with the joint maximum likelihood (JML) detector from [13]. In the referenced figures, we use $\eta ={\eta }_2/{\eta }_1={\eta }_{\min }$ and $\phi ={\phi }_2-{\phi }_1$. In Figure 3, we see the H-BER of the AH and the JCN detector. The right-hand figure zooms into the lower SNRs. It is clearly visible that for low SNRs, JCN is slightly better than AH (the error rate is of order ${10}^{-2}$ for both detectors), but for high SNRs, AH is remarkably better. In Figure 4, we compare H-BER of the AH and JML detector. Again, the right-hand figure zooms into lower SNRs. Apparently, the loss of AH w.r.t. the JML is about 0.5 dB in H-BER.

4.5. Other Numerical Results

In this subsection, we present the following.

1.

Decision regions for coherent and differential detectors.

2.

Comparison of H-BER performance of coherent vs. approximate coherent detector and coherent vs. ad hoc detector.

3.

H-BER performance of the ad hoc differential detector vs. the approximate coherent detector for the Rayleigh channel.

In all the figures, ${\eta }_1=1$, ${\eta }_2=\eta$, $\phi ={\phi }_2-{\phi }_1$. SNR is given with regard to the first source. Rayleigh fading channel is of the form

$$\begin{array}{cc}\hfill y& =h_1{q}^{\left(1\right)}+\eta h_2{q}^{\left(2\right)}+w,\hfill \end{array}$$

(57)

where $h_1,h_2\sim (0,{\sigma }^2)$. $\sigma$ is chosen to be $\sqrt{2}/2$ so that E$\left[\right|h_i{|}^2]=1$. Moreover, the channel attenuation coefficients $h_1$, $h_2$ are assumed to be the same for two consecutive observations. The channel parameter $\eta$ is fixed for the whole frame and it is the only parameter known to the AH detector in the channel model (57).

Observations follow. In Figure 5a, we see that the boundaries of decision regions of the coherent and the approximate coherent detector for SNR = 0 dB are quite close to each other. For higher SNR, boundaries are closer to each other. That results in practically the same H-BER performance of the two detectors as can be seen in Figure 6a. We can notice that the boundaries of decision regions for the approximate coherent detector consist of 4 line segments.

Decision regions for the ad hoc differential detector are 4-D subsets of ${ℝ}^4$. In Figure 5b, we have depicted decision regions for $y_1$, given fixed $y_0$. Decision regions of the JML detector are also shown. Here we have also shown the decision region for the detector that we get by marginalization of the criterion (32) by integration over $[{\phi }_1,{\phi }_2]\in {(0,2\pi )}^2$. The differential detector is denoted as JML2.

From Figure 6b, we conclude that the H-BER loss of the ad hoc detector w.r.t. the Coh detector is about 3.5 dB.

H-BER does change with $\phi$ in Figure 3, Figure 4 and Figure 6a,b by just a fraction of dB.

In Figure 7, we compare the ApC and AH detector for the Rayleigh channel. The AH detector knows only the channel parameter $\eta$, as given in the system model (57). We see that the knowledge of the magnitudes of subchannel attenuations for the AH detector is crucial and its absence results in very poor error performance. The ApC detector uses full knowledge of the channel parameters $h_1$ and $\eta h_2$.

5. Discussion

In this article, we have presented an AH differential detector of the XOR H-map, for two differentially encoded BPSK sources in the H-MAC. The proposed AH detector is very simple for evaluation, does not require the estimation of subchannel phases in the H-MAC channel, and the loss in its H-BER is only 3.5 dB with regard to the coherent detector. Moreover, we have derived the ApC detector, which has practically the same H-BER performance as the Coh detector. The analytical H-BER formula has been presented for the AH and coherent detectors. The AH differential detector has been compared to the other two differential detectors (JML and JCN). Additional results such as figures of H-BER and decision regions of detectors have been presented.