Non-Isolated Resolving Sets of Corona Graphs with Some Regular Graphs
Abstract
:1. Introduction
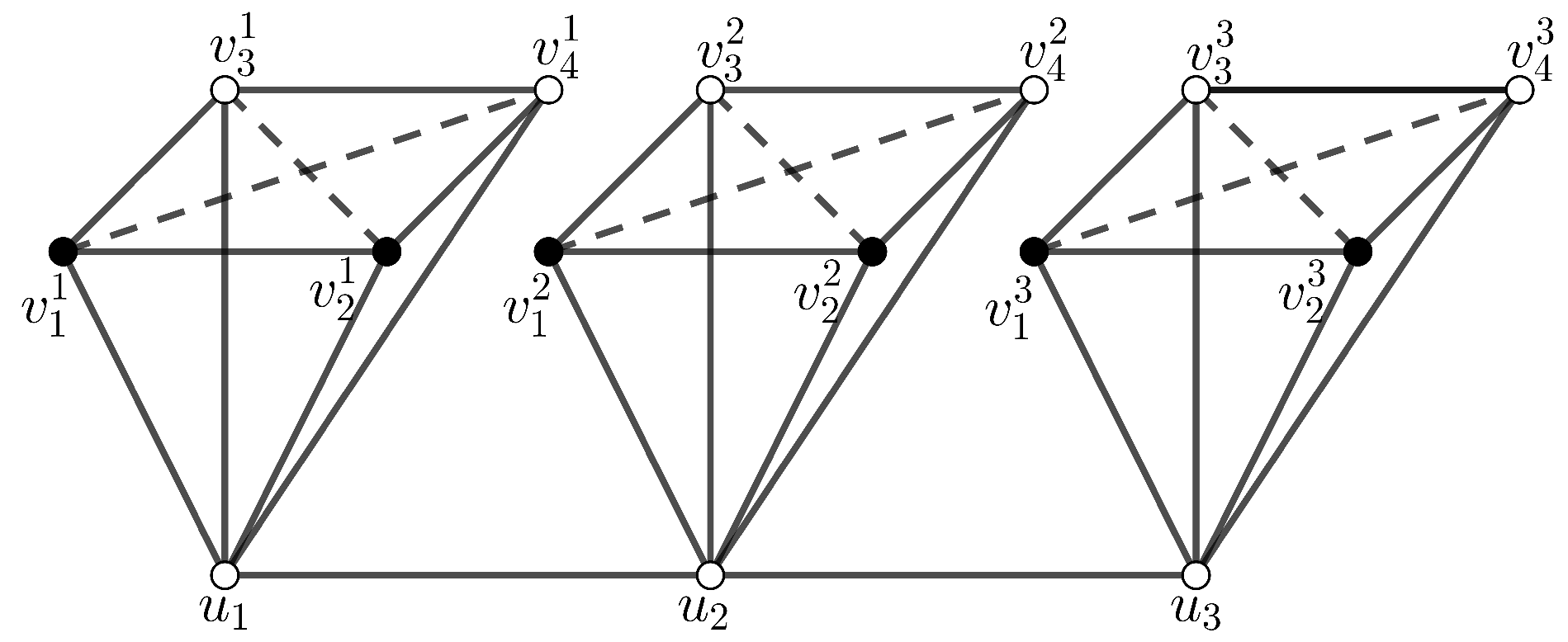
2. Non-Isolated Resolving Set of Where Is a -Regular Graph
3. Non-Isolated Resolving Set of Where Is a -Regular Graph
- 1.
- Let ;
- 2.
- Let ;
- 3.
- Choose two non-adjacent vertices in , say and and say another unlabeled vertex that is not adjacent to as ;
- 4.
- Let ;
- 5.
- Let be a vertex that is not adjacent to ;
- 6.
- If , then , and define , then repeat Step 5. Otherwise, go to Step 7;
- 7.
- Let be an induced subgraph of by ;
- 8.
- Define ;
- 9.
- If , then define , and repeat Step 3. Otherwise, finish.
- (i)
- If , then W is an -set of ;
- (ii)
- If , then .
- (i)
- Since , we have . Hence, W is also an -set of ;
- (ii)
- Since is a -regular graph, by Lemma 1, there is such that where and . Let W be an -set of and for every . Next, it is proven by contradiction. Suppose there is such that . As a consequence, there are two vertices u and v in such that . Since every is adjacent to all vertices in , we have . We obtain a contradiction.
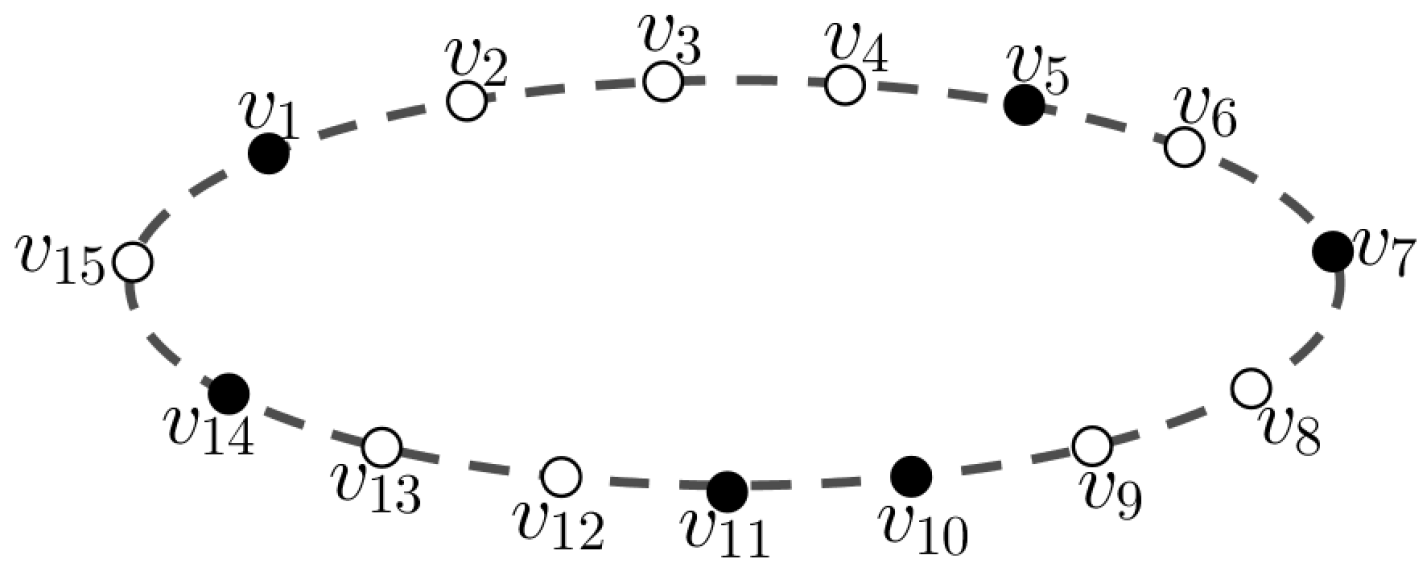
3.1. Resolvability of a Complete Graph Minus a Hamiltonian Cycle
- (i)
- Every gap of W contains at most three vertices;
- (ii)
- At most one gap of W contains three vertices;
- (iii)
- If a gap of W contains at least two vertices, then its neighboring gaps contain at most one vertex.
- (i)
- Suppose there is a gap of W containing four vertices for some . We obtain . We obtain a contradiction. Hence, every gap of W contains at most three vertices;
- (ii)
- Suppose there are two different gaps containing three vertices and for some k and l in with . We obtain . This is a contradiction. Therefore, the number of gaps of W containing three vertices is at most one;
- (iii)
- Suppose there are five vertices for some such that is the only vertex of W. Since and for every , we obtain . This is a contradiction. We conclude that if A is a gap of W containing at least two vertices, then the neighboring gaps of A contain at most one vertex.
- v belongs to a gap of size one of W:Let and be the end points of a gap containing v. Then, the vertex v has a distance of two to both and . Since , for every , we have or . This implies ;
- v belongs to a gap of size two of W:Let and be the end points of a gap containing v. Without loss of generality, let , then and . If there is with and and , then there is such that and . Therefore, for every , we obtain
- v belongs to a gap of size three of W:Let and be the end points of a gap containing v. Let , then . By Properties and of Lemma 3, no other vertex of has this representation. Now, let or . Without loss of generality, let , then and . If there is with , and , then there is such that and . Therefore, for every , we obtain .
- for some :The number of vertices in all gaps of W is at most . Therefore, . This implies that ;
- for some :The number of vertices in all gaps of W is at most . Therefore, . This means that .
- :Therefore, for some . Thus, . We define . Note that W contains vertices and satisfies Properties of Lemma 3;
- :Therefore, for some . Thus, . For , we define . For , we define . Note that W contains vertices and satisfies Properties of Lemma 3;
- :Therefore, for some . Thus, . We define . Note that W contains vertices and satisfies Properties of Lemma 3;
- :Therefore, for some . Thus, . For , we define . For , we define . Note that W contains vertices and satisfies Properties of Lemma 3;
- :Therefore, for some . Thus, . We define . Note that W contains vertices and satisfies Properties of Lemma 3.
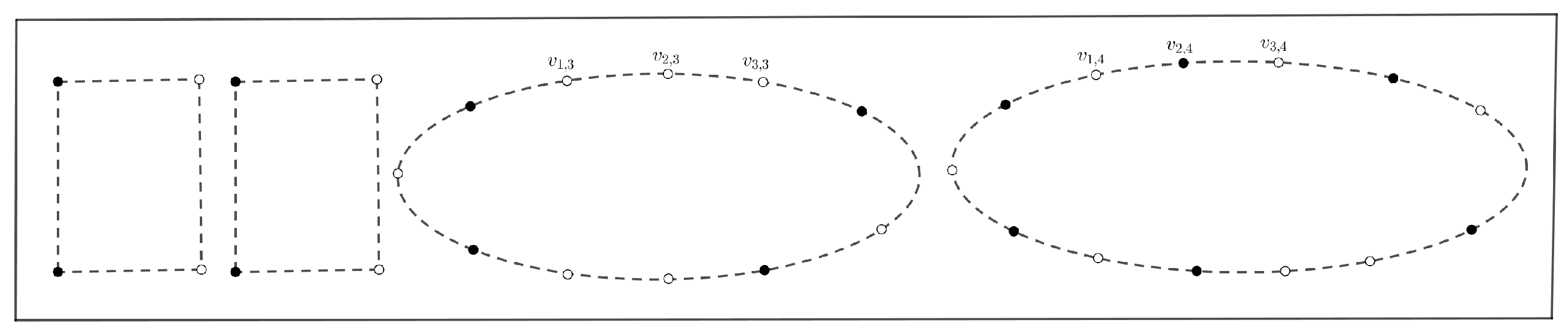
3.2. -Set of a -Regular Graph
- (i)
- Every gap of W contains at most three vertices;
- (ii)
- At most one gap of W contains three vertices.
- (i)
- Suppose there is a gap of W containing four vertices for some and . We obtain . We obtain a contradiction. Hence, every gap of W contains at most three vertices;
- (ii)
- By considering Lemma 4, suppose there are two different gaps containing three vertices in of and in of for some and with . We obtain . We have a contradiction. Hence, the number of gaps of W containing three vertices is at most one.
- For , we have and ;
- For , we have , and .
3.3. -Set of Where Is a -Regular Graph
- If , then there exist two vertices x and y in such that . This implies that , a contradiction;
- If , then contains an isolated vertex, a contradiction.
- x and y in for some :Let and . Since , we obtain ;
- and for some j and k in with :Let and for some a and b in . Since , we obtain .
- If , then there exist two vertices x and y in such that . This implies that , a contradiction;
- For , if contains an isolated vertex, then we have a contradiction. Otherwise, then there exist two vertices x and y in such that for every . This implies that , a contradiction.
- x and y in for some :Since is an -set of , we have . This means that ;
- and for some :If , then for some with and for any , we have . If , then for any , we have . Therefore, , and this means that ;
- and for some j and k in with :For any , we have but . Therefore, , so that ;
- x and y in :Let and for some j and k in with . For any , we have . Therefore . This means that .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Slater, P.J. Leaves of trees. Congr. Numer. 1975, 14, 549–559. [Google Scholar]
- Harary, F.; Melter, R.A. On the metric dimension of a graph. Ars Comb. 1976, 2, 191–195. [Google Scholar]
- Iswadi, H.; Baskoro, E.T.; Salman, A.N.M.; Simanjuntak, R. The metric dimension of graph with pendant edges. J. Comb. Math. Comb. Comput. 2008, 65, 139–145. [Google Scholar]
- Iswadi, H.; Baskoro, E.T.; Salman, A.N.M.; Simanjuntak, R. The resolving graph of amalgamation of cycles. Util. Math. 2010, 83, 121–132. [Google Scholar]
- Iswadi, H.; Baskoro, E.T.; Simanjuntak, R.; Salman, A.N.M. On the metric dimension of corona product of graphs. Far East J. Math. Sci. (FJMS) 2011, 52, 155–170. [Google Scholar]
- Saputro, S.W.; Baskoro, E.T.; Salman, A.N.M.; Suprijanto, D. The metric dimensions of a complete n-partite graph and its Cartesian product with a path. J. Comb. Math. Comb. Comput. 2009, 71, 283–293. [Google Scholar]
- Saputro, S.W.; Simanjuntak, R.; Uttunggadewa, S.; Assiyatun, H.; Baskoro, E.T. The metric dimension of the lexicographic product of graphs. Discret. Math. 2013, 313, 1045–1051. [Google Scholar] [CrossRef]
- Saputro, S.W.; Mardiana, N.; Purwasih, I.A. The metric dimension of comb product graphs. Matematički Vesn. 2017, 69, 248–258. [Google Scholar]
- Wang, J.; Mion, L.; Liu, Y. Characterization of n-vertex graphs of metric dimension n − 3 by metric matrix. Mathematics 2019, 7, 479. [Google Scholar] [CrossRef] [Green Version]
- Buczkowski, P.; Chartrand, G.; Poisson, C.; Zhang, P. On k-dimensional graphs and their bases. Period. Math. Hung. 2003, 46, 9–15. [Google Scholar] [CrossRef]
- Cáceres, J.; Hernando, C.; Mora, M.; Pelayo, I.M.; Puertas, M.L.; Seara, C.; Wood, D.R. On the metric dimension of Cartesian products of graphs. SIAM J. Discret. Math. 2007, 21, 423–441. [Google Scholar] [CrossRef] [Green Version]
- Hernando, C.; Mora, M.; Pelayo, I.M.; Seara, C.; Cáceres, J.; Puertas, M.L. On the metric dimension of some families of graphs. Electron. Discret. Math. 2005, 22, 129–133. [Google Scholar] [CrossRef]
- Chartrand, G.; Poisson, C.; Zhang, P. Resolvability and the upper dimension of graphs. Comput. Math. Appl. 2000, 39, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Estrada-Moreno, A. The k-metric dimension of a unicyclic graph. Mathematics 2021, 9, 2789. [Google Scholar] [CrossRef]
- González Yero, I. The Simultaneous strong resolving graph and the simultaneous strong metric dimension of graph families. Mathematics 2020, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Hernando, C.; Mora, M.; Pelayo, I.M.; Seara, C.; Wood, D.R. Extremal graph theory for metric dimension and diameter. Electron. J. Comb. 2010, 17, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Javaid, I.; Rahim, M.T.; Ali, K. Families of regular graphs with constant metric dimension. Util. Math. 2008, 75, 21–33. [Google Scholar]
- Khuller, S.; Raghavachari, B.; Rosenfeld, A. Landmarks in graphs. Discret. Appl. Math. 1996, 70, 217–229. [Google Scholar] [CrossRef] [Green Version]
- Chartrand, G.; Eroh, L.; Johnson, M.A.; Oellermann, O.R. Resolvability in graphs and the metric dimension of a graph. Discret. Appl. Math. 2000, 105, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Chartrand, G.; Zhang, P. The theory and applications of resolvability in graphs: A survey. Congr. Numer. 2003, 160, 47–68. [Google Scholar]
- Chitra, P.J.B.; Arumugam, S. Resolving sets without isolated vertices. Procedia Comput. Sci. 2015, 74, 38–42. [Google Scholar] [CrossRef] [Green Version]
- Hasibuan, I.M.; Salman, A.N.M.; Saputro, S.W. Non-isolated resolving sets of certain graphs Cartesian product with a path. J. Phys. Conf. Ser. 2018, 1008, 012045. [Google Scholar] [CrossRef] [Green Version]
- Abidin, W.; Salman, A.N.M.; Saputro, S.W. The non-isolated resolving number of some corona graphs. J. Phys. Conf. Ser. 2018, 1097, 012073. [Google Scholar] [CrossRef] [Green Version]
- Chartrand, G.; Lesniak, L.; Zhang, P. Graphs & Digraphs; Chapman and Hall/CRC: London, UK, 2010; pp. 401–402. [Google Scholar]
- Saputro, S.W. On local metric dimension of (n − 3)-regular graph. J. Comb. Math. Comb. Comput. 2016, 98, 43–54. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abidin, W.; Salman, A.; Saputro, S.W. Non-Isolated Resolving Sets of Corona Graphs with Some Regular Graphs. Mathematics 2022, 10, 962. https://doi.org/10.3390/math10060962
Abidin W, Salman A, Saputro SW. Non-Isolated Resolving Sets of Corona Graphs with Some Regular Graphs. Mathematics. 2022; 10(6):962. https://doi.org/10.3390/math10060962
Chicago/Turabian StyleAbidin, Wahyuni, Anm Salman, and Suhadi Wido Saputro. 2022. "Non-Isolated Resolving Sets of Corona Graphs with Some Regular Graphs" Mathematics 10, no. 6: 962. https://doi.org/10.3390/math10060962





