Estimation of Parameters of Different Equivalent Circuit Models of Solar Cells and Various Photovoltaic Modules Using Hybrid Variants of Honey Badger Algorithm and Artificial Gorilla Troops Optimizer
Abstract
:1. Introduction
- A new metaheuristic algorithm for estimating parameters of equivalent circuit models of solar cells and PV modules has been proposed.
- Two types of hybridization of algorithms used have been proposed.
- Statistical analysis of the results of these algorithms is examined.
- Performance of the proposed algorithms is compared with several well-known algorithms used in parameter estimation problems.
- The three equivalent circuit models of solar cells are addressed and investigated.
- The applicability and efficiency of the proposed methods are tested on commercial PV modules for different levels of temperature and irradiance.
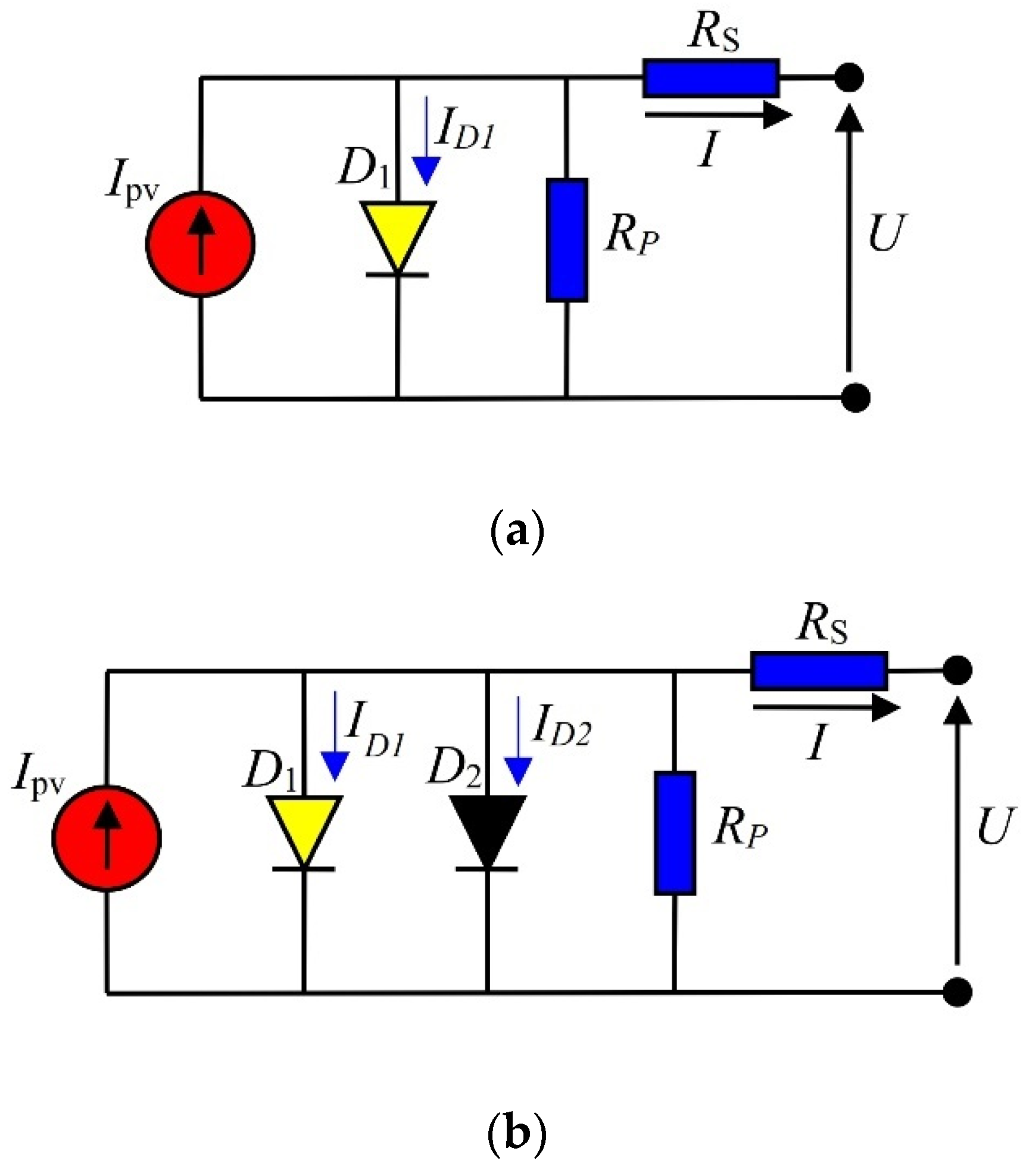
2. Solar Cell Equivalent Circuits
3. Proposed Hybrid Algorithms
| Algorithm 1: Complete pseudo-code of the artificial gorilla troops optimizer-honey badger algorithm (GTO-HBA) (Proposed 1). |
| 1: Set parameters N, C, β, and tmax |
| 2: Initialize the population using the GTO algorithm [60]: 3: Evaluate the fitness of each badger xi and assign it to fi 4: Save the best position xprey and assign it to fprey |
| 5: for t = 1 to tmax |
| 6: Update factor α 7: for i = 1 to N |
| 8: Calculate intensity Ii 9: if r < 0.5 |
| 10: Update the positions according to the digging phase 11: else 12: Update the positions according to the honey phase |
| 13: endif 14: Evaluate new positions and assign them to fnew 15: if fnew ≤ fi 16: set xi = xnew and fi = fnew |
| 17: endif 18: if fnew ≤ fprey 19: set xprey = xnew and fprey = fnew |
| 20: endif 21: end for 22: end for 23: Return xprey—the optimal solution |
| Algorithm 2: Complete pseudo-code of the honey badger algorithm and artificial gorilla troops optimizer (HBA-GTO) (Proposed 2). |
| 1: Set parameters N, N1, N2, p, β, and tmax |
| 2: Initialize the population of gorillas using HBA [30]: 3: Evaluate the fitness of each gorilla |
| 4: for t = 1 to tmax |
| 5: Update L and C 6: Conduct the exploration phase and calculated population GX(t) |
| 7: Evaluate the fitness of each gorilla and update the population X(t) 8: Determine the best gorilla—Silverback |
| 9: end for 10: Return Xsilverback—the optimal solution |
4. Numerical Results
5. Results Obtained for a Commercial PV Module
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony |
| ABC-DE | Artificial bee colony-differential evolution |
| ABC-TRR | Artificial bee colony-trust-region reflective algorithm |
| A&I | Analytical- and iterative-based methods |
| BC | Bézier curves |
| BIA | Bio-inspired algorithms |
| BHCS | Biogeography-based heterogeneous cuckoo search |
| BPFPA | Bee pollinator flower pollination algorithm |
| CGBO | Improved gradient-based optimization algorithm with chaotic drifts |
| CLSHADE | Chaotic successful history-based adaptive DE variants with linear population size reduction algorithm |
| CNMSMA | Chaotic Nelder–Mead slime mould algorithm |
| COA | Chaotic optimization approach |
| CPMPSO | Classified perturbation mutation-based particle swarm optimization |
| CS | Cuckoo search optimization |
| CSO | Cat swarm optimization |
| DDM | Double-diode model |
| DE | Differential evolution |
| DE-WOA | Hybrid DE with whale optimization algorithm |
| DSO | Drone squadron optimization |
| EHA–NMS | Eagle-based hybrid adaptive Nelder–Mead simplex algorithm |
| EHHO | Enhanced Harris hawk optimization |
| EO | Equilibrium optimizer method |
| GA | Genetic algorithm |
| GAMNU | Genetic algorithm based on non-uniform mutation |
| GBO | Gradient-based optimizer |
| GOFPANM | Generalized opposition-flower pollination algorithm-Nelder–Mead simplex method |
| GSK | Gaining–sharing knowledge-based algorithm |
| GTO | Gorilla troops optimizer |
| HBA | Honey badger algorithm |
| IJAYA | Improved JAYA optimization |
| IMO | Ions motion algorithm |
| ISCE | Improved shuffled complex evolution |
| ITLBO | Improved teaching–learning-based optimization |
| IWOA | Improved whale optimization algorithm |
| MADE | Memetic adaptive DE |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MLBSA | Multiple learning backtracking search algorithm |
| MPA | Marine-predators algorithm |
| MPSO | Modified particle swarm optimization |
| MSSO | Modified simplified swarm optimization algorithm |
| MSX 60 | Solarex’s multicrystalline 60 watts solar module |
| MTLBO | Modified teaching-–earning-based optimization |
| NM | Newton method |
| OBWOA | Opposition-based whale optimization algorithm |
| ORcr-IJADE | Onlooker-ranking-based and improved adaptive and differential evolution |
| PGJAYA | Performance-guided JAYA algorithm |
| Photowatt PWP | Photowatt solar panel of model PWP |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| RESs | Renewable energy sources |
| RTC | RadioTechnique Compelec |
| SDM | Single-diode model |
| SMA | Slime mould algorithm |
| SM55 | Shell monocrystalline PV module |
| STLBO | Simplified teaching–learning-based optimization |
| TDM | Triple-diode model |
| TLABC | Teaching–learning-based artificial bee colony |
| TLBO | Teaching–learning-based optimization |
| TLO | Teaching–learning optimization |
| TSO | Transient search optimization |
| TVA-CPSO | Time-varying acceleration coefficients PSO |
| WHHO | Whippy Harris hawks optimization |
| WOA | Whale optimization algorithm |
| WDO | Wind-driven optimization |
Appendix A
References
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Abdel Aleem, S.H.E.; Omar, N.; Ahmadi, A.; Alenezi, F.Q. Short-term solar power forecasting considering cloud coverage and ambient temperature variation effects. Renew. Energy 2018, 123, 793–805. [Google Scholar] [CrossRef]
- Ndegwa, R.; Simiyu, J.; Ayieta, E.; Odero, N. A Fast and Accurate Analytical Method for Parameter Determination of a Photovoltaic System Based on Manufacturer’s Data. J. Renew. Energy 2020, 2020, 7580279. [Google Scholar] [CrossRef]
- Ebeed, M.; Abdel Aleem, S.H.E. Overview of uncertainties in modern power systems: Uncertainty models and methods. In Uncertainties in Modern Power Systems; Zobaa, A.F., Abdel Aleem, S.H.E., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 1–34. ISBN 978-0-12-820491-7. [Google Scholar] [CrossRef]
- Zobaa, A.F.; Aleem, S.H.E.A.; Abdelaziz, A.Y. Classical and Recent Aspects of Power System Optimization; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128124413. [Google Scholar]
- Ciferri, D.; D’Errico, M.C.; Polinori, P. Integration and convergence in European electricity markets. Econ. Polit. 2020, 37, 463–492. [Google Scholar] [CrossRef] [Green Version]
- Shinde, P.; Boukas, I.; Radu, D.; de Villena, M.M.; Amelin, M. Analyzing trade in continuous intra-day electricity market: An agent-based modeling approach. Energies 2021, 14, 3860. [Google Scholar] [CrossRef]
- C2ES Renewable Energy. Available online: https://www.c2es.org/content/renewable-energy/ (accessed on 2 October 2021).
- Premkumar, M.; Karthick, K.; Sowmya, R. A review on solar PV based grid connected microinverter control schemes and topologies. Int. J. Renew. Energy Dev. 2018, 7, 171–182. [Google Scholar] [CrossRef]
- Dkhichi, F.; Oukarfi, B.; Fakkar, A.; Belbounaguia, N. Parameter identification of solar cell model using Levenberg-Marquardt algorithm combined with simulated annealing. Sol. Energy 2014, 110, 781–788. [Google Scholar] [CrossRef]
- Ćalasan, M.; Abdel Aleem, S.H.E.; Zobaa, A.F. On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on Lambert W function. Energy Convers. Manag. 2020, 210, 112716. [Google Scholar] [CrossRef]
- Ćalasan, M.; Abdel Aleem, S.H.E.; Zobaa, A.F. A new approach for parameters estimation of double and triple diode models of photovoltaic cells based on iterative Lambert W function. Sol. Energy 2021, 218, 392–412. [Google Scholar] [CrossRef]
- Saadaoui, D.; Elyaqouti, M.; Assalaou, K.; Ben hmamou, D.; Lidaighbi, S. Parameters optimization of solar PV cell/module using genetic algorithm based on non-uniform mutation. Energy Convers. Manag. X 2021, 12, 100129. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Dragicevic, T.; Rajasekar, N. A new hybrid bee pollinator flower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 2017, 135, 463–476. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L. Parameter estimation of photovoltaic models with memetic adaptive differential evolution. Sol. Energy 2019, 190, 465–474. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Xiong, G.; Li, L.; Mohamed, A.W.; Yuan, X.; Zhang, J. A new method for parameter extraction of solar photovoltaic models using gaining–sharing knowledge based algorithm. Energy Rep. 2021, 7, 3286–3301. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Mei, C.; Ding, Y.; Li, K. Teaching–learning–based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 2018, 212, 1578–1588. [Google Scholar] [CrossRef]
- Mathew, D.; Rani, C.; Kumar, M.R.; Wang, Y.; Binns, R.; Busawon, K. Wind-driven optimization technique for estimation of solar photovoltaic parameters. IEEE J. Photovolt. 2018, 8, 248–256. [Google Scholar] [CrossRef]
- Naeijian, M.; Rahimnejad, A.; Ebrahimi, S.M.; Pourmousa, N.; Gadsden, S.A. Parameter estimation of PV solar cells and modules using Whippy Harris Hawks Optimization Algorithm. Energy Rep. 2021, 7, 4047–4063. [Google Scholar] [CrossRef]
- Gude, S.; Jana, K.C. Parameter extraction of photovoltaic cell using an improved cuckoo search optimization. Sol. Energy 2020, 204, 280–293. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 171, 1843–1859. [Google Scholar] [CrossRef]
- Ridha, H.M. Parameters extraction of single and double diodes photovoltaic models using Marine Predators Algorithm and Lambert W function. Sol. Energy 2020, 209, 674–693. [Google Scholar] [CrossRef]
- Ćalasan, M.; Jovanović, D.; Rubežić, V.; Mujović, S.; Dukanović, S. Estimation of single-diode and two-diode solar cell parameters by using a chaotic optimization approach. Energies 2019, 12, 4209. [Google Scholar] [CrossRef] [Green Version]
- Premkumar, M.; Jangir, P.; Ramakrishnan, C.; Nalinipriya, G.; Alhelou, H.H.; Kumar, B.S. Identification of Solar Photovoltaic Model Parameters Using an Improved Gradient-Based Optimization Algorithm with Chaotic Drifts. IEEE Access 2021, 9, 62347–62379. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K. Hybridizing cuckoo search algorithm with biogeography-based optimization for estimating photovoltaic model parameters. Sol. Energy 2019, 180, 192–206. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Ndi, F.E.; Perabi, S.N.; Ndjakomo, S.E.; Ondoua Abessolo, G.; Mengounou Mengata, G. Estimation of single-diode and two diode solar cell parameters by equilibrium optimizer method. Energy Rep. 2021, 7, 4761–4768. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Yu, K.; Qu, B.; Yue, C.; Ge, S.; Chen, X.; Liang, J. A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 2019, 237, 241–257. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, S.; Yeh, W.; Chen, Z.; Wu, L. Parameters extraction of solar cell models using a modified simplified swarm optimization algorithm. Sol. Energy 2017, 144, 594–603. [Google Scholar] [CrossRef]
- Derick, M.; Rani, C.; Rajesh, M.; Farrag, M.E.; Wang, Y.; Busawon, K. An improved optimization technique for estimation of solar photovoltaic parameters. Sol. Energy 2017, 157, 116–124. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Liu, Y.; Heidari, A.A.; Ye, X.; Liang, G.; Chen, H.; He, C. Boosting slime mould algorithm for parameter identification of photovoltaic models. Energy 2021, 234, 121164. [Google Scholar] [CrossRef]
- Premkumar, M.; Babu, T.S.; Umashankar, S.; Sowmya, R. A new metaphor-less algorithms for the photovoltaic cell parameter estimation. Optik 2020, 208, 164559. [Google Scholar] [CrossRef]
- Szabo, R.; Gontean, A. Photovoltaic cell and module I-V characteristic approximation using Bézier curves. Appl. Sci. 2018, 8, 655. [Google Scholar] [CrossRef] [Green Version]
- Bana, S.; Saini, R.P. A mathematical modeling framework to evaluate the performance of single diode and double diode based SPV systems. Energy Rep. 2016, 2, 171–187. [Google Scholar] [CrossRef] [Green Version]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Parameter estimation method to improve the accuracy of photovoltaic electrical model. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization for electrical parameters estimation of photovoltaic module based on datasheet values. Energy Convers. Manag. 2020, 214, 112904. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Chakrabortty, R.K.; Sallam, K.; Ryan, M.J. An efficient teaching-learning-based optimization algorithm for parameters identification of photovoltaic models: Analysis and validations. Energy Convers. Manag. 2021, 227, 113614. [Google Scholar] [CrossRef]
- Gnetchejo, P.J.; Ndjakomo Essiane, S.; Dadjé, A.; Ele, P. A combination of Newton-Raphson method and heuristics algorithms for parameter estimation in photovoltaic modules. Heliyon 2021, 7, e06673. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- DIab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of Various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Cheng, Z.; Wang, H. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Z.; Long, C.; Cheng, S.; Lin, P.; Chen, Y.; Chen, H. Parameter extraction of photovoltaic models from measured I-V characteristics curves using a hybrid trust-region reflective algorithm. Appl. Energy 2018, 232, 36–53. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y. Parameter estimation of photovoltaic modules using a hybrid flower pollination algorithm. Energy Convers. Manag. 2017, 144, 53–68. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Whale optimisation algorithm for photovoltaic model identification. J. Eng. 2017, 2017, 1906–1911. [Google Scholar] [CrossRef]
- Jordehi, A.R. Time varying acceleration coefficients particle swarm optimisation (TVACPSO): A new optimisation algorithm for estimating parameters of PV cells and modules. Energy Convers. Manag. 2016, 129, 262–274. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Lin, P.; Wu, Y.; Cheng, S. Parameters identification of photovoltaic models using hybrid adaptive Nelder-Mead simplex algorithm based on eagle strategy. Appl. Energy 2016, 182, 47–57. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. An efficient parameters extraction technique of photovoltaic models for performance assessment. Sol. Energy 2017, 158, 192–206. [Google Scholar] [CrossRef]
- Ćalasan, M.; Zobaa, A.F.; Hasanien, H.M.; Abdel Aleem, S.H.E.; Ali, Z.M. Towards accurate calculation of supercapacitor electrical variables in constant power applications using new analytical closed-form expressions. J. Energy Storage 2021, 42, 102998. [Google Scholar] [CrossRef]
- Javidy, B.; Hatamlou, A.; Mirjalili, S. Ions motion algorithm for solving optimization problems. Appl. Soft Comput. J. 2015, 32, 72–79. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Ginidi, A.; Ghoneim, S.M.; Elsayed, A.; El-Sehiemy, R.; Shaheen, A.; El-Fergany, A. Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 2021, 13, 9459. [Google Scholar] [CrossRef]
- Liang, J.; Ge, S.; Qu, B.; Yu, K.; Liu, F.; Yang, H.; Wei, P.; Li, Z. Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 203, 112138. [Google Scholar] [CrossRef]
- Muangkote, N.; Sunat, K.; Chiewchanwattana, S.; Kaiwinit, S. An advanced onlooker-ranking-based adaptive differential evolution to extract the parameters of solar cell models. Renew. Energy 2019, 134, 1129–1147. [Google Scholar] [CrossRef]
- Chaibi, Y.; Malvoni, M.; Allouhi, A.; Mohamed, S. Data on the I–V characteristics related to the SM55 monocrystalline PV module at various solar irradiance and temperatures. Data Br. 2019, 26, 104527. [Google Scholar] [CrossRef]






















| # | Refs. | First Author | Year | Method | Model | Root Mean Square Error (RMSE) | Mean Absolute Error (MAE) | Mean Absolute Percentage Error (MAPE) |
|---|---|---|---|---|---|---|---|---|
| 1 | [32] | Ndi | 2021 | EO | SDM | 0.000776865 | 0.000678644363621 | 0.462865302508924 |
| 2 | [21] | Naeijian | 2021 | WHHO | SDM | 0.000791502 | 0.000667595306139 | 0.344470169829233 |
| 3 | [13] | Saadaou | 2021 | GAMNU | SDM | 0.000812621 | 0.000719474973281 | 0.643237501038952 |
| 4 | [17] | Xiong | 2021 | GSK | SDM | 0.000776134 | 0.000676554109096 | 0.451972461015800 |
| 5 | [33] | Kumar | 2020 | SMA | SDM | 0.000795243 | 0.000667150561147 | 0.332742958125476 |
| 6 | [34] | Jiao | 2020 | EHHO | SDM | 0.000786704 | 0.000701818945693 | 0.558833901459953 |
| 7 | [22] | Gude | 2020 | CSO | SDM | 0.000860194 | 0.000663573496324 | 0.210089090921584 |
| 8 | [18] | Li | 2019 | ITLBO | SDM | 0.000777792 | 0.000687239590168 | 0.502104166185744 |
| 9 | [35] | Yu | 2019 | PGJAYA | SDM | 0.000777792 | 0.000687239590168 | 0.502104166185744 |
| 10 | [29] | Chen | 2019 | BHCS | SDM | 0.000775415 | 0.000679675374715 | 0.455550255014124 |
| 11 | [23] | Merchaoui | 2018 | MPSO | SDM | 0.004359909 | 0.002889258774089 | 4.353156563261146 |
| 12 | [19] | Chen | 2018 | TLABC | SDM | 0.000775416 | 0.000679670632200 | 0.455459033518709 |
| 13 | [36] | Lin | 2017 | MSSO | SDM | 0.000809159 | 0.000665110052013 | 0.295109693517836 |
| 14 | [14] | Ram | 2017 | BPFPA | SDM | 0.000955513 | 0.000824210723789 | 0.736974713224005 |
| 15 | [37] | Derick | 2017 | WDO | SDM | 0.000894818 | 0.000721091048657 | 0.410871168713455 |
| 16 | [38] | Yu | 2017 | IJAYA | SDM | 0.000776055 | 0.000674909321295 | 0.443697941771721 |
| 17 | [17] | Xiong | 2021 | GSK | DDM | 0.000765347 | 0.000674714400538 | 0.477776103165468 |
| 18 | [13] | Saadaou | 2021 | GAMNU | DDM | 0.000795540 | 0.000671452693614 | 0.333198261209489 |
| 19 | [32] | Ndi | 2021 | EO | DDM | 0.006348583 | 0.006174565636472 | 2.943474469938229 |
| 20 | [21] | Naeijian | 2021 | WHHO | DDM | 0.000774553 | 0.000654593080672 | 0.327472776645842 |
| 21 | [39] | Liu | 2021 | CNMSMA | DDM | 0.000757922 | 0.000662676325841 | 0.426575266450123 |
| 22 | [33] | Kumar | 2020 | SMA | DDM | 0.007025646 | 0.004360131396396 | 7.646965757100302 |
| 23 | [34] | Jiao | 2020 | EHHO | DDM | 0.000764087 | 0.000671304856402 | 0.454160791097682 |
| 24 | [22] | Gude | 2020 | CSO | DDM | 0.000869770 | 0.000680544614180 | 0.300124951077260 |
| 25 | [26] | Ćalasan | 2019 | COA | DDM | 0.000757686 | 0.000667871337617 | 0.450126256899350 |
| 26 | [24] | Abd Elaziz | 2018 | ABC | TDM | 0.000990246 | 0.000771873120355 | 0.505954728856906 |
| 27 | 2018 | OBWOA | TDM | 0.000823136 | 0.000650108387227 | 0.218668597114990 | ||
| 28 | 2018 | STLBO | TDM | 0.000823698 | 0.000649122444713 | 0.215757981839370 | ||
| 29 | [40] | Premkumar | 2020 | R-II | TDM | 0.005125476 | 0.003367928190167 | 5.136372818754378 |
| 30 | 2020 | R-III | TDM | 0.002249998 | 0.001572560907759 | 2.495078551153684 | ||
| 31 | 2020 | PSO | TDM | 0.002171714 | 0.001543183004978 | 2.383178745442769 | ||
| 32 | 2020 | CS | TDM | 0.004569170 | 0.003033484788679 | 4.539593940311719 | ||
| 33 | 2020 | ABC | TDM | 0.002471743 | 0.001761292412332 | 2.292317731497820 | ||
| 34 | 2020 | TLO | TDM | 0.000779584 | 0.000654100267008 | 0.331628211492756 | ||
| 35 | Proposed Algorithm 1 | SDM | 0.000774655 | 0.000681168150469 | 0.455157210140345 | |||
| 36 | Proposed Algorithm 2 | SDM | 0.000774656 | 0.000681221910233 | 0.455412179465424 | |||
| 37 | Proposed Algorithm 1 | DDM | 0.000756129 | 0.000668726140277 | 0.457389890766874 | |||
| 38 | Proposed Algorithm 2 | DDM | 0.000755910 | 0.000662136081515 | 0.426224519512442 | |||
| 39 | Proposed Algorithm 1 | TDM | 0.000751879 | 0.000659656489694 | 0.420986462546710 | |||
| 40 | Proposed Algorithm 2 | TDM | 0.000752053 | 0.000663697106339 | 0.440229380526819 | |||
| # | Ipv (A) | I01 (μA) | n1 | RS (Ω) | RP (Ω) | I02 (μA) | n2 | I03 (μA) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.7607597037 | 0.32628893 | 1.48219300 | 0.03634099 | 54.20659400 | - | - | - |
| 2 | 0.76077551 | 0.32302031 | 1.48110808 | 0.03637710 | 53.71867407 | - | - | - |
| 3 | 0.76077400 | 0.32559540 | 1.48209600 | 0.03634020 | 53.89686000 | - | - | - |
| 4 | 0.76080000 | 0.32310000 | 1.48120000 | 0.03640000 | 53.72270000 | - | - | - |
| 5 | 0.76076000 | 0.32314000 | 1.48114000 | 0.03637000 | 53.71489000 | - | - | - |
| 6 | 0.76077500 | 0.32300000 | 1.48123800 | 0.03637500 | 53.74282000 | - | - | - |
| 7 | 0.76080000 | 0.32300000 | 1.48100000 | 0.03640000 | 53.71850000 | - | - | - |
| 8 | 0.76080000 | 0.32300000 | 1.48120000 | 0.03640000 | 53.71850000 | - | - | - |
| 9 | 0.76080000 | 0.32300000 | 1.48120000 | 0.03640000 | 53.71850000 | - | - | - |
| 10 | 0.76078000 | 0.32302000 | 1.48118000 | 0.03638000 | 53.71852000 | - | - | - |
| 11 | 0.76078700 | 0.31068300 | 1.47526200 | 0.03654600 | 52.88971000 | - | - | - |
| 12 | 0.76078000 | 0.32302000 | 1.48118000 | 0.03638000 | 53.71636000 | - | - | - |
| 13 | 0.76077700 | 0.32356400 | 1.48124400 | 0.03637000 | 53.74246500 | - | - | - |
| 14 | 0.76000000 | 0.31060000 | 1.47740000 | 0.03660000 | 57.71510000 | - | - | - |
| 15 | 0.76080000 | 0.32230000 | 1.48080000 | 0.03676800 | 57.74614000 | - | - | - |
| 16 | 0.76080000 | 0.32280000 | 1.48110000 | 0.03640000 | 53.75950000 | - | - | - |
| 17 | 0.76080000 | 0.25950000 | 1.46270000 | 0.03660000 | 54.93300000 | 0.47910000 | 1.99830000 | - |
| 18 | 0.76082700 | 0.32245246 | 1.48102800 | 0.03636440 | 53.11079000 | 0.00027392 | 1.47010100 | - |
| 19 | 0.76792000 | 0.39999000 | 2.00000000 | 0.03659000 | 54.17614000 | 0.26605000 | 1.46451000 | - |
| 20 | 0.76078094 | 0.22857400 | 1.45189500 | 0.03672887 | 55.42643282 | 0.727182 | 2 | - |
| 21 | 0.76078100 | 0.22597600 | 1.45101700 | 0.036740 | 55.48545 | 0.75068100 | 1.9999990 | - |
| 22 | 0.76076000 | 0.74874000 | 2.00000000 | 0.03677 | 55.71456 | 0.22652000 | 1.4546300 | - |
| 23 | 0.760769017 | 0.58618400 | 1.968451449 | 0.036598831 | 55.63943956 | 0.24096500 | 1.456910409 | - |
| 24 | 0.76080 | 0.22730 | 1.45130 | 0.03670 | 55.43270 | 0.73840000 | 1.99990 | - |
| 25 | 0.76078 | 0.22597 | 1.45102 | 0.03674 | 55.48542 | 0.749346 | 2.00000 | - |
| 26 | 0.760700 | 0.2000 | 1.4414 | 0.03687 | 55.8344 | 0.500000 | 1.90000 | 0.2100 |
| 27 | 0.760770 | 0.2353 | 1.4543 | 0.03668 | 55.4448 | 0.221300 | 2.00000 | 0.4573 |
| 28 | 0.760800 | 0.2349 | 1.4541 | 0.0367 | 55.2641 | 0.229700 | 2.00000 | 0.4443 |
| 29 | 0.760792 | 0.2600 | 1.4608 | 0.03660 | 54.9149 | 0.000006 | 1.14660 | 0.5700 |
| 30 | 0.760791 | 0.2100 | 1.7714 | 0.03670 | 55.3571 | 0.220000 | 1.45130 | 0.9900 |
| 31 | 0.760782 | 0.2500 | 1.4601 | 0.03660 | 55.3133 | 0.041000 | 1.74090 | 1.0000 |
| 32 | 0.760776 | 0.1400 | 1.4872 | 0.03630 | 53.7218 | 0.190000 | 1.47710 | 0.0310 |
| 33 | 0.760790 | 0.3200 | 1.8666 | 0.03670 | 55.4411 | 0.230000 | 1.45210 | 0.7400 |
| 34 | 0.760763 | 0.2800 | 1.4684 | 0.03650 | 55.3821 | 0.000670 | 1.54680 | 1.0000 |
| 35 | 0.76077537 | 0.320741243 | 1.48046987 | 0.0364 | 53.5397184 | - | - | - |
| 36 | 0.76077541 | 0.3207412 | 1.48047001 | 0.0364 | 53.5397 | - | - | - |
| 37 | 0.7607801 | 0.84162 | 1.999999 | 0.03679 | 55.73 | 0.2154505 | 1.44706 | - |
| 38 | 0.76078 | 0.841611 | 2.00000 | 0.0367905 | 55.72835 | 0.2154501 | 1.44704 | - |
| 39 | 0.7607602 | 0.876504 | 1.99504 | 0.0369201 | 55.6798 | 0.20441 | 1.442401 | 0.0001805 |
| 40 | 0.7607601 | 0.876499 | 1.99501 | 0.0369202 | 55.6801 | 0.204401 | 1.44241 | 0.0001801 |
| # | Refs. | First Author | Year | Method | Model | RMSE | MAE | MAPE |
|---|---|---|---|---|---|---|---|---|
| 1 | [42] | Bana | 2018 | NM | SDM | 0.101844933535061 | 0.086404559671331 | 7.989316753756794 |
| 2 | [41] | Szabo | 2018 | BC | SDM | 0.030722505654028 | 0.023915966897748 | 1.928605918749928 |
| 3 | [43] | Silva | 2016 | A&I | SDM | 0.018106614648430 | 0.015234044936426 | 1.804005972558074 |
| 4 | [44] | Villalva | 2009 | A&I | SDM | 0.028396627361794 | 0.020903325782359 | 1.703387713558635 |
| 5 | [12] | Calasan | 2021 | CLSHADE | DDM | 0.012028665165887 | 0.008871675551380 | 1.300255779491913 |
| 6 | [45] | Qais | 2020 | TSO | TDM | 0.017009785983445 | 0.014438913645570 | 1.467713460523862 |
| 7 | Proposed Algorithm 1 | SDM | 0.012105788990909 | 0.009207999217896 | 1.210171037317782 | |||
| 8 | Proposed Algorithm 2 | SDM | 0.012120811620560 | 0.009345995684596 | 1.276143583474973 | |||
| 9 | Proposed Algorithm 1 | DDM | 0.011955126049429 | 0.008847188231494 | 1.292653674324527 | |||
| 10 | Proposed Algorithm 2 | DDM | 0.011896989581563 | 0.008827736037378 | 1.286768018642119 | |||
| 11 | Proposed Algorithm 1 | TDM | 0.011683038647976 | 0.008837712415575 | 1.260645716394877 | |||
| 12 | Proposed Algorithm 2 | TDM | 0.011660925987728 | 0.008830639239597 | 1.256151650040435 | |||
| # | Ipv (A) | I01 (μA) | n1 | RS (Ω) | RP (Ω) | I02 (μA) | n2 | I03 (μA) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3.8084 | 4.8723 × 10−10 | 1.0003 | 0.3692 | 169.0471 | - | - | - |
| 2 | 3.808 | 1.22 × 10−9 | 1.045 | 0.316 | 146.08 | - | - | - |
| 3 | 3.7983 | 6.79 × 10−8 | 1.28 | 0.251 | 582.7278 | - | - | - |
| 4 | 3.808244 | 1.21946 × 10−9 | 1.045334 | 0.316000 | 146.081207 | - | - | - |
| 5 | 3.812527 | 0.12311 × 10−6 | 1.32290 | 0.226800 | 800 | 7.29990 × 10−11 | 1.98800 | - |
| 6 | 3.8019 | 3.3525 × 10−7 | 1.9346 | 0.22724 | 450.13 | 1 × 10−12 | 1.7208 | 6.4568 × 10−8 |
| 7 | 3.8127 | 0.14051 × 10−6 | 1.332513 | 0.22351 | 1105.5869 | - | - | - |
| 8 | 3.81268 | 0.14 × 10−6 | 1.3325 | 0.2235 | 1155.6258 | - | - | - |
| 9 | 3.812527 | 0.12312 × 10−6 | 1.32288 | 0.226805 | 805.46 | 7.30 × 10−11 | 1.98800 | - |
| 10 | 3.81252689 | 0.1231199 × 10−6 | 1.32286 | 0.226801 | 807.11 | 7.299 × 10−11 | 1.9881 | - |
| 11 | 3.81252 | 0.12314 × 10−6 | 1.32274 | 0.226756 | 831.01000 | 7.29990 × 10−11 | 1.98888 | 1.24 × 10−10 |
| 12 | 3.81253 | 0.12312 × 10−6 | 1.32271 | 0.2267586 | 827.51000 | 7.30000 × 10−11 | 1.99060 | 1.2488 × 10−10 |
| # | Refs. | First Author | Year | Method | Model | RMSE | MAE | MAPE |
|---|---|---|---|---|---|---|---|---|
| 1 | [27] | Premkumar | 2021 | CGBO | SDM | 0.002203160582196 | 0.001777355730246 | 0.391412974711076 |
| 2 | GBO | SDM | 0.002203160582196 | 0.001777355730246 | 0.391412974711076 | |||
| 3 | [46] | Basset | 2021 | MTLBO | SDM | 0.002192702293887 | 0.001732693097767 | 0.386396089379751 |
| 4 | [47] | Gnetchejo | 2021 | DSO | SDM | 0.005525262416993 | 0.004319124678700 | 6.249226276809913 |
| 5 | [25] | Ridha | 2020 | MPA | SDM | 0.002741282553112 | 0.002131950064861 | 0.661561491439685 |
| 6 | [48] | Basset | 2020 | EO | SDM | 0.002307739416553 | 0.001831385873737 | 0.525272290565770 |
| 7 | [61] | Liang | 2020 | CPMPSO | SDM | 0.002192702238676 | 0.001732692519390 | 0.386403196851621 |
| 8 | [35] | Yu | 2019 | PGJAYA | SDM | 0.002193558995652 | 0.001733161807074 | 0.384469167044506 |
| 9 | [62] | Muangkote | 2019 | ORcr-IJADE | SDM | 0.002192747605064 | 0.001732930882957 | 0.383436962669269 |
| 10 | [18] | Li | 2019 | ITLBO | SDM | 0.002192702300691 | 0.001732692943681 | 0.386396861783031 |
| 11 | 2019 | TLBO | SDM | 0.004291553746717 | 0.003496972143159 | 1.247781769889620 | ||
| 12 | [15] | Li | 2019 | MADE | SDM | 0.002192702238262 | 0.001732692528770 | 0.386403149832207 |
| 13 | [28] | Xiong | 2018 | WOA | SDM | 0.002657115956104 | 0.002085699153659 | 0.539623953519785 |
| 14 | [50] | Yu | 2018 | MLBSA | SDM | 0.002162931772907 | 0.001693675233514 | 0.388880476705581 |
| 15 | [28] | Xiong | 2018 | DE-WOA | SDM | 0.002192747607804 | 0.001732930797684 | 0.383437390120559 |
| 16 | [51] | Wu | 2018 | ABC-TRR | SDM | 0.002192747605338 | 0.001732930874429 | 0.383437005413906 |
| 17 | [16] | Gao | 2018 | ISCE | SDM | 0.002192747603968 | 0.001732930917066 | 0.383436791688368 |
| 18 | [28] | Xiong | 2018 | IWOA | SDM | 0.002192213422029 | 0.001731871744843 | 0.389108171505321 |
| 19 | [52] | Xu | 2017 | GOFPANM | SDM | 0.002192747602872 | 0.001732930951174 | 0.383436620706835 |
| 20 | [53] | Elazab | 2017 | WOA | SDM | 0.002335740096957 | 0.001841026675079 | 0.332600274029797 |
| 21 | [54] | Jordehi | 2016 | TVACPSO | SDM | 0.003934939903764 | 0.003196946998661 | 4.232444252386350 |
| 22 | [55] | Chen | 2016 | EHA-NMS | SDM | 0.002192747604790 | 0.001732930891484 | 0.383436919923165 |
| 23 | [58] | Javidy | 2015 | IMO | SDM | 0.002835333050835 | 0.002165750688947 | 0.381968187687215 |
| 24 | [27] | Premkumar | 2021 | CGBO | DDM | 0.002199165255522 | 0.001759965636308 | 0.343756630837216 |
| 25 | 2021 | GBO | DDM | 0.002199691952382 | 0.001769207464245 | 0.368397908487905 | ||
| 26 | [48] | Basset | 2020 | EO | DDM | 0.002416169330585 | 0.001882811345434 | 0.375619719216614 |
| 27 | [58] | Javidy | 2015 | IMO | DDM | 0.003177249323240 | 0.002272124722926 | 0.743764711488892 |
| 28 | Proposed Algorithm 1 | SDM | 0.002101381507033 | 0.001770256665782 | 0.529618617926409 | |||
| 29 | Proposed Algorithm 2 | SDM | 0.002104650458946 | 0.001774133525922 | 0.460871551281877 | |||
| 30 | Proposed Algorithm 1 | DDM | 0.002076434123783 | 0.001706530046156 | 1.026218805598722 | |||
| 31 | Proposed Algorithm 2 | DDM | 0.002072962280362 | 0.001701420988536 | 1.006077058292598 | |||
| 32 | Proposed Algorithm 1 | TDM | 0.002040806557869 | 0.001676862715116 | 0.667708048509709 | |||
| 33 | Proposed Algorithm 2 | TDM | 0.002041811785061 | 0.001685648251157 | 0.656010002550055 | |||
| # | Ipv (A) | I01 (μA) | n1 | RS (Ω) | RP (Ω) | I02 (μA) | n2 | I03 (μA) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.0305 | 3.48 | 48.6428 | 1.2013 | 981.9821 | - | - | - |
| 2 | 1.0305 | 3.48 | 48.6428 | 1.2013 | 981.9821 | - | - | - |
| 3 | 1.0305143 | 3.4823 | 48.6428349 | 1.2012710 | 981.9823732 | - | - | - |
| 4 | 1.032357 | 2.496596 | 47.33406 | 1.240547 | 748.32309 | - | - | - |
| 5 | 1.0273 | 4.51 | 49.6486 | 1.1781 | 1977.6535 | - | - | - |
| 6 | 1.0296 | 3.76 | 48.9340 | 1.1943 | 1139.0284 | - | - | - |
| 7 | 1.0305143 | 3.4823 | 48.6428348 | 1.2012710 | 981.9822493 | - | - | - |
| 8 | 1.0305 | 3.4818 | 48.642372 | 1.2013 | 981.8545 | - | - | - |
| 9 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98224 | - | - | - |
| 10 | 1.0305143 | 3.4823 | 48.6428349 | 1.201271 | 981.9821925 | - | - | - |
| 11 | 1.0357161 | 4.13 | 49.2820100 | 1.2222703 | 999.6274934 | - | - | - |
| 12 | 1.0305143 | 3.4823 | 48.6428348 | 1.2012710 | 981.9822603 | - | - | - |
| 13 | 1.0280 | 4.75 | 49.8593 | 1.1680 | 1712.8543 | - | - | - |
| 14 | 1.0309977 | 3.4279 | 48.583600 | 1.2026154 | 931.9237428 | - | - | - |
| 15 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98214 | - | - | - |
| 16 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98223 | - | - | - |
| 17 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98228 | - | - | - |
| 18 | 1.0305 | 3.4717 | 48.631284 | 1.2016 | 978.6771 | - | - | - |
| 19 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98232 | - | - | - |
| 20 | 1.0294212 | 3.8525 | 49.0306622 | 1.1906302 | 1179.9442886 | - | - | - |
| 21 | 1.031435 | 2.6386 | 47.556648 | 1.235611 | 821.59514 | - | - | - |
| 22 | 1.030514 | 3.482263 | 48.64284 | 1.201271 | 981.98225 | - | - | - |
| 23 | 1.0264 | 3.45 | 48.5924 | 1.2112 | 1899.6737 | - | - | - |
| 24 | 1.0305 | 3.48 | 48.6428 | 1.2013 | 981.8874 | 3.89 × 10−6 | 34.7828 | - |
| 25 | 1.0305 | 3.47 | 48.6314 | 1.2016 | 981.2677 | 0 | 50 | - |
| 26 | 1.0288 | 9.38 × 10−4 | 47.1325 | 1.1896 | 1310.6705 | 3.96 | 49.1369 | - |
| 27 | 1.0251 | 0 | 45.7618 | 1.2339 | 1849.8346 | 3.07 | 48.1472 | - |
| 28 | 1.03241 | 2.5538 | 47.48801 | 1.2386 | 752.8111 | - | - | - |
| 29 | 1.0323 | 2.554 | 47.48563 | 1.23861 | 772.8905 | - | - | - |
| 30 | 1.03242 | 2.5130 | 47.418 | 1.2393 | 744.724 | 3.89 × 10−6 | 50 | - |
| 31 | 1.0325 | 2.5150 | 47.421 | 1.23928 | 743.666 | 3.8885 × 10−6 | 49.88 | - |
| 32 | 1.0323818 | 2.512908 | 47.42295 | 1.2393 | 743.724 | 1.86 × 10−4 | 48.88 | 1.35 × 10−6 |
| 33 | 1.032383 | 2.512914 | 47.423 | 1.2393 | 753.659 | 1.16 × 10−3 | 48.93 | 1.05 × 10−6 |
| Algorithms | Best | Worst | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| Proposed 1 | 7.7465 × 10−4 | 7.8447 × 10−4 | 7.7591 × 10−4 | 7.7468 × 10−4 | 3.5901 × 10−6 |
| Proposed 2 | 7.7466 × 10−4 | 7.8842 × 10−4 | 7.7504 × 10−4 | 7.7472 × 10−4 | 3.9844 × 10−6 |
| GTO | 7.7488 × 10−4 | 7.8447 × 10−4 | 7.7501 × 10−4 | 7.7501 × 10−4 | 3.711 × 10−6 |
| HBA | 7.7524 × 10−4 | 8.5089 × 10−4 | 7.8427 × 10−4 | 7.7921 × 10−4 | 1.4697 × 10−5 |
| AO | 16.000 × 10−4 | 95.000 × 10−4 | 51.000 × 10−4 | 49.000 × 10−4 | 18.000 × 10−4 |
| PSO | 7.7453 × 10−4 | 8.5089 × 10−4 | 7.9619 × 10−4 | 7.9570 × 10−4 | 1.9585 × 10−5 |
| Algorithms | Proposed 1 Versus Proposed 2 | Proposed 1 Versus HBA | Proposed 1 Versus GTO | Proposed 1 Versus AO | Proposed 1 Versus PSO |
|---|---|---|---|---|---|
| p-value | 8.5641 × 10−4 | 8.1465 × 10−5 | 0.0103 | 3.01 × 10−11 | 2.8314 × 10−8 |
| Algorithms | Proposed 2 versus Proposed 1 | Proposed 2 versus HBA | Proposed 2 versus GTO | Proposed 2 versus AO | Proposed 2 versus PSO |
| p-value | 8.5641 × 10−4 | 5.1857 × 10−7 | 0.3112 | 3.01 × 10−11 | 2.9215 × 10−9 |
| Parameters | Ipv (A) | I0 (μA) | RS (Ω) | RP (Ω) | n |
|---|---|---|---|---|---|
| Value | 3.45884 | 0.041477 | 0.3876853 | 549.98057 | 1.28087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rawa, M.; Abusorrah, A.; Al-Turki, Y.; Calasan, M.; Micev, M.; Ali, Z.M.; Mekhilef, S.; Bassi, H.; Sindi, H.; Aleem, S.H.E.A. Estimation of Parameters of Different Equivalent Circuit Models of Solar Cells and Various Photovoltaic Modules Using Hybrid Variants of Honey Badger Algorithm and Artificial Gorilla Troops Optimizer. Mathematics 2022, 10, 1057. https://doi.org/10.3390/math10071057
Rawa M, Abusorrah A, Al-Turki Y, Calasan M, Micev M, Ali ZM, Mekhilef S, Bassi H, Sindi H, Aleem SHEA. Estimation of Parameters of Different Equivalent Circuit Models of Solar Cells and Various Photovoltaic Modules Using Hybrid Variants of Honey Badger Algorithm and Artificial Gorilla Troops Optimizer. Mathematics. 2022; 10(7):1057. https://doi.org/10.3390/math10071057
Chicago/Turabian StyleRawa, Muhyaddin, Abdullah Abusorrah, Yusuf Al-Turki, Martin Calasan, Mihailo Micev, Ziad M. Ali, Saad Mekhilef, Hussain Bassi, Hatem Sindi, and Shady H. E. Abdel Aleem. 2022. "Estimation of Parameters of Different Equivalent Circuit Models of Solar Cells and Various Photovoltaic Modules Using Hybrid Variants of Honey Badger Algorithm and Artificial Gorilla Troops Optimizer" Mathematics 10, no. 7: 1057. https://doi.org/10.3390/math10071057
APA StyleRawa, M., Abusorrah, A., Al-Turki, Y., Calasan, M., Micev, M., Ali, Z. M., Mekhilef, S., Bassi, H., Sindi, H., & Aleem, S. H. E. A. (2022). Estimation of Parameters of Different Equivalent Circuit Models of Solar Cells and Various Photovoltaic Modules Using Hybrid Variants of Honey Badger Algorithm and Artificial Gorilla Troops Optimizer. Mathematics, 10(7), 1057. https://doi.org/10.3390/math10071057











