The IRC Indices of Transformation and Derived Graphs
Abstract
:1. Introduction
2. Preliminaries
- (i)
- such that in G, or;
- (ii)
- , or vice versa such that in G.
- (i)
- such that in G, or;
- (ii)
- , or vice vera such that in G.
- (i)
- and .
- (ii)
- .
- (iii)
- and .
- (iv)
- and .
- (v)
- and .
- (i)
- , if and if ;
- (ii)
- , in G if and in G if ;
- (iii)
- , , in G if and in G if .
- (i)
- and .
- (ii)
- and .
- (iii)
- and .
- (iv)
- and .
- (v)
- and .
- (vi)
- and .
- (vii)
- and .
- (viii)
- and .
3. Application of the IRC Index in QSAR Modeling
3.1. Computational Details
- Step 1:
- Draw G on newGraph and compute its adjacency matrix A.
- Step 2:
- Input A into our program in MatLab to compute .
3.2. QSAR Modeling of Physicochemical Properties
4. The IRC Indices of Transformation Graphs
5. The IRC Indices of Derived Graphs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roy, K.; Kar, S.; Das, R.N. A Primer on QSAR/QSPR Modeling: Fundamental Concepts; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Allison, T.C.; Burgess, D.R., Jr. First-principles prediction of enthalpies of formation for polycyclic aromatic hydrocarbons and derivatives. J. Phys. Chem. A 2015, 119, 11329–11365. [Google Scholar] [CrossRef] [Green Version]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Redžepović, I.; Marković, S.; Furtula, B. On structural dependence of enthalpy of formation of catacondensed benzenoid hydrocarbons. MATCH Commun. Math. Comput. Chem. 2019, 82, 663–678. [Google Scholar]
- Yu, J.; Sumathi, R.; Green, W.H. Accurate and efficient method for predicting thermochemistry of polycyclic aromatic hydrocarbons-bond-centered group additivity. J. Am. Chem. Soc. 2004, 126, 12685–12700. [Google Scholar] [CrossRef] [PubMed]
- Zavitsas, A.A.; Matsunaga, N.; Rogers, D.W. Enthalpies of formation of hydrocarbons by hydrogen atom counting. Theoretical implications. J. Phys. Chem. A 2008, 112, 5734–5741. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, A.L.; Leal, J.P.; Falcao, A.O. Random forests for feature selection in QSPR models–an application for predicting standard enthalpy of formation of hydrocarbons. J. Cheminf. 2013, 5, 9–24. [Google Scholar] [CrossRef]
- Song, X.; Chai, L.; Zhang, J. Graph signal processing approach to QSAR/QSPR model learning of compounds. IEEE Trans. Pattern Anal. Mach. Intell. 2020, in press. [Google Scholar] [CrossRef]
- Dudek, A.Z.; Arodz, T.; Galvez, J. Computational methods in developing quantitative structure-activity relationships (QSAR): A review. Comb. Chem. High Throughput Screen. 2006, 9, 213–228. [Google Scholar] [CrossRef] [PubMed]
- Mauri, A.; Consonni, V.; Todeschini, R. Molecular Descriptors. Handbook of Computational Chemistry; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley-VCHL: Weinheim, Germany, 2009; Volume 1–2. [Google Scholar]
- Dearden, J.C. Advances in QSAR Modeling-Applications in Pharmaceutical, Chemical, Food, Agricultural and Environmental Sciences; Roy, K., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPR; Gordon & Breach: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Talevi, A.; Bellera, C.L.; Di Ianni, M.; Duchowicz, P.R.; Bruno-Blanch, L.E.; Castro, E.A. An integrated drug development approach applying topological descriptors. Curr. Comput. Aided Drug Des. 2012, 8, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Réti, T.; Sharafdini, R.; Dregelyi-Kiss, A.; Haghbin, H. Graph irregularity indices used as molecular descriptor in QSPR studies. MATCH Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Ascioglu, M.; Cangul, I.N. Sigma index and forgotten index of the subdivision and r-subdivision graphs. Proc. Jangjeon Math. 2018, 21, 375–383. [Google Scholar]
- Réti, T. On some properties of graph irregularity indices with a particular regard to the σ-index. Appl. Math. Comput. 2019, 344–345, 107–115. [Google Scholar] [CrossRef]
- Diudea, M.V.; Gutman, I.; Lorentz, J. Molecular Topology; Nova Science Publishers: New York, NY, USA, 2001. [Google Scholar]
- Collatz, L.; Sinogowitz, U. Spektren endlicher grafen. Abh. Math. Sem. Univ. Hamburg. 1957, 21, 63–77. [Google Scholar] [CrossRef]
- Bell, F.K. A note on the irregularity of a graph. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse problem for sigma index. MATCH Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals: Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Gutman, I.; Das, K.C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Furtula, A.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Réti, T.; Toth-Laufer, E. On the construction and comparison of graph irregularity indices. Kragujevac J. Sci. 2017, 39, 53–75. [Google Scholar] [CrossRef] [Green Version]
- Cioabă, S.M. Sums of powers of the degrees of a graph. Discrete Math. 2006, 306, 1959–1964. [Google Scholar] [CrossRef] [Green Version]
- Ilić, A.; Zhou, B. On reformulated Zagreb indices. Discret. Appl. Math. 2012, 160, 204–209. [Google Scholar] [CrossRef] [Green Version]
- Ranjini, P.S.; Lokesha, V.; Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 2013, 1, 116–121. [Google Scholar]
- Behzad, M. A criterion for the planarity of a total graph. Proc. Cambridge Philos. Soc. 1967, 63, 679–681. [Google Scholar] [CrossRef]
- Sampathkumar, E.; Chikkodimath, S.B. The semi-total graphs of a graph-I. J. Karnatak Univ.-Sci. 1973, 18, 274–280. [Google Scholar]
- Akiyama, J.; Hamada, T.; Yoshimura, I. Miscellaneous properties of middle graphs. TRU Math. 1974, 10, 41–53. [Google Scholar]
- Alon, N. Eigenvalues and expanders. Combinatorica 1986, 6, 83–89. [Google Scholar] [CrossRef]
- Wu, B.; Meng, J. Basic properties of total transformation graphs. J. Math. Study 2001, 34, 109–116. [Google Scholar]
- Xu, L.; Wu, B. Transformation graph G−+−. Discrete Math. 2008, 308, 5144–5148. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Wu, B. The transformation graph G++−. Aust. J. Comb. 2009, 44, 37–42. [Google Scholar]
- Stevanović, D.; Brankov, V.; Cvetković, D.; Simić, S. newGRAPH: A Fully Integrated Environment used for Research Process in Graph Theory. Available online: http://www.mi.sanu.ac.rs/newgraph/index.html (accessed on 21 February 2022).
- MATLAB 8.0 and Statistics Toolbox 8.1; The MathWorks, Inc.: Natick, MA, USA, 2022.
- Gutman, I.; Tošović, J. Testing the quality of molecular structure descriptors. Vertex-degree-based topological indices. J. Serb. Chem. Soc. 2013, 78, 805–810. [Google Scholar] [CrossRef]
- NIST Standard Reference Database. Available online: http://webbook.nist.gov/chemistry/ (accessed on 21 February 2022).
- Nikolić, S.; Trinajstić, N.; Baučić, I. Comparison between the vertex- and edge-connectivity indices for benzenoid hydrocarbons. J. Chem. Inf. Comput. Sci. 1998, 38, 42–46. [Google Scholar] [CrossRef]
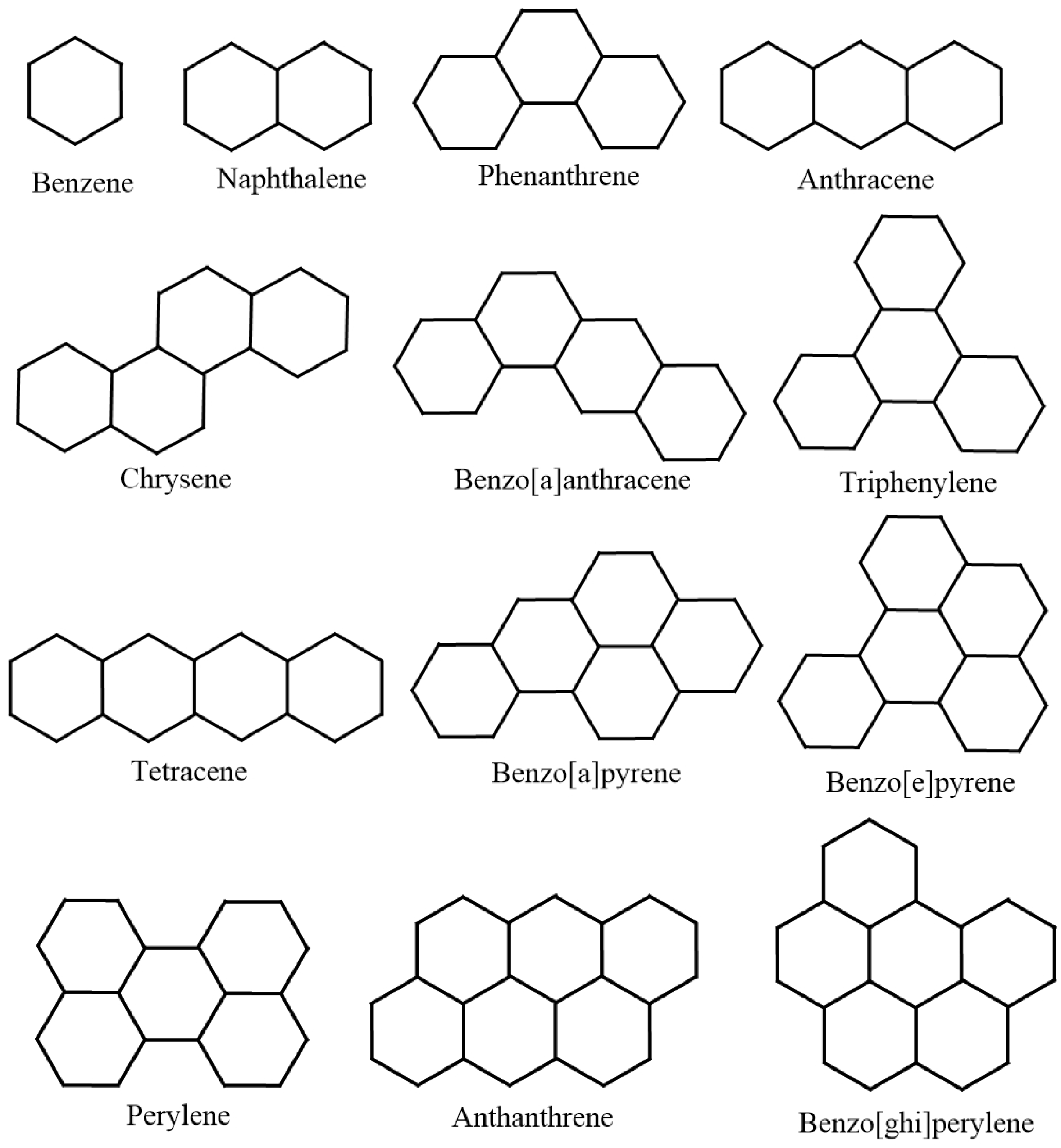
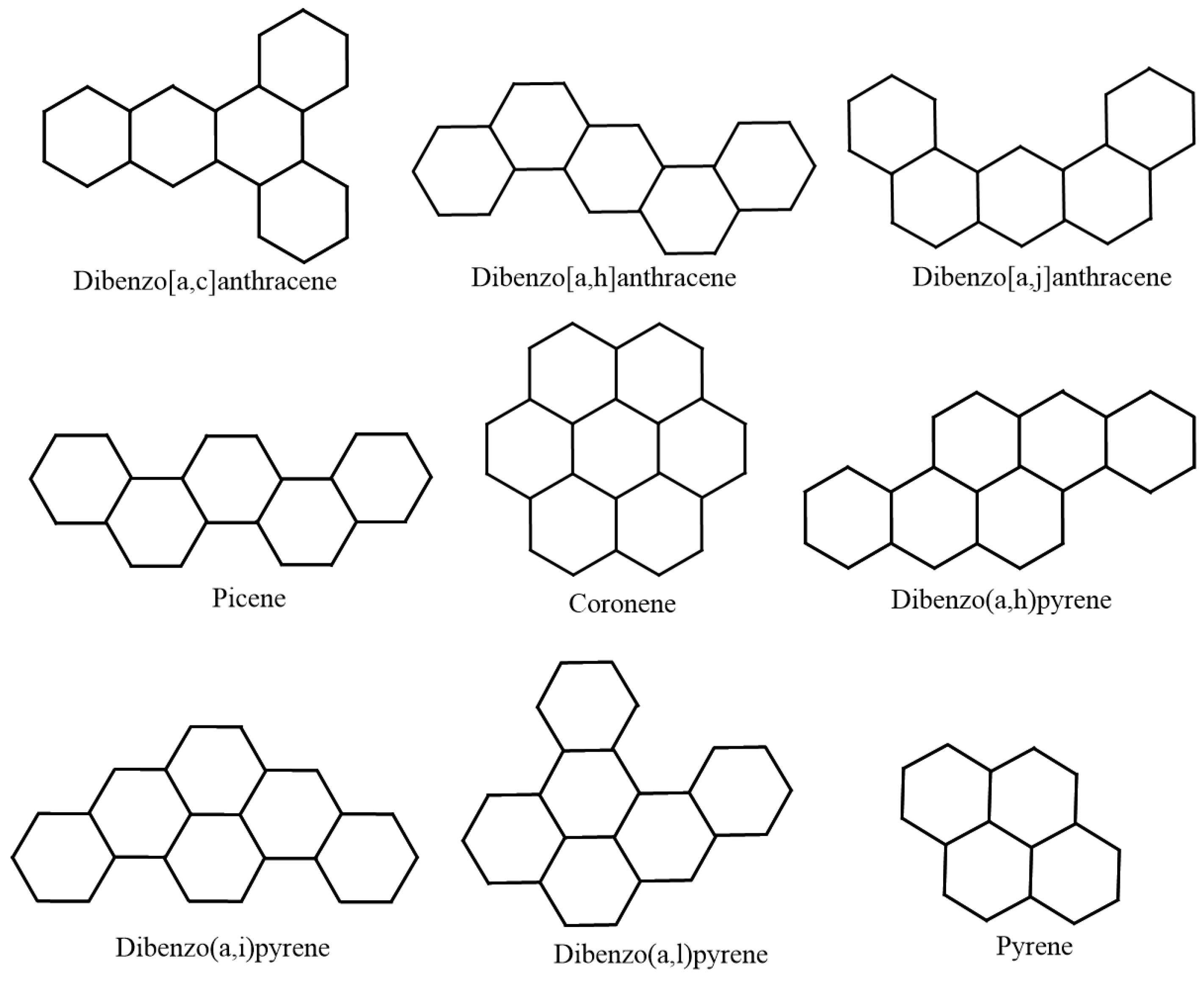
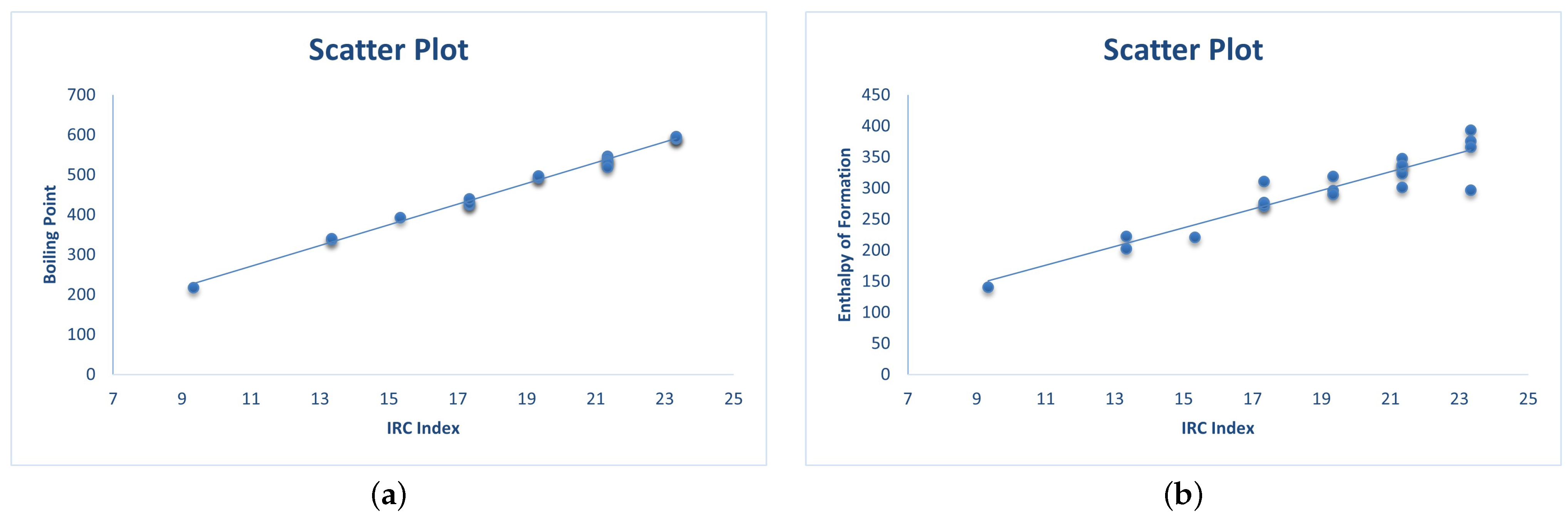
| Molecule | in °C | in kJ/mol | |
|---|---|---|---|
| Benzene | 80.1 | 75.2 | 0 |
| Naphthalene | 218 | 141 | 9.3333 |
| Phenanthrene | 338 | 202.7 | 13.3333 |
| Anthracene | 340 | 222.6 | 13.3333 |
| Chrysene | 431 | 271.1 | 17.3333 |
| Benzo[a]anthracene | 425 | 277.1 | 17.3333 |
| Triphenylene | 429 | 275.1 | 17.3333 |
| Tetracene | 440 | 310.5 | 17.3333 |
| Benzo[a]pyrene | 496 | 296 | 19.3333 |
| Benzo[e]pyrene | 493 | 289.9 | 19.3333 |
| Perylene | 497 | 319.2 | 19.3333 |
| Anthanthrene | 547 | 323 | 21.3333 |
| Benzo[ghi]perylene | 542 | 301.2 | 21.3333 |
| Dibenzo[a,c]anthracene | 535 | 348 | 21.3333 |
| Dibenzo[a,h]anthracene | 535 | 335 | 21.3333 |
| Dibenzo[a,j]anthracene | 531 | 336.3 | 21.3333 |
| Picene | 519 | 336.9 | 21.3333 |
| Coronene | 590 | 296.7 | 23.3333 |
| Dibenzo(a,h)pyrene | 596 | 375.6 | 23.3333 |
| Dibenzo(a,i)pyrene | 594 | 366 | 23.3333 |
| Dibenzo(a,l)pyrene | 595 | 393.3 | 23.3333 |
| Pyrene | 393 | 221.3 | 15.3333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Hayat, S.; Zhong, Y.; Peng, Z.; Réti, T. The IRC Indices of Transformation and Derived Graphs. Mathematics 2022, 10, 1111. https://doi.org/10.3390/math10071111
Luo H, Hayat S, Zhong Y, Peng Z, Réti T. The IRC Indices of Transformation and Derived Graphs. Mathematics. 2022; 10(7):1111. https://doi.org/10.3390/math10071111
Chicago/Turabian StyleLuo, Haichang, Sakander Hayat, Yubin Zhong, Zhongyuan Peng, and Tamás Réti. 2022. "The IRC Indices of Transformation and Derived Graphs" Mathematics 10, no. 7: 1111. https://doi.org/10.3390/math10071111
APA StyleLuo, H., Hayat, S., Zhong, Y., Peng, Z., & Réti, T. (2022). The IRC Indices of Transformation and Derived Graphs. Mathematics, 10(7), 1111. https://doi.org/10.3390/math10071111






