Mathematical Thinking and the VESS Model: A Descriptive Study

Abstract

Critical, creative, and flexible thinking is one of the educational priorities in the 21st Century, at a time in which the world is showing its most ephemeral and uncertain side. In this sense, visible thinking is a fundamental tool for achieving more significant and meaningful learning. The VESS (Meaningful Life with Balance and Wisdom) model, considering how we learn, provides different tools, such as the aforementioned, which facilitate learning. Thus, thinking, and, more specifically, the development of mathematical thinking through the VESS model, provides an open door towards the development of basic cognitive skills, such as attention, metacognition, and memory, and has a direct effect on the three areas of the early childhood education curriculum. The aim of the present work is to discover, in a descriptive manner, how the learning of the VESS model influences future teachers. In the present article, a series of descriptive, correlational, and survey-based models conducted at the University of Cordoba (Córdoba, Spain) are described. Beforehand, a validation of the instrument was performed, which obtained high goodness-of-fit indices, with an adequate validity and reliability.

1. Introduction

Spanish education is continuously changing in search of an inclusive educational praxis that considers every need and that is adapted to each of the existing capacities in the classroom. In this sense, different modifications have been implemented from the state educational legislation in favor of a type of pedagogy that allows the access and the permanence of all children, independently of their social, economic, or family situation, to the educational system.

Likewise, many active methodologies are being considered, such as that proposed by Rose (development neuropsychologist) and Meyer (pedagogist, psychologist, and graphic designer) in the 1990s, who defined Universal Design for Learning (UDL), which considers three basic aspects [1]. These are:

• Development of basic cognitive skills, considering what to learn, and having in mind an affective perspective (motivation, interest, self-regulation).
• Offering the students different types of representation and presentation of learning (different ways to show the information, improve comprehension through visible learning, graphical organizers).
• Providing options so that the students interact with the information and convert this information knowledge through language and the use of executive functions.

This line of thought is followed by the VESS model (Meaningful Life with Balance and Wisdom), an innovative and revolutionary example that combines different learning methodologies and that is supported by critical, rational, and visible thinking, neuroeducation, and the acquisition of adapted and meaningful learning from the area of development of the child [2]. It allows us to imagine a world that is more democratic, where the citizens are an active part of each and all of the decisions of the country and are active subjects of social change.

Therefore, this model is a tool that allows us to work on, from emotions and thinking, the basic cognitive skills, such as attention, perception, memory, metacognition, etc., which are useful in logical-mathematical learning, and all of this from an interactive perspective, where the teacher plays the role of a guide.

The development of all of these skills is acquired in the first years of life. Thus, from early childhood, the teacher must row in favor of mathematical development, considering the three areas that come into play in the early childhood curriculum (Royal Decree 1640/2006, from 29 December): languages, communication, and representation; knowledge about oneself; knowledge about the surroundings.

These areas, in the logical-mathematical and visuospatial development of the student, are very present and can or must be developed considering different methods, strategies, or tools that underlie in the VESS model, such as visible thinking, thinking routines, language of thinking, and habits of mind.

1.1. Visible Thinking and Mathematics

Visible thinking, proposed by [3], implies the most effective manner of comprehension for developing the thinking of students, and delves into the learning of contents through images and, in general, the living expression of thought.

Visible thinking has been present as a manner of communication and comprehension of human beings since the start of society. Mathematical procedures and the different specific areas of mathematics (algebra, calculus, trigonometry…) were developed, starting with symbols and simple and regulated rules. Thus, learning of mathematics implies a change in the brain structure since early childhood, and includes the development of simple mental and cognitive processes, such as comparison, analysis, organization of ideas, etc. [4].

According to [5], there are two ways to achieve this way of learning in our students, which consider the use of graphical resources or words to communicate and think better: through language of thinking and thinking routines.

Language of thinking fixes thoughts, allows their analysis, and turns them into words. Likewise, it socializes thought, it is a medium of intellectual progress, and allows the solving of problems [6].

This language is provided by communication, dialogic thinking, and reflective argumentation, either inductive or deductive, for the access of mathematical knowledge.

Thinking routines, according to [7], consist of performing simple and structured tasks to organize, explore, and summarize thoughts so that they are developed in a viable and efficient manner.

Thus, language of thinking, as well as thinking routines, imply a methodological innovation in the teaching–learning process of mathematics, which foments the construction of thought and promotes the implementation of habits of mind. In this sense, and transversally, it foments experience-based learning, exploration, and it awakens curiosity, which inevitably results in a greater degree of reflection and creativity [8].

Likewise, the authors of [9] conclude that co-operative learning favors basic cognitive skills, such as attention, perception, memory, or metacognition, which are involved in the comprehension, construction, and resolution of problems from a reflective perspective.

In this case, [10] establishes three dimensions which foment cognitive skills through co-operative learning, such as cognitive, motivational, and metacognitive dimensions.

Based on the above, we can affirm that knowledge of mathematics promotes creativity and reasoning ability, which allows students to connect ideas, resolve problems, etc., turning them into proactive individuals who are organized and unwavering when resolving a problem.

1.2. Development of Logical-Mathematical Thinking

When discussing mathematics and thinking, in truth, we are referring to a skill or ability to think in an applied manner through logical reasoning. Ref. [11] highlights the existence of seven types of intelligence, among which we find logical-mathematical intelligence. This intelligence is associated to deductive or inductive reasoning. It is utilized to resolve logic problems, and it has always been considered the most important intelligence.

Nevertheless, from the classrooms, the teaching of mathematics has always been taught from a static and rigid perspective. The stimulation of mathematical thinking must start from an early age, as it will not only be useful to the student in the resolution of academic math problems, but also in their everyday life. Moreover, this stimulation must be adapted to the age and personal characteristics of each child to achieve meaningful learning coming from a motivational process and with experiences closer to their reality, which allows students to learn in a constructive manner.

At present, then, an argument is made about the teaching of thinking skills that will lead us towards the solution of problems in a divergent manner—obtaining different conclusions; and not convergent—there is only one way to arrive to a logical solution [12].

In this sense, Ref. [13] posits two theories involved in the learning of mathematics: through absorption and cognition. The first has been historically used. Presently, we find ourselves in a time of change, and the VESS model, supported by cognitive foundations, advocates the teaching of mathematics from a perspective that is critical, rational, visible, creative, flexible, and dynamic.

1.3. The VESS Model from Mathematics and the Areas of the Curriculum

The VESS model is based on the use of different tools to achieve an integral development of the student that goes from emotional control to reach the maximum of cognitive skills through tools that promote good thinking. For this purpose, the author of [14] distinguishes four phases that can be used in a complementary way with some strategies promoted by the VESS model, which structure problem solving and facilitate comprehension acting as a means for the development of mathematical thinking.

1.3.1. Comprehension of The Problem: Visible Thinking

The context in which the students develop and the experiences they encounter or go through are very important in the construction or acquisition of cognitive and social skills. In this sense, everything they learn is conditioned by what was mentioned above and has a great repercussion in the manner in which they move, express, understand, or think.

Likewise, at schools, we must provide students with strategies that complement and associate the new knowledge with the aspects they know and which are present in their everyday lives. This is achieved through visible thinking (experimental activities, imagination games, social interaction, etc.) [15].

1.3.2. Design of a Solution Plan: Thinking Routines

Once the description of the problem is understood, it is important to organize the information and, for this, it is fundamental to establish guidelines that facilitate this process. This could be achieved through different thinking routines, which organize the information and allow for a better execution of the solution plan.

1.3.3. Execution of a Plan (Habits of Mind)

Once the information is organized, we must implement divergent thinking that allows us to choose the correct operation to solve the problem. For this, we could utilize habits of mind (reflecting, taking risks, managing the impulsivity of making any operation without thinking, considering different perspectives, connecting, reasoning with evidence, etc.).

1.3.4. Retrospective View (Metacognition, Language of Thinking, Socrative)

Lastly, once one has arrived to a result or a conclusion, we must think about the result and the process of problem resolution (metacognition) to reflect about our train of thought, and whether there was a mistake or some element we must improve. For this, we must use the language of thinking: expressing the conclusion obtained, verbally or creatively, and by listening. This second part, which encompasses the language of thinking, is fundamental in that listening to other perspectives leads to listening to others and, therefore, to the performance of activities as a group.

In this sense, an evaluation or comparison of results could be performed in a manner that is attractive, and new technologies could be used for this. More specifically, in this case, an evaluation tool, such as Socrative, could be utilized.

Socrative allows the evaluation and self-evaluation of knowledge in a specific moment in time and offers immediate feedback, which is fundamental for guiding the students between the places they are at to the one they want to reach [16]. Moreover, it can be used individually or as a group, and it also utilizes images to facilitate comprehension, which is extremely important for achieving meaningful learning.

Likewise, these four steps take into account three areas of the children’s curriculum: languages: communication and representation—present when one makes use of language of thinking; knowledge about themselves—present when critically and creatively thinking, which indirectly re-enforces self-esteem and self-concept, and takes into account motivational activities closely associated to the children that offer positive emotional feedback; knowledge of the surroundings—showing activities and problems closely associated to the children.

2. Theoretical–Practical Perspective of the Study

We live in an overconnected and liquid world, we receive information from everywhere and we have access to any type of information whenever we want. However, on many occasions, we are not capable of deciding and making our own decisions, making us not very autonomous people. The learning to learn competency is not practically worked on in schools.

For this reason, the contribution that this work makes to the academic world, and to education in particular, is important, since it shows a novel and innovative methodology that is based on co-operative learning and that focuses on critical, rational, creative, and visible thinking for problem solving from an early age. The application of the different ways of thinking allows the student to develop several basic cognitive skills, such as attention, perception, memory, metacognition, and comprehension. In this way, the learning of mathematics and logical-mathematical development occurs from an integral point of view, including the different tools that underlie the VESS model, thus addressing all areas of the curriculum. The area of “language, communication and representation” is worked through the language of thought—when students communicate their reasoning; the area of “knowledge of the environment” is shown by proposing activities close to the context in which children develop; finally, the area of “self-knowledge and personal autonomy” is shown through the use of different group dynamics—habits of mind and tools that structure thinking—thinking routines.

In order to understand in a practical way how to carry out the VESS model in the learning of mathematics, we will carry it out as an example, attending to the three areas of early childhood education, as mentioned above:

• Area 1: knowledge of the environment. The proposed activities should be based on the students’ zone of proximal development, so that they receive a more realistic idea of the problem posed. For example, if what they want to work on is spatial orientation, the space should be a familiar place, such as the neighborhood where they live. In this way, they will develop habits of mind, establishing mental movements.
• Area 2: languages, communication, and representation. When students read and understand a problem statement, they are able to explain the reasoning that led them to perform one operation or another. Sharing thoughts with others, apart from enriching the cognition process in learning, develops the students’ language, both verbal (with words) and creative (with drawings).
• Area 3: self-knowledge and personal autonomy. It is perhaps the area that develops in a more transversal way, since the fact that students communicate in an organized and structured way (thinking routines), asking themselves questions and establishing cognitive links, leads the student to be increasingly autonomous. In addition, if all activities are conducted in a co-operative way, this self-knowledge is accentuated, since critical thinking, emotions, and feelings towards others that define us individually are encouraged and enhanced.

All this is relevant because the VESS model fostering thinking from an early age is very important for making students future social agents of change. In this sense, future primary school teachers should be aware of this fact [17] and know that well-executed mathematical thinking improves or develops critical and creative thinking, fostering in students attitudes (moral dimension, ethics, empathy, companionship, etc.) and skills (attention, perception, memory, metacognition, etc.) necessary for human development. [18].

Objectives and Hypotheses

The main objective of this research is to “analyze the perception of the students of the Degree in Early Childhood Education, Primary Education and Master of Inclusive Education of the University of Cordoba on the learning of the VESS model”.

In turn, this main objective carries with it four specific objectives, each of which has a hypothesis associated with it:

• O1. To describe the perceptions of the students of Early Childhood Education, Primary Education, and Master of Inclusive Education of the University of Cordoba about the learning of the VESS model.
• H1. The VESS model, making use of co-operative learning and digital assessment tools, such as “Socrative”, fosters creativity and critical thinking of the students of the Higher Education Degree.
• O2. To analyze the differences in the means of the three dimensions that make up the questionnaire “Perceptions of university students about the VESS Model” and the independent variables corresponding to sex, age, and the type of school in which they studied.
• H2. There are differences in the perception that higher education students have of the VESS method according to age, sex, degree, and the type of school in which they studied.
• O3. To observe whether or not there is a relationship between the different dimensions that make up the questionnaire.
• H3. There are relationships between all the dimensions that make up the questionnaire.
• O4. To study the existence of a predictive model of the students’ expectations of the use of the VESS model according to their perception of it as a learning strategy, as well as their assessment of co-operative learning and evaluation through “Socrative”.
• H4. The development of co-operative learning and the use of Socrative are predictors of learning the VESS model.

3. Materials and Methods

To carry out this research we conducted several sessions with the study participants. The class dynamics we carried out were simple. First, we explained and contextualized what the VESS model consisted of and how Socrative was used to evaluate the learning obtained through the use of this methodology. Later, together, we created a series of activities based on the VESS model, that is to say, giving priority to visible, creative, and critical thinking, through the method’s own strategies, such as thinking routines, habits of mind, language of thought, etc. In this sense, and now in a small group, the students designed a pedagogical proposal that took into account all of the above. Finally, they filled in the questionnaire, previously elaborated by us to know what is the perception that the students of education have about the use of the VESS method, co-operative learning, and Socrative for the evaluation of learning.

3.1. Data Analysis

In order to respond to the previously stated objectives, we have carried out different analyses subsequent to the validation of the instrument created ad hoc. The analyses carried out are detailed below:

• Descriptive study of the three dimensions of which the instrument was composed, making use of measures of mean and standard dispersion.
• Analysis of variance using ANOVA and T-Student test.
• Correlational study between the three dimensions of the instrument through an analysis of bivariate correlations.
• Regression analysis based on the regression line coefficient using the “stepwise” method.

3.2. Sampling and Participants

The methodology used in this research is numerical in nature and follows a deductive, quantitative, and descriptive research strategy, which is important to be able to draw inferred conclusions that can be extrapolated to a larger sample group. The study sample was composed by 231 students enrolled in the Early Childhood Education, Primary Education, and Inclusive Education Master’s programs at the University of Cordoba (Córdoba, Spain). The sample was selected through the use of non-probabilistic, convenience sampling [19]. This is because we were only able to access the groups of students taught by the director of this study.

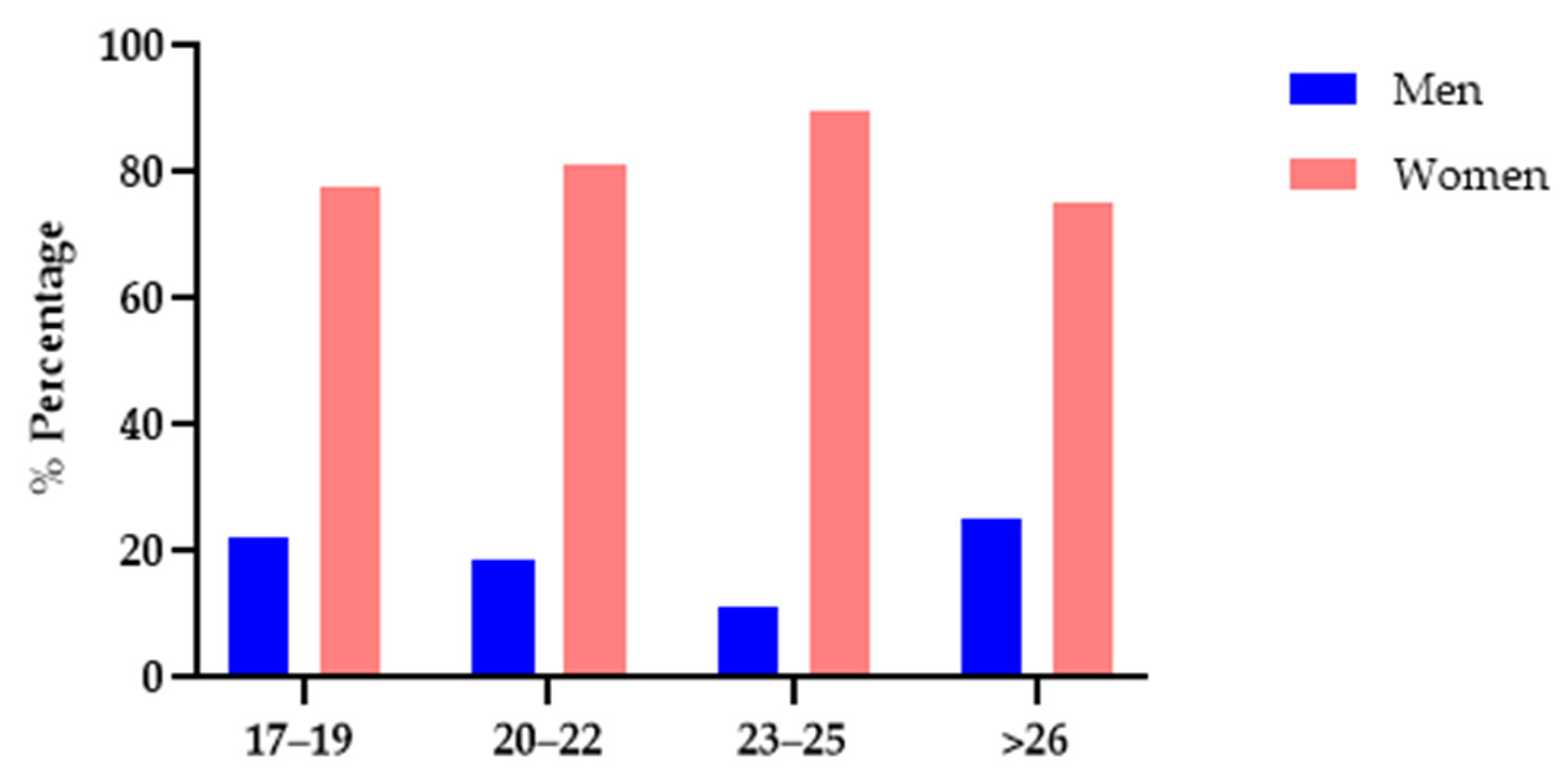
Among the students surveyed, 187 (80.95%) were women and 44 (19.05%) were men. Of these, 17 men and 57 women were aged between 17–19 years old; 16 men and 70 women were aged between 20 and 22 years old, and 5 men and 40 women were aged between 23 and 25 years old. Lastly, 6 men and 18 women were older than 26 years old.

Figure 1 shows a bar graph of the different students, distributed according to sex and age ranges.

Moreover, 127 (54.98%) participants were enrolled in the Early Childhood Education degree, 91 (39.39%) in the Primary Education degree, and 13 (5.63%) in the Masters in Inclusive Education degree.

Figure 2 combines the three variables that refer to the participants’ sex, age, and degree.

As for the schools where the students attended, it must be underlined that 170 (73.59%) attended a public school, 58 (25.11%) a concerted school, and 3 (1.30%) a private one.

3.3. Instrument

For the collection of data, a questionnaire was utilized. It was named Questionnaire on the Perception of the VESS Model in Higher Education. It was created exclusively for this research (ad hoc) and it was a polythematic, closed, short-question questionnaire, with the responses provided as Likert responses ranging from 1—complete disagreement to 5—complete agreement. The instrument was composed by 16 items distributed into 3 dependent variables or dimensions (VESS model, co-operative learning, and Socrative). Moreover, it was composed by a series of independent variables, such as sex, age, the type of school attended by each student, and the degree they were currently enrolled in. To find the validity of the instrument, it was subjected to an exploratory factorial analysis (EFA). With the help of the statistical package SPSS v25 and the software program Factory Analysis (10.8.04), an optimal implementation of parallel analysis [20] was performed, along with a process of extraction of common factors, “Robust Maximum Likelihood”, considering the “Promix” rotation procedure.

Likewise, it was possible to confirm the construct of the instrument through the Kaiser–Meyer–Olkin (KMO) index, which provided a result of 0.94; Bartlett’s sphericity test, with p = 0.000; root mean square residuals (RMSR) = 0.0379, with the model being adequate. The results showed that the total explained variance was 68.33%. The communalities oscillated between 0.308 for item 5 and 0.997 for item 8, with all of them found above 0.3 (

Table 1. Matrix of rotated factors.

Variable	F 1	F 2	F 3
V 1			0.431
V 2		0.391
V 3			0.498
V 4	0.359
V 5	0.308
V 6	0.336
V 7	0.446
V 8	0.997
V 9	0.529
V 10		0.622
V 11		0.614
V 12		0.867
V 13			0.573
V 14			0.730
V 15			0.662
V 16			0.575

).

Considering the results extracted from the EFA, a structure of the instrument shaped by three dimensions was found:

• Perspectives of the students on the VESS model.
• Co-operative learning.
• Socrative as an evaluation tool.

To confirm the structure obtained in the EFA, a confirmatory factorial analysis was performed (CFA). The CFA confirmed that the instrument was divided into three dimensions (perspectives of the students on the VESS model, co-operative learning, and Socrative). Thus, the factorial structure of the CFA showed a structure of 12 items, after 4 of them were eliminated due to factorial loads lower than 0.4.

To assess the fit of the model, the following were considered: chi-square statistic (X2 test) = 69.6; degrees of freedom (df) = 49; statistical significance value (p) = 0.028; X2/df = 1.42; comparative fit index (CFI) = 0.982; incremental adjustment index (IFI) = 0.983; standard adjustment index (NFI) = 0.944; TLI (Tuker–Lewis index) = 0.976; root mean square error of approximation (RMSEA) = 0.043; and expected cross-validation rate (ECVI) = 0.676. Given these results, it was concluded that the model fit was adequate, as the RMSEA value was lower than 0.060, and the value for the CFI, IFI, NFI, and TLI was above 0.90 [21,22].

The convergent and discriminant validity of the instrument was also verified, considering the indices recommended in the literature: composite reliability (CR), average variance extracted (AVE), maximum shared variance (MSV), and the maximal reliability H (MaxR(H)).

Lastly, the internal consistency of the questionnaire was verified, as a whole and for each of its dimensions separately (

Table 2. Internal consistency of the instrument.

Dimension	Reliability
Factor 1: Perspectives of the students on the VESS model	α = 0.832 (n = 4)
Factor 2: Cooperative learning	α = 0.782 (n = 4)
Factor 3. Socrative	α = 0.836 (n = 4)
Total	α = 0.892 (n = 12)

). All the factors of the instruments obtained coefficients higher than 0.600, an index that is considered acceptable [23].

4. Results

4.1. Descriptive Analyses

The following lines will describe the results of the mean, median, standard deviation, minimum, and maximum of the sample studied (

Table 3. Distribution of the frequencies of the items of the instrument.

Dimension	Items	(µ)	T (σ)
Factor 1. The VESS model	The VESS model considers diversity	4.12	0.765
	2. The VESS model foments creativity	4.54	0.617
	3. It makes sense to introduce the use of these methodologies in the Early Childhood Education classroom	3.73	1.13
	4. Through the VESS model, it is possible to work on contents from a holistic perspective	4.22	0.708
	5. Establishing thinking routines is necessary for guiding students in their learning process	4.37	0.659
	6. The VESS model foments learning through the externalization of thinking	4.30	0.741
	7. The VESS model allows for the organization of the content in the mind of children	4.38	0.654
Factor 2. Co-operative learning	8. I consider co-operative learning as a good method for developing my social competences	4.55	0.630
	9. Co-operative learning makes me feel as an active part of my own learning process	4.38	0.712
	10. The performance of the group improves if the activities planned by the teachers require reflection	4.22	0.755
	11. Working co-operatively is a manner of better understanding the content	4.36	0.738
	12. Co-operative learning allows me to come into an agreement between different opinions	4.32	0.764
Factor 3. Socrative	13. Socrative allows digital development in classrooms	4.49	0.638
	14. Socrative allows the participation of the students in real time	4.45	0.713
	15. Socrative actively involves all the students	4.41	0.757
	16. Socrative foments the creation of a play-based learning environment	4.34	0.721

), with the data from the final version of the instrument, shaped by 16 items.

Likewise, the descriptive values were high for the mean, as shown in

Table 4. Descriptive study of the dimensions.

	VESS Model	Co-Operative Learning	Socrative
Mean	4.32	4.32	4.42
Median	4.25	4.5	4.50
Std. Deviation	0.56	0.58	0.58
Minimum	2.25	2.50	2.75
Maximum	5.00	5.00	5.00

.

4.2. Inferential Study

This section describes the results from the mean comparison with Student’s t-test for a same group with respect to the different independent variables.

4.2.1. Dimension 1. “VESS Model”

This dimension encompasses seven items that deal with the opinion of the students enrolled in the Early Childhood Education, Primary Education, and the Masters in Inclusive Education degrees on the characteristics and/or benefits of the VESS model, related with the personal, evolutionary, and social development of the children, as well as thinking as a pedagogic tool.

With respect to the differences established according to sex in relation with the VESS model, the Student’s t-test indicated that statistically significant differences existed (T = 1.983, p = 0.049). The women had a slightly higher confidence with respect to the use of the VESS model than the men (μ = 4.27 vs. μ = 4.10).

To determine the influence of age, the type of school they attended, and the early childhood, primary, or Masters degrees in which the students were enrolled, multiple comparisons of the means were performed through an ANOVA. The results showed the existence of statistically significant differences between age and dimension 1 (F (3, 227) = 2.642; p = 0.05), although no statistically significant differences were found in any of the other two polytomous variables analyzed.

4.2.2. Dimension 2. “Cooperative Learning”

This dimension was composed of five items associated with the opinion of the students enrolled in the Early Childhood Education, Primary Education, and the Masters in Inclusive Education on co-operative learning as the basis of the VESS model, on aspects associated with the development of social competences, the access to active learning, or academic performance and the improvement of the reflective capacity.

The results showed that the students were partially in agreement on the use of co-operative learning as the basis of the VESS model (µ = 4.36; σ = 0.54).

As for the sex differences found in relation to co-operative learning as the basis of the VESS model, the Student’s t-test for independent samples showed that statistically significant differences did not exist.

To determine the influence of age, the type of school attended, and the degrees in which they were enrolled, multiple comparisons of the means were performed with an ANOVA. The results suggested that there was a statistically significant difference between age and the perception of the VESS model (F (3, 227) = 2.642; p = 0.05).

The analysis of variance performed to verify the existence of significant differences between age and co-operative learning also showed the existence of statistically significant differences (F (3, 227) = 3.269; p = 0.022).

Moreover, the results showed that the differences in means between age and the use of co-operative learning were greater between students older than 24, and lower for students aged between 20 and 22 years old; μ = 4.62 vs. μ = 4.26.

4.2.3. Dimension 3. “Socrative”

This dimension is composed of four items related with the opinion of the students enrolled in the Early Childhood Education, Primary Education, and the Masters in Inclusive Education on the use of Socrative as an evaluation and self-evaluation tool when utilizing the VESS model.

The results showed that the students were partially in agreement about the use of Socrative as an evaluation tool (µ = 4.42; σ = 0.58).

As for the differences found about Socrative according to sex, the Student’s t-test indicated the lack of statistically significant differences.

As for the students’ age and school they attended, it is important to highlight that statistically significant differences were not obtained. However, statistically significant differences were found with respect to the degree in which they were enrolled (early childhood education, primary school education, or Masters in inclusive education).

4.3. Correlational Study

Next, we will address the correlational study of the three dimensions that shaped the questionnaire, created ad hoc, and previously validated [24]. This study was performed to verify the relationships between the different factors of the data collection instrument. The data extracted from the Pearson’s correlation test are shown in

Table 5. Results of the bivariate correlations of the dimensions of the questionnaire on the perceptions of university students on the VESS Model.

		VESS Model	Co-Operative Learning	Socrative
VESS model	Pearson’s correlation	1	0.610 **	0.648 **
	Sig. (two-tailed)		0.000	0.000
	N	231	231	231
Co-operative learning	Pearson’s correlation	0.610 **	1	0.540 **
	Sig. (two-tailed)	0.000		0.000
	N	231	231	231
Socrative	Pearson’s correlation	0.648 **	0.540 **	1
	Sig. (two-tailed)	0.000	0.000
	N	231	231	231

** The correlation is significant at 0.01 (two-tailed).

.

Considering the data obtained, we can confirm the existence of a relationship between dimension 1 “Perspectives of the students on the VESS model”, with dimension 2 “Cooperative Learning”, and dimension 3 “Socrative”, as R = 0.610 and p = 0.000; R = 0.648 and p = 0.000; and R = 0.540 and p = 0.000, respectively, as there is a two-tailed level of significance at ns = 0.01. The relationship between them is high between dimensions 1 and 2, as well as dimension 1 and dimension 3, and moderate between 2 and 3, as highlighted by [25].

4.4. Regression Analysis Explanatory Models of the Expectations of the Students

To explain dimension 1 “VESS model”, as a function of the measurements of dimensions 2 “Cooperative learning” and 3 “Socrative”, a series of multiple linear regressions was performed [26] with a step-wise method to observe predictor variables and their relationship with the criterion variable, as shown in

Table 6. Coefficient of the regression line for the dependent variable “VESS Model”.

Model		Non-Standardized Coefficients		Standardized Coefficients	T	Sig.	Co-Linearity Statistics
		B	Std. Dev.	Beta			Tolerance	VIF
1	(Constant)	1.733	0.196		8.835	0.000
	dimension3	0.566	0.044	0.648	12.873	0.000	1.000	1.000
2	(Constant)	0.981	0.212		4.639	0.000
	dimension3	0.393	0.048	0.449	8.207	0.000	0.709	1.411
	dimension2	0.348	0.052	0.368	6.717	0.000	0.709	1.411

.

In the results obtained, it can be observed that the dimensions 3 and 2, “Socrative” and “Cooperative learning”, respectively, were predictor factors of dimension 1, “VESS Model”, for its perception, as β = 0.449, t (0.449) = 8.207, p < 0.01 and β = 0.368, t (368) = 6.717, p < 0.01, respectively. Thus, the regression line is statistically significant and the hypothesis of linear regression between the different dimensions analyzed can be accepted. For this, the adjusted R² value was 0.511, showing that 51.1% of the variable of the dimension “VESS Model” was explained by the two variables or dimensions previously mentioned [27].

5. Discussion

The descriptive analysis conducted on the contributions of the VESS model indicated that the students enrolled in the Early Childhood Education, Primary Education, and the Masters in Inclusive Education believed that it was intimately associated with an improvement in the social, evolutionary, and personal development of the student, and also thought that cooperative work was fundamental for the acquisition and improvement of social competences. The use of Socrative, on the other hand, was also in tune with respect to the improvement of the process of teaching and learning.

As for the expectations of the future teachers about the VESS model, the analysis showed that future teachers show great interest in its application, since they think that it is essential nowadays, especially because this method promotes mental processes and basic cognitive skills in students, encouraging the development of thinking and involving them directly in the pedagogical process itself.

For this purpose, authors such as [28,29] uphold the need to create sustained interest through time to also maintain the motivation of the students. For this, we must offer students activities that take into account diversity, that are supported on the social aspect, and that do not imply learning that is too abstract, but also consider a sphere that is closer to the reality of each student, to attain their own way of thinking. A type of thinking that not only involves cognitive development, but that is also holistic and which promotes “knowing how to co-habit, how to be, and what to do” [30].

Moreover, it was verified, in a generalized manner, that the VESS model promotes critical thinking and organized thinking in general, so that learning becomes meaningful [31]. Interpreting new realities and adapting to the social context in which we live requires a type of school that promotes and applies critical-reflective thinking that makes possible social transformation, which is strongly needed [32].

In this analysis, we verified the existence of differences in the different dimensions that shaped the questionnaire in relation with the independent variables analyzed (students’ sex, age, and type of school attended). In this case, the data obtained with respect to age indicated the existence of statistically significant differences between the VESS model itself, with a better perception from students older than 26, as compared to those aged 17–19, and co-operative learning, with a better evaluation again by those older than 26. Moreover, given the data obtained, we can confirm that the women had a better perception of the model than the men. This study also revealed the lack of statistically significant differences between the school attended by the participants and any of the three dimensions of the instrument, although there was a better predisposition towards the use of Socrative among the Early Childhood and Primary Education students. In general terms, these data are supported by other studies, which indicate that students, in general, prefer to learn through active methodologies that allow them to activate cognitive processes necessary for learning in an adapted and progressive manner that is not only based on learning by memorization, and new technologies, in some way, facilitate this [33,34].

When referring to the relationship between the dimensions of the questionnaire, there was a moderate correlation between dimensions 2 and 3, and a high correlation between dimension 1 and dimension 2, and between dimension 1 and dimension 3. Nevertheless, we were not able to contrast this data with previous studies, as we did not find studies that analyzed the relationship between the dimensions addressed in the present study.

Lastly, as for the explanatory models, it should be mentioned that the perceptions on the VESS model, group work as the basis of the method, and the use of the Socrative program as an evaluation tool were predictive factors of the expectations of Early Childhood Education students on the VESS model.

In this sense, co-operative learning and Socrative as tools that promote the possibility of achieving a common goal achieves higher student performance. Likewise, these two dimensions, as highlighted by [35], select four factors that have to do with the success obtained from them: motivation, social cohesion, cognitive development, and cognitive elaboration. Coincidentally, these are characteristics that also surround the VESS model itself and, therefore, can predict that good predisposition of the study participants towards it.

As stated by [36], we presently have a new way to share information and learn. The use of ICT is in vogue and brings with it the need to synchronize information. On the one hand, to work as a group and, on the other, it obliges us to evaluate and be critical with the information we receive.

6. Conclusions

In the end, considering the different dimensions used as the foundations, their importance in the society of information and communication in which we live, and considering that the current educational system needs a basic change in the manner of how the teaching–learning process is conducted, the approach offered by the present study on the perspective of Early Childhood Education students on the pedagogic contribution of the VESS model is primordial. Adapting to different learning rhythms, as well as fomenting activities that are interesting to students, is fundamental. Nevertheless, for this to occur, intrinsic motivation within the students must be present, which will help them learn, and this is provided, without a doubt, through the creation of meaning and thoughts about what is being learned [5].

Moreover, Ref. [34] backs the idea from the neuro-educational point of view and ensures that motivation and emotion in meaningful learning play a primordial role.

Nevertheless, this reflection for changing the world, or at least understanding it, considering the current needs, must begin from the institutions and teachers with respect to what is occurring in the classrooms, that is, a reflection on the actions must be conducted, to establish a relationship between the theoretical content and the tangible reality, as highlighted by [37]. To ensure that these ideas are more complete and efficient, they must be conducted together with the students themselves [36,37,38].

On the other hand, the addition of a digital resource grants additional value to the study, as it possesses both general and specific advantages, which enrich the environment of learning, and implies a teaching innovation that brings closer the exterior reality to the educational complexity found in the classroom [39]. As for the limitations we found, during the study, we must mainly underline the difficulty in accessing the classrooms to obtain the subjects needed for the study. A change in mentality is still needed between professors and teachers, which will give a green light to research studies within the classroom, so that they open their classroom doors to the entire education community.