Dynamic Behaviors of a Stochastic Eco-Epidemiological Model for Viral Infection in the Toxin-Producing Phytoplankton and Zooplankton System
Abstract
:1. Introduction
2. Preliminaries
3. Stochastic Boundedness
4. Extinction and Persistence of the Plankton
- 1.
- If then , and are extinct with probability one.
- 2.
- If then is persistent in the mean with probability one. Moreover, if the conditions and hold, then and are extinct with probability one, that is,
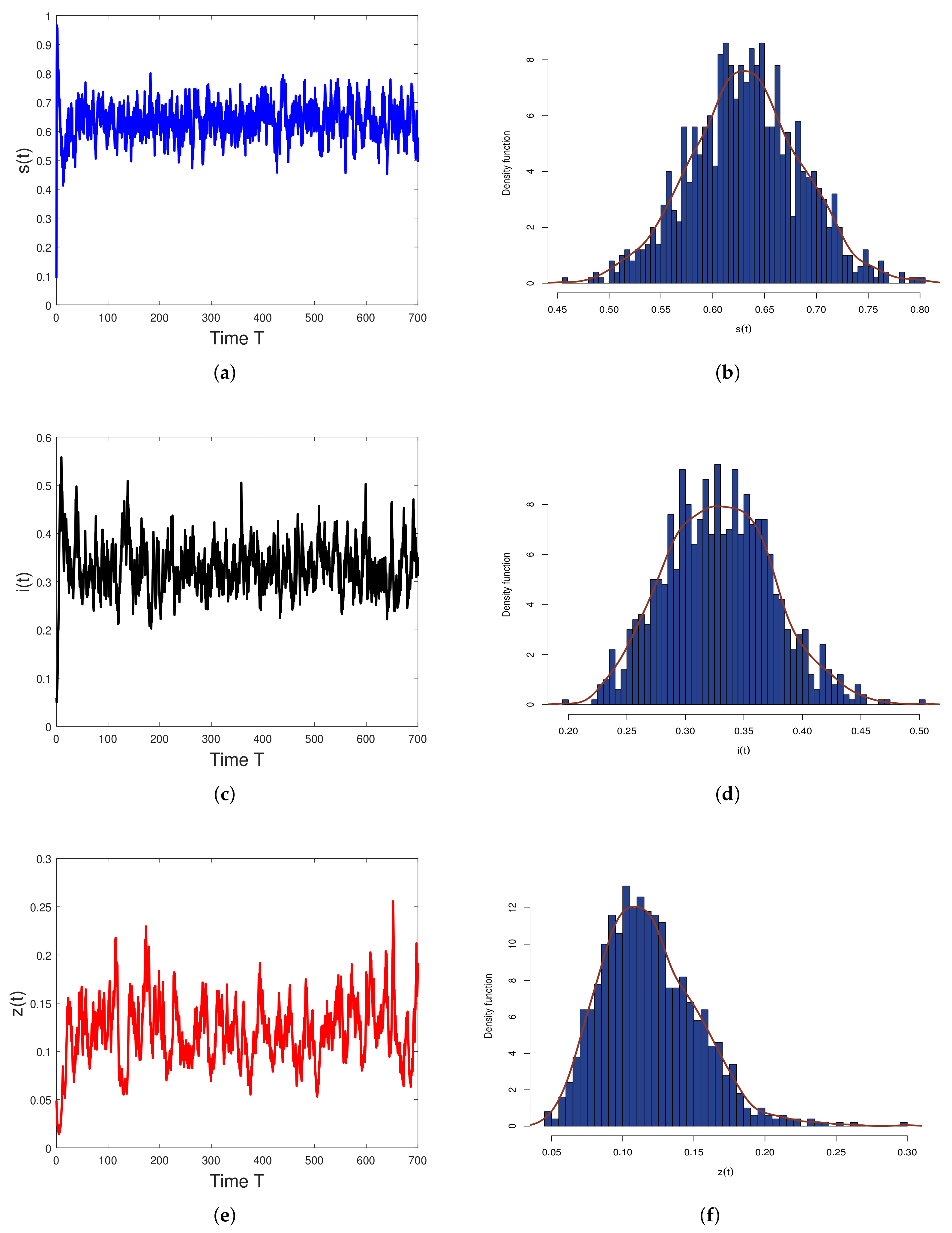
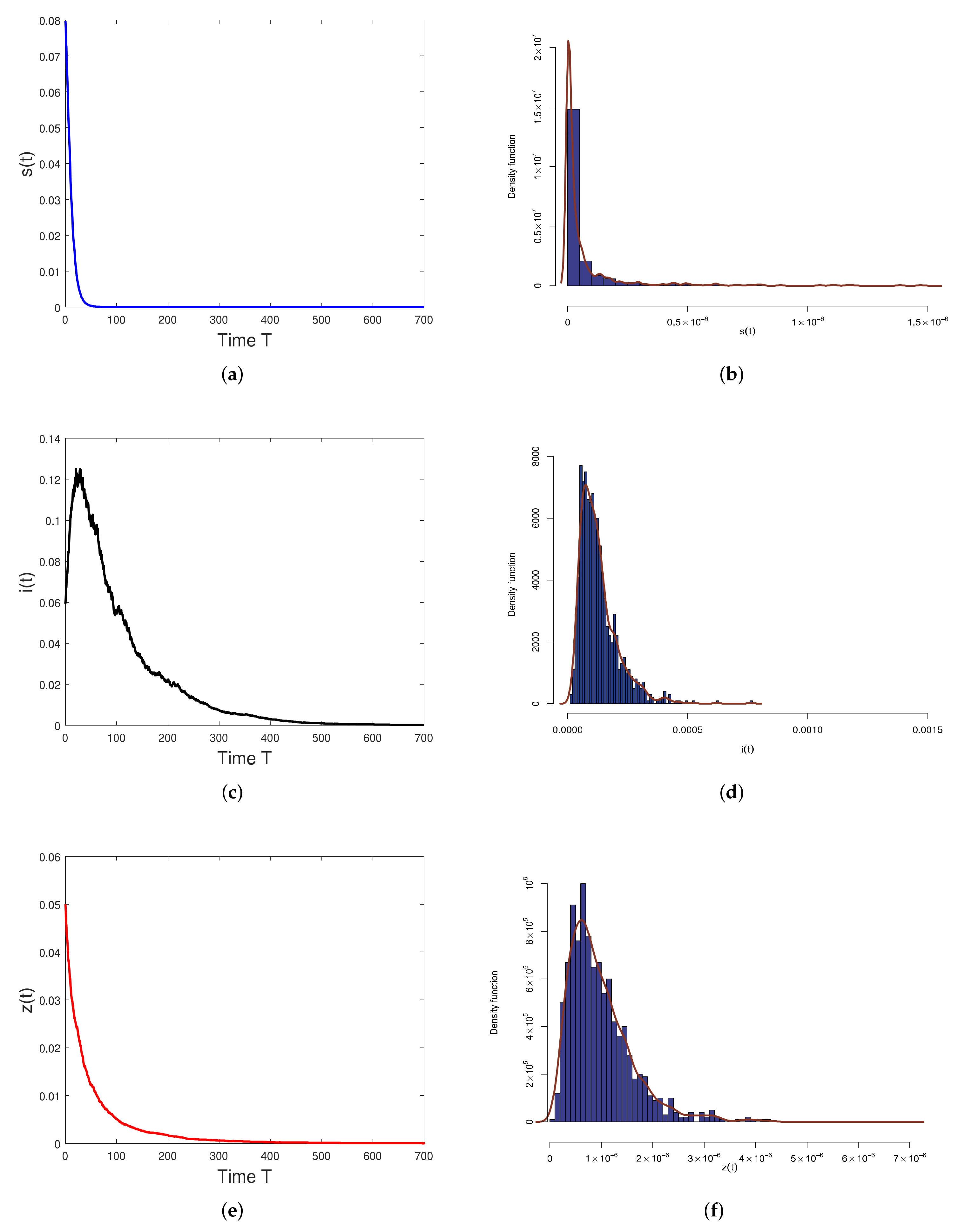
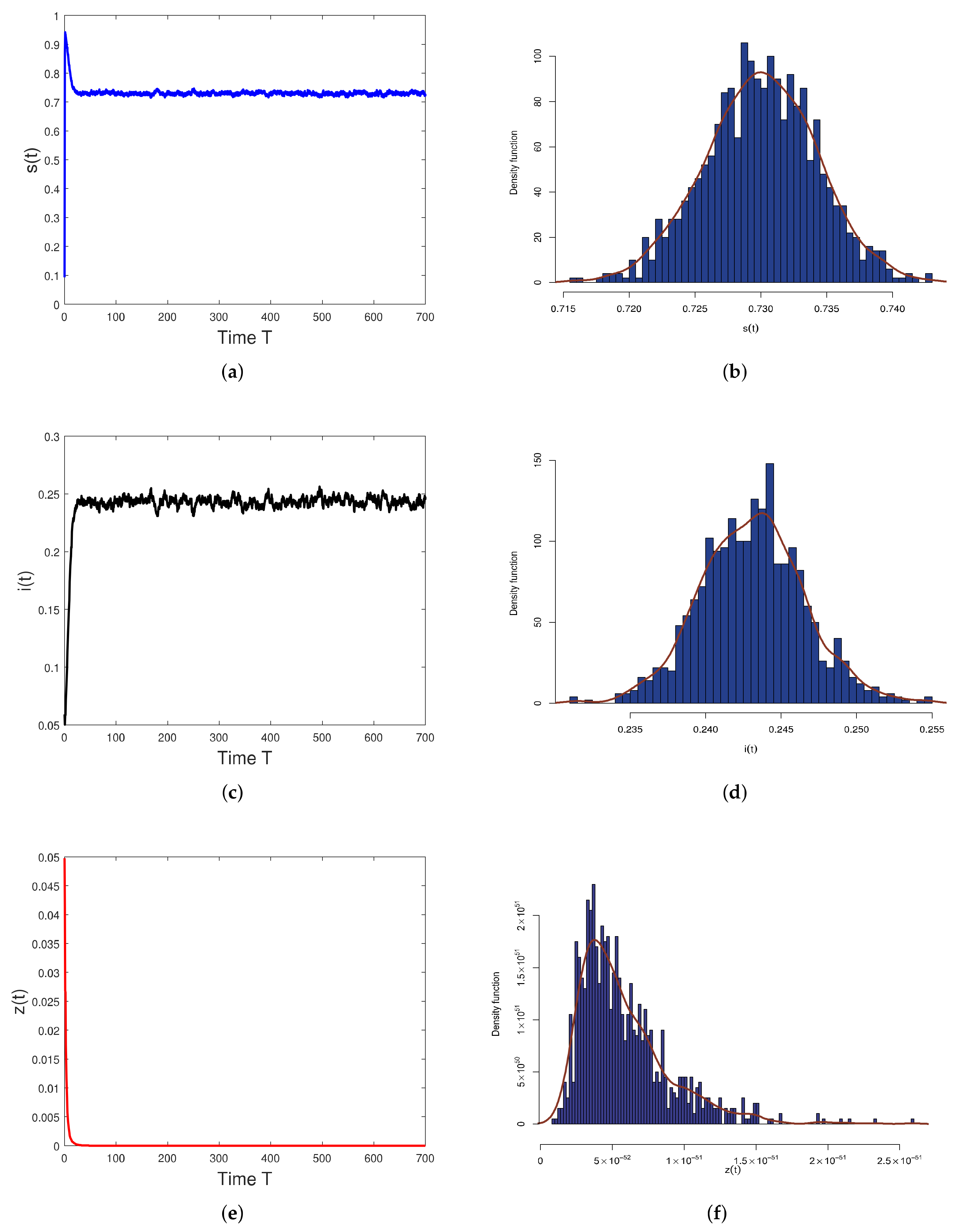
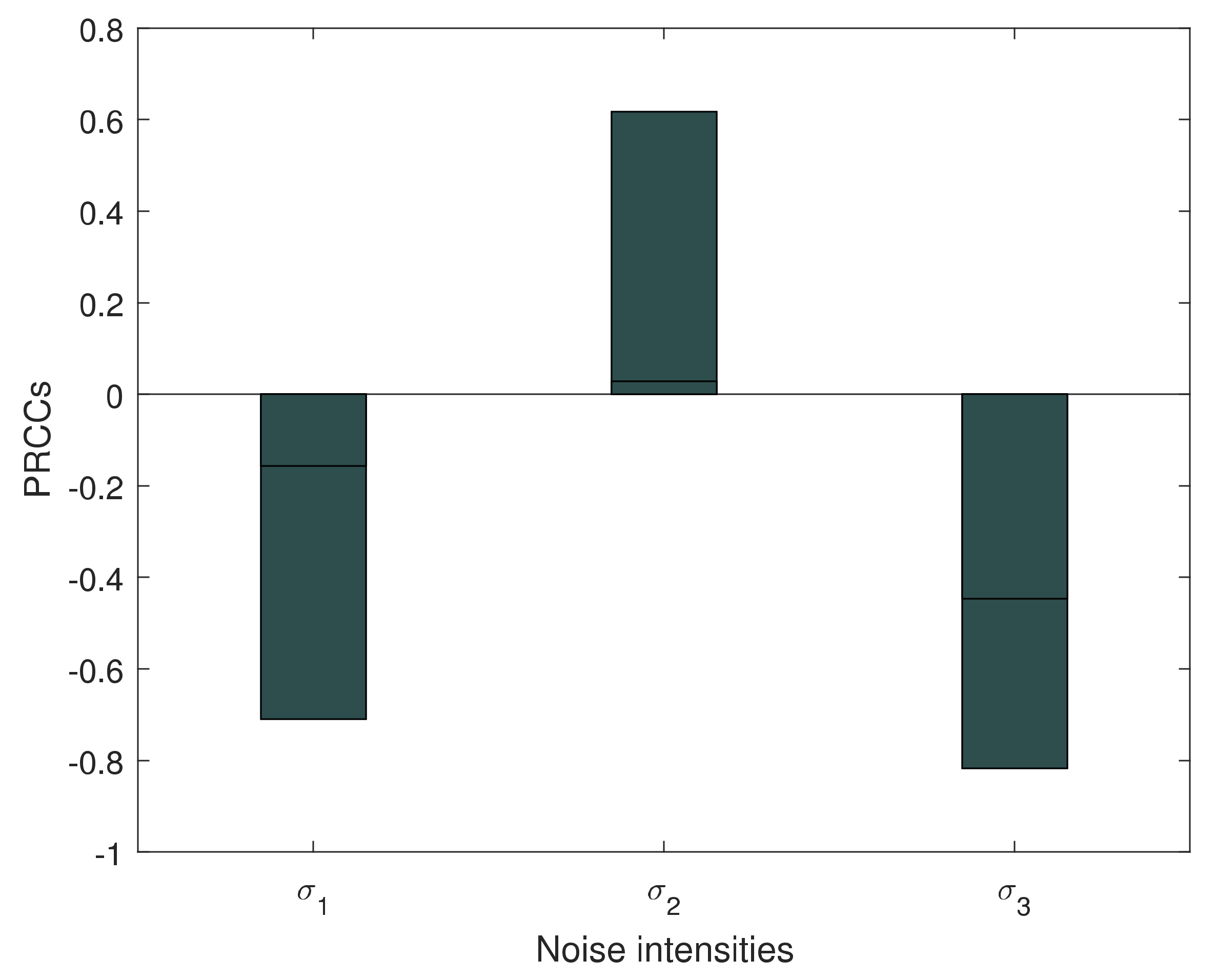
5. Numerical Simulations
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eilertsen, H.C.; Raa, J. Toxins in seawater produced by a common phytoplankter: Phaeocystis pouchetii. J. Mar. Biotechnol. 1995, 3, 115–119. [Google Scholar]
- Sahoo, D.; Mondal, S.; Samanta, G.P. Interaction among toxic phytoplankton with viral infection and zooplankton in presence of multiple time delays. Int. J. Dyn. Control 2021, 9, 308–333. [Google Scholar] [CrossRef]
- Beltrami, E.; Carroll, T. Modelling the role of viral disease in recurrent phytoplankton blooms. J. Math. Biol. 1994, 32, 857–919. [Google Scholar] [CrossRef]
- Truscott, J.E.; Brindley, J. Ocean plankton population as excitable media. Bull. Math. Biol. 1994, 4, 981–998. [Google Scholar] [CrossRef]
- Pal, R.; Basu, D.; Banerjee, M. Modelling of phytoplankton allelopathy with Monod-Haldane-type functional response—A mathematical study. BioSystems 2009, 136, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Yuan, S.; Zhang, T. Asymptotic properties of stochastic nutrient-plankton food chain models with nutrient recycling. Nonlinear Anal. Hybrid Syst. 2019, 34, 209–225. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H. Stability and selective harvesting of a phytoplankton-zooplankton System. J. Appl. Math. 2014, 2014, 684790. [Google Scholar] [CrossRef] [Green Version]
- Luo, J. Phytoplankton-zooplankton dynamics in periodic environments taking into account eutrophication. Math. Biol. 2013, 245, 126–136. [Google Scholar] [CrossRef]
- Sarkar, R.R.; Chattopadhayay, J. Occurrence of planktonic blooms under environmental fluctuations and its possible control mechanism-mathematical models and experimental observations. J. Theor. Biol. 2003, 224, 501–516. [Google Scholar] [CrossRef]
- Jang, R.J.; Allen, E.J. Deterministic and stochastic nutrient-phytoplankton- zooplankton models with periodic toxin producing phytoplankton. Appl. Math. Comput. 2015, 271, 52–67. [Google Scholar] [CrossRef]
- Chattopadhayay, J.; Sarkar, R.R.; Mandal, S. Toxinproducing plankton may act as a biological control for planktonic blooms—Field study and mathematical modelling. J. Theor. Biol. 2002, 215, 333–344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuhrman, J.A. Marine viruses and their biogeochemical and ecological effects. Nature 1999, 399, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Wommack, K.; Colwell, R. Virioplankton: Viruses in aquatic ecosystems. Microbiol. Mol. Biol. Rev. 2000, 64, 69–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suttle, C.; Chan, A. Marine cyanophages infecting oceanic and coastal strains of Synechococcus: Abundance, morphology, cross infectivity and growth characteristics. Mar. Ecol. Prog. Ser. 1993, 92, 69–109. [Google Scholar] [CrossRef]
- Mondal, A.; Pal, A.K.; Samanta, G.P. Rich dynamics of non-toxic phytoplankton, toxic phytoplankton and zooplankton system with multiple gestation delays. Int. J. Dyn. Control 2020, 8, 112–131. [Google Scholar] [CrossRef]
- Singh, B.; Chattopadhyay, J.; Sinha, S. A role of viral infection in a simple phytoplankton zooplankton system. J. Theor. Biol. 2004, 231, 153–166. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, L. Modelling and analysis of a predator-prey model with disease in the prey. Math. Biosci. 2001, 171, 59–82. [Google Scholar] [CrossRef]
- Chattopadhyay, J.; Pal, S. Viral infection on phytoplankton-zooplankton system—A mathematical model. Ecol. Model. 2002, 151, 15–28. [Google Scholar] [CrossRef]
- Gakkhar, S.; Negi, K. A mathematical model for viral infection in toxin producing phytoplankton and zooplankton system. Appl. Math. Comput. 2006, 179, 301–313. [Google Scholar] [CrossRef]
- Gakkhar, S.; Singh, A. A delay model for viral infection in toxin producing phytoplankton and zooplankton system. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3607–3620. [Google Scholar] [CrossRef]
- Thakur, N.K.; Srivastava, S.C.; Ojha, A. Dynamical study of an eco-epidemiological delay model for plankton system with toxicity. Iran. J. Sci. Technol. Trans. A 2021, 45, 283–304. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q. Bifurcation analysis and control of a plankton-fish model with a distribution delay. J. Mech. Med. Biol. 2011, 11, 857–879. [Google Scholar] [CrossRef]
- Nath, B.; Roy, P.; Das, K.P. Dynamics of nutrient-phytoplankton-zooplankton interaction in the presence of viral infection. Nonlinear Stud. 2019, 26, 197–217. [Google Scholar]
- Nath, B.; Roy, P.; Sahani, S.K.; Maiti, S.; Daset, K. Plankton dynamics in nutrient-phytoplankton-zooplankton model with viral infection in phytoplankton. Nonlinear Stud. 2020, 27, 1–24. [Google Scholar]
- Biswas, S.; Tiwari, P.K.; Kang, Y.; Samares, P. Effects of zooplankton selectivity on phytoplankton in an ecosystem affected by free-viruses and environmental toxins. Math. Biosci. Eng. 2019, 17, 1272–1317. [Google Scholar] [CrossRef]
- Wei, C.; Fu, Y. Stationary distribution and periodic solution of stochastic toxin-producing phytoplankton-zooplankton systems. Complexity 2020, 2020, 4627571. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Tian, Z.; Zhang, S.; Wei, C. The stationary distribution and ergodicity of a stochastic phytoplankton-zooplankton model with toxin-producing phytoplankton under regime switching. Physica A 2020, 537, 122728. [Google Scholar] [CrossRef]
- Yu, X.; Yuan, S.; Zhang, T. Survival and ergodicity of a stochastic phytoplankton-zooplankton model with toxin-producing phytoplankton in an impulsive polluted environment. Appl. Math. Comput. 2019, 347, 249–264. [Google Scholar] [CrossRef]
- Wang, H.; Liu, M. Stationary distribution of a stochastic hybrid phytoplankton-zooplankton model with toxin-producing phytoplankton. Appl. Math. Lett. 2020, 101, 106077. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D.; Lei, D. Dynamical behavior of a one predator and two independent preys system with stochastic perturbations. Physica A 2019, 515, 649–664. [Google Scholar] [CrossRef]
- Liu, C.; Yu, L.; Zhang, Q.; Li, Y. Dynamic analysis of a hybrid bioeconomic plankton system with double time delays and stochastic fluctuations. Appl. Math. Comput. 2018, 316, 115–137. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Ahmad, B. Stationary distribution and extinction of a stochastic predator-prey model with additional food and nonlinear perturbation. Appl. Math. Comput. 2018, 320, 226–239. [Google Scholar] [CrossRef]
- Cai, Y.; Mao, X. Stochastic prey-predator system with foraging arena scheme. Appl. Math. Model. 2018, 64, 357–371. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Yuan, S.; Zhang, T. Dynamic analysis of a stochastic eco-epidemiological model with disease in predators. Stud. Appl. Math. 2022, 1–38. [Google Scholar] [CrossRef]
- Feng, X.; Sun, J.; Wang, L.; Zhang, F.; Sun, S. Periodic Solutions for a Stochastic Chemostat Model with Impulsive Perturbation on the Nutrient. J. Biol. Syst. 2021, 29, 849–870. [Google Scholar] [CrossRef]
- Rihan, F.A.; Alsakaji, H.J. Persistence and extinction for stochastic delay differential model of prey predator system with hunting cooperation in predators. Adv. Differ. Equ. 2020, 2020, 124. [Google Scholar] [CrossRef]
- Rihan, F.A.; Alsakaji, H.J. Dynamics of a stochastic delay differential model for COVID-19 infection with asymptomatic infected and interacting peoples: Case study in the UAE. Results Phys. 2021, 28, 104658. [Google Scholar] [CrossRef]
- Rihan, F.A.; Alsakaji, H.J.; Rajivganthi, C. Stochastic SIRC epidemic model with time-delay for COVID-19. Adv. Differ. Equ. 2020, 2020, 502. [Google Scholar] [CrossRef]
- Jiang, D.; Shi, N.; Li, X. Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation. J. Math. Anal. Appl. 2008, 340, 588–597. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, N.; Watanabe, S. A comparison theorem for solutions of stochastic differential equations and its applications. Osaka J. Math. 1977, 14, 619–633. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Horwood Publishing: Chichester, UK, 2007; pp. 154–196. [Google Scholar]
- Higham, D. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Miao, Y.; Sun, S.; Wang, L. Dynamic Behaviors of a Stochastic Eco-Epidemiological Model for Viral Infection in the Toxin-Producing Phytoplankton and Zooplankton System. Mathematics 2022, 10, 1218. https://doi.org/10.3390/math10081218
Feng X, Miao Y, Sun S, Wang L. Dynamic Behaviors of a Stochastic Eco-Epidemiological Model for Viral Infection in the Toxin-Producing Phytoplankton and Zooplankton System. Mathematics. 2022; 10(8):1218. https://doi.org/10.3390/math10081218
Chicago/Turabian StyleFeng, Xiaomei, Yuan Miao, Shulin Sun, and Lei Wang. 2022. "Dynamic Behaviors of a Stochastic Eco-Epidemiological Model for Viral Infection in the Toxin-Producing Phytoplankton and Zooplankton System" Mathematics 10, no. 8: 1218. https://doi.org/10.3390/math10081218





