Optimizing PV Microgrid Isolated Electrification Projects—A Case Study in Ecuador
Abstract
1. Introduction
- A set of potential connections is established, indicating impossible wiring between different geographical points. This new constraint, motivated by local factors (explained in the following sections), is addressed through a decomposition strategy of the original problems that allows a more efficient solution process.
- A new objective function now incorporates the parametrized ponderation of the costs of microgrids versus individual systems. This novel feature is motivated by the electrification policies dictated by Ecuador’s national government, promoting microgrid configurations. However, the versatility of the formulation proposed here allows either one or the other configuration to be favored according to any policy makers’ decisions.
- For cultural reasons in the RAE, items shared by the members of a community cannot be stored on private ground. This requirement is reflected in the model by new constraints, which prevent microgrid generation units from being located at demand points.
2. Context Analysis for the Design of Stand-Alone Electrification Systems in the RAE
2.1. Overview of the Electrification Process in Ecuador
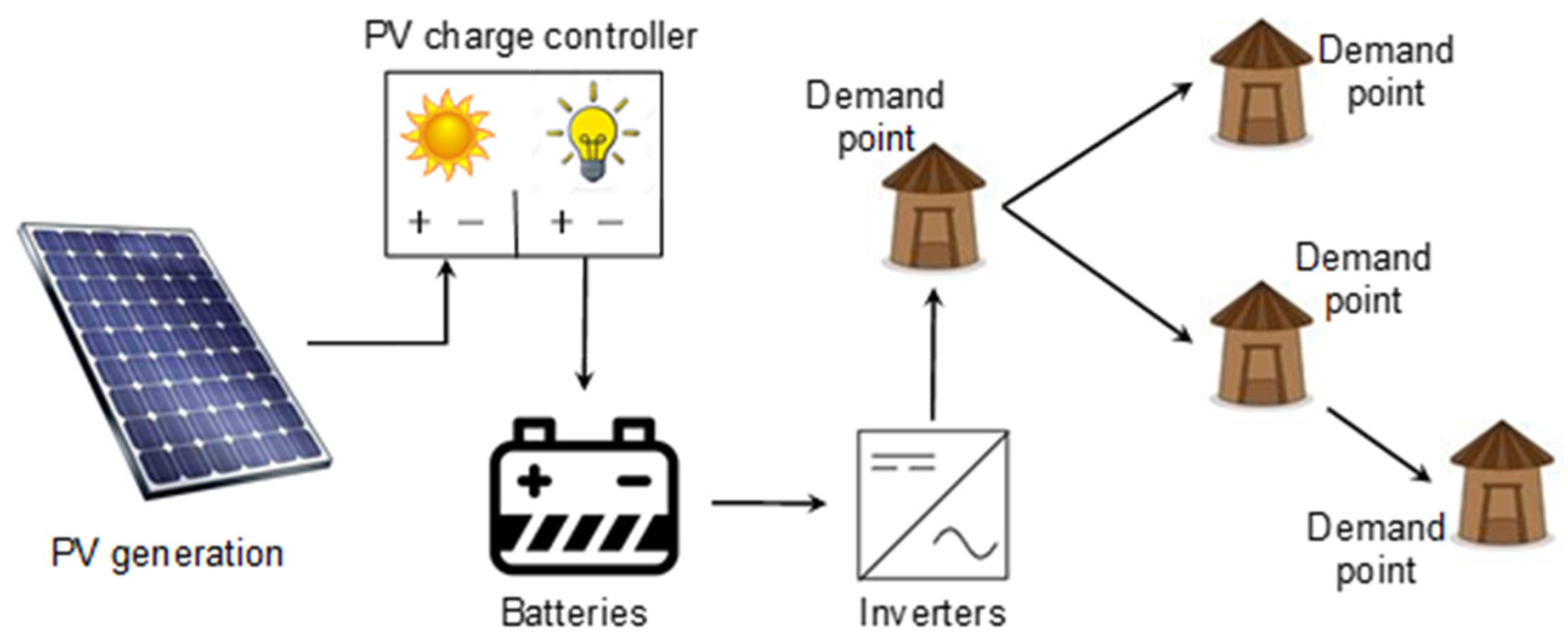
2.2. Technical Description of Stand-Alone Systems
2.3. Conditioning Factors for Stand-Alone Electrification Systems in the RAE
- (a)
- National and regional policies contemplate social aspects, such as opting for electrification designs including microgrids rather than individual systems. Indeed, the community-based management of joint installations provides social benefits, such as the coordination and cooperation of families sharing the same objectives. In order to encourage microgrid formation, priority is given to designs including such configurations, even though they entail a higher cost than individual supply systems (up to 20% higher, as proposed by MEER).
- (b)
- The institutional framework of electrification projects may ensure economies of scale (for instance, when equipment is purchased for district or regional projects) but may also restrict the technical characteristics of power generation and distribution items. In the case study presented here, the limiter boxes allow only two output cables, which may have an impact on the microgrid structure.
- (c)
- The communication paths available (rivers, airways) and the transportation means to get to the community in question have an impact on the technical equipment employed. Moreover, the current state of these paths may also involve space and weight limitations for the equipment units to be shipped. For instance, the varying water depth in a river (or landing strip dimensions) can limit the size of canoes (or aircraft) that can be used.
- (d)
- The property concept in some indigenous communities means that the equipment shared by the community cannot be physically installed at a demand point, which is private ground. So, non-demand points should be identified for potential microgrid generation. Furthermore, this means the construction of sheds for electric equipment storage within the area where PV panels are to be located in order to protect batteries, inverters and regulators from weather or animals. This incurs additional costs associated with the purchase and installation of these buildings.
- (e)
- In the Low Amazon region, the increased concern for environmental aspects leads to the development of underground connections rather than air connections. Indeed, despite the advantages of air microgrids in both practical (avoiding obstacles such as rivers, small buildings, etc.) and economic (cheaper installation and maintenance) terms, they have a negative environmental impact due to tree clearing around the microgrid installations. Underground wiring is also better protected from external agents (rain, animals) and presents technical advantages [51]. However, this policy involves constraints due to physical obstacles (river, ravine, floodable area, landing strip, etc.) that may prevent cable installation.
3. A Mathematical Model for the Design of Autonomous Rural Electrification Systems in the RAE
4. Case Study: Three Communities in the RAE
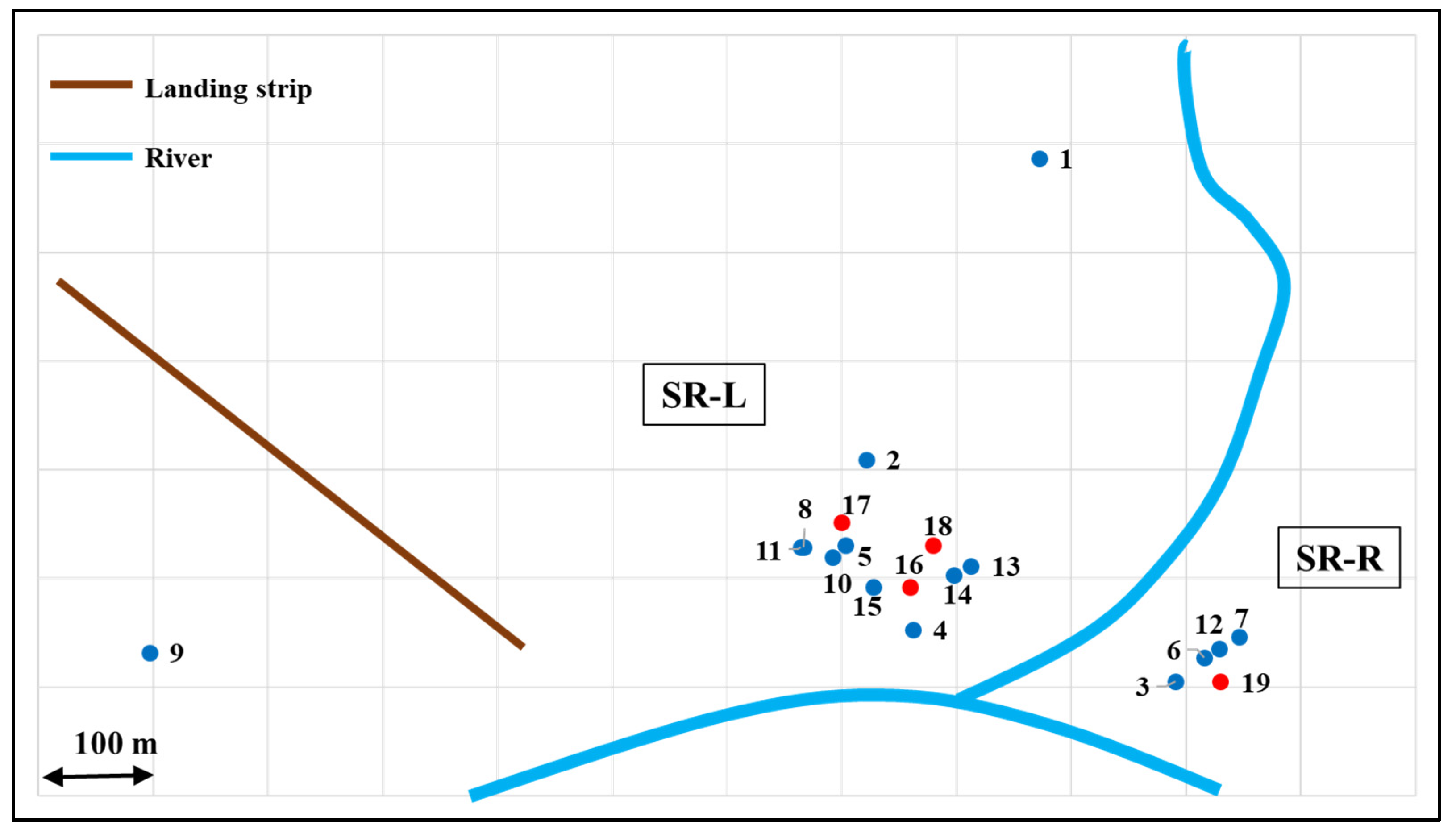
4.1. General Description of the Communities
4.2. Problem Data, Point Distribution and Pre-Processing
- Right side (SR-R), with 4 demand points and 1 potential generation point.
- Left side (SR-L), with 11 demand points and 3 potential generation points.
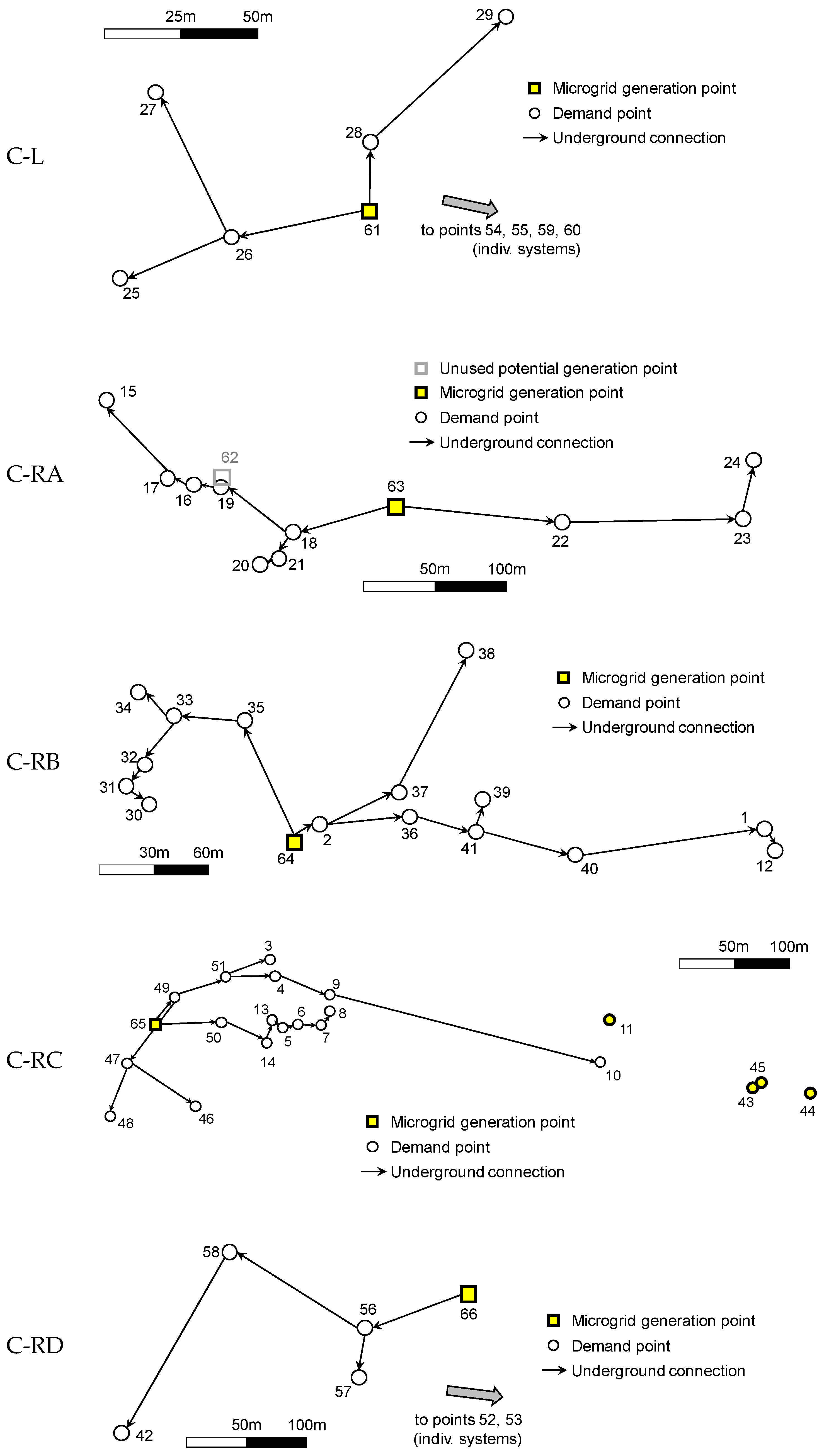
- Left side (C-L: orange points), 9 demand points and 1 potential generation point.
- Right side A (C-RA: green points), 10 demand points and 2 potential generation points.
- Right side B (C-RB: grey points), 15 demand points and 1 potential generation point.
- Right side C (C-RC: blue points), 20 demand points and 1 potential generation point.
- Right side D (C-RD: lilac points), 6 demand points and 1 potential generation point.
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://sdgs.un.org/goals (accessed on 18 January 2022).
- Blimpo, M.P.; Cosgrove-Davies, M. Electricity Access in Sub-Saharan Africa: Uptake, Reliability, and Complementary Factors for Economic Impact; World Bank, Africa Development Forum: Washington, DC, USA, 2019; Available online: https://openknowledge.worldbank.org/handle/10986/31333 (accessed on 18 January 2022).
- Jeuland, M.; Fetter, T.R.; Li, Y.; Pattanayak, S.K.; Usmani, F.; Bluffstone, R.A.; Chávez, C.; Girardeau, H.; Hassen, S.; Jagger, P.; et al. Is energy the golden thread? A systematic review of the impacts of modern and traditional energy use in low- and middle-income countries. Renew. Sustain. Energy Rev. 2021, 135, 110406. [Google Scholar] [CrossRef]
- Peters, J.; Sievert, M. Impacts of rural electrification revisited-the African context. J. Dev. Eff. 2016, 8, 327–345. [Google Scholar] [CrossRef]
- International Energy Agency World Energy Outlook: Electricity Access Database. 2017. Available online: https://www.iea.org/reports/world-energy-outlook-2017 (accessed on 19 January 2022).
- Sovacool, B.K. Deploying off-grid technology to eradicate energy poverty. Science 2012, 338, 47–48. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Alonso-Gómez, V. A review of photovoltaic systems: Design, operation and maintenance. Sol. Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Slednev, V.; Bertsch, V.; Ruppert, M.; Fichtner, W. Highly resolved optimal renewable allocation planning in power systems under consideration of dynamic grid topology. Comput. Oper. Res. 2018, 96, 280–292. [Google Scholar] [CrossRef]
- Hassan, Q. Evaluation and optimization of off-grid and on-grid photovoltaic power system for typical household electrification. Renew. Energy 2021, 164, 375–390. [Google Scholar] [CrossRef]
- Taye, B.Z.; Workineh, T.G.; Nebey, A.H.; Kefale, H.A. Rural electrification planning using Geographic Information System (GIS). Cogent Eng. 2020, 7, 1836730. [Google Scholar] [CrossRef]
- Ellman, D. The Reference Electrification Model: A Computer Model for Planning Rural Electricity Access. Master’s Thesis, Massachusetts Institute of Technology, Boston, MA, USA, 2015. [Google Scholar]
- Mentis, D.; Howells, M.; Rogner, H.; Korkovelos, A.; Arderne, C.; Zepeda, E.; Siyal, S.H.; Taliotis, C.; Bazilian, M.; de Roo, A.; et al. Lighting the World, The first global application of an open source, spatial electrification tool (OnSSET), with a focus on Sub-Saharan Africa. Environ. Res. Lett. Focus Energy Access Sustain. Dev. 2017, 12, 085003. [Google Scholar]
- Brown, T.; Hörsch, J.; Schlachtberger, D. PyPSA: Python for Power System Analysis. J. Open Re. Soft. 2018, 6, 4. [Google Scholar] [CrossRef]
- Eddy, J.; Miner, N.E.; Stamp, J. Sandia’s Microgrid Design Toolkit. Electr. J. 2017, 30, 62–67. [Google Scholar] [CrossRef]
- Bahramara, S.; Parsa Moghaddam, M.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Lal, D.K.; Dash, B.B.; Akella, A.K. Optimization of PV/wind/micro-hydro/diesel hybrid power system in HOMER for the study area. Int. J. Electr. Eng. Inform. 2011, 3, 307–325. [Google Scholar]
- Rozlan, M.B.M.; Zobaa, A.F.; Abdel Aleem, S.H.E. The optimisation of stand-alone hybrid renewable energy systems using HOMER. Int. Rev. Electr. Eng. 2011, 6, 1802–1810. [Google Scholar]
- Hossain, E.; Kabalci, E.; Bayindir, R.; Perez, R. Microgrid testbeds around the world: State of art. Energy Convers. Manag. 2014, 86, 132–153. [Google Scholar] [CrossRef]
- Wang, R.; Lam, C.M.; Hsu, S.C.; Chen, J.H. Life cycle assessment and energy payback time of a standalone hybrid renewable energy commercial microgrid: A case study of Town Island in Hong Kong. Appl. Energy 2019, 250, 760–775. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Peters, J.; Sievert, M.; Toman, M.A. Rural electrification through mini-grids: Challenges ahead. Energy Policy 2019, 132, 27–31. [Google Scholar] [CrossRef]
- Castilla, M.; Gómez, M.; Mercado, P.; Moreira, C.; Negroni, J.J.; Sosa, J.; Zambroni de Sousa, A.C. The growing state of distributed generation and microgrids in the Ibero-American region: A view from the RIGMEI network. In Proceedings of the 2014 IEEE Power & Energy Society Transmission and Distribution Latin American Conference & Exposition, Medellín, Colombia, 10–13 September 2014. [Google Scholar]
- Mahomed, S.; Shirley, R.; Tice, D.; Phillips, J. Business Model Innovations for Utility and Mini-Grid Integration: Insights from the Utilities 2.0 Initiative in Uganda. Energy and Economic Growth, Energy Insight Report. 2020. Available online: https://www.energyeconomicgrowth.org/publication/business-model-innovations-utility-and-mini-grid-integration-insights-utilities-20 (accessed on 19 January 2022).
- Tenenbaum, B.; Greacen, C.; Siyambalapitiya, T.; Knuckles, J. From the Bottom Up: How Small Power Producers and Mini-Grids Can Deliver Electrification and Renewable Energy in Africa; World Bank Group Report; Directions in Development—Energy and Mining: Washington, DC, USA, 2014; Available online: https://openknowledge.worldbank.org/handle/10986/16571 (accessed on 19 January 2022).
- Lukuyu, J.; Fetter, R.; Krishnapriya, P.P.; Williams, N.; Taneja, J. Building the supply of demand: Experiments in mini-grid demand stimulation. Dev. Eng. 2021, 6, 100058. [Google Scholar] [CrossRef]
- Rezaei, M.; Dowlatabadi, H. Off-grid: Community energy and the pursuit self-sufficiency in British Columbia’s remote and First Nations communities. Local Environ. 2015, 21, 789–807. [Google Scholar] [CrossRef]
- Leithon, J.; Werner, S.; Koivunen, V. Energy optimization through cooperative storage management: A calculus of variations approach. Renew. Energy 2021, 171, 1357–1370. [Google Scholar] [CrossRef]
- Domenech, B.; Ferrer-Martí, L.; Pastor, R. Including management and security of supply constraints for designing stand-alone electrification systems in developing countries. Renew. Energy 2015, 80, 359–369. [Google Scholar] [CrossRef]
- Ranaboldo, M.; Domenech, B.; Vilar, D.; Ferrer-Martí, L.; Pastor, R.; García-Villoria, A. Renewable energy projects to electrify rural communities in Cape Verde. Appl. Energy 2014, 118, 280–291. [Google Scholar] [CrossRef]
- Triadó-Aymerich, J.; Ferrer-Martí, L.; García-Villoria, A.; Pastor, R. MILP-based heuristics for the design of rural community electrification projects. Comput. Oper. Res. 2016, 71, 90–99. [Google Scholar] [CrossRef]
- Rojas-Zerpa, J.C.; Yusta, J.M. Application of multicriteria decision methods for electric supply planning in rural and remote areas. Renew. Sustain. Energy Rev. 2015, 52, 557–571. [Google Scholar] [CrossRef]
- Balderrama, S.; Lombardi, F.; Riva, F.; Canedo, W.; Colombo, E.; Quoilin, S. A two-stage linear programming optimization framework for isolated hybrid microgrids in a rural context: The case study of the “El Espino” community. Energy 2019, 188, 116073. [Google Scholar] [CrossRef]
- Blechinger, P.; Cader, C.; Bertheau, P.; Huyskens, H.; Seguin, R.; Breyer, C. Global analysis of the techno-economic potential of renewable energy hybrid systems on small islands. Energy Policy 2016, 98, 674–687. [Google Scholar] [CrossRef]
- Gómez, M.F.; Silveira, S. The last mile in the Brazilian Amazon—A potential pathway for universal electricity access. Energy Policy 2015, 82, 23–37. [Google Scholar] [CrossRef]
- Garces, E.; Tomei, J.; Franco, C.J.; Dyner, I. Lessons from last mile electrification in Colombia: Examining the policy framework and outcomes for sustainability. Energy Res. Soc. Sci. 2021, 79, 102156. [Google Scholar] [CrossRef]
- Fernández-Fuentes, M.H.; Eras-Almeida, A.A.; Egido-Aguilera, M.A. Characterization of Technological Innovations in Photovoltaic Rural Electrification, Based on the Experiences of Bolivia, Peru, and Argentina: Third Generation Solar Home Systems. Sustainability 2021, 13, 3032. [Google Scholar] [CrossRef]
- Barzola, J.; Espinoza, M.; Pavón, C.; Cabrera, F. Solar-wind renewable energy system for off-grid rural electrification in Ecuador. In Proceedings of the 14th LACCEI International Multi-Conference for Engineering, Education, and Technology, “Engineering Innovations for Global Sustainability”, San José, Costa Rica, 20–22 July 2016. [Google Scholar]
- Feron, S.; Heinrichs, H.; Cordero, R.R. Are the electrification efforts in the Ecuadorian Amazon sustainable? Sustainability 2016, 8, 443. [Google Scholar] [CrossRef]
- Ferrer-Martí, L.; Domenech, B.; García-Villoria, A.; Pastor, R. A MILP model to design hybrid wind–photovoltaic isolated rural electrification projects in developing countries. Eur. J. Oper. Res. 2013, 226, 293–300. [Google Scholar] [CrossRef]
- Escribano, G. Ecuador’s energy policy mix: Development versus conservation and nationalism with Chinese loans. Energy Policy 2013, 57, 152–159. [Google Scholar] [CrossRef]
- Agencia de Regulación y Control de Electricidad de Ecuador (ARCONEL). Revista Digital: Estadística del Sector Eléctrico Ecuatoriano 2017; Ministerio de Electricidad y Energía Renovable: Quito, Ecuador, 2017. Available online: https://www.controlrecursosyenergia.gob.ec/estadisticas-del-sector-electrico-ecuatoriano-buscar (accessed on 19 January 2022). (In Spanish)
- Cortés Valencia, I.V. Regulatory and Planning Approach to Rural Electrification in Isolated Areas of the Amazon: Bolivia, Brazil, Colombia, Ecuador and Peru. Master’s Thesis, Escuela Técnica Superior de Ingeniería, Universidad Pontífica Comillas, Madrid, Spain, 2016. [Google Scholar]
- Peláez-Samaniego, M.R.; García-Pérez, M.; Cortez, L.A.B.; Oscullod, J.; Olmedo, G. Energy sector in Ecuador: Current status. Energy Policy 2007, 35, 4177–4189. [Google Scholar] [CrossRef]
- Finer, M.; Jenkins, C.N. Proliferation of hydroelectric dams in the Andean Amazon and implications for Andes-Amazon connectivity. PLoS ONE 2012, 7, e0035126. [Google Scholar] [CrossRef]
- Robalino-López, A.; Mena-Nieto, A.; García-Ramos, J.E. System dynamics modeling for renewable energy and CO2 emissions: A case study of Ecuador. Energy Sustain. Dev. 2014, 20, 11–20. [Google Scholar] [CrossRef]
- Posso, F.; Sánchez, J.; Espinoza, J.L.; Siguencia, J. Preliminary estimation of electrolytic hydrogen production potential from renewable energies in Ecuador. Int. J. Hydrogen Energy 2016, 41, 2326–2344. [Google Scholar] [CrossRef]
- Ferrer-Martí, L.; Garwood, A.; Chiroque, J.; Ramírez, B.; Marcelo, O.; Garfí, M.; Velo, E. Evaluating and comparing three community small-scale wind electrification projects. Renew. Sustain. Energy Rev. 2012, 16, 5379–5390. [Google Scholar] [CrossRef]
- Tratural (Cia. Ltda). Estudio Homologación de Unidades de Propiedad (UP) y Unidades de Construcción (UC) de Sistemas Fotovoltaicos No Conectados a la Red; Ministerio de Electricidad y Energía Renovable: Quito, Ecuador, 2016. (In Spanish) [Google Scholar]
- Enginyeria Sense Fronteres (ESF); Empresa Eléctrica Ambato, Sociedad Anónima. Conceptos para la Gestión de Sistemas Fotovoltaicos Aislados; Ministerio de Electricidad y Energías Renovables: Quito, Ecuador, 2016. (In Spanish) [Google Scholar]
- Khan, A.A.; Malik, N.; Al-Arainy, A.; Alghuwainem, S. A review of condition monitoring of underground power cables. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 909–912. [Google Scholar]
- Trotter, P.A. A low-carbon way to increase energy access: How to scale mini-grids in developing countries. In Proceedings of the Applied Energy Symposium, MIT A+B, Boston, MA, USA, 22–24 May 2019. [Google Scholar]
- Taneja, J. If You Build It, Will They Consume? Key Challenges for Universal, Reliable, and Low-Cost Electricity Delivery in Kenya; Working Paper No. 491; Center for Global Development: Washington, DC, USA, 2018. [Google Scholar]
- Cader, C.; Blechinger, P.; Bertheau, P. Electrification planning with focus on hybrid mini-grids—A comprehensive modelling approach for the Global South. Enrgy. Proced. 2016, 99, 269–276. [Google Scholar] [CrossRef]
- Galleguillos-Pozo, R.; Domenech, B.; Ferrer-Martí, L.; Pastor, R. Design of stand-alone electrification systems using fuzzy mathematical programming approaches. Energy 2021, 228, 120639. [Google Scholar] [CrossRef]
- Baños, R.; Manzano-Agugliaro, F.; Montoya, F.G.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Domenech, B.; Ranaboldo, M.; Ferrer-Martí, L.; Pastor, R.; Flynn, D. Local and regional microgrid models to optimise the design of isolated electrification projects. Renew. Energy 2018, 119, 795–808. [Google Scholar] [CrossRef]
- Tomei, J.; Cronin, J.; Agudelo Arias, H.D.; Córdoba Machado, S.; Mena Palacios, F.M.; Toro Ortiz, Y.M.; Borja Cuesta, Y.E.; Palomino Lemus, R.; Murillo López, W.; Anandarajah, G. Forgotten spaces: How reliability, affordability and engagement shape the outcomes of last-mile electrification in Chocó, Colombia. Energy Res. Soc. Sci. 2020, 59, 101302. [Google Scholar] [CrossRef]
- Lambert, T.W.; Hittle, D.C. Optimization of autonomous village electrification systems by simulated annealing. Sol. Energy 2000, 68, 121–132. [Google Scholar] [CrossRef]
- Ferrer-Martí, L.; Pastor, R.; Capó, G.M.; Velo, E. Optimizing microwind rural electrification projects. A case study in Peru. J. Glob. Opt. 2011, 50, 127–143. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). World Energy Outlook: Electricity Access Database. 2021. Available online: https://www.iea.org/reports/world-energy-outlook-2021 (accessed on 19 January 2022).






| Feature | a.* | b.* | c.* | d.* | e.* | f.* | g.* | h.* |
|---|---|---|---|---|---|---|---|---|
| PV generation | X | X | X | X | X | X | X | |
| Battery storage | X | X | X | X | X | X | X | |
| Microgrid distribution | X | X | X | X | X | X | X | |
| Several microgrids | X | X | X | X | X | X | ||
| Individual supply | X | X | X | X | X | X | ||
| Versatile (microgrids vs. individual) | X | |||||||
| Forbidden connections | X | X | ||||||
| Restriction on microgrid generation points | X | |||||||
| Demand/non-demand points | X | X | X | X | X | |||
| Economic assessment | X | X | X | X | X | X | X | X |
| Additional installation costs | X | X | X | X |
| Parameter | Description | Unit |
|---|---|---|
| Demand points | ||
| P | Set of potential generation points, including the demand points. | - |
| D | Set of demand points, D ∈ P. | - |
| Lpd | Distance between two points p and d (p ∈ P, d ∈ D). | [m] |
| Lmax | Maximum length of a wire segment of the microgrid. | [m] |
| MPCpd | (p,d)-element of the matrix of potential connections (p ∈ P, d ∈ D). ∀p ∈ P, ∀d ∈ D, MPCpd ∈ {0,1}. | - |
| Qp | Subset of points to which point p can be directly connected with a wire segment (p ∈ P, d ∈ D: p ≠ d, MPCpd = 1, Lpd ≤ Lmax). | - |
| EDp | Energy demand at p (p ∈ D). | [Wh/day] |
| PDp | Power demand at p, considering the simultaneity factor (p ∈ D). | [W] |
| PV generation | ||
| S, NS | Set of PV panel types and maximum number of PV panels that can be placed at a point, respectively. | - |
| ESs | Energy generated by a PV panel of type s (s ∈ S). | [Wh/day] |
| PSs | Maximum power of a PV panel of type s (s ∈ S). | [W] |
| CSs | Cost of a PV panel of type s (s ∈ S). | [US$] |
| Z | Set of PV controller types. | - |
| PZz | Maximum power of a PV controller of type z (z ∈ Z). | [W] |
| CZz | Cost of a PV controller of type z (z ∈ Z). | [US$] |
| Electric equipment | ||
| B | Set of battery types. | - |
| EBb | Capacity of a battery of type b (b ∈ B). | [Wh] |
| CBb | Cost of a battery of type b (b ∈ B). | [US$] |
| ηb | Battery efficiency. | [%] |
| DB | Maximum discharge proportion admitted for the batteries. | [%] |
| DA | Required autonomy of the batteries. | [days] |
| I | Set of inverter types. | - |
| PIi | Maximum power of an inverter of type i (i ∈ I). | [W] |
| CIi | Cost of an inverter of type i (i ∈ I). | [US$] |
| ηi | Inverter efficiency. | [%] |
| CL | Cost of an electric meter device. | [US$] |
| Electricity distribution | ||
| C | Set of wire types. | - |
| RCc | Electric resistance (feed and return) of a wire of type c (c ∈ C). | [Ω/m] |
| ICc | Maximum intensity of a wire of type c (c ∈ C). | [A] |
| CCc | Cost of a wire of type c (feed and return), including the infrastructure (c ∈ C). | [US$/m] |
| Vn | Nominal voltage. | [V] |
| Vmin | Minimum voltage. | [V] |
| Vmax | Maximum voltage. | [V] |
| ηc | Wire efficiency. | [%] |
| Specific features for RAE electrification | ||
| CA | Cost of a shed for equipment storage. | [$US] |
| α | Accepted percentage of cost overhead of microgrids w.r.t. individual systems. | [%] |
| Cmax | Maximum number of output connections from a microgrid point. | - |
| Variable | Description | Unit |
|---|---|---|
| Integer non-negative variables | ||
| xsps | Number of PV panels of type s placed at point p (p ∈ P, s ∈ S). | - |
| xzpz | Number of PV controllers of type z placed at point p (p ∈ P, z ∈ Z). | - |
| xbpb | Number of batteries of type b placed at point p (p ∈ P, b ∈ B). | - |
| xipi | Number of inverters of type i placed at point p (p ∈ P, i ∈ I). | - |
| Float non-negative variables | ||
| fepd | Energy flow between points p and d (p ∈ P, d ∈ Qp). | [Wh/day] |
| fppd | Power flow between points p and d (p ∈ P, d ∈ Qp). | [W] |
| vp | Voltage at point p (vp ∈ [Vmin, Vmax], p ∈ P). | [V] |
| Binary variables | ||
| xgp | =1, if at least a wind turbine or PV panel is placed at point p (p ∈ P). | - |
| xcpdc | =1, if there is a wire of type c between the points p and d (p ∈ P, d ∈ Qp, c ∈ C). | - |
| xlp | =1, if point p (p ∈ D) belongs to a microgrid (involving a meter device). | - |
| Description | Parameter | Value | Unit |
|---|---|---|---|
| Electric equipment | |||
| Batteries: types | |B| | 2 | - |
| Batteries: capacity | EBb (b ∈ B) | 1800; 3600 | [Wh] |
| Batteries: cost | CBb (b ∈ B) | 300; 850 | [US$] |
| Batteries: efficiency | ηb | 85 | [%] |
| Batteries: maximum discharge | DB | 60 | [%] |
| Batteries: required autonomy | DA | 3 | [days] |
| Inverters: types | |I| | 2 | - |
| Inverters: maximum power | PIi (i ∈ I) | 600; 3600 | [W] |
| Inverters: cost | CIi (i ∈ I) | 400; 2000 | [US$] |
| Inverters: efficiency | ηi | 85 | [%] |
| Meter devices: cost | CL | 50 | [US$] |
| Demand points | |||
| Maximum length of wire segments | Lmax | 300 | [m] |
| Energy demand | EDp (p ∈ D) | 1000 | [Wh/day] |
| Power demand | PDp (p ∈ D) | 600 | [W] |
| PV generation | |||
| PV panel: types | |S| | 1 | - |
| PV panel: maximum number | NS | 40 | - |
| PV panel: energy generated | ESs (s ∈ S) | 1178.8 | [Wh/day] |
| PV panel: maximum power | PSs (s ∈ S) | 330 | [W] |
| PV panel: cost | CSs (s ∈ S) | 350 | [US$] |
| PV controllers: types | |Z| | 2 | - |
| PV controllers: maximum power | PZz (z ∈ Z) | 80; 2880 | [W] |
| PV controllers: cost | CZz (z ∈ Z) | 300; 700 | [US$] |
| Distribution equipment | |||
| Wires: types | |C| | 1 | - |
| Wires: electric resistance | RCc (c ∈ C) | 0.0016 | [Ω/m] |
| Wires: maximum intensity | ICc (c ∈ C) | 60 | [A] |
| Wires: cost | CCc (c ∈ C) | 3.94 | [US$/m] |
| Nominal voltage | Vn | 110 | [V] |
| Minimum voltage | Vmin | 105 | [V] |
| Maximum voltage | Vmax | 116 | [V] |
| Wires: efficiency | ηc | 90 | [%] |
| RAE’s specific features | |||
| Shed cost | CA | 1500 | [$US] |
| Cost overhead (microgrids vs. individual systems) | α | −20, 0, 20 | [%] |
| Maximum output connections in microgrids | Cmax | 2 | - |
| Community | Sub-Problem | Demand Points | α (%) | Obj. Func. (USD) | Real Cost (USD) | Configuration |
|---|---|---|---|---|---|---|
| Suraka | 12 | −20 | 34,800 | 34,800 | 12 individual systems | |
| 0 | 31,110 | 31,110 | One microgrid (all 12 users) | |||
| 20 | 25,925 | |||||
| Santa Rosa | SR-R | 4 | −20 | 11,600 | 11,600 | 4 individual systems |
| 0 | ||||||
| 20 | 10,231 | 12,277 | One microgrid (all 4 users) | |||
| SR-L | 11 | −20 | 31,900 | 31,900 | 11 individual systems | |
| 0 | 29,848 | 29,848 | One microgrid (9 users) and 2 individual systems | |||
| 20 | 25,840 | |||||
| Conambo | C-L | 9 | −20 | 26,100 | 26,100 | 9 individual systems |
| 0 | 25,925 | 25,925 | One microgrid (5 users) and 4 individual systems | |||
| 20 | 23,538 | |||||
| C-RA | 10 | −20 | 29,000 | 29,000 | 10 individual systems | |
| 0 | 27,463 | 27,463 | One microgrid (all 10 users) | |||
| 20 | 22,886 | |||||
| C-RB | 15 | −20 | 43,500 | 43,500 | 15 individual systems | |
| 0 | 39,353 | 39,353 | One microgrid (13 users) and 2 individual systems | |||
| 20 | 32,897 | 39,477 | One microgrid (all 15 users) | |||
| C-RC | 20 | −20 | 58,000 | 58,000 | 20 individual systems | |
| 0 | 53,649 | 53,649 | One microgrid (15 users) and 5 individual systems | |||
| 20 | 46,789 | 53,827 | One microgrid (16 users) and 4 individual systems | |||
| C-RD | 6 | −20 | 17,400 | 17,400 | 6 individual systems | |
| 0 | ||||||
| 20 | 17,252 | 19,543 | One microgrid (4 users) and 2 individual systems | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domenech, B.; Ferrer-Martí, L.; García, F.; Hidalgo, G.; Pastor, R.; Ponsich, A. Optimizing PV Microgrid Isolated Electrification Projects—A Case Study in Ecuador. Mathematics 2022, 10, 1226. https://doi.org/10.3390/math10081226
Domenech B, Ferrer-Martí L, García F, Hidalgo G, Pastor R, Ponsich A. Optimizing PV Microgrid Isolated Electrification Projects—A Case Study in Ecuador. Mathematics. 2022; 10(8):1226. https://doi.org/10.3390/math10081226
Chicago/Turabian StyleDomenech, Bruno, Laia Ferrer-Martí, Facundo García, Georgina Hidalgo, Rafael Pastor, and Antonin Ponsich. 2022. "Optimizing PV Microgrid Isolated Electrification Projects—A Case Study in Ecuador" Mathematics 10, no. 8: 1226. https://doi.org/10.3390/math10081226
APA StyleDomenech, B., Ferrer-Martí, L., García, F., Hidalgo, G., Pastor, R., & Ponsich, A. (2022). Optimizing PV Microgrid Isolated Electrification Projects—A Case Study in Ecuador. Mathematics, 10(8), 1226. https://doi.org/10.3390/math10081226







