Research on Location-Routing Problem of Maritime Emergency Materials Distribution Based on Bi-Level Programming

Abstract

To solve the location-routing problem of maritime emergency materials distribution (MEMD-LRP) of multi-agent joint decision, a bi-level programming model of MEMD-LRP is constructed. The model is established on the premise of considering the rescue time window and emergency materials distribution priority, aiming at the strong regional characteristics of maritime accidents, strong timeliness of maritime rescue, great difficulty of rescue, high cost of rescue, and so on. From the point of view of the emergency management department, the upper level makes the location decision to minimize the construction cost of the shore-based emergency materials reserves and the time satisfaction loss cost of the accident point. From the point of view of the commercial rescue unit, the lower level plans the routes by minimizing the cost of emergency material distribution, ship transportation, ship dispatch, and time penalty. A hybrid algorithm of the ant colony and tabu search is designed to solve the model, and an example is designed and analyzed based on the case of the Bohai Sea to verify the effectiveness of the model and algorithm. Modeling and algorithm design based on bi-level programming can help decision-makers at different levels in maritime emergency logistics systems to make more scientific and reasonable decisions to improve the service capability of the maritime emergency logistics system.

1. Introduction

Within the rapidly developing marine economy, the increase in marine economic activities has also brought huge security risks [1,2,3]. Various marine accidents have occurred in recent years [4,5,6], and these accidents cause huge losses to human life, property, and the marine ecological environment [7]. For example, at least 232 people were killed when a stowaway ship caught fire and sank in Italian waters in 2013. In 2015, a shipwreck occurred in the sea area of Russia Okhotsk, resulting in 56 deaths. The “Eastern Star” tourist ship capsized in 2015, a major catastrophic incident at sea that killed 442 people. Another example is the collision between “Sangji” and “Changfeng Crystal” in 2018; the volatilization and combustion of 130,000 tons of condensate contained in the Sangji caused serious pollution to the surrounding sea area and atmosphere and impacted marine ecology for decades. Therefore, the problems related to maritime emergencies have attracted more and more attention. The characteristics of maritime accidents are sudden, regional, time-efficient, and difficult and result in costly rescues, bringing great challenges to maritime emergency work. The collaborative optimization of the location of emergency materials reserves and emergency material distribution routes in maritime emergency logistics systems can improve the operation efficiency of the whole emergency logistics system and reduce the overall timeliness and cost of emergency logistics. Therefore, it is of great practical significance to research the location-routing problem of maritime emergency materials distribution (MEMD-LRP).

The study of the modern location problem (LP) can be traced back to 1909 [8], whereas the research on the vehicle-routing problem (VRP) came later (Dantaig et al., 1959) [9]. In the 1970s, Cooper first combined the LP with the transportation problem and proposed the transportation–location problem [10]. Subsequently, when studying the transportation–location problem, some scholars began to add the characteristics of multi-point transportation of the VRP. It was not until the 1980s that a real location-routing problem (LRP) emerged [11]. The LRP can be regarded as a joint decision problem of location and vehicle routing, which are interdependent and interactive. Distribution center location and vehicle routing arrangements belong to different levels of activities, and the LP must be solved at the strategic decision-making level to determine the number and location of facilities and the customers they serve at the same time. The VRP is determined at the tactical level or operation level to construct a specific route scheme to serve customers. The bi-level programming method is suitable for solving the joint decision problem of different levels of decision-makers; this method can consider the overall situation and the interests of each decision-making agent at the same time and ensure that the overall situation is given priority. Using a bi-level programming model to solve LRP can jointly optimize LP and VRP and reflect the hierarchy and integrity of the logistics system.

With the in-depth study of LRP by domestic and foreign scholars, LRP of emergency logistics has also become one of the topics of focus. The goal of LRP of emergency logistics is usually the shortest transportation time as the main goal while taking into account the lowest economic cost, the highest satisfaction of the accident points, and other goals. Moreover, there are multiple types of emergency materials transported in the LRP of emergency logistics. The current LRP of emergency logistics is usually based on the post-earthquake background, establishes multi-objective models, and designs a hybrid algorithm to solve the problem [12,13,14]. The existing research seldom takes into account that the LRP of emergency logistics requires the participation of multiple decision-makers and uses the bi-level programming method to solve the problem.

Therefore, to optimize the maritime emergency logistics system as a whole, it is necessary to study the MEMD-LRP while considering (a) rescue time window and distribution priority of different kinds of emergency materials from the perspective of joint participation and joint decision of multi-level agents and (b) the modeling idea of bi-level programming.

The contributions of this paper can be summarized as follows: (a) Taking the maritime emergency materials distribution with multi-agent participation as the decision-making background, the location routing problem is studied. We studied the overall layout of the maritime emergency logistics system based on a deterministic scenario. (b) A bi-level programming model considering the time window of accident points and the priority of multiple types of emergency materials distribution is constructed. The upper level makes the location decision and the lower level makes the route choice decision. (c) A hybrid algorithm of the ant colony and tabu search is designed to solve the bi-level programming model of MEMD-LRP.

This paper is divided into six parts. The second part summarizes the research related to this topic, and the third part gives a general description of the research problem. The fourth part gives the ant colony–tabu search algorithm to solve the problem in this paper. In the fifth part, an example is introduced to verify the effectiveness of the model and algorithm proposed in this paper, and the optimal decision is given. Finally, the sixth part summarizes this paper.

2. Literature Review

At present, there are rich research results on LRP, with most of this research focusing on various extended models and solution methods based on classical problems. For example, Wang et al. [15,16] carried out research on green LRP, Yu et al. [17] studied capacity-limited LRP, and Wang et al. [18,19] studied LRP with simultaneous pick-up and delivery. The solution methods of LRP-related research mainly include staged solutions and global solutions. In [16], the green LRP is decomposed into two sub-problems, namely the cumulative LRP (CumLRP) and the speed optimization problem (SOP), and each sub-problem is solved hierarchically. The solution results of the cumulative location routing and speed optimization algorithm (CLRSOA) are compared with the iterated local search algorithm. Reference [18] proposed a hybrid heuristic algorithm based on a tabu search to solve the LRP with simultaneous pick-up and delivery. The algorithm is divided into three stages: initialization, location, and routing. References [15,17] used a hybrid genetic algorithm (HGA), and [19] proposed a multi-start hybrid heuristic algorithm with path relinking (MHH-PR) composed of local search and a variable neighborhood descent algorithm to solve the LRP as a whole.

The research on the combination of LRPs and emergency logistics has also become a hot issue considered by scholars at home and abroad. The relevant research on LRPs of emergency logistics by domestic and overseas scholars in recent years is summarized in

Table 1. Summary of main features of related research on emergency logistics LRPs.

Author	Uncertainty	Maritime Emergency	Multiple Types of Emergency Materials	Time Window	Improved Algorithm
Liu et al. [13]				√	√
Tavana et al. [20]			√		√
Wei et al. [21]				√	√
Vahdani et al. [22]			√
Xue et al. [23]			√
Li et al. [24]		√	√
Ai et al. [25]		√			√
Ai et al. [26]		√			√
Shen et al. [14]	√				√
Zhang et al. [27]	√	√			√
Bozorgi-Amiri et al. [28]	√		√
Chang et al. [29]	√			√
Veysmoradi et al. [30]	√				√
Wu et al. [31]	√
Zhang et al. [32]	√				√
Hu et al. [33]	√		√		√
Liu et al. [34]	√		√
Xiong et al. [35]	√		√	√	√
Qin et al. [36]	√				√
Liu et al. [37]	√
Liu et al. [38]	√				√
This paper		√	√	√	√

.

Emergency rescue needs the joint action of multiple units and multiple departments. Government-led, functional departments cooperate, communicate, and coordinate with each other to carry out emergency rescue operations more reasonably and efficiently. Therefore, emergency logistics should be a joint decision-making activity with the participation of multi-level decision-makers. In the existing research on LRP with emergency logistics, some scholars consider the characteristics of multi-participation and multi-decision of emergency logistics by the government and enterprises and use the bi-level programming method to solve the problem from the perspective of multi-agent decision. To solve the problem of lack of road condition information increasing the uncertainty of disaster relief work within 72 h after an earthquake, Xu et al. [39] proposed a bi-level model based on a random fuzzy environment and designed an interactive genetic algorithm based on random fuzzy simulation to search the optimal solution of the bi-level model. Lou [40] studied (a) the expression of emergency logistics with the participation of the government and enterprises and (b) the post-disaster LRP. Lou [40] then established a bi-level programming model and designed a hybrid simulated annealing algorithm combined with tabu search technology. Safaei et al. [41] proposed a bi-objective, bi-level optimization model under an uncertain environment to design a complete disaster relief logistics operation framework, and the proposed nonlinear model was transformed into a single-level linear problem to solve. Chen et al. [42] established a bi-level programming model considering minimum allocation time and maximum allocation fairness and designed an improved differential evolution algorithm to solve the problem. Li et al. [43] established a multi-period, bi-level programming model for post-disaster road network emergency repair scheduling and disaster relief logistics problems and designed genetic algorithms to solve the problem. Considering the various characteristics of the two-level logistics emergency system, Zhou [44] studied transfer facility location and relief material transportation in the initial period after the earthquake. The grey mixed integer bi-level nonlinear programming model was established, and the genetic algorithm was designed. At present, few researchers have examined how to solve the LRP in emergency logistics using a bi-level programming method; the above research is all based on land disasters and emergencies.

Generally speaking, the research on the LRP of emergency logistics is rich and in-depth, and stochastic programming, robust optimization, and bi-level programming decision-making methods have also been applied to different forms of the LRP of emergency logistics. However, there are still some aspects worthy of further exploration. First, most of the existing studies focus on land disasters and emergencies, and few scholars consider using maritime emergencies as the background to optimize the overall layout of the maritime emergency logistics system. Among the above-mentioned references, only [24,25,26,27] explored the background of maritime emergencies. Second, most of the existing studies only consider a single kind of emergency material, and few scholars consider many kinds of emergency materials and the priority in distribution. Although many kinds of emergency materials are considered in [20,22,23,24,28,33,34,35,41,42], the priority of emergency materials distribution is only considered in [23]. However, the limitation of [23] is that it did not detail the joint decision-making of location and routing, and the location is not considered in the study. Third, most of the existing studies focus on the use of multi-objective models, without considering multiple decision-making agents and the application of bi-level programming methods. Different decision-making agents will lead to different decision-making problems. Location and route selection are activities at different levels that require a combined decision. The single-level programming method will separate the things that are originally related, and it cannot comprehensively analyze and solve the problems. References [39,40,41,42,43,44] adopt a bi-level programming method to solve the LRP of emergency logistics with the participation of multiple decision agents, but [40,41,42,43,44] do not consider that location and route selection are activities at different levels, making location decisions at the upper level and planning the route at the lower level. The biggest difference between maritime emergencies and other emergencies is that the environment is different. A dangerous situation at sea is sudden and harmful and can easily cause mass deaths and injuries. Maritime emergency operations are often carried out in harsh conditions, making rescue difficult. Therefore, the LRP of the maritime emergency network has higher requirements on time, which can deliver maritime emergency materials to the accident points in the shortest time as soon as possible. Due to the different environments, MEMD-LRP often needs a variety of professional emergency materials. There are many units and departments involved in the maritime emergency network, and problems in any link may lead to missing the best rescue opportunity. Therefore, the task of maritime rescue and coordination is also relatively heavy. The MEMD-LRP will definitely involve multiple decision-makers.

3. Problem Description and Model Construction

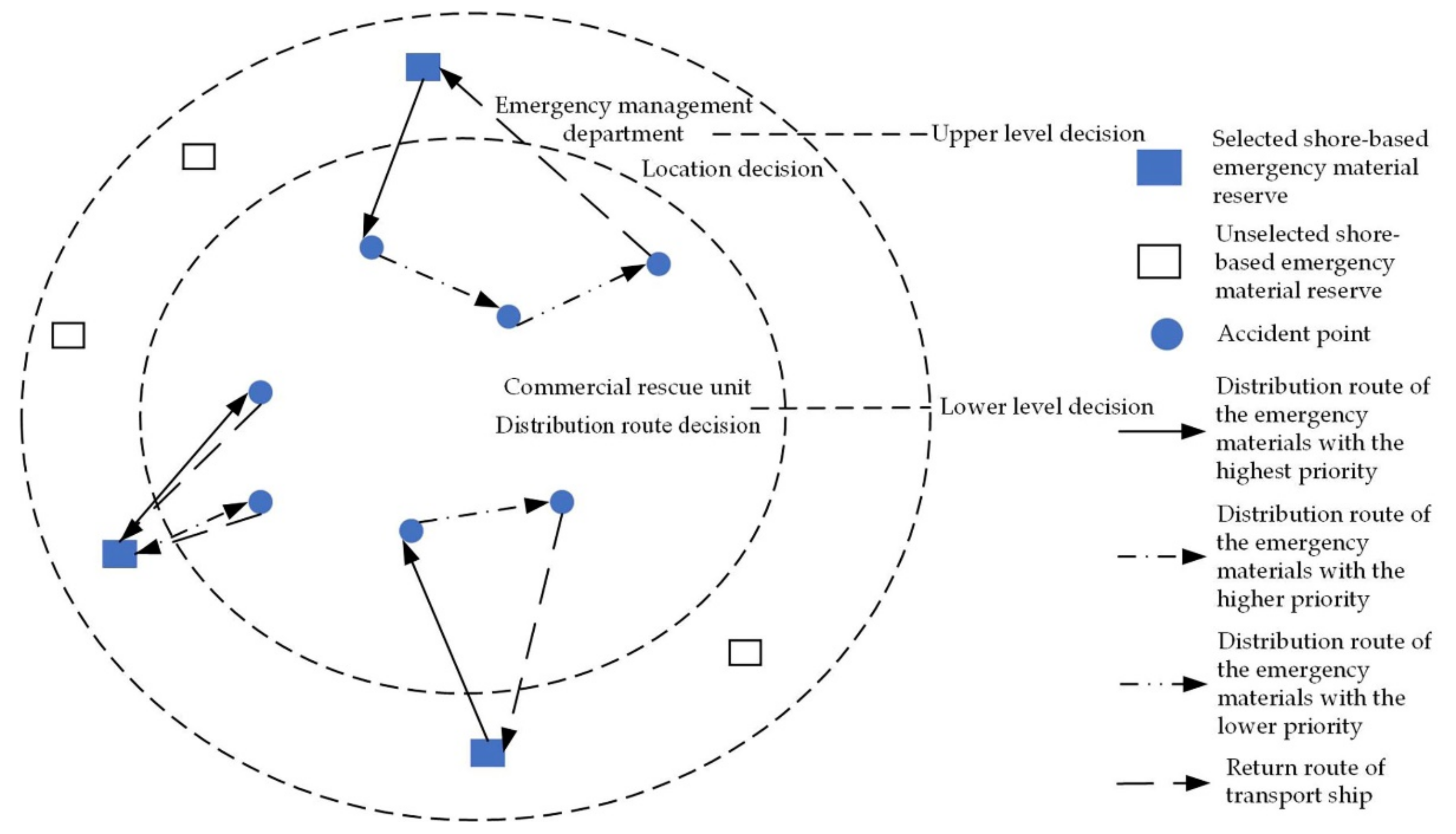
3.1. Problem Description

MEMD-LRP decisions require scientific and reasonable location selection of shore-based emergency materials reserves and distribution route planning of maritime emergency materials to achieve efficient scheduling of emergency materials and improve the overall operational efficiency of the maritime emergency logistics system. The problem can be described as follows: There are several shore-based candidate emergency materials reserves and several potential maritime accident points. Several suitable reserves are selected as distribution centers from the shore-based candidate emergency materials reserves. According to the information such as the location of potential accident points and the demand for emergency materials, under the constraints of meeting the time windows and other constraints, the commercial rescue unit reasonably plans the routes to distribute emergency materials with different priorities from the reserves to the accident points. The maritime logistics system and related elements studied in this paper are shown in Figure 1.

MEMD-LRP is a multi-level decision agent participation and joint decision problem. The bi-level programming method can be used to solve the practical problem of two-level decision-makers in the decision-making system; this problem can be described by bi-level programming. First, the upper decision-maker gives their decision. Then, under the decision given by the upper level, the lower decision-maker determines the optimal lower-level decision and feeds it back to the upper level. Next, the upper-level decision-maker adjusts the upper-level decision based on feedback from the lower-level decision-maker to make the best decision for the whole. The upper- and lower-level decision-makers influence each other but do not completely restrict each other; the upper-level decision is considered from a more overall point of view. In the research of this paper, the upper decision-maker is a member of the emergency management department. This upper decision-maker makes overall planning decisions on the location of emergency materials reserves while considering both the minimum total construction costs and the minimum loss costs of time satisfaction at the accident points. The lower decision-maker is a member of the commercial rescue unit. According to the location scheme given by the upper level, the lower level reasonably plans the distribution routes of emergency materials to minimize the cost of emergency materials distribution, ship transportation, ship dispatch, and time punishment. The upper decision-maker first makes the location decision; then, the lower decision-maker must respond to this decision. The lower decision-maker has a certain degree of independent decision-making power, and the rescue unit provides feedback on the distribution plan to the emergency management department. Then, the upper decision-maker must make another decision according to the response of the rescue unit to make the optimal decision for the whole emergency logistics system.

This paper has the following assumptions:

• Multiple candidate emergency materials reserves with known locations and unlimited capacity.
• Multiple potential accident points with known locations and the drift and diffusion of the accident points are not considered.
• Multiple levels of emergency materials with known priorities; the transportation order of materials is in the order of priority, and the unit distribution cost of different levels of emergency materials is different.
• The number of ships is sufficient, the transport ships are of the same type and capacity, and different levels of emergency materials can be mixed and loaded under the limitation of the time window of the accident point.
• The emergency materials in the candidate reserves are sufficient, the emergency material demand at the accident point is known, the emergency materials storage capacity of each reserve meets the rescue needs of multiple accident points, and the demand at each accident point does not exceed the storage capacity of a single emergency material reserve.
• Each accident point is rescued by only one emergency material reserve, and only one ship passes through the accident point in the process of emergency material distribution at each level, with time window restrictions.
• Each ship belongs to an emergency material reserve. Starting from the warehouse and returning to the warehouse after transporting the materials, each ship can serve multiple accident points under the condition of meeting the time window limit.

Variables and symbols are described as follows:

$I=\left\{i|i=\mathrm{1,2},\cdots ,\left|I\right|\right\}$ is the set of all candidate shore-based emergency material reserves;

$J=\left\{j|j=\mathrm{1,2},\cdots ,\left|J\right|\right\}$ is the set of all accident points;

$B=I\cup J$ is the set of all nodes in the network;

$K=\left\{k|k=\mathrm{1,2},\cdots ,\left|K\right|\right\}$ is the set of all ships;

$W=\left\{w|w=\mathrm{1,2},\cdots ,\left|W\right|\right\}$ is the set of emergency materials priority number;

$f_i$ is the fixed construction cost of the $i$ candidate material reserve;

$S_k$ is the transportation cost per unit distance of the $k$ ship;

$c_0$ is the fixed dispatch cost per ship;

$G$ is the fixed capacity per ship;

When $u_{jw}=1$, the accident point $j$ needs emergency materials of level $w$, and when $u_{jw}=0$, the emergency materials of level $w$ are not required at the accident point $j$;

$D_{jw}$ is the demand for emergency materials of level w at accident point $j$;

$C_{ijw}$ is the unit transportation cost of emergency materials of level $w$ transported from reserve $i$ to accident point $j$;

$V_{pqk}$ is the actual average velocity of ship $k$ from node $p$ to $q$ considering the influence of wind and water current;

$v_{pqk}$ is the average velocity of ship $k$ from node $p$ to $q$ in still water;

$v_1$ is the influence of the wind;

$v_2$ is the influence of the water current;

$d_{pq}$ is the shortest sailing distance from node $p$ to $q$;

$T_k$ is the time of ship $k$ loading and unloading unit materials;

$T_{Ejw}$ is the expected arrival time of emergency materials of level $w$ at accident point $j$;

$T_{Ljw}$ is the latest arrival time of level $w$ emergency materials that can be tolerated at the accident point $j$;

$T_{jw}$ is the actual arrival time of level $w$ emergency materials at accident point $j$;

$c_1$ is the time penalty cost caused by the arrival of emergency materials of level $w$ earlier than $T_{Ejw}$;

$c_2$ is the time penalty cost for the arrival of emergency materials of level $w$ later than $T_{Ejw}$ and earlier than $T_{Ljw}$;

$F\left(T_{jw}\right)$ is the time satisfaction function of the accident point $j$ in the transportation of emergency materials of level $w$;

$f\left(F\left(T_{jw}\right)\right)$ is the time satisfaction loss cost penalty coefficient function of the accident point $j$ in the transportation of emergency materials of level $w$;

$A$ is a sufficiently large positive number;

Decision variables:

$x_i=\left\{\begin{array}{l}1,\mathrm{Construct} \mathrm{an} \mathrm{emergency} \mathrm{material} \mathrm{reserve} \mathrm{at} \mathrm{the} \mathrm{point}\\ 0,\mathrm{Otherwise}\end{array}\right.;$

$y_{ij}=\left\{\begin{array}{l}1,\mathrm{Emergency} \mathrm{materials} \mathrm{reserve} i \mathrm{rescue} \mathrm{the} \mathrm{accident} \mathrm{point} j\\ 0,\mathrm{Otherwise}\end{array}\right.;$

$q_k=\left\{\begin{array}{l}1,\mathrm{The} \mathrm{ship} k \mathrm{put} \mathrm{into} \mathrm{use}\\ 0,\mathrm{Otherwise}\end{array}\right.;$

$z_{pqk}=\left\{\begin{array}{l}1,\mathrm{The} \mathrm{ship} k \mathrm{sails} \mathrm{from} \mathrm{node} p \mathrm{to} q\\ 0,\mathrm{Otherwise}\end{array}\right..$

3.2. Model Construction

3.2.1. The Time Penalty Cost Description of MEMD-LRP

The maritime emergency rescue has the characteristic of strong time-effectiveness, so this paper improves the time penalty cost function in [21,40,45] to obtain the time penalty cost in MEMD-LRP. When the ship $k$ transports a certain level of emergency materials to the accident point $j$, if it does not arrive at the expected time $T_{Ejw}$ of the accident point $j$, the time penalty cost will be incurred. Under no circumstances shall the time taken to arrive at the accident point $j$ exceed $T_{Ljw}$; otherwise, the ship $k$ cannot transport materials to the accident point. The relationship between time and the cost of time penalty is shown in Figure 2.

3.2.2. The Time Satisfaction Loss Cost Description of at Accident Points of MEMD-LRP

In this paper, the decision-making problem of the emergency management department is that of selecting a suitable shore-based emergency material reserve to meet the needs of all potential accident points, from the overall point of view. Both the construction cost and the time satisfaction of the accident points should be considered. To facilitate calculation, time satisfaction is converted into time satisfaction loss cost into the goal of upper-level decision-makers. When the ship $k$ transports a certain level of emergency materials to the accident point $j$ and does not arrive at the expected time $T_{Ejw}$ of the accident point $j$, the time satisfaction of the accident point $j$ will be lost. The greater the difference between the time when the emergency materials arrive at the accident point $j$ and $T_{Ejw}$, the greater the loss of time satisfaction is. According to the research results of [46], this paper selects the linear time satisfaction function to discuss the time satisfaction of the maritime accident points to the arrival time of emergency materials, and the functional relationship is set to $F\left(T_{jw}\right)$, and the loss cost of time satisfaction at the accident point is related to the demand for emergency materials at the accident point. The penalty coefficient of the loss cost of time satisfaction at the accident point is a piecewise function corresponding to time satisfaction, and the functional relationship is set to $\varphi \left(F\left(T_{jw}\right)\right)$.

The time satisfaction function expression of the accident point $j$ for the arrival time of a certain level of emergency materials is as follows:

$$F\left(T_{jw}\right)=\left\{\begin{array}{l}1,T_{jw}=T_{Ejw}\\ \frac{T_{Ejw}-T_{jw}}{T_{Ejw}},0\le T_{jw}<T_{Ejw}\\ \frac{T_{Ljw}-T_{jw}}{T_{Ljw}-T_{Ejw}},T_{Ejw}<T_{jw}\le T_{Ljw}\\ 0,T_{Ljw}<T_{jw}\end{array}\right.,\forall j\in J,w\in W$$

(1)

The function expression of the penalty coefficient of the time satisfaction loss cost of the accident point $j$ is as follows:

$$\varphi \left(F\left(T_{jw}\right)\right)=\left\{\begin{array}{l}0,F\left(T_{jw}\right)=1\\ 1,F\left(T_{jw}\right)=\frac{T_{Ejw}-T_{jw}}{T_{Ejw}},\forall j\in J,w\in W\\ 1,F\left(T_{jw}\right)=\frac{T_{Ljw}-T_{jw}}{T_{Ljw}-T_{Ejw}},\forall j\in J,w\in W\\ +\infty ,F\left(T_{jw}\right)=0\end{array}\right.$$

(2)

The total cost of the loss of time satisfaction at the accident points is as follows:

$${\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{w\in W}{x}_i\varphi \left(F\left(T_{jw}\right)\right)}}}{y}_{ij}{D}_{jw}$$

(3)

3.2.3. The Bi-Level Programming Model of MEMD-LRP

Upper model:

$$min{f}_1={\displaystyle \sum _{i\in I}{f}_i{x}_i+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{w\in W}{x}_i\varphi \left(F\left(T_{jw}\right)\right)}}}{y}_{ij}{D}_{jw}}$$

(4)

$$\mathrm{s.t.} 1\le {\displaystyle \sum _{i\in I}{x}_i\le I}$$

(5)

$$y_{ij}-x_i\le 0,\forall i\in I,j\in J$$

(6)

$$x_i\in \left\{0,1\right\}$$

(7)

The objective function (4) represents the minimization of the construction cost of emergency materials reserves and the loss cost of time satisfaction at the accident points. Constraint (5) indicates that the actual construction number of the emergency materials reserves cannot exceed the number of candidate emergency materials reserves. Constraint (6) indicates that materials can be transported only if they are selected as emergency materials reserves, and constraint (7) is the upper-level decision variable.

Lower model:

$$\begin{array}{l}min{f}_2={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{w\in W}{u}_{jw}{d}_{jw}{C}_{ijw}{y}_{ij}+{\displaystyle \sum _{p,q\in B}{\displaystyle \sum _{k\in K}{z}_{pqk}{d}_{pq}{S}_k+{\displaystyle \sum _{k\in K}{c}_0{q}_k+}}}}}}\\ {\displaystyle \sum _{w\in W}\left({\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{y}_{ij}\left(c_{1}max\left\{T_{Ejw}-T_{jw},0\right\}+c_{2}max\left\{T_{jw}-T_{Ejw},0\right\}\right)}}\right)}\end{array}$$

(8)

$$\mathrm{s.t.} {\displaystyle \sum _{i\in I}{y}_{ij}=1,\forall }j\in J$$

(9)

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{j\in J}{z}_{ijk}\ge x_i,\forall i\in I}}$$

(10)

$${\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{z}_{ijk}\le 1,\forall k\in K}}$$

(11)

$$z_{pqk}\le q_k,\forall p,q\in B,p\ne q,k\in K$$

(12)

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{p\in B}{z}_{pjk}{u}_{jw}=1,\forall j\in J,w\in W}}$$

(13)

$${\displaystyle \sum _{p,q\in B}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{D}_{jw}{u}_{jw}{y}_{ij}{z}_{pqk}\le G,\forall k\in K}}}$$

(14)

$${\displaystyle \sum _{k\in K}{z}_{pqk}=0,\forall p,q\in I}$$

(15)

$${\displaystyle \sum _{p\in B}{z}_{pqk}-{\displaystyle \sum _{p\in B}{z}_{qpk}}=0,\forall k\in K,q\in B}$$

(16)

$${\displaystyle \sum _{j\in J}{z}_{ijk}+{\displaystyle \sum _{j\in J}{z}_{jrk}}\le 1,\forall i,r\in I}$$

(17)

$$y_{ij}{D}_{j(w+1)}\le u_{jw}A,\forall i\in I,j\in J,w=1,\cdots ,\left|W\right|-1$$

(18)

$$T_{jw}\le T_{j(w+1)},\forall j\in J,w=1,\cdots ,\left|W\right|-1$$

(19)

$${\displaystyle \sum _{j\in J}{T}_{jw}}\le {\displaystyle \sum _{j\in J}{T}_{j(w+1)}},w=1,\cdots ,|W|-1$$

(20)

$$y_{ij}{T}_{jw}\le T_{Ljw},\forall i\in I,j\in J,w\in W$$

(21)

$$T_{iw}+T_k{D}_{iw}{z}_{ijk}+\frac{d_{ij}}{V_{ijk}}\le T_{Ljw},\forall i,j\in J,w\in W,z_{ijk}=1$$

(22)

$$y_{ij}\in \left\{0,1\right\},q_k\in \left\{0,1\right\},z_{pqk}\in \left\{0,1\right\}$$

(23)

In the bi-level programming model, the constraints of the upper model are also applicable to the lower model. The objective function (8) is the minimum sum of the distribution cost of different levels of emergency materials, ship transportation cost, ship dispatch cost, and time penalty cost. Constraint (9) indicates that each accident point is rescued by only one emergency materials reserve. Constraint (10) means that each selected emergency materials reserve is assigned to ships. Constraint (11) means that each ship is assigned to a selected emergency materials reserve. Constraint (12) indicates that only ships put into use can transport, and constraint (13) means that there is only one ship passing by each accident point during the distribution of emergency materials at each level. Constraint (14) means that the emergency materials demand at the accident points on the distribution route of each ship is less than or equal to the ship capacity. Constraint (15) indicates that any two emergency materials reserves cannot be transported, and constraint (16) means that ships entering from that point also sail out from that point. Constraint (17) means that the ship departing from the emergency materials reserve will finally return to the emergency materials reserve. Constraint (18) indicates that the emergency materials transported from the emergency material reserve $i$ to the accident point $j$ can be transported only after the transportation of the emergency materials of the previous level is completed. Constraints (19) and (20) indicate that the actual delivery time of high-priority emergency materials is strictly less than that of low-priority emergency materials. Constraint (21) indicates that the actual arrival time of the level $w$ emergency materials transported from the emergency material reserve $i$ to the accident point $j$ is less than or equal to the latest delivery time of the level $w$ emergency materials that can be tolerated at the accident point $j$. Constraint (22) represents the time window constraint of the ship in the process of serving multiple accident points, and constraint (23) is lower-level decision variables.

The calculation formula of the time when the ship $k$ arrives at the accident point $j$ is as follows:

$$T_{jw}=T_{iw}+T_k{D}_{iw}{z}_{ijk}+\frac{d_{ij}}{V_{ijk}},\forall i,j\in J,w\in W,z_{ijk}=1$$

(24)

The speed of ship $k$ will be affected by wind and water current, so the actual average velocity of ship $k$ is the vector superposition of the ship $k$ still water average velocity, wind velocity, and water current velocity. Because the research of this paper is in the prevention stage, it represents the overall layout of the maritime emergency logistics system. Therefore, it is assumed that the still water velocity of the ship, the wind velocity, and the water current velocity between nodes are constant [25,26]:

$$V_{ijk}=v_{ijk}+v_1+v_2$$

(25)

The bi-level programming model established in this paper has a bi-level hierarchical structure. The objective function and constraints of the upper-level optimization problem are not only related to the upper-level decision variable but also depend on the optimal solution of the lower-level optimization problem. At the same time, the optimal solution of the lower-level optimization problem is affected by the upper-level decision variable. The upper decision variable is $x_i$, the location decision that should be made, and the lower decision variables are $y_{ij},q_k,z_{pqk}$. According to the location decision, accident points should be assigned to each selected emergency materials reserve, and appropriate rescue routes should be designed. The lower-level decision variables depend on the upper-level decision variable. Once the upper-level variable is determined, the corresponding lower-level variables can be determined. Each upper solution $\left\{x_i\right\}$ corresponds to a lower solution $\{y_{ij},q_k,z_{pqk}\}$. It is only after the location decision of the upper level is completed that the lower level can allocate the accident points and plan the distribution routes of each emergency materials reserve to serve each accident point. The location decision of the upper level should be re-adjusted according to the response of the route decision of the lower level. Bi-level programming is used to emphasize the influence between upper and lower levels of decision-making; thus, bi-level programming usually cannot be solved independently.

4. Algorithm Design

The bi-level programming model is very difficult to solve. The model belongs to the NP-Hard problem, and there is no accurate solution algorithm [39,40]. The bi-level programming model constructed in this paper not only considers multiple emergency materials reserves, multiple accident points, and multiple types of emergency materials, but also considers factors such as emergency materials distribution priority, accident point time window, and accident point satisfaction loss cost. At the same time, the upper-level location result is the premise of lower-level route planning, which greatly impacts route planning. There are many model variables and constraints, which makes the model more difficult to solve. Ant colony algorithm is an approximate algorithm, which is used to solve a problem that no accurate algorithm has been found to solve so far. The algorithm has the characteristics of positive feedback, multi-point parallel search, and strong robustness, and it can be used to solve the problem in this paper. Although the ant colony algorithm has a strong global optimization ability, the local search ability is poor and the convergence speed is slow; the tabu search algorithm can jump out of the local optimal solution, and it is a global iterative optimization algorithm with strong local search ability. The combination of the two algorithms can avoid the algorithm falling into the local optimization and obtain the global optimal solution [47,48]. Therefore, according to the characteristics of bi-level programming in this paper and the existing algorithms for solving similar models [14,40,45], a hybrid algorithm of the ant colony and tabu search is designed.

4.1. Coding and Decoding

Suppose that there are $I$ candidate emergency materials reserves and $J$ accident points. First, the candidate emergency materials reserves and accident points are coded by real number coding. The ship’s route begins at the emergency materials reserve, then passes through the accident points, and finally returns to the emergency materials reserve. For example, the scheme code of starting from reserve 1 and passing through accident points 2, 3, 5, and 6 is 123561. Secondly, the double-level coding method is used to encode the ants. The first level code is the access priority code of the accident points, the real number coding with the code length $J$, and the change interval is [0, 1]. The code is sorted in ascending order to obtain the access order code $S_1$ of the accident point. The second-level code is the assigned code of the reserves, the real number coding with the length $J$, and the interval is $[1,I+0.999]$. After rounding down this code, the assigned reserves code S2 is obtained, indicating which reserve serves the accident point. For example, when $I=4$ and $J=6$, a randomly generated ant code can be $x$ = (0.3,0.5,0.2,0.41,0.6,0.7,1.8,2.3,1.5,3.6,4.1,4.2), and the first level code is $x_1$ = (0.3,0.5,0.2,0.41,0.6,0.7). The code is sorted in ascending order to obtain $S_1$ = (3,1,4,2,5,6), which means that accident point 3 is accessed first, then the priority is to visit incident point 1, then the priority is to visit incident point 4, then the priority is to access incident point 2, then the priority is to access incident point 5, and then priority is to access incident point 6. The code of the second level is $x_2$ = (1.8,2.3,1.5,3.6,4.1,4.2), rounded down to obtain $M$ = (1,2,1,3,4,4), indicating that accident point 3 is served by reserve 1, accident point 1 is served by reserve 2, accident point 4 is served by reserve 1, accident point 2 is served by reserve 3, accident point 5 is served by reserve 4, and accident point 6 is served by reserve 4. After ant colony decoding, the location and division of the accident points and distribution routes can be determined. A possible distribution route scheme real number coding is 4564. It is not possible to determine whether the resulting solution is feasible during the encoding and decoding process. Only when the optimal coding is obtained after several iterations of the algorithm and the optimal scheme and objective function values are obtained by decoding can we judge whether the scheme is feasible or not.

4.2. Ant Colony Movement

The core idea of the ant colony algorithm is that the ant colony moves in the direction of the maximum pheromone. For the current ant $i$, first randomly select $t$ other ants and identify the ant with the largest corresponding pheromone among the $t$ ants. This ant represents the maximum direction of the pheromones. Move the position of the current ant $i$ according to the following equation: $xnew=\left(1-speed\right)\times xi+speed\times xmax$, where $xnew$ is the new location of the ant, $speed$ is the movement speed of the ant, $xi$ is the location of the current ant $i$, and $xmax$ is the ant location in the maximum direction of pheromones. The above movement is carried out for each ant such that the whole ant colony moves simultaneously in the maximum pheromone direction.

4.3. Pheromone Update

Ants will leave a certain amount of pheromones as they move forward, and at the same time, all pheromones will volatilize at a certain rate. The ACO-TS algorithm designed in this paper uses the equation ${\tau }_i(gen+1)=(1-\rho ){\tau }_i(gen)$ to describe the volatilization of pheromones, where ${\tau }_i(gen+1)$ is the pheromone corresponding to the $i$ ant of the $gen+1$ generation, $\rho$ is the pheromone volatilization coefficient, and ${\tau }_i(gen)$ is the pheromone corresponding to the $i$ ant of the $gen$ generation. Equation ${\tau }_i(gen+1)={\tau }_i(gen+1)+\Delta {\tau }_i(gen+1)$ is used to describe the enhancement of pheromones, where $\Delta {\tau }_i(gen+1)=Q\frac{\max yj-yi}{\max yj-\min yj}$ is the pheromone increment of the $i$ ant of the $gen+1$ generation, $Q$ is the pheromone enhancement factor, $\max yj$ is the maximum sum of the upper and lower objective function values corresponding to all ants after dimension elimination, $\min yj$ is the minimum sum of the upper and lower objective function values corresponding to all ants after dimension elimination, and $yi$ is the sum of the upper and lower objective function values corresponding to the $i$ ant after dimension elimination.

4.4. Neighborhood Movement

The neighborhood moving method of the tabu search part is similar to the mutation operation of the genetic algorithm. It randomly generates a natural number $r$, changes the $r$ bit of the coding of the current solution, rearranges the coding, and generates a neighbor of the current solution. Then, it checks whether the current neighbor is in the tabu table.

4.5. Tabu Table Length

The length of the tabu table affects the search time, local search strategy, and wide search strategy. The long table is suitable for wide search and the short table has good locality. The tabu length of the tabu search algorithm designed in this paper is fixed, and the fixed constant is selected according to the scale of the problem.

4.6. Stop Criterion

The stop criterion of the tabu search algorithm is to set the maximum number of iterations, which is equal to the maximum number of iterations of the whole algorithm.

4.7. Specific Steps

The specific steps of the hybrid algorithm proposed in this paper can be summarized as follows, and the flow chart of the algorithm is shown in Figure 3.

Step 1: All candidate emergency materials reserves and accident points are numbered, and all different emergency materials reserve sets are calculated by the enumerating algorithm.

Step 2: Input a set of emergency materials reserves in which the initial number of reserves is equal to the number of candidate emergency reserves. Under the constraints of the time window and shipload, considering the priority of emergency materials distribution and the demand for each level of emergency materials at the accident points, the ant colony–tabu search algorithm is used to plan the routes. Then, the lower objective function is calculated, and the time satisfaction loss cost is returned to the upper objective function. Record the results of this location and route selection, as well as the values of the upper and lower level objective functions.

Step 2.1: Read the data and set the model parameters, the ant colony–tabu search algorithm parameters, and the number of iterations of the algorithm.

Step 2.2: Initialize the encoding and pheromone and decode to calculate the initialized lower-level objective function value, return the time satisfaction loss cost to the upper level to calculate the upper-level objective function value, and generate a tabu table.

Step 2.3: The ant colony moves in the direction of the maximum pheromone; decode to obtain the accident point served by each emergency materials reserve; divide the routes according to the time window, load, and priority constraints. The rules for dividing routes according to loads are as follows: the demand of the accident point is accumulated from the reserve, and when the cumulative demand is less than or equal to the ship capacity, the visited accident points are added to the current route; when the demand of the cumulative accident point is greater than the ship capacity, the front accident points join the route, allocate new ship to the current accident point, re-accumulate the demand of the accident point, and generate a new route. Calculate the time window constraints; calculate the lower objective function value, feed the time satisfaction loss cost back to the upper level, and calculate the upper objective function value. Update pheromones.

Step 2.4: The feasible solution generated by the ant colony algorithm is re-optimized as the initial solution of the tabu search algorithm.

Step 2.5: The candidate solution set is generated by neighborhood movement. If the generated domain is in the tabu table, it is regenerated until it does not exist in the tabu table. Decode and calculate the objective function values.

Step 2.6: The upper objective function is used as the evaluation function to evaluate the advantages and disadvantages of the candidate solution and update the solution.

Step 2.7: Update the tabu table, randomly select a feasible candidate solution to add to the tabu table, and remove the tabu of the first solution in the tabu table.

Step 2.8: Judge whether the maximum number of iterations of the algorithm is reached. If not, return to Step 2.3. If so, output and record the location and route selection results as well as the upper and lower level objective functions.

Step 3: Keep the number of emergency materials reserves in the set unchanged, update the set of emergency materials reserves, and return to Step 2. If there is no unselected set of emergency materials reserves containing the same number of reserves, then reduce the number of emergency materials reserves from the set of emergency materials reserves by 1, and return to Step 2.

Step 4: If the number of emergency materials reserves in the set is reduced to 1 and there is no unselected set of emergency materials reserves, the algorithm stops. The recorded results of location and route selection as well as the values of upper and lower objective functions are compared and analyzed, and the optimal location scheme and route selection scheme are obtained.

5. Results and Discussions

5.1. Introduction of a Numerical Example

To verify the effectiveness of the model and algorithm proposed in this paper, based on the real historical cases of the Bohai Sea, the example of this paper is designed according to the accident level, adding different priority emergency materials, accident point time windows, and other related information. Dalian Port, Yingkou Port, Tianjin Port, Qinhuangdao Port, Weifang Port, and Yantai Port are selected as candidate points for the construction of shore-based emergency materials reserves, and 40 collision and shipwreck accident points in the real historical cases in the Bohai Sea are selected as potential accident points. The attributes of the above two types of maritime accidents are similar, and collisions may lead to shipwrecks; thus, the types of materials needed are generally similar. Three levels of emergency materials are selected for rescue consumption, and some data are selected based on the optimal scheduling problem of emergency materials for major maritime accidents in [47]. Some of the information on the historical cases is shown in

Table 2. Information on some historical cases in the Bohai Sea area (data source: Maritime Safety Administration of the People’s Republic of China).

Date	Accident	Number of People Involved	Economic Loss (CNY 10,000)	Accident Level
9 November 2016	Collision accident between “Xiangping River Cargo 0306” and “Jihuanggang Fishing Boat 19”	3	92	Larger
18 December 2017	Collision accident between “Yongyue 66” and “Lushouyu 60687”	8	100	Larger
13 April 2017	Collision accident between “Haiyang 207” and “NanDongting 6”	2	625	General
18 September 2018	Collision accident between “C” and “W9099”	0	600	General
3 September 2019	Collision accident between “K” and “L23626”	1	200	General
22 September 2020	Collision accident between “XCH” and “Jileyu XXXXX”	0	30	Small

; the relevant data of candidate shore-based emergency materials reserves and accident points are shown in

Table 3. Data of candidate shore-based emergency materials reserves.

Number	Port	Longitude	Latitude	${\mathit{f}}_{\mathit{i}} (\mathbf{CNY} \mathrm{10,000})$
1	Dalian Port	121°39′17″	38°55′44″	20
2	Yingkou Port	122°06′00″	40°17′42″	18
3	Tianjin Port	117°42′05″	38°59′08″	20
4	Qinhuangdao Port	119°36′26″	39°54′24″	20
5	Weifang Port	120°19′05″	36°04′	18
6	Yantai Port	121°23′46.9″	37°32′51.8″	20

and

Table 4. Accident point data.

Number	Longitude	Latitude	${\mathit{D}}_{\mathbf{j}1} \left(\mathbf{Units}\right)$	${\mathbf{T}}_{\mathbf{E}\mathbf{j}1} \left(\mathbf{h}\right)$	${\mathbf{T}}_{\mathbf{L}\mathbf{j}1} \left(\mathbf{h}\right)$	Accident Level
1	118°06′1″	38°52′2″	8	1	7	Larger
2	119°13′.7	38°52′.3	6	2	8	General
3	119°29.6′	38°43.3′	6	2	8	General
4	117°51′.6	38°55′.5	5	2	8	General
5	119°08′.1	38°47′.3	0	0	0	Small
6	118°31′.9	38°42′.3	0	0	0	Small
7	120°25′.78	40°02′.95	7	1	7	Larger
8	120°50′.23	38°37′.44	8	1	7	Larger
9	121°33′15.54″	40°05′13.86″	7	1	7	Larger
10	121°48.80′	40°12.24′	6	1	7	Larger
11	120°10′.98	39°13′	8	1	7	Larger
12	120°07′.211	40°01′.560	7	1	7	Larger
13	121°12′.88	40°08′.59	5	2	8	General
14	120°48′00.96″	39°02′46.56″	6	2	8	General
15	121°08′49”.17	39°35′49”.18	5	2	8	General
16	120°35′48.42″	38°35′34.92″	4	2	8	General
17	121°09′	39°27′	5	2	8	General
18	121°01.08′	40°42.31′	5	2	8	General
19	122°01′.3	38°46′.2	6	2	8	General
20	118°11.39′	38°26.19′	8	1	7	Larger

. Due to space constraints, the relevant data of accident points only give the first-level emergency material demand and time windows of 20 accident points, and the distribution maps of candidate emergency materials reserves and potential accident points are shown in Figure 4. The main parameters of the model are set as $G=30$ units/ship, $V_{pqk}=25$ kn, $S_k=1$ CNY/n mile, $c_0=900$ CNY/ship, $T_k=0.05$ h/unit, $c_1=10$ CNY/h, $c_2=20$ CNY/h, $C_{ij1}=5$ CNY/unit, $C_{ij2}=4$ CNY/unit, and $C_{ij3}=3$ CNY/unit. When solving the problem, the relevant software is used to convert the longitude and latitude of the actual port location and the location of the accidents into Cartesian coordinates.

MATLAB R2017a (MathWorks Inc., Natick, The United States of America) was used to solve the model and algorithm designed in this paper and was run on a computer with an Intel(R) Core (TM) i7-10510U processor at 1.80 GHz with 16 GB RAM. The main parameters in the algorithm are the number of iterations $N$, ant population $m$, ant crawling speed $speed$, pheromone volatilization coefficient $\rho$, pheromone enhancement factor $Q$, tabu table length $L$, and so on. According to the characteristics of the numerical example in this paper and the results of multiple tests, the main parameters are set as $N=200$, $m=200$, $speed=0.05$, $\rho =0.5$, $Q=1$, and $L=10$.

5.2. Solution Result and Analysis

5.2.1. Algorithm Analysis

To verify the effectiveness of the proposed algorithm, the ant colony–tabu search algorithm and the ant colony algorithm without tabu search algorithm are used to solve the examples in this paper. The main parameters in the ant colony algorithm without tabu search algorithm are the number of iterations $N$, ant population $m$, ant crawling speed $speed$, pheromone volatilization coefficient $\rho$, pheromone enhancement factor $Q$, and so on, making $N=200$, $m=200$, $speed=0.05$, $\rho =0.5$, and $Q=1$.

When using the hybrid algorithm to experiment, it is found that when the number of shore-based emergency materials reserves is 1 under the current parameters, in all cases, three levels of emergency materials cannot be distributed to 40 accident points according to the priority of emergency materials within the specified time window, which can neither complete the distribution task nor accord with the actual situation of the Bohai Sea. When the number of shore-based emergency material reserves is 2–6, in most cases, the materials can be distributed to 40 accident points according to the priority of emergency materials within the specified time window. The sets of feasible emergency materials reserves and their results are shown in

Table 5. Ant colony–tabu search algorithm to obtain feasible set and its results.

Number of Reserves Constructed	Feasible Reserve Set	Upper Objective Function Value (CNY)	Lower Objective Function Value (CNY)
2	(1,4)	400,621	88,388.13
2	(1,5)	380,621	90,357.17
2	(2,3)	380,621	85,030.14
2	(2,5)	360,621	89,078.48
2	(3,6)	400,621	93,957.46
2	(4,6)	400,621	94,432.83
3	(1,2,3)	580,621	94,031.79
3	(1,2,4)	580,621	87,522.29
3	(1,3,4)	600,621	87,095.50
3	(1,3,5)	580,621	92,320.94
3	(1,3,6)	600,621	93,290.49
3	(1,4,5)	580,621	81,984.93
3	(1,4,6)	600,621	85,566.20
3	(2,3,4)	580,621	88,886.87
3	(2,4,5)	560,621	93,514.44
3	(2,4,6)	580,621	94,088.88
3	(2,5,6)	560,621	88,560.94
3	(3,4,6)	600,621	84,988.67
3	(3,5,6)	580,621	91,868.98
4	(1,2,3,4)	780,621	79,176.22
4	(1,2,3,5)	760,621	83,445.32
4	(1,2,3,6)	780,621	91,623.80
4	(1,2,4,5)	760,621	86,400.66
4	(1,2,5,6)	760,621	89,852.23
4	(1,3,4,5)	780,621	83,745.40
4	(1,3,4,6)	800,621	86,068.29
4	(1,3,5,6)	780,621	91,003.71
4	(1,4,5,6)	780,621	82,959.10
4	(2,3,4,5)	760,621	88,423.75
4	(2,3,4,6)	780,621	83,243.21
4	(2,3,5,6)	760,621	89,076.61
4	(2,4,5,6)	760,621	95,240.82
4	(3,4,5,6)	780,621	84,848.72
5	(1,2,3,4,5)	960,621	85,884.94
5	(1,2,3,4,6)	980,621	85,426.08
5	(1,2,3,5,6)	960,621	86,749.95
5	(1,2,4,5,6)	960,621	84,223.97
5	(1,3,4,5,6)	980,621	88,462.68
5	(2,3,4,5,6)	960,621	91,765.69
6	(1,2,3,4,5,6)	1160,621	86,693.65

.

Table 6. Ant colony algorithm to obtain feasible set and its result.

Number of Reserves Constructed	Feasible Reserve Set	Upper Objective Function Value (CNY)	Lower Objective Function Value (CNY)
3	(1,2,4)	580,621	99,227.50
5	(1,2,3,5,6)	960,621	103,418.47
6	(1,2,3,4,5,6)	1,160,621	87,152.38

shows the feasible sets of emergency materials reserves obtained by the ant colony algorithm and the results. In the course of the experiment, it is found that when the number of emergency materials reserves constructed is 1–2, the result obtained by the ant colony algorithm cannot distribute three levels of emergency materials to the accident points within the specified time window. When the number of emergency materials reserves constructed is 4, the ant colony algorithm cannot find the optimal solution under the current number of iterations. When the number of emergency materials reserves constructed is 3, 5, or 6, the number of feasible sets obtained by the ant colony algorithm is much less than that obtained by the ant colony–tabu search algorithm. When the set of feasible reserves is the same, the value of the lower objective function obtained by the ant colony–tabu search algorithm is smaller than that obtained by the ant colony algorithm.

Figure 5 shows the comparison of the average iterative times of the ant colony algorithm and ant colony–tabu search. It can be seen from the figure that the average iteration times are independent of the running times. In most cases, the average number of iterations of the ant colony–tabu search algorithm is larger than that of the ant colony algorithm. The figure shows that the ant colony algorithm combined with the tabu search algorithm has stronger optimization ability and effectively avoids the problem of falling into the local optimal solution. Based on the above analysis, the ant colony algorithm combined with the tabu search algorithm has stronger optimization ability than the ant colony algorithm and can avoid falling into local optimization and obtain a better global optimal solution quickly.

5.2.2. Solution Analysis

In bi-level programming, the upper and lower decision-makers influence each other, and the upper decision is considered more overall. The upper level gives the decision first; then, within the allowable scope of the upper-level decision, the lower level has the right to make independent decisions. Next, the upper level makes decisions in line with the overall interests according to the response of the lower level. The optimal decision is made based on the above principles. When the number of shore-based emergency materials reserves is 2, the optimal decision of the emergency management department is (2,5), that is, to build shore-based emergency material reserves in Yingkou Port and Weifang Port; the total cost of the upper level is CNY 360,621; and the total route planning the cost of commercial rescue unit is CNY 89,078.48. When the number of shore-based emergency materials reserves is 3, the optimal decision of the emergency management department is (2,5,6), that is, to build shore-based emergency materials reserves in Yingkou Port, Weifang Port, and Yantai Port, and the total cost of the upper level is CNY 560,621. The total cost of independent route planning by the commercial rescue unit is CNY 88,560.94. When the number of shore-based emergency materials reserves is 4, the optimal decision of the emergency management department is (1,2,3,5), that is, to build shore-based emergency materials reserves in Dalian Port, Yingkou Port, Tianjin Port, and Weifang Port; the total cost of the upper level is CNY 760,621; and the total cost of independent route planning of the commercial rescue unit is CNY 83,445.32. When the number of shore-based emergency materials reserves is 5, the optimal decision of the emergency management department is (1,2,4,5,6), that is, to build shore-based emergency materials reserves in Dalian Port, Yingkou Port, Qinhuangdao Port, Weifang Port, and Yantai Port; the total cost of the upper level is CNY 960,621; and the total cost of independent route planning of the commercial rescue unit is CNY 84,223.97. When the number of shore-based emergency materials reserves is 6, the optimal decision of the emergency management department is (1,2,3,4,5,6), that is, to build shore-based emergency materials reserves in Dalian Port, Yingkou Port, Tianjin Port, Qinhuangdao Port, Weifang Port, and Yantai Port; the total cost of the upper level is CNY 1,160,621; and the total cost of independent route planning of the commercial rescue unit is CNY 86,693.65. Among the above five decisions, when the number of emergency materials reserves constructed is 4, the total cost of the rescue unit planning routes is the lowest; however, when making its decision, the emergency management department should consider the maximization of its interests as a priority and choose the decision that minimizes total cost of the upper level. When the construction number of emergency materials reserves is 2, although the total cost of route planning of the lower rescue unit has increased, it is far less than the reduction of the construction cost of the upper location, which still achieves the goal of overall optimization of the emergency logistics system. Therefore, the optimal decision of the emergency management department is to build shore-based emergency materials reserves in Yingkou Port and Weifang Port. The location-routing result is shown in

Table 7. Location-routing result.

Reserves	Upper Total Cost (CNY)	Time Satisfaction Loss Cost (CNY)	Lower Total Cost (CNY)	Emergency Materials Distribution Cost (CNY)	Ship Dispatch Cost (CNY)	Shipping Cost (CNY)	Time Penalty Cost (CNY)
(2,5)	360,621	621	89,078.47	2494	64,800	7330.37	14,454.11

, the location-routing map is shown in Figure 6, and the emergency materials distribution route table (part) is shown in

Table 8. Emergency materials distribution route table (part).

Reserves	Accident Points of Reserves Service	Ship	Distribution Routes (Emergency Materials Level in Parentheses)
2	4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,29,31,32,34,37	1	0-7(1)-0
		2	0-15(1)-0
		3	0-37(1)-0
		4	0-11(1)-12(1)-0
		5	0-17(1)-19(1)-0
		6	0-13(1)-7(2)-0
		7	0-4(1)-17(2)-0
		8	0-34(1)-5(2)-0
		9	0-10(1)-19(2)-37(3)-0
		10	0-8(1)-32(1)-10(2)-0
5	1,2,3,20,21,22,23,24,25,26,27,28,30,33,35,36,38,39,40	1	0-1(1)-0
		2	0-24(1)-0
		3	0-26(1)-0
		4	0-39(1)-0
		5	0-35(1)-38(1)-0
		6	0-33(1)-20(1)-36(1)-30(1)-0
		7	0-3(1)-21(1)-23(1)-0
		8	0-27(1)-25(1)-2(1)-0
		9	0-22(1)-35(2)-40(2)-0
		10	0-28(1)-33(2)-2(2)-23(2)-24(3)-0

. The longest time for the commercial rescue unit to complete the distribution of first-level emergency materials is 7.8 h, the longest time for the second-level emergency materials is 14.6 h, and the longest time for the third-level emergency materials is 18.5 h.

The location of emergency materials reserves and the route optimization of emergency materials distribution are two important factors in the whole maritime emergency logistics system. The organic combination of the two to achieve overall optimization can avoid the limitation of considering only a single problem and realize the optimization of the whole maritime emergency logistics system. Maritime emergency logistics is jointly participated in and jointly decided by the emergency management department and commercial rescue unit. There is a game relationship between them, and their decisions affect each other. The emergency management department should give priority to maximizing its interests when considering the number and location of emergency materials reserves. Within the allowable range, the rescue unit will independently plan the routes to achieve the distribution goal, and the emergency management department will make decisions in line with the overall interests according to the route feedback of the rescue unit.

When the construction number of the emergency materials reserves is the same and the construction cost is the same, the emergency management department directly considers the interests of the rescue unit and selects the decision with the lowest cost at the lower level. When the number of emergency materials reserves constructed is the same and the construction cost is not much different, the emergency management department will consider the interests of the rescue unit and choose the option with the lowest lower and upper costs as small as possible to achieve overall optimization. For example, when the number of emergency materials reserves constructed is 4 in Table 5, the decision is made between the reserve sets of (1,2,3,4) and (2,4,5,6). When the number of emergency material reserve construction is different, the construction cost will vary greatly. However, the lower cost difference is not large at this time; therefore, the emergency management department gives priority to the decision to maximize its interests (such as the optimal decision with the number of reserves constructed being 2 and 4 in Table 5).

The maritime emergency rescue has strong regional characteristics, as can be seen from Figure 6. When the rescue unit plans the routes, they often distribute emergency materials according to the nearest principle. However, because different levels of emergency materials in this study can be mixed, cross-regional distribution can also exist on the premise of meeting the time window limit. The results show that the distribution cost of the rescue unit can be reduced as much as possible. The goal of this paper is to optimize the location of the emergency materials reserves and the distribution routes of emergency materials cooperatively. The overall layout of the maritime emergency logistics system should be carried out. The situation of cross-regional distribution is also conducive to the effective development of maritime emergency work. It can ensure that those accident points can also be effectively rescued when the emergency materials reserve nearest to the accident point is busy.

5.3. Management Implications

This study presents the following management implications and recommendations for relevant policies:

• For the emergency management department of the upper decision-maker, the emergency management department has the priority decision-making power. This department’s decision should consider the benefits of the commercial rescue unit of the lower-level decision-makers while maximizing their benefits to achieve global optimization. Under the premise of meeting the needs of the accident points, the construction number of emergency materials reserves does not need to be high; otherwise, excessive construction of emergency materials reserves will lose the significance of centralized distribution and increase unnecessary construction costs. When there is little difference in the lower cost and there is a large difference in the upper cost, priority can be given to the benefit maximization of the upper level. When the upper cost is the same or there is little difference, while the lower cost is significantly reduced, priority can be given to the benefits of the lower level to achieve global optimization.
• For the commercial rescue unit of the lower-level decision-maker, within the scope permitted by the emergency management department, the rescue unit independently plans the distribution routes of emergency materials to (a) distribute multi-level emergency materials to the accident points within the specified time window and (b) feed the route scheme back to the emergency management department in time. When planning the routes, priority should be given to the regionality of the accident points, and emergency materials should be distributed according to the principle of proximity; however, there can also be a cross-regional distribution within the scope of the time window.
• All participating units in the maritime emergency logistics system shall communicate and coordinate to (a) scientifically and reasonably select the location of the maritime emergency materials reserves and (b) plan the distribution routes of emergency materials to ensure that, in case of a maritime accident, the emergency materials can be delivered to the accident point in time and reliably, provide rescue capacity, control the impact of the accident to the minimum, reduce various losses caused by sudden maritime disasters, and effectively improve the emergency service capability of the maritime emergency logistics system.

6. Conclusions

This paper studies the problem of joint participation and joint decision-making of multi-level decision agents in MEMD-LRP. Using the method of bi-level programming, under the conditions of considering the time window and the priority of emergency materials distribution, the collaborative optimization of the location of shore-based emergency materials reserves and multi-level emergency materials distribution routes in the maritime emergency logistics system is realized, and the optimal decision for the maritime emergency logistics system is obtained.

This study is based on the scenario of parameter determination. In the future, it is planned to further consider the uncertainty of accident point demands and the uncertainty of maritime transportation time under the influence of wind and waves for modeling and analysis. In addition, based on a single type of ship transport, the mixed transport of multiple types of ships and the multimodal transport environment including aircraft and ships can be studied. In addition, future research can consider the scenario of the coexistence of public welfare relief and commercial rescue.