The Research on the Interactions between the Emerging and Developed Markets: From Region and Structural Break Perspectives
Abstract
:1. Introduction
2. Literature Review
3. Methodology
4. Data and Descriptive Statistics
5. Empirical Results
5.1. The Unit Root Test and the Cointegration Test
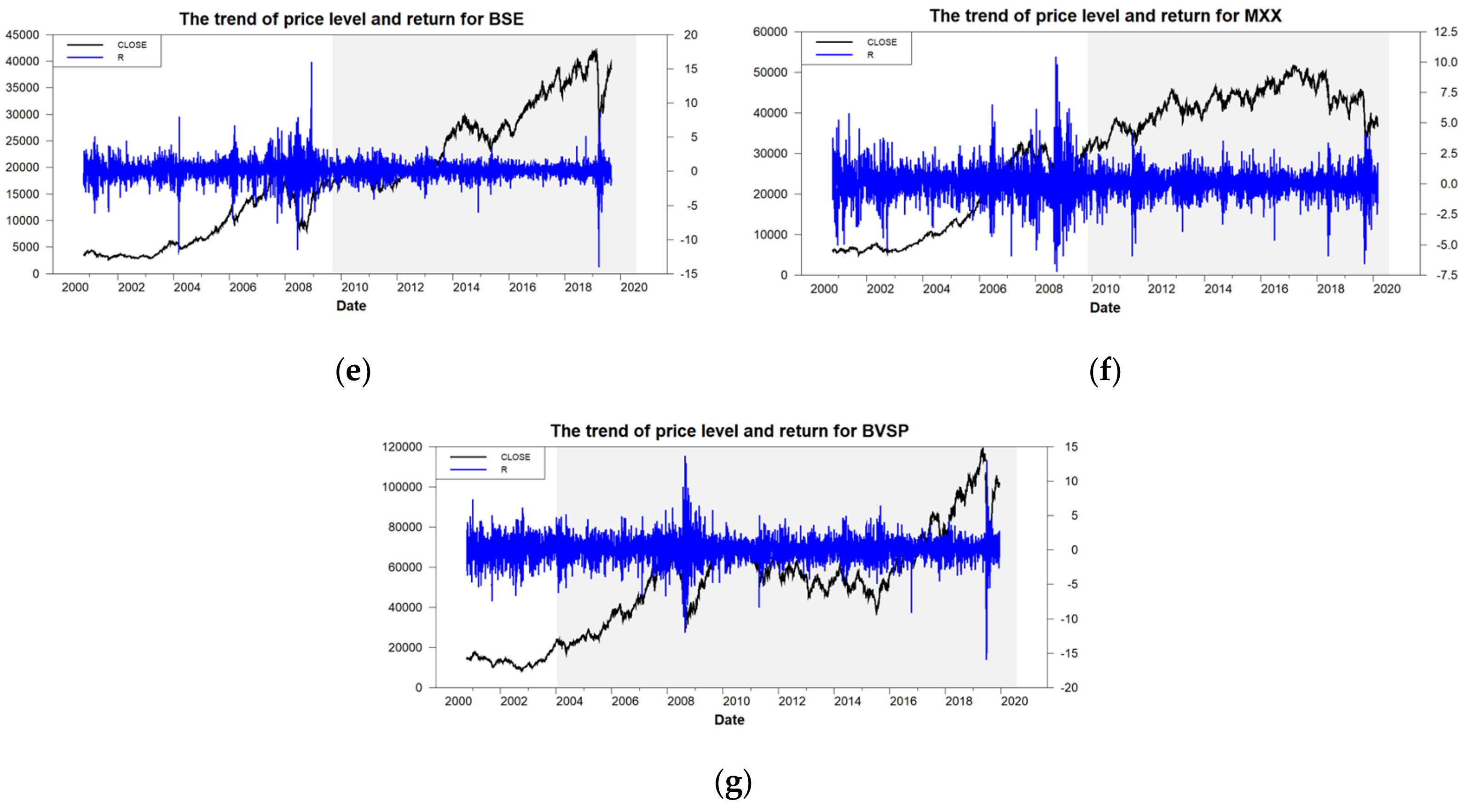
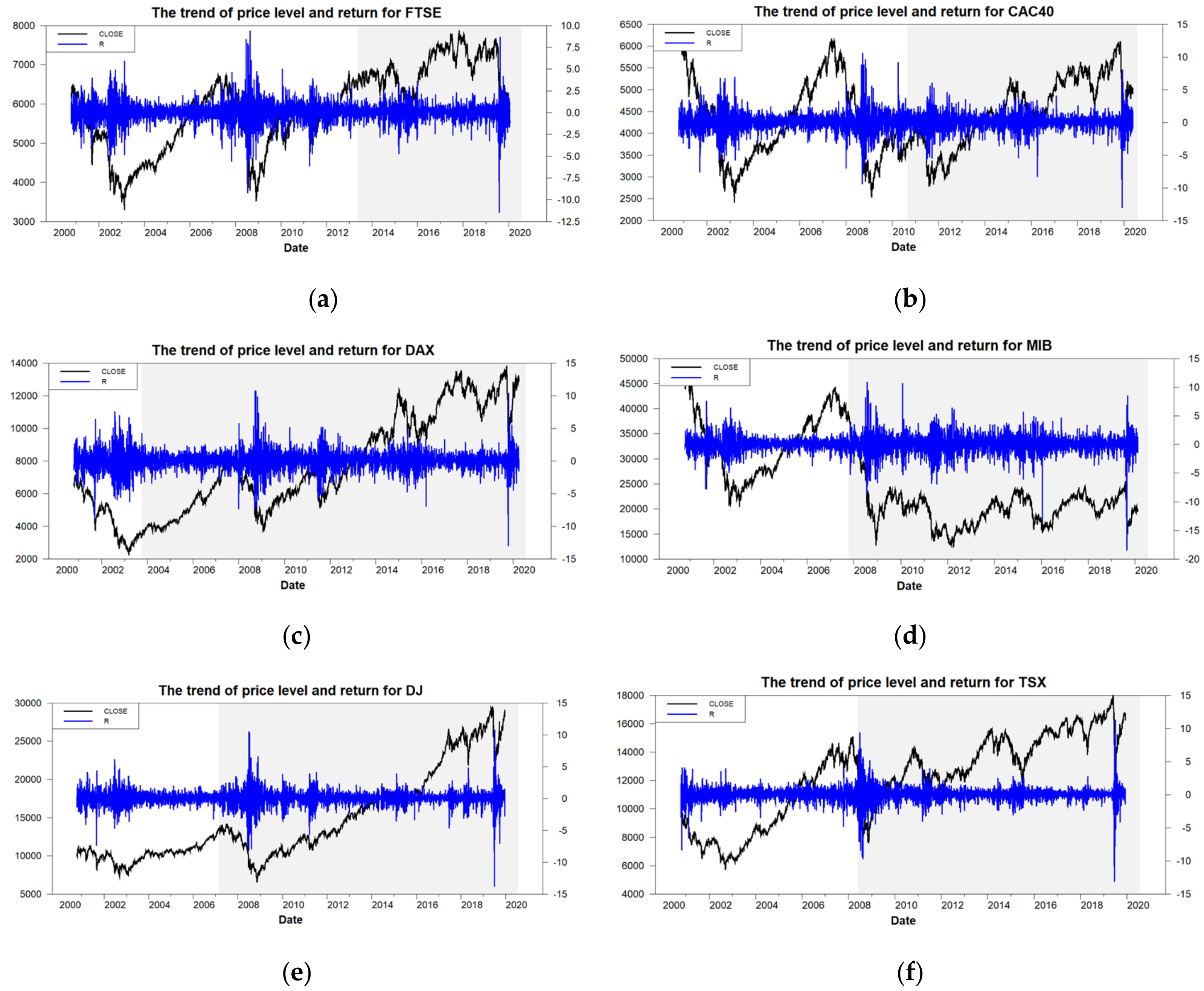
5.2. Confirm the Appropriateness of the Subperiods’ Settings on the B-EGARCH-SB Model
5.3. The Interactions between the Emerging and Developed Markets
5.4. The Impact of a Structural Break on the Interactions between the Emerging and Developed Markets
6. Discussion
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y. A test for volatility spillover with application to exchange rates. J. Econom. 2001, 103, 183–224. [Google Scholar] [CrossRef]
- Wei, K.C.J.; Liu, Y.J.; Yang, C.C.; Chaung, G.S. Volatility and price change spillover effects across the developed and emerging markets. Pac. Basin Financ. J. 1995, 3, 113–136. [Google Scholar] [CrossRef]
- Ng, A. Volatility spillover effects from Japan and the US to the Pacific–Basin. J. Int. Money Financ. 2000, 19, 207–233. [Google Scholar] [CrossRef]
- Miyakoshi, T. Spillovers of stock return volatility to Asian equity markets from Japan and the US. J. Int. Financ. Mark. Instig. Money 2003, 13, 383–399. [Google Scholar] [CrossRef]
- Wang, P.; Wang, P. Price and volatility spillovers between the Greater China Markets and the developed markets of US and Japan. Glob. Financ. J. 2010, 21, 304–317. [Google Scholar] [CrossRef]
- Lee, Y.H. Global and regional range-based volatility spillover effects. Emerg. Mark. Rev. 2013, 14, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Giles, D.E. Modelling volatility spillover effects between developed stock markets and Asian emerging stock markets. Int. J. Financ. Econ. 2015, 20, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Vo, X.V.; Ellis, C. International financial integration: Stock return linkages and volatility transmission between Vietnam and advanced countries. Emerg. Mark. Rev. 2018, 36, 19–27. [Google Scholar] [CrossRef]
- Bhar, R.; Nikolova, B. Return, volatility spillovers and dynamic correlation in the BRIC equity markets: An analysis using a bivariate EGARCH framework. Glob. Financ. J. 2009, 19, 203–218. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, W.; Zhang, J. Volatility spillovers between the Chinese and world equity markets. Pac. Basin Financ. J. 2012, 20, 247–270. [Google Scholar] [CrossRef]
- Allen, D.E.; Amram, R.; McAleer, M. Volatility spillovers from the Chinese stock market to economic neighbours. Math. Comput. Simul. 2013, 94, 238–257. [Google Scholar] [CrossRef] [Green Version]
- Gilenko, E.; Fedorova, E. Internal and external spillover effects for the BRIC countries: Multivariate GARCH-in-mean approach. Res. Int. Bus. Financ. 2014, 31, 32–45. [Google Scholar] [CrossRef]
- Yavas, B.F.; Rezayat, F. Country ETF returns and volatility spillovers in emerging stock markets, Europe and USA. Int. J. Emerg. Mark. 2016, 11, 419–437. [Google Scholar] [CrossRef]
- Majdoub, J.; Sassi, S.B. Volatility spillover and hedging effectiveness among China and emerging Asian Islamic equity indexes. Emerg. Mark. Rev. 2017, 31, 16–31. [Google Scholar] [CrossRef]
- McIver, R.P.; Kang, S.H. Financial crises and the dynamics of the spillovers between the U.S. and BRICS stock markets. Res. Int. Bus. Financ. 2020, 54, 101276. [Google Scholar] [CrossRef]
- Do, A.; Powell, R.; Yong, J.; Singh, A. Time-varying asymmetric volatility spillover between global markets and China’s A, B and H-shares using EGARCH and DCC-EGARCH models. N. Am. J. Econ. Financ. 2020, 54, 101096. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, B.; Pandey, A. Price and volatility spillovers across North American, European and Asian stock markets. Int. Rev. Financ. Anal. 2010, 19, 55–64. [Google Scholar] [CrossRef]
- Beirne, J.; Caporale, G.M.; Schulze-Ghattas, M.; Spagnolo, N. Global and regional spillovers in emerging stock markets: A multivariate GARCH-in-mean analysis. Emerg. Mark. Rev. 2010, 11, 250–260. [Google Scholar] [CrossRef] [Green Version]
- Chevallier, J.; Nguyen, D.K.; Siverskog, J.; Uddin, G.S. Market integration and financial linkages among stock markets in Pacific Basin countries. J. Empir. Financ. 2018, 46, 77–92. [Google Scholar] [CrossRef]
- Ballester, L.; Escrivá, A.M.; González-Urteaga, A. The Nexus between Sovereign CDS and Stock Market Volatility: New Evidence. Mathematics 2021, 9, 1201. [Google Scholar] [CrossRef]
- Su, X.; Liu, Z. Sector Volatility Spillover and Economic Policy Uncertainty: Evidence from China’s Stock Market. Mathematics 2021, 9, 1411. [Google Scholar] [CrossRef]
- Weber, E.; Zhang, Y. Common influences, spillover and integration in Chinese stock markets. J. Empir. Financ. 2012, 19, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Green, S.P. Equity Politics and Market Institutions: The Development of Stock Market Policy and Regulation in China, 1984–2003. 2004. Available online: http://ssrn.com/abstract=509342 (accessed on 1 March 2022).
- Eizaguirre, J.C.; Biscarri, J.G.; Hidalgo, F.P.D.G. Structural changes in volatility and stock market development: Evidence for Spain. J. Bank Financ. 2004, 28, 1745–1773. [Google Scholar] [CrossRef]
- Baba, Y.; Engle, R.F.; Kraft, D.K.; Kroner, K. Multivariate Simultaneous Generalized ARCH. Unpublished Manuscript, University of California. 1999. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.27.1240 (accessed on 1 March 2022).
- Engle, R.F.; Kroner, K.F. Multivariate simultaneous generalized ARCH. Econom. Theory 1995, 11, 122–150. Available online: https://www.jstor.org/stable/3532933 (accessed on 1 March 2022). [CrossRef]
- Su, J.B. The interrelation of stock markets in China, Taiwan and Hong Kong and their constructional portfolio’s value-at-risk estimate. J. Risk Model Valid. 2014, 8, 69–127. [Google Scholar] [CrossRef]
- Moschini, G.C.; Myers, R.J. Testing for constant hedge ratios in commodity markets: A multivariate GARCH approach. J. Empir. Financ. 2002, 9, 589–603. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–419. Available online: https://www.jstor.org/stable/2350970 (accessed on 1 March 2022). [CrossRef]
- Christie, A. The stochastic behavior of common stock variances: Value, leverage, and interest rate effects. J. Financ. Econ. 1982, 10, 407–432. [Google Scholar] [CrossRef]
- Su, J.B. Empirical analysis of long memory, leverage, and distribution effects for stock market risk estimates. N. Am. J. Econ. Financ. 2014, 30, 1–39. [Google Scholar] [CrossRef]
- Braione, M.; Scholtes, N.K. Forecasting value-at-risk under different distributional assumptions. Econometrics 2016, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Su, J.B.; Hung, K. The assessment of the United States quantitative easing policy: Evidence from global stock markets. Int. J. Financ. Econ. 2017, 22, 319–340. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and testing linear models with multiple structural changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. A test for normality of observations and regression residuals. Int. Stat. Rev. 1987, 55, 163–172. [Google Scholar] [CrossRef]
- Fuller, W.A. Introduction to Statistical Time Series; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Osterwald-Lenum, M. A note with quantiles of the asymptotic distribution of the maximum likelihood cointegration rank test statistics. Oxf. Bull. Econ. Stat. 1992, 53, 461–471. Available online: https://EconPapers.repec.org/RePEc:bla:obuest:v:54:y:1992:i:3:p:461-72 (accessed on 1 March 2022). [CrossRef]
- Johnson, C.R. Positive definite matrices. Am. Math. Mon. 1970, 77, 259–264. [Google Scholar] [CrossRef]
- Su, J.B. How do financial features affect volatility forecasts? Evidence from the oil market and other markets. Asia Pac. Manag. Rev. 2018, 23, 95–107. [Google Scholar] [CrossRef]


| Mean | SD | Max. | Min. | SK | KUR | J-B | Obs. | ||
|---|---|---|---|---|---|---|---|---|---|
| Panel A. The overall period | |||||||||
| XU100 | 0.0626 | 2.3730 | 17.764 | −20.330 | −0.3468 c | 9.712 c | 13,993 c | 1074 c | 3542 |
| RTSI | 0.0624 | 2.4110 | 17.764 | −20.779 | −0.4155 c | 9.625 c | 13,776 c | 1164 c | 3542 |
| JKSE | 0.0713 | 1.6112 | 13.624 | −12.925 | −0.3621 c | 11.093 c | 18,239 c | 932.9 c | 3542 |
| SSE | 0.0277 | 1.9904 | 45.160 | −12.763 | 3.1167 c | 78.069 c | 905,235 c | 8.67 | 3542 |
| BSE | 0.0654 | 1.7302 | 14.412 | −17.183 | −0.5450 c | 11.082 c | 18,302 c | 776.6 c | 3542 |
| MXX | 0.0526 | 1.4561 | 10.153 | −16.277 | −0.4461 c | 9.871 c | 14,499 c | 1306 c | 3542 |
| BVSP | 0.0540 | 2.1034 | 13.022 | −18.749 | −0.4944 c | 7.284 c | 7976 c | 2028 c | 3542 |
| FTSE | −0.0004 | 1.3964 | 10.870 | −11.512 | −0.3793 c | 8.767 c | 11,428 c | 2985 c | 3542 |
| CAC40 | −0.0057 | 1.6802 | 11.285 | −13.098 | −0.3133 c | 6.508 c | 6309 c | 2383 c | 3542 |
| DAX | 0.0185 | 1.7380 | 11.588 | −13.054 | −0.3638 c | 6.003 c | 5396 c | 2335 c | 3542 |
| MIB | −0.0224 | 1.8261 | 13.761 | −18.541 | −0.8237 c | 10.102 c | 15,463 c | 1144 c | 3542 |
| DJ | 0.0270 | 1.3578 | 10.764 | −12.577 | −0.6376 c | 11.107 c | 18,449 c | 4064 c | 3542 |
| TSX | 0.0126 | 1.2871 | 11.294 | −16.998 | −1.4318 c | 23.325 c | 81,506 c | 2154 c | 3542 |
| N225 | 0.0111 | 1.7027 | 11.805 | −12.715 | −0.3873 c | 6.035 c | 5464 c | 1444 c | 3542 |
| Panel B. The pre-SB period | |||||||||
| XU100 | 0.0855 | 2.9423 | 17.764 | −20.330 | −0.2487 c | 7.4985 c | 3943.89 c | 410.3 c | 1676 |
| RTSI | 0.1027 | 3.0401 | 17.764 | −18.992 | −0.1873 c | 6.8078 c | 2591.69 c | 544.0 c | 1338 |
| JKSE | 0.1174 | 1.8733 | 13.624 | −12.925 | −0.2982 c | 9.5211 c | 6984.90 c | 390.7 c | 1842 |
| SSE | 0.0180 | 1.9350 | 12.950 | −12.763 | −0.1973 c | 5.1914 c | 3299.20 c | 771.6 c | 2921 |
| BSE | 0.0910 | 2.0984 | 14.412 | −17.183 | −0.5462 c | 8.0961 c | 4527.30 c | 213.7 c | 1628 |
| MXX | 0.1012 | 1.7349 | 10.153 | −16.277 | −0.3997 c | 8.9867 c | 5596.33 c | 499.0 c | 1650 |
| BVSP | 0.0680 | 2.3039 | 12.933 | −12.225 | 0.0110 | 3.0426 c | 235.31 c | 8.542 | 610 |
| FTSE | 0.0033 | 1.4760 | 10.870 | −10.327 | −0.1260 b | 6.8439 c | 4395.25 c | 2491 c | 2249 |
| CAC40 | −0.0287 | 1.8192 | 11.285 | −11.476 | 0.0139 | 5.2222 c | 2037.51 c | 1656 c | 1793 |
| DAX | −0.1111 | 2.4495 | 8.005 | −9.790 | −0.0921 | 1.3016 c | 40.39 c | 226.6 c | 561 |
| MIB | −0.0058 | 1.4282 | 10.498 | −12.900 | −0.3739 c | 8.9981 c | 4385.43 c | 548.8 c | 1291 |
| DJ | 0.0154 | 1.2201 | 6.154 | −7.396 | −0.0752 | 3.6927 c | 667.59 c | 580.4 c | 1173 |
| TSX | 0.0252 | 1.1025 | 4.709 | −10.482 | −1.0141 c | 8.3560 c | 4300.71 c | 203.2 c | 1396 |
| N225 | −0.0479 | 1.8132 | 7.883 | −7.020 | 0.0742 | 0.9694 c | 26.57 c | 16.03 | 663 |
| Panel C. The post-SB period | |||||||||
| XU100 | 0.0419 | 1.7075 | 6.919 | −11.063 | −0.697 c | 4.069 c | 1438.6 c | 134.9 c | 1866 |
| RTSI | 0.0379 | 1.9320 | 9.727 | −20.779 | −0.911 c | 9.806 c | 9136.8 c | 69.7 c | 2204 |
| JKSE | 0.0214 | 1.2661 | 9.704 | −9.635 | −0.650 c | 9.138 c | 6035.4 c | 740.8 c | 1700 |
| SSE | 0.0732 | 2.2340 | 45.160 | −6.712 | 13.213 c | 268.109 c | 1,878,04 c | 0.682 | 621 |
| BSE | 0.0436 | 1.3399 | 11.573 | −11.327 | −0.459 c | 12.927 c | 13394 c | 724.1 c | 1914 |
| MXX | 0.0102 | 1.1583 | 5.618 | −7.336 | −0.625 c | 4.760 c | 1910.2 c | 898.9 c | 1892 |
| BVSP | 0.0511 | 2.0597 | 13.022 | −18.749 | −0.640 c | 8.561 c | 9154.5 c | 2203 c | 2932 |
| FTSE | −0.0071 | 1.2464 | 8.666 | −11.512 | −1.1052 c | 14.179 c | 11,095 c | 932.2 c | 1293 |
| CAC40 | 0.0177 | 1.5248 | 8.056 | −13.098 | −0.8544 c | 8.409 c | 5366 c | 882.3 c | 1749 |
| DAX | 0.0429 | 1.5678 | 11.588 | −13.054 | −0.4558 c | 8.356 c | 8776 c | 1764 c | 2981 |
| MIB | −0.0319 | 2.0195 | 13.761 | −18.541 | −0.8759 c | 9.065 c | 7996 c | 672.3 c | 2251 |
| DJ | 0.0328 | 1.4212 | 10.764 | −12.577 | −0.8113 c | 12.803 c | 16,440 c | 2930 c | 2369 |
| TSX | 0.0044 | 1.3943 | 11.294 | −16.998 | −1.5275 c | 25.682 c | 59,810 c | 1449 c | 2146 |
| N225 | 0.0247 | 1.6763 | 11.805 | −12.715 | −0.5169 c | 7.611 c | 7078 c | 1377 c | 2879 |
| ADF | PP | |||||||
|---|---|---|---|---|---|---|---|---|
| Price Level | First Difference | Price Level | First Difference | |||||
| No Trend | Trend | No Trend | Trend | No Trend | Trend | No Trend | Trend | |
| XU100 | −1.19 | −2.68 | −18.40 c | −18.40 c | −1.11 | −2.57 | −58.18 c | −58.18 c |
| RTSI | −1.14 | −2.61 | −15.21 c | −15.21 c | −1.11 | −2.58 | −58.52 c | −58.52 c |
| JKSE | −1.56 | −1.28 | −11.56 c | −11.62 c | −1.71 | −0.85 | −57.50 c | −57.52 c |
| SSE | −1.34 | −2.38 | −13.71 c | −13.74 c | −1.01 | −1.97 | −59.48 c | −59.48 c |
| BSE | −1.11 | −1.99 | −23.29 c | −23.30 c | −1.06 | −1.99 | −58.90 c | −58.89 c |
| MXX | −1.82 | −0.70 | −16.57 c | −16.66 c | −2.09 | −0.68 | −55.56 c | −55.62 c |
| BVSP | −1.22 | −2.09 | −16.49 c | −16.49 c | −1.09 | −1.91 | −59.97 c | −59.96 c |
| FTSE | −1.96 | −3.39 a | −14.54 c | −14.54 c | −2.08 | −3.42 b | −60.88 c | −60.87 c |
| CAC40 | −2.47 | −2.92 | −29.40 c | −29.42 c | −2.59 a | −3.01 | −59.63 c | −59.64 c |
| DAX | −0.83 | −3.60 b | −20.28 c | −20.30 c | −0.79 | −3.41 b | −58.63 c | −58.63 c |
| MIB | −2.53 | −2.61 | −16.54 c | −16.56 c | −2.36 | −2.51 | −59.52 c | −59.52 c |
| DJ | −0.30 | −2.55 | −13.58 c | −13.61 c | −0.39 | −2.61 | −63.22 c | −63.23 c |
| TSX | −1.26 | −2.85 | −15.30 c | −15.30 c | −1.17 | −3.25 a | −59.20 c | −59.19 c |
| N225 | −1.21 | −2.49 | −60.25 c | −60.26 c | −1.15 | −2.46 | −60.27c | −60.29 c |
| Xu-ft | 12.126 | 0.425 | 12.551 | 0.425 | rt-ft | 19.102 b | 0.502 | 19.604 a | 0.502 |
| Xu-ca | 10.621 | 1.013 | 11.634 | 1.013 | rt-ca | 11.781 | 0.287 | 12.068 | 0.287 |
| Xu-da | 14.374 a | 0.416 | 14.791 | 0.416 | rt-da | 21.360 c | 0.017 | 21.377 b | 0.017 |
| Xu-mi | 7.333 | 1.616 | 8.949 | 1.616 | rt-mi | 6.693 | 0.653 | 7.345 | 0.653 |
| Xu-dj | 7.084 | 0.134 | 7.218 | 0.134 | rt-dj | 12.363 | 0.048 | 12.411 | 0.048 |
| Xu-ts | 12.943 | 0.444 | 13.387 | 0.444 | rt-ts | 21.851 c | 0.258 | 22.109 b | 0.258 |
| Xu-n2 | 7.654 | 0.614 | 8.268 | 0.614 | rt-n2 | 8.973 | 0.028 | 9.001 | 0.028 |
| jk-ft | 15.289 a | 1.052 | 16.341 | 1.052 | ss-ft | 6.765 | 2.359 | 9.124 | 2.359 |
| jk-ca | 10.004 | 1.985 | 11.988 | 1.985 | ss-ca | 12.592 | 2.451 | 15.043 | 2.451 |
| jk-da | 9.408 | 1.452 | 10.860 | 1.452 | ss-da | 6.614 | 0.587 | 7.201 | 0.587 |
| jk-mi | 7.404 | 2.037 | 9.441 | 2.037 | ss-mi | 10.215 | 1.506 | 11.721 | 1.506 |
| jk-dj | 3.885 | 3.189 | 7.074 | 3.189 | ss-dj | 5.121 | 0.199 | 5.320 | 0.199 |
| jk-ts | 9.374 | 1.079 | 10.453 | 1.079 | ss-ts | 7.366 | 1.488 | 8.854 | 1.488 |
| jk-n2 | 5.066 | 2.471 | 7.538 | 2.471 | ss-n2 | 8.225 | 2.160 | 10.385 | 2.160 |
| bs-ft | 14.098 a | 0.130 | 14.228 | 0.130 | mx-ft | 13.717 | 3.169 | 16.886 | 3.169 |
| bs-ca | 11.837 | 0.107 | 11.944 | 0.107 | mx-ca | 9.721 | 4.552 | 14.272 | 4.552 |
| bs-da | 16.218 b | 0.032 | 16.250 | 0.032 | mx-da | 6.352 | 4.054 | 10.406 | 4.054 |
| bs-mi | 7.205 | 0.187 | 7.392 | 0.187 | mx-mi | 7.615 | 3.890 | 11.504 | 3.890 |
| bs-dj | 7.482 | 0.001 | 7.484 | 0.001 | mx-dj | 7.689 | 1.754 | 9.443 | 1.754 |
| bs-ts | 12.895 | 0.111 | 13.007 | 0.111 | mx-ts | 9.562 | 2.920 | 12.482 | 2.920 |
| bs-n2 | 7.390 | 0.042 | 7.432 | 0.042 | mx-n2 | 5.437 | 3.950 | 9.387 | 3.950 |
| bv-ft | 7.063 | 0.529 | 7.592 | 0.529 | |||||
| bv-ca | 10.541 | 0.659 | 11.200 | 0.659 | |||||
| bv-da | 4.408 | 0.299 | 4.706 | 0.299 | |||||
| bv-mi | 8.275 | 0.646 | 8.921 | 0.646 | |||||
| bv-dj | 3.251 | 0.027 | 3.278 | 0.027 | |||||
| bv-ts | 5.654 | 0.630 | 6.284 | 0.630 | |||||
| bv-n2 | 4.673 | 0.314 | 4.987 | 0.314 | |||||
| XU100-FTSE | XU100-CAC40 | XU100-DAX | XU100-MIB | XU100-DJ | XU100-TSX | XU100-N225 | Sum | |
|---|---|---|---|---|---|---|---|---|
| Pre-SB | 2000/10/16~ 2010/01/13 | - | 2000/10/16~ 2003/10/15 | 2000/10/16~ 2007/10/09 | 2000/10/16~ 2007/02/27 | 2000/10/16~ 2008/05/28 | 2000/10/16~ 2004/05/12 | |
| Post-SB | 2013/05/15~ 2020/07/28 | - | 2010/01/13~ 2020/07/28 | 2010/01/13~ 2020/07/28 | 2010/01/13~ 2020/07/28 | 2010/01/13~ 2020/07/28 | 2010/01/13~ 2020/07/28 | |
| LL | −12,319.22 (−12,307.01) | − | −13,202.77 (−13,181.63) | −13,373.04 (−13,341.68) | −12,269.78 (−12,245.46) | −11,934.13 (−11,909.50) | −13,600.69 (−13,557.08) | |
| LR | 23.98 b | - | 42.28 c | 62.72 c | 48.64 c | 49.26 c | 87.22 c | 6 |
| MAE | 2.7053 (2.7001) | - | 3.1172(3.0914) | 3.2339(3.2123) | 2.4365(2.4398) | 2.4387(2.4466) | 2.7952(2.7858) | 2(4) |
| RMSE | 7.7184 (7.7165) | - | 8.5565(8.5490) | 9.9569(9.9417) | 7.4856(7.4852) | 8.3094(8.2929) | 8.0160(8.0231) | 1(5) |
| () | 1.9570 (4.2445) | - | 8.7291 b(1.4409) | 3.1123(2.0789) | 0.0136 c(2.0214) | 5.9070 c(5.7799 a) | 1.1849(4.2360) | 3(1) |
| () | 10.793 c (5.2046a) | - | 48.013c(8.0897b) | 62.611 c(30.595 c) | 12.158 c(7.9315 b) | 5.3624 a (43.397 c) | 144.58 c(2.1254) | 6(5) |
| 7.3077 b | - | 1.3172 | 90.295 c | 16.323 c | 9.1210 b | 25.413 c | 5 | |
| () | 3.4005 (5.2454 a) | - | 0.5926(2.2128) | 3.1377(13.655 c) | 0.7000(2.2049) | 1.5030(7.9256 b) | 5.3099 a (12.373 c) | 1(4) |
| () | 2.593 (1.961) | - | 2.638(1.758) | 3.245(1.709) | 2.164(1.340) | 2.103(0.445) | 2.300(1.377) | |
| RTSI-FTSE | RTSI-CAC40 | RTSI-DAX | RTSI-MIB | RTSI-DJ | RTSI-TSX | RTSI-N225 | Sum | |
| Pre-SB | 2000/10/16~ 2008/01/23 | 2000/10/16~ 2008/01/23 | 2000/10/16~ 2003/10/15 | 2000/10/16~ 2007/10/09 | 2000/10/16~ 2007/02/27 | 2000/10/16~ 2008/01/23 | 2000/10/16~ 2004/05/12 | |
| Post-SB | 2013/05/15~ 2020/07/28 | 2010/09/01~ 2020/07/28 | 2008/01/23~ 2020/07/28 | 2008/01/23~ 2020/07/28 | 2008/01/23~ 2020/07/28 | 2008/05/28~ 2020/07/28 | 2008/01/23~ 2020/07/28 | |
| LL | −12,692.4 (−12,677.8) | −13,421.9 (−13,404.8) | −13,555.5 (−13,541.4) | −13,712.1 (−13,693.3) | −12,480.5 (−12,472.5) | −12,162.5 (−12,149.9) | −13,784.6 (−13,745.1) | |
| LR | 29.14 b | 34.3 c | 28.12 b | 37.46 c | 16.06 | 25.24 b | 78.98 c | 6 |
| MAE | 2.0570(2.0579) | 2.3111(2.3291) | 2.3750(2.4002) | 2.4634 (2.4646) | 2.0762(2.0898) | 2.0460(2.0568) | 2.3690(2.3584) | 6(1) |
| RMSE | 5.5180(5.5205) | 6.2396(6.2402) | 6.5154(6.5095) | 6.8188 (6.8214) | 5.7304(5.7346) | 5.9208(5.9163) | 6.0970(6.0756) | 4(3) |
| () | 2.6214(0.9844) | 1.9834(2.0542) | 0.1055(1.3241) | 9.3509 c(2.7657) | 0.7063(4.7977 a) | 1.4306(1.2099) | 14.752 c(0.1911) | 2(1) |
| () | 3.1115(22.913 c) | 46.630 c(4.7351 a) | 32.234 c(10.450 c) | 22.535 c(18.628 c) | 5.2858 a(5.7721 a) | 6.2926 b(6.0103 b) | 95.933 c(5.6198 a) | 6(7) |
| 1.1522 | 1.4935 | 0.9593 | 0.7305 | 2.1496 | 2.4627 | 5.1074 a | 1 | |
| () | 1.7919(2.3733) | 2.5016(0.08104) | 1.4701(0.6377) | 1.2448(1.6234) | 1.7917(3.3834) | 5.2013 a(11.794 c) | 0.5440(10.109 c) | 1(2) |
| () | 2.701(1.934) | 2.826(2.124) | 2.459(2.259) | 3.096(2.386) | 2.794(1.450) | 2.556(0.473) | 2.726(1.305) | |
| JKSE-FTSE | JKSE-CAC40 | JKSE-DAX | JKSE-MIB | JKSE-DJ | JKSE-TSX | JKSE-N225 | Sum | |
| Pre-SB | 2000/10/16~ 2011/01/12 | 2000/10/16~ 2010/09/01 | 2000/10/16~ 2003/10/15 | 2000/10/16~ 2007/10/09 | 2000/10/16~ 2007/02/27 | 2000/10/16~ 2008/05/28 | 2000/10/16~ 2004/05/12 | |
| Post-SB | 2013/05/15~ 2020/07/28 | 2011/01/12~ 2020/07/28 | 2011/01/12~ 2020/07/28 | 2011/01/12~ 2020/07/28 | 2011/01/12~ 2020/07/28 | 2011/01/12~ 2020/07/28 | 2011/01/12~ 2020/07/28 | |
| LL | −10,986.02 (−10,971.85) | −11,722.61 (−11,709.63) | −11,864.14 (−11,839.05) | −12,049.52 (−12,026.59) | −10,794.98 (−10,773.99) | −10,441.79 (−10,419.10) | −11,972.22 (−11,952.79) | |
| LR | 28.34 b | 25.96 b | 50.18 c | 45.86 c | 41.98 c | 45.38 c | 38.86 c | 7 |
| MAE | 1.5747(1.5803) | 1.8910(1.8937) | 1.8987(1.9058) | 2.0232(2.0218) | 1.4000(1.3921) | 1.4367(1.4153) | 2.0883(2.0894) | 4(3) |
| RMSE | 5.3189(5.3199) | 5.9638(5.9642) | 5.6038(5.6118) | 7.0081(6.9783) | 4.7924(4.7716) | 5.6947(5.6623) | 6.5592(6.5867) | 4(3) |
| () | 11.008 c(2.8001) | 2.3778(5.9817 a) | 17.194 c(4.5393) | 2.2015(1.5129) | 14.618 c(4.9716 a) | 0.3605(0.5264) | 3.6580(0.7792) | 3(2) |
| () | 4.8726 a(6.0281 b) | 20.548 c(0.7417) | 17.652 c(11.467c) | 29.806 c(11.818 c) | 0.5074(8.4995 b) | 10.072 c(30.524 c) | 32.478 c(10.928 c) | 6(6) |
| 0.4100 | 0.7582 | 1.0028 | 9.3453 c | 0.0782 | 6.7104 b | 8.9595 b | 3 | |
| () | 4.5370(1.9570) | 7.9884 b(0.8104) | 7.2664 b(3.6869) | 13.025 c(1.8152) | 24.246 c(1.0319) | 7.3548 b(17.984 c) | 10.881 c(18.010 c) | 6(2) |
| () | 2.082(0.766) | 2.747(0.671) | 2.226(0.682) | 3.114(0.674) | 1.534 (0.885) | 0.799 (0.355) | 1.819(0.611) |
| XU100(6) | RTSI(7) | JKSE(7) | SSE(7) | BSE(7) | MXX(5) | BVSP(7) | Sum(46) | |
|---|---|---|---|---|---|---|---|---|
| Panel A. The likelihood ratio test | ||||||||
| LR | 6 | 6 | 7 | 6 | 7 | 5 | 7 | 44 |
| Panel B. Volatility forecasting performance comparison | ||||||||
| MAE | 2(4) | 6(1) | 4(3) | 1(6) | 2(5) | 4(1) | 3(4) | 22(24) |
| RMSE | 1(5) | 4(3) | 4(3) | 2(5) | 1(6) | 1(4) | 7(0) | 20(26) |
| Panel C. The parameters equality tests | ||||||||
| 3 | 2 | 3 | 3 | 4 | 1 | 2 | 18 | |
| 1 | 1 | 2 | 1 | 0 | 1 | 2 | 8 | |
| 6 | 6 | 6 | 6 | 7 | 5 | 7 | 43 | |
| 5 | 7 | 6 | 5 | 4 | 5 | 5 | 37 | |
| 5 | 1 | 3 | 3 | 5 | 3 | 5 | 25 | |
| 1 | 1 | 6 | 7 | 5 | 1 | 2 | 23 | |
| 4 | 2 | 2 | 2 | 5 | 3 | 3 | 21 | |
| XU100-N225 | RTSI-N225 | JKSE-N225 | SSE-N225 | BSE-N225 | Sum | |
|---|---|---|---|---|---|---|
| Panel A. Return spillover | ||||||
| 0.0011 (0.0216) | 0.0292 (0.0625) | −0.0295 (0.0260) | 0.0053 (0.0236) | 0.0151 (0.0258) | 0 | |
| −0.0257 (0.0214) | 0.0098 (0.0192) | −0.0235 (0.0152) | 0.0573 (0.0275) b | −0.0138 (0.0113) | 1(+) | |
| 0.0498 (0.0176) c | 0.0111 (0.0166) | −0.0098 (0.0353) | −0.0467 (0.0352) | 0.0904 (0.0321) c | 2(+) | |
| 0.0975 (0.0162) c | 0.0101 (0.0139) | 0.0274 (0.0247) | −0.0166 (0.0149) | 0.1238 (0.0212) c | 2(+) | |
| Panel B. Volatility spillover | ||||||
| 0.1101 (0.0226) c | 0.1191 (0.0274) c | 0.0453 (0.0120) c | −0.0057 (0.0044) | 0.0224 (0.0086) c | 4(+) | |
| −0.0003 (0.0100) | 0.0371 (0.0120) c | 0.0143 (0.0108) | −0.0175 (0.0074)b | −0.0005 (0.0077) | 2(1+;1−) | |
| 0.0195 (0.0082) b | 0.0354 (0.0106) c | 0.0424 (0.0109) c | 0.0381 (0.0121)c | 0.0391 (0.0118) c | 5(+) | |
| 0.0131 (0.0138) | 0.0438 (0.0162) c | 0.0142 (0.0089) | −0.0168 (0.0103) | 0.0137 (0.0096) | 1(+) | |
| Panel C. Correlation | ||||||
| 0.0384 (0.0137) c | −0.3274 (0.2686) | 0.0397 (0.0126) c | −0.0018 (0.0021) | 0.0627 (0.0159) c | 3(+) | |
| 0.0166 (0.0051) c | 0.2284 (0.1075) b | 0.0236 (0.0056) c | 0.0045 (0.0023) b | 0.0395 (0.0064) c | 5(+) | |
| Panel D. Leverage effect | ||||||
| −0.0644 (0.0229) c | −0.0789 (0.0281) c | 0.0057 (0.0228) | −0.0767 (0.0187) c | −0.0308 (0.0194) | 3(−) | |
| −0.1157 (0.0190) c | −0.0980 (0.0201) c | −0.0976 (0.0202) c | −0.0675 (0.0179) c | −0.1008 (0.0162) c | 5(−) | |
| −0.0467 (0.0281) a | −0.0515 (0.0316) | −0.0301 (0.0254) | −0.0711 (0.0285) b | −0.0280 (0.0269) | 2(−) | |
| −0.1190 (0.0163) c | −0.1593 (0.0190) c | −0.1096 (0.0165) c | −0.1173 (0.0257) c | −0.0913 (0.0158) c | 5(−) | |
| MXX-TSX | BVSP-DJ | BVSP-TSX | Sum | |
|---|---|---|---|---|
| Panel A. Return spillover | ||||
| 0.0412(0.0240) a | 0.0389(0.0417) | −0.0343(0.0514) | 1(+) | |
| 0.0012(0.0181) | −0.0069(0.0178) | 0.1170(0.0252) c | 1(+) | |
| 0.0318(0.0126) b | 0.0142(0.0177) | 0.0298(0.0138) b | 2(+) | |
| 0.0259(0.0121) b | 0.0084(0.0049) a | 0.0197(0.0080) b | 3(+) | |
| Panel B. Volatility spillover | ||||
| −0.0017(0.0045) | 0.0110(0.0050) b | −0.0053(0.0050) | 1(+) | |
| 0.0105(0.0037)c | 0.0147(0.0032) c | 0.0039(0.0033) | 2(+) | |
| 0.0151(0.0045)c | 0.0313(0.0069) c | 0.0202(0.0057) c | 3(+) | |
| 0.0116(0.0044)c | 0.0283(0.0058) c | 0.0196(0.0050) c | 3(+) | |
| Panel C. Correlation | ||||
| 0.0081(0.0015) c | 0.0102(0.0042) b | 0.0150(0.0040) c | 3(+) | |
| 0.0054(0.0010) c | 0.0070(0.0016) c | 0.0119(0.0020) c | 3(+) | |
| Panel D. Leverage effect | ||||
| −0.0447(0.0084) c | −0.0294(0.0123) b | −0.0415(0.0114) c | 3(−) | |
| −0.0260(0.0095) c | −0.0284(0.0045) c | −0.0418(0.0069) c | 3(−) | |
| −0.0161(0.0089) a | −0.0850(0.0163) c | −0.0578(0.0152) c | 3(−) | |
| −0.0721(0.0077) c | −0.0528(0.0063) c | −0.0854(0.0072) c | 3(−) | |
| XU100-DJ | XU100-TSX | RTSI-DJ | RTSI-TSX | JKSE-DJ | JKSE-TSX | Sum | |
|---|---|---|---|---|---|---|---|
| Panel A. Return spillover | |||||||
| 0.4035(0.0562) c | 0.3328(0.0487) c | −0.0306(0.0548) | 0.0072(0.0532) | 0.2160(0.0297)c | 0.2512(0.0287) c | 4(+) | |
| 0.1176(0.0287) c | 0.1465(0.0343) c | 0.0155(0.0271) | 0.0124(0.0307) | 0.2289(0.0210)c | 0.2398(0.0285) c | 4(+) | |
| −0.0091(0.0084) | 0.0110(0.0076) | 0.0057(0.0098) | 0.0056(0.0084) | −0.0594(0.0159)c | −0.0117(0.0141) | 1(−) | |
| 0.0109(0.0098) | −0.0002(0.0091) | −0.0035(0.0094) | −0.0048(0.0063) | −0.0129(0.0164) | −0.0009(0.0135) | 0 | |
| Panel B. Volatility spillover | |||||||
| 0.0203(0.0088) b | 0.0136(0.0095) | 0.0237(0.0106) b | 0.0248(0.0084) c | 0.0315(0.0131) b | 0.0086(0.0126) | 4(+) | |
| −0.0017(0.0044) | −0.0015(0.0037) | 0.0085(0.0053) | 0.0098(0.0038) b | 0.0346(0.0122) c | 0.0536(0.0072) c | 3(+) | |
| 0.0123(0.0057) b | 0.0072(0.0047) | 0.0179(0.0064) c | 0.0066(0.0058) | 0.0261(0.0069) c | 0.0392(0.0047) c | 4(+) | |
| 0.0110(0.0079) | −0.0018(0.0065) | 0.0239(0.0088) c | 0.0032(0.0072) | 0.0092(0.0058) | 0.0190(0.0042) c | 2(+) | |
| Panel C. Correlation | |||||||
| 0.0076(0.0050) | 0.0209(0.0054) c | 0.0046(0.0078) | 0.1653(0.0923) a | 0.0033(0.0022) | 0.0056(0.0019) c | 3(+) | |
| 0.0215(0.0050) c | 0.0191(0.0042) c | 0.0006(0.0014) | 0.0510(0.0572) | 0.0030(0.0014) b | 0.0026(0.0010) b | 4(+) | |
| Panel D. Leverage effect | |||||||
| −0.0272(0.0141) a | −0.0232(0.0134) a | −0.0456(0.0176) c | −0.0371(0.0165) b | −0.0080(0.0196) | −0.0439(0.0191) b | 5(−) | |
| −0.0413(0.0142) c | −0.0468(0.0142) c | −0.0647(0.0173) c | −0.0634(0.0152) c | −0.0979(0.0256) c | −0.0986(0.0267) c | 6(−) | |
| −0.1433(0.0235) c | −0.0720(0.0179) c | −0.1556(0.0258) c | −0.0616(0.0189)c | −0.1288(0.0242) c | −0.0659(0.0172) c | 6(−) | |
| −0.1186(0.0132) c | −0.1218(0.0150) c | −0.1654(0.0152) c | −0.1370(0.0173) c | −0.1470(0.0160) c | −0.1529(0.0144) c | 6(−) | |
| SSE−DJ | SSE−TSX | BSE−DJ | BSE−TSX | MXX−N225 | BVSP−N225 | Sum | |
| Panel A. Return spillover | |||||||
| 0.0380(0.0208) a | 0.0485(0.0294) a | 0.1730(0.0289) c | 0.2340(0.0314) c | −0.0170(0.0268) | 0.0132(0.0378) | 4(+) | |
| 0.1337(0.0284) c | 0.1298(0.0364) c | 0.2095(0.0214)c | 0.2539(0.0244) c | −0.0385(0.0140)c | 0.0029(0.0197) | 5(4+;1−) | |
| 0.0241(0.0134) a | 0.0082(0.0114) | −0.0288(0.0148) a | −0.0071(0.0126) | 0.2720(0.0391) c | 0.1247(0.0269) c | 4(3+;1−) | |
| −0.0295(0.0201) | −0.0144(0.0088) | −0.0035(0.0143) | −0.0100(0.0131) | 0.2878(0.0231) c | 0.1970(0.0117) c | 2(+) | |
| Panel B. Volatility spillover | |||||||
| −0.0149(0.0042) c | −0.0046(0.0053) | −0.0241(0.0069) c | −0.0201(0.0074) c | 0.0178(0.0038) c | 0.0261(0.0099) c | 5(2+;3−) | |
| −0.0002(0.0036) | −0.0022(0.0046) | 0.0113(0.0058) a | 0.0118(0.0071) a | −0.0087(0.0041) b | 0.0167(0.0092) a | 4(3+;1−) | |
| 0.0015(0.0054) | 0.0165(0.0043) c | −0.0024(0.0058) | 0.0177(0.0054) c | 0.0392(0.0095) c | 0.0519(0.0161) c | 4(+) | |
| −0.0006(0.0061) | −0.0092(0.0074) | 0.0039(0.0065) | 0.0111(0.0064) a | −0.0001(0.0100) | 0.0349(0.0142) b | 2(+) | |
| Panel C. Correlation | |||||||
| 0.0453(0.0550) | 0.1021(0.0683) | 0.0069(0.0033) b | 0.0130(0.0036) c | 0.6043(0.1398) c | 0.0296(0.0120) b | 4(+) | |
| 0.1049(0.0375) c | 0.1033(0.0648) | 0.0122(0.0032) c | 0.0094(0.0027) c | 0.3993(0.0470) c | 0.0105(0.0043) b | 5(+) | |
| Panel D. Leverage effect | |||||||
| −0.0419(0.0114) c | −0.0291(0.0122) b | −0.0761(0.0171) c | −0.0635(0.0147) c | −0.0835(0.0233) c | −0.0620(0.0247) b | 6(−) | |
| 0.0015(0.0186) | −0.0796(0.0209) c | −0.0953(0.0169) c | −0.0867(0.0169) c | −0.0962(0.0171) c | −0.0789(0.0142) c | 5(−) | |
| −0.1277(0.0194) c | −0.0879(0.0188) c | −0.1403(0.0215) c | −0.0646(0.0156) c | −0.0349(0.0312) | −0.0323(0.0296) | 4(−) | |
| −0.1085(0.0145) c | −0.1562(0.0218) c | −0.1251(0.0133) c | −0.1264(0.0149) c | −0.1148(0.0146) c | −0.1064(0.0169) c | 6(−) | |
| XU100-FTSE | XU100-DAX | XU100-MIB | RTSI-FTSE | RTSI-CAC40 | RTSI-DAX | RTSI-MIB | Sum | |
|---|---|---|---|---|---|---|---|---|
| Panel A. Return spillover | ||||||||
| 0.0399(0.0365) | 0.0084(0.0365) | 0.0901(0.0425) b | 0.1002(0.0495) b | 0.0275(0.0396) | 0.0297(0.0458) | 0.0135(0.0462) | 2(+) | |
| 0.0729(0.0325) b | 0.0195(0.0216) | 0.0100(0.0169) | 0.0000(0.0377) | −0.0113(0.0255) | 0.0131(0.0223) | 0.0051(0.0163) | 1(+) | |
| 0.0068(0.0079) | −0.0011(0.0095) | 0.0103(0.0097) | 0.0144(0.0089) | 0.0286(0.0113) b | 0.0261(0.0192) | 0.0238(0.0102) b | 2(+) | |
| 0.0329(0.0136) b | 0.0145(0.0134) | 0.0280(0.0177) | 0.0007(0.0139) | 0.0035(0.0137) | 0.0058(0.0125) | −0.0000(0.0153) | 1(+) | |
| Panel B. Volatility spillover | ||||||||
| 0.0013(0.0028) | 0.0230(0.0066) c | 0.0131(0.0059) b | 0.0175(0.0075) b | 0.0436(0.0116) c | 0.0479(0.0112) c | 0.0156(0.0067) b | 6(+) | |
| 0.0018(0.0037) | 0.0071(0.0040) a | 0.0188(0.0039) c | 0.0050(0.0066) | −0.0039(0.0055) | 0.0132(0.0066) b | −0.0067(0.0032) b | 4(3+;1−) | |
| −0.0011(0.0027) | 0.0015(0.0039) | −0.0064(0.0032) b | −0.0023(0.0040) | 0.0006(0.0046) | 0.0076(0.0058) | −0.0046(0.0029) | 1(−) | |
| −0.0049(0.0039) | −0.0048(0.0058) | 0.0034(0.0054) | −0.0104(0.0055) a | −0.0029(0.0066) | −0.0013(0.0073) | 0.0066(0.0052) | 1(−) | |
| Panel C. Correlation | ||||||||
| 0.0158(0.0041) c | 0.0415(0.0204) b | 0.0257(0.0061) c | 0.0015(0.0013) | 0.0015(0.0015) | 0.3916(0.3676) | 0.0186(0.0258) | 3(+) | |
| 0.0098(0.0030) c | 0.0311(0.0065) c | 0.0332(0.0064) c | −0.0001(0.0013) | −0.0000(0.0008) | 0.0612(0.0788) | 0.0083(0.0230) | 3(+) | |
| Panel D. Leverage effect | ||||||||
| −0.0042(0.0083) | −0.0271(0.0152) a | −0.0205(0.0122) a | −0.0482(0.0157) c | −0.0594(0.0162) c | −0.0557(0.0226) b | −0.0462(0.0149) c | 6(−) | |
| −0.0310(0.0125) b | −0.0414(0.0121) c | −0.0490(0.0121) c | −0.0778(0.0212) c | −0.0973(0.0199) c | −0.0912(0.0178) c | −0.0660(0.0142) c | 7(−) | |
| −0.0932(0.0096) c | −0.1217(0.0228) c | −0.1043(0.0158) c | −0.1737(0.0212) c | −0.1652(0.0220) c | −0.1312(0.0299) c | −0.1436(0.0206) c | 7(−) | |
| −0.1151(0.0162) c | −0.0935(0.0116) c | −0.0866(0.0116) c | −0.1597(0.0183) c | −0.1605(0.0162) c | −0.1583(0.0167) c | −0.1169(0.0120) c | 7(−) | |
| JKSE−FTSE | JKSE−CAC40 | JKSE−DAX | JKSE−MIB | SSE−FTSE | SSE−CAC40 | SSE−DAX | Sum | |
| Panel A. Return spillover | ||||||||
| 0.1290(0.0212) c | 0.1030(0.0181) c | 0.0678(0.0227) c | 0.0937(0.0245) c | 0.0892(0.0206) c | 0.0452(0.0019) c | 0.0300(0.0184) | 6(+) | |
| 0.0795(0.0231) c | 0.1015(0.0165) c | 0.1045(0.0138) c | 0.0782(0.0128) c | 0.0982(0.0348) c | 0.0877(0.0318) c | 0.0811(0.0263) c | 7(+) | |
| −0.0277(0.0125) b | −0.0481(0.0157) c | −0.0467(0.0425) | −0.0427(0.0174) b | 0.0009(0.0084) | 0.0004(0.0118) | 0.0198(0.0490) | 3(−) | |
| 0.0113(0.0207) | 0.0067(0.0221) | 0.0173(0.0224) | −0.0036(0.0254) | −0.0307(0.0134) b | −0.0198(0.0160) | −0.0260(0.0184) | 1(−) | |
| Panel B. Volatility spillover | ||||||||
| 0.0072(0.0061) | 0.0160(0.0068) b | 0.0185(0.0057) c | 0.0075(0.0068) | 0.0010(0.0030) | −0.0000(0.0029) | −0.0074(0.0036) b | 3(2+;1−) | |
| 0.0039(0.0079) | −0.0082(0.0062) | −0.0080(0.0066) | −0.0151(0.0050) c | −0.0063(0.0071) | −0.0157(0.0059) c | −0.0228(0.0085) c | 3(−) | |
| 0.0138(0.0040) c | 0.0067(0.0040) a | 0.0276(0.0088) c | −0.0154(0.0044) c | 0.0112(0.0028) c | 0.0083(0.0032) b | 0.0270(0.0097) c | 7(6+;1−) | |
| 0.0033(0.0054) | 0.0025(0.0049) | 0.0057(0.0055) | 0.0024(0.0043) | 0.0060(0.0057) | 0.0024(0.0060) | −0.0017(0.0083) | 0 | |
| Panel C. Correlation | ||||||||
| 0.0088(0.0028) c | 0.0128(0.0046) c | 0.0143(0.0089) | 0.0088(0.0037) b | 0.0012(0.0009) | 0.0008(0.0015) | 0.0216(0.0557) | 3(+) | |
| 0.0080(0.0028) c | 0.0093(0.0037) b | 0.0135(0.0047) c | 0.0097(0.0041) b | 0.0023(0.0012) a | 0.0026(0.0024) | 0.0914(0.0854) | 5(+) | |
| Panel D. Leverage effect | ||||||||
| −0.0338(0.0131) c | −0.0322(0.0132) b | 0.0041(0.0260) | −0.0119(0.0160) | −0.0276(0.0102) c | −0.0269(0.0095) c | −0.1203(0.0245) c | 5(−) | |
| −0.0650(0.0221) c | −0.0779(0.0202) c | −0.0964(0.0217) c | −0.0920(0.0199) c | −0.0632(0.0181) c | −0.0602(0.0168) c | −0.0767(0.0189) c | 7(−) | |
| −0.1223(0.0139) c | −0.1158(0.0144) c | −0.1289(0.0251) c | −0.1104(0.0169) c | −0.1537(0.0130) c | −0.1707(0.0188) c | −0.1888(0.0347) c | 7(−) | |
| −0.1338(0.0186) c | −0.1351(0.0155) c | −0.1307(0.0164) c | −0.1032(0.0138) c | −0.1165(0.0251) c | −0.1306(0.0213) c | −0.1211(0.0254) c | 7(−) | |
| SSE−MIB | BSE−FTSE | BSE−CAC40 | BSE−DAX | BSE−MIB | Sum | |||
| Panel A. Return spillover | ||||||||
| 0.0292(0.0165) a | 0.1295(0.0237) c | 0.1249(0.0204) c | 0.0911(0.0148) c | 0.1154(0.0240) c | 5(+) | |||
| 0.0712(0.0281) b | 0.0683(0.0233) c | 0.0731(0.0160) c | 0.0757(0.0166) c | 0.0716(0.0110) c | 5(+) | |||
| −0.0004(0.0144) | 0.0075(0.0118) | −0.0010(0.0138) | 0.0649(0.0250) c | 0.0143(0.0157) | 1(+) | |||
| −0.0270(0.0181) | 0.0069(0.0195) | −0.0209(0.0176) | −0.0145(0.0194) | −0.0170(0.0081) b | 1(−) | |||
| Panel B. Volatility spillover | ||||||||
| −0.0092(0.0036) b | −0.0002(0.0030) | 0.0020(0.0025) | 0.0001(0.0039) | −0.0070(0.0044) | 1(−) | |||
| −0.0217(0.0061) c | −0.0046(0.0039) | −0.0085(0.0025) c | −0.0082(0.0043) a | −0.0152(0.0037) c | 4(−) | |||
| −0.0124(0.0044) c | 0.0027(0.0022) | 0.0016(0.0019) | 0.0065(0.0058) | −0.0183(0.0039) c | 2(−) | |||
| −0.0047(0.0072) | 0.0000(0.0036) | 0.0029(0.0030) | 0.0050(0.0036) | −0.0015(0.0041) | 0 | |||
| Panel C. Correlation | ||||||||
| −0.0001(0.0015) | 0.0093(0.0032) c | 0.0132(0.0028)c | 0.0071(0.0065) | 0.0154(0.0056) c | 3(+) | |||
| 0.0116(0.0087) | 0.0115(0.0032) c | 0.0144(0.0019)c | 0.0161(0.0038) c | 0.0294(0.0072) c | 4(+) | |||
| Panel D. Leverage effect | ||||||||
| −0.0304(0.0116) c | −0.0190(0.0104) a | −0.0215(0.0101) b | −0.0421(0.0203) b | −0.0338(0.0143) b | 5(−) | |||
| −0.0830(0.0192) c | −0.0747(0.0166) c | −0.0616(0.0089) c | −0.0762(0.0142) c | −0.0939(0.0148) c | 5(−) | |||
| −0.1607(0.0224) c | −0.1089(0.0119) c | −0.1023(0.0128) c | −0.1525(0.0224) c | −0.1134(0.0156)c | 5(−) | |||
| −0.1487(0.0249) c | −0.1100(0.0156) c | −0.1086(0.0119) c | −0.0999(0.0134) c | −0.0873(0.0114) c | 5(−) | |||
| MXX-FTSE | MXX-DAX | MXX-MIB | BVSP-FTSE | BVSP-CAC40 | BVSP-DAX | BVSP-MIB | Sum | |
|---|---|---|---|---|---|---|---|---|
| Panel A. Return spillover | ||||||||
| −0.0038(0.0130) | 0.0321(0.0046) c | −0.0031(0.0217) | 0.0265(0.0487) | −0.0339(0.0329) | 0.0363(0.0329) | 0.0209(0.0095) b | 2(+) | |
| −0.0547(0.0200) c | −0.0255(0.0145) a | −0.0114(0.0111) | 0.0038(0.0369) | 0.0218(0.0219) | 0.0751(0.0204) c | 0.0362(0.0172) b | 4(2+;2−) | |
| 0.0900(0.0105) c | 0.0389(0.0437) | 0.0898(0.0176) c | 0.0335(0.0177) a | 0.0698(0.0181) c | 0.0026(0.0025) | 0.0994(0.0178) c | 5(+) | |
| 0.0669(0.0196) c | 0.0976(0.0226) c | 0.0960(0.0255) c | 0.0487(0.0125) c | 0.0793(0.0117) c | 0.0651(0.0108) c | 0.0726(0.0151) c | 7(+) | |
| Panel B. Volatility spillover | ||||||||
| 0.0019(0.0026) | −0.0009(0.0032) | −0.0043(0.0034) | 0.0034(0.0049) | 0.0056(0.0036) | 0.0091(0.0041) b | 0.0144(0.0064) b | 2(+) | |
| −0.0008(0.0029) | −0.0101(0.0039) c | −0.0128(0.0031) c | 0.0035(0.0045) | −0.0025(0.0030) | 0.0016(0.0042) | −0.0012(0.0037) | 2(−) | |
| 0.0087(0.0026) c | 0.0147(0.0062) b | −0.0152(0.0046) c | 0.0029(0.0045) | 0.0152(0.0050) c | 0.0304(0.0069) c | 0.0160(0.0084) a | 6(5+;1−) | |
| 0.0050(0.0032) | 0.0050(0.0047) | −0.0069(0.0044) | 0.0031(0.0041) | 0.0135(0.0042) c | 0.0198(0.0048) c | 0.0251(0.0099) b | 3(+) | |
| Panel C. Correlation | ||||||||
| 0.0153(0.0030) c | 0.0473(0.0104) c | 0.0283(0.0058) c | 0.0189(0.0072) c | 0.0199(0.0064) c | 0.0882(0.0201) c | 0.0519(0.0162) c | 7(+) | |
| 0.0130(0.0027) c | 0.0230(0.0047) c | 0.0257(0.0054) c | 0.0133(0.0038) c | 0.0138(0.0028) c | 0.0317(0.0064) c | 0.0465(0.0103) c | 7(+) | |
| Panel D. Leverage effect | ||||||||
| −0.0287(0.0075) c | −0.0328(0.0203) | −0.0237(0.0119) b | −0.0150(0.0145) | −0.0395(0.0135) c | −0.0389(0.0182) b | −0.0432(0.0200) b | 5(−) | |
| −0.0351(0.0151) b | −0.0520(0.0126) c | −0.0685(0.0130) c | −0.0358(0.0128) c | −0.0326(0.0085) c | −0.0510(0.0093) c | −0.0482(0.0081) c | 7(−) | |
| −0.1013(0.0094) c | −0.0679(0.0195) c | −0.0813(0.0143) c | −0.1488(0.0217) c | −0.1035(0.0189) c | −0.0833(0.0201) c | −0.1139(0.0218) c | 7(−) | |
| −0.0997(0.0133) c | −0.0910(0.0115) c | −0.0747(0.0102) c | −0.1092(0.0132) c | −0.1094(0.0088) c | −0.0934(0.0105) c | −0.0818(0.0095) c | 7(−) | |
| Geographical Location | Emerging Stock Indices | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Asia (5) | America (3) | Asia–America (12) | Asia–Europe (19) | America–Europe (7) | SUM (46) | XU100 (6) | RTSI (7) | MXX (5) | BVSP (7) | JKSE (7) | SSE (7) | BSE (7) | |||
| Panel A. Return spillover | |||||||||||||||
| 0 | 1(+) | 8(+) | 13(+) | 2(+) | 24(+) | 3(+) | 1(+) | 2(+) | 1(+) | 6(+) | 5(+) | 6(+) | |||
| 1(+) | 1(+) | 9(8+;1−) | 13(+) | 4(2+;2−) | 28(25+;3−) | 3(+) | 0 | 3(−) | 3(+) | 6(+) | 7(+) | 6(+) | |||
| 2(+) | 2(+) | 5(3+;2−) | 6(3+;3−) | 5(+) | 20(15+;5−) | 1(+) | 2(+) | 4(+) | 5(+) | 4(−) | 1(+) | 3(2+;1−) | |||
| 2(+) | 3(+) | 2(+) | 3(1+;2−) | 7(+) | 17(15+;2−) | 2(+) | 0 | 5(+) | 7(+) | 0 | 1(−) | 2(1+;1−) | |||
| 1 (10%) | 2 (33.3%) | 17 (70.8%) | 26 (68.4%) | 6 (42.9%) | 60.8% | 52 (56.5%) | 6 (50%) | 1 (7.1%) | 5 (50%) | 4 (28.6%) | 12 (85.7%) | 12 (85.7%) | 12 (85.7%) | 78.6% | |
| 4 (40%) | 5 (83.3%) | 7 (29.2%) | 9 (23.7%) | 12 (85.7%) | 62% | 37 (40.2%) | 3 (25%) | 2 (14.3%) | 9 (90%) | 12 (85.7%) | 4 (28.6%) | 2 (14.3%) | 5 (35.7%) | 75.7% | |
| 2 (20%) | 3 (50%) | 13 (54.2%) | 19 (50%) | 7 (50%) | 44 (47.8%) | 4 (33.3%) | 3 (21.4%) | 6 (60%) | 6 (42.9%) | 10 (71.4%) | 6 (42.9%) | 9 (64.3%) | |||
| 3 (30%) | 4 (66.7%) | 11 (45.8%) | 16 (42.1%) | 11 (78.6%) | 45 (48.9%) | 5 (41.7%) | 0 (0%) | 8 (80%) | 10 (71.4%) | 6 (42.9%) | 8 (57.1%) | 8 (57.1%) | |||
| 10% | 16.7% | −8.4% | −7.9% | 28.6% | 1.1% | 8.4% | −21.4% | 20% | 28.5% | −28.5% | 14.2% | −7.2% | |||
| Panel B. Volatility spillover | |||||||||||||||
| 4(+) | 1(+) | 9(6+;3−) | 10(8+;2−) | 2(+) | 26(21+;5−) | 4(+) | 7(+) | 1(+) | 4(+) | 4(+) | 3(−) | 3(1+;2−) | |||
| 2(1+;1−) | 2(+) | 7(6+;1−) | 11(3+;8−) | 2(−) | 24(12+;12−) | 2(+) | 4(3+;1−) | 4(1+;3−) | 2(+) | 3(2+;1−) | 4(−) | 5(2+;3−) | |||
| 5(+) | 3(+) | 8(+) | 10(6+;4−) | 6(5+;1−) | 32(27+;5−) | 3(2+;1−) | 2(+) | 5(4+;1−) | 6(+) | 7(6+;1−) | 6(5+;1−) | 3(2+;1−) | |||
| 1(+) | 3(+) | 4(+) | 1(−) | 3(+) | 12(11+;1−) | 0 | 3(2+;1−) | 1(+) | 6(+) | 1(+) | 0 | 1(+) | |||
| 6 (60%) | 3 (50%) | 16 (66.7%) | 21 (55.3%) | 4 (28.6%) | 38.1% | 50 (54.3%) | 6 (50%) | 11 (78.6%) | 5 (50%) | 6 (42.9%) | 7 (50%) | 7 (50%) | 8 (57.1%) | 35.7% | |
| 6 (60%) | 6 (100%) | 12 (50%) | 11 (28.9%) | 9 (64.3%) | 71.1% | 44 (47.8%) | 3 (25%) | 5 (35.7%) | 6 (60%) | 12 (85.7%) | 8 (57.1%) | 6 (42.9%) | 4 (28.6%) | 60.7% | |
| 9 (90%) | 4 (66.7%) | 17 (70.8%) | 20 (52.6%) | 8 (57.1%) | 58 (63%) | 7 (58.3%) | 9 (64.3%) | 6 (60%) | 10 (71.4%) | 11 (78.6%) | 9 (64.3%) | 6 (42.9%) | |||
| 3 (30%) | 5 (83.3%) | 11 (45.8%) | 12 (31.6%) | 5 (35.7%) | 36 (39.1%) | 2 (16.7%) | 7 (50%) | 5 (50%) | 8 (57.1%) | 4 (28.6%) | 4 (28.6%) | 6 (42.9%) | |||
| −60% | 16.6% | −25% | −21% | −21.4% | −23.9% | −41.6% | −14.3% | −10% | −14.3% | −50% | −35.7% | 0% | |||
| Panel C. Correlative relation | |||||||||||||||
| 3(+)(60%) | 3(+)(100%) | 7(+)(58.3%) | 9(+)(47.4%) | 7(+)(100%) | 29(+)(63%) | 5(+)(83.3%) | 1(+)(14.3%) | 5(+)(100%) | 7(+)(100%) | 5(+)(71.4%) | 0(0%) | 6(+)(85.7%) | |||
| 5(+)(100%) | 3(+)(100%) | 9(+)(75%) | 12(+)(63.2%) | 7(+)(100%) | 36(+)(78.2%) | 6(+)(100%) | 1(+)(14.3%) | 5(+)(100%) | 7(+)(100%) | 7(+)(100%) | 3(+)(42.9%) | 7(+)(100%) | |||
| 8 (80%) | 6 (100%) | 16 (66.7%) | 21 (55.3%) | 14 (100%) | 44.7% | 65(70.7%) | 11 (91.7%) | 2 (14.3%) | 10 (100%) | 14 (100%) | 12 (85.7%) | 3 (21.4%) | 13 (92.9%) | 85.7% | |
| 40% | 0% | 16.7% | 15.8% | 0% | 15.2% | 16.7% | 0% | 0% | 0% | 28.6% | 42.9% | 14.3% | |||
| Panel D. Leverage effect | |||||||||||||||
| 3(−) | 3(−) | 11(−) | 16(−) | 5(−) | 38(−) | 5(−) | 7(−) | 4(−) | 6(−) | 3(−) | 7(−) | 6(−) | |||
| 5(−) | 3(−) | 11(−) | 19(−) | 7(−) | 45(−) | 6(−) | 7(−) | 5(−) | 7(−) | 7(−) | 6(−) | 7(−) | |||
| 2(−) | 3(−) | 10(−) | 19(−) | 7(−) | 41(−) | 6(−) | 6(−) | 4(−) | 6(−) | 6(−) | 7(−) | 6(−) | |||
| 5(−) | 3(−) | 12(−) | 19(−) | 7(−) | 46(−) | 6(−) | 7(−) | 5(−) | 7(−) | 7(−) | 7(−) | 7(−) | |||
| 8 (80%) | 6 (100%) | 22 (91.7%) | 35 (92.1%) | 12 (85.7%) | 20% | 83 (90.2%) | 11 (91.7%) | 14 (100%) | 9 (90%) | 13 (92.9%) | 10 (71.4%) | 13 (92.9%) | 13 (92.9%) | 28.6% | |
| 7 (70%) | 6 (100%) | 22 (91.7%) | 38 (100%) | 14 (100%) | 30% | 87 (94.6%) | 12 (100%) | 13 (92.9%) | 9 (90%) | 13 (92.9%) | 13 (92.9%) | 14 (100%) | 13 (92.9%) | 10% | |
| 5 (50%) | 6 (100%) | 21 (87.5%) | 35 (92.1%) | 12 (85.7%) | 79 (85.9%) | 11 (91.7%) | 13 (92.9%) | 8 (80%) | 12 (85.7%) | 9 (64.3%) | 14 (100%) | 12 (85.7%) | |||
| 10 (100%) | 6 (100%) | 23 (95.8%) | 38 (100%) | 14 (100%) | 91 (98.9%) | 12 (100%) | 14 (100%) | 10 (100%) | 14 (100%) | 14 (100%) | 13 (92.9%) | 14 (100%) | |||
| 50% | 0% | 8.3% | 7.9% | 14.3% | 13% | 8.3% | 7.1% | 20% | 14.3% | 35.7% | −7.1% | 14.3% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.-B. The Research on the Interactions between the Emerging and Developed Markets: From Region and Structural Break Perspectives. Mathematics 2022, 10, 1246. https://doi.org/10.3390/math10081246
Su J-B. The Research on the Interactions between the Emerging and Developed Markets: From Region and Structural Break Perspectives. Mathematics. 2022; 10(8):1246. https://doi.org/10.3390/math10081246
Chicago/Turabian StyleSu, Jung-Bin. 2022. "The Research on the Interactions between the Emerging and Developed Markets: From Region and Structural Break Perspectives" Mathematics 10, no. 8: 1246. https://doi.org/10.3390/math10081246
APA StyleSu, J.-B. (2022). The Research on the Interactions between the Emerging and Developed Markets: From Region and Structural Break Perspectives. Mathematics, 10(8), 1246. https://doi.org/10.3390/math10081246






