Temperature Distribution in the Flow of a Viscous Incompressible Non-Newtonian Williamson Nanofluid Saturated by Gyrotactic Microorganisms
Abstract
:1. Introduction
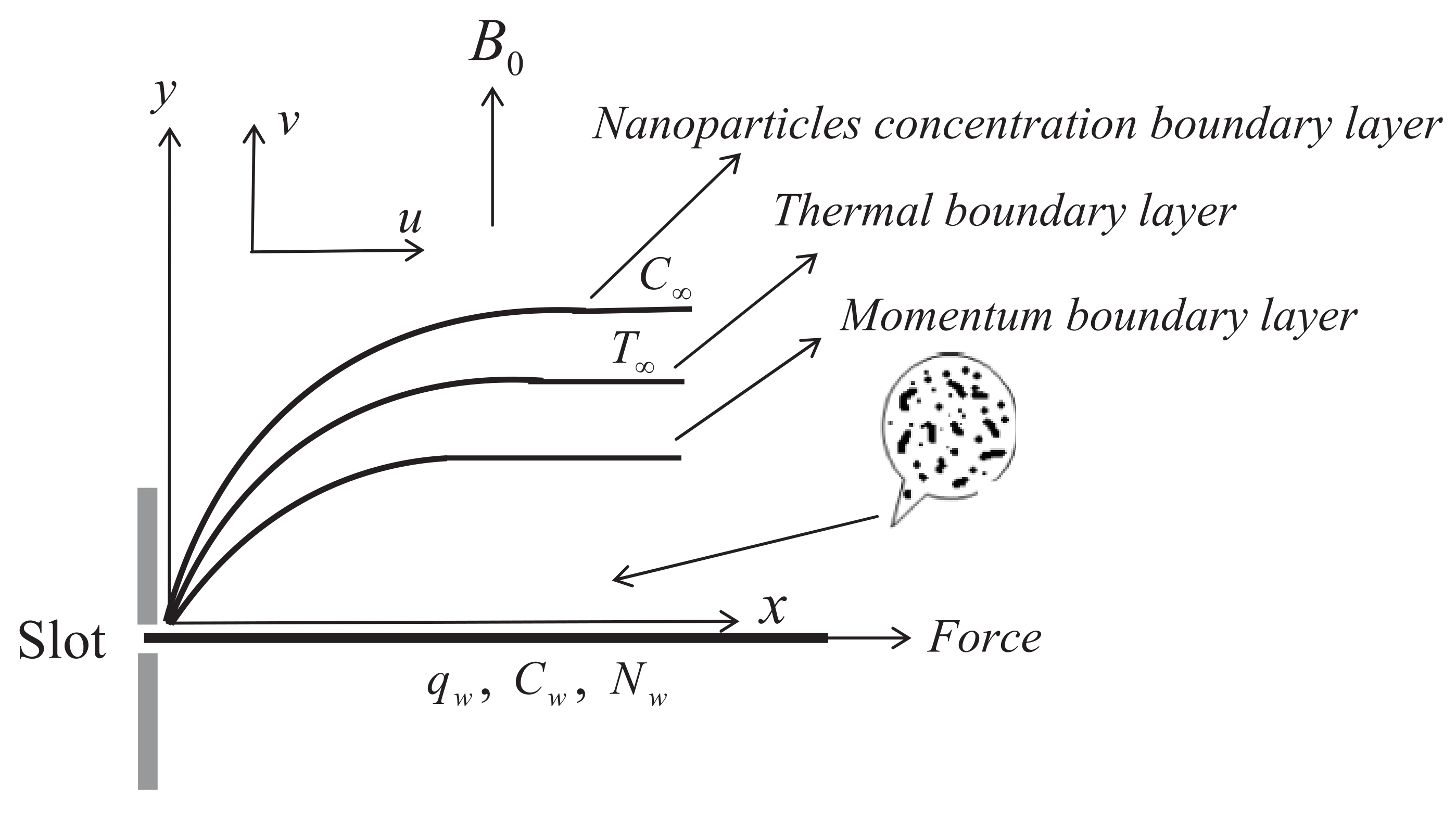
2. Mathematical Formulations
3. Numerical Solution
4. Verification of the Numerical Method
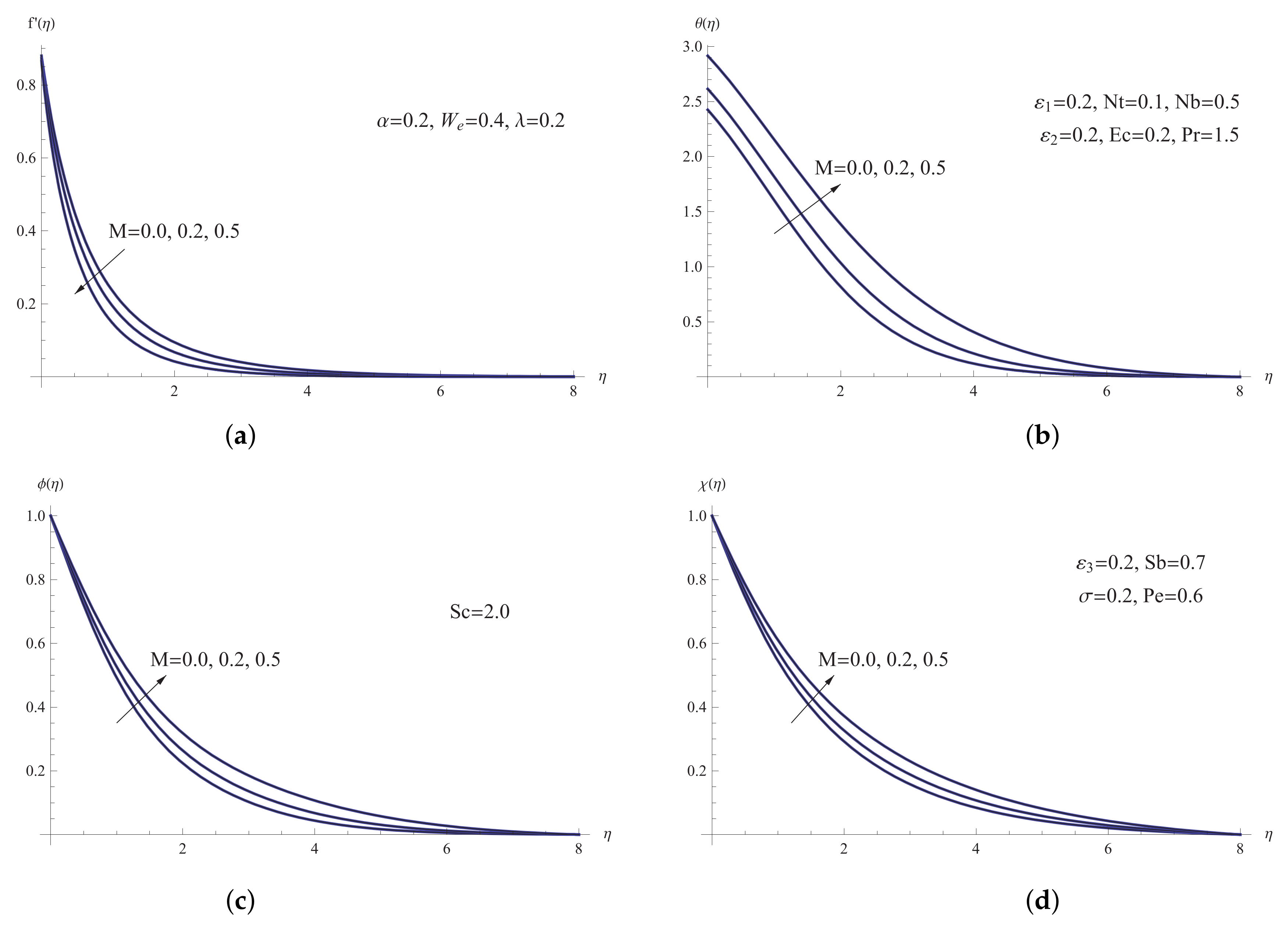
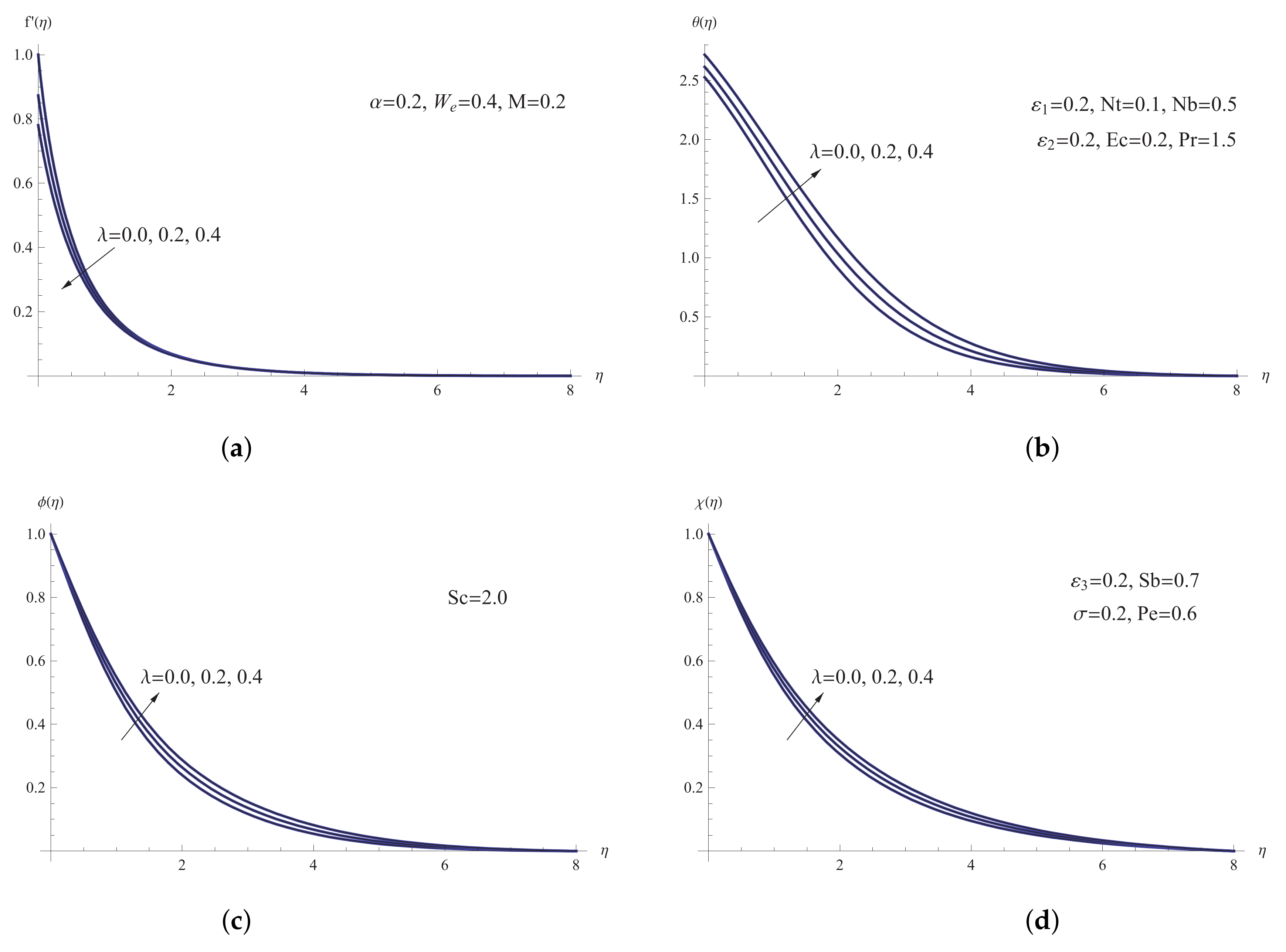
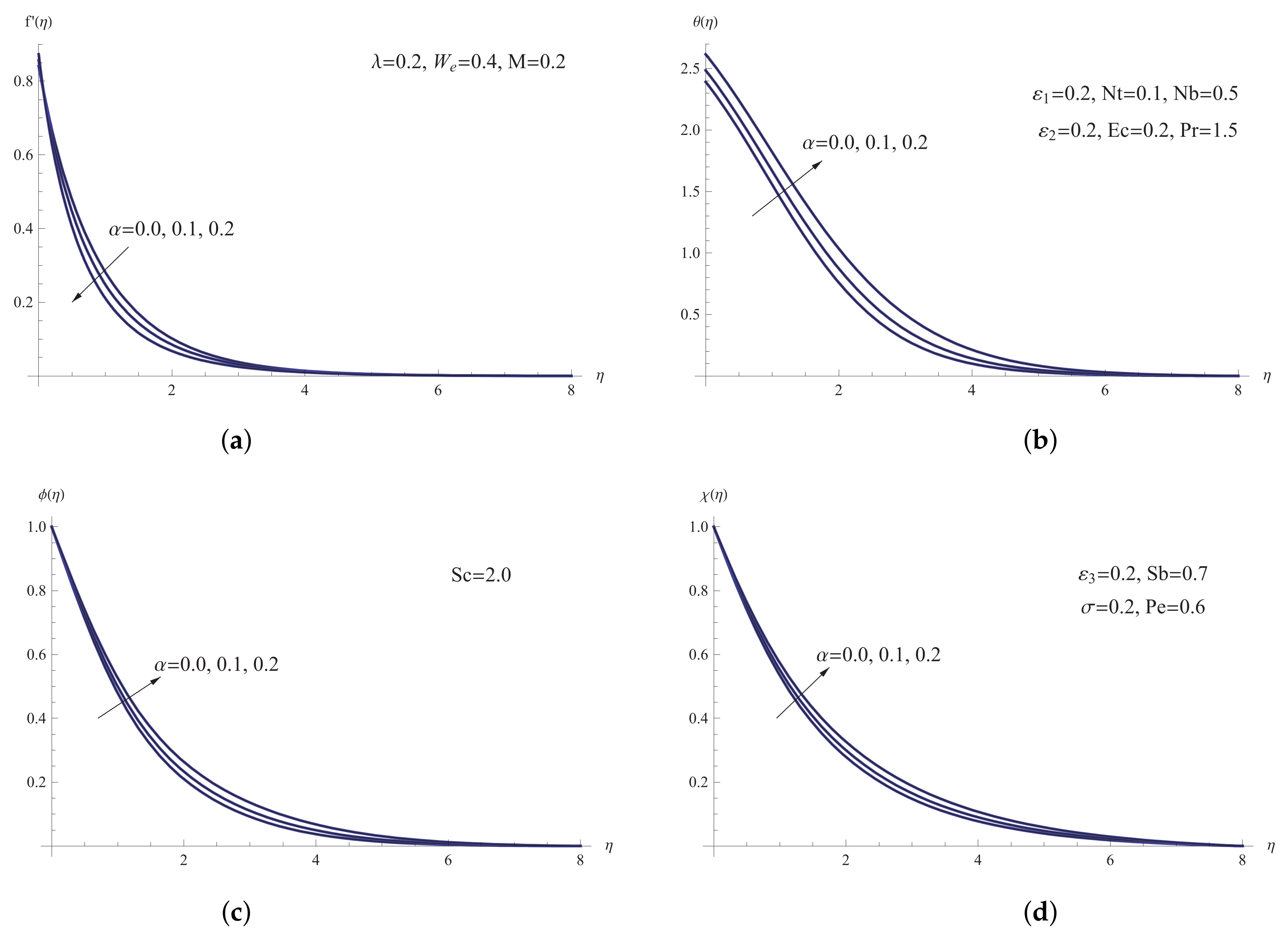
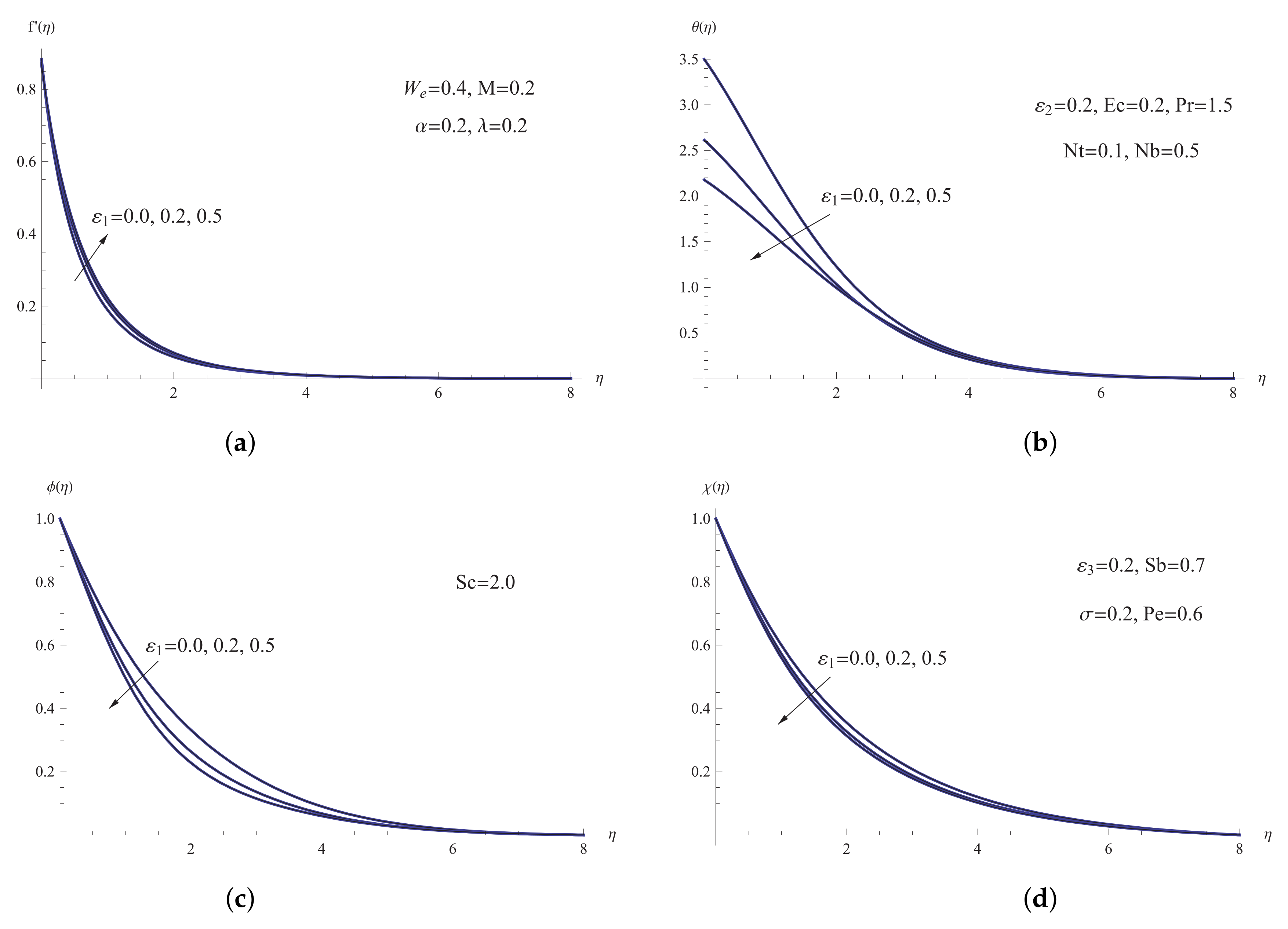
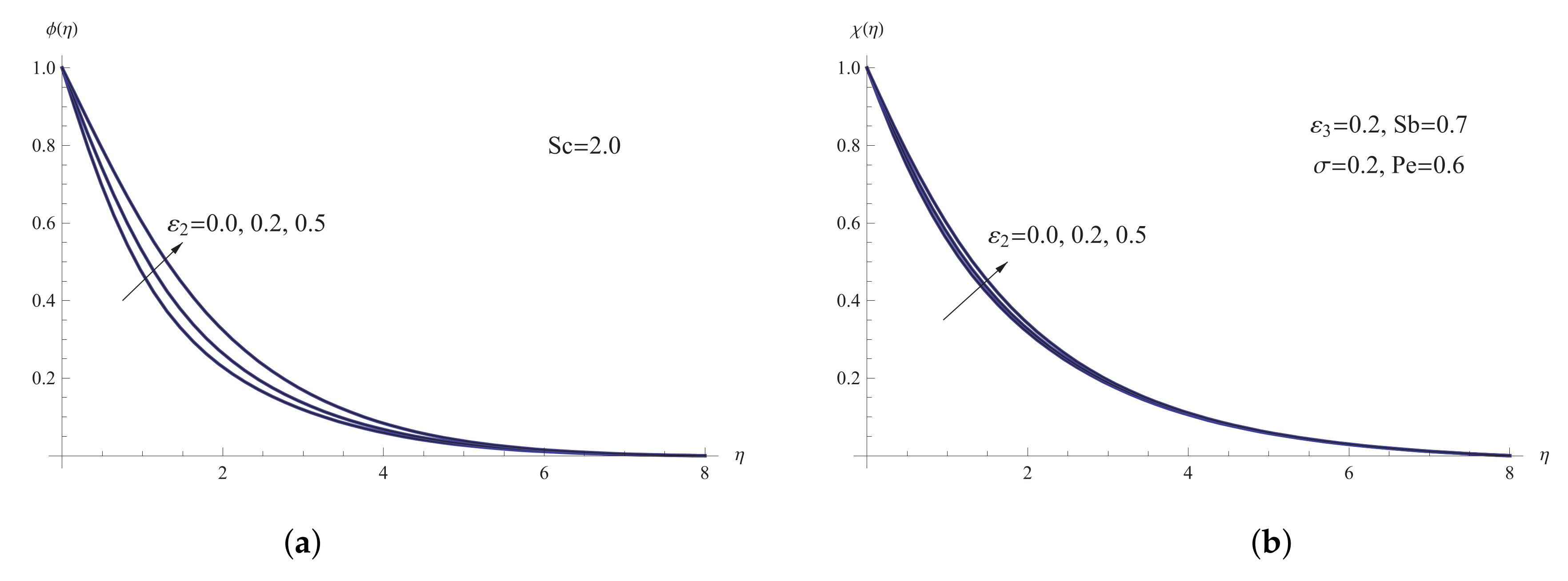
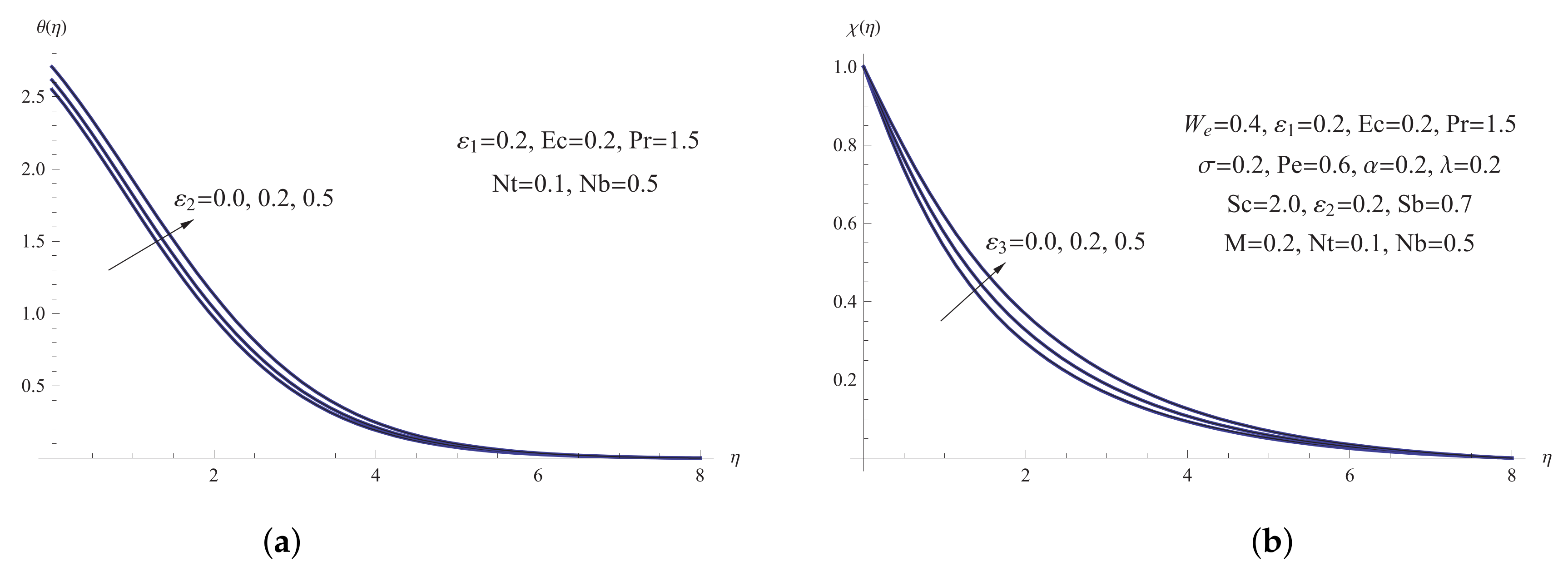
5. Results and Discussion
6. Conclusions
- The fluid temperature and thickness of the thermal boundary layer are improved by higher values of Eckert number, mass diffusivity parameter, viscosity parameter, and slip velocity parameter;
- The slip velocity parameter, viscosity parameter, and magnetic number are responsible for dropping the rate of mass heat transfer;
- The viscous forces are created by boosting the magnetic number, Eckert number, and viscosity parameter, causing a reduction in fluid velocity;
- The microorganism transfer rate is reduced by greater values of the magnetic number, slip velocity parameter, Eckert number, and viscosity parameter, whereas the thermal conductivity parameter improves it;
- The Nusselt number lowers when the magnetic number, slip velocity parameter, and viscosity parameter are estimated more accurately;
- In the future, we intend to expand on this research by looking into mass flux and how it affects flow through porous media.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Constant |
| Chemotaxis factor | |
| Magnetic field strength | |
| C | Concentration of nanofluid |
| Specific heat at constant pressure | |
| Nanofluid concentration at the surface | |
| Nanofluid concentration away from the surface | |
| Skin-friction coefficient | |
| Brownian diffusion coefficient | |
| Diffusivity of microorganisms | |
| Thermophoretic diffusion coefficient | |
| Eckret number | |
| f | Dimensionless stream function |
| M | Magnetic parameter |
| N | Density of motile microorganisms |
| Brownian motion parameter | |
| Nanoparticle Sherwood number | |
| Thermophoresis parameter | |
| Local Nusselt number | |
| Microbe concentration at the surface | |
| Ambient microbe concentration | |
| Prandtl number | |
| Surface heat flux | |
| Local Reynolds number | |
| Bioconvection Schmidt number | |
| Schmidt number | |
| Sherwood number | |
| T | Nanofluid temperature |
| Ambient temperature | |
| u | Velocity component in the x-direction |
| Sheet velocity | |
| v | Velocity component in the y-direction |
| Greatest speed of microorganism | |
| Cartesian coordinates | |
| Greek symbols | |
| Coefficient of viscosity | |
| Ambient nanofluid viscosity | |
| Nanofluid thermal conductivity | |
| Ambient nanofluid thermal conductivity | |
| Williamson coefficient | |
| Slip velocity parameter | |
| Bioconvection parameter | |
| Electrical conductivity | |
| Dimensionless density of motile microorganisms | |
| Dimensionless concentration | |
| Dimensionless temperature | |
| Density of the nanofluid | |
| Ambient density of the nanofluid | |
| Kinematic viscosity | |
| Ambient kinematic viscosity | |
| Viscosity parameter | |
| Similarity variable | |
| Thermal conductivity parameter | |
| Mass diffusivity parameter | |
| Microorganism diffusivity parameter | |
| Superscripts | |
| ′ | Differentiation with respect to |
| ∞ | Free stream condition |
| w | Wall condition |
References
- Choi, U.S.S. Enhancing thermal conductivity of fluids with nanoparticles, developments and application of non-Newtonian flows. ASME J. Heat Transf. 1995, 66, 99–105. [Google Scholar]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Vasu, V.; Rama Krishna, K.; Kumar, A.C.S. Analytical prediction of forced convective heat transfer of fluids embedded with nanostructured materials (nanofluids). Pramana J. Phys. 2007, 69, 411–421. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Lopez, R.J.; Khan, W.A. Heat and mass transfer in nanofluid over an unsteady stretching sheet using Buongiorno’s model. Eur. Phys. J. Plus 2016, 131, 16. [Google Scholar] [CrossRef]
- Alali, E.; Megahed, M.A. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev. 2022, 11, 463–472. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, S.T. Flow and heat transfer analysis of Williamson nanofluid. Appl. Nanosci. 2014, 4, 1005–1012. [Google Scholar] [CrossRef] [Green Version]
- Krishnamurthy, M.R.; Prassanakumara, B.C.; Gireesha, B.J.; Gorla, R.S.R. Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Eng. Sci. Technol. Int. J. 2016, 19, 53–61. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.; Malik, M.Y.; Salahuddin, T.; Rehman, K.U.; Naseer, M.; Khan, I. Numerical study for MHD peristaltic flow of Williamson nanofluid in an endoscope with partial slip and Journal wall properties. Int. Heat Mass Transf. 2017, 114, 1181–1187. [Google Scholar]
- Mabood, F.; Ibrahim, S.M.; Lorenzini, G.; Lorenzini, E. Radiation effects on Williamson nanofluid flow over a heated surface with magnetohydrodynamics. Int. J. Heat Technol. 2017, 35, 196–204. [Google Scholar] [CrossRef]
- Khan, M.; Salahuddin, T.; Malik, M.Y.; Mallawi, F.O. Change in viscosity of Williamson nanofluid flow due to thermal and solutal stratification. Int. J. Heat Mass Transf. 2018, 126, 941–948. [Google Scholar] [CrossRef]
- Loganathan, K.; Rajan, S. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J. Therm. Anal. Calorim. 2020, 141, 2599–2612. [Google Scholar] [CrossRef]
- Kamran, A.; Tanvir, A.; Taseer, M.; Metib, A. Heat transfer characteristics of MHD flow of Williamson nanofluid over an exponential permeable stretching curved surface with variable thermal conductivity. Case Stud. Therm. Eng. 2021, 28, 101544. [Google Scholar]
- Ahmed, K.; Akbar, T. Numerical investigation of magnetohydrodynamics Williamson nanofluid flow over an exponentially stretching surface. Adv. Mech. Eng. 2021, 13, 16878140211019875. [Google Scholar] [CrossRef]
- Waqas, S.H.; Khan, S.U.; Imran, M.; Bhatti, M.M. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Hayat, T.; Bashir, Z.; Qayyum, S.; Alsaedi, A. Nonlinear radiative flow of nanofluid in presence of gyrotactic microorganisms and magnetohydrodynamic. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3039–3055. [Google Scholar] [CrossRef]
- Khan, S.U.; Shehzad, S.A.; Ali, N. Bioconvection flow of magnetized Williamson nanoliquid with motile organisms and variable thermal conductivity. Appl. Nanosci. 2020, 10, 3325–3336. [Google Scholar] [CrossRef]
- Sankad, G.; Ishwar, M.; Dhange, M. Varying wall temperature and thermal radiation effects on MHD boundary layer liquid flow containing gyrotactic microorganisms. Partial. Differ. Equ. Appl. Math. 2021, 4, 100092. [Google Scholar]
- Yusuf, T.A.; Mabood, F.; Prasannakumara, B.C.; Ioannis, E.S. Magneto-bioconvection flow of Williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 2021, 6, 109. [Google Scholar] [CrossRef]
- Megahed, A.M. Improvement of heat transfer mechanism through a Maxwell fluid flow over a stretching sheet embedded in a porous medium and convectively heated. Math. Comput. Simul. 2021, 187, 97–109. [Google Scholar] [CrossRef]
- Amirsom, N.; Uddin, M.; Ismail, A. Three dimensional stagnation point flow of bionanofluid with variable transport properties. Alex. Eng. J. 2016, 55, 1983–1993. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Thirupathi, T.; Satya Narayana, P.V. Micropolar fluid flow induced due to a stretching sheet with heat source/sink and surface heat flux boundary condition effects. J. Appl. Comput. Mech. 2019, 5, 816–826. [Google Scholar]
- Zhou, S.S.; Khan, M.I.; Qayyum, S.; Prasannakumara, B.C.; Kumar, R.N.; Khan, S.U.; Gowda, R.P.; Chu, Y.M. Nonlinear mixed convective Williamson nanofluid flow with the suspension of gyrotactic microorganisms. Int. J. Mod. Phys. B 2021, 35, 2150145. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Q.; Javed, T. The modified decomposition method and Pade approximants for the MHD flow over a non-linear stretching sheet. Nonlinear Anal. Real World Appl. 2009, 10, 966–973. [Google Scholar] [CrossRef]
- Mabood, F.; Mastroberardino, A. Melting heat transfer on MHD convective flow of a nanofluid over a stretching sheet with viscous dissipation and second order slip. J. Taiwan Inst. Chem. Eng. 2015, 57, 62–68. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, W.A.; Waqas, M.; Kadry, S.; Chu, Y.M.; Nazeer, M. Role of dipole interactions in Darcy-Forchheimer first-order velocity slip nanofluid flow of Williamson model with Robin conditions. Appl. Nanosci. 2020, 10, 5343–5350. [Google Scholar] [CrossRef]

| M | Hayat et al. [25] | Present Work |
|---|---|---|
| 0 | 1.00000 | 1.000000001 |
| 1 | 1.41421 | 1.414207989 |
| 5 | 2.44948 | 2.449479804 |
| 10 | 3.31662 | 3.316624669 |
| M | Mabood and Mastroberardino [26] | Present Work |
|---|---|---|
| 10 | 3.3166247 | 3.316624669 |
| 50 | 7.1414284 | 7.141428353 |
| 100 | 10.049875 | 10.04988001 |
| 500 | 22.383029 | 22.38302853 |
| 1000 | 31.638584 | 31.63858342 |
| M | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.600491 | 0.412248 | 0.579751 | 0.542643 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505161 |
| 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.670821 | 0.343003 | 0.487964 | 0.457065 |
| 0.2 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.746086 | 0.395622 | 0.577339 | 0.537076 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505161 |
| 0.2 | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.549154 | 0.367881 | 0.508204 | 0.477407 |
| 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.796625 | 0.418147 | 0.595505 | 0.557137 |
| 0.2 | 0.2 | 0.1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.719606 | 0.402434 | 0.571268 | 0.534082 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505161 |
| 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.2 | 0.584102 | 0.285624 | 0.488075 | 0.473978 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505161 |
| 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.2 | 0.660554 | 0.459025 | 0.563998 | 0.519245 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.639832 | 0.392205 | 0.670139 | 0.557869 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505161 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.629451 | 0.369405 | 0.418768 | 0.455989 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.576694 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.505051 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.635508 | 0.382405 | 0.540179 | 0.429340 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 0.647482 | 0.411927 | 0.540144 | 0.507516 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.617545 | 0.345041 | 0.539406 | 0.501026 |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.0 | 0.587747 | 0.296533 | 0.536391 | 0.493252 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Areshi, M.; Alrihieli, H.; Alali, E.; Megahed, A.M. Temperature Distribution in the Flow of a Viscous Incompressible Non-Newtonian Williamson Nanofluid Saturated by Gyrotactic Microorganisms. Mathematics 2022, 10, 1256. https://doi.org/10.3390/math10081256
Areshi M, Alrihieli H, Alali E, Megahed AM. Temperature Distribution in the Flow of a Viscous Incompressible Non-Newtonian Williamson Nanofluid Saturated by Gyrotactic Microorganisms. Mathematics. 2022; 10(8):1256. https://doi.org/10.3390/math10081256
Chicago/Turabian StyleAreshi, Mounirah, Haifaa Alrihieli, Elham Alali, and Ahmed M. Megahed. 2022. "Temperature Distribution in the Flow of a Viscous Incompressible Non-Newtonian Williamson Nanofluid Saturated by Gyrotactic Microorganisms" Mathematics 10, no. 8: 1256. https://doi.org/10.3390/math10081256




