Stress State in an Eccentric Elastic Ring Loaded Symmetrically by Concentrated Forces
Abstract
:1. Introduction
2. Theoretical Analysis
2.1. Stress Function in Bipolar Coordinates for a Compact Disk
- obtaining the Airy function for the compact disk;
- finding the auxiliary potential required for generating the total potential.
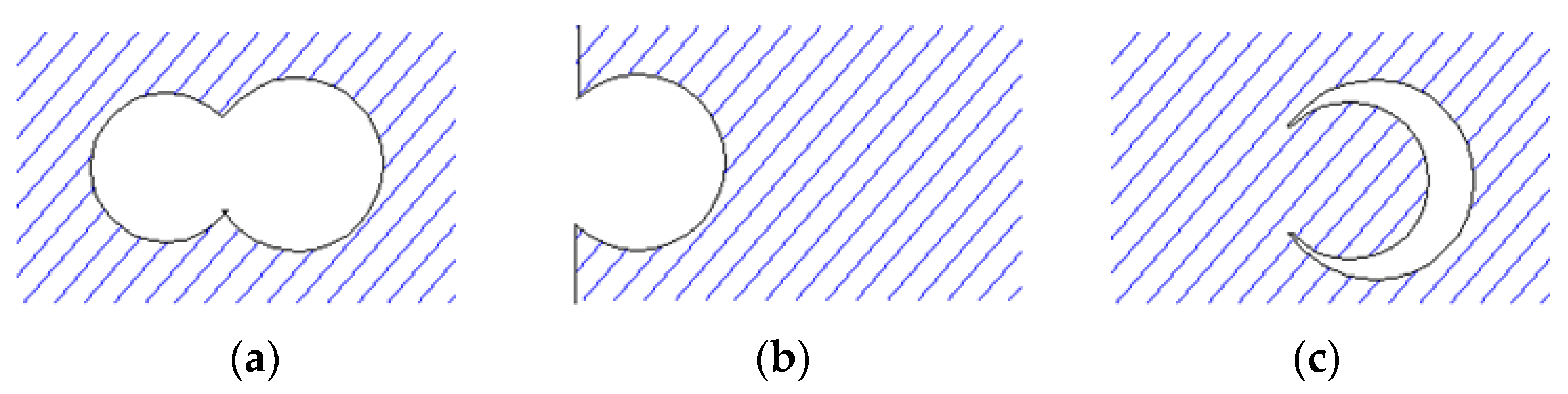
2.2. Stress Function in Bipolar Coordinates for an Eccentric Ring
- -
- for a given sequence of values of the number of terms of Fourier series, the components of the bipolar stresses are represented on the contour of the hole;
- -
- the fulfilment of boundary conditions is examined.
3. Results
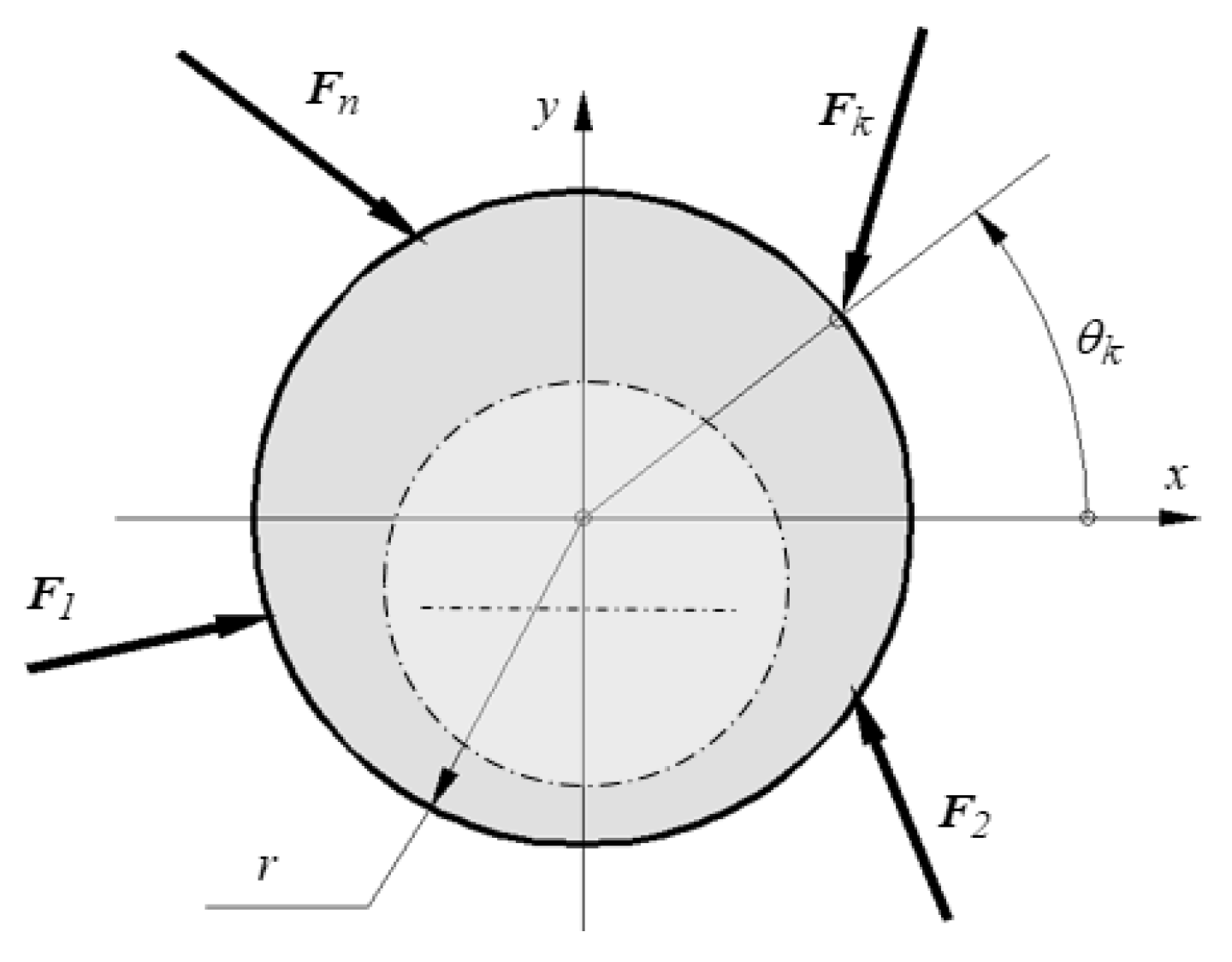
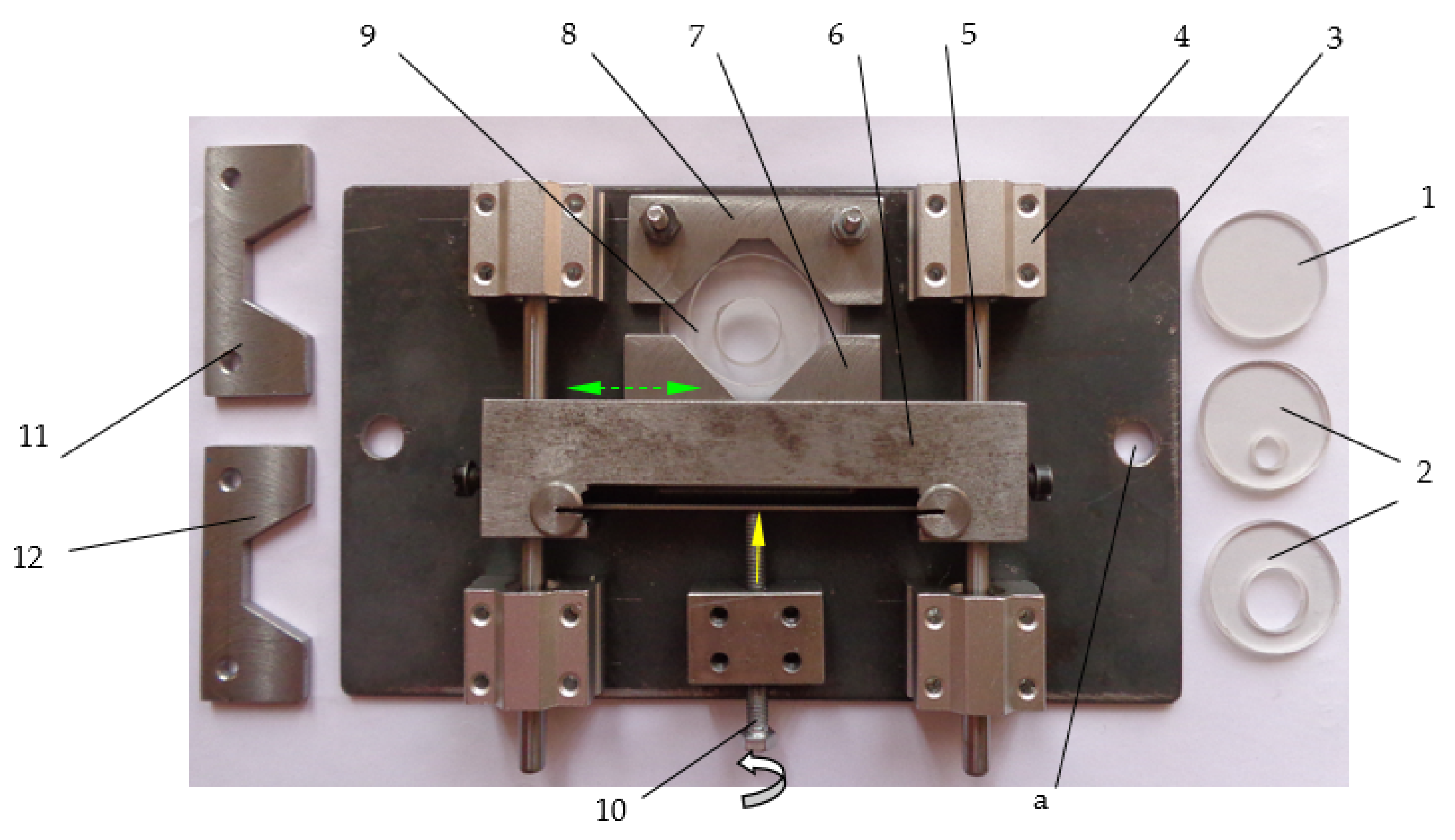
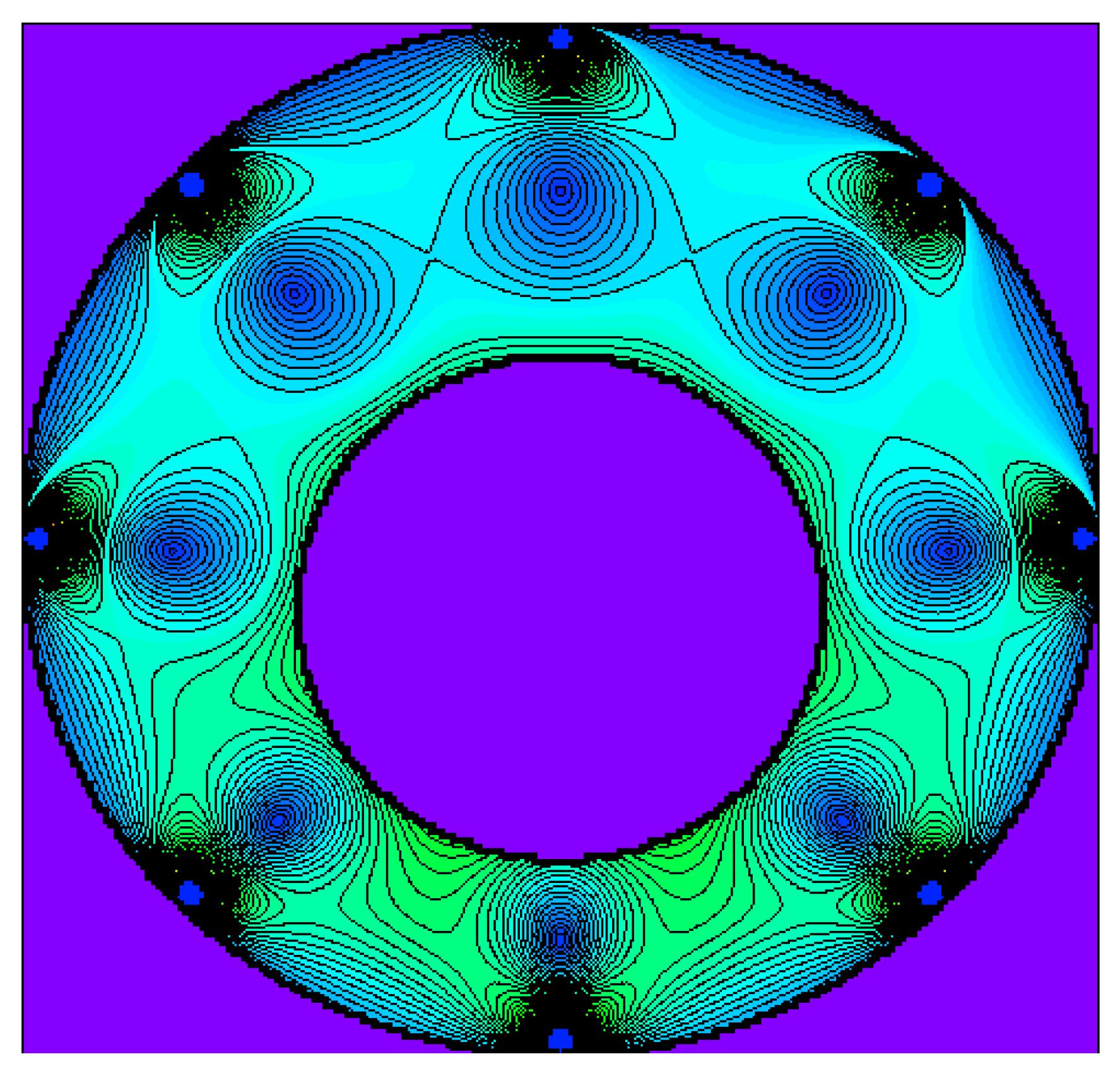
3.1. Experimental Device
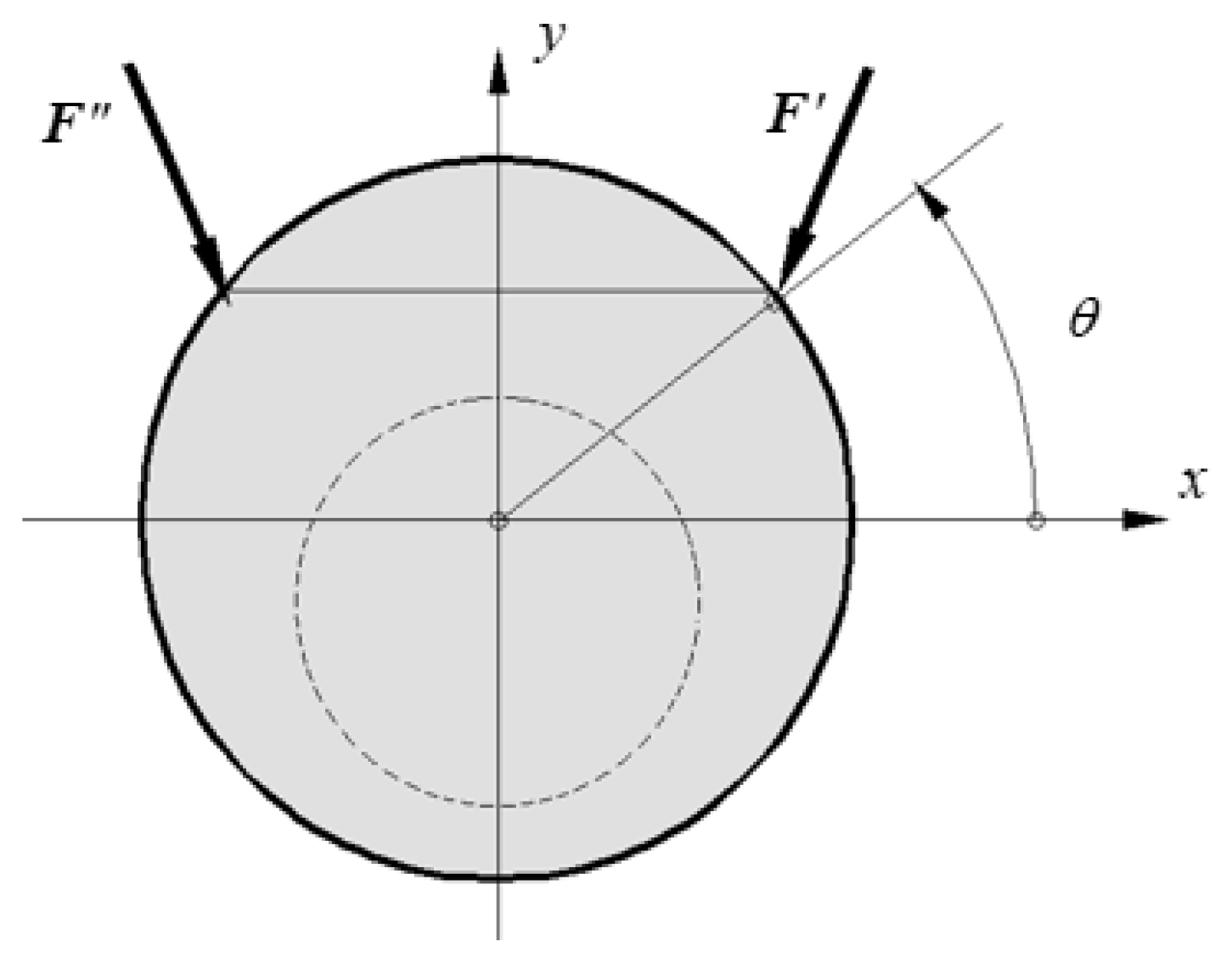
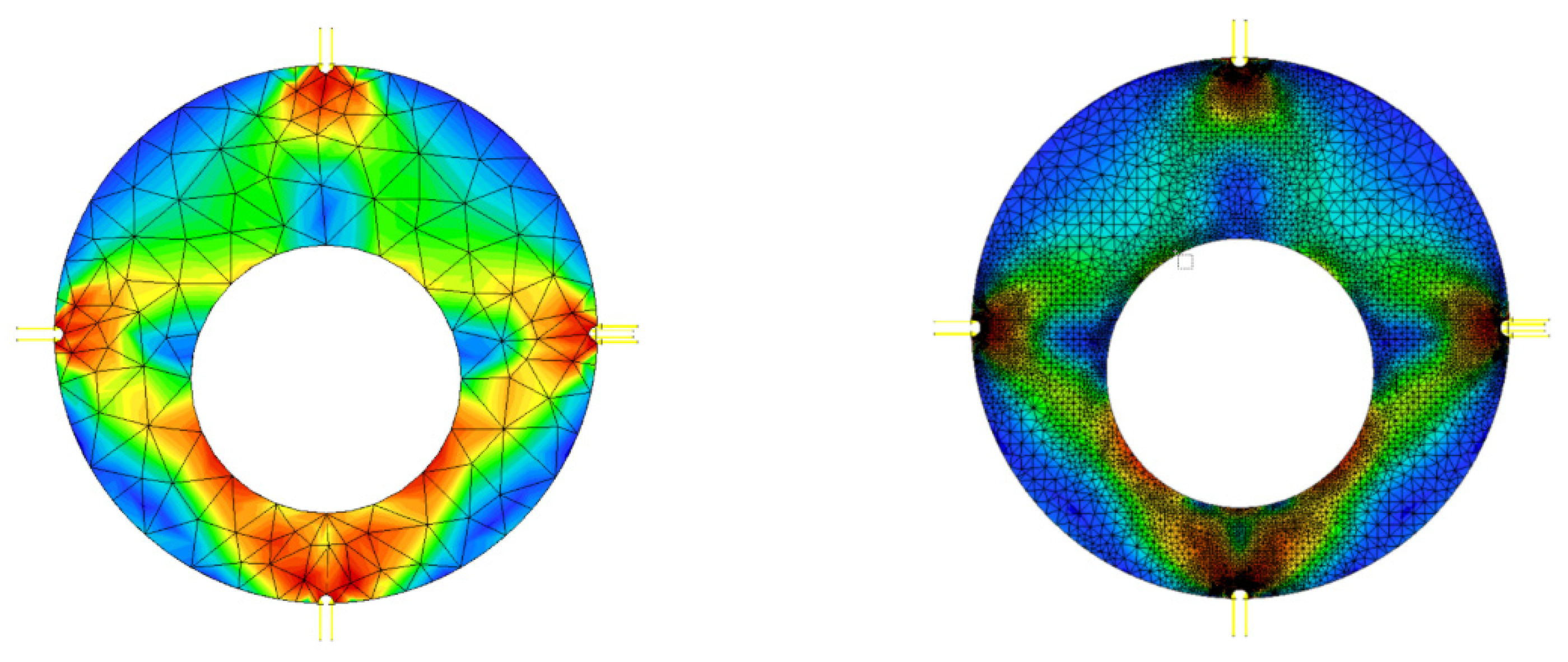
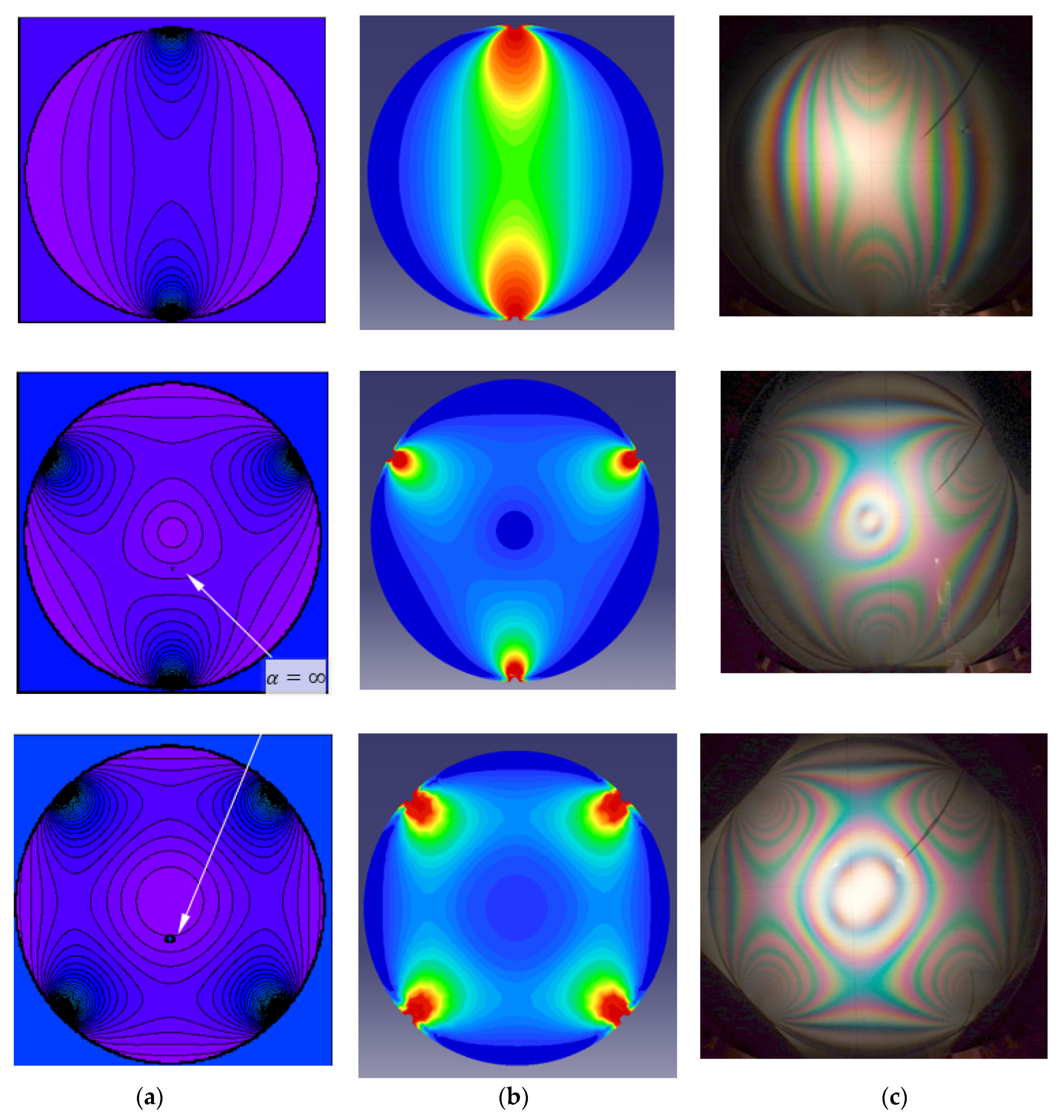
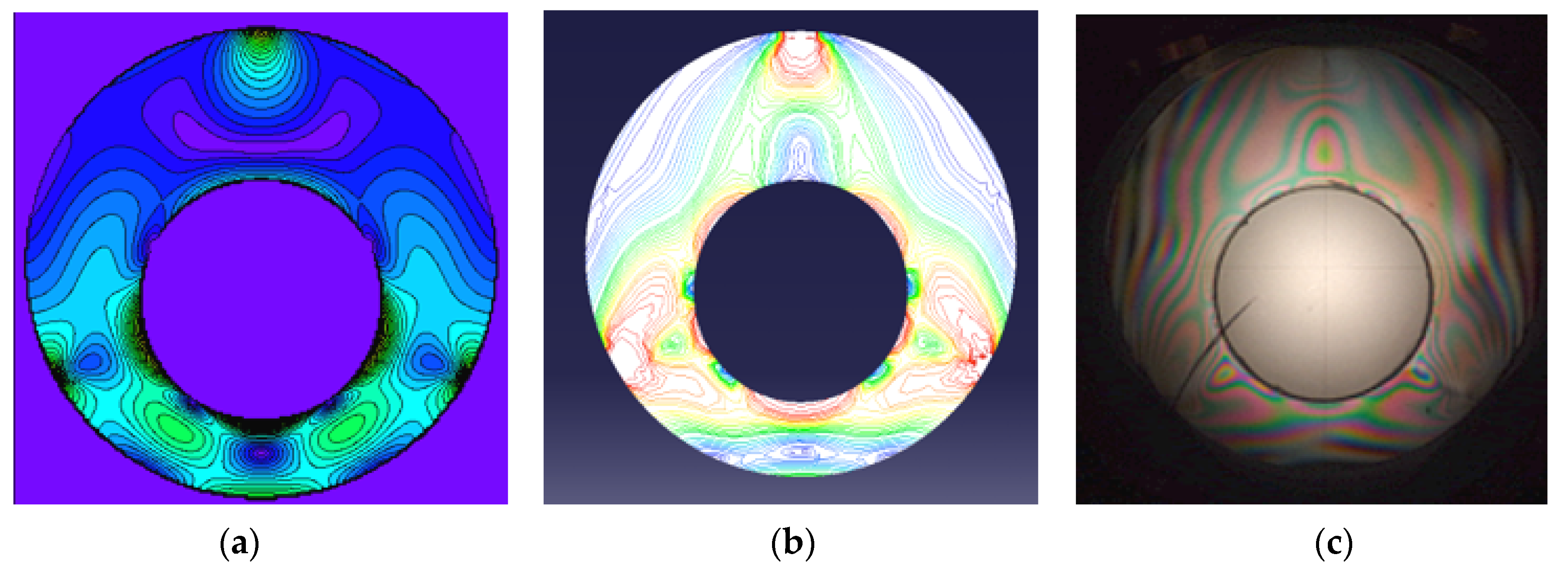
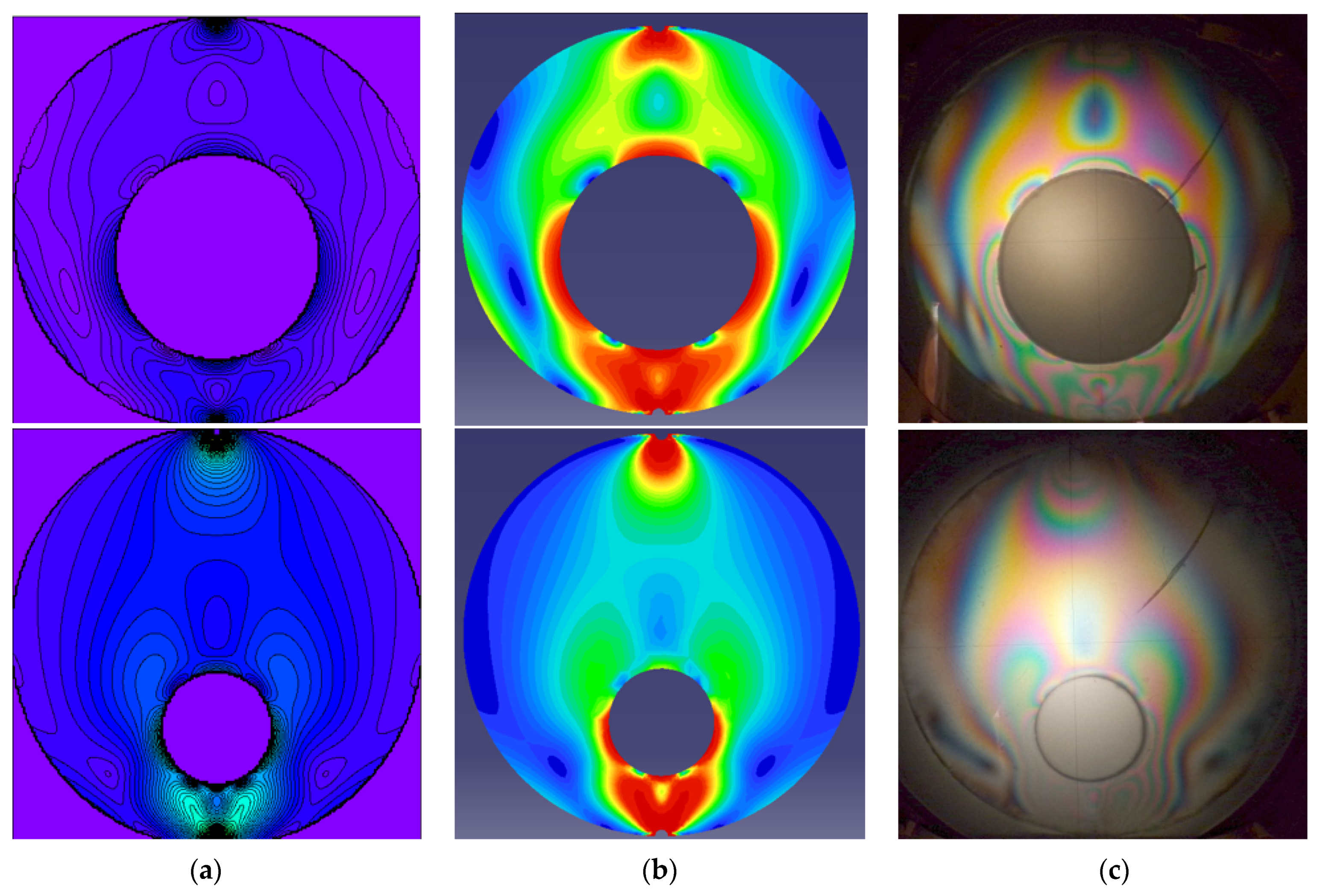
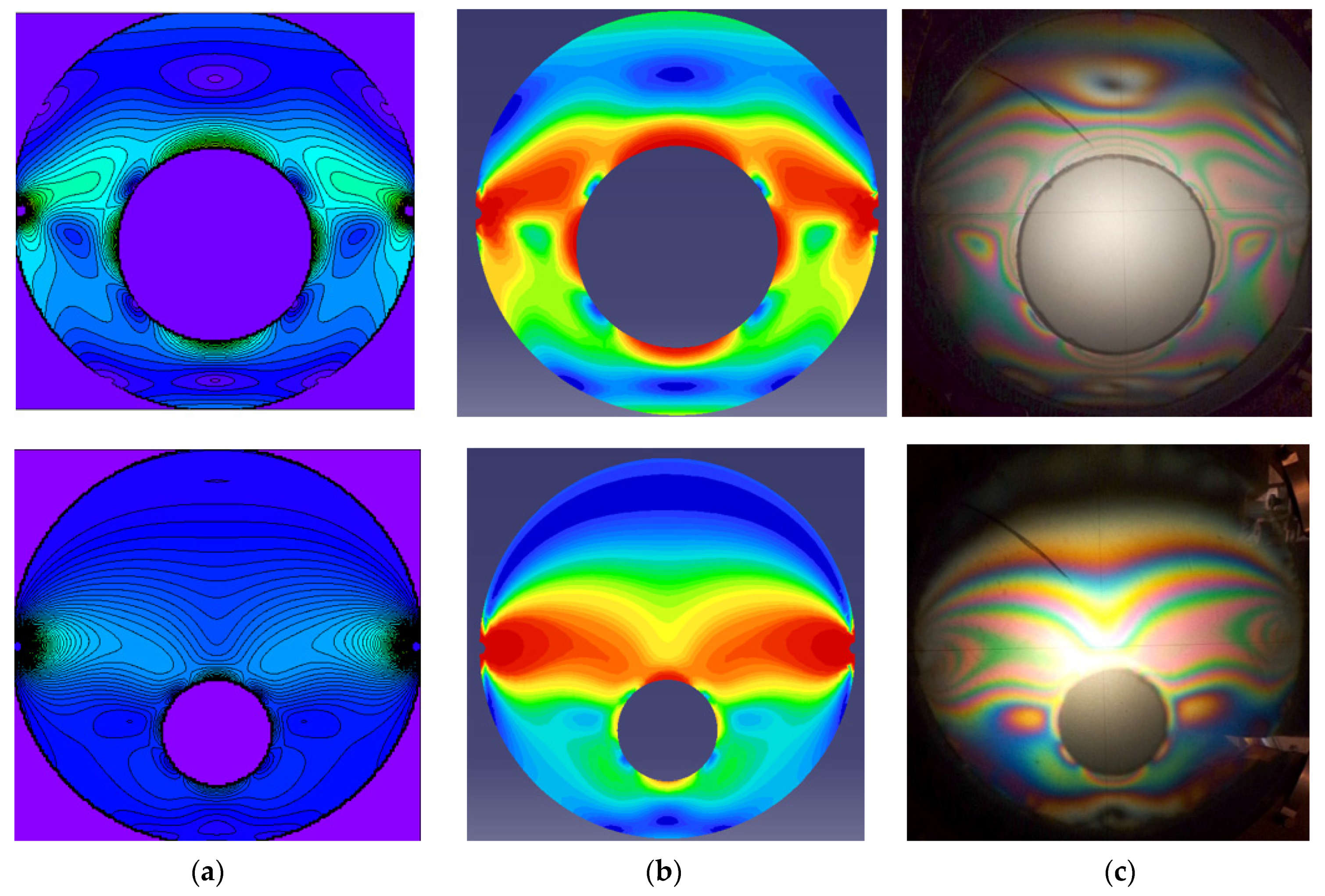
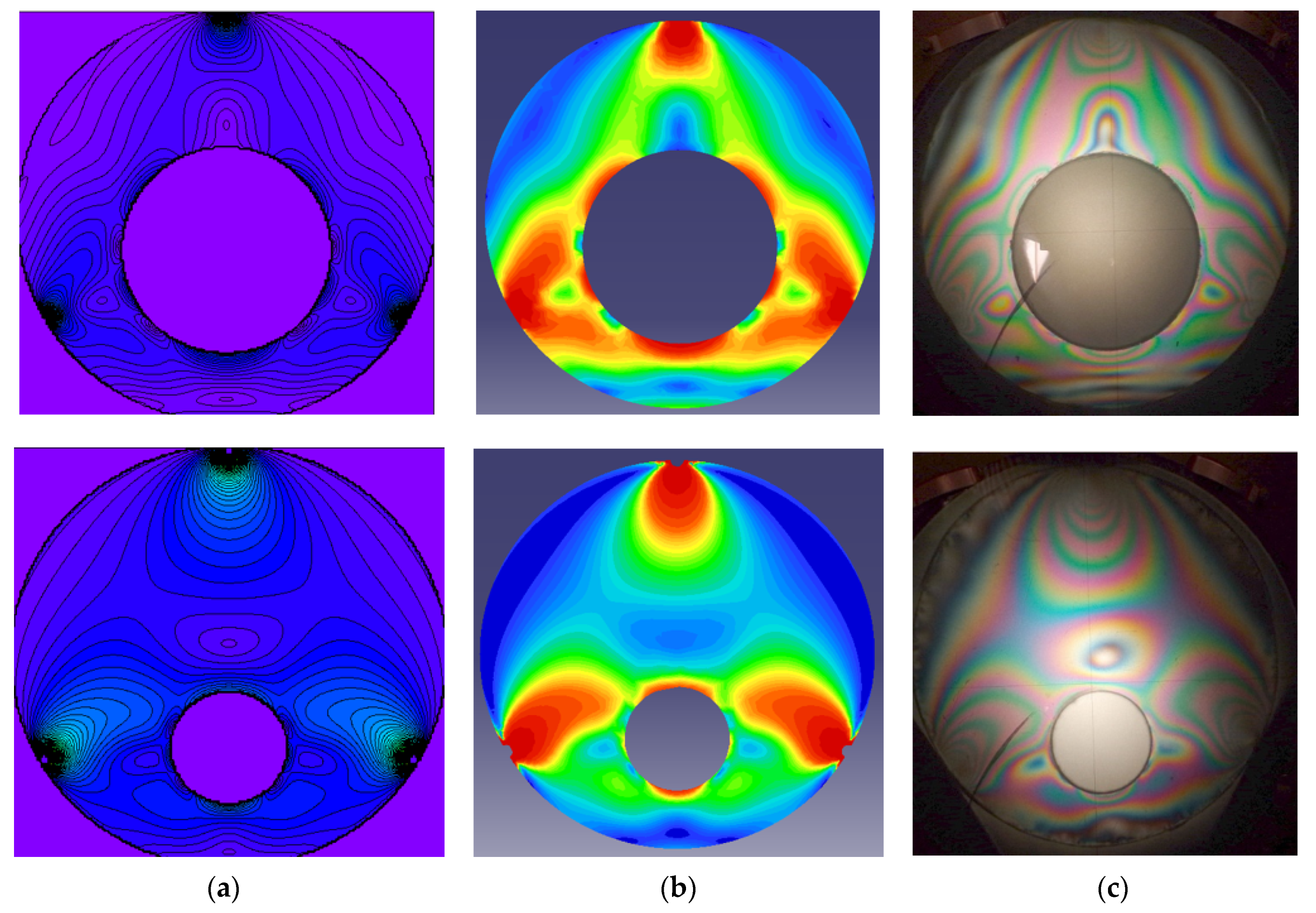
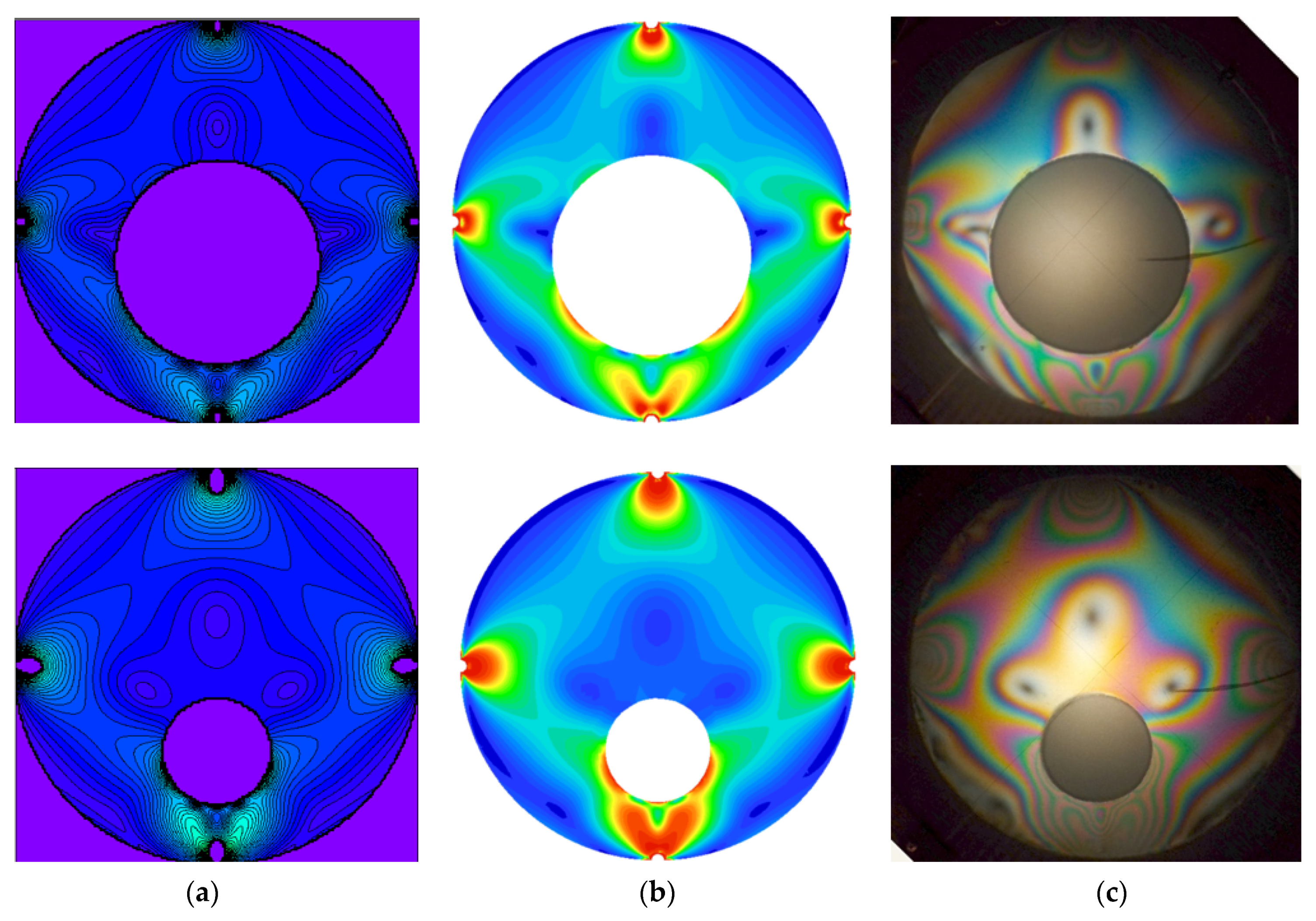
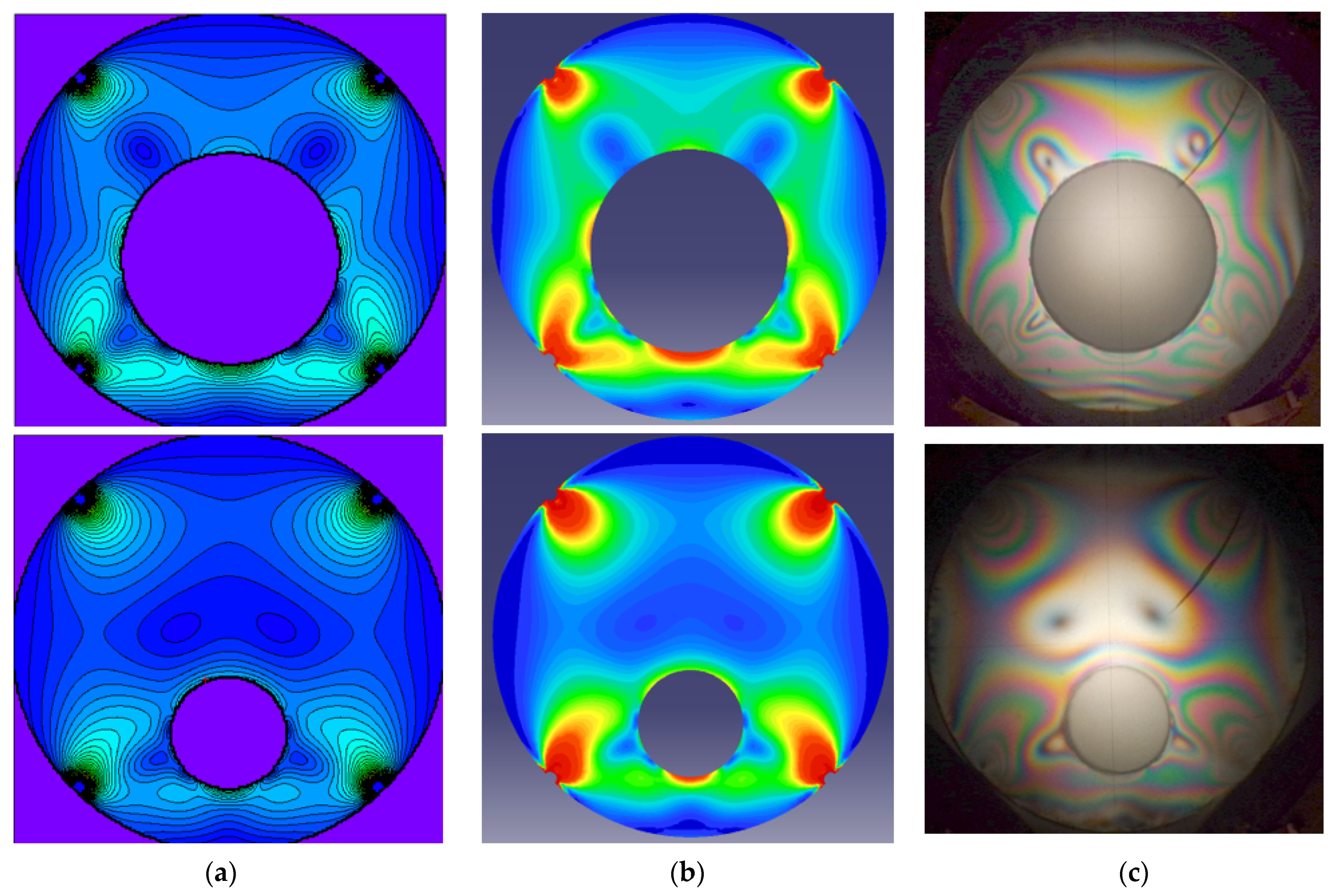
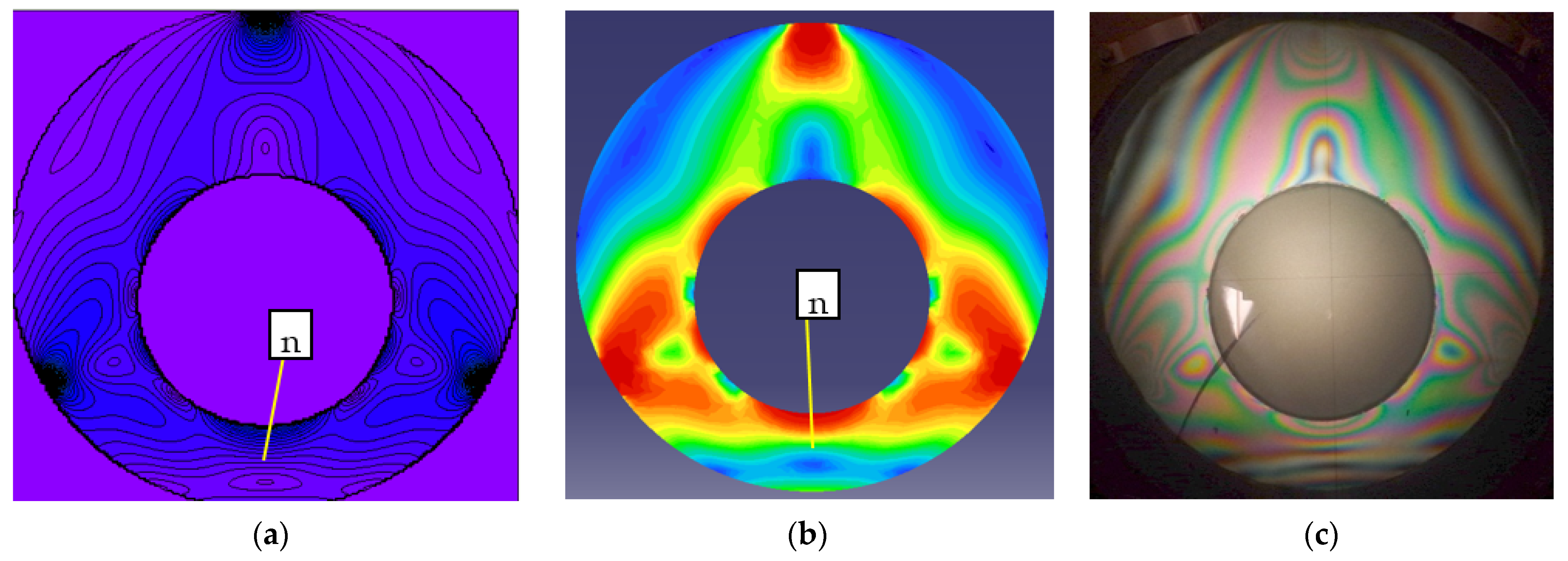
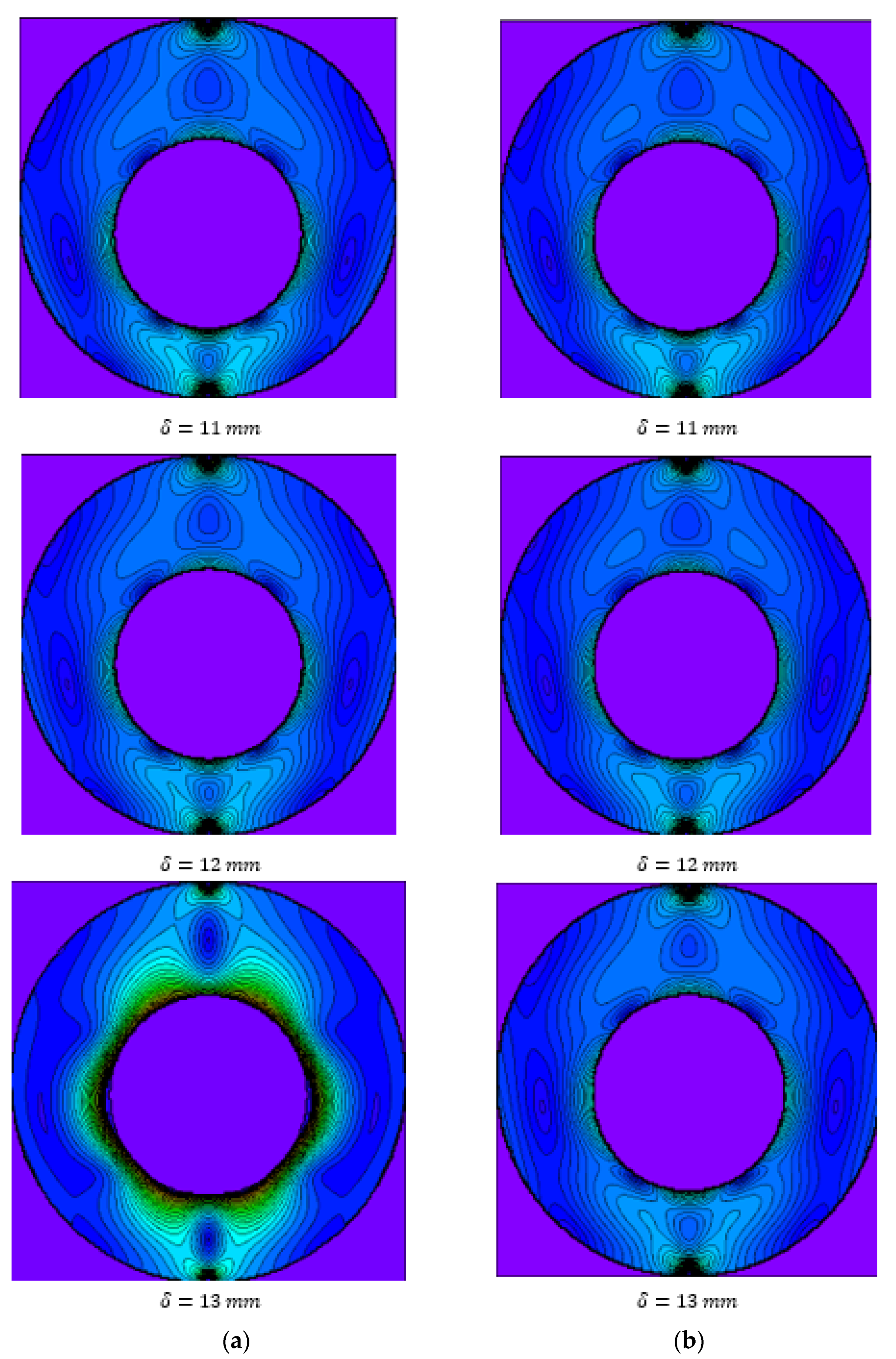
3.2. Comparison of Analytical, Numerical and Experimental Results
- Equation (32) is used for ;
- for , the equations are as follows:
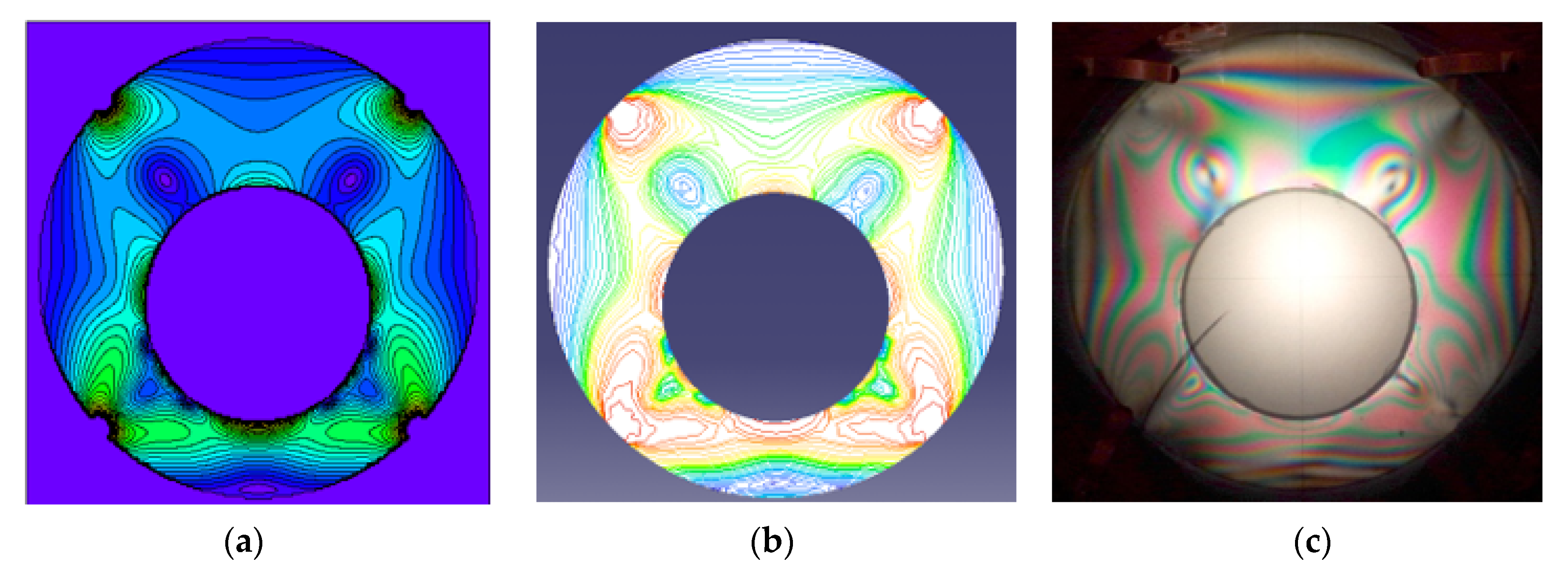
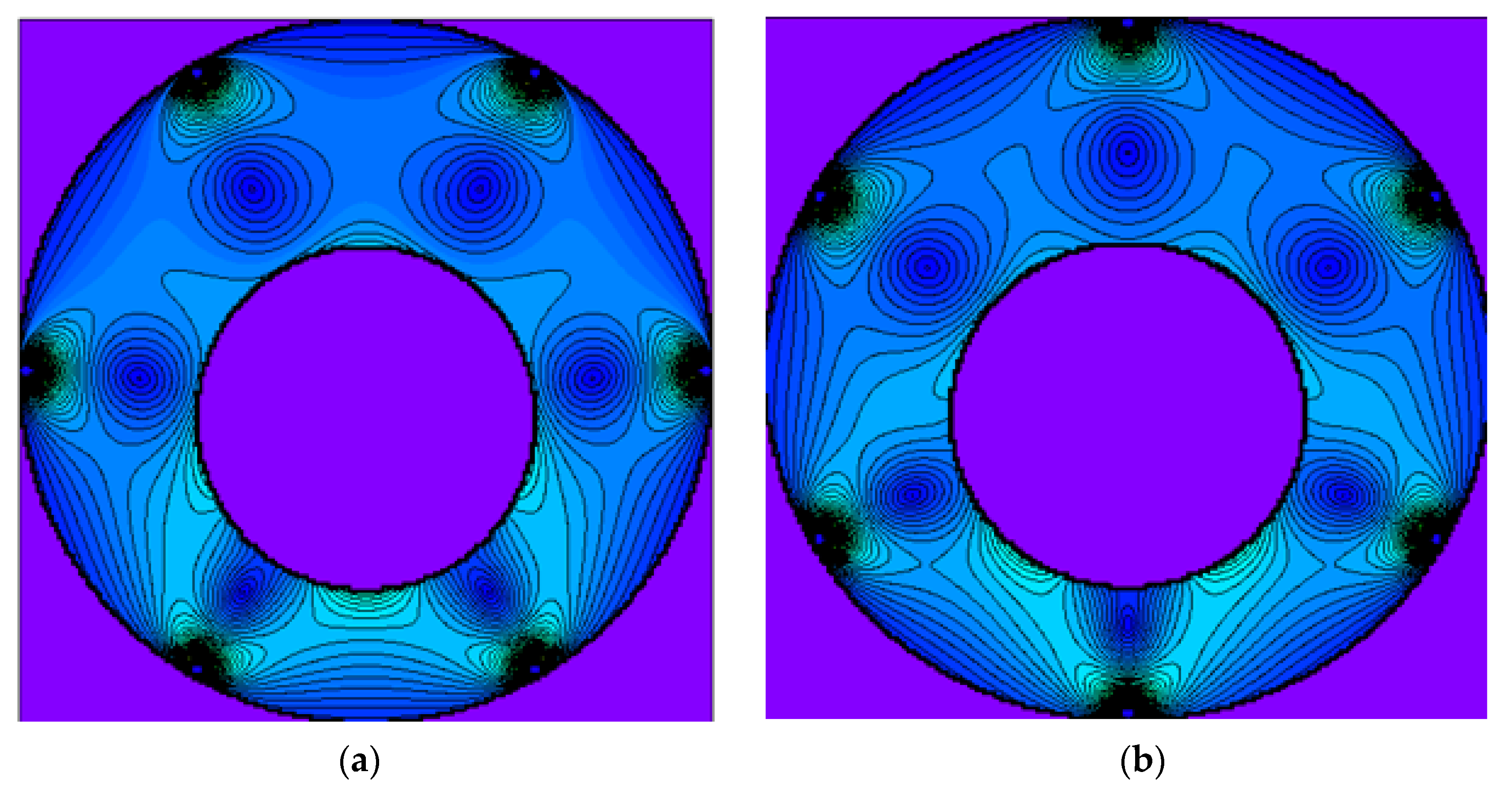
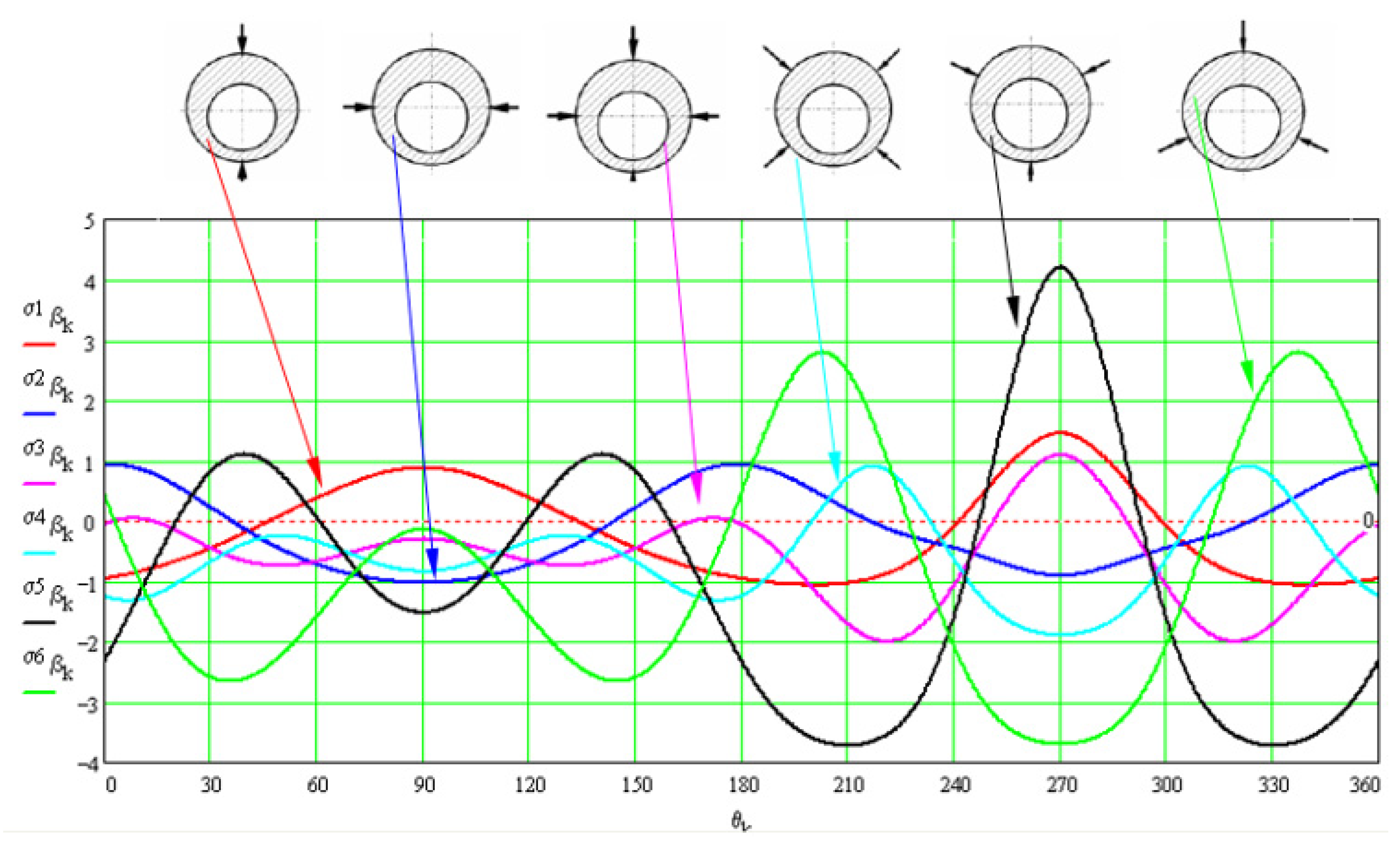
3.3. Stress Concentration Effect of the Hole
4. Discussion
5. Conclusions
- The paper presents the analytical, numerical and experimental analysis of the stress state in an elastic eccentric ring loaded on the outer boundary by a system of concentrated forces, symmetrical with respect to the axis of the centres.
- The analytical solution assumes finding the Airy function for the eccentric ring as a sum of two potentials expressed in bipolar coordinates, one for the compact disk and the other the auxiliary potential necessary to impose boundary conditions. A particular situation refers to imposing boundary conditions upon the stress state on the outer contour (compared to the conditions imposed onto concentrated forces) which leads to very cumbersome calculus. These mathematical aspects are revealed in the paper.
- A contribution to be highlighted is obtaining the optimum number of terms of the total potential form the Fourier series expansion for the compact disk potential.
- The theoretical solution was validated by numerical analysis performed by means of the FEM, and a good agreement was found between the principal shear stresses.
- An experimental method was also used for qualitative validation of the analytical results. The photoelastic images of the stresses obtained on the elastic specimen reveal the same principal elements, the shape of the isochromatic curves and the position of the stress concentration. A broad photoelastic quantitative analysis necessitates extra resources and will be the subject of future research.
- We must emphasise the excellent agreement between the isochromatic patterns found analytically, numerically and experimentally for two geometries of the ring and six different symmetrical loadings that proves the correctness of the theoretical solution.
- The analytical solution can be applied for symmetrical loadings with distributed normal forces considering that the distributed forces are equivalent to a system of concentrated forces and using the superposition principle. The experimental device constructed for symmetrical loading of the specimens can be adapted to the general loading state.
- Developing a theoretical model of an elastic ring loaded on the outer contour with arbitrary concentrated forces.
- Developing a general theoretical model of an elastic ring loaded on both contours with arbitrary concentrated forces.
- As an experiment, obtaining a more precise isoclinic grid using a digital polariscope for the studied models.
- The isoclinic grids are extremely important since they contain the singular points of the model, the points through which all the isoclinic curves pass. The positions of the singular points are intrinsic characteristics of the stress state, and the coordinates of these points can be used as parameters for the quantitative validation of the models.
- Using the lateral extensometers on the polariscope in establishing the isopachic curves for the complete characterisation of the stress state from the elastic eccentric ring.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tikhonov, A.N.; Samarskii, A.A. Equations of Mathematical Physics (Dover Books on Physics), Reprint ed.; Courier Corporation: North Chelmsford, MA, USA, 2011. [Google Scholar]
- Kozhanov, A.I. Hyperbolic Equations with Unknown Coefficients. Symmetry 2020, 12, 1539. [Google Scholar] [CrossRef]
- Busto, S.; Dumbser, M.; Río-Martín, L. Staggered Semi-Implicit Hybrid Finite Volume/Finite Element Schemes for Turbulent and Non-Newtonian Flows. Mathematics 2021, 9, 2972. [Google Scholar] [CrossRef]
- Bschorr, O.; Raida, H.-J. One-Way Wave Equation Derived from Impedance Theorem. Acoustics 2020, 2, 12. [Google Scholar] [CrossRef] [Green Version]
- Ayub, A.; Sabir, Z.; Shah, S.Z.H.; Mahmoud, S.R.; Algarni, A.; Sadat, R.; Ali, M.R. Aspects of infinite shear rate viscosity and heat transport of magnetized Carreau nanofluid. Eur. Phys. J. Plus 2022, 137, 247. [Google Scholar] [CrossRef]
- Shah, S.L.; Ayub, A.; Dehraj, S.; Wahab, H.A.; Sagayam, K.M.; Ali, M.R.; Sadat, R.; Sabir, Z. Magnetic dipole aspect of binary chemical reactive Cross nanofluid and heat transport over composite cylindrical panels. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Wahab, H.A.; Balubaid, M.; Mahmoud, S.R.; Ali, M.R.; Sadat, R. Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Mousa, M.M.; Ali, M.R.; Ma, W.X. A combined method for simulating MHD convection in square cavities through localized heating by method of line and penalty-artificial compressibility. J. Taibah Univ. Sci. 2021, 15, 208–217. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Shah, S.Z.H.; Wahab, H.A.; Sadat, R.; Ali, M.R. Effects of homogeneous-heterogeneous and Lorentz forces on 3-D radiative magnetized cross nanofluid using two rotating disks. Int. Commun. Heat Mass Transf. 2022, 130, 105778. [Google Scholar] [CrossRef]
- Solomon, L. Elasticite Lineaire; Masson et Cie Editeurs: Paris, France, 1968; p. 753. [Google Scholar]
- Popinceanu, N.; Gafitanu, M.; Diaconescu, E.; Cretu, S.; Mocanu, D.R. Fundamental Problems of Rolling Contact (in Romanian) Probleme Fundamentale Ale Contactului Cu Rostogolire; Technical University of Cluj-Napoca: Bucuresti, Romania, 1985; p. 454. [Google Scholar]
- Jafari, M.; Hoseyni, S.A.M.; Altenbach, H.; Craciun, E.-M. Optimum Design of Infinite Perforated Orthotropic and Isotropic Plates. Mathematics 2020, 8, 569. [Google Scholar] [CrossRef] [Green Version]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. 1959, 252, 561–569. [Google Scholar]
- Kirsch, G. Die Theorie der Elastizitat und die Bedurfnisse der Festigkeitslehre. Zantralblatt Verlin Dtsch. Ing. 1898, 42, 797–807. [Google Scholar]
- Horii, H.; Nemat-Nasser, S. Elastic fields of interacting inhomogeneities. Int. J. Solids Struct. 1985, 21, 731–745. [Google Scholar] [CrossRef]
- Greenwood, J.A. Exact formulae for stresses around circular holes and inclusions. Int. J. Mech. Sci. 1989, 31, 219–227. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 2nd ed; McGraw-Hill Book Company: New York, NY, USA, 1951; pp. 11–27. [Google Scholar]
- Flamant, A. Sur la répartition des pressions dans un solide rectangulaire chargé transversalement. Comptes Rendus L’académiedes Sci. 1892, 114, 1465. [Google Scholar]
- Hertz, H. On the distribution of stress in an elastic right circular cylinder. In Miscellaneous Papers; Wentworth Press: London, UK, 1884; p. 15. Available online: https://archive.org/details/miscellaneouspap00hertuoft/page/n7/mode/2up?ref=ol&view=theater (accessed on 23 February 2022).
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Berlin/Heidelberg, Germany, 1977; p. 732. [Google Scholar]
- Pöschl, T. Uber eine particular losung des biharmonischen problems für den anbeuraum einer ellipse. Mat. Z. 1921, 11, 89–96. [Google Scholar] [CrossRef] [Green Version]
- Savin, G.N. Stress Concentration around Holes; Pergamon Press: Oxford, UK, 1961; p. 430. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F.; Zhuming, B. Peterson’s Stress Concentration Factors; John Wiley & Sons: Hoboken, NJ, USA, 2008; p. 560. [Google Scholar]
- Howland, R.C.; Knight, R.C. Stress functions for a plate containing groups of circular holes. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 238, 357–392. [Google Scholar]
- Green, A.E. General bi-harmonic analysis for a plate containing circular holes. Proc. R. Soc. A Math. Phys. Eng. Sci. 1940, 176, 121–139. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Yue, Z.Q.; Lee, C.F.; Tham, L.G.; Yang, Z.F. Stress solution of multiple elliptic hole problem in plane elasticity. J. Eng. Mech. 2003, 129, 1394–1407. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, A. An Analytic Algorithm of Stresses for Any Double Hole Problem in Plane Elastostatics. J. Appl. Mech. 2001, 68, 350–353. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Lu, A.Z.; Yue, Z.Q.; Yang, Z.F. An efficient and accurate iterative stress solution for an infinite elastic plate around two elliptic holes, subjected to uniform loads on the hole boundaries and at infinity. Eur. J. Mech. A Solids 2009, 28, 189–193. [Google Scholar] [CrossRef]
- Lu, A.-Z.; Xu, Z.; Zhang, N. Stress analytical solution for an infinite plane containing two holes. Int. J. Mech. Sci. 2017, 128–129, 224–234. [Google Scholar] [CrossRef]
- Zeng, X.-T.; Lu, A.-Z.; Zhang, N. Analytical stress solution for an infinite plate containing two oval holes. Eur. J. Mech. A Solids 2018, 67, 291–304. [Google Scholar] [CrossRef]
- Jeffery, G.B. Plane stress and plane strain in bipolar coordinates. Philos. Trans. R. Soc. Lond. 1920, 221, 582–593. [Google Scholar]
- Khomasuridze, N. Solution of some elasticity boundary value problems in bipolar coordinates. Acta Mech. 2007, 189, 207–224. [Google Scholar] [CrossRef]
- Chen, J.T.; Shieh, H.C.; Lee, Y.T.; Lee, J.W. Bipolar coordinates, image method and the method of fundamental solutions for Green’s functions of Laplace problems containing circular boundaries. Eng. Anal. Bound. Elem. 2011, 35, 236–243. [Google Scholar] [CrossRef]
- Ling, C.-B. On the stresses in a plate containing two circular holes. J. Appl. Phys. 1948, 19, 77–82. [Google Scholar] [CrossRef]
- Zimmerman, R.W. Second-Order Approximation for the Compression of an Elastic Plate Containing a Pair of Circular Holes. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Und Mech. 1988, 68, 575–577. [Google Scholar] [CrossRef]
- Haddon, R.A. Stresses in an infinite plate with two unequal circular holes. Q. J. Mech. Appl. Math. 1967, 20, 277–291. [Google Scholar] [CrossRef]
- Salerno, V.L.; Mahoney, J.B. Stress solution for an infinite plate containing two arbitrary circular holes under equal biaxial stresses. J. Manuf. Sci. Eng. 1968, 90, 656–665. [Google Scholar] [CrossRef]
- Ting, K.; Chen, K.T.; Yang, W.S. Applied alternating method to analyze the stress concentration around interacting multiple circular holes in an infinite domain. Int. J. Solids Struct. 1999, 36, 533–556. [Google Scholar] [CrossRef]
- Toshihiro, I.; Kazyu, M. Stress concentrations in a plate with two unequal circular holes. Int. J. Eng. Sci. 1980, 18, 1077–1090. [Google Scholar] [CrossRef]
- Lim, M.; Yu, S. Stress concentration for two nearly touching circular holes. arXiv 2017, arXiv:1705.10400. [Google Scholar]
- Barjansky, A. Distorsion of Boussinesq Field Due to Circular Hole. Quart. Appl. Math. 1944, 2, 16–30. [Google Scholar] [CrossRef] [Green Version]
- Evan-Iwanowski, R.M. Distortion of Boussinesq field by circular hole. Quart. Appl. Math. 1962, 19, 359–365. [Google Scholar] [CrossRef] [Green Version]
- Alaci, S.; Diaconescu, E. Concentrated force acting on the boundary of an elastic half-plane with circular hole. In Proceedings of the 2nd World Tribology Congress, Vienna, Austria, 3–7 September 2001; pp. 175–177. [Google Scholar]
- Alaci, S. Applications of Bipolar Coordinates in Plane Elastostatics. Part I. Theoretical Results; Matrixrom: Bucuresti, Romania, 2020; pp. 259–290. (In Romanian) [Google Scholar]
- Proskura, A.V.; Freidin, A.; Kolesnikova, A.L.; Morozov, N.F.; Romanov, A.E. Plane elasticity solution for a half-space weakened by a circular hole and loaded by a concentrated force. J. Mech. Behav. Mater. 2013, 22, 11–25. [Google Scholar] [CrossRef]
- Tamate, O. On a contact problem of an elastic half-plane with a circular hole: 2nd Report, The Case of Frictionless Contact. Trans. Jpn. Soc. Mech. Eng. 1964, 30, 1212–1219. [Google Scholar] [CrossRef]
- Sen Gupta, A.M. Stresses due to diametral forces on a circular disk with an eccentric hole. J. App. Mech. 1955, 22, 263–266. [Google Scholar] [CrossRef]
- Gupta, D.P. Stresses due to diametral forces in tension on an eccentric hole of a circular disc. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 1960, 40, 246–252. [Google Scholar] [CrossRef]
- Solov’ev, I.I. The action of a concentrated force on an eccentric ring. J. Appl. Math. Mech. 1958, 22, 701–705. [Google Scholar] [CrossRef]
- Desai, P.; Pandya, V. Airy’s Stress Solution for Isotropic Rings with Eccentric Hole Subjected to Pressure. Int. J. Mech. Solids 2017, 12, 211–233. [Google Scholar]
- Radi, E.; Strozzi, A. Jeffery solution for an elastic disk containing a sliding eccentric circular inclusion assembled by interference fit. Int. J. Solids Struct. 2009, 46, 4515–4526. [Google Scholar] [CrossRef] [Green Version]
- Richardson, M.K. Interference stresses in a half plane containing an elastic disk of the same material. J. Appl. Mech. 1969, 36, 128–130. [Google Scholar] [CrossRef]
- Herráez-Galindo, C.; Torres-Lagares, D.; Martínez-González, Á.-J.; Pérez-Velasco, A.; Torres-Carranza, E.; Serrera-Figallo, M.-A.; Gutiérrez-Pérez, J.-L. A Comparison of Photoelastic and Finite Elements Analysis in Internal Connection and Bone Level Dental Implants. Metals 2020, 10, 648. [Google Scholar] [CrossRef]
- Gao, G.; Mao, D.; Jiang, R.; Li, Z.; Liu, X.; Lei, B.; Bian, J.; Wu, S.; Fan, B. Investigation of Photoelastic Property and Stress Analysis for Optical Polyimide Membrane through Stress Birefringence Method. Coatings 2020, 10, 56. [Google Scholar] [CrossRef] [Green Version]
- Nishii, Y.; Sameshima, G.T.; Tachiki, C. Digital Photoelastic Analysis of TAD-Supported Maxillary Arch Distalization. Appl. Sci. 2022, 12, 1949. [Google Scholar] [CrossRef]
- Vieira, F.G.; Scari, A.S.; Magalhães Júnior, P.A.A.; Martins, J.S.R.; Magalhães, C.A. Analysis of Stresses in a Tapered Roller Bearing Using Three-Dimensional Photoelasticity and Stereolithography. Materials 2019, 12, 3427. [Google Scholar] [CrossRef] [Green Version]
- Surendra, K.V.N.; Simha, K.R.Y. Characterizing Frictional Contact Loading via Isochromatics. Exp. Mech. 2014, 54, 1011–1030. [Google Scholar] [CrossRef]
- Surendra, K.V.N.; Simha, K.R.Y. Digital image analysis around isotropic points for photoelastic pattern recognition. Opt. Eng. 2015, 54, 081209. [Google Scholar] [CrossRef]
- Frocht, M.M. Factors of stress concentration determined by photoelasticity. J. Appl. Mech. Trans. ASME 1935, 57, 597–598. [Google Scholar]
- Frocht, M.M. Photoelasticity; John Wiley and Sons: Hoboken, NJ, USA, 1941; Volume 1, p. 523. [Google Scholar]
- Durelli, A.J.; Shukla, A. Identification of isochromatics fringes. Exp. Mech. 1983, 23, 111–119. [Google Scholar] [CrossRef]
- Mirsayar, M.M. Calculation of stress intensity factors for an interfacial notch of a bi-material joint using photoelasticity. Eng. Solid Mech. 2013, 1, 149–153. [Google Scholar] [CrossRef]
- Yamamoto, T.; Masao, E.; Kosho, M. Stress concentration in the vicinity of a hole defect under conditions of Hertzian contact. Tribol. Trans. 1982, 25, 511–518. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Sajjan, S.S. Photo Elastic and Finite Element Analysis of Circular Ring Subjected to Diametral Compression. Int. J. Eng. Res. Technol. 2017, 6, 344–346. [Google Scholar]
- Wahl, A.M.; Beeuwkes, R.J. Stress Concentration Produced by Holes and Notches. Trans. ASME 1934, 56, 617–625. [Google Scholar]
- Coker, E.G.; Filon, L.N.G. A Treatise on Photo-Elasticity, 2nd ed.; Cambridge University Press: London, UK, 1957. [Google Scholar]
- Baek, T.H.; Kim, M.S. Separation of Isochromatics and Isoclinics from Photoelastic Fringes in a Circular Disk by Phase Measuring Technique. KSME Int. J. 2002, 16, 175–181. [Google Scholar] [CrossRef]
- Ramesh, K.; Sasikumar, S. Digital photoelasticity: Recent developments and diverse applications. Opt. Lasers Eng. 2020, 135, 106186. [Google Scholar] [CrossRef]
- Hawong, J.-S.; Nam, J.-H.; Kim, K.-H.; Kwon, O.-S.; Kwon, G.; Par, S.-H. A study on the development of photoelastic experimental hybrid method for colour isochromatics (I). J. Mech. Sci. Technol. 2010, 24, 1279–1287. [Google Scholar] [CrossRef]
- Nam, J.-H.; Hawong, J.-S.; Kwon, G.; Shin, D.-C.; Mose, B.; Park, S.-H. A study on the development of photoelastic experimental hybrid method for colour isochromatics (II). J. Mech. Sci. Technol. 2011, 25, 1797–1809. [Google Scholar] [CrossRef]
- Alaci, S.; Ciornei, F.-C.; Filote, C. Theoretical and experimental stress states in diametrically loaded eccentric rings. J. Balk. Tribol. Assoc. 2016, 22, 2959–2979. [Google Scholar]




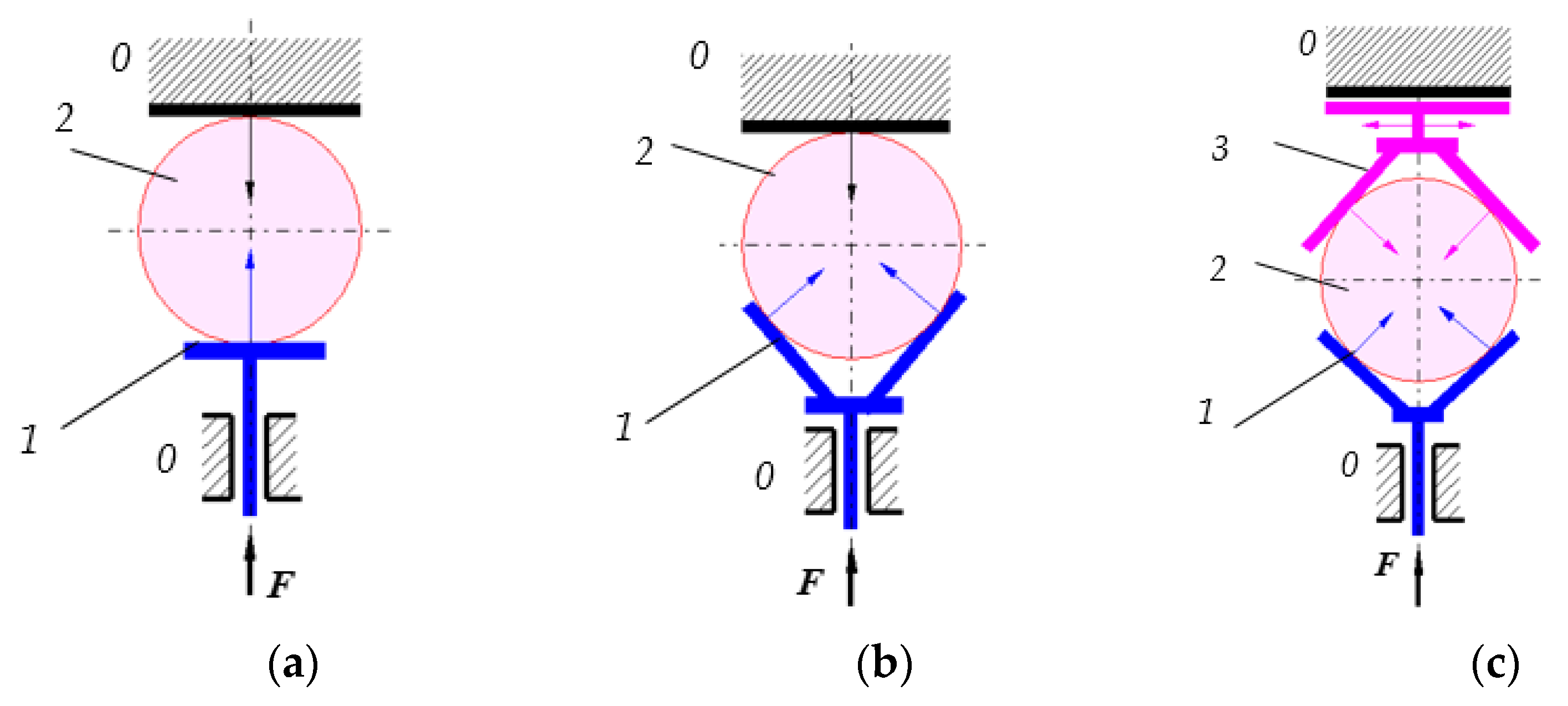



| Case a | Case b | Case c | Case d | Case e | Case f | |
|---|---|---|---|---|---|---|
| Loading scheme |  |  | 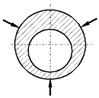 |  | 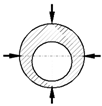 |  |
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaci, S.; Ciornei, F.-C.; Romanu, I.-C. Stress State in an Eccentric Elastic Ring Loaded Symmetrically by Concentrated Forces. Mathematics 2022, 10, 1314. https://doi.org/10.3390/math10081314
Alaci S, Ciornei F-C, Romanu I-C. Stress State in an Eccentric Elastic Ring Loaded Symmetrically by Concentrated Forces. Mathematics. 2022; 10(8):1314. https://doi.org/10.3390/math10081314
Chicago/Turabian StyleAlaci, Stelian, Florina-Carmen Ciornei, and Ionut-Cristian Romanu. 2022. "Stress State in an Eccentric Elastic Ring Loaded Symmetrically by Concentrated Forces" Mathematics 10, no. 8: 1314. https://doi.org/10.3390/math10081314
APA StyleAlaci, S., Ciornei, F.-C., & Romanu, I.-C. (2022). Stress State in an Eccentric Elastic Ring Loaded Symmetrically by Concentrated Forces. Mathematics, 10(8), 1314. https://doi.org/10.3390/math10081314





