Categorification of Integer Sequences via Brauer Configuration Algebras and the Four Subspace Problem

Abstract

The four subspace problem is a known matrix problem, which is equivalent to determining all the indecomposable representations of a poset consisting of four incomparable points. In this paper, we use solutions of this problem and invariants associated with indecomposable projective modules with some suitable Brauer configuration algebras to categorify the integer sequence encoded in the OEIS as A100705 and some related integer sequences.

1. Introduction

Ringel and Fahr introduced the theory of categorification of integer sequences in [1]. According to them, a categorification of a sequence of numbers means instead of considering these numbers suitable objects in a category (for instance, as a representation of quivers), the numbers in question occur as invariants of the objects; equally, numbers may be visualized by isomorphisms of objects’ functional relations by functorial ties.

Before the introduction of the notion of categorification of integer sequences, Ringel and Fahr started their research in [2], where they used the theory of representation of the 3-Kronecker quiver and Gabriel’s covering theory to obtain an interpretation of Fibonacci numbers in terms of some Coxeter reflections. In their seminal paper [1], Ringel and Fahr generalized these results. They categorified Fibonacci numbers using dimension vectors of indecomposable $\mathsf{\Lambda }$-modules instead of the 3-Kronecker algebra. Furthermore, they used appropriated filtrations, exact sequences, and Auslander–Reiten sequences associated with some suitable Fibonacci modules to categorify identities of the following type:

$$\begin{array}{cc}\hfill f_{t+1}& =f_{t-1}+f_t,\hfill \\ \hfill f_{2t+1}& =1+\underset{i=1}{\sum ^t}{f}_{2i},\hfill \\ \hfill f_{2t}& =\underset{i=1}{\sum ^t}{f}_{2i-1},\hfill \\ \hfill f_{t-2}+f_{t+2}& =3f_t.\hfill \end{array}$$

(1)

where $f_i$ denotes the ith Fibonacci number such that

$$f_i=f_{i-1}+f_{i-2},f_0=f_1=1,\mathrm{for}i\ge 2.$$

(2)

In [3], Ringel thoroughly discussed the role of hereditary Artin algebras in the categorification of Catalan numbers with the form $\frac{1}{n+1}\left(\genfrac{}{}{0pt}{}{2n}{n}\right)$. He introduced Dynkin functions, which associate a real number, a set, or a sequence to a Dynkin diagram. According to him, a Dynkin function f provides a vector $f\left({\Delta }_n\right)$ of the form $(f\left({\mathbb{A}}_n\right),f\left({\mathbb{B}}_n\right),f\left({\mathbb{C}}_n\right),f\left({\mathbb{D}}_n\right),f\left({\mathbb{E}}_6\right),$$f\left({\mathbb{E}}_7\right),f\left({\mathbb{E}}_8\right),f\left({\mathbb{F}}_4\right),f\left({\mathbb{G}}_2\right))$, where $f\left({\Delta }_n\right)$ is a sequence (a real number) if ${\Delta }_n\in \{{\mathbb{A}}_n,{\mathbb{B}}_n,{\mathbb{C}}_n,{\mathbb{D}}_n\}$ (${\Delta }_n\in \{{\mathbb{E}}_6,{\mathbb{E}}_7,{\mathbb{E}}_8$, ${\mathbb{F}}_4$ and ${\mathbb{G}}_2\}$). For instance, if $f\left({\Delta }_n\right)=sinc\left({\Delta }_n\right)=$ the number of sincere indecomposable modules, it holds that, $sinc\left({\Delta }_n\right)=(1,n,n,n-2,7,16,44,10,4)$. The Dynkin function $r\left({\Delta }_n\right)=$ the number of indecomposable modules (the number of positive roots) has associated the vector $(\left(\genfrac{}{}{0pt}{}{n+1}{2}\right),n^2,n^2,n(n-1),36,63,120,24,6)$. $a\left({\Delta }_n\right)$ the number of antichains in $\mathrm{mod}\mathsf{\Lambda }$, and $t_n\left({\Delta }_n\right)$ the number of tilting modules are also examples of Dynkin functions.

As a task for the future, Ringel proposed, in [3], creating an On-Line Encyclopedia of Dynkin Functions (OEDF), giving complete information on all types of Dynkin functions, just as the On-Line Encyclopedia of Integer Sequences (OEIS) does for integer sequences.

Contributions

In this work, instead of Dynkin algebras, we use Brauer configuration algebras and indecomposable representations of the category of representations of a poset consisting of four incomparable points, also called a tetrad, to categorify integer sequences.

Combinatorial information arising from some preprojective representations of the tetrad is used to build Brauer configuration algebras so that the number of summands in the heart $ht\left(P\right)=\mathrm{rad}P/\mathrm{soc}P$ of an appropriated indecomposable projective module P over an algebra of this type is given by the combinatorial data arisen from the tetrad. This procedure allows giving a categorification of the integer sequence A100705 in the OEIS and some related integer sequences.

We recall that finding indecomposable representations of four incomparable points is a well-known matrix problem called the four subspace problem (FSP). The solution of this problem is essentially equivalent to determining all of the socle-projective indecomposable representations of the four subspace quiver F shown in Figure 1 [4]:

Figure 2 shows how Brauer configuration algebras and solutions of the four subspace problem are related to the main results (targets of green arrows) presented in this paper.

This paper is organized as follows. In Section 2, we recall definitions and notation used throughout the paper. In particular, we recall the notion of path algebra, Brauer configuration algebra and the four subspace problem. In Section 3, we give our main results. We define and enumerate cycles associated with some preprojective representations of the tetrad, giving a relationship between the number of cycles and nontruncated vertices of indecomposable modules over some suitable Brauer configuration algebras. Concluding remarks are given in Section 4.

2. Background and Related Work

In this section, we introduce some definitions and notations to be used throughout the paper. In particular, it is given a brief overview regarding Brauer configuration algebras, and the four subspace problem.

2.1. Path Algebras

This section is focused on the theory of representation of basic algebras associated with finite connected quivers (oriented graphs) [5].

If $\mathbb{F}$ is an algebraic closed field, then a path algebra$\mathbb{F}Q$ is an algebra generated by the paths of a quiver $Q=(Q_0,Q_1,s,t)$, where $Q_0$ and $Q_1$ are sets and $s,t$ are maps such that $s,t:Q_1\to Q_0$, elements of the set $Q_0$ ($Q_1$) are said to be the vertices (arrows) of the quiver Q.

If $\alpha \in Q_1$ then the vertex $s\left(\alpha \right)$ ($t\left(\alpha \right)$) is the source (target) of the arrow $\alpha$ [5].

An ideal I of a path algebra $\mathbb{F}Q$ is generated by relations. These relations are nothing but paths with the same starting and ending points. The two-sided ideal generated by the arrows (paths of length greater than or equal to l) of Q is denoted by $R_Q$ ($R_Q^l$). An ideal I is said to be admissible, if there is an integer $m\ge 2$ such that $R_Q^m\subseteq I\subseteq R_Q^2$. $R_Q$ is said to be the arrow ideal of $\mathbb{F}Q$.

If I is an admissible ideal of $\mathbb{F}Q$, the pair $(Q,I)$ is said to be a bound quiver. The quotient algebra $\mathbb{F}Q/I$ is said to be a bound quiver algebra  [4,5]. It is worth noticing that, any basic algebra is isomorphic to a bound algebra $\mathbb{F}Q/I$ if I is a suitable admissible ideal.

2.2. Brauer Configuration Algebras

Green and Schroll introduced Brauer configuration algebras as a generalization of Brauer graph algebras [6,7].Their definition is as follows:

A Brauer configuration algebra ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}$ (or simply $\mathsf{\Lambda }$ if no confusion arises) is a bound quiver algebra induced by a Brauer configuration $\mathsf{\Gamma }=({\mathsf{\Gamma }}_0,{\mathsf{\Gamma }}_1,\mu ,\mathcal{O})$, where:

• ${\mathsf{\Gamma }}_0$ is a finite set of vertices.
• ${\mathsf{\Gamma }}_1$ is a collection of polygons, which are multisets consisting of vertices (vertices repetition allowed), ${\mathsf{\Gamma }}_1=\{U_i\mid 1\le i\le n\}$ for some suitable integer n. Any polygon $U_i$ contains more than one vertex.
• $\mu$ is a map from the set of vertices ${\mathsf{\Gamma }}_0$ to the set of positive integers $\mathbb{N}\setminus \left\{0\right\}={\mathbb{N}}^{+}$, $\mu :{\mathsf{\Gamma }}_0\to {\mathbb{N}}^{+}.$
• $\mathcal{O}$ is given by associating a linear order < to each collection of polygons where nontruncated vertices occur. Such ordering is a way of registering how vertices occur in polygons. For instance, if a vertex $\alpha \in {\mathsf{\Gamma }}_0$ occurs in polygons $U_{i_i},U_{i_2},\dots ,U_{i_m}$, for suitable indices $i_1,i_2,\dots ,i_m\in \{1,2,3,\dots ,n\}$, then the ordering < can be defined in such a way that:

  $$U_{i_1}^{{\alpha }_1}<U_{i_2}^{{\alpha }_2}<\cdots <U_{i_m}^{{\alpha }_m},{\alpha }_{i_s}>0.$$

  (3)

  where, $U_{i_s}^{{\alpha }_s}=\underset{{\alpha }_s-times}{\underbrace{U_{i_s}<\cdots <U_{i_s}}}$ means that vertex $\alpha$ occurs ${\alpha }_s$ in polygon $U_{i_s}$, denoted $occ(\alpha ,U_{i_s})$.
  The sequence (3) is said to be the successor sequence at vertex $\alpha$ denoted $S_{\alpha }$. Note that for the sake of clarity, if a vertex ${\alpha }^{\prime }\ne \alpha$ also occur in polygons $U_{i_i},U_{i_2},\dots ,U_{i_m}$, then we keep such polygons ordering if it has already been defined.
• If $\alpha \in {\mathsf{\Gamma }}_0$ then there is at least one polygon $U_i$ such that $\alpha \in U_i$.

If $\alpha \in {\mathsf{\Gamma }}_0$ then the valency $val\left(\alpha \right)$ of $\alpha$ is given by the identity

$$val\left(\alpha \right)=\sum _{U\in {\mathsf{\Gamma }}_1}occ(\alpha ,U).$$

(4)

If $\alpha \in {\mathsf{\Gamma }}_0$ is such that $\mu \left(\alpha \right)val\left(\alpha \right)=1$ then $\alpha$ is said to be truncated (it occurs once in just one polygon). Otherwise $\alpha$ is a non-truncated vertex. A Brauer configuration without truncated vertices is said to be reduced.

In [8], Cañadas et al. introduced Algorithm 1 to build the Brauer quiver $Q_{\mathsf{\Gamma }}$ and the Brauer configuration algebra ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}=\mathbb{F}{Q}_{\mathsf{\Gamma }}/I_{\mathsf{\Gamma }}$ induced by a Brauer configuration $\mathsf{\Gamma }$, where $I_{\mathsf{\Gamma }}$ is an admissible ideal generated by suitable relations associated with the vertices occurrences.

Algorithm 1: Construction of a Brauer configuration algebra.

1. Input A reduced Brauer configuration $\mathsf{\Gamma }=({\mathsf{\Gamma }}_0,{\mathsf{\Gamma }}_1,\mu ,\mathcal{O})$. 2. Output The Brauer configuration algebra ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}=\mathbb{F}{Q}_{\mathsf{\Gamma }}/I_{\mathsf{\Gamma }}$ 3. Construct the quiver $Q_{\mathsf{\Gamma }}=({\left(Q_{\mathsf{\Gamma }}\right)}_0,{\left(Q_{\mathsf{\Gamma }}\right)}_1,s:{\left(Q_{\mathsf{\Gamma }}\right)}_1\to {\left(Q_{\mathsf{\Gamma }}\right)}_0,t:{\left(Q_{\mathsf{\Gamma }}\right)}_1\to {\left(Q_{\mathsf{\Gamma }}\right)}_0)$ (a) ${\left(Q_{\mathsf{\Gamma }}\right)}_0={\mathsf{\Gamma }}_1$, (b) For each cover $U_i<U_{i+1}\in {\mathsf{\Gamma }}_1$ define an arrow $a\in {\left(Q_{\mathsf{\Gamma }}\right)}_1$, such that $s\left(a\right)=U_i$ and $t\left(a\right)=U_{i+1}$, (c) Each relation $U_i<U_i$ defines a loop in $Q_{\mathsf{\Gamma }}$, (d) Each ordered set $S_{\alpha }$ defines a cycle $C_{\alpha }=S_{\alpha }\cup \{U_{i_m}<U_{i_1}\}$ in $Q_{\mathsf{\Gamma }}$ called special cycle. Special cycles are obtained from successor sequences by defining a suitable circular relation, without loss of generality, we assume that a relation of the form $U_{i_m}<U_{i_1}$ holds in special cycles. 4. Define the path algebra $\mathbb{F}{Q}_{\mathsf{\Gamma }}$, 5. Construct the admissible ideal $I_{\mathsf{\Gamma }}$, which is generated by the following relations: (a) If ${\alpha }_i,{\alpha }_j\in U$, $U\in {\mathsf{\Gamma }}_1$ and $C_{{\alpha }_i},C_{{\alpha }_j}$ are corresponding special cycles then $C_{{\alpha }_i}^{\mu \left({\alpha }_i\right)}-C_{{\alpha }_j}^{\mu \left({\alpha }_j\right)}=0$, (b) If $C_{{\alpha }_i}$ is a special cycle associated with the vertex ${\alpha }_i$ then $C^{\mu \left({\alpha }_i\right)}a=0$, if a is the first arrow of $C_{{\alpha }_i}$, (c) If $\alpha ,{\alpha }^{\prime }\in {\mathsf{\Gamma }}_0$, $\alpha \ne {\alpha }^{\prime }$, $a,b\in {\left(Q_{\mathsf{\Gamma }}\right)}_1$, $a\ne b$, $ab\notin C_{\alpha }$ for any $\alpha \in {\mathsf{\Gamma }}_0$ then $ab=0$, if $a\in C_{\alpha }$, $b\in C_{{\alpha }^{\prime }}$ and $ab\in \mathbb{F}{Q}_{\mathsf{\Gamma }}$, (d) If a is a loop associated with a vertex $\alpha$ with $val\left(\alpha \right)=1$ and $\mu \left(\alpha \right)>1$ then $a^{\mu \left(\alpha \right)+1}=0$. 6. ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}=\mathbb{F}{Q}_{\mathsf{\Gamma }}/I_{\mathsf{\Gamma }}$ is the Brauer configuration algebra. 7. For the construction of a basis of ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}$ follow the next steps: (a) For each $U\in {\mathsf{\Gamma }}_1$ choose a nontruncated vertex ${\alpha }_U$ and exactly one special $\alpha$-cycle $C_{{\alpha }_U}$ at U, (b) Define: $$\begin{array}{cc}\hfill A& =\{\overline{p}\mid pisaproperprefixofsome{C}_{\alpha }^{\mu \left(\alpha \right)}\},\hfill \\ \hfill B& =\{\overline{C_{{\alpha }_U}^{\mu \left(\alpha \right)}}\mid U\in {\mathsf{\Gamma }}_1\}.\hfill \end{array}$$ (c) $A\cup B$ is a $\mathbb{F}$-basis of ${\mathsf{\Lambda }}_{\mathsf{\Gamma }}$.

Henceforth, there is no possibility of confusion. Notations Q, I, and $\mathsf{\Lambda }$ will be assumed for a quiver, an admissible ideal, and the Brauer configuration algebra induced by a fixed Brauer configuration $\mathsf{\Gamma }$.

Since polygons in Brauer configurations are multisets, we will often assume that such polygons are given by words w of the form

$$\begin{array}{cc}\hfill w& =y_1^{f_1}{y}_2^{f_2}\dots y_{t-1}^{f_{t-1}}{y}_t^{f_t}\hfill \end{array}$$

(5)

where for each i, $1\le i\le t$, $y_i$ is an element of the polygon called vertex and $f_i$ is the frequency of the vertex $y_i$. In other words, $f_i$ is the number of times that a vertex occurs in a polygon. In particular, if vertices $y_i$ in a polygon V of a Brauer configuration are integer numbers then the corresponding word w will be interpreted as a partition of an integer number $n_V$ associated with the polygon V, where it is assumed that each vertex $y_i$ is a part of the partition, $f_i$ is the number of times that the part $y_i$ occurs in the partition. Furthermore, $n_V={\displaystyle \sum _{i=1}^t}{f}_i{y}_i$.

The following Theorem 1 gives some properties of Brauer configuration algebras [6,9].

Theorem 1

([6], Theorem B, Proposition 2.7, Theorem 3.10, Corollary 3.12, Proposition 3.2, Proposition 3.5, Proposition 3.8). The following results hold for a Brauer configuration algebra $\mathsf{\Lambda }=\mathbb{F}Q/I$ induced by a Brauer configuration $\mathsf{\Gamma }=({\mathsf{\Gamma }}_0,{\mathsf{\Gamma }}_1,\mu ,\mathcal{O})$.

1.

There is a bijection between ${\mathsf{\Gamma }}_1$ and the set of indecomposable projective Λ-modules.

2.

I is admissible, and Λ is a multiserial symmetric algebra.

3.

If P is an indecomposable projective Λ-module corresponding to a polygon V in Γ. Then $\mathrm{rad}P={\displaystyle \sum _{i=1}^r}{U}_i$, where r is the number of (non-truncated) vertices of V, $U_i$ is an indecomposable uniserial module for any i. Furthermore, $U_i\cap U_j$ being a simple Λ-module for any $i,j$. Moreover, if Λ is connected, then an uniserial projective Λ-module U is isomorphic to the indecomposable projective Λ-module associated with a 2-gon V having a truncated vertex.

4.

The number of summands in the heart $ht\left(P\right)=\mathrm{rad}P/\mathrm{soc}P$ of an indecomposable projective Λ-module P such that ${\mathrm{rad}}^{2}P\ne 0$ equals the number of non-truncated vertices of the polygons in Γ corresponding to P counting repetitions.

5.

If Γ is connected then Λ is indecomposable as an algebra.

6.

If ${\mathsf{\Lambda }}^{\prime }$ is a Brauer configuration algebra obtained from Λ by removing a truncated vertex of a polygon in ${\mathsf{\Gamma }}_1$ with $d\ge 3$ vertices then Λ is isomorphic to ${\mathsf{\Lambda }}^{\prime }$.

Proposition 1 and Theorem 2 give formulas for the dimensions and the center of a Brauer configuration algebra [6,9].

Proposition 1

([6], Proposition 3.13). Let Λ be a Brauer configuration algebra associated with the Brauer configuration Γ and let $\mathcal{C}=\{C_1,\dots ,C_t\}$ be a full set of equivalence class representatives of special cycles. Assume that for $i=1,\dots ,t$, $C_i$ is a special ${\alpha }_i$-cycle where ${\alpha }_i$ is a non-truncated vertex in Γ. Then

$${\dim }_{\mathbb{F}}\mathsf{\Lambda }=2|Q_0|+\sum _{{\mathcal{C}}_i\in \mathcal{C}}|C_i|(n_i|C_i|-1),$$

(6)

where $|Q_0|$ denotes the number of vertices of Q, $|C_i|$ denotes the number of arrows in the ${\alpha }_i$-cycle $C_i$ and $n_i=\mu \left({\alpha }_i\right)$.

Please note that the dimension of a Brauer configuration algebra $\mathsf{\Lambda }$ induced by a reduced Brauer configuration $\mathsf{\Gamma }$ is given by the following identity (7).

$${\dim }_{\mathbb{F}}\mathsf{\Lambda }=2\left|{\mathsf{\Gamma }}_1\right|+\sum _{{\alpha }_i\in {\mathsf{\Gamma }}_0}val\left({\alpha }_i\right)(\mu \left(i\right)val\left({\alpha }_i\right)-1).$$

(7)

Theorem 2

([9], Theorem 4.9). Let Γ be a reduced and connected Brauer configuration and let Q be its induced quiver and let Λ be the induced Brauer configuration algebra such that ${\mathrm{rad}}^2\mathsf{\Lambda }\ne 0$ then the dimension of the center of Λ denoted ${\dim }_{\mathbb{F}}Z\left(\mathsf{\Lambda }\right)$ is given by the formula:

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}Z\left(\mathsf{\Lambda }\right)& =1+\sum _{\alpha \in {\mathsf{\Gamma }}_0}\mu \left(\alpha \right)+|{\mathsf{\Gamma }}_1|-|{\mathsf{\Gamma }}_0|+\#\left(LoopsQ\right)-|{\mathcal{C}}_{\mathsf{\Gamma }}|.\hfill \end{array}$$

where, ${\mathcal{C}}_{\mathsf{\Gamma }}=\{\alpha \in {\mathsf{\Gamma }}_0\mid val\left(\alpha \right)=1,and\mu \left(\alpha \right)>1\}$.

2.3. The Four Subspace Problem (FSP)

The four subspace problem is another example of a matrix problem; in this case if $\mathbb{F}$ is an arbitrary field then a quadruple of finite-dimensional $\mathbb{F}$-vector spaces is a system of the form

$$U=(U_0,U_1,U_2,U_3,U_4)$$

where $U_0$ is a finite-dimensional $\mathbb{F}$-vector space and $U_1,\dots ,U_4$ is an ordered collection of four subspaces of $U_0$. Two quadruples are said to be isomorphic if there exists a $\mathbb{F}$-space isomorphism $\phi :U_0\to V_0$ such that $\phi \left(U_i\right)=V_i$ for all i. Furthermore, a quadruple U is decomposable ($U=U^{\prime }\oplus U^{″}$) if some non-trivial direct sum decomposition $U_0=U_0^{\prime }\oplus U_0^{″}$ satisfies the identity $U_i=(U_i\cap U_0^{\prime })\oplus (U_i\cap U_0^{″})$ for each $i\in \{1,\dots ,4\}$ [10].

The four subspace problem consists of classifying all indecomposable quadruples up to isomorphism; it is equivalent to determine indecomposable representations of four incomparable points or a tetrad.

Given two matrix representations $M=(M_{x_i},\mid 1\le i\le 4)$ and $M^{\prime }=(M_{x_i}^{\prime },\mid 1\le i\le 4)$ of the tetrad then M and $M^{\prime }$ are said to be equivalent or isomorphic, if one can be turned into the other by means of the following admissible transformations:

1.

$\mathbb{F}$-elementary transformations of rows of the whole matrix.

2.

$\mathbb{F}$-elementary transformations of columns of matrixes $M_{x_i}$.

FSP was solved by Gelfand and Ponomarev in 1970 for $\mathbb{F}$ algebraically closed [11], and by Nazarova (1967–1974) for the arbitrary case [12]. An advance to this problem was made by Brenner [13,14] who described the indecomposable quadruples with non-zero defect $\partial \left(U\right)={\displaystyle \sum _{i=1}^4}\dim U_i-2\dim U_0$ (called non-regular) in particular she extended the results of Gelfand and Ponomarev to the case of a skew field $\mathbb{F}$. Afterwards, in 2004 Zavadskij and Medina gave an elementary solution of this problem [10].

2.4. Binomial Trees and Integer Partitions

In this paper, graphical interpretations of integer partitions are used to obtain some of the main results. This approach deals with the construction of binomial trees. In particular, we use binomial trees, which appear in many fields of the mathematics, they are binary trees with the shape given in Figure 3 [15]:

Figure 4 illustrates the form of $T_4$.

Please note that at each level, $T_4$ gives integer partitions of numbers 1, 2, and 3 (without taking into account 0 as a part). Often, these types of trees are said to be partition trees, which can be used to store partitions of a given positive integer n or of all positive integers $\le n$.

3. Main Results

In this section, the number of suitable cycles associated with indecomposable representations of the tetrad is related to combinatorial information arising from the indecomposable projective modules over some Brauer configuration algebras to categorify integer sequences.

3.1. Cycles Associated with a Preprojective Representation of Type IV

For $n\ge 1$, we consider $(2n+2)\times (4n+3)$-matrixes of type ${\mathcal{C}}_n$, whose rows and columns are partitioned by four adjacent matrix blocks (from the left to the right), $U_1,U_2,U_3$ and $U_4$ denoted $(A_1,A_1^{\prime });(A_2,A_2^{\prime });(A_3,A_3^{\prime }),(A_4,A_4^{\prime })$, respectively. $A_i$ and $A_i^{\prime }$ are matrixes vertically adjacent (blocks of type $A_i$ as well as those of type $A_i^{\prime }$ are horizontally adjacent) of the same size, three of the four blocks $U_i$ consists of $(n+1)\times (n+1)$-matrixes, and the remaining block consists of two $(n+1)\times n$-matrixes.

If U is a matrix of type ${\mathcal{C}}_n$ then ith row (jth column) $i_U^R$ ($j_U^C$) of U is given by the union

$$i_U^R=\left\{\begin{array}{cc}\underset{m=1}{\stackrel{4}{\cup }}{i}_{A_m}^R,\hfill & \mathrm{if}{i}_U^R\subset \underset{m=1}{\stackrel{4}{\cup }}{A}_m,\hfill \\ \underset{m=1}{\stackrel{4}{\cup }}{i}_{A_m^{\prime }}^R,\hfill & \mathrm{if}{i}_U^R\subset \underset{m=1}{\stackrel{4}{\cup }}{A}_m^{\prime },\hfill \end{array}\right.$$

where $i_{A_m}^R$ and $i_{A_m^{\prime }}^R$ are corresponding rows in the matrixes $A_m$ and $A_m^{\prime }$, $m=1,\dots ,4$.

The jth column $j_U^C$ of U is given by the union

$$j_U^C=j_{A_s}^C\cup j_{A_s^{\prime }}^C\mathrm{if}{j}_U^C\subset A_s\cup A_s^{\prime },$$

The following is a typical shape of a matrix U of type ${\mathcal{C}}_n$:

$$U=\begin{array}{|cccc|}\hline A_1& A_2& A_3& A_4\\ A_1^{\prime }& A_2^{\prime }& A_3^{\prime }& A_4^{\prime }\\ \hline\end{array}$$

Matrixes of type ${\mathcal{C}}_n$ have associated cycles which are connected by an oriented graph whose construction is as follows:

1.

(Vertices) By definition any matrix U of type ${\mathcal{C}}_n$ is defined by a word w whose letters are the symbols $U_1,U_2,U_3$ and $U_4$, i.e., $w=U_{\sigma \left(1\right)}{U}_{\sigma \left(2\right)}{U}_{\sigma \left(3\right)}{U}_{\sigma \left(4\right)}$ where $\sigma$ is a permutation of four elements. For the sake of clarity, later on, we assume that the matrix blocks of a matrix U of type ${\mathcal{C}}_n$ are organized according to $w=U_{\sigma \left(1\right)}{U}_{\sigma \left(2\right)}{U}_{\sigma \left(3\right)}{U}_{\sigma \left(4\right)}$ with $\sigma \left(i\right)=i$, $1\le i\le 4$. Blocks $U_1$ and $U_4$ are said to be external blocks, whereas blocks $U_2$ and $U_3$ are internal blocks.

2.

Fix three rows $i_{A_{i_1}}^R$, $i_{A_{i_2}}^R$ and $i_{A_{i_2}^{\prime }}^{\prime R}$. In this case, $U_{i_1}$ is a $(2n+2)\times (n+1)$-matrix block, whereas $U_{i_2}$ is a $(2n+2)\times n$-matrix block. Thus, according to our choice, $i_1\in \{1,2,3\}$ and $i_2=4$.

3.

Entries of matrix U of type ${\mathcal{C}}_n$ are either pivoting or exterior vertices (or entries). We consider rows $i_{A_4}^R$ and $i_{A_4^{\prime }}^{\prime R}$, which do not contain pivoting entries. If $P_{A_m^r}$ denotes the set of pivoting entries of the matrix $A_m^r$, $r=0,1$, $m=1,\dots ,4$ with $A_i^0=A_i$, $A_i^1=A_i^{\prime }$. Then $|P_{A_i^r}|=|P_{A_j^r}|=n+1$, if $i,j\in \{1,2,3\}$ and $|P_{A_4}|=|P_{A_4^{\prime }}|=n$.

4.

Without loss of generality, we assume that the starting and ending vertex are the same and belong to $i_{A_1}^R\subset U_1$, it is a pivoting vertex. Furthermore, $i_{A_{i_2}}^R\subset A_4$ and ${i^{\prime }}_{A_{i_2}^{\prime }}^R\subset A_4^{\prime }$.

5.

According to the assumption introduced in 1, the sequence of vertices connected by a cycle $\mathcal{C}$ is of the form,

$$\begin{array}{cc}\hfill {\mathcal{C}}_0& =\{a_{i_1,j_1},a_{i_1^{\prime },j_1}^{\prime },b_{i_1^{\prime },j_1^{\prime }}^{\prime },b_{i_2,j_1^{\prime }},c_{i_2,j_2},c_{i_3^{\prime },j_2}^{\prime },d_{i_3^{\prime },j_2^{\prime }}^{\prime }\}\cup \{d_{i_4,j_2^{\prime }},c_{i_4,j_3},c_{i_4^{\prime },j_3}^{\prime },b_{i_4^{\prime },j_4^{\prime }}^{\prime }\}\hfill \\ \hfill & \cup \{b_{i_1,j_4^{\prime }},a_{i_1,j_1}\}.\hfill \end{array}$$

(8)

where entries $(a,a^{\prime })$, $(b,b^{\prime })$, $(c,c^{\prime })$ and $(d,d^{\prime })$ correspond, respectively, to the blocks $(A_1,A_1^{\prime })$, $(A_2,A_2^{\prime })$, $(A_3,A_3^{\prime })$ and $(A_4,A_4^{\prime })$.

6.

Any cycle contains the fixed vertices $a_{i_1,j_1}$, $a_{i_1^{\prime },j_1}^{\prime }$, $b_{i_1^{\prime },j_1^{\prime }}^{\prime }$, $b_{i_2,j_1}$ and $c_{i_2,j_2}$, which is a pivoting entry. Entries of the form $d_{j_{A_{i_2}}^{\prime R},j_2}^{\prime }\notin {\mathcal{C}}_0$. No horizontal arrow has an entry $d_{j_{A_{i_2}}^R,j}\in A_4$ as its ending vertex.

7.

Vertices $a_{i_1,j_1}\in A_1$, $b_{i_1^{\prime },j_1^{\prime }}^{\prime }\in A_2^{\prime }$, $c_{i_2,j_2}\in A_3$, $d_{i_3^{\prime },j_2^{\prime }}^{\prime }\in A_4^{\prime }$, $c_{i_4,j_3}\in A_3$ and $b_{i_4^{\prime },j_4^{\prime }}^{\prime }\in A_2^{\prime }$ are pivoting entries.

8.

(Arrows) arrows in $\mathcal{C}$ connect alternatively pivoting entries with exterior entries. They are defined as follows:

(a)

Arrows in $\mathcal{C}$ are either horizontal (→, ←) or vertical (↑, ↓). We let ${\mathcal{C}}_1$ denote the set of arrows of $\mathcal{C}$. We write, $X\to Y$, $X\leftarrow Y$, $X\uparrow Y$ and $X\downarrow Y$, the different ways of connecting matrixes of the different blocks $U_i$. According to the sequence of vertices, the first vertical arrow of the cycle $\mathcal{C}$ is of the form $A_1\downarrow A_1^{\prime }$.

(b)

Since we are assuming cycles associated with a word of the form $w=U_1{U}_2{U}_3{U}_4$, therefore horizontal arrows connect adjacent matrixes $A_i$ ($A_i^{\prime }$) with $A_{i+1}$ ($A_{i+1}^{\prime }$) (conversely, $A_{i+1}$ ($A_{i+1}^{\prime }$) with $A_i$ ($A_i^{\prime }$)). The first horizontal arrow in our case is of the form $A_1^{\prime }\to A_2^{\prime }$. Vertical arrows connect matrixes in the form $A_i\uparrow A_i^{\prime }$ or $A_i^{\prime }\downarrow A_i$. External blocks are connected by a unique vertical arrow (either $A_1\downarrow A_1^{\prime }$ iff $A_4\uparrow A_4^{\prime }$ or $A_1^{\prime }\uparrow A_1$ iff $A_4\downarrow A_4^{\prime }$). Two arrows, $U_2\overrightarrow{\leftarrow }{U}_3$, $U_3\overrightarrow{\leftarrow }{U}_4$ connect internal matrix blocks ($A_2\to A_3$ iff $A_2^{\prime }\leftarrow A_3^{\prime }$, $A_3\to A_4$ iff $A_3^{\prime }\leftarrow A_4^{\prime }$). Two vertical arrows connect internal matrix blocks $A_2\downarrow \downarrow A_2^{\prime }$ or $A_2\uparrow \uparrow A_2^{\prime }$; the same conditions satisfy matrixes $A_3$ and $A_3^{\prime }$.

(c)

Each horizontal arrow is preceded by a unique vertical arrow, and unless the first arrow, any vertical arrow is preceded by an horizontal arrow.

(d)

No row or column of a matrix $A_m^r$ in a matrix block $U_m$, $r=0,1$, $m=1,\dots ,4$ is visited by arrows of $\mathcal{C}$ more than once.

Please note that any matrix U of type ${\mathcal{C}}_n$ can be described in the form $(U,U_i,n\mid 1\le i\le 4)$. We let $(i_{A_1}^R,j_{A_4}^R,j_{A_4^{\prime }}^{\prime R},P_{A_i^r}\mid 1\le i\le 4,r\in \{0,1\})$ denote the set of all cycles associated with a matrix U of type ${\mathcal{C}}_n$ and ${\mathcal{C}}_U=|(i_{A_1}^R,j_{A_4}^R,j_{A_4^{\prime }}^{\prime R},P_{A_i^r}\mid 1\le i\le 4,r\in \{0,1\})|$ its corresponding cardinal.

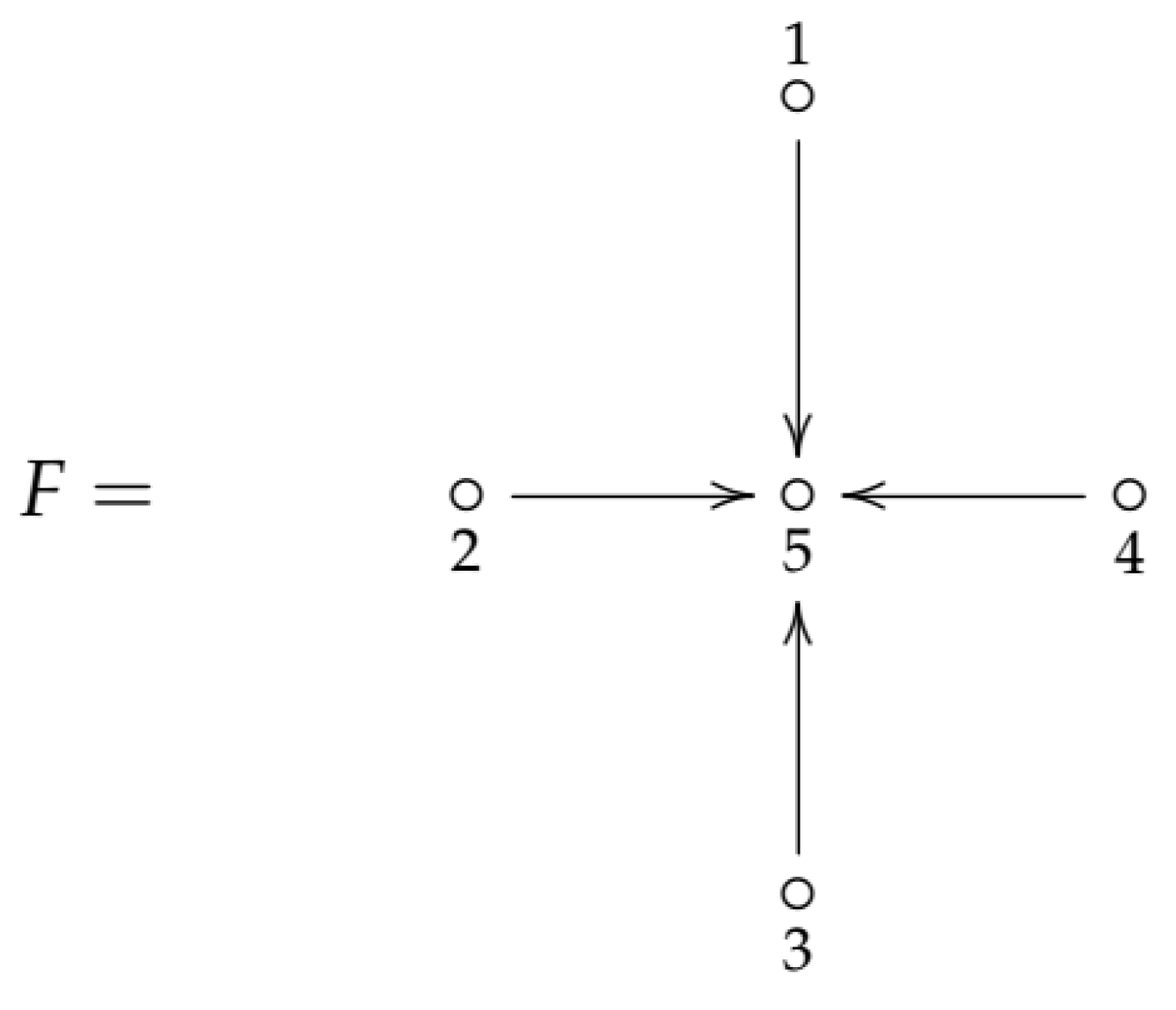
In this work, we establish an identity between the number of cycles associated with preprojective representations of type IV of the tetrad and an integer number (in the sense of (5)) defined by the indecomposable projective modules over some Brauer configuration algebras. Figure 5 shows the canonical matrix presentation of such preprojective representations where $I_n$ is an $n\times n$ identity matrix, $I_n^{\uparrow }$ ($I_n^{\downarrow }$) is an $(n+1)\times n$-matrix, obtained by adding a row of zeros at the top (at the bottom) of an $n\times n$-identity matrix. n is said to be the order of the representation.

The following Figure 6 gives an example of a cycle of type

$$(1_{A_1}^R,1_{A_4}^R,4_{A_4^{\prime }}^R,P_{A_i^r}=\underset{\underset{r=0,1}{1\le i\le 3}}{\cup }{d}_i^r\cup \underline{d_4}\cup d_4^{\prime }\mid r\in \{0,1\})$$

associated with a preprojective representation of order $n=3$ of the tetrad, black arrows connect fixed vertices of the corresponding cycles, whereas $d_i^r$ ($\underline{d_4}$) denote the set of diagonal (subdiagonal) entries used to define the pivoting vertices.

3.2. Categorification of the Sequence A100705 and Some Related Integer Sequences

In this section, elements of the integer sequence $h_n=n^3+{(n+1)}^2$, $n\ge 1$ are interpreted as the number of cycles associated with preprojective representations of the tetrad. Such interpretation allows categorifying this integer sequence (encoded in the OEIS as A100705). Moreover, some new Brauer configuration algebras are defined to obtain alternative categorifications of others types of integer sequences.

Firstly, we note that the Brauer configuration (10) allows seeing each polygon $V_n$ as a partition of the number $h_n$ into two parts of the form $\{n,n+1\}$ where n occurs ${\left(n\right)}^2$ times and $n+1$ occurs $n+1$ times. Assuming the classical notation for partitions [16] each number $h_n$ can be expressed as follows:

$$\begin{array}{cc}\hfill h_n& ={\left(n\right)}^{\left(n^2\right)}{(n+1)}^{(n+1)},n\ge 1,\hfill \end{array}$$

(9)

we let $P_n$ denote such a partition. The partition tree $T_{P_n}$ associated with each partition of the form $P_n$ is obtained by assuming the notation given in Figure 7.

In this case, $T_{P_n}$ has a root node with $n+1$ children, n of them have n children and the last one has $n+1$ children in such a way that in the last level of $T_{P_n}$, n of these children represent a partition of the form ${\left(n\right)}^{(n-1)}{(n+1)}^{\left(1\right)}$ and the last one represents a partition of the form ${\left(n\right)}^{\left(n\right)}{(n+1)}^{\left(1\right)}$. Partition trees of the form $T_{P_n}$ are used in the proof of Theorem 4.

Now we consider Brauer configuration algebras of the form ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}=\mathbb{F}{Q}_{{\mathsf{\Gamma }}_n}/J$ induced by the Brauer configuration ${\mathsf{\Gamma }}_n$ such that For $n\ge 2$ fixed, ${\mathsf{\Gamma }}_n=({\mathsf{\Gamma }}_0,{\mathsf{\Gamma }}_1,\mu ,\mathcal{O})$ with

1.

 

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_0& =\{1,2,3,\cdots ,n,n+1\},\hfill \\ \hfill {\mathsf{\Gamma }}_1& ={\{V_t=t^{\left(t^2\right)}{(t+1)}^{(t+1)}\}}_{1\le t\le n},i.e.,\mathrm{occ}(t,V_t)=t^2,\mathrm{occ}(t+1,V_t)=t+1.\hfill \end{array}$$

(10)

2.

The orientation $\mathcal{O}$ is defined in such a way that for $2\le i\le n$ at vertexi, $V_{i-1}^{(i,<)}<V_i^{(i^2,<)}$, where $V_x^{(y,<)}$ means that the polygon $V_x$ occurs y times in the successor sequence of the corresponding vertex, in particular, $V_{i-1}<V_i$. At the vertex $n+1$, the successor sequence has the form $V_n^{(n+1,<)}$, in this case, $V_{n,1}<V_{n,2}<\cdots <V_{n,n}<V_{n,n+1}$ where $V_{n,i}$ denotes the ith occurrence of the polygon $V_n$ in the sequence.

3.

The multiplicity function $\mu$ is such that $\mu \left(j\right)=1$, for any $j\in {\mathsf{\Gamma }}_0$.

Figure 8 shows a part of the quiver $Q_{{\mathsf{\Gamma }}_n}$ associated with the Brauer configuration ${\mathsf{\Gamma }}_n$; it is worth noting that there is no arrow connecting vertex 1 with any other vertex provided that it is truncated (see Theorem 1, item 5), moreover, we use the symbol $[x_j;y_j]$ to denote that the vertex $x_j$ occurs $y_j$ times at the polygon $h_j=j^3+{(j+1)}^2$ (see identity (5)). Furthermore, $c_j^i$ is a set of loops $\{c_{j_y}^i\mid 1\le y\le \mathrm{occ}(x_j,h_j)-1,2\le i\le n+1\}$. For instance, at 17 there are associated the loops, $c_{{17}_1}^2,c_{{17}_2}^2,c_{{17}_3}^2$ and $c_{{17}_1}^3,c_{{17}_2}^3$.

The following are examples of polygons in a Brauer configuration ${\mathsf{\Gamma }}_n$:

$$\begin{array}{cc}\hfill 5& =\left(1\right)+(2+2)={\left(1\right)}^{\left(1\right)}{\left(2\right)}^{\left(2\right)},\hfill \\ \hfill 17& =(2+3)+(2+3)+(2+2+3)={\left(2\right)}^{\left(4\right)}{\left(3\right)}^{\left(3\right)},\hfill \\ \hfill 43& =(3+3+4)+(3+3+4)+(3+3+4)+(3+3+3+4)={\left(3\right)}^{\left(9\right)}{4}^{\left(4\right)},\hfill \\ \hfill 89& =(4+4+4+5)+(4+4+4+5)+(4+4+4+5)+(4+4+4+5)+(4+4+4+4+5)\hfill \\ \hfill ⋮& =⋮\hfill \end{array}$$

(11)

The ideal J is generated by the following relations where for a fixed $2\le l\le n+1$, $P_{h_j}^{i,l}$ is the product of i loops of type l ($1\le i\le \mathrm{occ}(l,h_j)-1$) attached to the polygon $h_j$ with $y_j-1$ being the total number of such loops ($y_j\in \{j^2,j\}$):

1.

$c_{j_x}^u{c}_{j_y}^v$, if $u\ne v$, for all the possible values of u, v, x, y and j,

2.

$c_{j_x}^t{c}_{j_y}^t=c_{j_y}^t{c}_{j_x}^t$, for all the possible values of x, y, t, and j,

3.

${(c_{j_x}^t)}^2$ for all the possible values of j, t and x,

4.

$c_{j_x}^h{\alpha }_{h+1}$; ${\alpha }_h{c}_{{(j+1)}_x}^{h+1}$; $c_{j_x}^h{\beta }_{h-1}$; ${\beta }_h{c}_{{(j-1)}_x}^{h-1}$, ${\alpha }_j{\beta }_j$ for all the possible values of $h,j$ and x,

5.

${\alpha }_i{\alpha }_{i+1}$; ${\beta }_{j+1}{\beta }_j$, $2\le i\le n-1$, $2\le j\le n-1$,

6.

If

$$\begin{array}{cc}\hfill {\epsilon }_j^1& =P_{h_j}^{u,j}{\alpha }_j{P}_{h_{j+1}}^{y_{j+1}-1,j}{\beta }_j{P}_{h_j}^{y_j-(1+u),j},\hfill \\ \hfill {\epsilon }_j^2& ={\alpha }_j{P}_{h_{j+1}}^{y_{j+1}-1,j}{\beta }_j{P}_{h_j}^{y_j-1,j},\hfill \\ \hfill {\epsilon }_j^3& =P_{h_{j+1}}^{u,j}{\beta }_j{P}_{h_j}^{y_j-1,j}{\alpha }_j{P}_{h_{j+1}}^{y_{j+1}-(1+u),j},\hfill \\ \hfill {\epsilon }_j^4& ={\beta }_j{P}_{h_j}^{y_j-1,j}{\alpha }_j{P}_{h_{j+1}}^{y_{j+1}-1,j},\hfill \\ \hfill {\epsilon }_{j+1}^5& =P_{h_{j+1}}^{v,j+1}{\alpha }_{j+1}{P}_{h_{j+2}}^{y_{j+2}-1,j+1}{\beta }_{j+1}{P}_{h_{j+1}}^{y_{j+1}-(1+v),j+1},\hfill \\ \hfill {\epsilon }_{j+1}^6& ={\alpha }_{j+1}{P}_{h_{j+2}}^{y_{j+2}-1,j+1}{\beta }_{j+1}{P}_{h_{j+1}}^{y_{j+1}-1,j+1},\hfill \\ \hfill {\epsilon }_{j+1}^7& =P_{h_{j+2}}^{v,+1}{\beta }_{j+1}{P}_{h_{j+1}}^{y_{j+1}-1,j+1}{\alpha }_{j+1}{P}_{h_{j+2}}^{y_{j+2}-(1+v),j+1},\hfill \\ \hfill {\epsilon }_{j+1}^8& ={\beta }_{j+1}{P}_{h_{j+1}}^{y_{j+1}-1,j+1}{\alpha }_{j+1}{P}_{h_{j+2}}^{y_{j+2}-1,j+1},\hfill \end{array}$$

(12)

then there are relations of the form ${\epsilon }_s^r-{\epsilon }_{s^{\prime }}^{r^{\prime }}$ where $r,r^{\prime }\in \{1,\dots ,8\}$, $r\ne r^{\prime }$ and $s,s^{\prime }\in \{j,j+1\}$, for all the possible values of u, v and j,

7.

${\epsilon }_j^2{\alpha }_j$, ${\epsilon }_j^4{\beta }_j$, ${\epsilon }_{j+1}^6{\alpha }_{j+1}$, ${\epsilon }_j^8{\beta }_{j+1}$.

The following results prove that the number of cycles associated with preprojective representations of type IV are invariant under admissible transformations.

Theorem 3.

For $n\ge 2$, let, $(U,U_i,n\mid 1\le i\le 4)$, $(U^{\prime },U_i^{\prime },n\mid 1\le i\le 4)$, ${\mathcal{C}}_U$ and ${\mathcal{C}}_{U^{\prime }}$ be two matrixes of type ${\mathcal{C}}_n$ with corresponding sets of cycles ${\mathcal{C}}_U$ and ${\mathcal{C}}_{U^{\prime }}$ defined by systems of the form $(i_{A_1}^R,j_{A_4}^R,j_{A_4^{\prime }}^{\prime R},P_{A_i^r}\mid 1\le i\le 4,r\in \{0,1\})$ and $(f_{B_1}^R,g_{B_4}^R,g_{B_4^{\prime }}^{\prime R},P_{B_i^r}\mid 1\le i\le 4,r\in \{0,1\})$, respectively. Then $|{\mathcal{C}}_U|=|{\mathcal{C}}_{U^{\prime }}|$.

Proof. 

Any cycle $\mathcal{C}\in (i_{A_1}^R,j_{A_4}^R,j_{A_4^{\prime }}^{\prime R},P_{A_i^r}\mid 1\le i\le 4,r\in \{0,1\})$ with set of vertices of the form (8) corresponds uniquely to a cycle ${\mathcal{C}}^{\prime }\in (f_{B_1}^R,g_{B_4}^R,{g^{\prime }}_{B_4^{\prime }}^R,P_{B_i^r}\mid 1\le i\le 4,r\in \{0,1\})$, via the identification $\sigma :U{\mid }_{{\mathcal{C}}_0}\to U^{\prime }{\mid }_{{\mathcal{C}}_0^{\prime }}$ such that $\sigma (t_{i,j})={\mathfrak{t}}_{i,j}$, for any vertex $t_{i,j}\in {\mathcal{C}}_0$, where

$$\begin{array}{cc}\hfill {\mathcal{C}}_0^{\prime }& =\{{\mathfrak{a}}_{i_1,j_1},{\mathfrak{a}}_{i_1^{\prime },j_1}^{\prime },{\mathfrak{b}}_{i_1^{\prime },j_1^{\prime }}^{\prime },{\mathfrak{b}}_{i_2,j_1^{\prime }},{\mathfrak{c}}_{i_2,j_2},{\mathfrak{c}}_{i_3^{\prime },j_2}^{\prime },{\mathfrak{d}}_{i_3^{\prime },j_2^{\prime }}^{\prime }\}\cup \{{\mathfrak{d}}_{i_4,j_2^{\prime }},{\mathfrak{c}}_{i_4,j_3},{\mathfrak{c}}_{i_4^{\prime },j_3}^{\prime },{\mathfrak{b}}_{i_4^{\prime },j_4^{\prime }}^{\prime }\}\hfill \\ \hfill & \cup \{{\mathfrak{b}}_{i_1,j_4^{\prime }},{\mathfrak{a}}_{i_1,j_1}\}.\hfill \end{array}$$

(13)

Entries $(\mathfrak{a},{\mathfrak{a}}^{\prime })$, $(\mathfrak{b},{\mathfrak{b}}^{\prime })$, $(\mathfrak{c},{\mathfrak{c}}^{\prime })$ and $(\mathfrak{d},{\mathfrak{d}}^{\prime })$ belong, respectively, to the blocks $(B_1,B_1^{\prime })$, $(B_2,B_2^{\prime })$, $(B_3,B_3^{\prime })$ and $(B_4,B_4^{\prime })$ of $U^{\prime }$.

In this case, $t_{i,j}\in P_{A_i^r}$ if and only if ${\mathfrak{t}}_{i,j}\in P_{B_i^r}$. In general, a copy ${\mathcal{C}}^{\prime }\in (f_{B_1}^R,g_{B_4}^R,{g^{\prime }}_{B_4^{\prime }}^R,P_{B_i^r}\mid 1\le i\le 4,r\in \{0,1\}$ of a cycle $\mathcal{C}\in (i_{A_1}^R,j_{A_4}^R,{j^{\prime }}_{A_4^{\prime }}^R,P_{A_i^r}\mid 1\le i\le 4,r\in \{0,1\})$ can be built taking into account that an initial exterior vertex $t_{f,j}\in \mathcal{C}$ has a vertex ${\mathfrak{t}}_{f,j^{\prime }}\in \sigma \left({\mathcal{C}}_0\right)$ as its corresponding initial exterior copy and ${\mathcal{C}}^{\prime }$ visits the same rows in the same order as those visited previously by $\mathcal{C}$. We are done. □

The next corollary shows that the number of cycles associated with an indecomposable representation of type IV of the tetrad is invariant under admissible matrix transformations.

Corollary 1.

If for $n\ge 2$, U and $U^{\prime }$ are equivalent preprojective representations of the tetrad of type IV with corresponding sets of cycles ${\mathcal{C}}_U$ and ${\mathcal{C}}_{U^{\prime }}$ then $|{\mathcal{C}}_U|=|{\mathcal{C}}_{U^{\prime }}|$.

Proof. 

Matrix presentations of preprojective representations of type IV of the tetrad are of type ${\mathcal{C}}_n$. □

The following theorem regards Brauer configuration algebra ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}$ and its connection with the number of cycles associated with a preprojective representation of the tetrad of type IV. Recall that the notation $n_V$ (see (5)) is adopted for the integer number associated with the polygon V, in this case V is interpreted as an integer partition of $n_V$.

Theorem 4.

For $n\ge 2$ fixed and $1\le i\le n$ the number $n_{V_i}=i^3+{(i+1)}^2$ associated with the the polygon $V_i=h_i\in {\mathsf{\Gamma }}_1$ (see Figure 5 and Formulas $\left(10\right)$ is the number of cycles associated with an indecomposable preprojective representation of type $\mathrm{IV}$ and order $i+1$. Moreover, the identification of numbers $n_{V_i}$ with partitions of the form ${\left(i\right)}^{\left(i^2\right)}{(i+1)}^{(i+1)}$ defines a bijection between indecomposable projective modules over the Brauer configuration algebra ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}$ and preprojective representations of type $\mathrm{IV}$ of the tetrad.

Proof. 

According to Theorem 1, in order to prove that there exists the required bijection, it suffices to find out the number of cycles associated with a given preprojective representation of type IV. To do that, we fix a representation $U^n$ of this type of order $n\ge 2$, and denote its different blocks as follows:

$$U^n=\begin{array}{|cccc|}\hline A& B& C& D\\ A^{\prime }& B^{\prime }& C^{\prime }& D^{\prime }\\ \hline\end{array}$$

We note that all the cycles associated with $U^n$ can be seen as trees $T_{c_{(n+1),(n+1)}}$ which have the entry $c_{(n+1),(n+1)}$ as root node with n branches whose successors are given by entries

$$c_{1,(n+1)}^{\prime },c_{2,(n+1)}^{\prime },\dots ,c_{n,(n+1)}^{\prime }.$$

Each entry $c_{i,(n+1)}^{\prime }$ has $n-1$ branches if $i\ne n$, whereas $c_{n,(n+1)}^{\prime }$ has n branches. Moreover, all of these entries give rise to an arrow

$$c_{i,(n+1)}^{\prime }\to d_{j,i},$$

for some entry $d_{j,i}\in D$. Actually, $d_{j,i}$ is a successor root of $c_{i,(n+1)}^{\prime }$ with $(n-1)$ branches in the tree whenever $j\in \{1,\dots ,n\}$ and $i\ne 1$. If $i=1$ then $d_{1,j}$ has by construction n branches in $C^{\prime }$. Therefore, the structure of $T_{c_{(n+1),(n+1)}}$ has the shape given in Figure 9.

Which corresponds to the partition tree $T_{P_{(n-1)}}$ of $h_{(n-1)}={(n-1)}^3+{\left(n\right)}^2$, thus the correspondence $T_{P_{(n-1)}}\to T_{c_{(n+1),(n+1)}}$ is a bijection between indecomposable preprojective representations of type IV of the tetrad and polygons of the Brauer configuration (10). □

As an example, the following Figure 10 illustrates the diagram of $T_{c_{4,4}}$ such that the number of vertices in the last level gives the number of associated cycles (described in the proof of Theorem 4) with the indecomposable representation of the tetrad $U^3$:

The number of cycles associated with the indecomposable preprojective representation of the tetrad $U^3$ (shown in Figure 11) equals the second term of the integer sequence A100705. Actually, the number of cycles associated with $U^n$ is given by $h_{(n-1)}={(n-1)}^3+{\left(n\right)}^2$, $n\ge 2$, which is the $(n-1)$th term of this sequence. Black arrows denote the common part of all these cycles.

The following results are consequences of Theorems 1 and 2, and Proposition 1.

Corollary 2.

For $n\ge 2$ fixed and $2\le i\le n$, the number of summands in the heart of the indecomposable projective module $V_i$ over the algebra ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}$ is $i^2+i+1$.

Proof. 

Since for any indecomposable projective module $V_i$, it holds that ${\mathrm{rad}}^2{V}_i\ne 0$ then the result follows from Theorem 1 and the definition of the polygon $V_i$ which has $i^2+i+1$ nontruncated vertices counting repetitions. □

Corollary 3.

For $n\ge 2$ fixed, ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}={\displaystyle \sum _{m=2}^n}{\left(m(m+1)\right)}^2-\frac{1}{3}(n-3)(n+1)(n+2)$. Furthermore, ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_{n+1}}/G_{n+1}=2(1-t_n)+{\left[(n+1)(n+2)\right]}^2$, where for $i\ge 1$, $t_i$ denotes the ith triangular number. Furthermore, $G_{n+1}$ is a $\mathbb{F}$-subspace of ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_{n+1}}$ isomorphic to ${\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}$.

Proof. 

It is enough to observe that for $n\ge 2$ and $2\le j<n+1$, it holds that $val\left(j\right)=j^2+j$, whereas $val\left(1\right)=1$ and $val(n+1)=n+1$. The theorem holds as a consequence of Proposition 1. □

Corollary 4.

For $n\ge 2$ fixed, it holds that

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}\right)& =\frac{n(n+1)(n+2)}{3}+1,\hfill \\ \hfill {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_{n+1}}\right)/Z_{n+1}& =2t_{n+1},\hfill \end{array}$$

(14)

where $Z_{n+1}$ is a $\mathbb{F}$-subspace of $Z\left({\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_{n+1}}\right)$ isomorphic to $Z\left({\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}\right)$.

Proof. 

Since ${\mathrm{rad}}^2{\mathsf{\Lambda }}_{{\mathsf{\Gamma }}_n}\ne 0$, the result is a consequence of Theorem 2 with $\mu \left(i\right)=1$, for any $2\le i\le n+1$, $|{\mathsf{\Gamma }}_0|=n$, $|{\mathsf{\Gamma }}_1|=n$, $\mathrm{occ}(i,h_i)+\mathrm{occ}(i+1,h_i)=i^2+i+1$, $2\le i\le n$, and $\mathrm{occ}(2,h_1)=2$. □

Remark 1.

Note that Corollaries 2–4 are categorifications of the integer sequences $n^2+n+1$ (encoded in the OEIS as A002061), ${\displaystyle \sum _{m=2}^n}{\left(m(m+1)\right)}^2-\frac{1}{3}(n-3)(n+1)(n+2)$, and $\frac{n(n+1)(n+2)}{3}+1$ (which is the sequence A064999). Elements of the sequence A064999 appear as coefficients (in the case $t=3$) of the generating polynomial of a n-twist knot with the form $P_n\left(x\right)={\displaystyle \sum _{t\ge 0}}{a}_{n,t}{x}^t$. Furthermore, the sequence ${\displaystyle \sum _{t=2}^n}{\left(t(t+1)\right)}^2={\displaystyle \sum _{1\le i<j\le n}}{(j-i)}^3$ is encoded A024166 in the OEIS.

Partition trees $T_{P_j}$ associated with numbers $n_{V_j}=j^3+{(j+1)}^2$ in the proof of Theorem 4 define a sequence of Brauer configuration algebras ${\mathsf{\Lambda }}_{E^j}$, $j\ge 2$ induced by Brauer configurations $E^j$ whose set of vertices are 4-vertex paths contained in such trees. In order to describe Brauer configurations $E^j$, we assume the notation $L_{i_2,i_3+1}^{i_1}$ for the $i_2$th, 4-vertex path occurring in a third ramification of size $i_1$ in the partition tree $T_{P_{i_3}}$. In fact, vertices in $E^j$ define a labeling of 4-vertex paths in partition trees $T_{P_i}$, $1\le i\le j$. As an example, the five 4-vertex paths of $T_{P_1}$ belong to $P^1=P_1^1\cup P_2^1\cup P_2^2$, where $P_1^1=\left\{L_{1,1}^1\right\}$, $P_2^2=\{L_{1,2}^2,L_{2,2}^2,L_{3,2}^2,L_{4,2}^2\}$, and $P_2^1=⌀$. The seventeen 4-vertex paths $P^2$ of $T_{P_2}=T_{c_4,4}$ are given by the following identities:

$$\begin{array}{cc}\hfill P^2& =P_2^2\cup P_3^2\cup P_3^3,\hfill \\ \hfill P_3^2& =\{L_{5,3}^2,L_{6,3}^2,L_{7,3}^2,L_{8,3}^2\},\hfill \\ \hfill P_3^3& =\{L_{1,3}^3,L_{2,3}^3,L_{3,3}^3,L_{4,3}^3,L_{5,3}^3,L_{6,3}^3,L_{7,3}^3,L_{8,3}^3,L_{9,3}^3\}.\hfill \end{array}$$

(15)

For $j\ge 2$ fixed, $1\le h_i\le i^2$, $i^2+1\le h_i^{\prime }\le i^3$, and $1\le h_{i+1}\le {(i+1)}^2$. The Brauer configuration $E^j=(E_0^j,E_1^j,{\mu }^j,{\mathcal{O}}^j)$ is defined in the following fashion:

1.

 

$$\begin{array}{cc}\hfill E_0^j& =\{L_{h_i,i}^i,L_{h_i^{\prime },i+1}^i,L_{h_{i+1},i+1}^{i+1}\mid 2\le i\le j\}\cup \{L_{1,1}^1\},\hfill \\ \hfill E_1^j& =\{T_{P_i}\mid 1\le i\le j\},\hfill \\ \hfill T_{P_i}& =P^i=P_i^i\cup P_{i+1}^i\cup P_{i+1}^{i+1},\hfill \\ \hfill P_i^i& =\{L_{1,i}^i,L_{2,i}^i,\dots ,L_{i^2,i}^i\},fori\ge 2,\hfill \\ \hfill P_{i+1}^i& =\{L_{i^2+1,i+1}^i,L_{i^2+2,i+1}^i,\dots ,L_{i^3,i+1}^i\},fori\ge 2,\hfill \\ \hfill P_{i+1}^{i+1}& =\{L_{1,i+1}^{i+1},L_{2,i+1}^{i+1},\dots ,L_{{(i+1)}^2,i+1}^{i+1}\},fori\ge 2.\hfill \end{array}$$

(16)

2.

The orientation ${\mathcal{O}}^j$ for successor sequences is defined by the usual order of natural numbers, i.e., any successor sequence has the form $T_{P_1}^{(s_{j_1})}<T_{P_2}^{(s_{j_2})}<\cdots <T_{P_{j-1}}^{(s_{j_{(j-1)}})}<T_{P_j}^{(s_{j_j})}$, for some nonnegative integers $s_{j_m}$ ($s_{j_m}=0$, means that the vertex does not occur in the polygon $T_{P_m}$).

3.

${\mu }^j$ is a multiplicity function such that, ${\mu }^j\left(L\right)=2$ for any $L\in \{L_{1,1}^1\}\cup P_{i+1}^i\cup P_{j+1}^{j+1}$, $2\le i\le j$, ${\mu }^j\left(L\right)=1$, otherwise. This multiplicity function is defined to avoid the presence of truncated vertices in the configuration.

Figure 12 shows the Brauer quiver $Q_{E^j}$, where notation $c_{L_{h_r,s}^i}$ means that the corresponding polygon has associated loops of type $c_{L_{h_r,i+1}^i}$, $c_{L_{h_m,j+1}^{j+1}}$, $i^2+1\le h_r\le i^3$, $1\le h_m\le {(i+1)}^2$ defined by vertices $L_{h_r,s}^i$ ($h_1=1$). In this case, ${\alpha }_{L_{i_r,s}^i}$ (${\beta }_{L_{i_r,s}^i}$) denotes arrows determined by polygons $T_{P_{(i-1)}}$ and $T_{P_i}$, $1\le i_r\le i^2$, $i\ge 2$. Loops $c_{L_{h_6,6}^6}$ in the diagram appear if $j=5$. If $j>5$ then at the vertex $T_{P_5}$ there are associated only loops of type $c_{L_{h_5,5}^5}$ and in the vertex $T_{P_j}$ there are attached loops of the form $c_{L_{h_j,j}^j}$ and $c_{L_{h_{j+1},j+1}^{j+1}}$.

The ideal J in this case is generated by the following set of relations defined for all the possible values of $h,i,j,m,t,t^{\prime }$ and u:

1.

${(c_{L_{j,m}^i})}^2$,

2.

$c_{L_{h_j,j}^j}{c}_{L_{h_{(j+1)},j+1}^{j+1}}$,

3.

$c_{L_{h_j,m}^i}{\alpha }_{L_{i_j,m+1}^{i+1}}$,

4.

${\alpha }_{L_{i_j,m}^i}{c}_{L_{h_{(j+1)},m}^i}$,

5.

${\alpha }_{L_{i_{(j-1)},j}^j}{c}_{L_{h_{(j+1)},j+1}^{j+1}}$,

6.

$c_{L_{h_j,m}^i}{\beta }_{L_{i_{(j-1)},m}^i}$,

7.

$c_{L_{h_{(j+1)},j+1}^{j+1}}{\beta }_{L_{i_{(j-1)},j}^j}$,

8.

${\beta }_{L_{i_j,m}^i}{c}_{L_{h_j,m-1}^{i-1}}$,

9.

${\alpha }_{L_{i_j,m}^i}{\alpha }_{L_{i_{(j+1)},m+1}^{i+1}}$,

10.

${\beta }_{L_{i_j,m}^i}{\beta }_{L_{i_{(j-1)},m-1}^{i-1}}$,

11.

$s_{L_{t,u}^i}^{2}a$, where a is the first arrow of the special cycle $s_{L_{t,u}^i}$ associated with the vertex $L_{t,u}^i$,

12.

$s_{L_{t,i}^i}^2-s_{L_{t^{\prime },i}^i}^2$, $s_{L_{t,i}^i}^2-s_{L_{h,i+1}^i}^2$, $s_{L_{t,i}^i}^2-s_{L_{m,i+1}^{i+1}}^2$.

If we let ${\mathsf{\Lambda }}_{E^j}$ denote the algebra $\mathbb{F}{Q}_{E^j}/J$, then the following result categorifies sequence $h_n=n^3+{(n+1)}^2$, $n\ge 1$, by considering its elements as invariants of objects of the category $\mathrm{mod}{\mathsf{\Lambda }}_{E^j}$.

Theorem 5.

For $j\ge 2$ fixed and $1\le i\le j$, the number of summands in the heart of the indecomposable projective module $T_{P_i}$ over the algebra ${\mathsf{\Lambda }}_{E^j}$ is $h_i$.

Proof. 

Since for any indecomposable projective module $T_{P_i}$, it holds that ${\mathrm{rad}}^2{T}_{P_i}\ne 0$ then the theorem follows from Theorem 1 and the definition of the polygon $T_{P_i}$ which has $i^3+{(i+1)}^2$ nontruncated vertices counting repetitions. □

Numbers in the sequence A100705 appear by computing the dimension of quotient spaces of the form ${\mathsf{\Lambda }}_{E^{i+1}}/F_{i+1}$, where $F_{i+1}$ is a $\mathbb{F}$-subspace of ${\mathsf{\Lambda }}_{E^{i+1}}$ isomorphic to ${\mathsf{\Lambda }}_{E^i}$. Actually the following results hold.

Theorem 6.

For $j\ge 2$ fixed, it holds that ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{E^j}=\frac{(j+1)(j+2)(2j+3)}{6}+{(\frac{j(j+1)}{2})}^2+2j-1$. Furthermore, ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{E^{n+1}}-{\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{E^n}=h_{n+1}+2$, where $h_n=n^3+{(n+1)}^2$, $n\ge 2$.

Proof. 

Please note that $|E_1^j|=j$, and $E_0^j=H_1\cup H_2$, where $H_1=\{L_{h_{i,i}^1}^i\mid 2\le i\le j+1\}$ and $H_2=\{L_{h_{m,m+1}^2}^m\mid 1\le m\le j\}$, $L_{h_{1,2}^2}^1=L_{1,1}^1$, $1\le h_i^1\le i^2$, $1\le h_m^2\le m^3-m^2$ (terms $L_{h_{s,m+1}^2}^m$ correspond bijectively to vertices $L_{m^2+s,m+1}^m\in P_{m+1}^m$). If $x\in H_1$ then $val(x)=2$ and ${\mu }^j(x)=1$, whereas, if $y\in H_2$ then $val(y)=1$ and ${\mu }^j(y)=2$. The result follows bearing in mind that $val(L_{h_{1,2}^2}^1)=1$, ${\mu }^j(L_{h_{1,2}^2}^1)=2$ and that for i and m fixed, there are $i^2$ vertices of type $H_1$, $1\le i\le j+1$ and $m^3-m^2$ vertices of type $H_2$, $2\le m\le j$. We are done. □

Theorem 7.

For $j\ge 3$, ${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{E^j}\right)-{\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{E^{(j-1)}}\right)=j^3-j^2+1$.

Proof. 

Since ${\mathrm{rad}}^2{\mathsf{\Lambda }}_{E^j}\ne 0$, $|E_0^j|={\displaystyle \sum _{i=1}^j}{i}^3+{(j+1)}^2$ and the number of loops in the quiver $Q_{E^j}$ equals $|{\mathcal{C}}_{E^j}|$ then ${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{E^j}\right)={\displaystyle \sum _{i=1}^j}(i^3-i^2)+(j+2)$. We are done. □

The sequence $j^3-j^2+1$ appears encoded in the OEIS as A100104.

3.3. The Trace Norm Associated with Preprojective Representations of the Tetrad

If Q is a quiver and ${\left\{{\sigma }_i\right\}}_{1\le i\le n}$ is the set of singular values of the corresponding $m\times n$ adjacency matrix $M\left(Q\right)$ with ${\sigma }_1\ge {\sigma }_2\ge \dots {\sigma }_{n-1}\ge {\sigma }_n$ then the trace norm of Q, denoted ${\left|\right|M\left(Q\right)\left|\right|}_{*}$ is given by the following identity:

$${\left|\right|M\left(Q\right)\left|\right|}_{*}=\underset{i=1}{\sum ^{\min \{m,n\}}}{\sigma }_i.$$

(17)

The trace norm $\left|\right|M(T_{P_{(n-1)}}){\left|\right|}_{*}$ of the partition trees $T_{P_{(n-1)}}$ associated with preprojective representations of type IV is another way to obtain real-valued sequences. In fact, the following result holds:

Theorem 8.

For each $n\ge 3$, $\left|\right|M(T_{P_{(n-1)}}){\left|\right|}_{*}=(n+2)\sqrt{n}+n(n-1)\sqrt{n-1}$.

Proof. 

For each $n\ge 3$, the underlying tree $\overline{T_{P_{(n-1)}}}\in \mathsf{\Omega }(h_n+i_n,i_n)$, where $\mathsf{\Omega }(n,y)$ is the graphs family with n vertices and y ramifications, $h_n=n^3+{(n+1)}^2$, and $i_n=n^2+2$. Thus, for each n, $T_{P_{(n-1)}}$ has the shape shown in Figure 13.

Where $\left(x\right)$ denotes that the corresponding vertex has x children. Therefore, the associated characteristic polynomial has the form $P_n\left(\lambda \right)={(\lambda -n)}^{n+2}{(\lambda -(n-1))}^{n(n-1)}{\lambda }^{n^3+{(n+1)}^2}$. Furthermore, the corresponding singular values have the form ${\sigma }_1=0$, ${\sigma }_2=\sqrt{n}$ and ${\sigma }_3=\sqrt{n-1}$ up to multiplicities. □

4. Concluding Remarks

Brauer configuration algebras and the four subspace problem allow categorifying integer sequences. The integer sequence A100705 in the OEIS corresponds to the number of cycles associated with a preprojective representation of type IV of the tetrad. On the other hand, each number in the sequence A100705 gives the number of summands at the heart of an indecomposable projective module over a suitable Brauer configuration algebra. Dimensions of the Brauer configuration algebras and corresponding centers involved in the different processes are an alternative way to categorify integer sequences.

It is known that there are six types of indecomposable representations of the tetrad [10]. This paper focuses on categorifying some integer sequences associated with the indecomposable representation of type IV of such a poset. It is an open question to establish what kind of cycles or quivers can be related to the other type of indecomposable representations. Enumerating these quivers will give rise to the categorification of new integer sequences.

Applying the techniques proposed in this paper on modules over general algebras as the Cohen-Macaulay modules is an interesting task for the future.