Bending and Buckling of FG-GRNC Laminated Plates via Quasi-3D Nonlocal Strain Gradient Theory
Abstract
:1. Introduction
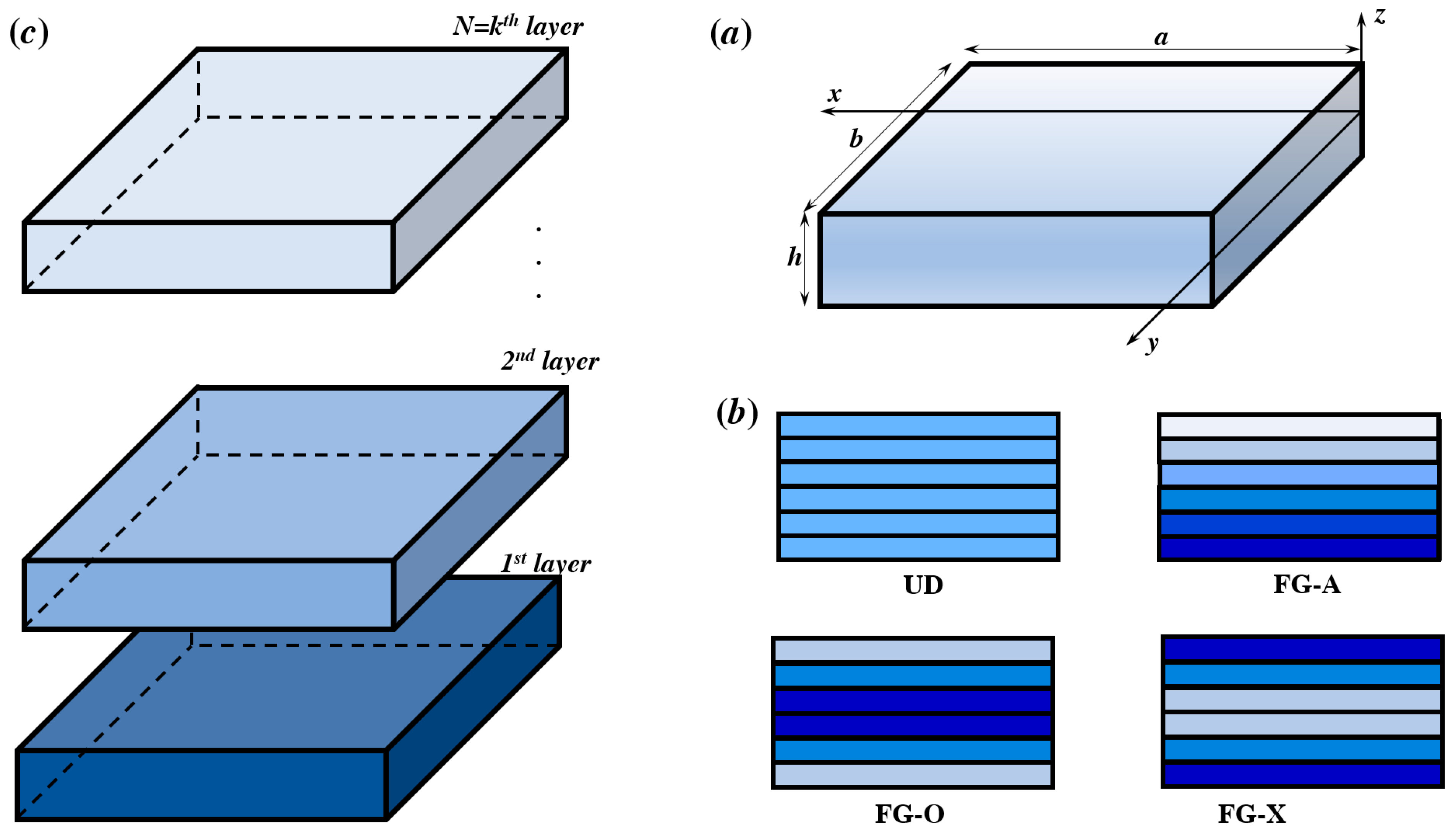
2. Mathematical Formulation of FG-GRNC Plate
2.1. Material Distribution and Graduation
2.2. Basic Equations
2.3. Nonlocal Strain Gradient Elasticity Theory
2.4. Equilibrium Equations
3. Analytical Solution
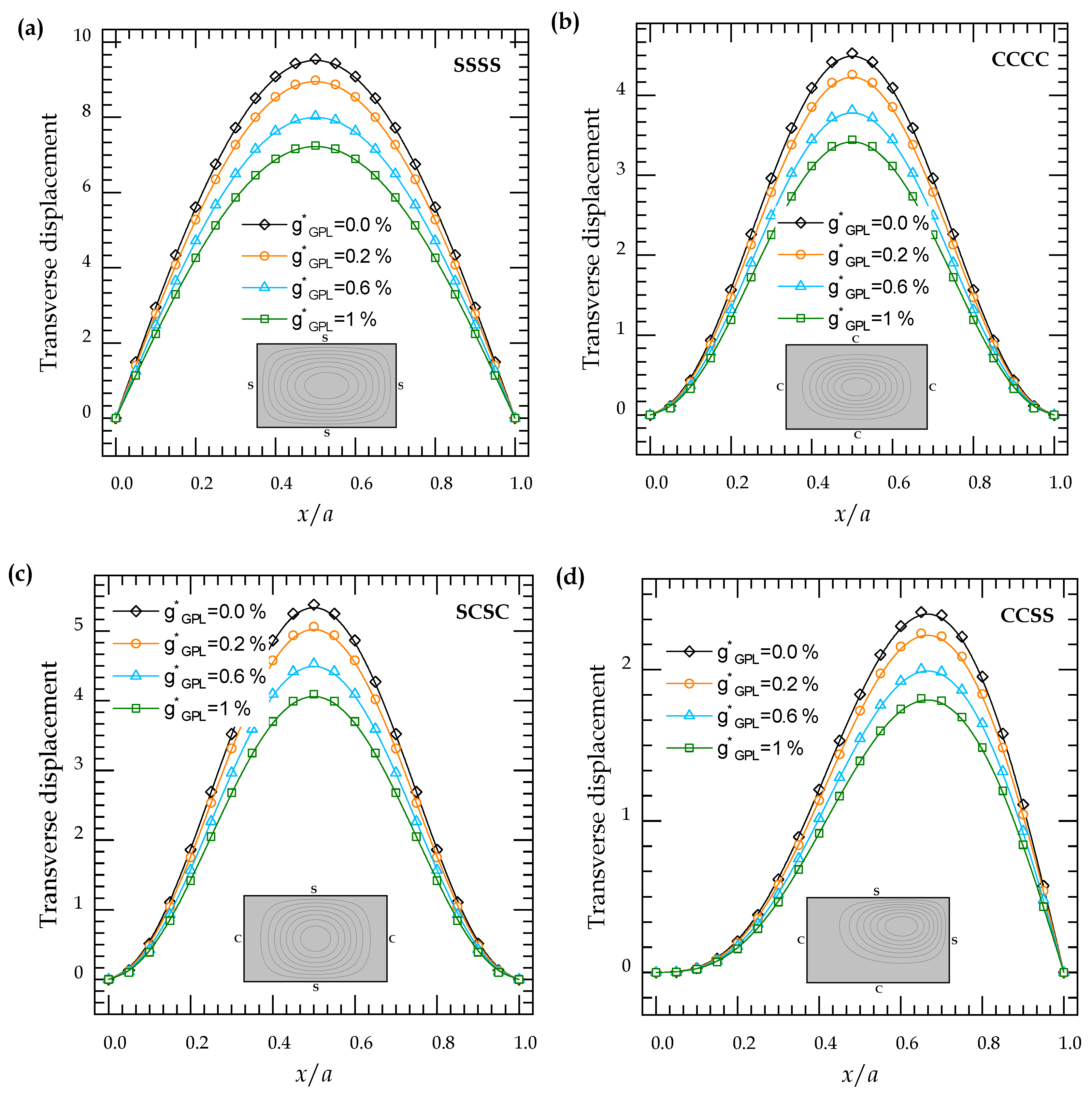
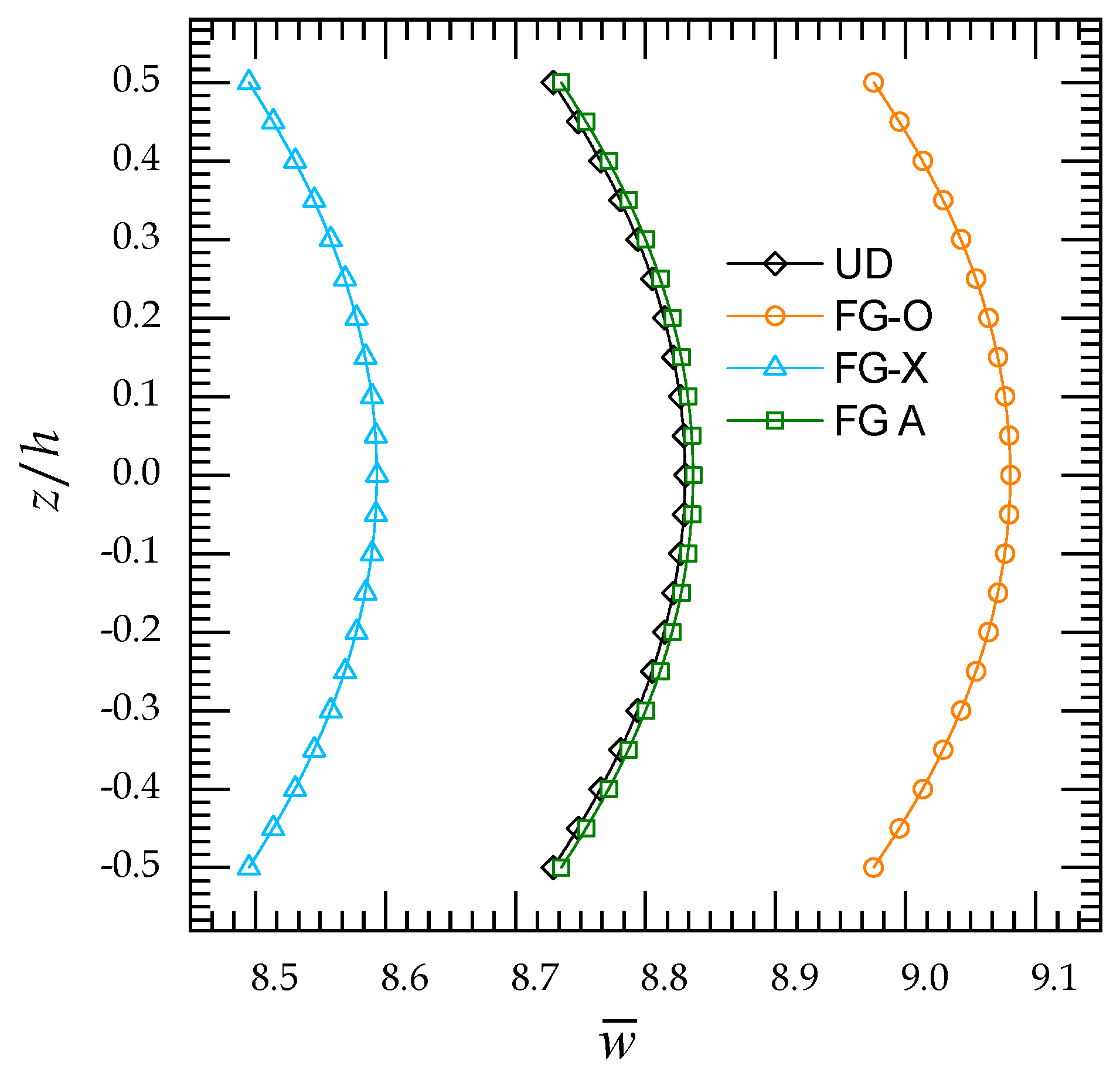
4. Numerical Results
4.1. Verification Analysis
4.2. Parametric Study
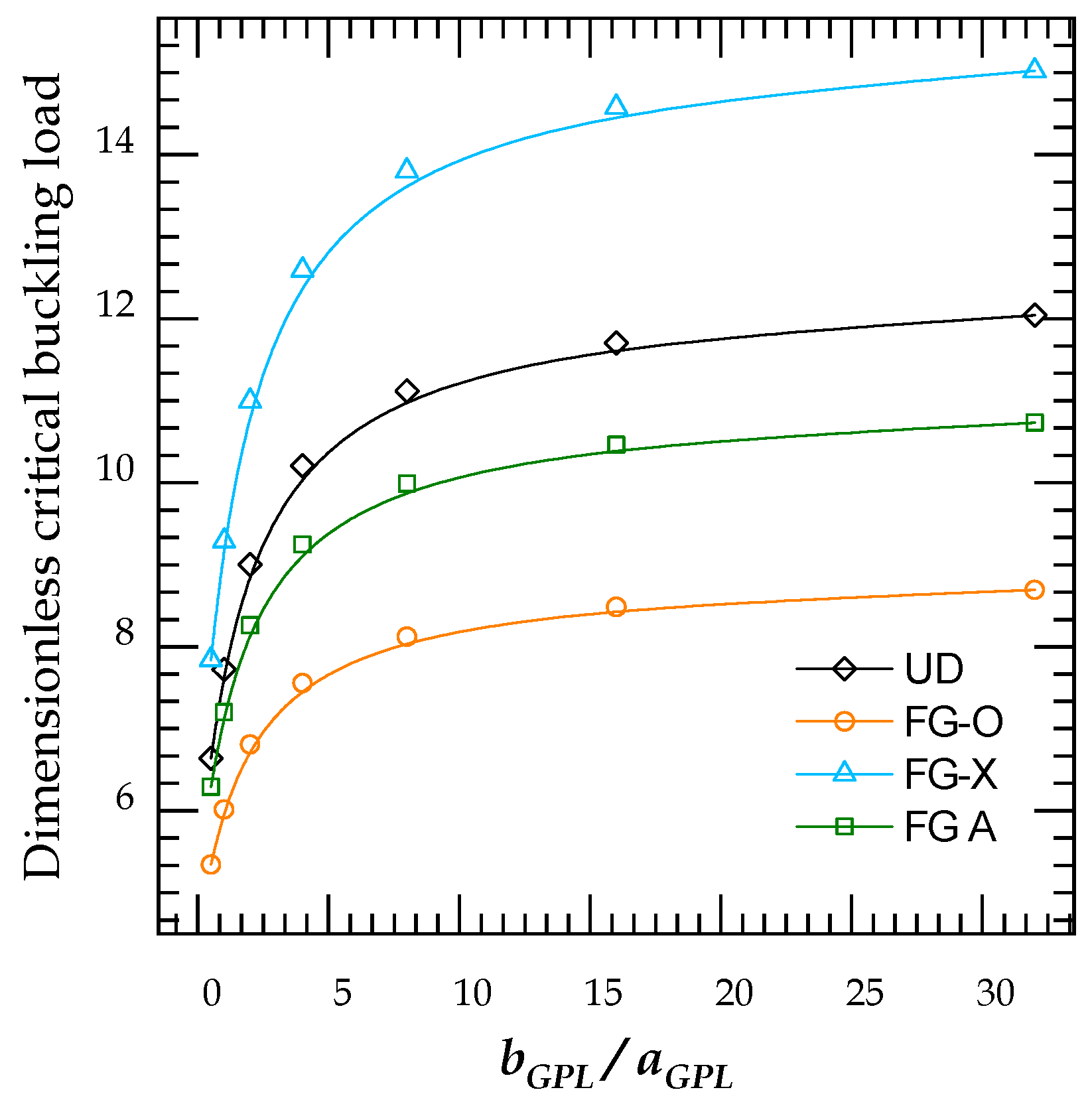
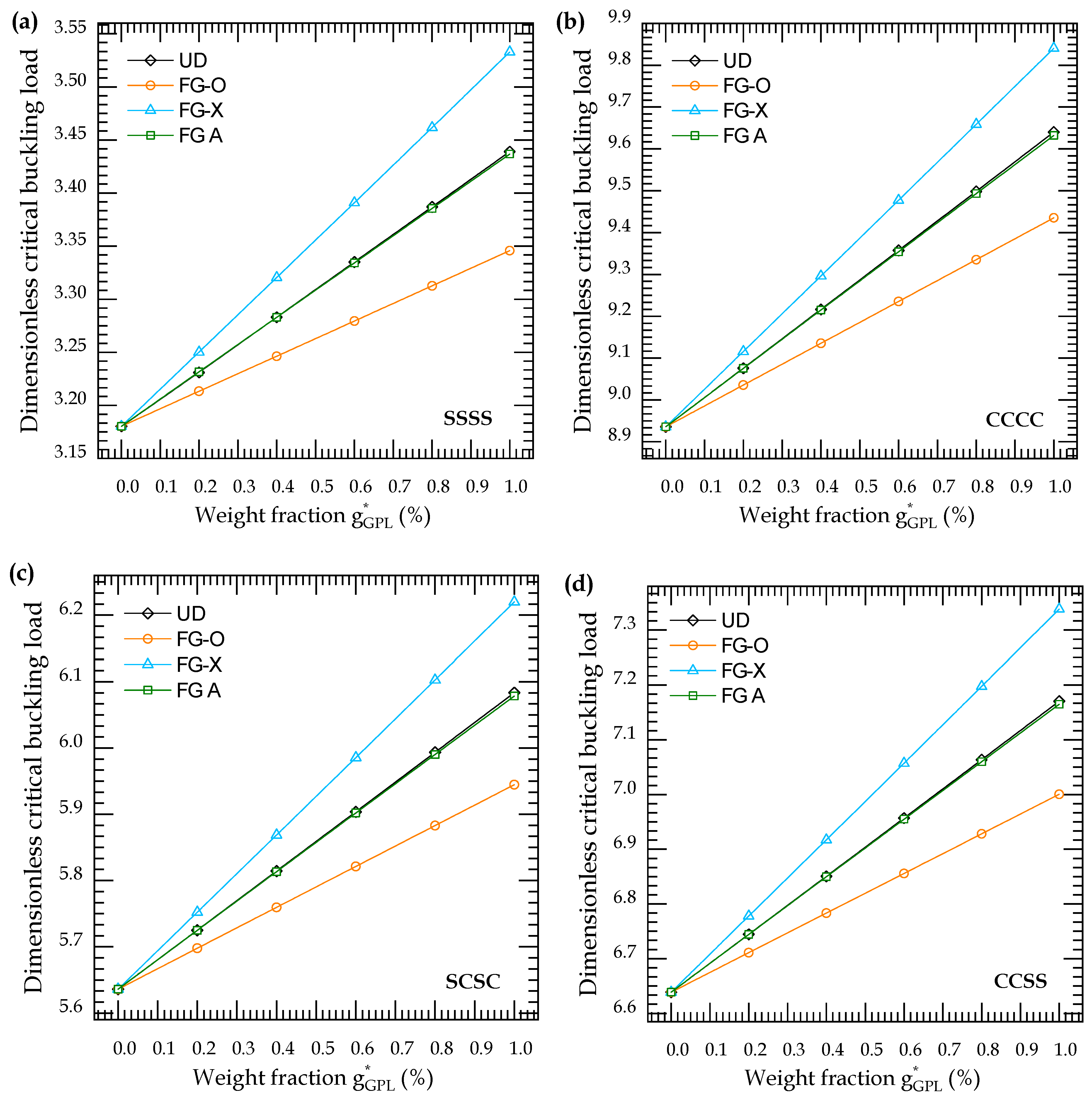
4.2.1. Buckling Analysis
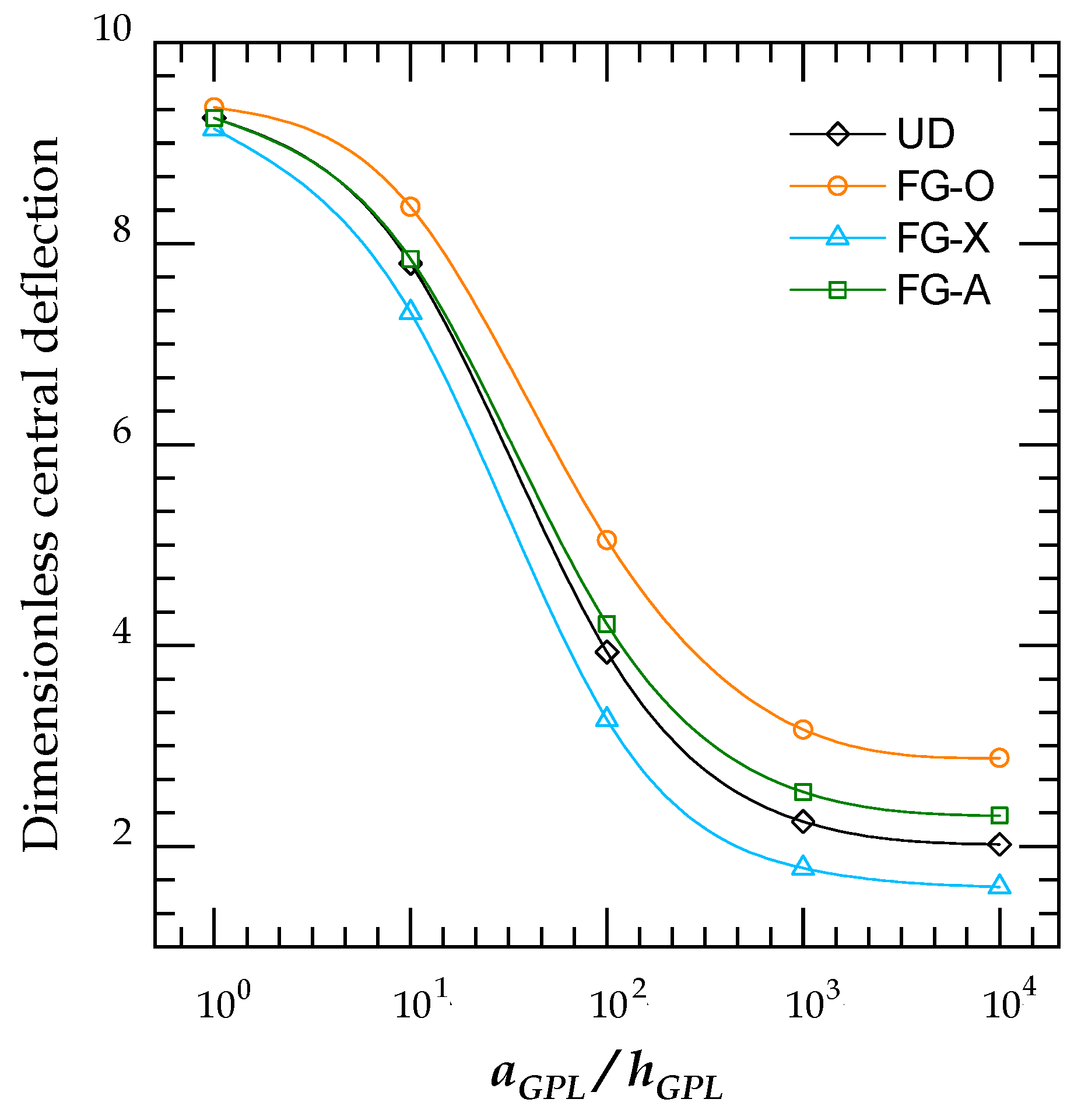
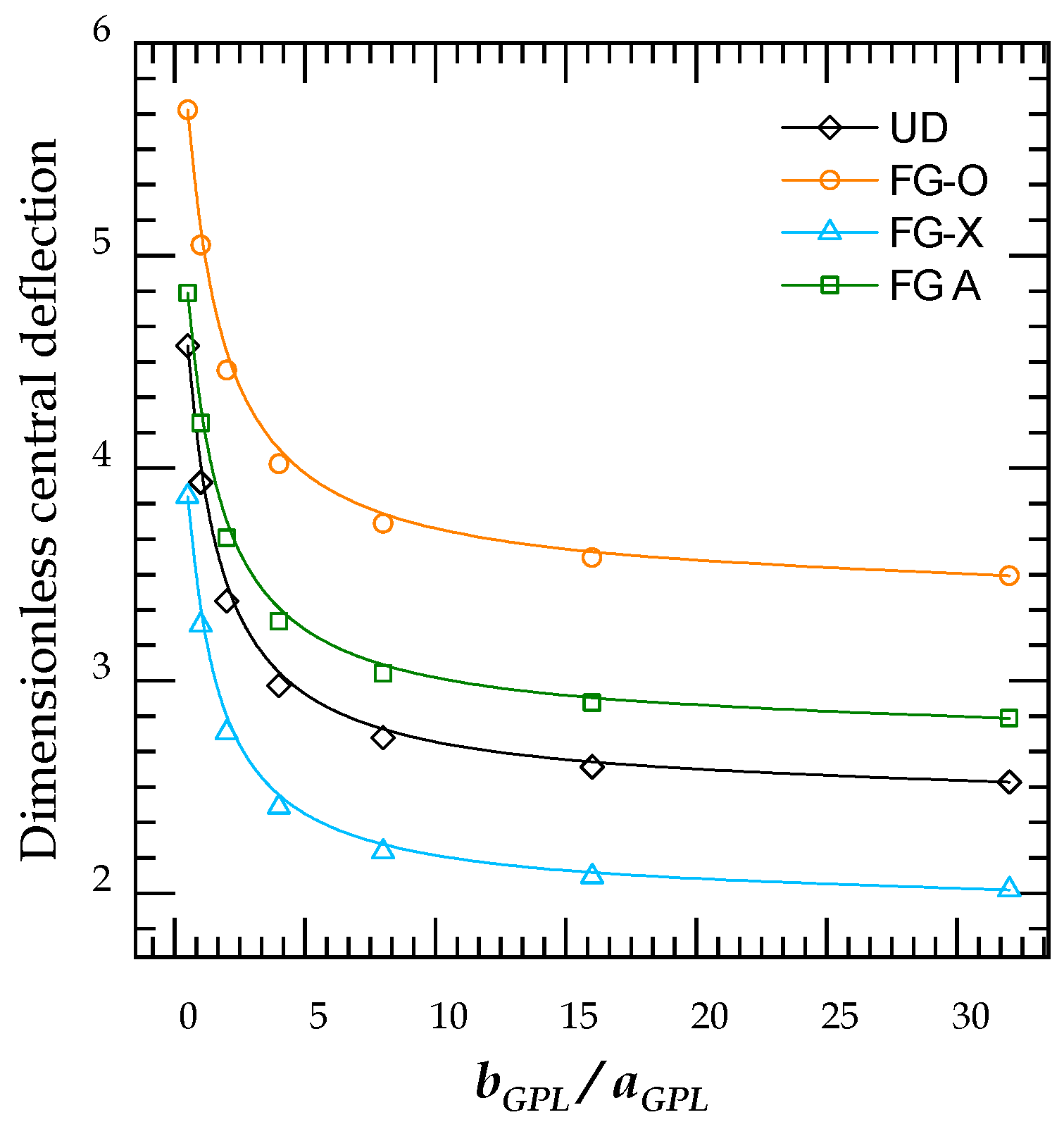
4.2.2. Bending Analysis
5. Conclusions
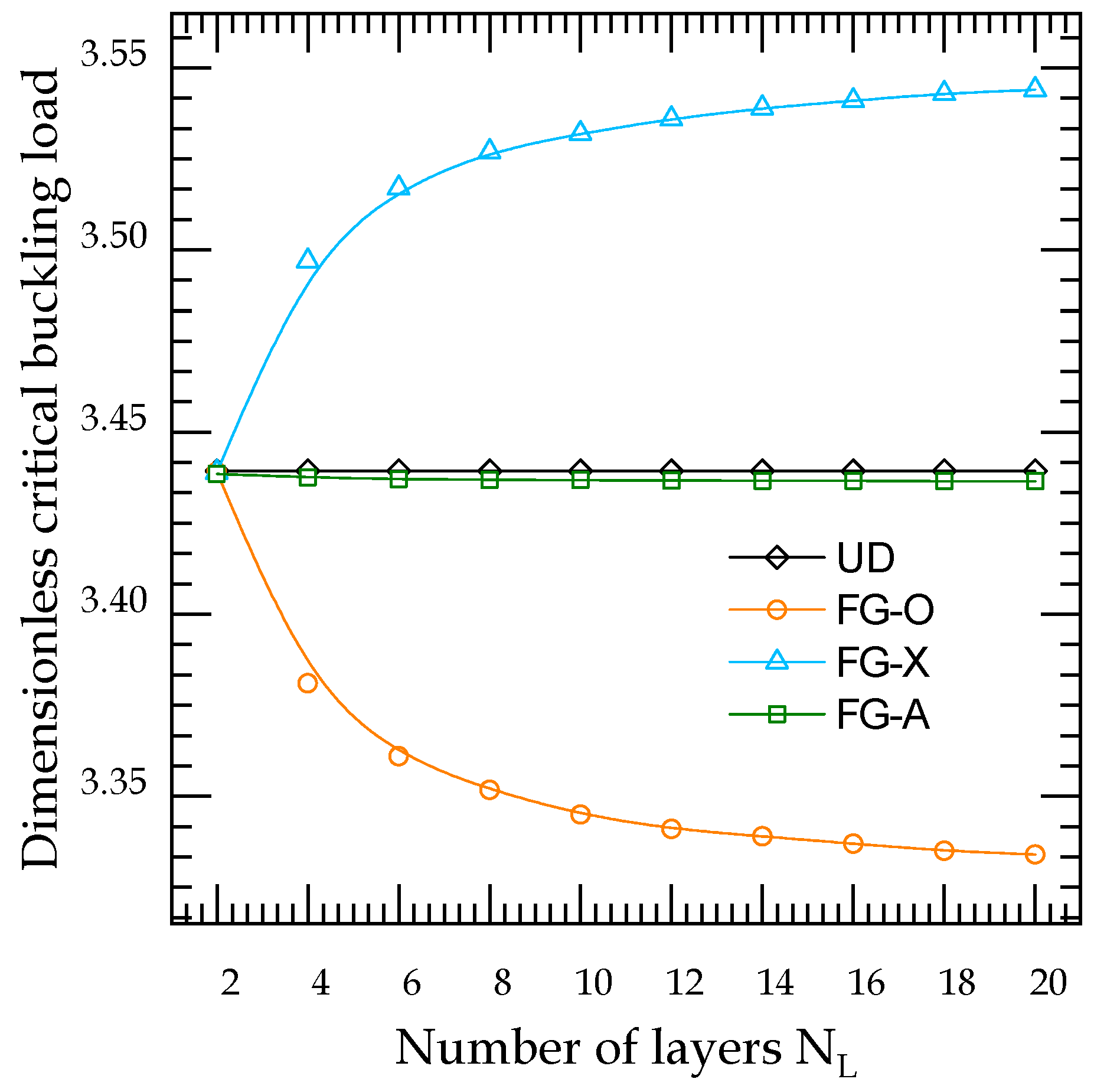
- Unlike the FG-X GRNC plates, the increase in the number of layers leads to an improvement in the FG-X GRNC plate stiffness; therefore, the critical buckling load increases and the central deflection decreases.
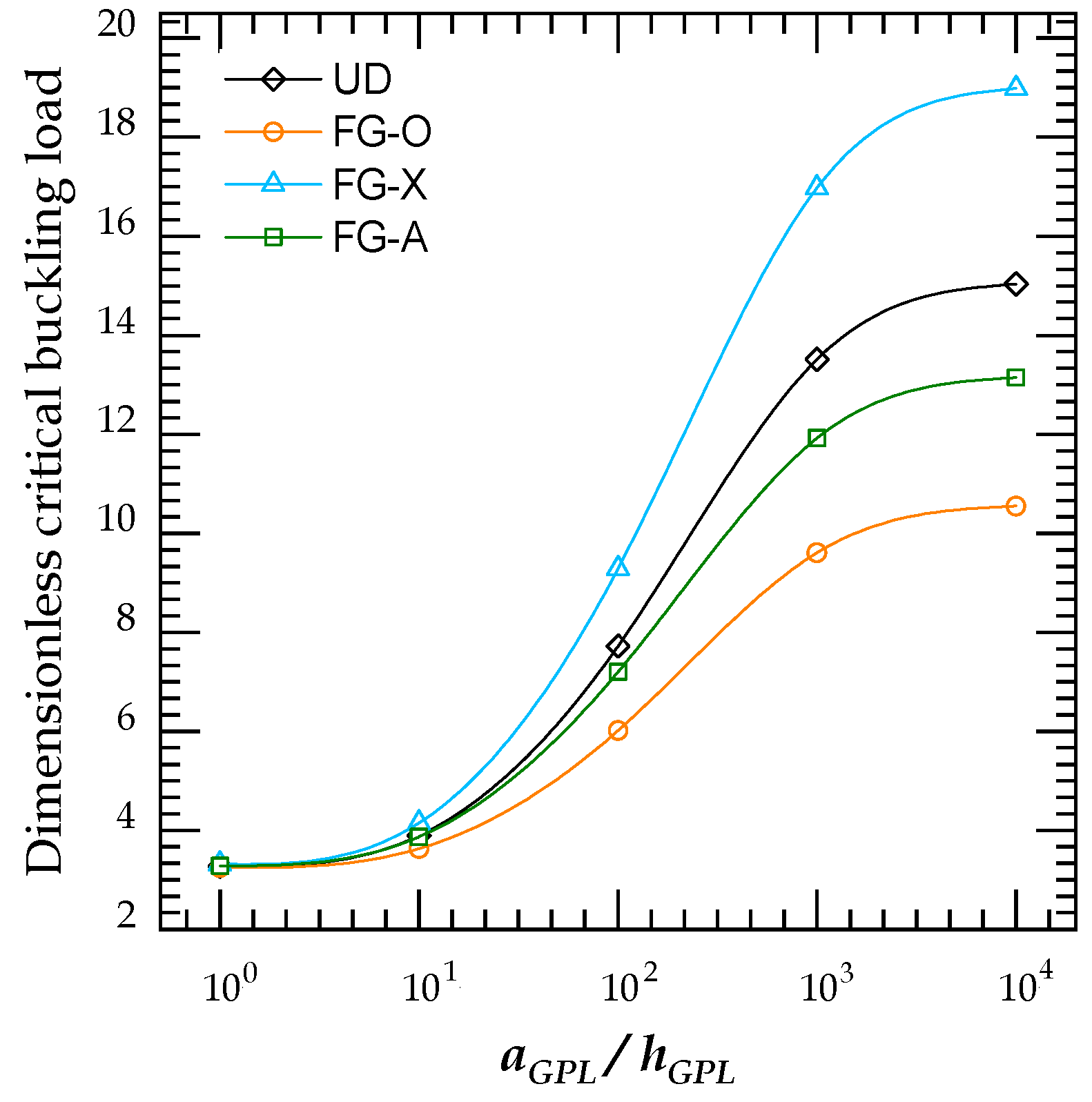
- Both increasing the weight fraction and the number of layers can improve the stiffness of the GRNC plates.
- The inclusion of thickness stretching has a significant effect on the response of the GRNC plate, especially for the fully clamped plate.
- The inclusion of a nonlocal parameter leads to a decrease in buckling loads and an increase in transverse displacements, while the opposite is found when increasing the length-scale parameter.
- The FG-X reinforcement pattern has the better response under in-plane and transverse loadings, among the other analyzed distributions, due to their higher stiffness.
- Increasing the length-to-width and length-to-thickness ratios result in increasing the total stiffness of the GRNC plate and consequently lead to higher critical buckling loads and lower transverse displacements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.S.; Xiang, Y.; Lin, F. Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin-Walled Struct. 2017, 118, 229–237. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y.; Lin, F. Nonlinear bending of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations in thermal environments. Compos. Struct. 2017, 170, 80–90. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Liu, A.; Fu, J. Nonlinear buckling analysis of functionally graded graphene reinforced composite shallow arches with elastic rotational constraints under uniform radial load. Materials 2018, 11, 910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Macias, E.; Rodriguez-Tembleque, L.; Saez, A. Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos. Struct. 2018, 186, 123–138. [Google Scholar] [CrossRef]
- Dong, Y.H.; He, L.W.; Wang, L.; Li, Y.H.; Yang, J. Buckling of spinning functionally graded graphene reinforced porous nanocomposite cylindrical shells: An analytical study. Aerosp. Sci. Technol. 2018, 82, 466–478. [Google Scholar] [CrossRef]
- Daikh, A.A.; Megueni, A. Thermal buckling analysis of functionally graded sandwich plates. J. Therm. Stresses 2018, 41, 139–159. [Google Scholar] [CrossRef]
- Liu, D.; Kitipornchai, S.; Chen, W.; Yang, J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos. Struct. 2018, 189, 560–569. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Li, Z.; Kitipornchai, S.; Yang, J. Three-dimensional free vibration and bending analyses of functionally graded graphene nanoplatelets-reinforced nanocomposite annular plates. Compos. Struct. 2019, 229, 111453. [Google Scholar] [CrossRef]
- Polit, O.; Anant, C.; Anirudh, B.; Ganapathi, M. Functionally graded graphene reinforced porous nanocomposite curved beams: Bending and elastic stability using a higher-order model with thickness stretch effect. Compos. Part B Eng. 2019, 166, 310–327. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, Y.; Liu, A.; Fu, J.; Wu, D. Nonlinear in-plane buckling of fixed shallow functionally graded graphene reinforced composite arches subjected to mechanical and thermal loading. Appl. Math. Model. 2019, 70, 315–327. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar] [CrossRef]
- Anirudh, B.; Ganapathi, M.; Anant, C.; Polit, O. A comprehensive analysis of porous graphene-reinforced curved beams by finite element approach using higher-order structural theory: Bending, vibration and buckling. Compos. Struct. 2019, 222, 110899. [Google Scholar] [CrossRef]
- Tam, M.; Yang, Z.; Zhao, S.; Yang, J. Vibration and buckling characteristics of functionally graded graphene nanoplatelets reinforced composite beams with open edge cracks. Materials 2019, 12, 1412. [Google Scholar] [CrossRef] [Green Version]
- Tam, M.; Yang, Z.; Zhao, S.; Zhang, H.; Zhang, Y.; Yang, J. Nonlinear bending of elastically restrained functionally graded graphene nanoplatelet reinforced beams with an open edge crack. Thin-Walled Struct. 2020, 156, 106972. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira AJ, M.; Tran, T.D.; Phung-Van, P. Free vibration, buckling and bending analyses of multilayer functionally graded graphene nanoplatelets reinforced composite plates using the NURBS formulation. Compos. Struct. 2019, 220, 749–759. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira AJ, M.; Tran, T.D.; Phung-Van, P. A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos. Struct. 2020, 234, 111695. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Attia, M.A.; Wagih, A. Predictive model for indentation of elasto-plastic functionally graded composites. Compos. Part B Eng. 2020, 197, 108129. [Google Scholar] [CrossRef]
- Rahimi, A.; Alibeigloo, A.; Safarpour, M. Three-dimensional static and free vibration analysis of graphene platelet–reinforced porous composite cylindrical shell. J. Vib. Control 2020, 26, 1627–1645. [Google Scholar] [CrossRef]
- Shahgholian, D.; Safarpour, M.; Rahimi, A.R.; Alibeigloo, A. Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh–Ritz method. Acta Mech. 2020, 231, 1887–1902. [Google Scholar] [CrossRef]
- Hamed, M.A.; Mohamed, S.A.; Eltaher, M.A. Buckling analysis of sandwich beam rested on elastic foundation and subjected to varying axial in-plane loads. Steel Compos. Struct. 2020, 34, 75–89. [Google Scholar] [CrossRef]
- Hamed, M.A.; Abu-bakr, R.M.; Mohamed, A.S.; Eltaher, M.A. Influence of Axial Load Function and Optimization on Static Stability of Sandwich Functionally Graded Beams with Porous Core. Eng. Comput. 2020, 36, 1929–1946. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Yang, J.; Zhou, D.; Liu, W. Static response of functionally graded graphene platelet–reinforced composite plate with dielectric property. J. Intell. Mater. Syst. Struct. 2020, 31, 2211–2228. [Google Scholar] [CrossRef]
- Daikh, A.A.; Guerroudj, M.; El Adjrami, M.; Megueni, A. Thermal buckling of functionally graded sandwich beams. Adv. Mater. Res. 2020, 1156, 43–59. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D. On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comput. Methods Appl. Mech. Eng. 2020, 359, 112767. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y.; Nix, W.D.; Hutchinson, J.W. Mechanism-based strain gradient plasticity—I. Theory. J Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Couple-Stresses on Stress Concentrations; Columbia University: New York, NY, USA, 1962. [Google Scholar]
- Koiter, W.T. Couple stresses in the theory of elasticity. Proc. Koninklijke Nederl. Akaad Wetensch 1964, 67, 20. [Google Scholar]
- Gurtin, M.E.; Ian Murdoch, A. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M.; Rabczuk, T. Nonlinear bending of functionally graded porous micro/nano-beams reinforced with graphene platelets based upon nonlocal strain gradient theory. Compos. Struct. 2018, 186, 68–78. [Google Scholar] [CrossRef]
- Emam, S.A.; Eltaher, M.A.; Khater, M.E.; Abdalla, W.S. Postbuckling and free vibration of multilayer imperfect nanobeams under a pre-stress load. Appl. Sci. 2018, 8, 2238. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, F.; Barati, M.R. Damping vibration analysis of graphene sheets on viscoelastic medium incorporating hygro-thermal effects employing nonlocal strain gradient theory. Compos. Struct. 2018, 185, 241–253. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari MS, A.; Tounsi, A. Buckling analysis of porous FGM sandwich nanoplates due to heat conduction via nonlocal strain gradient theory. Eng. Res. Express 2019, 1, 015022. [Google Scholar] [CrossRef]
- Fattahi, A.M.; Sahmani, S.; Ahmed, N.A. Nonlocal strain gradient beam model for nonlinear secondary resonance analysis of functionally graded porous micro/nano-beams under periodic hard excitations. Mech. Based Des. Struct. Mach. 2019, 48, 403–432. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Rabczuk, T. Static analysis of functionally graded anisotropic nanoplates using nonlocal strain gradient theory. Compos. Struct. 2019, 227, 111249. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Civalek, Ö. A nonlocal strain gradient refined plate theory for dynamic instability of embedded graphene sheet including thermal effects. Compos. Struct. 2019, 220, 209–220. [Google Scholar] [CrossRef]
- Daikh, A.A.; Drai, A.; Houari, M.S.A.; Eltaher, M.A. Static analysis of multilayer nonlocal strain gradient nanobeam reinforced by carbon nanotubes. Steel Compos. Struct. 2020, 36, 643–656. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Viscoelastic wave propagation analysis of axially motivated double-layered graphene sheets via nonlocal strain gradient theory. Waves Random Complex Media 2020, 30, 157–176. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N. Nonlinear stability and vibration of imperfect CNTs by Doublet mechanics. Appl. Math. Comput. 2020, 382, 125311. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.A. Nonlinear buckling and free vibration of curved CNTs by doublet mechanics. Smart Struct. Syst. 2020, 26, 213–226. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng. Comput. 2020, 37, 2823–2836. [Google Scholar] [CrossRef]
- Daikh, A.A.; Zenkour, A.M. Bending of functionally graded sandwich nanoplates resting on Pasternak foundation under different boundary conditions. J. Appl. Comput. Mech. 2020, 6, 1245–1259. [Google Scholar] [CrossRef]
- Daikh, A.A.; Drai, A.; Bensaid, I.; Houari MS, A.; Tounsi, A. On vibration of functionally graded sandwich nanoplates in the thermal environment. J. Sandw. Struct. Mater. 2020, 23, 2217–2244. [Google Scholar] [CrossRef]
- Torabi, J.; Ansari, R.; Zabihi, A.; Hosseini, K. Dynamic and pull-in instability analyses of functionally graded nanoplates via nonlocal strain gradient theory. Mech. Based Des. Struct. Mach. 2020, 50, 588–608. [Google Scholar] [CrossRef]
- Xiao, W.S.; Dai, P. Static analysis of a circular nanotube made of functionally graded bi-semi-tubes using nonlocal strain gradient theory and a refined shear model. Eur. J. Mech.-A/Solids 2020, 82, 103979. [Google Scholar] [CrossRef]
- Chaleshtari MH, B.; Jafari, M.; Khoramishad, H.; Craciun, E.M. Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes. Mathematics 2021, 9, 311. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Malikan, M.; Dimitri, R.; Tornabene, F. Nonlocal elasticity analysis of moderately thick porous functionally graded plates in a hygro-thermal environment. Compos. Struct. 2021, 255, 112925. [Google Scholar] [CrossRef]
- Abo-Bakr, R.M.; Abo-Bakr, H.M.; Mohamed, S.A.; Eltaher, M.A. Optimal Weight for Buckling of FG Beam under Variable Axial Load using Pareto Optimality. Compos. Struct. 2020, 258, 113193. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Abdalla, A.W.; Othman, R.; Almitani, K.H.; Eltaher, M.A. Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Wagih, A.; Othman, R.; Almitani, K.H.; Eltaher, M.A. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics 2022, 10, 408. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. A new quasi 3D nonlocal plate theory for vibration and buckling of FGM nanoplates. Int J. Appl. Mech. 2017, 9, 1750008. [Google Scholar] [CrossRef]
- Zenkour, A.M. Bending analysis of functionally graded sandwich plates using a simple four-unknown shear and normal deformations theory. J. Sandw. Struct. Mater. 2013, 15, 629–656. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Thai, H.-T. Dynamic stability of viscoelastic porous FG nanoplate under longitudinal magnetic field via a nonlocal strain gradient quasi-3D theory. Compos. B Eng. 2019, 175, 107164. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari MS, A.; Eltaher, M.A. A novel nonlocal strain gradient Quasi-3D bending analysis of sigmoid functionally graded sandwich nanoplates. Compos. Struct. 2020, 262, 113347. [Google Scholar] [CrossRef]
- Amir, S.; Arshid, E.; Rasti-Alhosseini SM, A.; Loghman, A. Quasi-3D tangential shear deformation theory for size-dependent free vibration analysis of three-layered FG porous micro rectangular plate integrated by nanocomposite faces in hygrothermal environment. J. Stresses 2020, 43, 133–156. [Google Scholar] [CrossRef]
- Shahraki, H.; Tajmir Riahi, H.; Izadinia, M.; Talaeitaba, S.B. Buckling and vibration analysis of FG-CNT-reinforced composite rectangular thick nanoplates resting on Kerr foundation based on nonlocal strain gradient theory. J. Vib. Control. 2020, 26, 277e305. [Google Scholar] [CrossRef]
- Khadir, A.I.; Daikh, A.A.; Eltaher, M.A. Novel four-unknowns quasi 3D theory for bending, buckling and free vibration of functionally graded carbon nanotubes reinforced composite laminated nanoplates. Adv. Nano Res. 2021, 11, 621–640. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Daikh, A.A.; Eltaher, M.A. Novel quasi 3D theory for mechanical responses of FG-CNTs reinforced composite nanoplates. Adv. Nano Res. 2022, 12, 117–137. [Google Scholar] [CrossRef]
- Affdl, J.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Reddy, J.N. A general non-linear third-order theory of plates with moderate thickness. Int. J. Non-Linear Mech. 1990, 25, 677–686. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K.P. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solid 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Thai, H.T.; Nguyen, T.K.; Vo, T.P.; Lee, J. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. Eur. J. Mech.-A/Solids 2014, 45, 211–225. [Google Scholar] [CrossRef] [Green Version]
- Sahmani, S.; Aghdam, M.M. Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams. Compos. Struct. 2017, 179, 77–88. [Google Scholar] [CrossRef]
- Wu, H.; Yang, J.; Kitipornchai, S. Parametric instability of thermo-mechanically loaded functionally graded graphene reinforced nanocomposite plates. Int. J. Mech. Sci. 2018, 135, 431–440. [Google Scholar] [CrossRef] [Green Version]
- Gholami, R.; Ansari, R. Nonlinear stability and vibration of pre/post-buckled multilayer FG-GPLRPC rectangular plates. Appl. Math. Model. 2019, 65, 627–660. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Thermal buckling and postbuckling of functionally graded graphene nanocomposite plates. Mater. Des. 2017, 132, 430–441. [Google Scholar] [CrossRef] [Green Version]
- Zenkour, A. Benchmark trigonometric and 3-D elasticity solutions for an exponentially graded thick rectangular plate. Arch. Appl. Mech. 2007, 77, 197–214. [Google Scholar] [CrossRef]
- Bessaim, A.; Houari, M.S.; Tounsi, A.; Mahmoud, S.R.; Bedia, E.A.A. A new higher-order shear and normal deformation theory for the static and free vibration analysis of sandwich plates with functionally graded isotropic face sheets. J. Sandw. Struct. Mater. 2013, 15, 671–703. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.; Carrera, E.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M.M. Static analysis of functionally graded sandwich plates according to a hyperbolic theory considering Zig-Zag and warping effects. Adv. Eng. Softw. 2012, 52, 30–43. [Google Scholar] [CrossRef]
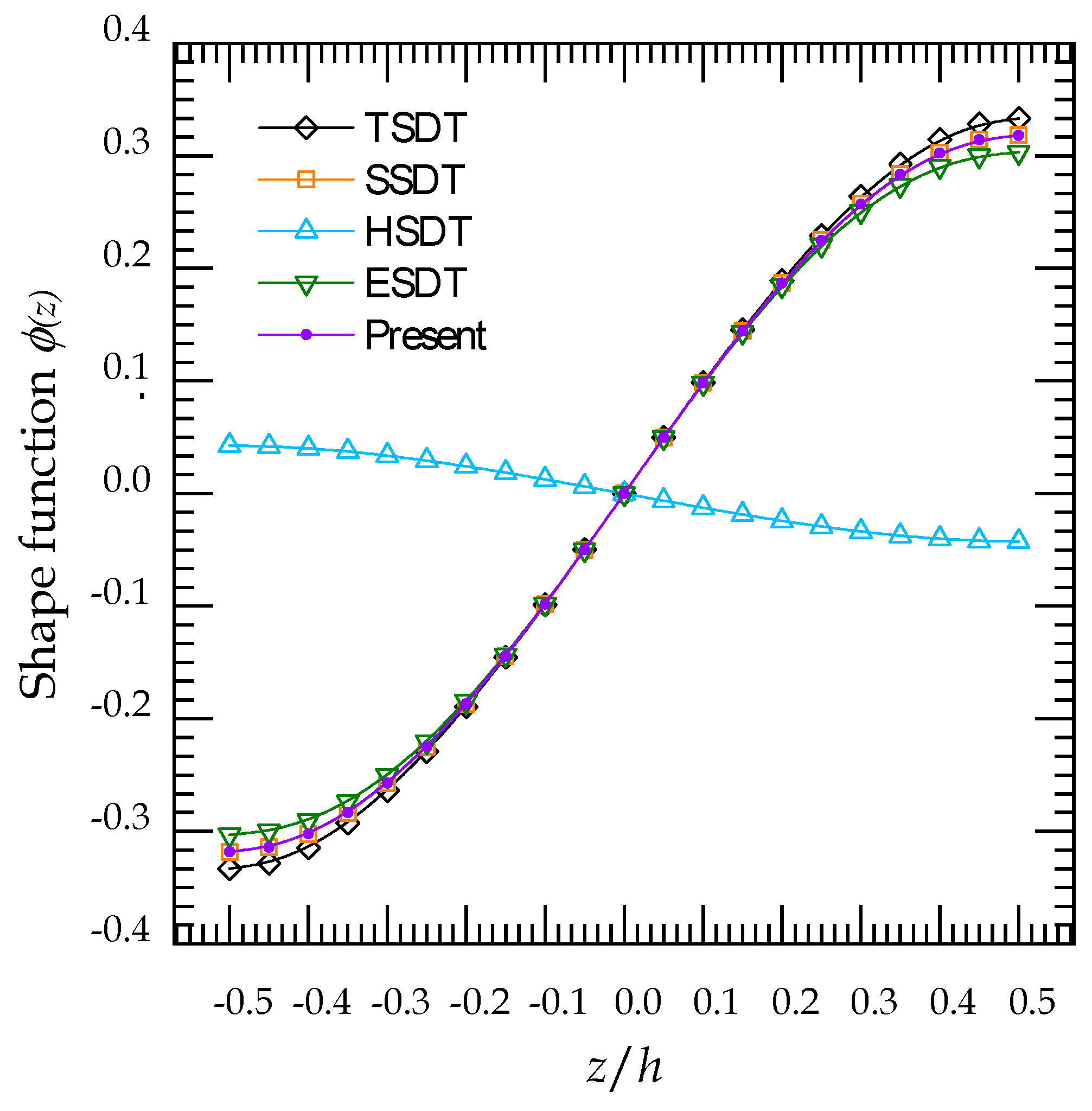







| Theory | Description | |
|---|---|---|
| Reddy [66] | TSDT | |
| Touratier [67] | SSDT | |
| Soldatos et al. [68] | HSDT | |
| Karama et al. [69] | ESDT | |
| Present |
| Boundary Conditions | ||||
|---|---|---|---|---|
| SSSS | ||||
| CCCC | ||||
| CCSS | ||||
| SCSC | ||||
| References | Pattern | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SSSS | CCCC | SCSC | ||||||||
| UD | FG-O | FG-X | UD | FG-O | FG-X | UD | FG-O | FG-X | ||
| 0.0 | Wu et al. [75] | 0.0310 | 0.0310 | 0.0310 | 0.0675 | 0.0675 | 0.0675 | 0.0520 | 0.0520 | 0.0520 |
| Gholami [74] | 0.0311 | 0.0311 | 0.0311 | 0.0680 | 0.0680 | 0.0680 | 0.0523 | 0.0523 | 0.0523 | |
| Thai et al. [18] | 0.0309 | 0.0309 | 0.0309 | 0.0735 | 0.0735 | 0.0735 | − | − | − | |
| Present | 0.0310 | 0.0310 | 0.0310 | 0.0757 | 0.0757 | 0.0757 | 0.0492 | 0.0492 | 0.0492 | |
| Present | 0.0318 | 0.0318 | 0.0318 | 0.0894 | 0.0894 | 0.0894 | 0.0564 | 0.0564 | 0.0564 | |
| 0.1 | Wu et al. [75] | 0.0413 | 0.0366 | 0.0460 | 0.0899 | 0.0809 | 0.0984 | 0.0692 | 0.0622 | 0.0760 |
| Gholami [74] | 0.0414 | 0.0368 | 0.0462 | 0.0906 | 0.0811 | 0.0987 | 0.0697 | 0.0626 | 0.0761 | |
| Thai et al. [18] | 0.0412 | 0.0376 | 0.0448 | 0.0980 | 0.0910 | 0.1044 | − | − | − | |
| Present | 0.0413 | 0.0376 | 0.0450 | 0.1009 | 0.0927 | 0.1083 | 0.0656 | 0.0601 | 0.0707 | |
| Present | 0.0424 | 0.0385 | 0.0461 | 0.1190 | 0.1098 | 0.1272 | 0.0751 | 0.0690 | 0.0803 | |
| 0.3 | Wu et al. [75] | 0.0619 | 0.0478 | 0.0758 | 0.1346 | 0.1072 | 0.1597 | 0.1037 | 0.0823 | 0.1235 |
| Gholami [74] | 0.0620 | 0.0480 | 0.0759 | 0.1351 | 0.1084 | 0.1599 | 0.1041 | 0.0828 | 0.1238 | |
| Thai et al. [18] | 0.0618 | 0.0509 | 0.0726 | 0.1469 | 0.1252 | 0.1655 | − | − | − | |
| Present | 0.0620 | 0.0504 | 0.0728 | 0.1512 | 0.1259 | 0.1722 | 0.0983 | 0.0813 | 0.1130 | |
| Present | 0.0635 | 0.0517 | 0.0745 | 0.1784 | 0.1496 | 0.2012 | 0.1125 | 0.0936 | 0.1283 | |
| 0.5 | Wu et al. [75] | 0.0825 | 0.0588 | 0.1055 | 0.1794 | 0.1331 | 0.2207 | 0.1382 | 0.1021 | 0.1709 |
| Gholami [74] | 0.0826 | 0.0592 | 0.1057 | 0.1801 | 0.1348 | 0.2211 | 0.1386 | 0.1026 | 0.1721 | |
| Thai et al. [18] | 0.0824 | 0.0641 | 0.1003 | 0.1957 | 0.1590 | 0.2262 | − | − | − | |
| Present | 0.0827 | 0.0632 | 0.1004 | 0.2016 | 0.1586 | 0.2353 | 0.1311 | 0.1022 | 0.1548 | |
| Present | 0.0847 | 0.0648 | 0.1027 | 0.2376 | 0.1887 | 0.2741 | 0.1499 | 0.1179 | 0.1752 | |
| 1 | Thai et al. [18] | 0.1338 | 0.0971 | 0.1695 | 0.3177 | 0.2428 | 0.3773 | − | − | − |
| Present | 0.1342 | 0.0951 | 0.1690 | 0.3274 | 0.2399 | 0.3918 | 0.2128 | 0.1544 | 0.2586 | |
| Present | 0.1375 | 0.0975 | 0.1729 | 0.3853 | 0.2856 | 0.3853 | 0.2432 | 0.1781 | 0.2915 | |
| Zenkour [58] FSDT | 0.19607 | 1.97576 | 0.19099 |
| Zenkour [58] TSDT | 0.19606 | 2.04985 | 0.23857 |
| Zenkour [58] SSDT | 0.19605 | 2.05452 | 0.24618 |
| Neves [35] | 0.1961 | 1.9947 | 0.2538 |
| Present | 0.19605 | 2.05438 | 0.24634 |
| Zenkour [58] | 0.19487 | 2.00773 | 0.23910 |
| Bessaim [77] | 0.19486 | 1.99524 | 0.2461 |
| Neves [78] | 0.1949 | 2.0066 | 0.2459 |
| Present | 0.19429 | 1.99547 | 0.24559 |
| Pattern | Theory | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0% | 0.2% | 0.6% | 1.0% | ||||||
| UD | TSDT | 3.1043 | 3.1638 | 3.1547 | 3.2151 | 3.2560 | 3.3181 | 3.3580 | 3.4218 |
| SSDT | 3.1046 | 3.1811 | 3.1550 | 3.2326 | 3.2562 | 3.3361 | 3.3583 | 3.4402 | |
| HSDT | 3.1043 | 3.1638 | 3.1547 | 3.2150 | 3.2560 | 3.3181 | 3.3580 | 3.4218 | |
| ESDT | 3.1054 | 3.2277 | 3.1558 | 3.2797 | 3.2571 | 3.3843 | 3.3592 | 3.4895 | |
| Present | 3.1046 | 3.1803 | 3.1550 | 3.2318 | 3.2562 | 3.3352 | 3.3583 | 3.4393 | |
| FG-O | TSDT | 3.1043 | 3.1638 | 3.1364 | 3.1966 | 3.2007 | 3.2621 | 3.2652 | 3.3279 |
| SSDT | 3.1046 | 3.1811 | 3.1367 | 3.2141 | 3.2011 | 3.2803 | 3.2657 | 3.3467 | |
| HSDT | 3.1043 | 3.1638 | 3.1364 | 3.1965 | 3.2007 | 3.2620 | 3.2652 | 3.3278 | |
| ESDT | 3.1054 | 3.2277 | 3.1376 | 3.2613 | 3.2021 | 3.3285 | 3.2667 | 3.3959 | |
| Present | 3.1046 | 3.1803 | 3.1367 | 3.2133 | 3.2011 | 3.2795 | 3.2657 | 3.3459 | |
| FG-X | TSDT | 3.1043 | 3.1638 | 3.1730 | 3.2337 | 3.3113 | 3.3742 | 3.4509 | 3.5160 |
| SSDT | 3.1046 | 3.1811 | 3.1732 | 3.2511 | 3.3115 | 3.3918 | 3.4510 | 3.5338 | |
| HSDT | 3.1043 | 3.1638 | 3.1730 | 3.2336 | 3.3113 | 3.3742 | 3.4510 | 3.5160 | |
| ESDT | 3.1054 | 3.2277 | 3.1740 | 3.2982 | 3.3122 | 3.4401 | 3.4516 | 3.5831 | |
| Present | 3.1046 | 3.1803 | 3.1732 | 3.2502 | 3.3115 | 3.3910 | 3.4510 | 3.5329 | |
| FG-A | TSDT | 3.1043 | 3.1638 | 3.1545 | 3.2150 | 3.2545 | 3.3172 | 3.3541 | 3.4194 |
| SSDT | 3.1046 | 3.1811 | 3.1548 | 3.2325 | 3.2548 | 3.3351 | 3.3544 | 3.4377 | |
| HSDT | 3.1043 | 3.1638 | 3.1545 | 3.2149 | 3.2545 | 3.3172 | 3.3540 | 3.4194 | |
| ESDT | 3.1054 | 3.2277 | 3.1556 | 3.2796 | 3.2557 | 3.3833 | 3.3553 | 3.4869 | |
| Present | 3.1046 | 3.1803 | 3.1548 | 3.2317 | 3.2548 | 3.3343 | 3.3544 | 3.4368 | |
| Pattern | Theory | Boundary Conditions | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SSSS | CCCC | SCSC | CCSS | ||||||
| Uniaxial in-plane loading | |||||||||
| UD | TSDT | 3.3580 | 3.4218 | 8.1882 | 9.6157 | 5.3242 | 6.0649 | 6.5004 | 7.1422 |
| SSDT | 3.3583 | 3.4402 | 8.1903 | 9.6414 | 5.3253 | 6.0843 | 6.5017 | 7.1718 | |
| HSDT | 3.3580 | 3.4218 | 8.1882 | 9.6150 | 5.3242 | 6.0645 | 6.5004 | 7.1417 | |
| ESDT | 3.3592 | 3.4895 | 8.19598 | 9.7008 | 5.3282 | 6.1320 | 6.5051 | 7.2442 | |
| Present | 3.3583 | 3.4393 | 8.1903 | 9.6405 | 5.3253 | 6.0835 | 6.5016 | 7.1706 | |
| FG-O | TSDT | 3.2652 | 3.3279 | 7.9932 | 9.4090 | 5.1913 | 5.9252 | 6.3369 | 6.9712 |
| SSDT | 3.2657 | 3.3467 | 7.9965 | 9.4363 | 5.1930 | 5.9455 | 6.33896 | 7.0018 | |
| HSDT | 3.2652 | 3.3278 | 7.9931 | 9.4082 | 5.1912 | 5.9248 | 6.3368 | 6.9706 | |
| ESDT | 3.2667 | 3.3959 | 8.0031 | 9.4967 | 5.1965 | 5.9937 | 6.3430 | 7.0745 | |
| Present | 3.2657 | 3.3459 | 7.9965 | 9.4353 | 5.1930 | 5.9447 | 6.3389 | 7.0006 | |
| FG-X | TSDT | 3.4509 | 3.5160 | 8.3809 | 9.8182 | 5.4561 | 6.2026 | 6.6627 | 7.3114 |
| SSDT | 3.4510 | 3.5338 | 8.3815 | 9.8419 | 5.4564 | 6.2209 | 6.6630 | 7.3398 | |
| HSDT | 3.4510 | 3.5160 | 8.3810 | 9.8178 | 5.4562 | 6.2024 | 6.6628 | 7.3111 | |
| ESDT | 3.4516 | 3.5831 | 8.3859 | 9.8997 | 5.4587 | 6.2678 | 6.6657 | 7.4115 | |
| Present | 3.4510 | 3.5329 | 8.3815 | 9.8408 | 5.4563 | 6.2200 | 6.6630 | 7.3385 | |
| FG-A | TSDT | 3.3541 | 3.4194 | 8.1796 | 9.6077 | 5.3184 | 6.0599 | 6.4933 | 7.1367 |
| SSDT | 3.3544 | 3.4377 | 8.1817 | 9.6334 | 5.3195 | 6.0793 | 6.4945 | 7.1662 | |
| HSDT | 3.3540 | 3.4194 | 8.1796 | 9.6071 | 5.3184 | 6.0596 | 6.4933 | 7.1362 | |
| ESDT | 3.3553 | 3.4869 | 8.1873 | 9.6926 | 5.3224 | 6.1268 | 6.4980 | 7.2385 | |
| Present | 3.3544 | 3.4368 | 8.1817 | 9.6323 | 5.31947 | 6.0784 | 6.4945 | 7.1650 | |
| Biaxial in-plane loading | |||||||||
| UD | TSDT | 1.6790 | 1.7109 | 4.0941 | 4.8078 | 3.0424 | 3.4656 | 3.2502 | 3.5711 |
| SSDT | 1.6791 | 1.7201 | 4.0952 | 4.8207 | 3.0430 | 3.4767 | 3.2508 | 3.5859 | |
| HSDT | 1.6790 | 1.7109 | 4.0941 | 4.8075 | 3.0424 | 3.4654 | 3.25019 | 3.5709 | |
| ESDT | 1.6796 | 1.7448 | 4.0980 | 4.8504 | 3.0447 | 3.5040 | 3.25256 | 3.6221 | |
| Present | 1.6791 | 1.7197 | 4.0952 | 4.8202 | 3.0430 | 3.4763 | 3.2508 | 3.5853 | |
| FG-O | TSDT | 1.6326 | 1.6640 | 3.9966 | 4.7045 | 2.9665 | 3.3858 | 3.1685 | 3.4856 |
| SSDT | 1.6329 | 1.6733 | 3.9983 | 4.7182 | 2.9675 | 3.3974 | 3.1695 | 3.5009 | |
| HSDT | 1.6326 | 1.6639 | 3.9965 | 4.7041 | 2.9664 | 3.3855 | 3.1684 | 3.4853 | |
| ESDT | 1.6334 | 1.6979 | 4.0015 | 4.7484 | 2.9694 | 3.4249 | 3.1715 | 3.5373 | |
| Present | 1.6329 | 1.6729 | 3.9983 | 4.7177 | 2.9674 | 3.3970 | 3.1695 | 3.5003 | |
| FG-X | TSDT | 1.7255 | 1.7580 | 4.1905 | 4.9091 | 3.11776 | 3.5443 | 3.3313 | 3.6557 |
| SSDT | 1.7255 | 1.7669 | 4.1908 | 4.9209 | 3.1179 | 3.5548 | 3.3315 | 3.6699 | |
| HSDT | 1.7255 | 1.7580 | 4.1905 | 4.9089 | 3.1178 | 3.5442 | 3.3314 | 3.6555 | |
| ESDT | 1.7258 | 1.7915 | 4.1929 | 4.9499 | 3.1192 | 3.5816 | 3.3329 | 3.7057 | |
| Present | 1.7255 | 1.7665 | 4.1907 | 4.9204 | 3.1179 | 3.5543 | 3.3315 | 3.6692 | |
| FG-A | TSDT | 1.6770 | 1.7097 | 4.0898 | 4.8038 | 3.0391 | 3.4628 | 3.2467 | 3.5684 |
| SSDT | 1.6772 | 1.7188 | 4.0909 | 4.8167 | 3.0397 | 3.4739 | 3.2473 | 3.5831 | |
| HSDT | 1.6770 | 1.7097 | 4.0898 | 4.8035 | 3.0391 | 3.4626 | 3.2466 | 3.5681 | |
| ESDT | 1.6776 | 1.7434 | 4.0937 | 4.8463 | 3.0414 | 3.5010 | 3.2490 | 3.6192 | |
| Present | 1.6772 | 1.7184 | 4.0908 | 4.8162 | 3.0397 | 3.4734 | 3.2473 | 3.5825 | |
| Pattern | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| UD | 0 | 3.4393 | 3.4410 | 3.4427 | 3.4444 | 3.4461 | 3.4478 |
| 1 | 3.4376 | 3.4393 | 3.4410 | 3.4427 | 3.4444 | 3.4461 | |
| 2 | 3.4359 | 3.4376 | 3.4393 | 3.4410 | 3.4427 | 3.4444 | |
| 3 | 3.4343 | 3.4360 | 3.4376 | 3.4393 | 3.4410 | 3.4427 | |
| 4 | 3.4326 | 3.4343 | 3.4360 | 3.4376 | 3.4393 | 3.4410 | |
| 5 | 3.4309 | 3.4326 | 3.4343 | 3.4360 | 3.4376 | 3.4393 | |
| FG-O | 0 | 3.3459 | 3.3475 | 3.3492 | 3.3508 | 3.35247 | 3.3541 |
| 1 | 3.3442 | 3.3459 | 3.3475 | 3.3492 | 3.3508 | 3.3525 | |
| 2 | 3.3426 | 3.3442 | 3.3459 | 3.3475 | 3.34916 | 3.3508 | |
| 3 | 3.3409 | 3.3426 | 3.3442 | 3.3459 | 3.3475 | 3.3492 | |
| 4 | 3.3393 | 3.3409 | 3.3426 | 3.3442 | 3.3459 | 3.3475 | |
| 5 | 3.3376 | 3.3393 | 3.3409 | 3.3426 | 3.3442 | 3.3459 | |
| FG-X | 0 | 3.5329 | 3.5347 | 3.5364 | 3.5382 | 3.5399 | 3.5417 |
| 1 | 3.5312 | 3.5329 | 3.5347 | 3.5364 | 3.5382 | 3.5399 | |
| 2 | 3.5295 | 3.5312 | 3.5330 | 3.5347 | 3.5364 | 3.5382 | |
| 3 | 3.5277 | 3.5295 | 3.5312 | 3.5329 | 3.5347 | 3.5364 | |
| 4 | 3.5260 | 3.5277 | 3.5295 | 3.5312 | 3.5329 | 3.5346 | |
| 5 | 3.5242 | 3.5260 | 3.5277 | 3.5294 | 3.5312 | 3.5329 | |
| FG-A | 0 | 3.4368 | 3.4385 | 3.4402 | 3.4419 | 3.4436 | 3.4453 |
| 1 | 3.4351 | 3.4368 | 3.4385 | 3.4402 | 3.4419 | 3.4436 | |
| 2 | 3.4334 | 3.4351 | 3.4368 | 3.4385 | 3.4402 | 3.4419 | |
| 3 | 3.4318 | 3.4335 | 3.4351 | 3.4368 | 3.4385 | 3.4402 | |
| 4 | 3.4301 | 3.4317 | 3.4334 | 3.4351 | 3.4368 | 3.4385 | |
| 5 | 3.4284 | 3.4301 | 3.4318 | 3.4335 | 3.4351 | 3.4368 | |
| a/h | b/a | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | ||
| 5 | 0.5 | 12.5221 | 12.4559 | 12.4266 | 12.4116 | 12.4027 | 12.3968 | 12.3926 | 12.3895 | 12.3871 | 12.3851 |
| 1 | 6.1508 | 6.0762 | 6.0495 | 6.0361 | 6.0281 | 6.0227 | 6.0189 | 6.0161 | 6.0139 | 6.0121 | |
| 2 | 4.0620 | 4.0035 | 3.9833 | 3.9731 | 3.9670 | 3.9630 | 3.9601 | 3.9580 | 3.9563 | 3.9549 | |
| 3 | 3.6483 | 3.5942 | 3.5756 | 3.5662 | 3.5606 | 3.5569 | 3.5542 | 3.5522 | 3.5507 | 3.5494 | |
| 10 | 0.5 | 4.0620 | 4.0035 | 3.9833 | 3.9731 | 3.9670 | 3.9630 | 3.9601 | 3.9580 | 3.9563 | 3.9549 |
| 1 | 1.7197 | 1.6906 | 1.6808 | 1.6759 | 1.6729 | 1.6710 | 1.6696 | 1.6685 | 1.6677 | 1.6676 | |
| 2 | 1.0904 | 1.0713 | 1.0648 | 1.0616 | 1.0597 | 1.0584 | 1.0575 | 1.0568 | 1.0563 | 1.0558 | |
| 3 | 0.9719 | 0.9547 | 0.9489 | 0.9460 | 0.9443 | 0.9431 | 0.9423 | 0.9417 | 0.9412 | 0.9408 | |
| 20 | 0.5 | 1.0904 | 1.0713 | 1.0648 | 1.0616 | 1.0597 | 1.0584 | 1.0575 | 1.0568 | 1.0563 | 1.0558 |
| 1 | 0.4426 | 0.4345 | 0.4318 | 0.4304 | 0.4296 | 0.4291 | 0.4287 | 0.4284 | 0.4282 | 0.4280 | |
| 2 | 0.2776 | 0.2725 | 0.2708 | 0.2699 | 0.2694 | 0.2691 | 0.2688 | 0.2687 | 0.2685 | 0.2684 | |
| 3 | 0.2469 | 0.2424 | 0.2407 | 0.2401 | 0.2396 | 0.2393 | 0.2391 | 0.2390 | 0.2388 | 0.2387 | |
| 30 | 0.5 | 0.4912 | 0.4823 | 0.4793 | 0.4778 | 0.4769 | 0.4763 | 0.4759 | 0.4755 | 0.4753 | 0.4751 |
| 1 | 0.1978 | 0.1941 | 0.1929 | 0.1923 | 0.1919 | 0.1917 | 0.1915 | 0.1913 | 0.1913 | 0.1912 | |
| 2 | 0.1238 | 0.1215 | 0.1207 | 0.1203 | 0.1201 | 0.1200 | 0.1199 | 0.1198 | 0.1197 | 0.1197 | |
| 3 | 0.1109 | 0.1080 | 0.1073 | 0.1070 | 0.1068 | 0.1067 | 0.1066 | 0.1065 | 0.1064 | 0.1064 | |
| Pattern | Theory | ||||||
|---|---|---|---|---|---|---|---|
| UD | TSDT | 0.0655 | 8.8951 | 2.0541 | 1.0157 | 0.2386 | |
| 0.0548 | 8.8308 | 2.0699 | 1.0040 | 0.2385 | |||
| SSDT | 0.0646 | 8.8943 | 2.0554 | 1.0164 | 0.2462 | ||
| 0.0538 | 8.7868 | 2.2564 | 0.9992 | 0.2449 | |||
| HSDT | 0.0656 | 8.8951 | 2.0540 | 1.0157 | 0.2379 | ||
| 0.0549 | 8.8305 | 2.0527 | 1.0039 | 0.2379 | |||
| ESDT | 0.0634 | 8.8919 | 2.0566 | 1.0169 | 0.2538 | ||
| 0.0529 | 8.6629 | 2.4104 | 0.9852 | 0.2511 | |||
| Present | 0.0646 | 8.8943 | 2.0554 | 1.0163 | 0.2463 | ||
| 0.0538 | 8.7891 | 2.2406 | 0.9994 | 0.2451 | |||
| FG-O | TSDT | 0.0641 | 9.1477 | 2.0124 | 0.9925 | 0.2459 | |
| 0.0531 | 9.0807 | 2.0299 | 0.9809 | 0.2459 | |||
| SSDT | 0.0631 | 9.1463 | 2.0136 | 0.9931 | 0.2534 | ||
| 0.0520 | 9.0327 | 2.2165 | 0.9760 | 0.2520 | |||
| HSDT | 0.0642 | 9.1478 | 2.0123 | 0.9924 | 0.2452 | ||
| 0.0532 | 9.0806 | 2.0126 | 0.9809 | 0.2453 | |||
| ESDT | 0.0619 | 9.1434 | 2.0147 | 0.9936 | 0.2608 | ||
| 0.0511 | 8.9017 | 2.3699 | 0.9619 | 0.2580 | |||
| Present | 0.0631 | 9.1463 | 2.0136 | 0.9931 | 0.2535 | ||
| 0.0520 | 9.0350 | 2.2009 | 0.9762 | 0.2522 | |||
| FG-X | TSDT | 0.0669 | 8.6555 | 2.0938 | 1.0380 | 0.2310 | |
| 0.0566 | 8.5937 | 2.1080 | 1.0261 | 0.2310 | |||
| SSDT | 0.0661 | 8.6554 | 2.0951 | 1.0387 | 0.2388 | ||
| 0.0556 | 8.5537 | 2.2941 | 1.0215 | 0.2377 | |||
| HSDT | 0.0670 | 8.6554 | 2.0936 | 1.0380 | 0.2303 | ||
| 0.0567 | 8.5933 | 2.0908 | 1.0260 | 0.2304 | |||
| ESDT | 0.0650 | 8.6537 | 2.0964 | 1.0394 | 0.2466 | ||
| 0.0548 | 8.4366 | 2.4485 | 1.0075 | 0.2441 | |||
| Present | 0.0661 | 8.6554 | 2.0951 | 1.0387 | 0.2390 | ||
| 0.0556 | 8.5559 | 2.2781 | 1.0218 | 0.2378 | |||
| FG-A | TSDT | 0.0956 | 8.9054 | 2.1339 | 0.9736 | 0.2368 | |
| 0.0763 | 8.8369 | 2.1394 | 0.9559 | 0.2368 | |||
| SSDT | 0.0947 | 8.9046 | 2.1353 | 0.9742 | 0.2444 | ||
| 0.0752 | 8.7931 | 2.3353 | 0.9514 | 0.2432 | |||
| HSDT | 0.0957 | 8.9054 | 2.1338 | 0.9735 | 0.2361 | ||
| 0.0764 | 8.8367 | 2.1213 | 0.9558 | 0.2362 | |||
| ESDT | 0.0935 | 8.9023 | 2.1366 | 0.9747 | 0.2519 | ||
| 0.0742 | 8.6693 | 2.4971 | 0.9383 | 0.2493 | |||
| Present | 0.0947 | 8.9047 | 2.1352 | 0.9742 | 0.2445 | ||
| 0.0752 | 8.7954 | 2.3187 | 0.9516 | 0.2433 |
| Pattern | Boundary Conditions | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SSSS | CCCC | SCSC | CCSS | ||||||
| Epoxy | 0.0% | 9.6211 | 9.5058 | 5.2610 | 4.5170 | 6.0683 | 5.3675 | 1.9881 | 1.8313 |
| UD | 0.1% | 9.5437 | 9.4295 | 5.2186 | 4.4819 | 6.0194 | 5.3255 | 1.9721 | 1.8168 |
| 0.2% | 9.4674 | 9.3543 | 5.1768 | 4.4472 | 5.9712 | 5.2840 | 1.9563 | 1.8025 | |
| 0.6% | 9.1729 | 9.0639 | 5.0153 | 4.3132 | 5.7851 | 5.1239 | 1.8953 | 1.7474 | |
| 1.0% | 8.8943 | 8.7891 | 4.8626 | 4.1864 | 5.6090 | 4.9724 | 1.8377 | 1.6952 | |
| FG-O | 0.1% | 9.5716 | 9.4568 | 5.2316 | 4.4919 | 6.0351 | 5.3383 | 1.9773 | 1.8214 |
| 0.2% | 9.5226 | 9.4081 | 5.2025 | 4.4671 | 6.0024 | 5.3094 | 1.9666 | 1.8115 | |
| 0.6% | 9.3310 | 9.2182 | 5.0891 | 4.3704 | 5.8746 | 5.1968 | 1.9249 | 1.7733 | |
| 1.0% | 9.1463 | 9.0350 | 4.9804 | 4.2779 | 5.7518 | 5.0888 | 1.8848 | 1.7366 | |
| FG-X | 0.1% | 9.5160 | 9.4025 | 5.2057 | 4.4719 | 6.0037 | 5.3127 | 1.9669 | 1.8123 |
| 0.2% | 9.4129 | 9.3011 | 5.1514 | 4.4276 | 5.9404 | 5.2590 | 1.9461 | 1.7936 | |
| 0.6% | 9.0200 | 8.9147 | 4.9442 | 4.2582 | 5.6988 | 5.0537 | 1.8668 | 1.7224 | |
| 1.0% | 8.6554 | 8.5559 | 4.7517 | 4.1006 | 5.4743 | 4.8628 | 1.7931 | 1.6562 | |
| FG-A | 0.1% | 9.5438 | 9.4296 | 5.2187 | 4.4819 | 6.0194 | 5.3255 | 1.9721 | 1.8168 |
| 0.2% | 9.4679 | 9.3546 | 5.1770 | 4.4473 | 5.9715 | 5.2842 | 1.9564 | 1.8026 | |
| 0.6% | 9.1770 | 9.0664 | 5.0173 | 4.3146 | 5.7875 | 5.1255 | 1.8961 | 1.7479 | |
| 1.0% | 8.9047 | 8.7954 | 4.8677 | 4.1898 | 5.6151 | 4.9764 | 1.8397 | 1.6965 | |
| Pattern | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| UD | 0 | 8.7891 | 8.7848 | 8.7805 | 8.7762 | 8.7718 | 8.7675 |
| 1 | 8.7935 | 8.7891 | 8.7848 | 8.7805 | 8.7762 | 8.7718 | |
| 2 | 8.7978 | 8.7935 | 8.7891 | 8.7848 | 8.7805 | 8.7762 | |
| 3 | 8.8022 | 8.7978 | 8.7935 | 8.7891 | 8.7848 | 8.7805 | |
| 4 | 8.8065 | 8.8022 | 8.7978 | 8.7935 | 8.7891 | 8.7848 | |
| 5 | 8.8108 | 8.8065 | 8.8021 | 8.7978 | 8.7935 | 8.7891 | |
| FG-O | 0 | 9.0350 | 9.0306 | 9.0261 | 9.0217 | 9.0172 | 9.0128 |
| 1 | 9.0395 | 9.0350 | 9.0306 | 9.0261 | 9.0217 | 9.0173 | |
| 2 | 9.0440 | 9.0395 | 9.0350 | 9.0306 | 9.0261 | 9.0217 | |
| 3 | 9.0484 | 9.0440 | 9.0395 | 9.0350 | 9.0306 | 9.0262 | |
| 4 | 9.0529 | 9.0484 | 9.0440 | 9.0395 | 9.0350 | 9.0306 | |
| 5 | 9.0573 | 9.0529 | 9.0484 | 9.0440 | 9.0395 | 9.0350 | |
| FG-X | 0 | 8.5559 | 8.5517 | 8.5475 | 8.5433 | 8.5391 | 8.5349 |
| 1 | 8.5602 | 8.5559 | 8.5517 | 8.5475 | 8.5433 | 8.5391 | |
| 2 | 8.5644 | 8.5602 | 8.5559 | 8.5517 | 8.5475 | 8.5433 | |
| 3 | 8.5686 | 8.5644 | 8.5602 | 8.5559 | 8.5517 | 8.5475 | |
| 4 | 8.5728 | 8.5686 | 8.5644 | 8.5602 | 8.5559 | 8.5517 | |
| 5 | 8.5771 | 8.5728 | 8.5686 | 8.5644 | 8.5602 | 8.5559 | |
| FG-A | 0 | 8.7954 | 8.7911 | 8.7868 | 8.7824 | 8.7781 | 8.7738 |
| 1 | 8.7998 | 8.7954 | 8.7911 | 8.7868 | 8.7824 | 8.7781 | |
| 2 | 8.8041 | 8.7998 | 8.7954 | 8.7911 | 8.7868 | 8.7824 | |
| 3 | 8.8085 | 8.8041 | 8.7998 | 8.7954 | 8.7911 | 8.7868 | |
| 4 | 8.8128 | 8.8084 | 8.8041 | 8.7998 | 8.7954 | 8.7911 | |
| 5 | 8.8171 | 8.8128 | 8.8084 | 8.8041 | 8.7998 | 8.7954 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghandourah, E.E.; Daikh, A.A.; Alhawsawi, A.M.; Fallatah, O.A.; Eltaher, M.A. Bending and Buckling of FG-GRNC Laminated Plates via Quasi-3D Nonlocal Strain Gradient Theory. Mathematics 2022, 10, 1321. https://doi.org/10.3390/math10081321
Ghandourah EE, Daikh AA, Alhawsawi AM, Fallatah OA, Eltaher MA. Bending and Buckling of FG-GRNC Laminated Plates via Quasi-3D Nonlocal Strain Gradient Theory. Mathematics. 2022; 10(8):1321. https://doi.org/10.3390/math10081321
Chicago/Turabian StyleGhandourah, Emad E., Ahmed A. Daikh, Abdulsalam M. Alhawsawi, Othman A. Fallatah, and Mohamed A. Eltaher. 2022. "Bending and Buckling of FG-GRNC Laminated Plates via Quasi-3D Nonlocal Strain Gradient Theory" Mathematics 10, no. 8: 1321. https://doi.org/10.3390/math10081321






