New Fundamental Results on the Continuous and Discrete Integro-Differential Equations

Abstract

This work studies certain perturbed and un-perturbed nonlinear systems of continuous and discrete integro-delay differential equations (IDDEs). Using the Lyapunov–Krasovskii functional (LKF) method and the Lyapunov–Razumikhin method (LRM), uniform asymptotic stability (UAS), uniform stability (US), integrability and boundedness of solutions as well as exponential stability (ES) and instability of solutions are discussed. In this paper, five new theorems and a corollary are given and three numerical applications are provided with their simulations. With this work, we aim to make new contributions to the theory of the continuous and discrete integro-differential equations.

1. Introduction

Mathematical models called integro-differential equations, integral equations, integro-delay differential equations (IDDEs), ordinary differential equations, and so forth, are very attractive and interesting equations in the literature thanks to their very effective roles in numerous scientific fields and applications. In the past and in recent years, an extensive literature, such as a large number of books [1,2,3,4,5,6] and papers [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44], has been devoted to discussions of uniform stability, uniform asymptotically stability, exponential stability, instability, integrability, boundedness, etc., of these kinds of mathematical models. However, in the literature, we only find the work of Crisci et al. ([14], Theorem 2.2) that is on the behaviors of continuous and discrete IDDEs.

We would now like to introduce the related work of Crisci et al. ([14], Theorem 2.2).

In 1995, the authors ([14], Theorem 2.2) dealt with the AS of the continuous and discrete system of IDDEs:

$$\dot{y}\left(t\right)=G(t,y\left(t\right))+H(t,y\left(t\right))\underset{t-\tau }{\overset{t}{\int }}k(t,s,y(s\left)\right)ds,$$

(1)

where $G\in C({\mathbb{R}}^{+}\times {\mathbb{R}}^n,{\mathbb{R}}^n)$, $H\in C({\mathbb{R}}^{+}\times {\mathbb{R}}^n,{\mathbb{R}}^{n\times n})$, $k\in C({\mathbb{R}}^{+}\times [-\tau ,\infty )\times {\mathbb{R}}^n,{\mathbb{R}}^n)$, $G(t,0)=H(t,0)=k(t,s,0)=0$.

In Crisci et al. ([14], Theorem 2.2), a theorem was proved, which includes sufficient conditions, on the asymptotic stability of the system (1).

In this work, by virtue of the continuous and discrete system (1), i.e., the result of Crisci et al. ([14], Theorem 2.2) and that in the references section of this paper, we consider the continuous and discrete nonlinear perturbed system of IDDEs:

$$\begin{array}{cc}\hfill \dot{y}\left(t\right)=& -G(t,y\left(t\right))+H(t,y\left(t\right),y(t-\tau ))\underset{t-\tau }{\overset{t}{\int }}K(t,s,y(s\left)\right)ds\hfill \\ \hfill & +S(t,y(t),y(t-\tau \left)\right),\hfill \\ \hfill & x\left(t\right)=\varphi \left(t\right),t\in [-\tau ,0],\hfill \end{array}$$

(2)

where $y\in {\mathbb{R}}^n$, $t\in [-\tau ,\infty )$, $\tau \in \mathbb{R},$$\tau >0$. We assume that $\varphi \in C\left(\right[-\tau ,0],\mathbb{R})$, $\varphi$ is the initial condition (function), G is the same as in system (1), $H\in C({\mathbb{R}}^{+}\times {\mathbb{R}}^n\times {\mathbb{R}}^n,{\mathbb{R}}^{n\times n}),$ $K\in C({\mathbb{R}}^{+}\times [-\tau ,\infty )\times {\mathbb{R}}^n,{\mathbb{R}}^n)$, $G(t,0)=H(t,0,0)=K(t,s,0)=0$ and $S\in C({\mathbb{R}}^{+}\times {\mathbb{R}}^n\times {\mathbb{R}}^n,{\mathbb{R}}^n).$ The continuity of the functions G, H, K and S is a sufficient condition for the existence of the solutions of the system of IDDEs (2). We also assume that the functions G, H, K and S satisfy the Lipschitz condition with respect to the variables y and $y(t-\tau )$. This condition guarantees the uniqueness of solutions of the system of IDDEs (2).

The aim of this work is to obtain some new findings on the fundamental properties of solutions of the continuous and discrete unperturbed system (2) when $S(.)=S(t,y(t),y(t-\tau \left)\right)=0$ and the continuous and discrete perturbed system (2). Here, our goal is to produce five new results, a corollary, three examples and their numerical simulations, on the fundamental properties of solutions such as UAS, ES, instability, the integrability of the unperturbed continuous and discrete system and boundedness of the solutions of the perturbed continuous and discrete system. Next, the LKF method and the LRM are used as basic techniques to carry out the purpose of this paper. We note that LKM and LRM have very effective roles during the studies of the fundamental properties of solutions of ODEs, functional differential equations (FDEs), IDEs, IDDEs and so on, provided that they construct suitable LFs or LKFs. In this way, we note that the results of this paper are more general, i.e., Theorems 3–7 are new and they have more general results on the continuous and discrete IDDEs. Briefly, Theorems 3–7 have made new contributions to the relevant literature, which are explained in detail before the references in this paper.

2. Basic Results

Consider general non-autonomous FDE:

$$\dot{y}\left(t\right)=F(t,y_t),$$

(3)

where $F:\mathbb{R}\times C\to {\mathbb{R}}^n$ is a continuous mapping, $F(t,0)=0$. For some $\tau >0,$$C=C([-\tau ,0],{\mathbb{R}}^n),$$\varphi :[-\tau ,0]\to {\mathbb{R}}^n$ and $\tau >0$. For any $a\ge 0,$ some $t_0\ge 0,$ and $y\in C([t_0-\tau ,t_0+a],{\mathbb{R}}^n),$ we have $y_t=y(t+\theta )$ for $\theta \in [-\tau ,0]$ and $t\ge t_0.$ Let $y\in {\mathbb{R}}^n$. The norm $∥.∥$ is described as:

$$∥y∥=\sum _{i=1}^n\left|y_i\right|.$$

Next, let $X\in {\mathbb{R}}^{n\times n}.$ Then, $∥X∥$ is described as:

$$∥X∥=\underset{1\le j\le n}{max}\left(\sum _{i=1}^n\left|x_{ij}\right|\right).$$

Without mention, $y\left(t\right)$ is represented by y. For any $\varphi \in C$, let:

$${∥\varphi ∥}_C=\underset{\theta \in [-\tau ,0]}{sup}∥\varphi \left(\theta \right)∥={∥\varphi \left(\theta \right)∥}_{[-\tau ,0]}$$

and

$$C_H=\{\varphi :\varphi \in C\mathrm{and}{∥\varphi ∥}_C\le H_0<\infty \},H_0\in \mathbb{R},H_0>0.$$

Throughout this paper, it is assumed that the uniqueness of solutions of FDE (3) is held. We should also note that the nonlinear continuous and discrete systems IDDEs (1) and (2) are particular cases of FDE (3).

Let $y\left(t\right)=y(t,t_0,\varphi )$ be a solution of FDE (3) on $[t_0-\tau ,t_0]$, $t_0\ge 0$, such that $y\left(t\right)=\varphi \left(t\right)$, $\forall t\in [t_0-\tau ,t_0],$ where $\varphi \in C([t_0-\tau ,t_0],{\mathbb{R}}^n).$ Let the functional,

$$V_1:{\mathbb{R}}^{+}\times C_H\to {\mathbb{R}}^{+},{\mathbb{R}}^{+}=[0,\infty ),C_H={\{\varphi :\varphi \in C\mathrm{and}\parallel \varphi \parallel }_C\le H_0<\infty \},V_1(t,0)=0,$$

be a continuous in t and $\varphi .$ Further, let $\frac{d}{dt}{V}_1(t,y_t)$ represent the derivative of functional $V_1(t,y_t)$ on the right through any solution of FDE (3).

Firstly, we present the result of Crisci et al. ([14], Theorem 2.2), which is given by the below theorem, Theorem 1.

Theorem 1.

(Crisci et al. ([14], Theorem 2.2)). Let

$$a>\underset{t>0}{sup}\underset{0}{\overset{\infty }{\int }}\kappa (t+s,t)ds,$$

where

$$a=\underset{t\ge 0,y\in D}{sup}\gamma \left(g(t,y)\right),$$

$$g(t,y)=\frac{\partial G(t,y)}{\partial y},$$

$\gamma \left(g\right(t,y\left)\right)$ is the logarithmic norm of the matrix $g(t,y)$, D is in some neighborhood of the origin and k is defined as $∥k(t,s,y)∥\le \kappa (t,s)∥y∥,$ and $\kappa (t,s)$ is a continuous non-negative function. Then the trivial solution of the continuous and discrete system of IDDEs (1) is asymptotically stable.

It is worth presenting that the LKF $V=V(t,y),$

$$V=∥y\left(t\right)∥+\underset{0}{\overset{\infty }{\int }}ds\underset{t-s}{\overset{t}{\int }}\kappa (\tau +s,\tau )∥y\left(\tau \right),∥d\tau$$

was defined and used by Crisci et al. ([14], Theorem 2.2) to prove the mentioned theorem.

Next, the below theorem is a key result of this paper during the proofs

Theorem 2.

(Burton ([2], Theorem 4.2.9)). Assume that the below conditions (A1)–(A3) are held:

(A1) 

The functional$V_1(t,y_t)$is locally Lipschitz in$y_t,$i.e., for every compact$S\subset {\mathbb{R}}^n$and$\gamma >t_0,$

there is a$A_{\gamma s}\in \mathbb{R}$ with $A_{\gamma s}>0$ such that:

$$|V_1(t,y_t)-V_1(t,x_t)|\le A_{\gamma s}{∥y-x∥}_{[t_0-\tau ,t]}$$

for all $t\in [t_0,\gamma ]$ and $x,y\in C([t_0-\tau ,t_0],S).$

(A2) 

$Z:{\mathbb{R}}^{+}\times C_H\to {\mathbb{R}}^{+}$ is a continuous functional such that it is one sided locally Lipschitz in $t,$ i.e.,

$$Z(t_2,\varphi )-Z(t_1,\varphi )\le A(t_2-t_1),0<t_1<t_2<\infty ,A>0,A\in \mathbb{R},\varphi \in C_H.$$

(A3) 

There are four strictly increasing functions ω, ${\omega }_1$, ${\omega }_2$, ${\omega }_3:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ with value 0 at 0 such that:

$$\omega \left(∥\varphi \left(0\right)∥\right)+Z(t,\varphi )\le V_1(t,\varphi )\le {\omega }_1\left(∥\varphi \left(0\right)∥\right)+Z(t,\varphi ),$$

$$Z(t,\varphi )\le {\omega }_2\left({∥\varphi ∥}_C\right),$$

and

$$\frac{d}{dt}{V}_1(t,y_t)\le -{\omega }_3\left(∥y\left(t\right)∥\right),$$

$\forall t\in {\mathbb{R}}^{+}$ and $\forall y\in C_H.$ Then, the trivial solution $y\left(t\right)=0$ of FDE (3) is uniformly asymptotically stable.

3. Analysis of Solutions by LKF Method

We consider unperturbed system:

$$\dot{y}\left(t\right)=-G(t,y\left(t\right))+H(t,y\left(t\right),y(t-\tau ))\underset{t-\tau }{\overset{t}{\int }}K(t,s,y(s\left)\right)ds.$$

(4)

System (4) was obtained from system (2) when $S(.)=S(t,y(t),y(t-\tau \left)\right)=0.$

We now construct sufficient conditions, which are needed in the proofs of Theorems 3–5.

Assumption 1.

We need the below conditions through the proofs of our new results.

(C1) 

$$G(t,0)=H(t,0,0)=K(t,s,0)\equiv 0,$$

$$sgn{y}_i\left(t\right)G_i(t,y\left(t\right))>0forall{y}_i\left(t\right)\ne 0,y_i\left(t\right)\in \mathbb{R},$$

$$∥G(t,y(t\left)\right)∥\ge G_0∥y\left(t\right)∥,$$

$$∥H(t,y(t),y(t-\tau \left)\right)K(t,s,y(s\left)\right)∥\le K_1(t,s)∥y\left(s\right)∥,$$

$$K_1(t,s)\in C[{\mathbb{R}}^{+}\times {\mathbb{R}}^{+},{\mathbb{R}}^{+}]\mathrm{for}\mathrm{all}{t}_0\le s,t;$$

(C2) 

$$\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥du\le K_L<\infty ,\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du<\infty ,$$

$$G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du\ge g_0$$

for$0\le t,u,$where$g_0>0,$$G_0>0,$ $K_L>0,$ $g_0,G_0,K_L\in \mathbb{R};$

(C3) 

$$G(t,0)=H(t,0,0)=K(t,s,0)\equiv 0,$$

$$sgn{y}_i\left(t\right)G_i(t,y\left(t\right))>0forall{y}_i\left(t\right)\ne 0,y_i\left(t\right)\in \mathbb{R},$$

$$∥G(t,y(t\left)\right)∥\ge G_0∥y\left(t\right)∥,$$

$$∥H(t,y(t),y(t-\tau \left)\right)K(t,s,y(s\left)\right)∥\le K_1(t,s)∥y\left(s\right)∥,$$

where $K_1(t,s)\in C[{\mathbb{R}}^{+}\times {\mathbb{R}}^{+},{\mathbb{R}}^{+}]$ such that $0\le K_1(t,s)\le K_0$ for all $t_0\le s,t,$

$$G_0-\tau K_0>{\varsigma }_0,K_0\in \mathbb{R},{\varsigma }_0\in \mathbb{R},K_0>0,{\varsigma }_0>0;$$

(C4) 

$$G(t,0)=H(t,0,0)=K(t,s,0)\equiv 0,$$

$$sgn{y}_i\left(t\right)G_i(t,y\left(t\right))<0,\mathrm{for}\mathrm{all}{y}_i\left(t\right)\ne 0,y_i\left(t\right)\in \mathbb{R},$$

$$∥G(t,y(t\left)\right)∥\ge G_0∥y\left(t\right)∥,$$

$$∥H(t,y(t),y(t-\tau \left)\right)K(t,s,y(s\left)\right)∥\le K_1(t,s)∥y\left(s\right)∥,$$

where $K_1(t,s)\in C[{\mathbb{R}}^{+}\times {\mathbb{R}}^{+},{\mathbb{R}}^{+}]$ such that $0\le K_1(t,s)\le K_0,$ for all $t_0\le s,t,$

$$G_0-\tau K_0>{\varsigma }_0,K_0\in \mathbb{R},{\varsigma }_0\in \mathbb{R},K_0>0,{\varsigma }_0>0.$$

(C5) 

Let $s_0\in C[{\mathbb{R}}^{+},\mathbb{R}]$ such that

$$∥S(.)∥=∥S(t,y(t),y(t-\tau \left)\right)∥\le \left|s_0\left(t\right)\right|∥y\left(t\right)∥,$$

$$\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥du\le K_L<\infty ,\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du<\infty ,$$

and

$$G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du-\left|s_0\left(t\right)\right|\ge 0$$

for $0\le t,u,$ where $g_0>0,$$G_0>0,$$K_L>0,$ $g_0,G_0,K_L\in \mathbb{R}.$

It should be noted that throughout the proofs of Theorems 3–5 and Corollary 1 as a basic tool, we utilize the LKF $\mathsf{\Lambda }:=$$\mathsf{\Lambda }(t,y_t)$ defined by:

$$\begin{array}{cc}\hfill \mathsf{\Lambda }(t,y_t)& :=∥y∥+\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds\hfill \\ \hfill & =\left|y_1\right|+...+\left|y_n\right|+\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds,\hfill \end{array}$$

(5)

in which $\sigma >0,$ $\sigma \in \mathbb{R},$ we choose σ in the proof.

The first new result, i.e., the UAS result, is given by Theorem 3.

Theorem 3.

If conditions (C1) and (C2) are held, then the trivial solution of the unperturbed continuous and discrete system (4) is uniformly asymptotically stable.

Proof. 

As the steps of this proof, we will show that the LKF satisfies conditions (A1)–(A3) of Theorem 2 step by step, respectively.

First, in view of the LKF (5), we see that the LKF $\mathsf{\Lambda }$ is positive definite.

As for condition (A1) of Burton ([2], Theorem 4.2.9)), it is notable that:

$$\begin{array}{cc}\hfill |\mathsf{\Lambda }(t,y_t)-\mathsf{\Lambda }(t,x_t)|\le & \left|∥y∥-∥x∥\right|\hfill \\ \hfill & +\sigma \left|\underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds-\underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥x\left(s\right)∥duds\right|\hfill \\ \hfill =& \left|∥y∥-∥x∥\right|+\sigma \left|\underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥\left[∥y\left(s\right)∥-∥x\left(s\right)∥\right]duds\right|\hfill \\ \hfill \le & \left|∥y∥-∥x∥\right|+\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)-x\left(s\right)∥duds\hfill \\ \hfill \le & \left|∥y∥-∥x∥\right|+\sigma K_L\underset{t-\tau }{\overset{t}{\int }}∥y\left(s\right)-x\left(s\right)∥ds\hfill \\ \hfill \le & \sum _{i=1}^n\left|y_i-x_i\right|+\sigma \tau K_L\underset{t-\tau \le s\le t}{sup}∥y\left(s\right)-x\left(s\right)∥\hfill \\ \hfill & =∥y\left(t\right)-x\left(t\right)∥+\sigma \tau K_L\underset{t-\tau \le s\le t}{sup}∥y\left(s\right)-x\left(s\right)∥\hfill \\ \hfill & \le M\underset{t-\tau \le s\le t}{sup}∥x\left(s\right)-y\left(s\right)∥,\hfill \end{array}$$

where $M:=1+\sigma \tau K_L.$ As a result of this analysis, it is now seen that the LKF $\mathsf{\Lambda }$ satisfies the locally Lipschitz condition in $y_t,$ i.e., condition (A1) has been verified.

For the coming step, let:

$$Z(t,y_t):=\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds.$$

Then, using condition (C2), it therefore follows that:

$$\begin{array}{cc}\hfill Z(t,y_t)& =\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds\hfill \\ \hfill & =\sigma \underset{t-\tau }{\overset{t}{\int }}C(t,s,y(s\left)\right)ds,\hfill \end{array}$$

where

$$C(t,s,y\left(s\right))=\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥du.$$

Next, we have:

$$\begin{array}{cc}\hfill Z(t,y_t)& =\sigma \underset{t-\tau }{\overset{t}{\int }}C(t,s,y(s\left)\right)ds\hfill \\ \hfill & \le \sigma \tau K_L\underset{t-\tau \le s\le t}{sup}∥y\left(s\right)∥\hfill \\ \hfill & =\sigma \tau K_L{∥y\left(s\right)∥}_{[t-\tau ,t]},\hfill \end{array}$$

where $K_L>0$ is the Lipschitz constant.

Let $t_1>0,$ $t_2>0$ and $t_1<t_2<\infty .$

As for the next step, we derive that:

$$\begin{array}{cc}\hfill Z(t_2,\varphi )-Z(t_1,\varphi )=& \sigma \underset{t_2-\tau }{\overset{t_2}{\int }}C(t,s,\varphi (s\left)\right)ds-\sigma \underset{t_1-\tau }{\overset{t_1}{\int }}C(t,s,\varphi (s\left)\right)ds\hfill \\ \hfill =& \sigma \underset{t_2-\tau }{\overset{t_2}{\int }}C(t,s,\varphi (s\left)\right)ds+\sigma \underset{t_1}{\overset{t_1-\tau }{\int }}C(t,s,\varphi (s\left)\right)ds\hfill \\ \hfill & +\sigma \underset{t_1-\tau }{\overset{t_2-\tau }{\int }}C(t,s,\varphi (s\left)\right)ds-\sigma \underset{t_1-\tau }{\overset{t_2-\tau }{\int }}C(t,s,\varphi (s\left)\right)ds\hfill \\ \hfill =& \sigma \underset{t_1}{\overset{t_2}{\int }}C(t,s,\varphi (s\left)\right)ds-\sigma \underset{t_1-\tau }{\overset{t_2-\tau }{\int }}C(t,s,\varphi (s\left)\right)ds\hfill \\ \hfill \le & \sigma \underset{t_1}{\overset{t_2}{\int }}C(t,s,\varphi (s\left)\right)ds=\sigma \underset{t_1}{\overset{t_2}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥\varphi \left(s\right)∥duds\hfill \\ \hfill \le & \sigma K_L\underset{t_1}{\overset{t_2}{\int }}∥\varphi \left(s\right)∥ds\hfill \\ \hfill \le & \sigma K_L\underset{t_1}{\overset{t_2}{\int }}{H}_{0}ds=\sigma K_L{H}_0(t_2-t_1).\hfill \end{array}$$

As a result of the above analysis, we see that the LKF $\mathsf{\Lambda }$ satisfies condition (A2).

By virtue of the derivative of the LKF $\mathsf{\Lambda }$ along the continuous and discrete unperturbed system of IDDEs (4), we now derive that:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}^{+}(t,y_t)=& \sum _{i=1}^n{\dot{y}}_i\left(t\right)sgn{y}_i(t+0)+\sigma \underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥∥y\left(t\right)∥du\hfill \\ \hfill & -\sigma \underset{t}{\overset{\infty }{\int }}∥K_1(u,t-\tau )∥∥y(t-\tau )∥du-\sigma \underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds.\hfill \end{array}$$

(6)

According to condition (C1), it follows that:

$$\begin{array}{cc}\hfill \sum _{i=1}^n{\dot{y}}_i\left(t\right)sgn{y}_i(t+0)& \le -∥G(t,y(t\left)\right)∥+∥H(t,y(t),y(t-\tau \left)\right)∥\underset{t-\tau }{\overset{t}{\int }}∥K(t,s,y(s\left)\right)∥ds\hfill \\ \hfill & \le -∥G(t,y(t\left)\right)∥+\underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds.\hfill \end{array}$$

(7)

Thanks to (6) and (7), we derive that:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}^{+}(t,y_t)\le & -∥G(t,y(t\left)\right)∥+\underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds+\sigma \underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥∥y\left(t\right)∥du\hfill \\ \hfill & -\sigma \underset{t}{\overset{\infty }{\int }}∥K_1(u,t-\tau )∥∥y(t-\tau )∥du-\sigma \underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds\hfill \\ \hfill \le & -∥G(t,y(t\left)\right)∥+\underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds\hfill \\ \hfill & +\sigma \underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥∥y\left(t\right)∥du-\sigma \underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds.\hfill \end{array}$$

(8)

Let us choose $\sigma =1$. Next, using (8) and condition (C2), we have:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}^{+}(t,y_t)& \le -∥G(t,y(t\left)\right)∥+∥y\left(t\right)∥\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du\hfill \\ \hfill & \le -\left[G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du\right]∥y\left(t\right)∥\hfill \\ & \le -g_0∥y\left(t\right)∥<0,∥y\left(t\right)∥\ne 0.\hfill \end{array}$$

(9)

Let ${\omega }_1=∥y∥,$ ${\omega }_2=\sigma \tau K_L{∥y\left(s\right)∥}_{[t-\tau ,t]}$ and ${\omega }_3=g_0∥y∥$. According to the above discussion, conditions (A1)–(A3) of Theorem 2 (Burton ([2], Theorem 4.2.9)) are fulfilled. Thus, the trivial solution of the continuous and discrete unperturbed system (4) is uniformly asymptotically stable. □

Corollary 1.

If conditions (C1) and (C2) are held, then the trivial solution of the continuous and discrete unperturbed system (4) is uniformly stable.

Proof. 

Due to Theorem 3, the trivial solution of the continuous and discrete unperturbed system (4) is stable. To see the stability is uniform, let $y\in {\mathbb{R}}^n$ and $\left|y\right|$ be any norm, let C denote the Banach space of the functions $\varphi \in C([t_0-\tau ,t_0],{\mathbb{R}}^n)$ with

$${∥\varphi ∥}_{t_0}=\underset{t_0-\tau \le t\le t_0}{sup}\left|\varphi \left(t\right)\right|.$$

We suppose that $y\left(t\right)$ is a solution of the continuous and discrete unperturbed system (4) on $[t_0-\tau ,\beta ),$ $\beta >0,$ such that $y\left(t\right)=\varphi \left(t\right)$ on $\varphi \in [t_0-\tau ,t_0],$ $t_0\ge 0.$ By virtue of the LKF $\mathsf{\Lambda }(t,y_t),$ which is decreasing, using (5) and (C2), we have:

$$\begin{array}{cc}\hfill ∥y(t,t_0,\varphi )∥& \le \mathsf{\Lambda }(t,y_t)\le \mathsf{\Lambda }(t_0,\varphi \left(t_0\right))\hfill \\ \hfill & \le ∥\varphi \left(t_0\right)∥+\sigma \underset{t_0-\tau }{\overset{t_0}{\int }}\underset{t_0}{\overset{\infty }{\int }}∥K_1(u,s)∥∥\varphi \left(s\right)∥duds\hfill \\ \hfill & \le ∥\varphi \left(t_0\right)∥+\sigma K_L\underset{t_0-\tau }{\overset{t_0}{\int }}∥\varphi \left(s\right)∥ds\hfill \\ \hfill & \le ∥\varphi \left(t_0\right)∥+\sigma K_L\underset{t_0-\tau \le s\le t_0}{sup}∥\varphi \left(s\right)∥\hfill \\ \hfill & \le (1+\sigma K_L){∥\varphi ∥}_{t_0}.\hfill \end{array}$$

Then, for given $\epsilon >0,$ choose $\delta =\left(\frac{1}{1+\sigma K_L}\right)\frac{\epsilon }{2}$ such that for any solution $y\left(t\right)$ of the continuous and discrete unperturbed system of (4), if $∥\varphi \left(t\right)∥<\delta$ for $t\in [t_0-\tau ,t_0],$ then:

$$∥y(t,t_0,\varphi )∥\le (1+\sigma K_L)\delta \le \frac{\epsilon }{2}\mathrm{for}\mathrm{all}t\ge t_0.$$

Here, the number $\delta$ is independent of the constant $t_0.$ By virtue of the last inequality, we arrive at the solution $y\left(t\right)\equiv 0$ of the continuous and discrete unperturbed system (4), which is US. Hence, the proof is completed. □

The next result discusses the integrability of solutions of the continuous and discrete unperturbed system of IDDEs (4).

Theorem 4.

If conditions (C1) and (C2) are held, then the norm of solutions of the continuous and discrete unperturbed system (4) are integrable in the sense of Lebesgue on ${\mathbb{R}}^{+},$ ${\mathbb{R}}^{+}=[t_0,\infty ).$

Proof. 

From Theorem 3, we have the inequality (9). Integrating the inequality (9), we derive:

$$\mathsf{\Lambda }(t,y_t)-\mathsf{\Lambda }(t_0,\varphi \left(t_0\right))\le -g_0\underset{t_0}{\overset{t}{\int }}∥y\left(s\right)∥ds\mathrm{for}\mathrm{all}t\ge t_0.$$

It is notable that the LKF $\mathsf{\Lambda }$ is decreasing. Therefore, it follows that:

$$\underset{t_0}{\overset{t}{\int }}∥y\left(s\right)∥ds\le g_0^{-1}\mathsf{\Lambda }(t_0,\varphi \left(t_0\right))-g_0^{-1}\mathsf{\Lambda }(t,y_t)\le g_0^{-1}\mathsf{\Lambda }(t_0,\varphi \left(t_0\right)).$$

Hence, we conclude that:

$$\underset{t_0}{\overset{\infty }{\int }}∥y\left(s\right)∥ds\le g_0^{-1}\mathsf{\Lambda }(t_0,\varphi \left(t_0\right))\equiv \mathrm{is}\mathrm{a}\mathrm{positive}\mathrm{constant}\mathrm{provided}\mathrm{that}\varphi \left(t_0\right)\ne 0.$$

This result confirms that the solutions of the continuous and discrete unperturbed system of IDDEs (4) are integrable on ${\mathbb{R}}^{+},$ ${\mathbb{R}}^{+}=[t_0,\infty ).$ □

Theorem 5.

If conditions (C1) and (C5) are held, then the solutions of the perturbed continuous and discrete system of IDDEs (2) are bounded at infinity.

Proof. 

The derivative of LKF (5) along the continuous and discrete perturbed system (2) and conditions (C1) and (C5) give that:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}^{+}(t,y_t)& \le -\left[G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du\right]∥y\left(t\right))∥+∥S(t,y(t),y(t-\tau \left)\right)∥\hfill \\ \hfill & \le -\left[G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du-\left|s_0\left(t\right)\right|\right]∥y\left(t\right))∥\le 0,\hfill \end{array}$$

i.e.,

$$\frac{d}{dt}{\mathsf{\Lambda }}^{+}(t,y_t)\le 0.$$

Hence, we know that the LKF $\mathsf{\Lambda }$ is decreasing. Integrating, we derive:

$$\mathsf{\Lambda }(t,y_t)\le \mathsf{\Lambda }(t_0,\varphi \left(t_0\right))={\mathsf{\Lambda }}_0(>0)\in \mathbb{R},\mathrm{for}\mathrm{all}t\ge t_0,$$

provided that $\varphi \left(t_0\right)\ne 0.$ Next,

$$\underset{t\to \infty }{lim}∥y\left(t\right)∥\le \underset{t\to \infty }{lim}{\mathsf{\Lambda }}_0={\mathsf{\Lambda }}_0.$$

Thus, the solution $y\left(t\right)$ is bounded at infinity. The proof was completed. □

Theorem 6.

The trivial solution of the continuous and discrete unperturbed system (4) is ES if condition (C3) is held.

Proof. 

Let ${\mathsf{\Lambda }}_1:={\mathsf{\Lambda }}_1(t,y)$ be an LF defined by:

$${\mathsf{\Lambda }}_1(t,y):=∥y∥=\left|y_1\right|+...+\left|y_n\right|.$$

(10)

As the next step, by the derivative of the LF ${\mathsf{\Lambda }}_1$ in (10) with respect to the continuous and discrete unperturbed system (4) and condition (C3), we have:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}_1^{+}(t,y\left(t\right))& =\sum _{i=1}^n{\dot{y}}_i\left(t\right)sgn{y}_i(t+0)\hfill \\ \hfill & \le -∥G(t,y(t\left)\right)∥+∥H(t,y(t),y(t-\tau \left)\right)∥\underset{t-\tau }{\overset{t}{\int }}∥K(t,s,y(s\left)\right)∥ds\hfill \\ \hfill & \le -∥G(t,y(t\left)\right)∥+\underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds\hfill \\ \hfill & \le -G_0∥y\left(t\right)∥+K_0\underset{t-\tau }{\overset{t}{\int }}∥y\left(s\right)∥ds.\hfill \end{array}$$

(11)

For the next step, consider the integral term,

$$K_0\underset{t-\tau }{\overset{t}{\int }}∥y\left(s\right)∥ds,$$

which is available in (11).

Letting $s=t+\xi$ gives $ds=d\xi$. Hence, for $s=t-\tau$ and $s=t,$ it follows that $\xi =-\tau$ and $\xi =0$, respectively.

Using the Razumikhin condition on the set

$$s\in [-\tau ,0],$$

we get:

$$\begin{array}{cc}\hfill K_0\underset{t-\tau }{\overset{t}{\int }}∥y\left(s\right)∥ds& =K_0\underset{-\tau }{\overset{0}{\int }}∥x(t+\xi )∥d\xi <K_0\underset{-\tau }{\overset{0}{\int }}∥y\left(t\right)∥d\xi \hfill \\ \hfill & =K_0∥y\left(t\right)∥\underset{-\tau }{\overset{0}{\int }}d\xi =K_0\tau ∥y\left(t\right)∥.\hfill \end{array}$$

(12)

Then, from (10)–(12), it follows that:

$$\frac{d}{dt}{\mathsf{\Lambda }}_1^{+}(t,y\left(t\right))\le -(G_0-\tau K_0)∥y\left(t\right)∥\le -{\varsigma }_0{\mathsf{\Lambda }}_1(t,y\left(t\right)),$$

where ${\varsigma }_0<G_0-\tau K_0$ and is defined by condition (C4).

As for the next step, it is clear that:

$$\frac{{\dot{\mathsf{\Lambda }}}_1^{+}(t,y\left(t\right))}{{\mathsf{\Lambda }}_1(t,y\left(t\right))}\le -{\varsigma }_{0}dt.$$

Integrating these terms, we derive that:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1(t,y\left(t\right))& \le {\mathsf{\Lambda }}_1(t_0,\varphi \left(t_0\right))exp(-{\varsigma }_0(t-t_0))\hfill \\ \hfill & =∥\varphi \left(t_0\right)∥exp(-{\varsigma }_0(t-t_0)),t\ge t_0.\hfill \end{array}$$

It is now notable that:

$$∥y\left(t\right)∥\le ∥\varphi \left(t_0\right)∥exp(-{\varsigma }_0(t-t_0)),t\ge t_0.$$

Thus, the trivial solution of the continuous and discrete unperturbed system of (4) is exponentially stable. Thus, this result completes the proof of Theorem 6. □

Theorem 7.

If condition (C4) is held, then the trivial solution of the continuous and discrete system (4) is unstable.

Proof. 

Here, we again use the LF ${\mathsf{\Lambda }}_1:={\mathsf{\Lambda }}_1(t,y)$ given in Theorem 5:

$${\mathsf{\Lambda }}_1(t,y):=∥y∥=\left|y_1\right|+...+\left|y_n\right|.$$

It is obvious that:

$${\mathsf{\Lambda }}_1(t,y)=\left|y_1\right|+...+\left|y_n\right|>0.$$

As for the next step, differentiating the LF ${\mathsf{\Lambda }}_1$ and using condition (C4), we have:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathsf{\Lambda }}_1^{+}(t,y\left(t\right))& =\sum _{i=1}^n{\dot{y}}_i\left(t\right)sgn{y}_i(t+0)\hfill \\ \hfill & \ge ∥G(t,y(t\left)\right)∥-∥H(t,y(t),y(t-\tau \left)\right)∥\underset{t-\tau }{\overset{t}{\int }}∥K(t,s,y(s\left)\right)∥ds\hfill \\ \hfill & \ge ∥G(t,y(t\left)\right)∥-\underset{t-\tau }{\overset{t}{\int }}∥K_1(t,s)∥∥y\left(s\right)∥ds\hfill \\ \hfill & \ge G_0∥y\left(t\right)∥-K_0\underset{t-\tau }{\overset{t}{\int }}∥y\left(s\right)∥ds.\hfill \\ & \ge (G_0-\tau K_0)∥y\left(t\right)∥>0,∥y\left(t\right)∥\ne 0.\hfill \end{array}$$

Thus, the trivial solution of the continuous and discrete unperturbed system of IDDEs (4) is unstable and the proof of Theorem 7 is finished. □

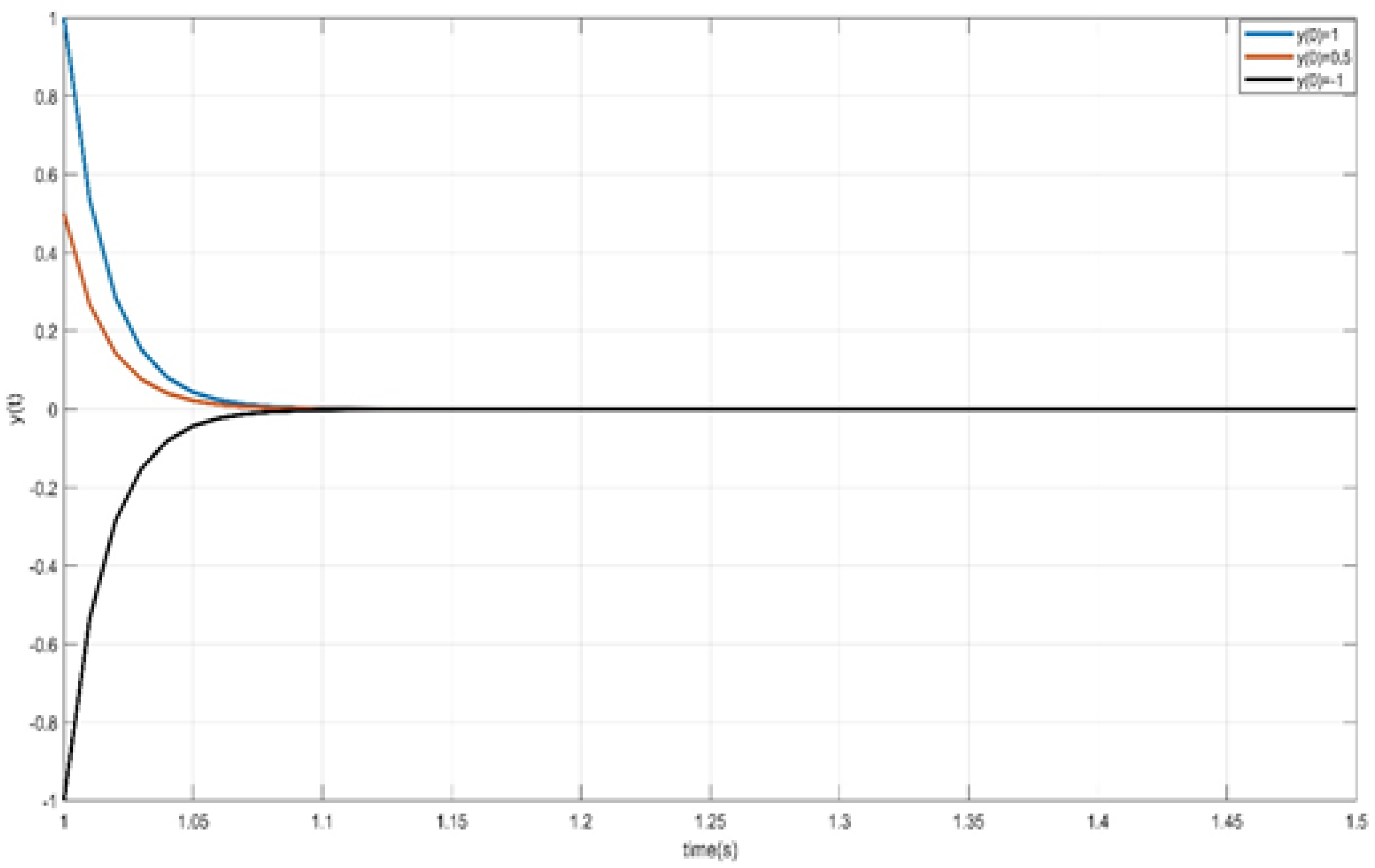
4. Numerical Applications

Example 1.

Consider the continuous and discrete scalar IDDE:

$$\begin{array}{cc}\hfill \dot{y}=& -\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)y\hfill \\ \hfill & +\frac{siny}{t^2+1+exp\left(y^2\right)+y^2(t-1)}\underset{t-1}{\overset{t}{\int }}\frac{siny\left(s\right)}{t^2+s^2+1+y^2\left(s\right)}ds,t\ge 1.\hfill \end{array}$$

(13)

Next, comparing the continuous and discrete IDDE (13) with a continuous and discrete unperturbed system of IDDEs (4), the below estimates are derived:

$$\tau =1$$

is the delay term;

$$G(t,y)=\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)y,$$

$$G(t,0)=0;$$

$$H(.)=H(t,y\left(t\right),y(t-1))=\frac{y}{t^2+1+exp\left(y^2\right)+y^2(t-1)},$$

$$H(t,0,0)=0;$$

$$K(.)=K(t,s,y\left(s\right))=\frac{siny\left(s\right)}{t^2+s^2+1+y^2\left(s\right)},$$

$$K(t,s,0)=0.$$

Hence, we derive the below relations:

$$sgnyG(t,y)=\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)ysgny>0,$$

$$y\ne 0,$$

$$y\in \mathbb{R};$$

$$\left|G(t,y)\right|\ge 20\pi \left|y\right|=G_0\left|y\right|,G_0=20\pi ;$$

$$\begin{array}{cc}\hfill \left|H(.)K(.)\right|& =\frac{\left|siny\right|}{t^2+1+exp\left(y^2\right)+y^2(t-1)}\times \frac{\left|siny\left(s\right)\right|}{s^2+t^2+1+y^2\left(s\right)}\hfill \\ \hfill & \le \frac{1}{s^2+t^2+1+y^2\left(s\right)}\left|y\left(s\right)\right|\hfill \\ \hfill & \le \frac{1}{s^2+t^2+1}\left|y\left(s\right)\right|=K_1(t,s)\left|y\left(s\right)\right|,\hfill \end{array}$$

where

$$K_1(t,s)=\frac{1}{s^2+t^2+1}\ge 0;$$

$$K_1(t,s)=\frac{1}{s^2+t^2+1}\le 1=K_0;$$

$$K_1(u,s)=\frac{1}{s^2+u^2+1};$$

$$K_1(u,t)=\frac{1}{t^2+u^2+1};$$

$$\begin{array}{cc}\hfill \underset{t}{\overset{\infty }{\int }}\left|K_1(u,s)\right|du& =\underset{t}{\overset{\infty }{\int }}\frac{1}{s^2+u^2+1}du\hfill \\ \hfill & \le \underset{t}{\overset{\infty }{\int }}\frac{1}{u^2+1}du=\frac{\pi }{2}-arctgt\le \frac{\pi }{4}=K_L<\infty ;\hfill \\ \hfill \underset{t}{\overset{\infty }{\int }}\left|K_1(u,t)\right|du& =\underset{t}{\overset{\infty }{\int }}\frac{1}{t^2+u^2+1}du\hfill \\ \hfill & \le \underset{t}{\overset{\infty }{\int }}\frac{1}{u^2+1}du=\frac{\pi }{2}-arctgt\le \frac{\pi }{4}<\infty ;\hfill \end{array}$$

$$G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du=20\pi -\frac{\pi }{2}+arctgt\ge \frac{39\pi }{2}=g_0$$

$$G_0-\tau K_0=20\pi -1>0.$$

According to the above information, conditions (C1)–(C3) of Theorems 3 and 4, Corollary 1 and Theorem 6 are held. By virtue of these reasons, the trivial solution of nonlinear continuous and discrete scalar IDDE (13) is uniformly asymptotically stable, uniformly stable, exponentially stable and the absolute value of the solutions is integrable.

Hence, by the mentioned stability concepts, we mean that, by making a sufficiently small change in initial data, then the given conditions will not allow the solutions to remarkably deviate from the desired behaviors.

In Figure 1, the continuous and discrete scalar IDDE (13) is solved by MATLAB.

Example 2.

Consider the scalar continuous and discrete scalar IDDE:

$$\begin{array}{cc}\hfill \dot{y}=& -\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)y\hfill \\ \hfill & +\frac{siny}{t^2+1+exp\left(y^2\right)+y^2(t-1)}\underset{t-1}{\overset{t}{\int }}\frac{siny\left(s\right)}{t^2+s^2+1++y^2\left(s\right)}ds\hfill \\ \hfill & +\frac{yexp\left(t\right)}{1+exp\left(2t\right)+exp\left(y^2\right)+exp\left(y^2(t-1)\right)},t\ge 1.\hfill \end{array}$$

(14)

Next, comparing continuous and discrete scalar IDDE (14) with the continuous and discrete unpertubed system of IDDEs (4), it follows that

$$S(.)=S(t,y,y(t-1))=\frac{yexp\left(t\right)}{1+exp\left(2t\right)+exp\left(y^2\right)+exp\left(y^2(t-1)\right)},$$

and the delay term τ, the functions $G(.)$, $H(.)$, $K(.)$ and $K_1(.)$ are the same as in Example 1. Thus, it is not needed to verify the conditions related to the functions $G(.)$, $H(.)$, $K(.)$ and $K_1(.)$.

As for the function $S(.)$, it is obvious that:

$$\left|S(.)\right|=\frac{\left|y\right|exp\left(t\right)}{1+exp\left(2t\right)+exp\left(y^2\right)+exp\left(y^2(t-1)\right)}\le \frac{\left|y\right|exp\left(t\right)}{1+exp\left(2t\right)}=\left|s_0\left(t\right)\right|\left|y\right|,$$

where

$$\left|s_0\left(t\right)\right|=exp\left(t\right){[1+exp(2t\left)\right]}^{-1}.$$

Next,

$$G_0-\underset{t}{\overset{\infty }{\int }}∥K_1(u,t)∥du-\left|s_0\left(t\right)\right|=20\pi -\frac{\pi }{2}+arctgt-\frac{exp\left(t\right)}{1+exp\left(2t\right)}>0.$$

Thus, conditions (C1) and (C5) of Theorem 5 are satisfied. By virtue of this information, the solutions of the continuous and discrete scalar IDDE (14) are bounded at infinity. This means that, under given conditions, every path of the solutions of IDDE (14) will remain inside a circle as $t\to \infty$.

In Figure 2, the continuous and discrete scalar IDDE (14) is solved by MATLAB.

Example 3.

Consider the continuous and discrete scalar IDDE:

$$\begin{array}{cc}\hfill \dot{y}=& \left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)y\hfill \\ \hfill & +\frac{siny}{t^2+1+exp\left(y^2\right)+y^2(t-1)}\underset{t-1}{\overset{t}{\int }}\frac{siny\left(s\right)}{t^2+s^2+1++y^2\left(s\right)}ds,t\ge 1.\hfill \end{array}$$

(15)

Next, comparing continuous and discrete scalar IDDE (15) with continuous and discrete unperturbed system of IDDEs (4), it follows that:

$$G(t,y)=-\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)y,$$

$$G(t,0)=0;$$

the delay term $\tau =1$, the functions $H(.)$ and $K(.)$ are the same as in Example 1. Thus, it is not needed to show again the estimates related to the functions $H(.)$ and $K(.)$. Next, it is clear that:

$$sgnyG(t,y)=-\left(20\pi +\frac{exp\left(t\right)}{(exp\left(t\right)+1)(1+y^2)}\right)ysgny<0,$$

$$y\ne 0,$$

$$y\in \mathbb{R};$$

$$\left|G(t,y)\right|\ge 20\pi \left|y\right|=G_0\left|y\right|,G_0=20\pi .$$

As for the last step, considering the estimates of the functions $H(.)$, $K(.)$ and the last one, we have

$$G_0-\tau K_0=20\pi -1>0.$$

With this information, condition (C4) of Theorem 7 is held. For these reasons, the trivial solution of continuous and discrete scalar IDDE (15) is unstable. This means that, under given conditions, every path of the solutions of IDDE (15) will not remain inside a circle.

In Figure 3, the continuous and discrete scalar IDDE (15) is solved by MATLAB.

5. Contributions

(1)

The systems of this paper, i.e., the continuous and discrete systems of IDDEs (2) and IDDEs (4), extend and improve the continuous and discrete system of IDDEs (1), which were studied by Crisci et al. ([14], Theorem 2.2). This is the first contribution of this paper.

(2)

In Crisci et al. ([14], Theorem 2.2), the LKF

$$V=∥y\left(t\right)∥+\underset{0}{\overset{\infty }{\int }}ds\underset{t-s}{\overset{t}{\int }}\kappa (\tau +s,\tau )∥y\left(\tau \right)∥d\tau$$

was constructed and used as a main tool to prove Theorem 1, i.e., Theorem 2.2 of Crisci et al. ([14], Theorem 2.2). In this paper, we define a novel LKF, such as

$$\mathsf{\Lambda }(t,y_t):=∥y∥+\sigma \underset{t-\tau }{\overset{t}{\int }}\underset{t}{\overset{\infty }{\int }}∥K_1(u,s)∥∥y\left(s\right)∥duds$$

to prove the UAS of the trivial solution of the unperturbed system (4). Here, the LKF $\mathsf{\Lambda }(t,y_t)$ was also used to prove Corollary 1, Theorems 4 and 5. The LKF $\mathsf{\Lambda }(t,y_t)$ is different from the LKF V of Crisci et al. ([14], Theorem 2.2). Next, the LKF $\mathsf{\Lambda }(t,y_t)$ can lead more suitable conditions related to Theorems 3–5. This is the second contribution of this paper.

(3)

In the paper of Crisci et al. ([14], Theorem 2.2), the AS of the trivial solution of system (1) is proved by the LKF method, see Theorem 1. In this paper, instead of the AS result, we proved the UAS of the trivial solution of the unperturbed system (4) by Theorem 3. The UAS implies the AS; however, on the contrary, the AS does not imply the UAS. Our result, Theorem 3, is stronger than Theorem 1, i.e., Crisci et al. ([14], Theorem 2.2). This is the third contribution of this paper.

(4)

In this paper, we used the LRM method to prove the ES and instability of the trivial solution of the continuous and discrete unperturbed system of IDDEs (4) via the LF defined by:

$${\mathsf{\Lambda }}_1(t,y):=∥y∥=\left|y_1\right|+...+\left|y_n\right|.$$

In the relevant literature, we did not find a paper on the properties of solutions of continuous and discrete perturbed system of IDDEs (2) and unperturbed system of IDDEs (4), where the LRM method is used as a basic technique to prove those kinds of results. Here, the effectiveness of the LRM can be seen from Theorems 6 and 7. This is the fourth contribution of this paper.

(5)

Crisci et al. ([14], Theorem 2.2) investigated the AS of the trivial solution of the continuous and discrete system of IDDEs (1). In this paper, we discussed the UAS, US, ES, instability of the trivial solution, integrability of non-trivial solutions of the continuous and discrete scalar unperturbed system (4) as well as the boundedness of non-trivial solutions at infinity of the continuous and discrete scalar perturbed system of IDDEs (2), which includes and extends the continuous and discrete system of IDDEs (1). Thus, we establish five new results and a corollary on the fundamental properties of solutions. This is the fifth contribution of this paper to the topic of the paper and the qualitative theory of solutions.

(6)

In Crisci et al. ([14], Theorem 2.2), no examples were given as an application of Theorem 1. Here, in particular cases of the continuous and discrete systems (2) and (4), we constructed three examples and solved them by MATLAB software. The conditions of Theorems 3–7 are held by Examples 1–3. Hence, the applications of Theorems 3–7 were provided. This is the sixth contribution of this paper.

(7)

In this paper the boundedness theorem, Theorem 5, was proved the use of Gronwall’s inequality was not needed. Hence, Theorem 5 has less restrictive conditions.

6. Conclusions

In this work, certain systems of continuous and discrete IDDEs were taken into consideration. Five theorems and a corollary related to the fundamental qualitative concepts, such as the US, UAS, ES, integrability, instability and boundedness of solutions of that systems of continuous and discrete IDDEs, were proved with the help of the LKF method and the LRM. In particular cases, as numerical applications of the obtained results, Examples 1–3 were solved by utilizing the 4th order Runge–Kutta method via MATLAB. The results of this work make contributions to the theory of continuous and discrete IDDEs and Crisci et al. ([14], Theorem 2.2).