Approximation by Tensor-Product Kind Bivariate Operator of a New Generalization of Bernstein-Type Rational Functions and Its GBS Operator
Abstract
:1. Introduction
2. Construction of Tensor-Product Kind Bivariate Operator
3. Approximation Results
4. GBS Operator
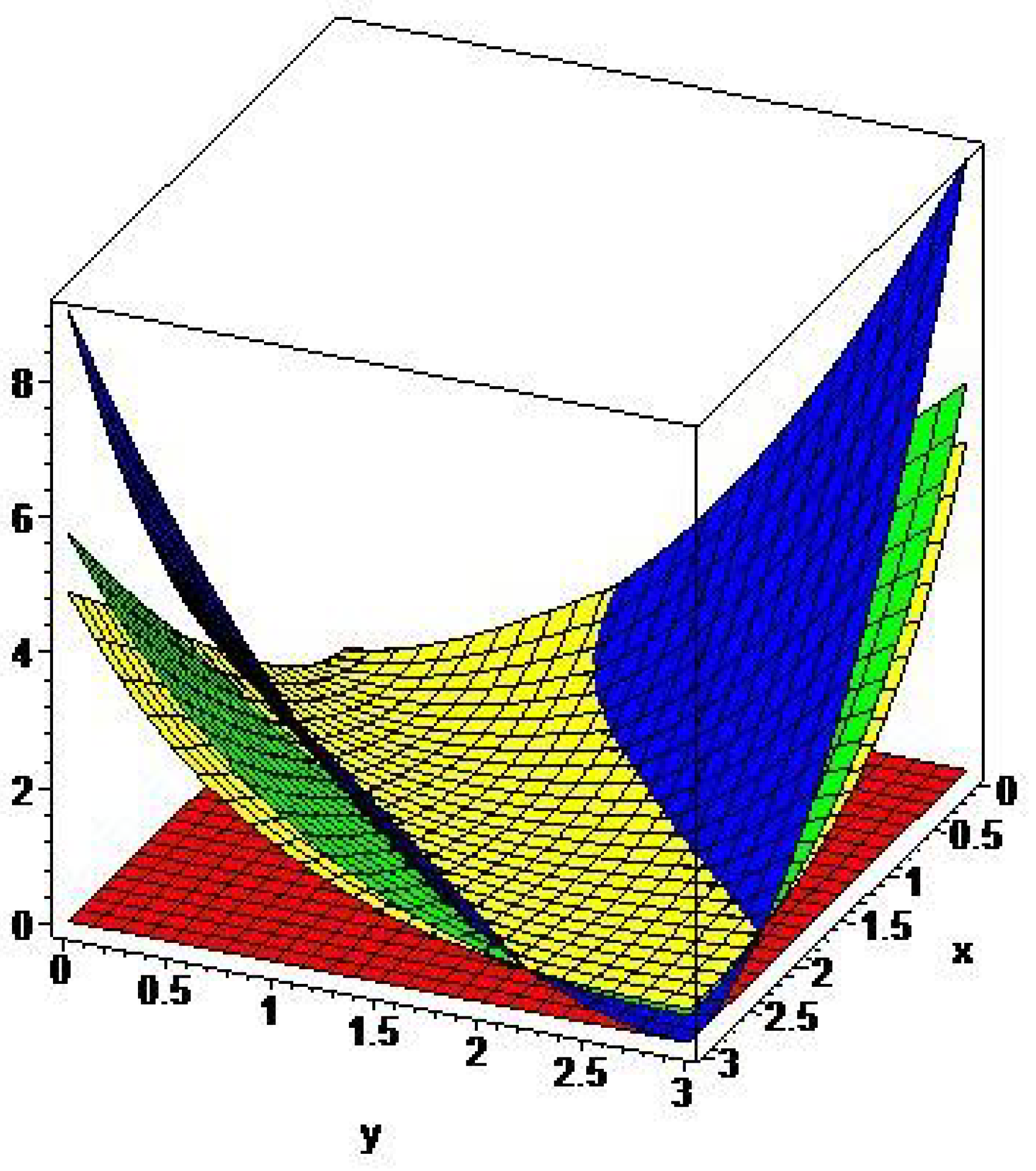
5. Graphical Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balázs, K. Approximation by Bernstein type rational funcitons. Acta Math. Acad. Sci. Hung. 1975, 26, 123–124. [Google Scholar] [CrossRef]
- Atakut, Ç.; İspir, N. On Bernstein type rational functions of two variables. Math. Slovaca 2004, 54, 291–301. [Google Scholar] [CrossRef]
- Atakut, Ç. On derivatives Bernstein type rational functions of two variables. Appl. Math. Comput. 2011, 218, 673–677. [Google Scholar] [CrossRef]
- Özkan, E.Y.; Aksoy, G. On a new generalization of Bernstein-type rational functions and its approximation. Mathematics 2022, 10, 973. [Google Scholar] [CrossRef]
- Acu, A.M.; Acar, T.; Muraru, C.-V.; Radu, V.A. Some approximation properties by a class of bivariate operators. Math. Methods Appl. Sci. 2018, 42, 5551–5565. [Google Scholar] [CrossRef]
- Agrawal, P.N.; Acu, A.M.; Chauhan, R.; Garg, T. Approximation of Bögel continuous functions and deferred weighted A-statistical convergence by Bernstein-Kantorovich type operators on a triangle. J. Math. Inequal. 2021, 15, 1695–1711. [Google Scholar] [CrossRef]
- Başcanbaz-Tunca, G.; Erençin, A.; Olgun, A. Quantitative estimates for bivariate Stancu operators. Math. Methods Appl. Sci. 2019, 42, 5241–5250. [Google Scholar] [CrossRef]
- Agrawal, P.N.; Kajla, A.; Kumar, D. Modified ρ-Bernstein operators for functions of two variables. Numer. Funct. Anal. Optim. 2021, 42, 1073–1095. [Google Scholar] [CrossRef]
- İspir, N. Quantitative estimates for GBS operators of Chlodowsky-Szász type. Filomat 2017, 31, 1175–1184. [Google Scholar] [CrossRef]
- Özkan, E.Y. Approximation properties of bivariate complex q-Balazs-Szabados operators of tensor product kind. J. Inequal. Appl. 2014, 2014, 20. [Google Scholar] [CrossRef] [Green Version]
- Özkan, E.Y. Approximation by complex bivariate Balazs-Szabados operators. Bull. Malays. Math. Sci. Soc. 2016, 39, 1–16. [Google Scholar] [CrossRef]
- Özkan, E.Y. Qantitative estimates for the tensor product (p,q)-Balázs-Szabados operators and associated generalized Boolean sum operators. Filomat 2020, 34, 779–793. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Zhou, Z. Durrmeyer type (p,q)-Baskakov operators for functions of one and two variables. J. Comput. Anal. Appl. 2019, 27, 481–501. [Google Scholar]
- Srivastava, H.M.; Ansari, K.J.; Özger, F.; Ödemiş Özger, Z. A Link between approximation theory and summability methods via four-dimensional infinite matrices. Mathematics 2021, 9, 1895. [Google Scholar] [CrossRef]
- Cai, Q.-B.; Ansari, K.J.; Temizer Ersoy, M.; Özger, F. Statistical blending-type approximation by a class of operators that includes shape parameters λ and α. Mathematics 2022, 10, 1149. [Google Scholar] [CrossRef]
- Volkov, V.I. On the convergence of sequences of linear positive operators in the space of continuous functions of two variables. Dokl. Akad. Nauk. SSSR (N.S.) 1957, 115, 17–19. (In Russian) [Google Scholar]
- Anastassiou, G.A.; Gal, S.G. Approximation Theory: Moduli of Continuity and Global Smoothness Preservation; Birkhäuser: Boston, MA, USA, 2000. [Google Scholar]
- Bögel, K. Mehr dimensionale Differentiation von Funktionen mehrerer Veränderlicher. J. Reine Angew. Math. 1934, 170, 197–217. [Google Scholar] [CrossRef]
- Bögel, K. Über die mehrdimensionale Integration und beschränkte Variation. J. Reine Angew. Math. 1935, 173, 5–29. [Google Scholar] [CrossRef]
- Bögel, K. Über die mehrdimensionale Differentiation. Jahresber. Dtsch. Math. Ver. 1962, 65, 45–71. [Google Scholar]
- Badea, C.; Cottin, C. Korovkin-type theorems for generalized Boolean sum operators. Approximation theory (Kecskemét, 1900). Colloq. Math. Soc. János Bolyai. 1990, 58, 51–68. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özkan, E.Y.; Aksoy, G. Approximation by Tensor-Product Kind Bivariate Operator of a New Generalization of Bernstein-Type Rational Functions and Its GBS Operator. Mathematics 2022, 10, 1418. https://doi.org/10.3390/math10091418
Özkan EY, Aksoy G. Approximation by Tensor-Product Kind Bivariate Operator of a New Generalization of Bernstein-Type Rational Functions and Its GBS Operator. Mathematics. 2022; 10(9):1418. https://doi.org/10.3390/math10091418
Chicago/Turabian StyleÖzkan, Esma Yıldız, and Gözde Aksoy. 2022. "Approximation by Tensor-Product Kind Bivariate Operator of a New Generalization of Bernstein-Type Rational Functions and Its GBS Operator" Mathematics 10, no. 9: 1418. https://doi.org/10.3390/math10091418





