A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor
Abstract
:1. Introduction
2. Fundamental Concepts of Fractional Derivatives in the Caputo Sense
3. Model with Vaccination
4. Mathematical Analysis
4.1. Local and Global Existence and Uniqueness of Solution
- (i) is Lebesgue measurable on with respect to t ,
- (ii) is continuous on with respect to x ,
- (iii) There exists a real-valued function such that for almost every and all .
4.2. Basic Reproductive Number
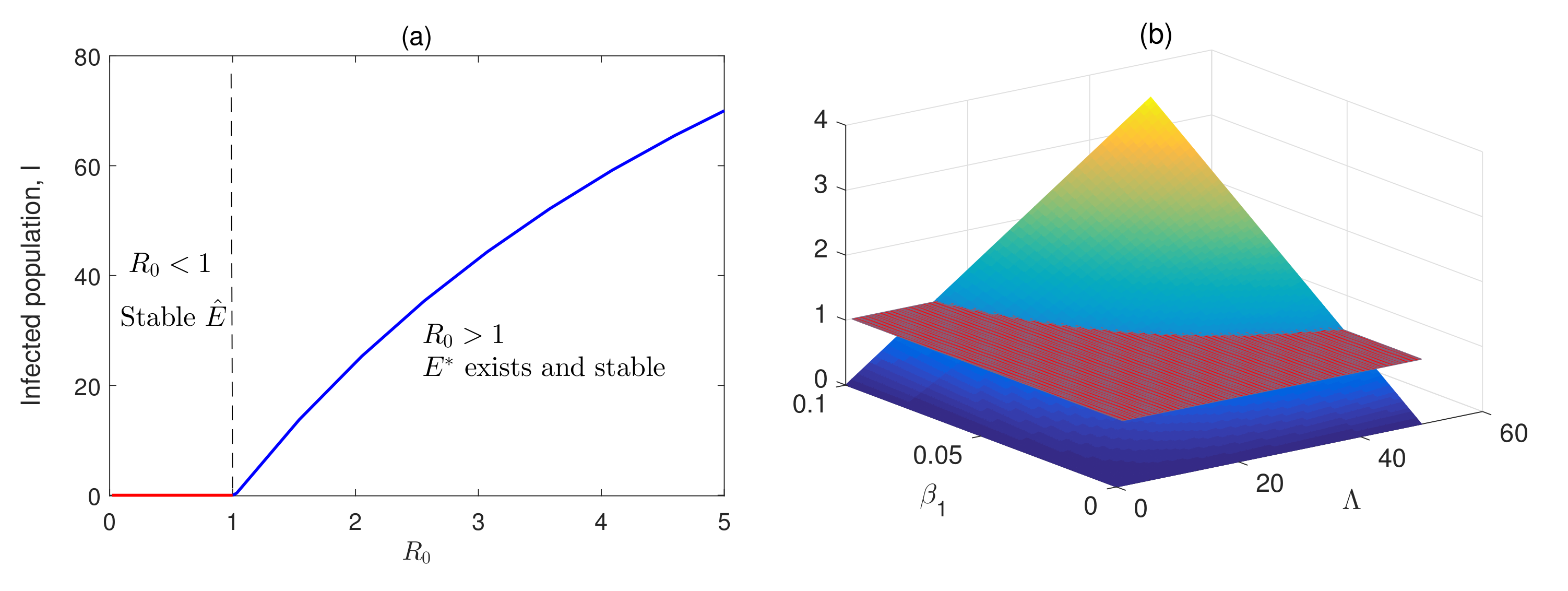
5. Existence of Equilibria and Stability
- (A)
- When , , then are in the interior of and have a unique interaction and . Moreover, at the given interaction point system (17) attains a unique endemic equilibrium, .
- (B)
- There is no interaction point of these three curves in the interior of whenever , as the model has a disease-free equilibrium when .
Stability of Equilibria
- (i)
- Define , , and as the Routh–Hurwitz discriminants where, , , andWhen and if the below conditionsare satisfied, then the equilibrium point E is locally asymptotically stable.
- (ii)
- If , , and , then then the equilibrium point E is unstable.
- (iii)
- If the inequalities , , , , and hold, then E is locally asymptotically stable, and unstable if , , , and .
- (iv)
- If the conditions , , , , and hold, then for E is locally asymptotically stable.
- (v)
- A necessary condition for the steady state E to be locally asymptotically stable is .
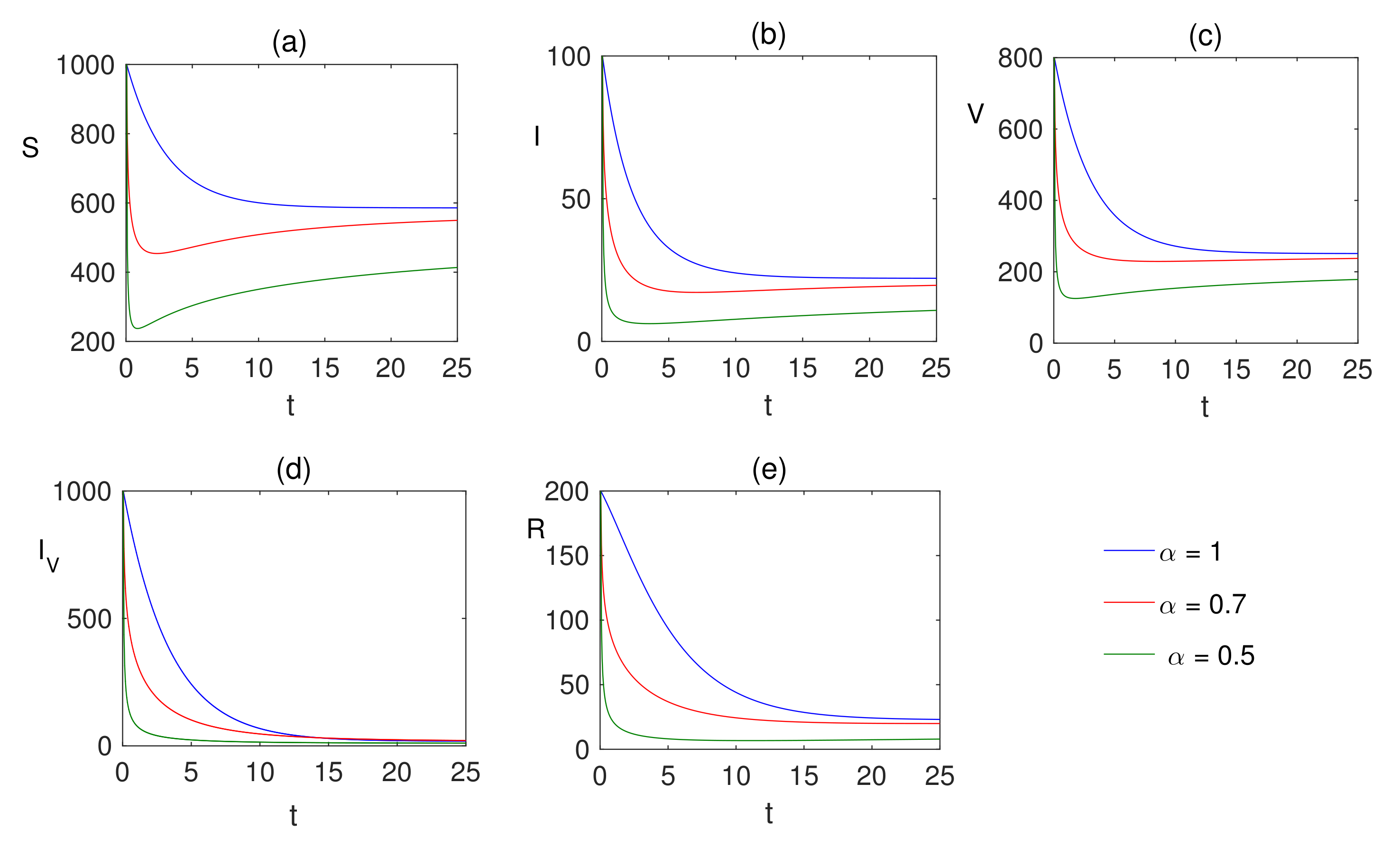
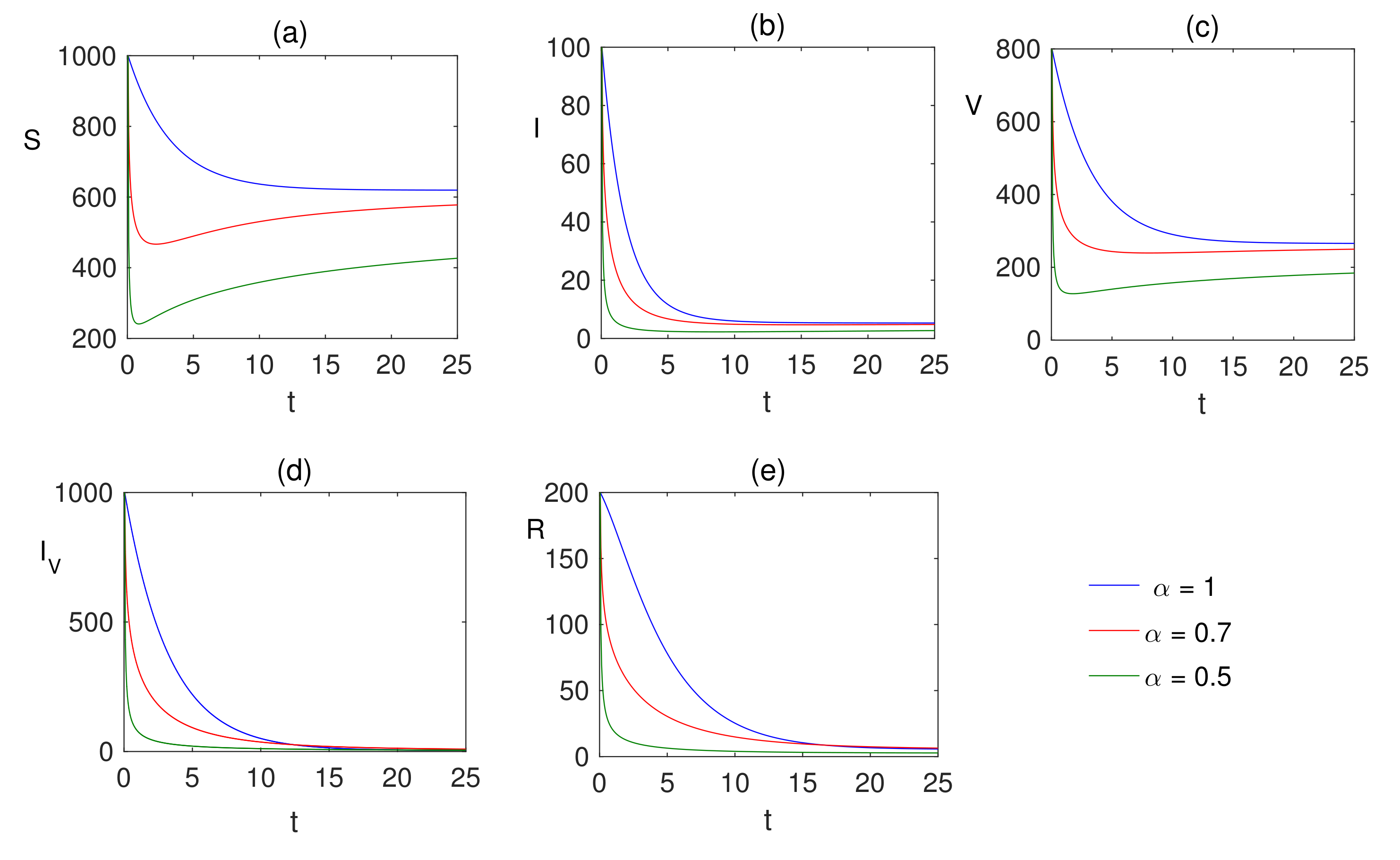
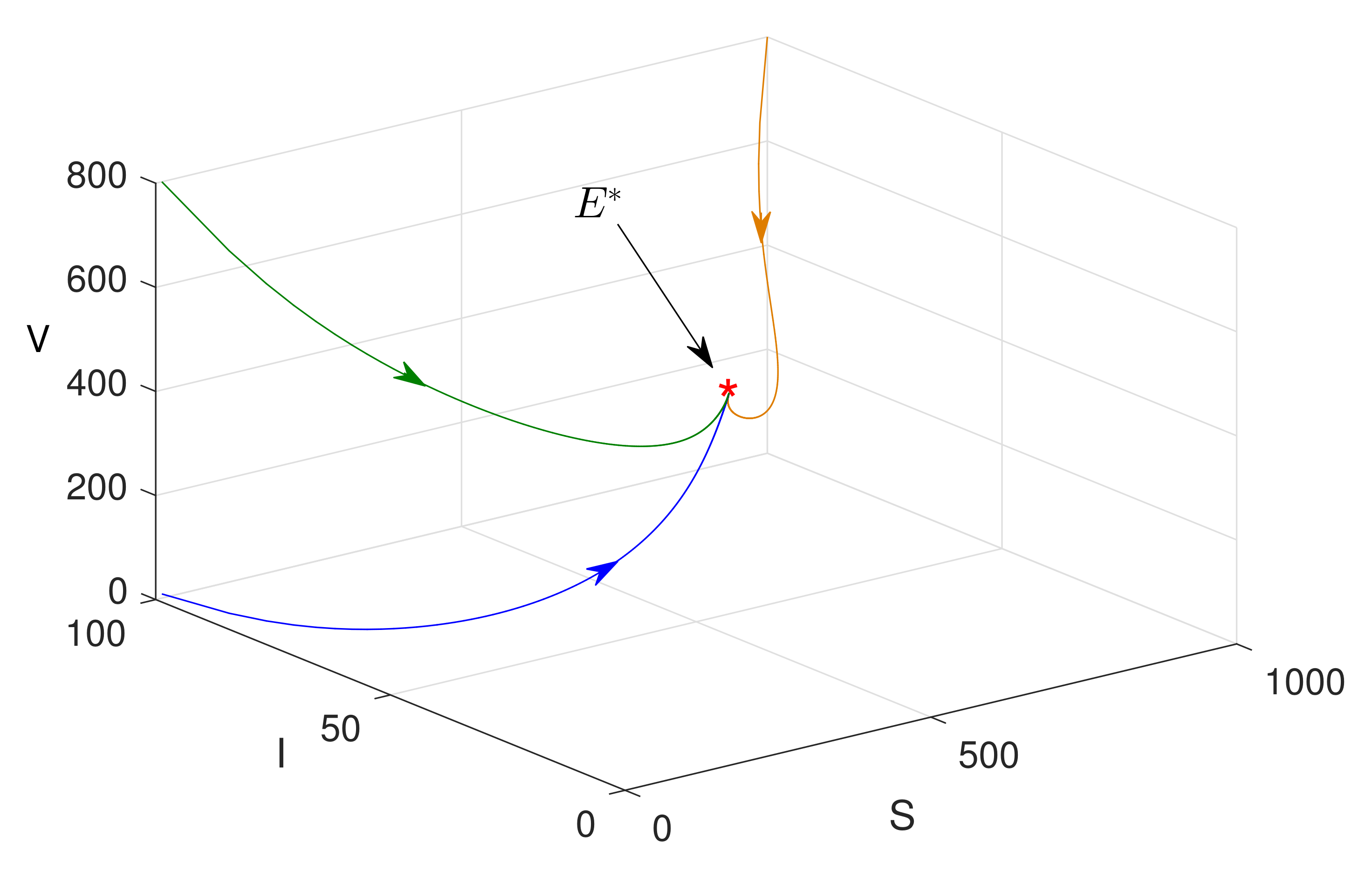
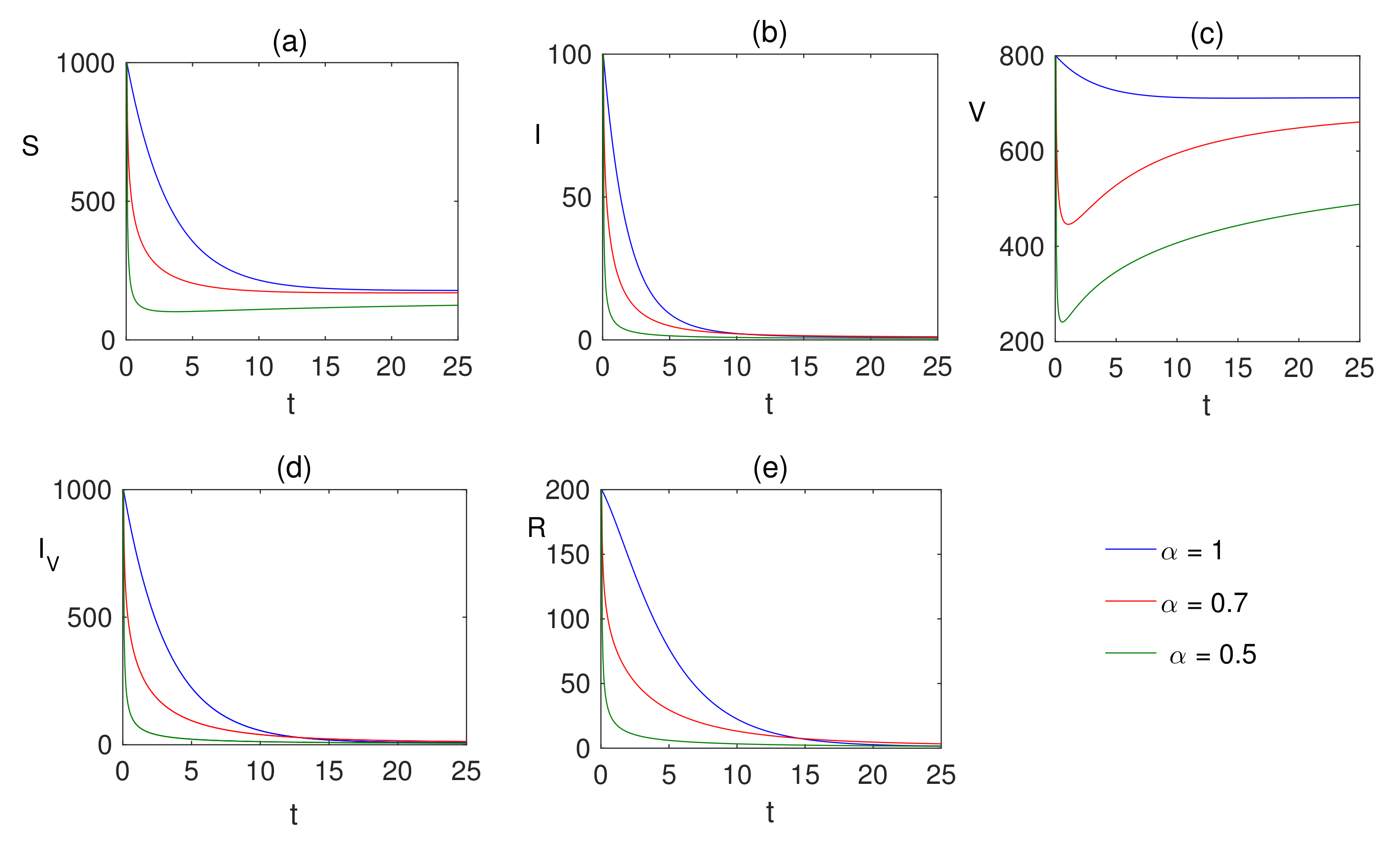
6. Numerical Simulations
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biscayart, C.; Angeleri, P.; Lloveras, S.; Chaves, T.d.S.S.; Schlagenhauf, P.; Rodríguez-Morales, A.J. The next big threat to global health? 2019 novel coronavirus (2019-nCoV): What advice can we give to travellers?—Interim recommendations January 2020, from the Latin-American society for Travel Medicine (SLAMVI). Travel Med. Infect. Dis. 2020, 33, 101567. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Khan, H.; Shah, K.; Khan, A. Fractional order mathematical modeling of COVID-19 transmission. Chaos Solitons Fractals 2020, 139, 110256. [Google Scholar] [CrossRef] [PubMed]
- Sparrow, A.K.; Brosseau, L.M.; Harrison, R.J.; Osterholm, M.T. Protecting Olympic participants from Covid-19—The urgent need for a risk-management approach. N. Engl. J. Med. 2021, 385, e2. [Google Scholar] [CrossRef]
- Jamali, A.A. COVID-19 VACCINES. J. Peoples Univ. Med. Health Sci. Nawabshah (JPUMHS) 2020, 10, 1–2. [Google Scholar]
- Zou, L.; Ruan, F.; Huang, M.; Liang, L.; Huang, H.; Hong, Z.; Yu, J.; Kang, M.; Song, Y.; Xia, J.; et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020, 382, 1177–1179. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Ahmad, B. A fractional-order differential equation model of COVID-19 infection of epithelial cells. Chaos Solitons Fractals 2021, 147, 110952. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Al Basir, F.; Almuqrin, M.A.; Mondal, J.; Khan, I. SARS-CoV-2 infection with lytic and non-lytic immune responses: A fractional order optimal control theoretical study. Results Phys. 2021, 26, 104260. [Google Scholar] [CrossRef]
- Mondal, J.; Samui, P.; Chatterjee, A.N. Optimal control strategies of non-pharmaceutical and pharmaceutical interventions for COVID-19 control. J. Interdiscip. Math. 2021, 24, 125–153. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Al Basir, F. A model for SARS-COV-2 infection with treatment. Comput. Math. Methods Med. 2020, 2020, 1352982. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gumel, A.B.; Ruan, S.; Day, T.; Watmough, J.; Brauer, F.; Van den Driessche, P.; Gabrielson, D.; Bowman, C.; Alexander, M.E.; Ardal, S.; et al. Modelling strategies for controlling SARS outbreaks. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2004, 271, 2223–2232. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020, 5, 323–337. [Google Scholar] [CrossRef]
- Samui, P.; Mondal, J.; Khajanchi, S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals 2020, 140, 110173. [Google Scholar] [CrossRef]
- Guariglia, E. Riemann zeta fractional derivative—Functional equation and link with primes. Adv. Differ. Equ. 2019, 2019, 261. [Google Scholar] [CrossRef]
- Torres-Hernandez, A.; Brambila-Paz, F. An approximation to zeros of the Riemann zeta function using fractional calculus. arXiv 2020, arXiv:2006.14963. [Google Scholar] [CrossRef]
- Li, C.; Dao, X.; Guo, P. Fractional derivatives in complex planes. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1857–1869. [Google Scholar] [CrossRef]
- Guariglia, E. Fractional calculus, zeta functions and Shannon entropy. Open Math. 2021, 19, 87–100. [Google Scholar] [CrossRef]
- Závada, P. Operator of fractional derivative in the complex plane. Commun. Math. Phys. 1998, 192, 261–285. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Ullah, S.; Okosun, K.; Shah, K. A fractional order pine wilt disease model with Caputo–Fabrizio derivative. Adv. Differ. Equ. 2018, 2018, 410. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- DarAssi, M.H.; Safi, M.A.; Khan, M.A.; Beigi, A.; Aly, A.A.; Alshahrani, M.Y. A mathematical model for SARS-CoV-2 in variable-order fractional derivative. Eur. Phys. J. Spec. Top. 2022. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Baleanu, D.; Abadi, M.H.; Jajarmi, A.; Vahid, K.Z.; Nieto, J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Ahmed, I.; Baba, I.A.; Yusuf, A.; Kumam, P.; Kumam, W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv. Differ. Equ. 2020, 2020, 394. [Google Scholar] [CrossRef]
- Kozioł, K.; Stanisławski, R.; Bialic, G. Fractional-order sir epidemic model for transmission prediction of covid-19 disease. Appl. Sci. 2020, 10, 8316. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Torres, D.F. Mathematical Analysis of a Fractional COVID-19 Model Applied to Wuhan, Spain and Portugal. Axioms 2021, 10, 135. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S.; Nieto, J.J. A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics 2021, 9, 1321. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Roy, A.K.; Basir, F.A.; Roy, P.K. A vivid cytokines interaction model on psoriasis with the effect of impulse biologic (TNF-alpha inhibitor) therapy. J. Theor. Biol. 2019, 474, 63–77. [Google Scholar] [CrossRef] [PubMed]
- Segel, L.; Slemrod, M. The quasi-steady-state assumption: A case study in perturbation. SIAM Rev. 1989, 31, 446–477. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef] [Green Version]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [Green Version]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Rihan, F.A.; Baleanu, D.; Lakshmanan, S.; Rakkiyappan, R. On Fractional SIRC Model with Salmonella Bacterial Infection. Abstr. Appl. Anal. 2014, 2014, 136263. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A. On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Ro¨ssler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- Cao, X.; Datta, A.; Al Basir, F.; Roy, P.K. Fractional-order model of the disease psoriasis: A control based mathematical approach. J. Syst. Sci. Complex. 2016, 29, 1565–1584. [Google Scholar] [CrossRef]
- Ahmad, S.W.; Sarwar, M.; Rahmat, G.; Shah, K.; Ahmad, H.; Mousa, A.A.A. Fractional order model for the coronavirus (COVID-19) in Wuhan, China. Fractals 2021, 30, 2240007. [Google Scholar] [CrossRef]
- Spencer, J.; Shutt, D.; Moser, S.; Clegg, H.; Wearing, H.; Mukundan, H.; Manore, C. Epidemiological Parameter Review and Comparative Dynamics of Influenza, Respiratory Syncytial Virus, Rhinovirus, Human Coronavirus, and Adenovirus. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Maji, C.; Al Basir, F.; Mukherjee, D.; Ravichandran, C.; Nisar, K. COVID-19 propagation and the usefulness of awareness based control measures: A mathematical model with delay. AIMS Math. 2022, 7, 12091–12105. [Google Scholar] [CrossRef]

| Dependent Variables | Description | ||
|---|---|---|---|
| S | Susceptible Population | ||
| I | Infected Population | ||
| V | vaccinated population | ||
| Infected population | |||
| after vaccination | |||
| R | Recovered Population | ||
| Parameter | Description | Values | Reference |
| Birth rate (per week) | 270 | [42] | |
| Probability of vaccination | 0–1 | - | |
| Infection rate without vaccination | 0.0075 | [2,11] | |
| Infection rate after vaccination | 0.0007 | [11] | |
| Fear effect before vaccination | 0.02–2 | Assumed | |
| Fear effect after vaccination | 0.02–2 | Assumed | |
| natural death rate | 0.3 | [2] | |
| Recovery rate before vaccination | 0.01 | [43] | |
| Recovery rate before vaccination | 0.3 | [43] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, A.N.; Basir, F.A.; Ahmad, B.; Alsaedi, A. A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor. Mathematics 2022, 10, 1451. https://doi.org/10.3390/math10091451
Chatterjee AN, Basir FA, Ahmad B, Alsaedi A. A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor. Mathematics. 2022; 10(9):1451. https://doi.org/10.3390/math10091451
Chicago/Turabian StyleChatterjee, Amar Nath, Fahad Al Basir, Bashir Ahmad, and Ahmed Alsaedi. 2022. "A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor" Mathematics 10, no. 9: 1451. https://doi.org/10.3390/math10091451
APA StyleChatterjee, A. N., Basir, F. A., Ahmad, B., & Alsaedi, A. (2022). A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor. Mathematics, 10(9), 1451. https://doi.org/10.3390/math10091451









