The Optical Solutions of the Stochastic Fractional Kundu–Mukherjee–Naskar Model by Two Different Methods

Abstract

In this paper, we focus on the stochastic fractional Kundu–Mukherjee–Naskar equation perturbed in the Stratonovich sense by the multiplicative Wiener process. To gain new elliptic, rational, hyperbolic and trigonometric stochastic solutions, we use two different methods: the Jacobi elliptic function method and the $(G^{\prime }/G)$-expansion method. Because of the significance of the Kundu-Mukherjee equation in a magnetized plasma, the obtained solutions are useful in understanding many remarkable physical phenomena. Furthermore, we show the effect of the multiplicative Wiener process on the obtained solutions of the Kundu–Mukherjee–Naskar equation.

1. Introduction

In chemistry, physics, engineering, biology, geophysics and climate dynamics, among other fields [1,2,3,4], the advantages of taking random effects in simulating, analyzing, predicting and modeling compound phenomena have been vastly recognized. Moreover, the presence of noises has been shown to give rise to some statistical features and essential phenomena, such as ergodic behavior forced by degenerate noise and a unique invariant measure. Simultaneously, stochastic perturbations in a physical system cannot be prevented, and they can not be neglected in some cases.

On the other hand, fractional differential Equations (FDEs) have been displayed to be more precise than classical one in explaining complex physical phenomena in the real world. FDEs have drawn the interest of scientists and researchers over the last two decades. The principle of fractional derivative has been utilized to define a variety of phenomena, such as viscoelastic materials, signal processing, fluid dynamics porous medium, ocean wave, photonic, electromagnetism, chaotic systems, propagation of waves, optical fiber communication, plasma physics, nuclear physics and others.

It is critical in nonlinear science to determine the analytic solutions of nonlinear evolution partial differential equations. Therefore, several analytical methods have been developed to deal with these sorts of nonlinear problems, such as the Jacobi elliptic function [5,6], perturbation [7,8,9], sine-cosine [10,11], Hirota’s function [12], $(\frac{G^{\prime }}{G})$-expansion [13,14,15], $exp(-\varphi (\varsigma ))$-expansion [16], tanh-sech [17,18], Riccati-Bernoulli sub-ODE [19], Darboux transformation [20], etc.

To get a better degree of quality consistency, we recognize here the following stochastic fractional-space Kundu–Mukherjee–Naskar equation (SFKMNE) perturbed by the multiplicative Wiener process:

$$i{u}_t+a{\mathbb{T}}_{xy}^{\alpha }u+ibu(u{\mathbb{T}}_x^{\alpha }{u}^{\ast }-u^{\ast }{\mathbb{T}}_x^{\alpha }u)+i\sigma u\circ {\mathcal{W}}_t=0,$$

(1)

where u denotes the optical soliton profile, ${\mathbb{T}}^{\alpha }$ is the conformable derivative (CD) [21], $a,b$ are positive constants, $\sigma$ is the noise strength, $u\circ {\mathcal{W}}_t$ is the multiplicative Wiener process in the Stratonovich sense and $\mathcal{W}(t)$ is the standard Wiener process (SWP).

Kundu and Mukherjee [22] proposed Equation (1) in 2013 with $\alpha =1$ and $\sigma =0$. It is attained from the fundamental hydrodynamic equations as a two-dimensional nonlinear Schrödinger equation. This Equation (1) can be utilized to explain ion-acoustic waves, oceanic rogue waves and optical fiber wave propagation in a magnetized plasma [23,24,25,26]. Many research works have been focused on Equation (1) to investigate soliton propagation into an optical fiber. As a result, numerous mathematical methods have been used to obtain exact solutions, such as extended trial function [27], trial Equation [28], modified simple Equation [29], Jacobi elliptic functions and Weierstrass [30] and Lie symmetry [31].

We do not investigate here the uniqueness and existence of the solutions, which is a well-known issue (see, for instance [32,33]).

Our motivation in this article is to get the analytical stochastic fractional solutions of the SFKMNE (1). We employ two various techniques, i.e., the Jacobi elliptic function method and the $(G^{\prime }/G)$-expansion method, to acquire solutions of elliptic, trigonometric, hyperbolic and rational functions. Furthermore, to examine the influence of the Wiener process on the solutions of SFKMNE (1), we utilize Matlab tools to create 2D and 3D graphs for several of the analytical solutions generated in this work.

The document is organized as follows: In Section 2, we define and give a few properties of the SWP and CD. In Section 3, we employ an appropriate wave transformation to get the wave equation of the SFKMNE (1), while in Section 4, to create the exact solutions of the SFKMNE (1), we use diverse approaches. In Section 5, the influence of the Wiener process on the derived solutions is investigated. The paper ends with a conclusion section.

2. Preliminaries

We present here some definitions and properties of SWP and CD. First, let us define SWP $\mathcal{W}(t)$ as follows:

Definition 1.

Stochastic process ${\{\mathcal{W}(t)\}}_{t\ge 0}$ is said to be an SWP if the following conditions hold:

1.

$\mathcal{W}(0)=0,$

2.

$\mathcal{W}(t)$ is a continuous function of $t\ge 0$,

3.

$\mathcal{W}({\tau }_2)-\mathcal{W}({\tau }_1)$ is independent for ${\tau }_1<{\tau }_2$,

4.

$\mathcal{W}({\tau }_2)-\mathcal{W}({\tau }_1)$ has a Gaussian distribution with mean 0 and variance ${\tau }_2-{\tau }_1$.

We should mention that the two most commonly utilized variants of the stochastic integral are Stratonovich and Itô [34]. Modeling problems mainly determine what form is appropriate; even so, once it is chosen, an equivalent equation of the other type can be created using the same solutions. Thus, the the next relation can be used to swap between Itô (denoted by ${\int }_0^t\mathrm{\Theta }d\mathcal{W}$) and Stratonovich (denoted by ${\int }_0^t\mathrm{\Theta }\circ d\mathcal{W}$):

$${\int }_0^t\mathrm{\Theta }(\tau ,Z_{\tau })d\mathcal{W}(\tau )={\int }_0^t\mathrm{\Theta }(\tau ,Z_{\tau })\circ d\mathcal{W}(\tau )-\frac{1}{2}{\int }_0^t\mathrm{\Theta }(\tau ,Z_{\tau })\frac{\partial \mathrm{\Theta }(\tau ,Z_{\tau })}{\partial z}d\tau ,$$

(2)

where $\mathrm{\Theta }$ is supposed to be sufficiently regular and $\{Z_t,$$t\ge 0\}$ is a stochastic process.

Definition 2

([21]). The CD of $\varphi :{\mathbb{R}}^{+}\to \mathbb{R}$ of order $\alpha \in (0,1]$ is defined as

$${\mathbb{T}}_x^{\alpha }\varphi (x)=\underset{h\to 0}{lim}\frac{\varphi (x+h{x}^{1-\alpha })-\varphi (x)}{h}.$$

Theorem 1

([21]). Let $\varphi ,\mathrm{\Psi }:{\mathbb{R}}^{+}\to \mathbb{R}$ be differentiable, and also let α be a differentiable function, then:

$${\mathbb{T}}_x^{\alpha }(\varphi \circ \mathrm{\Psi })(x)=x^{1-\alpha }{\mathrm{\Psi }}^{\prime }(x)\varphi (\mathrm{\Psi }(x)).$$

Let us exhibit some features of the CD:

1.

${\mathbb{T}}_x^{\alpha }[c_1\varphi (x)+c_2\mathrm{\Psi }(x)]=c_1{\mathbb{T}}_x^{\alpha }\varphi (x)+c_2{\mathbb{T}}_x^{\alpha }\mathrm{\Psi }(x),$

2.

${\mathbb{T}}_x^{\alpha }[C]=0$, where C is a constant,

3.

${\mathbb{T}}_x^{\alpha }[x^{\hslash }]=\hslash x^{\hslash -\alpha },\hslash \in \mathbb{R},$

4.

${\mathbb{T}}_x^{\alpha }\mathrm{\Psi }(x)=x^{1-\alpha }\frac{d\mathrm{\Psi }}{dx}.$

3. Wave Equation for SFKMNE

We use the following wave transformation to obtain the wave equation for the SFKMNE (1):

$$u(x,y,t)=\phi (\mu )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(3)

with:

$$\mu =\frac{{\mu }_1}{\alpha }{x}^{\alpha }+\frac{{\mu }_2}{\alpha }{y}^{\alpha }+{\mu }_{3}t,\theta =\frac{-{\theta }_1}{\alpha }{x}^{\alpha }-\frac{{\theta }_2}{\alpha }{y}^{\alpha }+{\theta }_{3}t,$$

where $\phi$ is a deterministic function and ${\mu }_k,$${\theta }_k$ are nonzero constants for $k=1,2,3$. Plugging Equation (3) into Equation (1) and using:

$$\begin{array}{ccc}\hfill \frac{du}{dt}& =& ({\mu }_3{\phi }^{\prime }+i{\theta }_3\phi -\sigma \phi {\mathcal{W}}_t-\frac{1}{2}{\sigma }^2\phi )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \\ & =& ({\mu }_3{\phi }^{\prime }+i{\theta }_3\phi -\sigma \phi \circ {\mathcal{W}}_t)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \end{array}$$

(4)

and:

$$\begin{array}{ccc}\hfill {\mathbb{T}}_x^{\alpha }u& =& ({\mu }_1{\phi }^{\prime }-i{\theta }_1\phi )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \\ \hfill {\mathbb{T}}_x^{\alpha }{u}^{\ast }& =& ({\mu }_1{\phi }^{\prime }+i{\theta }_1\phi )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}\hfill \\ \hfill {\mathbb{T}}_{xy}^{\alpha }u& =& [{\mu }_1{\mu }_2{\phi }^{″}-i({\theta }_1{\mu }_2+{\theta }_2{\mu }_1){\phi }^{\prime }-{\theta }_1{\theta }_2\phi ]e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \end{array}$$

we get for the imaginary part:

$${\mu }_3=a({\theta }_1{\mu }_2+{\theta }_2{\mu }_1),$$

and for the real part:

$$a{\mu }_1{\mu }_2{\phi }^{″}-2b{\theta }_1{\phi }^3{e}^{(-2\sigma \mathcal{W}(t)-2{\sigma }^{2}t)}-({\theta }_1{\theta }_2+{\theta }_3)\phi =0.$$

(5)

We get by taking expectation $\mathbb{E}(·)$:

$$a{\mu }_1{\mu }_2{\phi }^{″}-2b{\theta }_1{\phi }^3{e}^{-2{\sigma }^{2}t}\mathbb{E}(e^{-2\sigma \mathcal{W}(t)})-({\theta }_1{\theta }_2+{\theta }_3)\phi =0.$$

(6)

Since $\mathcal{W}(t)$ is a standard Gaussian process, $\mathbb{E}(e^{\lambda \mathcal{W}(t)})=e^{\frac{{\lambda }^2}{2}t}$ for any real constant $\lambda .$ Now, Equation (6) becomes:

$${\phi }^{″}-{\ell }_1{\phi }^3-{\ell }_2\phi =0,$$

(7)

where:

$${\ell }_1=\frac{2b{\theta }_1}{a{\mu }_1{\mu }_2}\mathrm{and}{\ell }_2=\frac{{\theta }_1{\theta }_2+{\theta }_3}{a{\mu }_1{\mu }_2}.$$

(8)

To calculate the value of the parameter N, which will be needed later in this paper, we balance ${\phi }^3$ with ${\phi }^{″}$ in Equation (7) to get:

$$N=1.$$

(9)

4. The Exact Solutions of the SFKMNE

To achieve the solutions of Equation (7), we employ two various methods, i.e., the Jacobi elliptic function [6] and the $(G^{\prime }/G)$-expansion method [13]. Therefore, we get the exact solutions of the SFKMNE (1).

4.1. The Jacobi Elliptic Function Method

We assume the solutions of Equation (7) has the following form (with $N=1$):

$$\phi (\mu )=a+bsn(\delta \mu ),$$

(10)

where $sn(\delta \mu )=sn(\delta \mu ,m)$ is the Jacobi elliptic sine function for $0<m<1$ and $a,b$, $\delta$ are undefined constants. By differentiating Equation (10) two times, we get:

$${\phi }^{″}(\mu )=-(m^2+1)b{\delta }^{2}sn(\delta \mu )+2m^{2}b{\delta }^{2}s{n}^3(\delta \mu ).$$

(11)

Plugging Equations (10) and (11) into Equation (7), we have:

$$(2m^{2}b{\delta }^2-{\ell }_1{b}^3)s{n}^3(\delta \mu )-3{\ell }_{1}a{b}^{2}s{n}^2(\delta \mu )$$

$$-[(m^2+1)b{\delta }^2+3{\ell }_1{a}^{2}b+{\ell }_{2}b]sn(\delta \mu )-({\ell }_1{a}^3+a{\ell }_2)=0.$$

Balancing coefficient of ${[sn(\delta \mu )]}^k$ to zero for $k=0,1,2,3$, we have:

$${\ell }_1{a}^3+a{\ell }_2=0,$$

$$(m^2+1)b{\delta }^2+3{\ell }_1{a}^{2}b+{\ell }_{2}b=0,$$

$$3{\ell }_{1}a{b}^{2}s{n}^2=0,$$

and:

$$2m^{2}b{\delta }^2-{\ell }_1{b}^3=0.$$

When we solve the previously mentioned equations, we get:

$$a=0,b=\pm \sqrt{\frac{-2m^2{\ell }_2}{(m^2+1){\ell }_1}}{\delta }^2=\frac{-{\ell }_2}{(m^2+1)}.$$

Thus, the solution of Equation (7), by using (10), is:

$$\phi (\mu )=\pm \sqrt{\frac{-2m^2{\ell }_2}{(m^2+1){\ell }_1}}sn(\frac{-{\ell }_2}{(m^2+1)}\mu ).$$

Therefore, the solutions of SFKMNE (1) have the form:

$$u(x,y,t)=\pm \sqrt{\frac{-2m^2{\ell }_2}{(m^2+1){\ell }_1}}sn\left(\sqrt{\frac{-{\ell }_2}{(m^2+1)}}\mu \right)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(12)

for ${\ell }_2<0$ and ${\ell }_1>0.$ If $m\to 1$, then the solution of Equation (12) becomes:

$$u(x,y,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}tanh\left(\sqrt{\frac{-{\ell }_2}{2}}\mu \right)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(13)

Similarly, we can change $sn$ in (10) by $dn$ and $cn$ to attain the following solutions of Equation (7):

$$\phi (\mu )=\pm \sqrt{\frac{2m^2{\ell }_2}{(2-m^2){\ell }_1}}dn(\frac{-{\ell }_2}{(2-m^2)}\mu ),$$

and:

$$\phi (\mu )=\pm \sqrt{\frac{-2m^2{\ell }_2}{(2m^2-1){\ell }_1}}cn(\frac{-{\ell }_2}{(2m^2-1)}\mu ),$$

respectively. Therefore, the SFKMNE (1) has the following solutions:

$$u(x,y,t)=\pm \sqrt{\frac{-2m^2{\ell }_2}{(2m^2-1){\ell }_1}}dn\left(\sqrt{\frac{-{\ell }_2}{(2m^2-1)}}\mu \right)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(14)

for ${\ell }_2<0$, ${\ell }_1>0,$ and:

$$u(x,y,t)=\pm \sqrt{\frac{-2m^2{\ell }_2}{(2m^2-1){\ell }_1}}cn\left(\sqrt{\frac{-{\ell }_2}{(2m^2-1)}}\mu \right)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(15)

for $\frac{{\ell }_2}{(2m^2-1)}<0$, ${\ell }_1>0$. If $m\to 1$, then the solutions (14) and (15) take the form:

$$u(x,y,t)=\pm \sqrt{\frac{-2{\ell }_2}{{\ell }_1}}\sec \mathrm{h}\left(\sqrt{-{\ell }_2}\mu )\right)e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(16)

for ${\ell }_2<0$, ${\ell }_1>0.$

4.2. The $(G^{\prime }/G)$-Expansion Method

We apply here the $(G^{\prime }/G)$-expansion method [13] to find the solutions of Equation (7). As a result, we have the solutions of the SFKMNE (1). To start, let us suppose that the solutions of (7) have the form (with $N=1$):

$$\phi ={\hslash }_0+{\hslash }_1\frac{G^{\prime }}{G},$$

(17)

where G solves:

$$G^{″}+\lambda G^{\prime }+\nu G=0,$$

(18)

where $\lambda ,\nu$ are undefined constants. Putting Equation (17) into Equation (7) and using Equation (18), we obtain:

$$\begin{array}{ccc}& & (2{\hslash }_1-{\ell }_1{\hslash }_1^3){[\frac{G^{\prime }}{G}]}^3+(3\lambda {\hslash }_1-3{\ell }_1{\hslash }_0{\hslash }_1^2){[\frac{G^{\prime }}{G}]}^2\hfill \\ & & +({\lambda }^2{\hslash }_1+2{\hslash }_1\nu -3{\ell }_1{\hslash }_1{\hslash }_0^2-{\ell }_2{\hslash }_1)[\frac{G^{\prime }}{G}]\hfill \end{array}$$

$$+(\nu \lambda {\hslash }_1-{\ell }_1{\hslash }_0^2{\hslash }_1-{\ell }_2{\hslash }_0)=0.$$

Equating each coefficient of ${[\frac{G^{\prime }}{G}]}^k$ by zero for $k=0,1,2,3$, we attain:

$$2{\hslash }_1-{\ell }_1{\hslash }_1^3=0,$$

$$3\lambda {\hslash }_1-3{\ell }_1{\hslash }_0{\hslash }_1^2=0,$$

$${\lambda }^2{\hslash }_1+2{\hslash }_1\nu -3{\ell }_1{\hslash }_1{\hslash }_0^2-{\ell }_2{\hslash }_1=0,$$

and:

$$\nu \lambda {\hslash }_1-{\ell }_1{\hslash }_0^3-{\ell }_2{\hslash }_0=0.$$

Solving this system, we have:

$${\hslash }_1=\pm \sqrt{\frac{2}{{\ell }_1}},\lambda =\lambda ,{\hslash }_0=\pm \frac{\lambda }{\sqrt{2{\ell }_1}},\nu =\frac{{\lambda }^2}{4}+\frac{{\ell }_2}{2}.$$

(19)

The roots of auxiliary Equation (18) are:

$$(\frac{-\lambda }{2}\pm \sqrt{\frac{-{\ell }_2}{2}}).$$

There are three cases for solutions of Equation (18) rely on the value of ${\ell }_2.$

Case 1.

If ${\ell }_2=0$, then:

$$G(\mu )=c_{1}exp(\frac{-\lambda }{2}\mu )+c_2\mu exp(\frac{-\lambda }{2}\mu ),$$

where $c_1,c_2$ are constants. Hence, the solution of Equation (7), by using Equation (17), is:

$$\phi (\mu )=\pm \frac{\lambda }{\sqrt{2{\ell }_1}}\pm \sqrt{\frac{2}{{\ell }_1}}[\frac{-\lambda }{2}+\frac{c_{2}exp(\frac{-\lambda }{2}\mu )}{c_{1}exp(\frac{-\lambda }{2}\mu )+c_2\mu exp(\frac{-\lambda }{2}\mu )}].$$

(20)

Consequently, the SFKMNE (1) has the exact solution:

$$u(x,y,t)=\pm \{\frac{\lambda }{\sqrt{2{\ell }_1}}+\sqrt{\frac{2}{{\ell }_1}}[\frac{-\lambda }{2}+\frac{c_{2}exp(\frac{-\lambda }{2}\mu )}{c_{1}exp(\frac{-\lambda }{2}\mu )+c_2\mu exp(\frac{-\lambda }{2}\mu )}]\}{e}^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(21)

where $\mu =\frac{{\mu }_1}{\alpha }{x}^{\alpha }+\frac{{\mu }_2}{\alpha }{y}^{\alpha }-a({\theta }_1{\mu }_2+{\theta }_2{\mu }_1)t.$

Case 2.

If ${\ell }_2<0$, then:

$$G(\mu )=c_{1}exp[(\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu ]+c_{2}exp[(\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu ].$$

Therefore, the solution of Equation (7) is:

$$\begin{array}{ccc}\hfill \phi (\mu )& =& \pm \frac{\lambda }{\sqrt{2{\ell }_1}}\pm \sqrt{\frac{2}{{\ell }_1}}[\frac{c_1(\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )}{c_{1}exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )+c_{2}exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}\hfill \\ & & +\frac{c_2(\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}{c_{1}exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )+c_{2}exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}].\hfill \end{array}$$

(22)

Consequently, the solutions of the SFKMNE (1) is:

$$\begin{array}{ccc}\hfill u(x,y,t)& =& \pm \{\frac{\lambda }{\sqrt{2{\ell }_1}}+\sqrt{\frac{2}{{\ell }_1}}[\frac{c_1(\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )}{c_{1}exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )+c_{2}exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}\hfill \\ & & +\frac{c_2(\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}{c_{1}exp((\frac{-\lambda }{2}+\sqrt{\frac{-{\ell }_2}{2}})\mu )+c_{2}exp((\frac{-\lambda }{2}-\sqrt{\frac{-{\ell }_2}{2}})\mu )}]\}{e}^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \end{array}$$

(23)

where $\mu =\frac{{\mu }_1}{\alpha }{x}^{\alpha }+\frac{{\mu }_2}{\alpha }{y}^{\alpha }-a({\theta }_1{\mu }_2+{\theta }_2{\mu }_1)t.$

Case 3.

If ${\ell }_2>0$, then:

$$G(\mu )=exp(\frac{-\lambda }{2}\mu )[c_{1}cos(\sqrt{\frac{{\ell }_2}{2}}\mu )+c_{2}sin(\sqrt{\frac{{\ell }_2}{2}}\mu )].$$

Hence, the solution of Equation (7) is:

$$\phi (\mu )=\pm \frac{\lambda }{\sqrt{2{\ell }_1}}\pm \sqrt{\frac{2}{{\ell }_1}}[\frac{-\lambda }{2}+\frac{-c_1\sqrt{\frac{{\ell }_2}{2}}sin(\sqrt{\frac{{\ell }_2}{2}}\mu )+c_2\sqrt{\frac{{\ell }_2}{2}}cos(\sqrt{\frac{{\ell }_2}{2}}\mu )}{c_{1}cos(\sqrt{\frac{{\ell }_2}{2}}\mu )+c_{2}sin(\sqrt{\frac{{\ell }_2}{2}}\mu )}].$$

(24)

Consequently, the solutions of the SFKMNE (1) is:

$$\begin{array}{ccc}\hfill u(x,y,t)& =& \{\frac{\lambda }{\sqrt{2{\ell }_1}}\pm \sqrt{\frac{2}{{\ell }_1}}[\frac{-\lambda }{2}+\hfill \\ & & +\frac{-c_1\sqrt{\frac{{\ell }_2}{2}}sin(\sqrt{\frac{{\ell }_2}{2}}\mu )+c_2\sqrt{\frac{{\ell }_2}{2}}cos(\sqrt{\frac{{\ell }_2}{2}}\mu )}{c_{1}cos(\sqrt{\frac{{\ell }_2}{2}}\mu )+c_{2}sin(\sqrt{\frac{{\ell }_2}{2}}\mu )}]\}{e}^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},\hfill \end{array}$$

(25)

where $\mu =\frac{{\mu }_1}{\alpha }{x}^{\alpha }+\frac{{\mu }_2}{\alpha }{y}^{\alpha }-a({\theta }_1{\mu }_2+{\theta }_2{\mu }_1)t.$

Special Cases:

Case 1: If we put $c_2=0$ and $\lambda =0$ in Equation (25), then:

$$u(x,y,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}tan(\sqrt{\frac{{\ell }_2}{2}}\mu )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(26)

Case 2: If we put $c_1=0$ and $\lambda =0$ in Equation (25), then:

$$u(x,y,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}cot(\sqrt{\frac{{\ell }_2}{2}}\mu )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(27)

Case 3: If we put $c_1=c_2=1$ and $\lambda =0$ in Equation (25), then:

$$u(x,y,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}[sec(\sqrt{2{\ell }_2}\mu )+tan(\sqrt{2{\ell }_2}\mu )]e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(28)

Case 4: If we put $c_1=c_2=1$ and $\lambda =\sqrt{2{\ell }_1}$ in Equation (25), then:

$$u(x,y,t)=[\pm 1\mp 2\sqrt{\frac{{\ell }_2}{{\ell }_1}}(\frac{1}{1+cot(\sqrt{2{\ell }_2}\mu )})]e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(29)

Case 5: If we put $c_1=c_2=1$ and $\lambda =-\sqrt{2{\ell }_1}$ in Equation (25), then:

$$u(x,y,t)=[\mp 1\pm 2\sqrt{\frac{{\ell }_2}{{\ell }_1}}(\frac{1}{1+tan(\sqrt{2{\ell }_2}\mu )})]e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(30)

Case 6: If we put $c_1=c_2=1$ and $\lambda =0$ in Equation (23), then:

$$u(x,y,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}tanh(\sqrt{\frac{-{\ell }_2}{2}}\mu )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)}.$$

(31)

Case 7: If we put $c_1=1,c_2=-1$ and $\lambda =0$ in Equation (23), then:

$$u(x,y,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}coth(\sqrt{\frac{-{\ell }_2}{2}}\mu )e^{(i\theta -\sigma \mathcal{W}(t)-{\sigma }^{2}t)},$$

(32)

where $\mu =\frac{{\mu }_1}{\alpha }{x}^{\alpha }+\frac{{\mu }_2}{\alpha }{y}^{\alpha }-a({\theta }_1{\mu }_2+{\theta }_2{\mu }_1)t.$

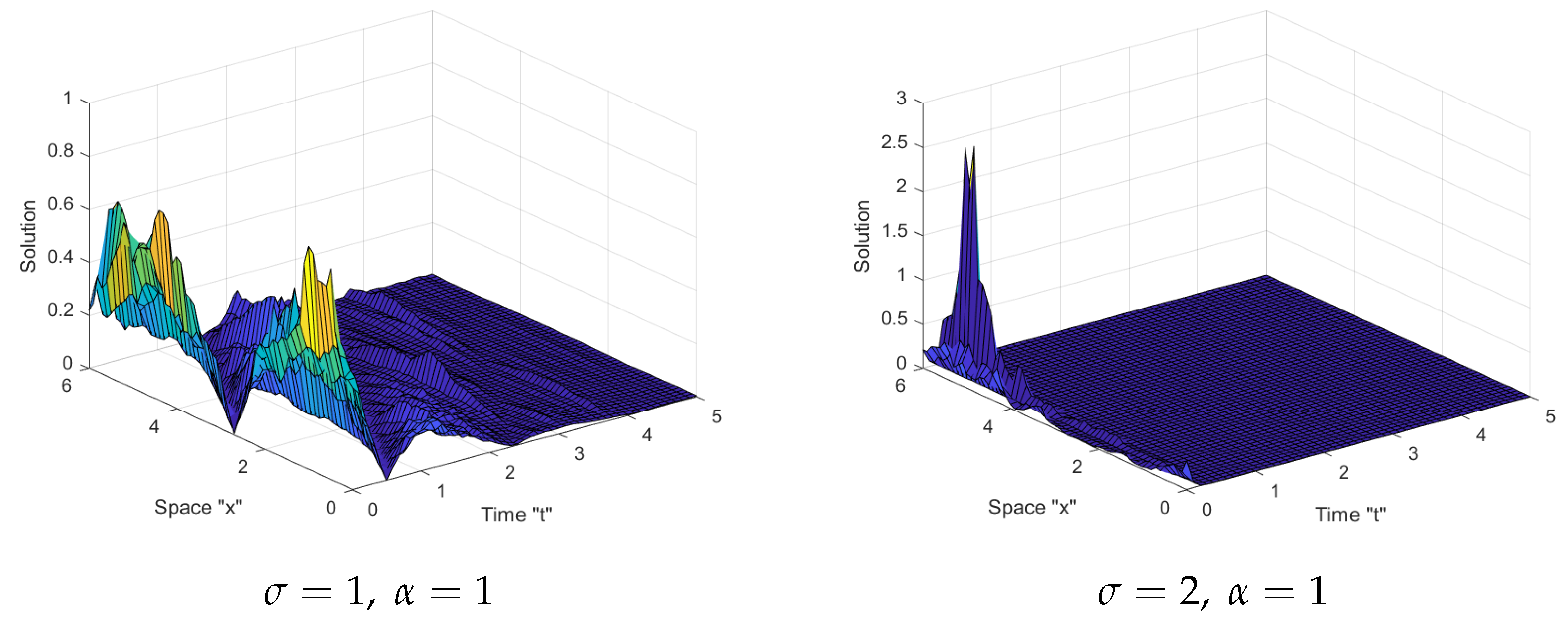
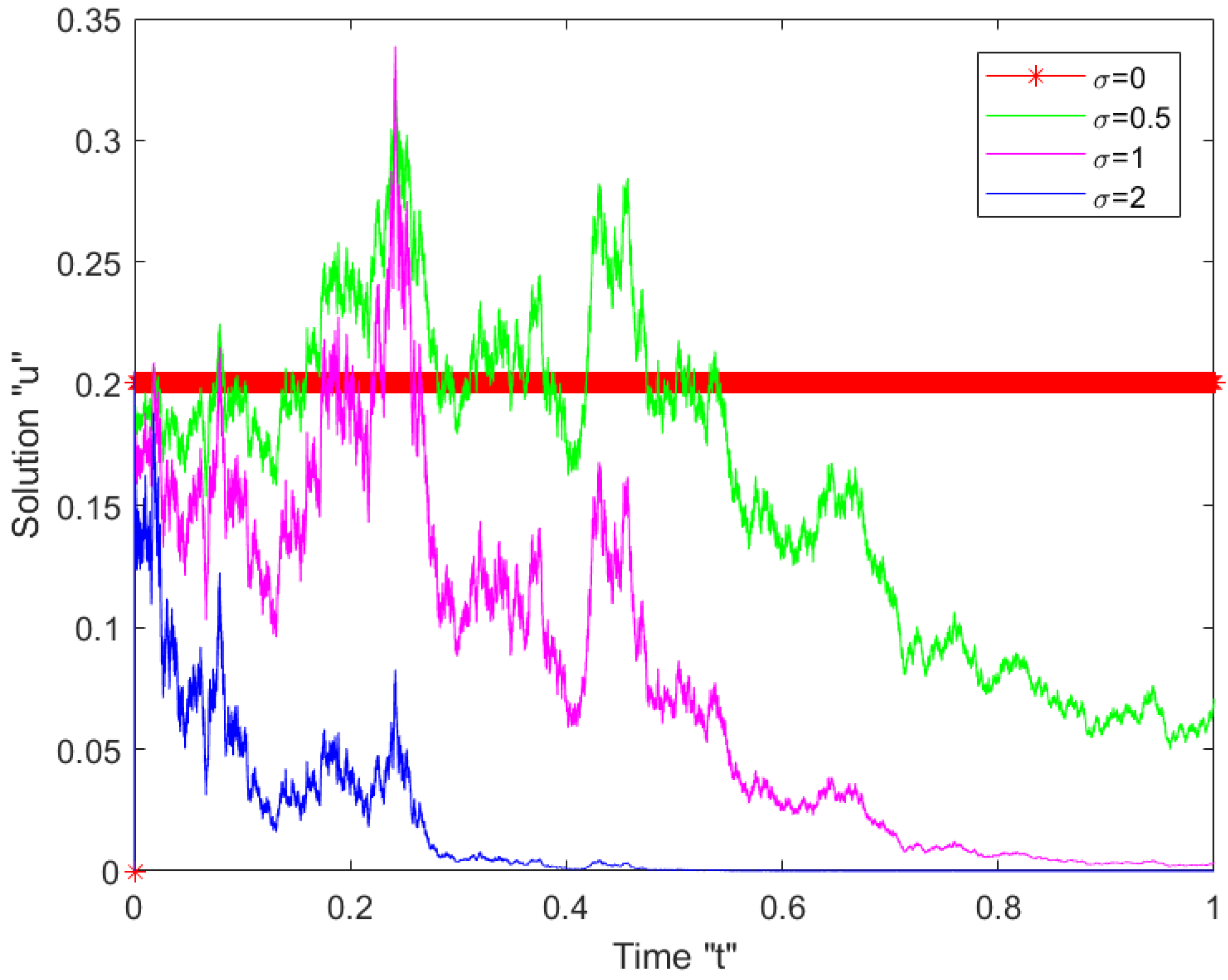
5. The Influence of Noise on SFKMNE Solutions

Here, the influence of noise on the exact solutions of the SFKMNE (1) is discussed. We provide a series of simulations for different values of $\alpha$ (the fractional derivative order) and $\sigma$ (noise intensity). Fix the parameters ${\mu }_1={\mu }_2={\theta }_1={\theta }_2=1,{\theta }_3=-2,m=0.5,$$a=2$ and $b=1$. We use MATLAB tools (see for instance [35]) to plot our figures. In Figure 1 and Figure 2, if $\sigma =0,$ we see that the surface fluctuates for different values of $\alpha$.

While in Figure 2 and Figure 3 below, we observe that after small transit patterns, the surface flattens significantly when noise is added and increased $\sigma =1,2$.

In Figure 4, we present a 2D graph of the u in (12) with $\sigma =0,0.5,1,2$ and with $\alpha =1$, which emphasize the results above.

6. Conclusions

We presented a broad range of exact solutions to the stochastic fractional Kundu–Mukherjee–Naskar model (1). We applied two different methods, i.e., the Jacobi elliptic function method and the $(G^{\prime }/G)$-expansion, to acquire elliptic, hyperbolic, trigonometric and rational stochastic fractional solutions. Such solutions are vital for appreciating some basically difficult complex phenomena. The obtained solutions will be highly beneficial for future investigations, such as ion-acoustic waves, oceanic rogue waves and optical fiber wave propagation in a magnetized plasma. Finally, the effect of noise on the analytical solution of the SFKMNE (1) is demonstrated. Since the multiplicative noise was addressed in this article, we may consider the additive noise in future work.