Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions
Abstract
:1. Introduction
2. An Analysis of the Inverse Coefficient Problem with Measured Data
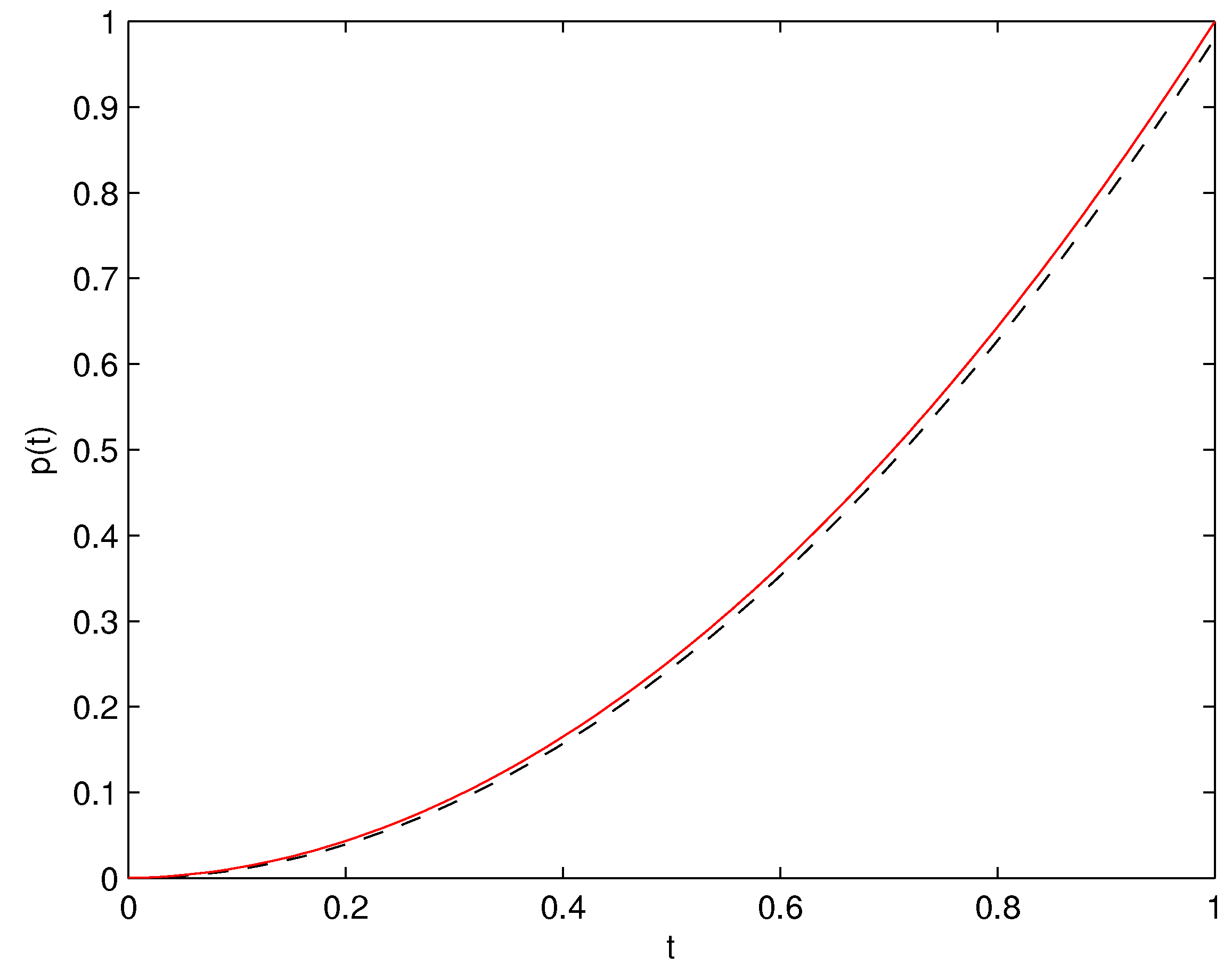
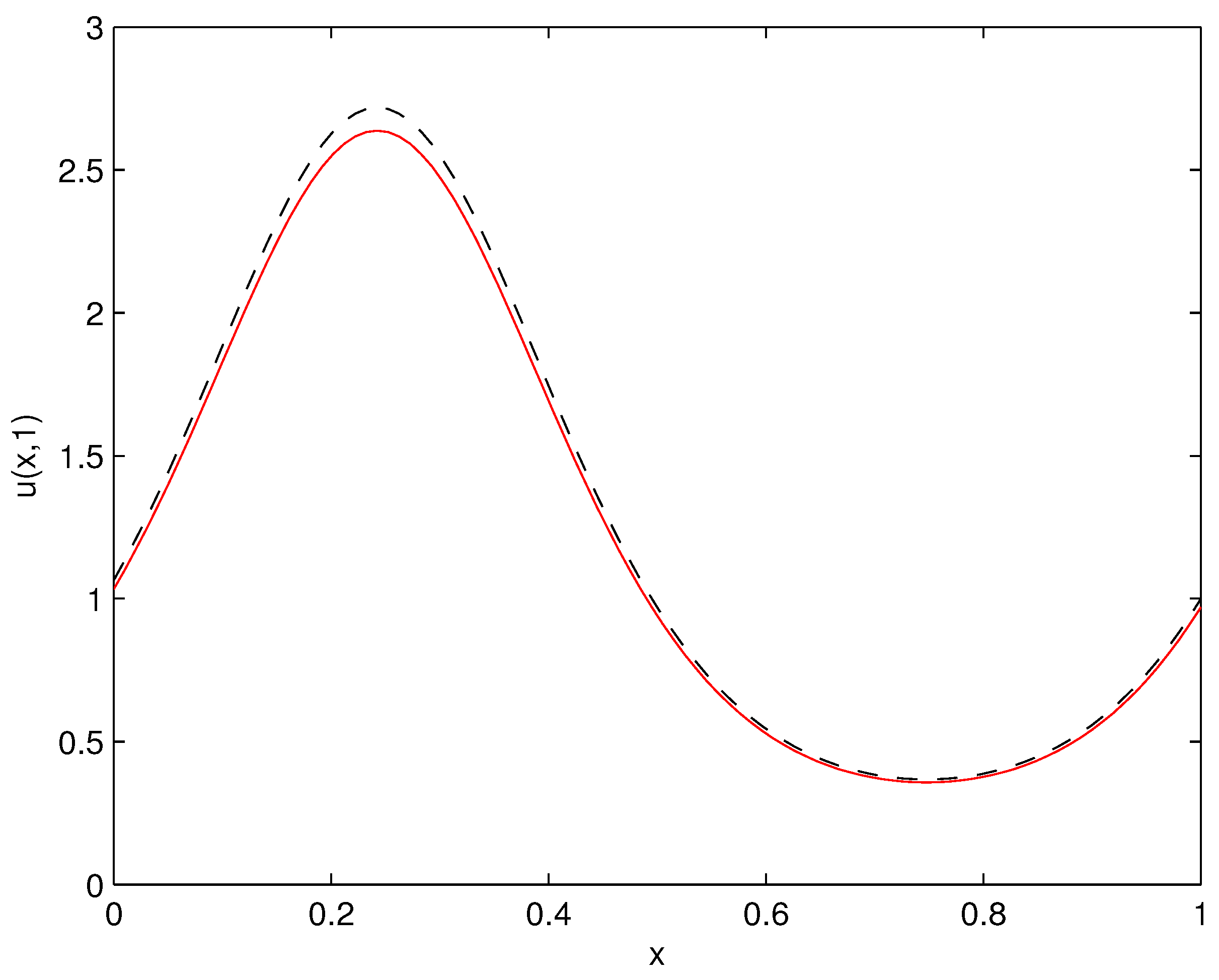
3. Numerical Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, T.; Zhang, Z.Q. Reconstruction of a time-dependent source term in a time-fractional diffusion equation. Eng. Anal. Bound. Elem. 2013, 37, 23–31. [Google Scholar] [CrossRef]
- Caepinteri, A.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Li, Z.; Yamamoto, M. Uniqueness for inverse problems of determining orders of multi-term time-fractional derivatives of diffusion equation. Appl. Anal. 2015, 94, 570–579. [Google Scholar] [CrossRef] [Green Version]
- Djrbashian, M.M. Differential operators of fractional order and boundary value problems in the complex domain. In The Gohberg Anniversary Collection; Springer: Berlin/Heidelberg, Germany, 1989; pp. 153–172. [Google Scholar]
- Mittag-Leffler, G.M. Sur la nouvelle fonction eα (x). CR Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Humbert, P. Quelques résultats relatifs à la fonction de mittag-leffler. C. R. Hebd. Des Seances Acad. Des Sci. 1953, 236, 1467–1468. [Google Scholar]
- Cannon, J.R.; Lin, Y. Determination of source parameter in parabolic equations. Mechanica 1992, 27, 85–94. [Google Scholar] [CrossRef]
- Dehghan, M. Identification of a time-dependent coefficient in a partial differential equation subject to an extra measurement. Numer. Methods Partial. Differ. Equ. 2004, 21, 621–622. [Google Scholar] [CrossRef]
- Luchko, Y. Initial boundary value problems for the one dimensional time-fractional diffusion equation. Frac. Calc. Appl. Anal. 2012, 15, 141–160. [Google Scholar] [CrossRef] [Green Version]
- Ozbilge, E. Identification of the unknown diffusion coefficient in a quasi-linear parabolic equation by semigroup approach with mixed boundary conditions. Math. Meth. Appl.Sci. 2008, 31, 1333–1344. [Google Scholar] [CrossRef]
- Renardy, M.; Rogers, R.C. An Introduction to Partial Differential Equations; Springer: New York, NY, USA, 2004. [Google Scholar]
- Showalter, R.E. Monotone Operators in Banach Spaces and Nonlinear Partial Differential Equations; American Mathematical Society: Waltham, MA, USA, 1997. [Google Scholar]
- Wei, H.; Chen, W.; Sun, H.; Li, X. A coupled method for inverse source problem of spatial fractional anomalous diffusion equations. Inverse Probl. Sci. Eng. 2010, 18, 945–956. [Google Scholar] [CrossRef]
- Chen, W.; Fu, Z.J. Boundary particle method for inverse cauchy problems of inhomogeneous helmholtz equations. J. Mar. Sci. Technol. 2009, 17, 157–163. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, X. Inverse source problem for a fractional diffusion equation. Inverse Probl. 2011, 27, 035010. [Google Scholar] [CrossRef]
- Francesco, M.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. arXiv 2007, arXiv:0702419. [Google Scholar]
- Gorenflo, R.; Mainardi, F.; Moretti, D.; Paradisi, P. Time fractional diffusion: A discrete random walk approach. Nonlinear Dyn. 2002, 29, 129–143. [Google Scholar] [CrossRef]
- Plociniczak, L. Analytical studies of a time-fractional porous medium equation. Derivation, approximation and applications. Commun. Nonlinear Sci. Num. Simul. 2015, 24, 169–183. [Google Scholar] [CrossRef] [Green Version]
- Baglan, I. Determination of a coefficient in a quasilinear parabolic equation with periodic boundary condition. Inverse Probl. Sci. Eng. 2015, 23, 884–900. [Google Scholar] [CrossRef]
- Ozbilge, E.; Demir, A. Identification of unknown coefficient in time fractional parabolic equation with mixed boundary conditions via semigroup approach. Dynam. Syst. Appl. 2015, 24, 341–348. [Google Scholar]
- Ozbilge, E.; Demir, A. Inverse problem for a time-fractional parabolic equation. J. Inequal. Appl. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Ozbilge, E.; Demir, A. Semigroup approach for identification of the unknown diffusion coefficient in a linear parabolic equation with mixed output data. Bound. Value Probl. 2013, 2013, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Özkum, G.; Demir, A.; Erman, S.; Korkmaz, E.; Özgür, B. On the inverse problem of the fractional heat-like partial differential equations: Determination of the source function. Adv. Math. Phys. 2013, 2013, 476154. [Google Scholar] [CrossRef] [Green Version]
- Ozbilge, E.; Demir, A. Identification of the unknown coefficient in a quasi-linear parabolic equation by a semigroup approach. J. Inequal. Appl. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Ozbilge, E.; Demir, A. Distinguishability of a source function in a time fractional inhomogeneous parabolic equation with robin boundary condition. Hacet. J. Math. Stat. 2018, 47, 1503–1511. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A.; Ozbilge, E. An improved version of residual power series method for space-time fractional problems. Adv. Math. Phys. 2022, 2022, 6174688. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A.; Ozbilge, E. A novel approach for the solution of fractional diffusion problems with conformable derivative. Numer. Methods Partial. Differ. Equ. 2021, 1–18. [Google Scholar] [CrossRef]
- Demir, A.; Bayrak, M.A.; Ozbilge, E. A new approach for the approximate analytical solution of space-time fractional differential equations by the homotopy analysis method. Adv. Math. Phys. 2019, 2019, 5602565. [Google Scholar] [CrossRef] [Green Version]
- Cetinkaya, S.; Demir, A. Diffusion equation including a local fractional derivative and weighted inner product. J. Appl. Math. Comput. Mech. 2022, 21, 19–27. [Google Scholar] [CrossRef]
- Bulut, A.; Hacioglu, I. The energy of all connected cubic circulant graphs. Linear Multilinear Algebra 2020, 68, 679–685. [Google Scholar] [CrossRef]
- Bulut, A.; Hacioglu, I. Asymptotic energy of connected cubic circulant graphs. Akce Int. J. Graphs Comb. 2021, 18, 25–28. [Google Scholar] [CrossRef]
- Hacioglu, I.; Bulut, A.; Kaskaloglu, K. The minimal and maximal energies of all cubic circulant graphs. Akce Int. J. Graphs Comb. 2021, 18, 148–153. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozbilge, E.; Kanca, F.; Özbilge, E. Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions. Mathematics 2022, 10, 1479. https://doi.org/10.3390/math10091479
Ozbilge E, Kanca F, Özbilge E. Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions. Mathematics. 2022; 10(9):1479. https://doi.org/10.3390/math10091479
Chicago/Turabian StyleOzbilge, Ebru, Fatma Kanca, and Emre Özbilge. 2022. "Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions" Mathematics 10, no. 9: 1479. https://doi.org/10.3390/math10091479
APA StyleOzbilge, E., Kanca, F., & Özbilge, E. (2022). Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions. Mathematics, 10(9), 1479. https://doi.org/10.3390/math10091479





