Revisiting the Formula for the Ramanujan Constant of a Series

Abstract

The main contribution of this paper is to propose a closed expression for the Ramanujan constant of alternating series, based on the Euler–Boole summation formula. Such an expression is not present in the literature. We also highlight the only choice for the parameter a in the formula proposed by Hardy for a series of positive terms, so the value obtained as the Ramanujan constant agrees with other summation methods for divergent series. Additionally, we derive the closed-formula for the Ramanujan constant of a series with the parameter chosen, under a natural interpretation of the integral term in the Euler–Maclaurin summation formula. Finally, we present several examples of the Ramanujan constant of divergent series.

1. Introduction

When a series diverges [1], it may still be necessary to obtain assertive information related to that series. A relevant problem, in mathematical physics, is to give meaning to infinities that are obtained from divergent series. Indeed, several summation methods were developed for this purpose. For example, Grandi’s series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}$ has the value $1/2$ attributed under the Abel, Euler, Cesàro, and Borel summation methods [2,3,4]. A widely used method to regularize divergent series, whose systematic approach was given by G.H. Hardy [2], uses the theory of zeta functions [5,6,7]. Riemann’s zeta function $\zeta \left(s\right)$, defined by ${\sum }_{n=1}^{\infty }{n}^{-s}$, arises in many areas of mathematics, and it is a very interesting object of study (see, for example: [8,9,10]). In this context, another approach is the Ramanujan summation method [11,12,13]. Such a technique establishes a relationship between the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ and a constant $C\left(f\right)$, which S. Ramanujan called “the constant of a series”. Later, Hardy [2] (p. 327) defined it as “the Euler–Maclaurin constant of f”. Such a constant is often known under the name of Ramanujan constant of a series (RCS). Following these concepts, it is desirable that a unique constant should be determined for each divergent series [14,15].

In Chapter VI of his second notebook, Ramanujan introduced formulae for obtaining a constant for a given series [13]. Analogues of these formulae appear in several key works, [2,11,12,16], just to cite a few. However, we note that, sometimes, the values presented as the Ramanujan constant for a given divergent series disagree with those obtained for other summation methods for the same series. Such a fact can be explained by looking at the definition for the RCS given by Hardy [2] (pp. 325–327), where the constant depends on a non-negative real parameter a. The RCS is, therefore, defined as a family of constants, from which, according to Hardy [2] (p. 327), the adequate value of the parameter a should be chosen for each special case studied. Moreover, Hardy [2] (p. 346) and B.C. Berndt [11] (p. 133) noted that the theory regarding the Ramanujan summation “demand great caution in their application” and “readers should keep in mind that his findings frequently lead to incorrect results”, respectively. The objectives of this manuscript are (i) to present the natural choice for the parameter a with which the values obtained for the RCS in the formula proposed by Hardy agree with those obtained for other summations methods, (ii) to present a version of the formula for the RCS with the parameter a selected, and (iii) to give a new closed formula for the RCS for alternating series.

Section 2 introduces the fundamental aspects of the Euler–Maclaurin summation formula (EMSF). Section 3 discusses the adjustment on the formula for the RCS, considering a specific value for the parameter a. Additionally, it presents some examples with the values obtained as a Ramanujan constant agreeing with those obtained for other summation methods, including some new examples. Section 4 addresses the Ramanujan constant for convergent series when the considered parameter a is that adopted in Section 3. Section 5 establishes a version of the Ramanujan constant for alternating series based on the Euler–Boole summation formula (EBSF). Additionally, several examples show the applicability of the proposed approach. Finally, Section 6 outlines the final remarks.

2. The Euler–Maclaurin and the Euler–Boole Summation Formulas

The EMSF is a powerful tool that enables the replacing of a finite sum of a function $f\left(x\right)$ with a combination of the derivatives and the integral of $f\left(x\right)$. This result was derived independently by L. Euler and by C. Maclaurin [17,18,19]. Due to the importance of the EMSF, Hardy dedicated the last chapter in [2] to this topic, where he wrote the expression

$${\displaystyle \sum _{m=1}^{n}f\left(m\right)\sim {\int }_a^{n}f\left(x\right)dx+C+\frac{1}{2}f\left(n\right)+\sum _{r=1}^{\infty }{(-1)}^{r-1}\frac{B_r}{\left(2r\right)!}{f}^{(2r-1)}\left(n\right),}$$

(1)

for a non-negative real parameter a, where $B_r$ denotes the Bernoulli numbers [20,21,22,23]. Note that Formula (1), written according to Hardy’s notation, includes the non-null Bernoulli numbers with positive signs: Hardy considered $B_1=1/6$, $B_2=1/30$, etc. (with a shift when compared with the modern notation). Note that the first Bernoulli number, $1/2$, is also present in Formula (1), with a positive sign, although written separately [2] (pp. 318, 320). It is supposed that the function f is sufficiently regular as x increases and that the magnitude of its kth derivative must decrease when k increases. Hardy called the constant $C=C\left(f\right)$ “the Euler–Maclaurin constant ” related to the function f. Hardy established a relation between C and the Ramanujan summation of the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ (denoted by Hardy as $(\mathfrak{R},a)$), for a non-negative real parameter a, so that

$${\displaystyle f\left(1\right)+f\left(2\right)+\cdots +f\left(x\right)+\cdots =C\left(f\right)(\mathfrak{R},a),}$$

(2)

where x denotes a non-negative real variable [2] (p. 327).

Many different arguments are known to derive the EMSF (see, for example, [2,15,21,23,24,25]). Commonly the EMSF of a function f that is infinitely differentiable is represented either as [3]

$${\displaystyle \sum _{k=b}^{n-1}f\left(k\right)={\int }_b^{n}f\left(x\right)dx-\frac{1}{2}f\left(x\right){|}_b^n+\sum _{m=1}^{\infty }\frac{B_{2m}}{\left(2m\right)!}{f}^{(2m-1)}\left(x\right){|}_b^n,}$$

(3)

for $b,n\in \mathbb{N}$, with $0<b<n$, or as [3]

$${\displaystyle \sum _{k=b}^{n}f\left(k\right)={\int }_b^{n}f\left(x\right)dx+\frac{\left(f\left(n\right)+f\left(b\right)\right)}{2}+\sum _{m=1}^{\infty }\frac{B_{2m}}{\left(2m\right)!}{f}^{(2m-1)}\left(x\right){|}_b^n,}$$

(4)

where the series in Equations (3) and (4) can diverge [2] (p. 320). Since the letter a is reserved to denote the parameter on the formula for the RCS, as written by Hardy [2] (p. 327), in the Equations (3) and (4), we use the letter b at the inferior bound limits of the sum and the integral. For functions f that are only differentiable until some finite order $r\in \mathbb{N}$, the EMSF with remainder can be written as

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{k=b}^{n}f\left(k\right)}& =& {\displaystyle {\int }_b^{n}f\left(x\right)dx+\frac{\left(f\left(n\right)+f\left(b\right)\right)}{2}}\hfill \\ \hfill & & {\displaystyle +\sum _{m=1}^{\lfloor r/2\rfloor }\frac{B_{2m}}{\left(2m\right)!}{f}^{(2m-1)}\left(x\right){|}_b^n-{\int }_b^n\frac{{\overline{B}}_r\left(\{1-x\}\right)}{r!}{f}^{\left(r\right)}\left(x\right)dx,}\hfill \end{array}$$

(5)

where ${\overline{B}}_r(·)$ are the periodic Bernoulli polynomials of index r and period 1 [26,27,28], $\left\{x\right\}:=x-\lfloor x\rfloor$ denotes the fractional part of $x\in \mathbb{R}$, and $\lfloor x\rfloor$ stands for the integer part of $x\in \mathbb{R}$. The remainder term for the EMSF was introduced by S.D. Poisson in 1823 [29]. The expression for the remainder used in Equation (5) appears in [25] (p. 96).

An analogous result of the EMSF, adapted for alternating series, is the EBSF. For an alternating function f that is infinitely differentiable and with derivatives absolutely integrable, it holds that

$${\displaystyle \sum _{m=b}^{n-1}{(-1)}^{m}f(m+h)=\frac{1}{2}\sum _{k=0}^{\infty }\frac{E_k\left(h\right)}{k!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)+{(-1)}^b{f}^{\left(k\right)}\left(b\right)\right),}$$

(6)

for $h\in (0,1)$ and $b\le n-1$, where $E_n\left(x\right)$ are the Euler polynomials [26,30,31]. If the alternating function f is only r times differentiable and $f^{\left(r\right)}$ is integrable on $(b,n)$, then the EBSF can be expressed as

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=b}^{n-1}{(-1)}^{m}f(m+h)}& =& \hfill {\displaystyle \frac{1}{2}\sum _{k=0}^{r-1}\frac{E_k\left(h\right)}{k!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)+{(-1)}^b{f}^{\left(k\right)}\left(b\right)\right)}\\ \hfill & & \hfill {\displaystyle +\frac{1}{2(r-1)!}{\int }_b^n{f}^{\left(r\right)}\left(x\right){\overline{E}}_{r-1}\left(\{h-x\}\right)dx,}\end{array}$$

(7)

where ${\overline{E}}_r(·)$ are the periodic Euler polynomials of index r and period 1. The formula (7) is due to G. Boole [32].

3. Ramanujan Constant of a Series

Ramanujan introduced a summability method in his second notebook, chapter VI (present in the rare book [13], and commented in Chapter 6 of [11]). Hardy [2] (p. 327) considered that the Ramanujan summation had a basis in a version of the EMSF (1). Moreover, he analyzed the consequences coming from a property of a given series called by Ramanujan by the constant of a series: the constant $C(f;a)$, in Equations (1) and (2) [11] (pp. 143–144). In his definition for the RCS [2] (p. 327), Hardy established that the constant depends on $f\left(x\right)$ and on

$${\displaystyle F\left(x\right)={\int }_a^{x}f\left(t\right)dt,}$$

(8)

i.e., it depends on $f\left(x\right)$ and on a non-negative real parameter a, and stated that such a constant gives another definition for the sum of a divergent series. This is a sufficient reason to look with care at the formula for the RCS.

Ramanujan started by writing

$${\displaystyle {\phi }_f\left(x\right)=f\left(1\right)+f\left(2\right)+\cdots +f\left(x\right),}$$

(9)

for describing a kind of interpolation function for the partial sums $s_n={\sum }_{k=1}^{n}f\left(k\right)$ that should satisfy the condition ${\phi }_f\left(0\right)=0$. He probably used a version of the EMSF (1) to write the function ${\phi }_f$ in an asymptotic expansion that can be expressed as

$${\displaystyle {\phi }_f\left(x\right)=C+\int f\left(x\right)dx+\frac{1}{2}f\left(x\right)+\sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(x\right),}$$

(10)

in which, $C=C(f;a)$ appears, that is, the constant that Ramanujan treated “like the center of gravity of a series” [11,13].

In 1995, B. Candelpergher [33] introduced an algebraic framework to define summation methods that can be adapted to cover the method introduced by Ramanujan. More about this algebraic framework can be read in [12,34,35]. Using a version of the EMSF with remainder (5), Candelpergher [12,34] has chosen $a=1$ and, thus, wrote the constant $C_r(f;1)$ as

$${\displaystyle C_r(f;1)=\frac{f\left(1\right)}{2}-\sum _{k=1}^r\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right)+{\int }_1^{\infty }\frac{{\overline{B}}_{2r+1}\left(\left\{x\right\}\right)}{(2r+1)!}{f}^{(2r+1)}\left(x\right)dx.}$$

(11)

Supposing that $f\in C^{\infty }$ and that the integral is convergent for a large enough r, the constant $C_r(f;1)$ does not depend on r and can be written only as $C(f;1)$. Using Formula (11), Candelpergher presented in [12] (p. 5) two initial examples and, for $f\left(x\right)=1$ and $f\left(x\right)=x$, he obtained $C(1;1)=\frac{f\left(1\right)}{2}=\frac{1}{2}$ and $C(x;1)=\frac{1}{2}-\frac{B_2}{2}=\frac{5}{12}$, respectively. However, we verify that the values $-\frac{1}{2}$ and $-\frac{1}{12}$ are assigned to the series ${\sum }_{n=1}^{\infty }1$ and ${\sum }_{n=1}^{\infty }n$, respectively, under the smoothed sum method (see [3] or [36] (pp. 88–104)). In the following, we present the adequate value for the parameter a that permits us to obtain, for the Ramanujan constant of a given divergent series, the same value obtained with other summation methods.

In Chapter XIII of the seminal work [2], specifically in Equations (13.5.9), (13.5.13), and (13.6.4), Hardy wrote the term $-F\left(1\right)$, which was neither included in Formula (11) given in [12] (pp. 4–8), nor in the equivalent formula in [11] (pp. 134–135). This is a kind of overlooked term of the RCS. To recover such a term for a series that does not alternate the sign, we revisit the formulas for the RCS in proposition 1, choosing $a=0$ and giving a natural interpretation for the integral term in the EMSF. To make the contribution more clear, namely the choice of $a=0$ that leads the RCS $C(f;0)$ to agree with the values obtained for other summation methods, we highlight a property satisfying Hardy’s formula for the RCS given in [2] (pp. 325–327), herein denoted by $C(f;a)$, as follows.

Property 1.

The Ramanujan constant of a given series can be obtained by the sum of all constants that do not depend on n in the development of the series under a proper summation formula.

For series ${\sum }_{n=1}^{\infty }f\left(n\right)$ in which the general term does not alternate the sign, the proper summation formula indicated in Property 1 is the EMSF (4) with $b=1$. In this case, the RCS depends on a non-negative real parameter a. For alternating series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}f\left(n\right)$, the proper summation formula is the EBSF (6) with $b=1$.

Proposition 1.

Let ${\sum }_{n=1}^{\infty }f\left(n\right)$ be a series where $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is a function integrable on $(0,n)$ for any $n\in \mathbb{N}$, and, as parameter of the integral (8), choose $a=0$. If the function f is only r times differentiable and if $\left({\overline{B}}_r\left(\{1-x\}\right)\right)f^{\left(r\right)}\left(x\right)$ is integrable on $(0,n)$ for any $n\in \mathbb{N}$, where ${\overline{B}}_r(·)$ are the periodic Bernoulli polynomials of index r, then the Ramanujan constant of the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ depending on r and with the parameter $a=0$ is given by

$${\displaystyle C_r(f;0)=-{\int }_0^{1}f\left(x\right)dx+\frac{f\left(1\right)}{2}-\sum _{k=1}^{\lfloor r/2\rfloor }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right)+{\int }_0^1\frac{B_r(1-x)}{r!}{f}^{\left(r\right)}\left(x\right)dx,}$$

(12)

where $B_r(·)$ are the Bernoulli polynomials of index r and $B_{2k}$ are the Bernoulli numbers.

If $f\in C^{\infty }$ and the series ${\sum }_{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right)$ is convergent, then the Ramanujan constant of the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ with the parameter $a=0$ is given as

$${\displaystyle C(f;0)=-{\int }_0^{1}f\left(x\right)dx+\frac{f\left(1\right)}{2}-\sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right).}$$

(13)

Proof. 

We look at the integral term ${\int }_b^{n}f\left(x\right)dx$ in the EMSF (5), using the fundamental theorem of calculus as follows. Let F be the primitive of f on $(0,n)$ that vanishes in $x=0$, i.e.,

$${\displaystyle {\int }_b^{n}f\left(x\right)dx=F\left(x\right){|}_b^n=F\left(n\right)-F\left(b\right),\mathrm{where}F\mathrm{satisfies}F\left(0\right)=0.}$$

(14)

Then, we can write

$${\displaystyle {\int }_b^{n}f\left(x\right)dx=F\left(n\right)-F\left(b\right)=\left(F\left(n\right)-F\left(0\right)\right)-\left(F\left(b\right)-F\left(0\right)\right)={\int }_0^{n}f\left(x\right)dx-{\int }_0^{b}f\left(x\right)dx}$$

(15)

and, choosing $b=1$, with the purpose of arriving at a formula for $C(f;0)$, we rewrite the EMSF (5) as

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{k=1}^{n}f\left(k\right)}& =& {\displaystyle C_r(f;0)+{\int }_0^{n}f\left(x\right)dx+\frac{f\left(n\right)}{2}}\hfill \\ \hfill & & {\displaystyle +\sum _{k=1}^{\lfloor r/2\rfloor }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(n\right)-{\int }_0^n\frac{{\overline{B}}_r\left(\{1-x\}\right)}{r!}{f}^{\left(r\right)}\left(x\right)dx,}\hfill \end{array}$$

(16)

where

$${\displaystyle C_r(f;0)=-{\int }_0^{1}f\left(x\right)dx+\frac{f\left(1\right)}{2}-\sum _{k=1}^{\lfloor r/2\rfloor }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right)+{\int }_0^1\frac{{\overline{B}}_r\left(\{1-x\}\right)}{r!}{f}^{\left(r\right)}\left(x\right)dx}$$

(17)

is a constant satisfying the Property 1.

Taking $n\to \infty$, we arrive at

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{k=1}^{\infty }f\left(k\right)}& =& \hfill {\displaystyle C_r(f;0)+{\int }_0^{\infty }f\left(x\right)dx+\underset{n\to \infty }{lim}\left(\frac{f\left(n\right)}{2}+\sum _{k=1}^{\lfloor r/2\rfloor }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(n\right)\right)}\\ \hfill & & \hfill {\displaystyle -{\int }_0^{\infty }\frac{{\overline{B}}_r\left(\{1-x\}\right)}{r!}{f}^{\left(r\right)}\left(x\right)dx,}\end{array}$$

(18)

where the Ramanujan constant $C_r(f;0)$ depending on r of the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ is given in (17). Replacing the last integral in (17) by ${\int }_0^1\frac{B_r(1-x)}{r!}{f}^{\left(r\right)}\left(x\right)dx$, we obtain Formula (12).

The bound limits of the integral in the remainder terms in Equations (16) and (17) are proposed under the same argument as for the primitive F for f, which should vanish at $x=0$. Observe that, in Equation (17), all derivatives are evaluated at $x=1$, whereas the primitives are evaluated at $x=1$ and vanish at $x=0$, respecting the numeric character of the constant.

When the function f is infinitely differentiable, the remainder term does not appears in Equations (16) and (17). If the series ${\sum }_{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right)$ is convergent, then it is possible to write ${\displaystyle C(f;0)=\underset{r\to \infty }{lim}{C}_r(f;0)}$ and thus to obtain

$${\displaystyle C(f;0)=-{\int }_0^{1}f\left(x\right)dx+\frac{f\left(1\right)}{2}-\sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}{f}^{(2k-1)}\left(1\right),}$$

(19)

the formula given in (13) for the RCS.

To apply Equation (12) or Equation (13), we must evaluate ${\int }_0^{1}f\left(x\right)dx$ using the primitive F of the function f, which vanishes at $x=0$. □

Remark 1.

Proposition 1 presents Formula (12) for the constant $C_r(f;0)$ that depends on r, but such a constant may not be a good approximation for the RCS $C(f;0)$ for low orders r due to the presence of the remainder term ${\int }_0^1\frac{B_r(1-x)}{r!}{f}^{\left(r\right)}\left(x\right)dx$.

With the formulae (12) and (13) for the RCS, obtained with the choice of $a=0$ for the parameter, the Ramanujan summation is now useful for obtaining constants for divergent series that agree with those obtained from others summation methods.

In the following, we revisit the two previous examples by applying Formula (13).

Example 1.

The series ${\sum }_{n=1}^{\infty }1$ and ${\sum }_{n=1}^{\infty }{n}^s$ for $s\ge 1$.

For ${\sum }_{n=1}^{\infty }1$, where $f\left(n\right)=1$, we obtain

$${\displaystyle C(1;0)=-{\int }_0^{1}dx+\frac{f\left(1\right)}{2}=-\left(x\right){|}_0^1+\frac{1}{2}=-1+\frac{1}{2}=-\frac{1}{2}.}$$

(20)

For ${\sum }_{n=1}^{\infty }n$, where $f\left(n\right)=n$, we obtain

$${\displaystyle C(n;0)=-{\int }_0^{1}xdx+\frac{f\left(1\right)}{2}-\frac{B_2}{2}=-\left(\frac{x^2}{2}\right){|}_0^1+\frac{1}{2}-\frac{B_2}{2}=-\frac{1}{12}.}$$

(21)

The values now given to the Ramanujan constant for the series ${\sum }_{n=1}^{\infty }1$ and ${\sum }_{n=1}^{\infty }n$ under Formula (13) are the expected values, agreeing with the those obtained under other summation methods. Applying Formula (13), we obtain

$${\displaystyle C(n^2;0)=0;C(n^3;0)=\frac{1}{120};\cdots }$$

(22)

Remark 2.

Two desired properties for a given summation method are shift-invariance and linearity. We observe that the RCS is linear, but it is not shift-invariant. Since Formulae (12) and (13) are composed of a combination of linear operators acting on f, then $C(f;0)$ has the property of linearity. However, the RCS in Expression (20) serves as a counterexample for the shift-invariance of $C(f;0)$. If the series ${\sum }_{n=1}^{\infty }1$, for which $C(1;0)=-\frac{1}{2}$, was invariant, we would have

$${\displaystyle \sum _{n=1}^{\infty }{a}_n=a_1+\sum _{n=2}^{\infty }{a}_n=a_1+\sum _{n=1}^{\infty }{a}_{n+1}\Rightarrow \sum _{n=1}^{\infty }1=1+\sum _{n=1}^{\infty }1,}$$

(23)

that is, in terms of $C(0;1)$, we would have

$$C(1;0)=1+C(1;0)\Rightarrow =-\frac{1}{2}=1-\frac{1}{2},$$

(24)

an absurd.

For the next example, the following lemma is necessary:

Lemma 1.

The series ${\displaystyle \sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}}$ is convergent.

The well known Lemma 1 can be proved using the convergence of the series

$${\displaystyle \sum _{k=0}^{\infty }\frac{B_k}{k!}{t}^n=\frac{t}{e^t-1}}$$

(25)

for all t such that $\left|t\right|<2\pi$, or using the approximation $|B_{2k}|\sim 4\sqrt{\pi k}{\left(\frac{k}{\pi e}\right)}^{2k}$, valid for large k (and when $k\to \infty$) [37] (p. 143), after applying the ratio test for series.

Example 2.

The series ${\sum }_{n=1}^{\infty }{e}^{n-1}$ and ${\sum }_{n=1}^{\infty }{e}^n$.

We start by computing the constant $C(f;0)$ for the series ${\sum }_{n=1}^{\infty }{e}^{n-1}$.

For the term $-F\left(x\right)$, we calculate $F\left(x\right)=\int e^{x-1}dx=e^{x-1}+c$ and, imposing the condition $F\left(0\right)=0$, we arrive at $F\left(x\right)=e^{x-1}-e^{-1}$. Thus, we obtain

$${\displaystyle F\left(1\right)={\int }_0^1{e}^{x-1}dx=\frac{e-1}{e}.}$$

(26)

The term $f\left(1\right)/2$ returns the value $1/2$. The derivatives return $f^{\left(n\right)}\left(1\right)=e^0=1$ for all $n\in \mathbb{N}$.

Then, using Formula (13), we obtain

$${\displaystyle C(e^{n-1};0)=-\frac{e-1}{e}+\frac{1}{2}-\sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}.}$$

(27)

From Lemma 1, the last series is convergent, and, then, a numerical approximation to $C(e^{(n-1)};0)$ can be obtained:

$${\displaystyle C(e^{n-1};0)\approx -0.2140972662.}$$

(28)

For the constant $C(f;0)$ for the series ${\sum }_{n=1}^{\infty }{e}^n$, we can evaluate the constant $C(e^n;0)$ by choosing to apply Formula (13) or to use the linearity of the RCS, taking ${\sum }_{n=1}^{\infty }{e}^n$ = $e{\sum }_{n=1}^{\infty }{e}^{n-1}$. In both cases, we arrive at

$${\displaystyle C(e^n;0)\approx -0.5819767082.}$$

(29)

Unfortunately, just like other summation methods, the Ramanujan summation cannot apply to all divergent series. One example of a series that is not summable under the RCS is the harmonic series ${\sum }_{n=1}^{\infty }\frac{1}{n}$. In addition to the function $f\left(x\right)=\frac{1}{x}$ not being defined for $x=0$; we cannot evaluate $C(\frac{1}{n};0)$ by Formula (13) because the integral ${\int }_0^1(1/x)dx$ is divergent.

4. Ramanujan Constant for Convergent Series

Ramanujan wrote “if $f\left(1\right)+f\left(2\right)+\cdots +f\left(x\right)$ be a convergent series then its constant is the sum of the series” [13]. In this section, we study the RCS applied to convergent series, when the parameter $a=0$ is chosen, and we conclude that, in this case, the RCS $C(f;0)$ may not be equal to the sum of the series ${\sum }_{n=1}^{\infty }f\left(n\right)$ in the classical sense. However, for such cases, we provide a possible interpretation for $C(f;0)$ applied to convergent series, when the parameter $a=0$ is chosen. Let us start with the following example.

Example 3.

The convergent series ${\sum }_{n=1}^{\infty }(1/2^n)$.

It is known that ${\sum }_{n=1}^{\infty }(1/2^n)=1$.

Considering the function $f\left(x\right)=2^{-x}$ and applying Formula (13) to the series ${\sum }_{n=1}^{\infty }(1/2^n)$, for the term $F\left(x\right)$, we obtain $F\left(x\right)=\int 2^{-x}dx=\frac{2^{-x}}{log\left(2\right)}+c$ and, imposing the condition $F\left(0\right)=0$, we arrive at $F\left(x\right)=\frac{2^{-x}}{log\left(2\right)}+\frac{1}{log\left(2\right)}$. Thus, we obtain

$${\displaystyle F\left(1\right)={\int }_0^1{2}^{-x}dx=\frac{1}{log\left(4\right)}.}$$

(30)

The term $f\left(1\right)/2$ returns the value $1/4$. The derivatives of f are given by $f^{\left(n\right)}\left(x\right)={(-1)}^n{(log(2\left)\right)}^n/2^x$ for all $n\in \mathbb{N}$.

Then, using Formula (13) for the RCS, we obtain

$${\displaystyle C(2^{-n};0)=-\frac{1}{log\left(4\right)}+\frac{1}{4}+\sum _{k=1}^{\infty }\frac{B_{2k}}{\left(2k\right)!}\frac{{(log(2\left)\right)}^{2k-1}}{2},}$$

(31)

where the last series is convergent (it is verifiable by the same argument that proves Lemma 1). A numerical approximation to $C(2^{-n};0)$ evaluates until $k=4$, returning

$${\displaystyle C(2^{-n};0)\approx -0.4426975208,}$$

(32)

a number clearly different to 1, the classical sum of the series ${\sum }_{n=1}^{\infty }1/2^n$.

To gives a clear interpretation for the RCS for a convergent series when the parameter $a=0$ is chosen, we look again at the EMSF (1) and at the RCS Formula (13). For the function $f\left(x\right)=2^{-x}$ and considering $n\to \infty$ in the Formula (1), the only terms remaining are

$$\sum _{m=1}^{\infty }{2}^{-m}\sim {\int }_0^{\infty }{2}^{-x}dx+C,$$

(33)

and we can rewrite

$${\displaystyle C\sim \sum _{m=1}^{\infty }{2}^{-m}-{\int }_0^{\infty }{2}^{-x}dx=1-\frac{1}{log\left(2\right)}\approx 1-1.4426950408.}$$

(34)

Therefore, the value obtained for the RCS $C(2^{-n};0)$ of the convergent series ${\sum }_{n=1}^{\infty }(1/2^n)$, evaluated by Formula (13), is a good approximation for the difference between the infinite sum of the terms $f\left(n\right)=2^{-n}$, starting at $n=1$, and the improper integral of the function $f\left(x\right)=2^{-x}$, beginning at $x=0$.

This example indicates a possible interpretation of the RCS for a type of convergent series when $a=0$: the RCS $C(f;0)$ can evaluates the difference between the infinite sum of the terms $f\left(n\right)$, starting at $n=1$, and the improper integral of the function $f\left(x\right)$, beginning at $x=0$.

5. Ramanujan Constant for Alternating Series

Hardy [2] (p. 327) states that the Ramanujan summation and RCS are “primarily adapted to series of positive terms”. However, we easily extrapolate this assertion for: “the RCS is adapted to series of terms that do not alternate signs”; indeed, if, in the derivation of the EMSF, we consider all terms $f\left(n\right)$ negative, i.e., $f\left(n\right)=-g\left(n\right)$ for some function $g\left(n\right)\ge 0,\forall n\in \mathbb{N}$, before taking $n\to \infty$ in the derivation of Formulae (12) and (13), it is possible put the negative signs as evidence. This allows us to conclude that $C(f;a)=C(-g;a)=-C(g;a)$.

Example 4.

Series with only negative terms.

Applying Formula (13), or revisiting the previous examples, we can write:

$$\begin{array}{ccc}\hfill C(-1;0)& =& 1/2\hfill \\ \hfill C(-n;0)& =& 1/12\hfill \\ \hfill C(-n^3;0)& =& {\displaystyle -1/120}\hfill \\ \hfill C(-e^n;0)& \approx & 0.5819767082\hfill \\ \hfill C(-2^{-n};0)& \approx & 0.4422377977.\hfill \end{array}$$

(35)

However, since the EMSF is not appropriate for series with alternating terms, Formulae (12) and (13) are also not appropriate for evaluating the RCS for series with alternating terms.

In entries 9 and 10 of Chapter 6 of his VI Notebook [13], Ramanujan approached the constant for alternating series. However, we do not find a clear formula for evaluating the Ramanujan constant of an alternating series (RCAS) anywhere in the literature. In the following, based on the EBSF, we propose a way to evaluate the RCAS. The closed formulae for the RCAS are given in Propositions 2 and 3. We observe that the RCAS does not depend on the parameter a, i.e., a unique constant can be determined as a constant to each alternating series that diverges.

Proposition 2.

Let ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}f\left(n\right)$ be an alternating series, where $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is a function absolutely integrable on $(0,n)$ for any $n\in \mathbb{N}$. If the function f is only r times differentiable and if $\left({\overline{E}}_r\left(\{1-x\}\right)\right)f^{\left(r\right)}\left(x\right)$ is absolutely integrable on $(0,n)$ for any $n\in \mathbb{N}$, then the Ramanujan constant of the alternating series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}f\left(n\right)$ depending on r is given by

$${\displaystyle C_r\left({(-1)}^{n-1}f\left(n\right)\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}\sum _{k=1}^{r-1}\frac{E_k\left(1\right)}{k!}{f}^{\left(k\right)}\left(1\right)-{\int }_0^1\frac{E_{r-1}(1-x)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx,}$$

(36)

where $E_r(·)$ are the Euler polynomials of index r.

Proof. 

We choose the EBSF with remainder (7) and initially rewrite only its left side as

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=b+1}^n{(-1)}^{m-1}f(m-1+h)}& =& \hfill {\displaystyle \frac{1}{2}\sum _{k=0}^{r-1}\frac{E_k\left(h\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)+{(-1)}^b{f}^{\left(k\right)}\left(b\right)\right)}\\ \hfill & & \hfill {\displaystyle +{\int }_b^n\frac{{\overline{E}}_{r-1}\left(\{h-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx.}\end{array}$$

(37)

Then, choosing $b=1$ and considering the extreme case $h=1$, we obtain

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=2}^n{(-1)}^{m-1}f\left(m\right)}& =& \hfill {\displaystyle \frac{1}{2}\sum _{k=0}^{\infty }\frac{E_k\left(1\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)-f^{\left(k\right)}\left(1\right)\right)}\\ \hfill & & \hfill {\displaystyle +{\int }_1^n\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx.}\end{array}$$

(38)

Without a loss of generality, to guarantee that the first term of the alternating series ${\sum }_{m=1}^{\infty }{(-1)}^{m-1}f\left(m\right)$ is positive, we consider that $f\left(n\right)\ge 0,\forall n\in \mathbb{N}$, with $f\left(1\right)>0$. Then, we sum the term $f\left(1\right)$ on both sides of Equation (38), i.e,

$$\begin{array}{ccc}\hfill {\displaystyle f\left(1\right)+\sum _{m=2}^n{(-1)}^{m-1}f\left(m\right)}& =& \hfill {\displaystyle f\left(1\right)+\frac{1}{2}\sum _{k=0}^{\infty }\frac{E_k\left(1\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)-f^{\left(k\right)}\left(1\right)\right)}\\ \hfill & & \hfill {\displaystyle +{\int }_1^n\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx.}\end{array}$$

(39)

After rearranging terms, we arrive at the following EBSF-like formula with remainder

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=1}^n{(-1)}^{m-1}f\left(m\right)}& =& \hfill {\displaystyle \frac{f\left(1\right)}{2}+\frac{{(-1)}^{n-1}f\left(n\right)}{2}+\frac{1}{2}\sum _{k=1}^{\infty }\frac{E_k\left(1\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)-f^{\left(k\right)}\left(1\right)\right)}\\ \hfill & & \hfill {\displaystyle +{\int }_1^n\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx.}\end{array}$$

(40)

Then, since $\left({\overline{E}}_{r-1}\left(\{1-x\}\right)\right)f^{\left(r\right)}\left(x\right)$ is supposed to be absolutely integrable on $(0,n)$ for any $n\in \mathbb{N}$, we can rewrite the integral in the remainder term as

$$\begin{array}{ccc}\hfill {\displaystyle {\int }_1^n\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx}& =& {\displaystyle {\int }_0^n\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx}\hfill \\ \hfill & & {\displaystyle -{\int }_0^1\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx.}\hfill \end{array}$$

(41)

Note that the last integral can be expressed as ${\int }_0^1\frac{E_r(1-x)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx$ because the considered interval is $(0,1)$. Then, we take $n\to \infty$ to obtain

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{k=1}^{\infty }{(-1)}^{m-1}f\left(m\right)}& =& \hfill {\displaystyle C_r\left({(-1)}^{n-1}f\left(n\right)\right)+\frac{1}{2}\underset{n\to \infty }{lim}\left(\sum _{k=0}^{r-1}\frac{E_k\left(1\right)}{k!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)\right)\right)}\\ \hfill & & \hfill {\displaystyle +{\int }_0^{\infty }\frac{{\overline{E}}_{r-1}\left(\{1-x\}\right)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx,}\end{array}$$

(42)

where

$${\displaystyle C_r\left({(-1)}^{n-1}f\left(n\right)\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}\sum _{k=1}^{r-1}\frac{E_k\left(1\right)}{k!}{f}^{\left(k\right)}\left(1\right)-{\int }_0^1\frac{E_{r-1}(1-x)}{2(r-1)!}{f}^{\left(r\right)}\left(x\right)dx}$$

(43)

is the formula for the RCAS depending on r given in Equation (36). □

Proposition 3.

Let ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}f\left(n\right)$ be an alternating series, where $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is a function absolutely integrable on $(0,n)$ for any $n\in \mathbb{N}$. If $f\in C^{\infty }$ and the series ${\sum }_{k=1}^{\infty }\frac{E_k\left(1\right)}{k!}{f}^{\left(k\right)}\left(1\right)$ is convergent, then the Ramanujan constant of the alternating series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}f\left(n\right)$ is given as

$${\displaystyle C\left({(-1)}^{n-1}f\left(n\right)\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}\sum _{k=1}^{\infty }\frac{E_k\left(1\right)}{k!}{f}^{\left(k\right)}\left(1\right),}$$

(44)

where $E_k(·)$ are the Euler polynomials of index k.

Proof. 

Suppose that $f\in C^{\infty }$. We start by rewriting only the left side of Equation (6) as follows:

$${\displaystyle \sum _{m=b+1}^n{(-1)}^{m-1}f(m-1+h)=\frac{1}{2}\sum _{k=0}^{\infty }\frac{E_k\left(h\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)+{(-1)}^b{f}^{\left(k\right)}\left(b\right)\right).}$$

(45)

Then, as in the proof of Proposition 2, choosing $b=1$ and considering $h=1$, supposing that $f\left(n\right)\ge 0,\forall n\in \mathbb{N}$, with $f\left(1\right)>0$, summing $f\left(1\right)$ on both sides and rearranging the terms, we arrive at the EBSF-like formula:

$${\displaystyle \sum _{m=1}^n{(-1)}^{m-1}f\left(m\right)=\frac{f\left(1\right)}{2}+\frac{{(-1)}^{n-1}f\left(n\right)}{2}+\frac{1}{2}\sum _{k=1}^{\infty }\frac{E_k\left(1\right)}{\left(k\right)!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)-f^{\left(k\right)}\left(1\right)\right).}$$

(46)

Taking $n\to \infty$, we obtain

$${\displaystyle \sum _{k=1}^n{(-1)}^{m-1}f\left(m\right)=C\left({(-1)}^{n-1}f\left(n\right)\right)+\frac{1}{2}\underset{n\to \infty }{lim}\left(\sum _{k=0}^{\infty }\frac{E_k\left(1\right)}{k!}\left({(-1)}^{n-1}{f}^{\left(k\right)}\left(n\right)\right)\right),}$$

(47)

where

$${\displaystyle C\left({(-1)}^{n-1}f\left(n\right)\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}\sum _{k=1}^{\infty }\frac{E_k\left(1\right)}{k!}{f}^{\left(k\right)}\left(1\right)}$$

(48)

is the formula for the RCAS given in Equation (44). □

Example 5.

The Grandi’s series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}$.

For the Grandi’s series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}$, which is an alternating series with first term positive, we can apply Formula (44) to obtain the RCAS. We work with the constant function $f\left(x\right)=1$. We obtain the value $1/2$ for the term $f\left(1\right)/2$. Since the derivatives of $f=1$ are all null, the term $f\left(1\right)/2$ is the single non-null term in Formula (44). We conclude that

$${\displaystyle C\left({(-1)}^{n-1}\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}·0=\frac{1}{2}.}$$

(49)

The same value is recovered for the Grandi’s series under Abel, Euler, Cesàro, and Borel summation methods.

Example 6.

The Euler’s alternating series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}n$.

It is known that the series ${\sum }_{n=1}^{\infty }{(-1)}^{n-1}n$ receives the value $1/4$ under other summability methods, such as the Abel or Euler summability method [3].

Now, we apply Formula (44) for evaluating the constant $C\left({(-1)}^{n-1}n\right)$ of the Euler’s alternating series. The considered function is $f\left(x\right)=x$. We obtain the value $1/2$ for the term $f\left(1\right)/2$, and the derivatives of $f=x$ are all null, except for the first, which returns the value 1. As the Euler polynomial of order 1 evaluated at $x=1$ returns $1/2$, we conclude that

$${\displaystyle C\left({(-1)}^{n-1}n\right)=\frac{f\left(1\right)}{2}-\frac{1}{2}·\frac{1}{2}·1=\frac{1}{2}-\frac{1}{4}=\frac{1}{4}.}$$

(50)

This is the same value obtained for Euler’s alternating series under the Abel and Euler summation methods.

Example 7.

The series of coefficients of the Grünwald–Letnikov fractional derivatives.

For a given function f defined in an interval $I=(a,b)\in \mathbb{R}$, the Grünwald–Letnikov fractional operator of order $\alpha$ is defined as [38,39,40,41]:

$${\displaystyle {}^{GL}{D}_{a,x}^{\alpha }f\left(x\right)=\underset{h\to 0}{lim}\left(\frac{1}{h^{\alpha }}\sum _{k=0}^{\lfloor n\rfloor }\frac{{(-1)}^k\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(k+1)\mathsf{\Gamma }(\alpha -k+1)}f(x-kh)\right),nh=x-a.}$$

(51)

If $\alpha >0$, then the operator is a fractional derivative; otherwise, if $\alpha <0$, then the operator is a fractional integral. The series of coefficients of the Grünwald–Letnikov fractional operator of order $\alpha$ is given by ${\sum }_{k=0}^{\infty }\frac{{(-1)}^k\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(k+1)\mathsf{\Gamma }(\alpha -k+1)}$, or, adjusting the initial term at $k=1$, by

$${\displaystyle \sum _{k=1}^{\infty }\frac{{(-1)}^{k-1}\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }\left(k\right)\mathsf{\Gamma }(\alpha -k+2)}.}$$

(52)

This adjustment is needed in order to evaluate the RCAS. The general term of the series (52) can be written as ${(-1)}^{x-1}f\left(x\right)$, where the function $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is

$${\displaystyle f\left(x\right)=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }\left(x\right)\mathsf{\Gamma }(\alpha -x+2)}.}$$

(53)

Formula (44) is appropriate for functions that are infinitely differentiable, and Expression (36) is appropriate for use when the function f is only $C^r\left({\mathbb{R}}_{+}\right)$ (or infinitely differentiable, but with a large computational cost for evaluating it). In this example, both formulae can be considered.

We apply (44) for calculations until $k=5$ to obtain an idea of the behavior of the RCAS depending on $\alpha$. The term $f\left(1\right)/2$ returns the value $1/2$, for any $\alpha$. The first derivative of the function f is

$${\displaystyle f^{\prime }\left(x\right)=\frac{\mathsf{\Gamma }(\alpha +1)\left[{\mathsf{\Psi }}^{\left(0\right)}(\alpha -x+2)-{\mathsf{\Psi }}^{\left(0\right)}\left(x\right)\right]}{\mathsf{\Gamma }\left(x\right)\mathsf{\Gamma }(\alpha -x+2)},}$$

(54)

where ${\mathsf{\Psi }}^{\left(0\right)}=\frac{{\mathsf{\Gamma }}^{\prime }\left(x\right)}{\mathsf{\Gamma }\left(x\right)}$ is the polygamma function of order 0 [31]. Applying this derivative at $x=1$ and multiplying by $E_1\left(1\right)=1/2$, we obtain

$${\displaystyle E_1\left(1\right)f^{\prime }\left(1\right)=\frac{1}{2}\frac{\mathsf{\Gamma }(\alpha +1)\left[{\mathsf{\Psi }}^{\left(0\right)}(\alpha +1)+\gamma \right]}{\mathsf{\Gamma }(\alpha +1)}=\frac{1}{2}\left({\mathsf{\Psi }}^{\left(0\right)}(\alpha +1)+\gamma \right),}$$

(55)

where $\gamma =-{\mathsf{\Psi }}^{\left(0\right)}\left(1\right)$ is the Euler–Mascheroni constant [21,24,31].

The numerical values for $f^{\prime }\left(1\right)$, $f^{\prime \prime \prime }\left(1\right)$ and for $f^{\left(5\right)}\left(1\right)$ are listed in

Table 1. Numerical approximations of $C\left({(-1)}^{n-1}f\right)$, using Formula (44), evaluated until $k=5$, for some values of $\alpha >0$ (derivatives).

$\mathit{\alpha }$	$\mathit{C}\left(\mathit{f}\right)$ (Approx.)	$\mathit{f}\left(1\right)/2$	${\mathit{f}}^{\prime }\left(1\right)$	${\mathit{f}}^{\prime \prime \prime }\left(1\right)$	${\mathit{f}}^{\left(5\right)}\left(1\right)$
1.0	0.12768...	1/2	1.00000	−3.86960...	20.01700...
0.9	0.14600...	1/2	0.93339...	−3.77359...	20.17390...
0.8	0.16674...	1/2	0.86220...	−3.63987...	20.09654...
0.7	0.19032...	1/2	0.78576...	−3.46229...	19.73062...
0.6	0.21722...	1/2	0.70326...	−3.23321...	19.00819...
0.5	0.24808...	1/2	0.61370...	−2.94313...	17.84321...
0.4	0.28369...	1/2	0.51583...	−2.58002...	16.12527...
0.3	0.32508...	1/2	0.40802...	−2.12835...	13.71045...
0.2	0.37361...	1/2	0.28817...	−1.56776...	10.40765...
0.1	0.43107...	1/2	0.15346...	−0.87089...	5.95769...
0.0	0.50000	1/2	0.00000	0.00000	0.00000

and

Table 2. Numerical approximations of $C\left({(-1)}^{n-1}f\right)$, using Formula (44), evaluated until $k=5$, for some values of $\alpha <0$ (integrals).

$\mathit{\alpha }$	$\mathit{C}\left(\mathit{f}\right)$ (Approx.)	$\mathit{f}\left(1\right)/2$	${\mathit{f}}^{\prime }\left(1\right)$	${\mathit{f}}^{\prime \prime \prime }\left(1\right)$	${\mathit{f}}^{\left(5\right)}\left(1\right)$
0.0	0.50000	1/2	0.00000	0.00000	0.00000
−0.1	0.58394...	1/2	−0.17771...	1.09864...	−7.98264...
−0.2	0.68820...	1/2	−0.38779...	2.50451...	−18.76023...
−0.3	0.82099...	1/2	−0.64280...	4.34089...	−33.53336...
−0.4	0.99583...	1/2	−0.96340...	6.81072...	−54.28752...
−0.5	1.23668...	1/2	−1.38629...	10.27548...	−84.57035...
−0.6	1.59176...	1/2	−1.98416...	15.45152...	−131.43019...
−0.7	2.17134...	1/2	−2.92530...	23.99865...	−211.22288...
−0.8	3.30615...	1/2	−4.71182...	40.87168...	−372.81743...
−0.9	6.64434...	1/2	−9.84653...	90.77350...	−859.96457...
−1.0	$+\infty$	1/2	$-\infty$	$+\infty$	$-\infty$

, for some values of $\alpha$, as well as the numerical approximations for the RCAS, evaluated until $k=5$. The other successive derivatives can be calculated, but the associated computational cost grows considerably. We remember that $\frac{E_1\left(1\right)}{1!}=\frac{1}{2}$, $\frac{E_3\left(1\right)}{3!}=-\frac{1}{24}$, and $\frac{E_5\left(1\right)}{5!}=\frac{1}{240}$, and that the derivatives of even order of the function f do not influence the value of the RCAS because $E_{2k}\left(1\right)=0$ for all $k\in \mathbb{N}$.

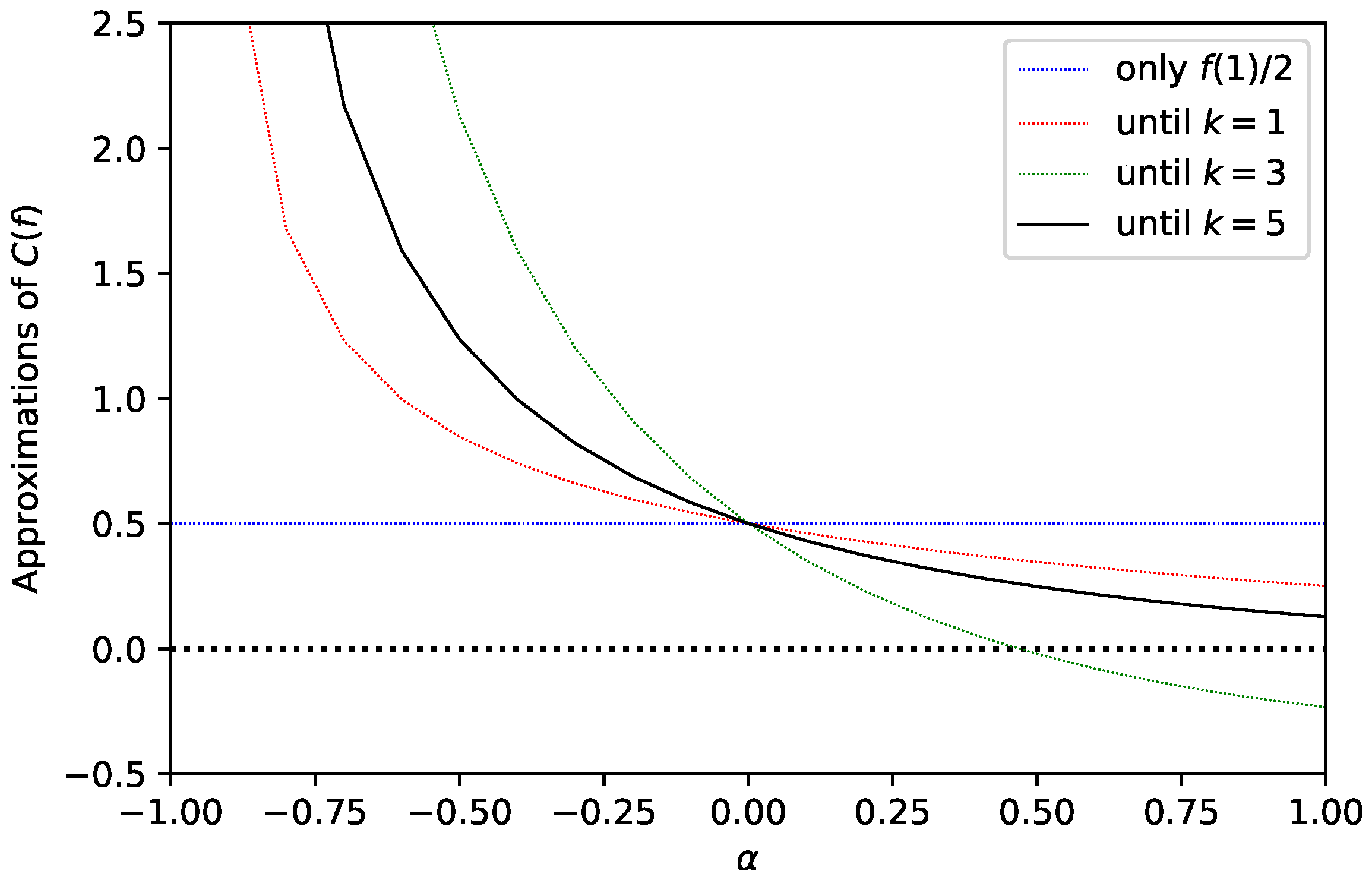
In Figure 1, it is possible to see the evolution of the constants when we add the consecutive terms. From Figure 1 and Table 1 and Table 2, it is possible to conclude that the RCAS for the series

$${\displaystyle \sum _{n=1}^{\infty }\frac{{(-1)}^{n-1}}{\mathsf{\Gamma }(-n+2)}}$$

(56)

(obtained choosing $\alpha =0$) is exactly the value $1/2$. For other values of $\alpha$, one needs to consider more terms in (44) to obtain a better approximation.

6. Conclusions

Divergent series appear in many fields of science, such as number theory, quantum theory, and mathematical physics, among others. A common issue is to give meaning to a divergent series. Regularization methods are used for such purposes. In this context, the RCS appears as a method with the potential to solve such a problem for a class of functions. Regarding the Ramanujan summation, Ramanujan himself stated “If $f\left(1\right)+f\left(2\right)+\cdots +f\left(x\right)$ be a convergent series then its constant is the sum of the series” and “We can substitute this constant... instead of its divergent infinite series”. The importance of the RCS can be understood throughout his own words, especially the last cited phrase.

The definition for the RCS given by Hardy [2] (pp. 325–327) includes a parameter a and maintains flexibility, which permits its use in several problems. However, when a divergent series already has a known value obtained for other summation methods, it is expected that the same value can be obtained as a constant for each summation method that is applicable to it, including the RCS. When the RCS $C(f;a)$ is considered with the parameter $a=0$, the RCS $C(f;0)$ agrees with the value obtained for any other summation method that is applicable to the divergent series considered.

We hope that Expressions (12) and (13) help to obtain applicable values as constants for several divergent series, where the general term does not alternate sign, as well as with Formulae (36), (44) for alternating series, thus helping to promote the Ramanujan summation theory as a technique for regularizing divergent series.

To emphasize the importance of regularization techniques for divergent series, we cite some examples of the applicability of such techniques. We highlight: (i) the zeta function regularization was applied, for example, to prove Lerch’s formula in number theory [42] and to evaluate the Casimir energy in mathematical physics [43], and (ii) the smoothed sum method [3,36] was also applied to revisit the Casimir effect [44,45]. Several applications of regularization techniques are given in references [46,47,48,49,50,51]. Some recent developments can be found in references [52,53,54,55].