A New Mathematical Model of COVID-19 with Quarantine and Vaccination
Abstract
:1. Introduction
2. Mathematical Model
Biological Assumptions of the Model
- We assume that individuals to be vaccinated are selected from individuals who have not been exposed to or immunized against the virus.
- The vaccination may not provide full protection for every person in the vaccine class. In this instance, we suppose that vaccinated people get the virus when they are exposed to it.
3. Basic Definitions
4. Mathematical Analysis of System (1)
Positivity and Boundedness of the Solutions
5. Equilibrium Points of the Model
5.1. Basic Reproduction Number
5.2. Global Stability of Disease-Free Equilibrium Point
- For is globally asymptotically stable.
- for where is an M-matrix (the off-diagonal elements of B are nonnegative), and is the region where the model makes biological sense.
5.3. Stability of
6. Sensitivity Analysis
7. Numerical Scheme for System (1)
Numerical Scheme
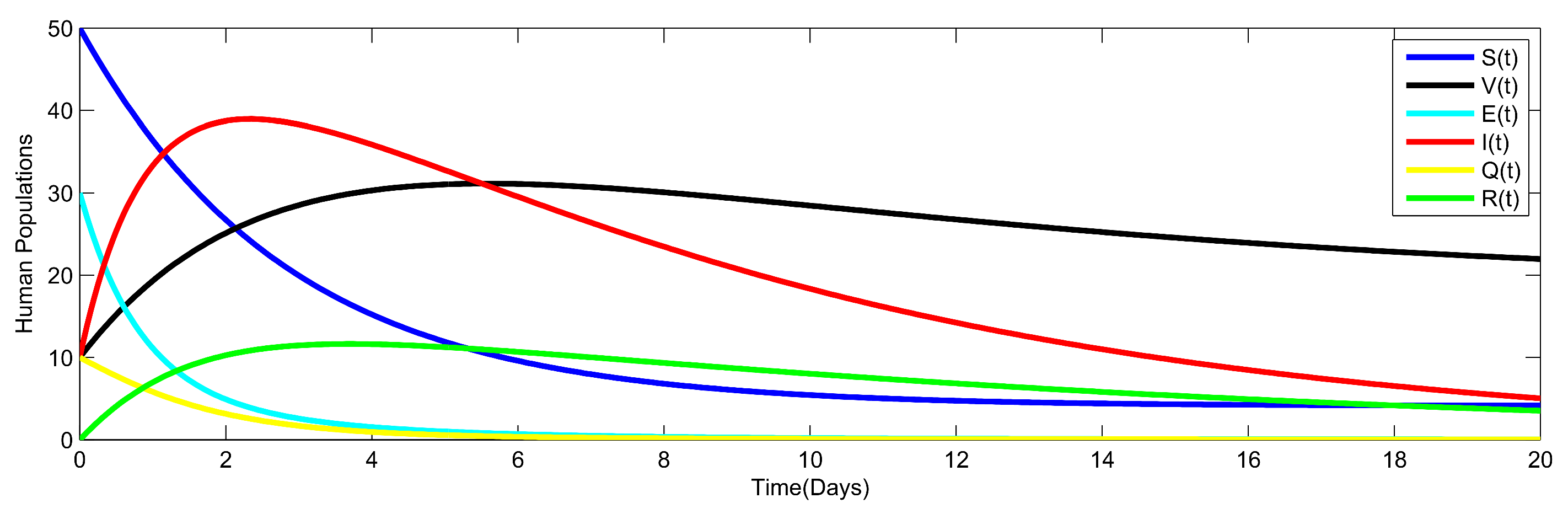
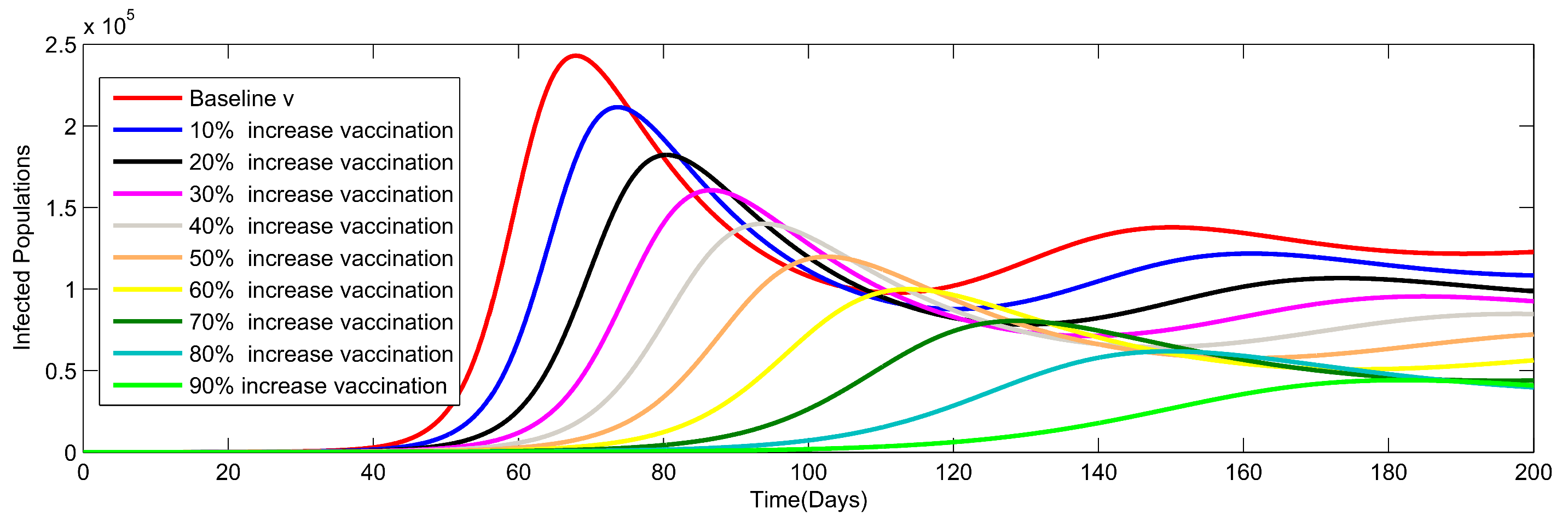
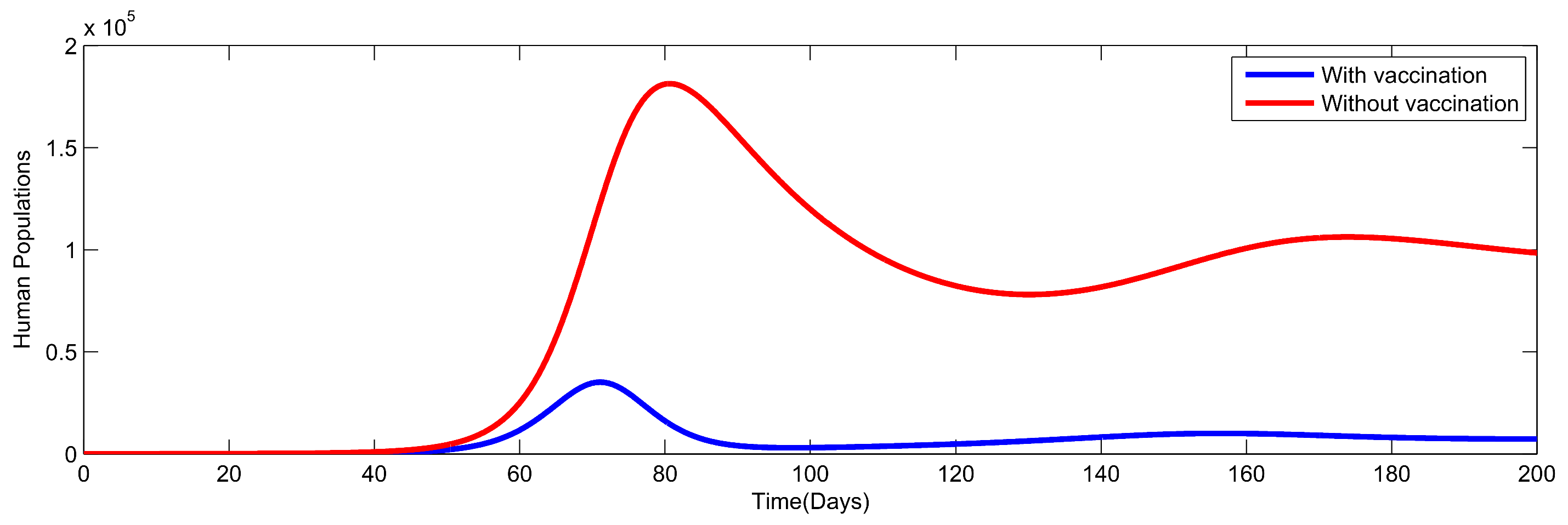
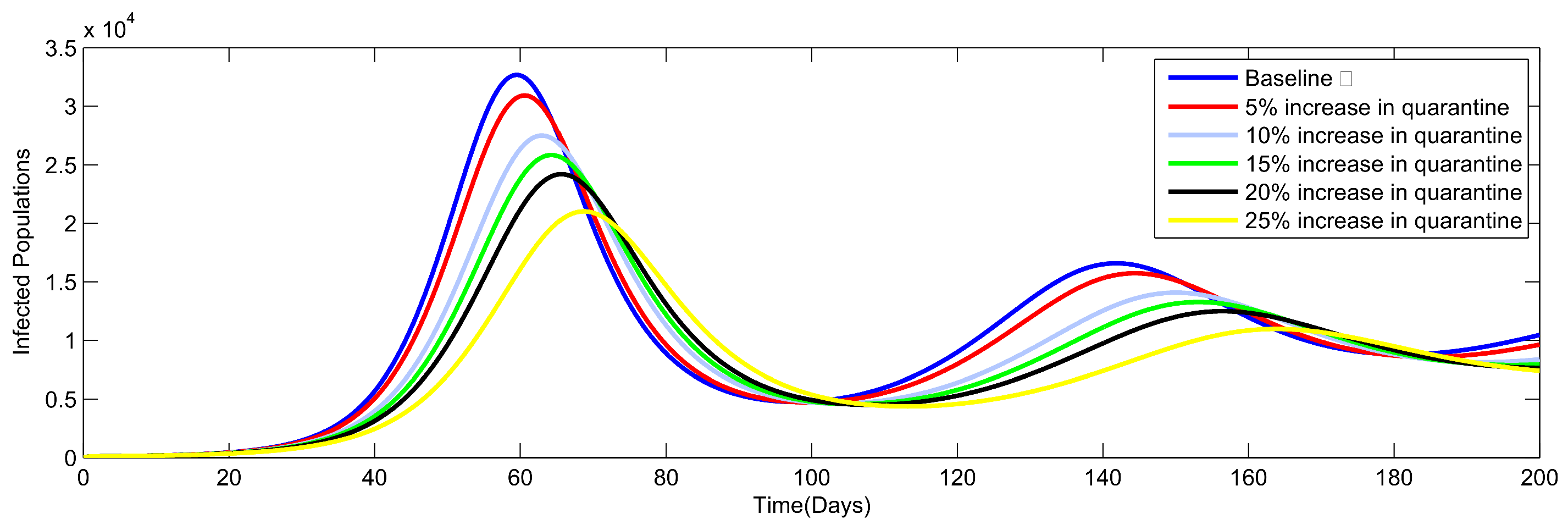
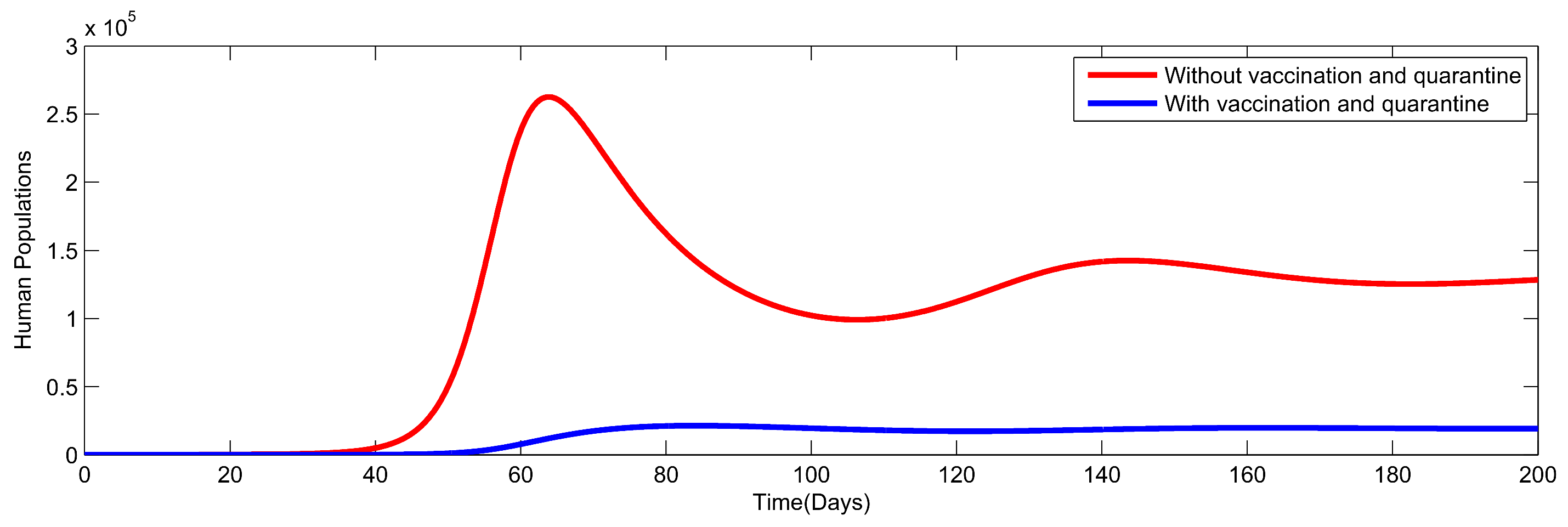
8. Numerical Simulation
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report—99; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report—73; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Trawicki, M.B. Deterministic seirs epidemic model for modeling vital dynamics, vaccinations, and temporary immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef] [Green Version]
- Din, A.; Shah, K.; Seadawy, A.; Alrabaiah, H.; Baleanu, D. On a new conceptual mathematical model dealing the current novel Coronavirus-19 infectious disease. Results Phys. 2020, 19, 103510. [Google Scholar] [CrossRef] [PubMed]
- Haq, I.U.; Ali, N.; Ahmad, H.; Nofal, T.A. On the fractional-order mathematical model of COVID-19 with the effects of multiple non-pharmaceutical interventions. AIMS Math. 2022, 7, 16017–16036. [Google Scholar] [CrossRef]
- Haq, I.U.; Ali, N.; Nisar, K.S. An optimal control strategy and grünwald-letnikov finite-difference numerical scheme for the fractional-order COVID-19 model. Math. Model. Numer. Simul. Appl. 2022, 2, 108–116. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Khan, T.; Zaman, G. Mathematical analysis of spread and control of the novel corona virus (COVID-19) in China. Chaos Solitons Fractals 2020, 141, 110286. [Google Scholar] [CrossRef]
- Chen, Y.; Bi, K.; Zhao, S.; Ben-Arieh, D.; Wu, C.-H.J. Modeling individual fear factor with optimal control in a disease-dynamic system. Chaos Solitons Fractals 2017, 104, 531–545. [Google Scholar] [CrossRef]
- Hsieh, Y.-H. Middle East respiratory syndrome Coronavirus (mers-cov) nosocomial outbreak in South Korea: Insights from modeling. PeerJ 2015, 3, e1505. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Lee, S.; Chu, C.; Choe, S.; Hong, S.; Shin, Y. The characteristics of middle eastern respiratory syndrome coronavirus transmission dynamics in south korea. Osong Public Health Res. Perspect. 2016, 7, 49–55. [Google Scholar] [CrossRef] [Green Version]
- Bi, K.; Chen, Y.; Wu, C.-H.J.; Ben-Arieh, D. A memetic algorithm for solving optimal control problems of zika virus epidemic with equilibriums and backward bifurcation analysis. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105176. [Google Scholar] [CrossRef]
- Chen, C.; Hsiao, C. Haar wavelet method for solving lumped and distributed-parameter systems. IEEE Proc.-Control Theory Appl. 1997, 144, 87–94. [Google Scholar] [CrossRef]
- Aziz, I. New algorithms for the numerical solution of nonlinear fredholm and volterra integral equations using haar wavelets. J. Comput. Appl. Math. 2013, 239, 333–345. [Google Scholar] [CrossRef]
- Lepik, Ü. Numerical solution of differential equations using haar wavelets. Math. Comput. Simul. 2005, 68, 127–143. [Google Scholar] [CrossRef]
- Lepik, Ü. Haar wavelet method for nonlinear integro-differential equations. Appl. Math. Comput. 2006, 176, 324–333. [Google Scholar] [CrossRef]
- Lepik, Ü. Solving pdes with the aid of two-dimensional haar wavelets. Comput. Math. Appl. 2011, 61, 1873–1879. [Google Scholar] [CrossRef] [Green Version]
- Lepik, Ü. Application of the haar wavelet transform to solving integral and differential equations. Proc. Est. Acad. Sci. Phys. Math. 2007, 56, 28–46. [Google Scholar] [CrossRef]
- Lepik, Ü. Solving fractional integral equations by the haar wavelet method. Appl. Math. Comput. 2009, 214, 468–478. [Google Scholar] [CrossRef]
- Majak, J.; Pohlak, M.; Eerme, M. Application of the haar wavelet-based discretization technique to problems of orthotropic plates and shells. Mech. Compos. Mater. 2009, 45, 631–642. [Google Scholar] [CrossRef]
- Jain, S. Numerical analysis for the fractional diffusion and fractional buckmaster equation by the two-step laplace adam-bashforth method. Eur. Phys. J. Plus 2018, 133, 1–11. [Google Scholar] [CrossRef]
- Rihan, F.; Al-Mdallal, Q.; AlSakaji, H.; Hashish, A. A fractional-order epidemic model with time-delay and nonlinear incidence rate. Chaos Solitons Fractals 2019, 126, 97–105. [Google Scholar] [CrossRef]
- Hajji, M.A.; Al-Mdallal, Q. Numerical simulations of a delay model for immune system-tumor interaction. Sultan Qaboos Univ. J. Sci. 2018, 23, 19–31. [Google Scholar] [CrossRef]
- Lai, C.-C.; Shih, T.-P.; Ko, W.-C.; Tang, H.-J.; Hsueh, P.-R. Severe acute respiratory syndrome coronavirus 2 (Sars-Cov-2) and Coronavirus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef]
- Babaaghaie, A.; Maleknejad, K. Numerical solutions of nonlinear two-dimensional partial volterra integro-differential equations by haar wavelet. J. Comput. Appl. Math. 2017, 317, 643–651. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 2010, 216, 2276–2285. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Islam, R. Mathematical Analysis of Epidemiological Model of Virus Transmission Dynamics in Perspective of Bangladesh. Ph.D. Thesis, Khulna University of Engineering & Technology (KUET), Khulna, Bangladesh, 2018. [Google Scholar]
- Majak, J.; Shvartsman, B.; Karjust, K.; Mikola, M.; Haavajõe, A.; Pohlak, M. On the accuracy of the haar wavelet discretization method. Compos. Part B Eng. 2015, 80, 321–327. [Google Scholar] [CrossRef]
- Yavuz, M.; Coşar, F.Ö.; Günay, F.; Özdemir, F.N. A new mathematical modeling of the COVID-19 pandemic including the vaccination campaign. Open J. Model. Simul. 2021, 9, 299–321. [Google Scholar] [CrossRef]
- Diagne, M.; Rwezaura, H.; Tchoumi, S.; Tchuenche, J. A mathematical model of COVID-19 with vaccination and treatment. Comput. Math. Methods Med. 2021, 2021, 1250129. [Google Scholar] [CrossRef]



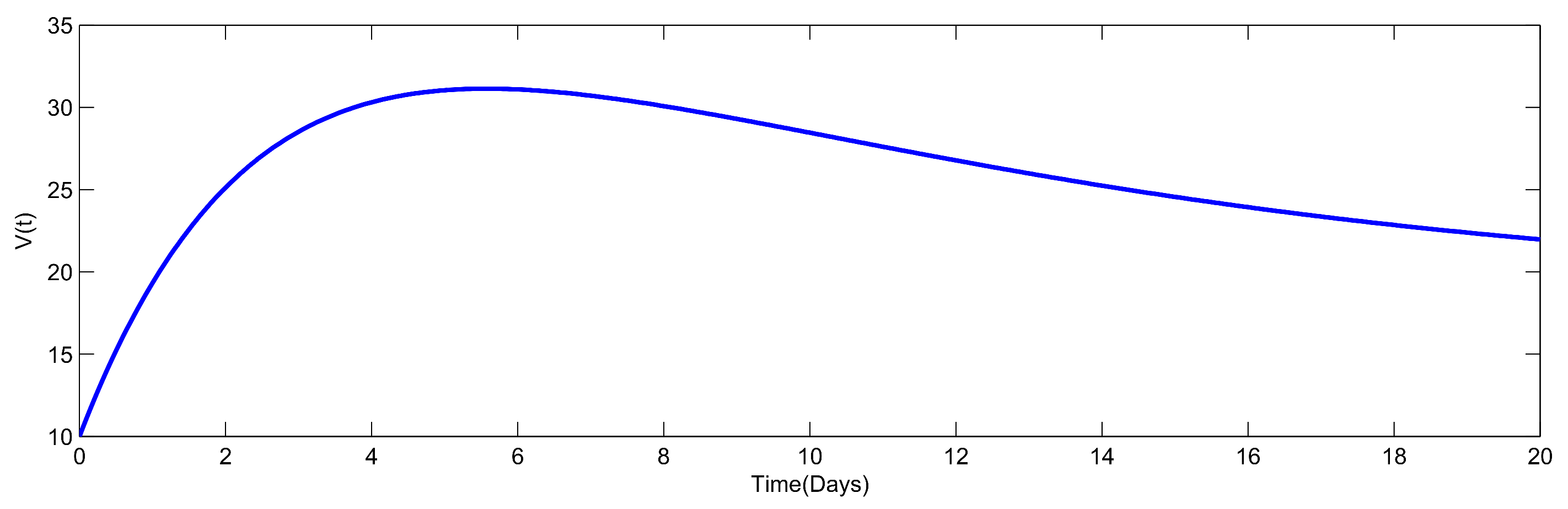

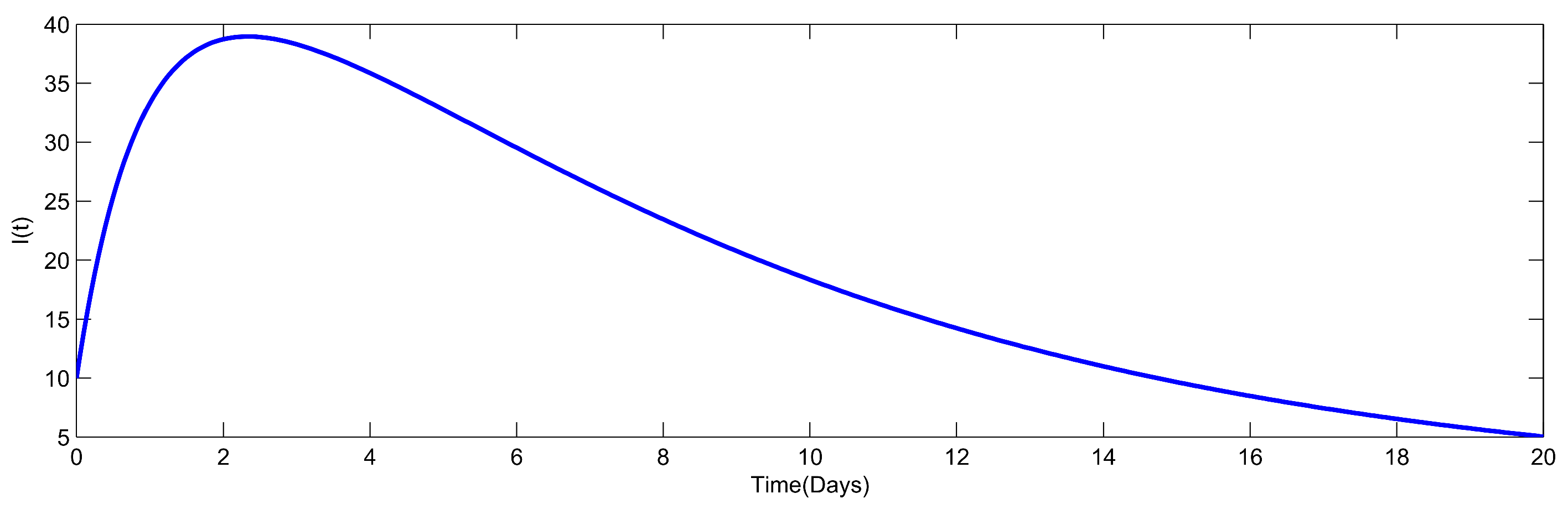
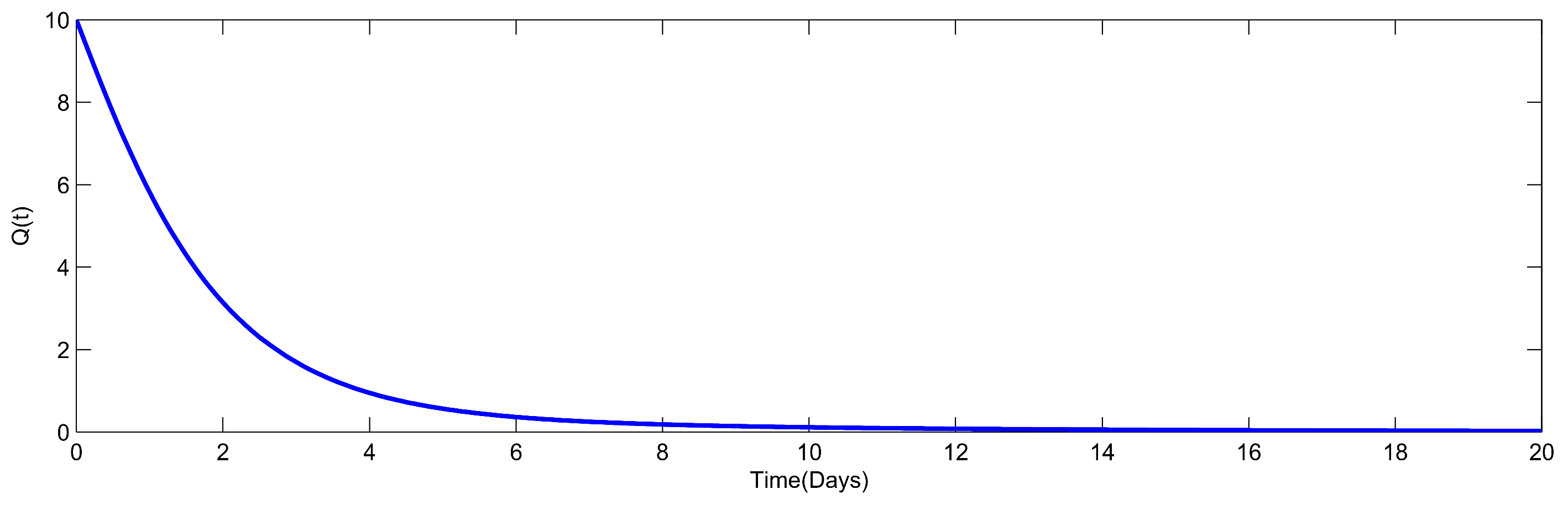
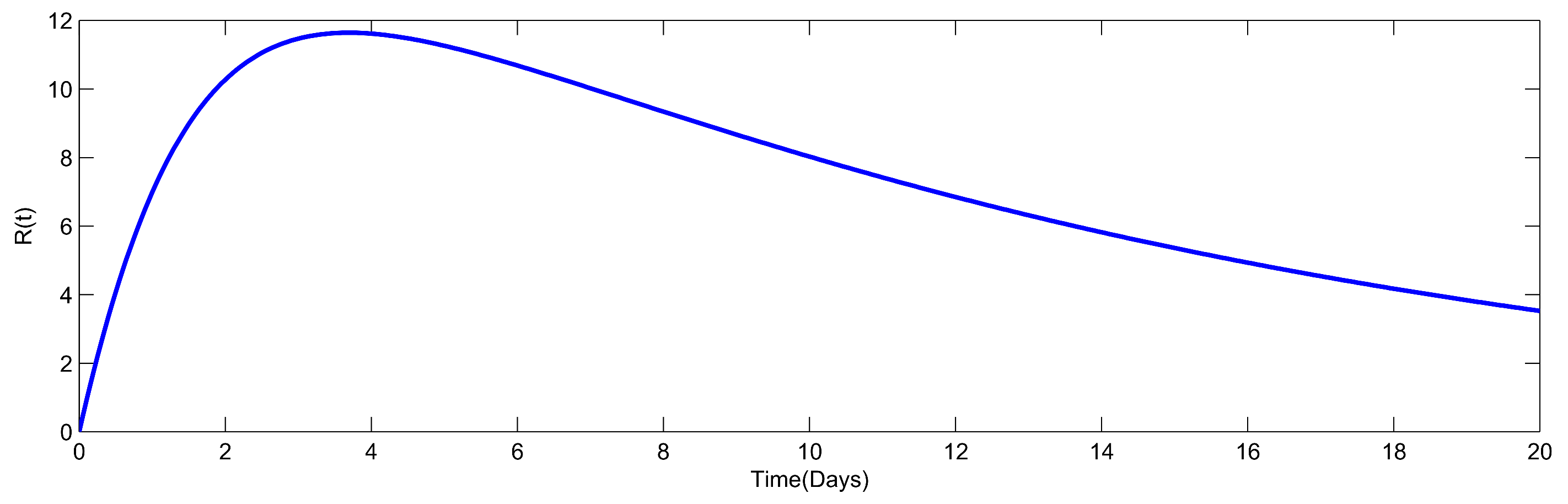

| Parameters | Parameters Sensitivity Index |
|---|---|
| = | |
| = | |
| = | |
| = | |
| = | |
| = | |
| = | |
| ==0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haq, I.U.; Ullah, N.; Ali, N.; Nisar, K.S. A New Mathematical Model of COVID-19 with Quarantine and Vaccination. Mathematics 2023, 11, 142. https://doi.org/10.3390/math11010142
Haq IU, Ullah N, Ali N, Nisar KS. A New Mathematical Model of COVID-19 with Quarantine and Vaccination. Mathematics. 2023; 11(1):142. https://doi.org/10.3390/math11010142
Chicago/Turabian StyleHaq, Ihtisham Ul, Numan Ullah, Nigar Ali, and Kottakkaran Sooppy Nisar. 2023. "A New Mathematical Model of COVID-19 with Quarantine and Vaccination" Mathematics 11, no. 1: 142. https://doi.org/10.3390/math11010142
APA StyleHaq, I. U., Ullah, N., Ali, N., & Nisar, K. S. (2023). A New Mathematical Model of COVID-19 with Quarantine and Vaccination. Mathematics, 11(1), 142. https://doi.org/10.3390/math11010142







