Control of a Hydraulic Generator Regulating System Using Chebyshev-Neural-Network-Based Non-Singular Fast Terminal Sliding Mode Method
Abstract
:1. Introduction
2. Mathematical Modeling
3. Control Design
3.1. Structure of ChNN
3.2. ChNN-Based FTSMC
4. Numerical Results
4.1. Fixed Point Stabilization
4.2. Periodic Orbit Tracking
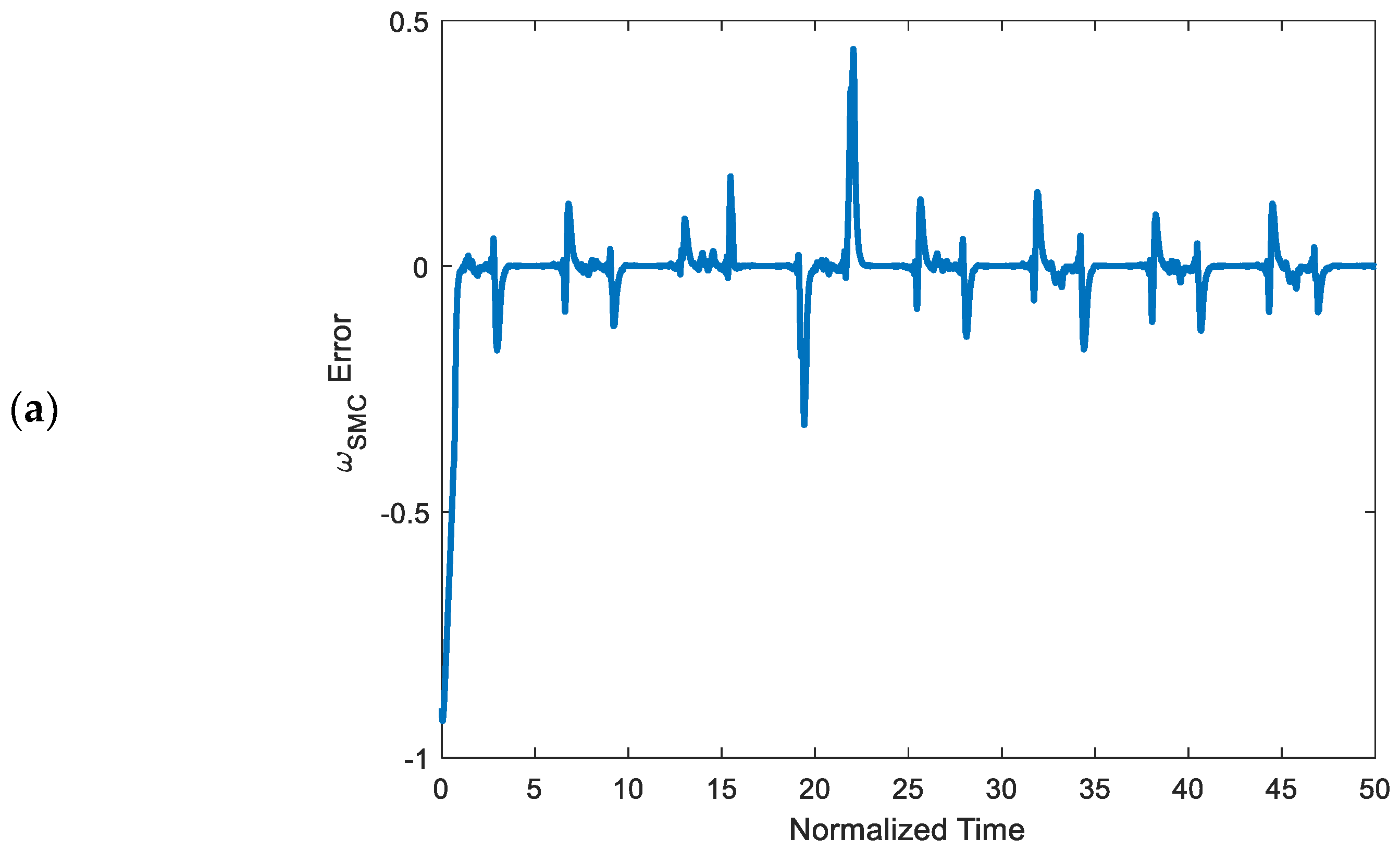
4.3. Robustness Test against Random Noise
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ChNN | Chebyshev neural network. |
| FTSMC | Fast terminal sliding mode control. |
| HTGS | Hydro-turbine governing system. |
| PID | Proportional–integral–derivative. |
| SMC | Sliding mode control. |
References
- Qu, F.; Guo, W. Robust H∞ control for hydro-turbine governing system of hydropower plant with super long headrace tunnel. Int. J. Electr. Power Energy Syst. 2020, 124, 106336. [Google Scholar] [CrossRef]
- Li, R.; Arzaghi, E.; Abbassi, R.; Chen, D.; Li, C.; Li, H.; Xu, B. Dynamic maintenance planning of a hydro-turbine in operational life cycle. Reliab. Eng. Syst. Saf. 2020, 204, 107129. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.; Tolo, S.; Patelli, E.; Jiang, Y. Model validation and stochastic stability of a hydro-turbine governing system under hydraulic excitations. Int. J. Electr. Power Energy Syst. 2018, 95, 156–165. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Chen, D.; Zhang, H.; Wang, F.; Zhang, X.; Wu, Y. Hamiltonian model and dynamic analyses for a hydro-turbine governing system with fractional item and time-lag. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-J. A new integral transform operator for solving the heat-diffusion problem. Appl. Math. Lett. 2017, 64, 193–197. [Google Scholar] [CrossRef]
- Yang, X.-J.; Abdel-Aty, M.; Cattani, C. A new general fractional-order derivataive with Rabotnov fractional-exponential kernel applied to model the anomalous heat transfer. Therm. Sci. 2019, 23, 1677–1681. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Yang, X.; Zhang, J. Stability analysis of hydro-turbine governing system including surge tanks under interconnected operation during small load disturbance. Renew. Energy 2018, 133, 1426–1435. [Google Scholar] [CrossRef]
- Li, C.; Mao, Y.; Zhou, J.; Zhang, N.; An, X. Design of a fuzzy-PID controller for a nonlinear hydraulic turbine governing system by using a novel gravitational search algorithm based on Cauchy mutation and mass weighting. Appl. Soft Comput. 2017, 52, 290–305. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, L.; Guo, Y.; Qian, J.; Zhang, C. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets. Nonlinear Dyn. 2014, 76, 1921–1933. [Google Scholar] [CrossRef] [Green Version]
- Trivedi, C.; Gandhi, B.K.; Cervantes, M.J.; Dahlhaug, O.G. Experimental investigations of a model Francis turbine during shutdown at synchronous speed. Renew. Energy 2015, 83, 828–836. [Google Scholar] [CrossRef]
- Garcia, F.J.; Uemori, M.K.I.; Echeverria, J.J.R.; da Costa Bortoni, E. Design Requirements of Generators Applied to Low-Head Hydro Power Plants. IEEE Trans. Energy Convers. 2015, 30, 1630–1638. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.-T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Iqbal, J.; Ullah, M.; Khan, S.G.; Khelifa, B.; Ćuković, S. Nonlinear Control Systems-A Brief Overview of Historical and Recent Advances. Nonlinear Eng. 2017, 6, 301–312. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sari, N.N.; Pham, V.-T.; Alsaadi, F.E.; Hayat, T. Optimal adaptive higher order controllers subject to sliding modes for a carrier system. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2019, 87, 105943. [Google Scholar] [CrossRef]
- Yousefpour, A.; Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Stabilization of nonlinear vibrations of carbon nanotubes using observer-based terminal sliding mode control. Trans. Inst. Meas. Control. 2019, 42, 1047–1058. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2019, 130, 109400. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Palm, R. Robust control by adaptive Non-singular Terminal Sliding Mode. Eng. Appl. Artif. Intell. 2017, 59, 205–217. [Google Scholar] [CrossRef]
- Yao, Q.; Jahanshahi, H.; Batrancea, L.M.; Alotaibi, N.D.; Rus, M.-I. Fixed-Time Output-Constrained Synchronization of Unknown Chaotic Financial Systems Using Neural Learning. Mathematics 2022, 10, 3682. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yao, Q.; Khan, M.I.; Moroz, I. Unified neural output-constrained control for space manipulator using tan-type barrier Lyapunov function. Adv. Space Res. 2022, in press. [Google Scholar] [CrossRef]
- Alsaade, F.W.; Yao, Q.; Bekiros, S.; Al-Zahrani, M.S.; Alzahrani, A.S.; Jahanshahi, H. Chaotic attitude synchronization and anti-synchronization of master-slave satellites using a robust fixed-time adaptive controller. Chaos Solitons Fractals 2022, 165, 112883. [Google Scholar] [CrossRef]
- Yao, Q.; Jahanshahi, H.; Moroz, I.; Bekiros, S.; Alassafi, M.O. Indirect neural-based finite-time integral sliding mode control for trajectory tracking guidance of Mars entry vehicle. Adv. Space Res. 2022, in press. [Google Scholar] [CrossRef]
- Lu, Y.-S. Sliding-Mode Disturbance Observer with Switching-Gain Adaptation and Its Application to Optical Disk Drives. IEEE Trans. Ind. Electron. 2009, 56, 3743–3750. [Google Scholar] [CrossRef]
- Chen, M.; Chen, W.-H. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int. J. Adapt. Control Signal Process. 2009, 24, 51–64. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Castillo, O. Application of Variable-Order Fractional Calculus in Neural Networks: Where Do We Stand? Eur. Phys. J. Spec. Top. 2022, 231, 1–4. [Google Scholar] [CrossRef]
- Li, Y.; Wei, X.; Li, Y.; Dong, Z.; Shahidehpour, M. Detection of False Data Injection Attacks in Smart Grid: A Secure Federated Deep Learning Approach. IEEE Trans. Smart Grid 2022, 13, 4862–4872. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Egusquiza, M.; Chen, D.; Li, F.; Behrens, P.; Egusquiza, E. A review of dynamic models and stability analysis for a hydro-turbine governing system. Renew. Sustain. Energy Rev. 2021, 144, 110880. [Google Scholar] [CrossRef]
- Ding, X.; Sinha, A. Hydropower Plant Frequency Control Via Feedback Linearization and Sliding Mode Control. J. Dyn. Syst. Meas. Control 2016, 138, 074501. [Google Scholar] [CrossRef]
- Ding, X.; Sinha, A. Hydropower Plant Load Frequency Control Via Second-Order Sliding Mode. J. Dyn. Syst. Meas. Control 2017, 139, 074503. [Google Scholar] [CrossRef]
- Ling, D.J. Bifurcation and Chaos of Hydraulic Turbine Governor; Nanjing Hohai University: Nanjing, China, 2007. [Google Scholar]
- Li, C.; Sprott, J.C.; Mei, Y. An infinite 2-D lattice of strange attractors. Nonlinear Dyn. 2017, 89, 2629–2639. [Google Scholar] [CrossRef]
- Vyas, B.Y.; Das, B.; Maheshwari, R.P. Improved Fault Classification in Series Compensated Transmission Line: Comparative Evaluation of Chebyshev Neural Network Training Algorithms. IEEE Trans. Neural Netw. Learn. Syst. 2014, 27, 1631–1642. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Wu, Q.-X.; Cui, R. Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems. ISA Trans. 2012, 52, 198–206. [Google Scholar] [CrossRef]
- The Math Works, Inc. MATLAB, Version 2020a; The Math Works, Inc.: Natick, MA, USA, 2020; Available online: Https://Www.Mathworks.Com/ (accessed on 28 May 2020).
- Yuan, X.; Chen, Z.; Yuan, Y.; Huang, Y.; Li, X.; Li, W. Sliding mode controller of hydraulic generator regulating system based on the input/output feedback linearization method. Math. Comput. Simul. 2016, 119, 18–34. [Google Scholar] [CrossRef]













| Periodic Response | Var | MSE | ITAE |
|---|---|---|---|
| SMC | 0.0093 | 0.0094 | 2178.2 |
| NNNFTSMC | 0.0026 | 0.0027 | 200.7 |
| Step Response | Var | MSE | ITAE |
|---|---|---|---|
| SMC | 0.0072 | 0.0074 | 314.1 |
| NNNFTSMC | 0.0026 | 0.0027 | 126.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaadi, F.E.; Yasami, A.; Alsubaie, H.; Alotaibi, A.; Jahanshahi, H. Control of a Hydraulic Generator Regulating System Using Chebyshev-Neural-Network-Based Non-Singular Fast Terminal Sliding Mode Method. Mathematics 2023, 11, 168. https://doi.org/10.3390/math11010168
Alsaadi FE, Yasami A, Alsubaie H, Alotaibi A, Jahanshahi H. Control of a Hydraulic Generator Regulating System Using Chebyshev-Neural-Network-Based Non-Singular Fast Terminal Sliding Mode Method. Mathematics. 2023; 11(1):168. https://doi.org/10.3390/math11010168
Chicago/Turabian StyleAlsaadi, Fawaz E., Amirreza Yasami, Hajid Alsubaie, Ahmed Alotaibi, and Hadi Jahanshahi. 2023. "Control of a Hydraulic Generator Regulating System Using Chebyshev-Neural-Network-Based Non-Singular Fast Terminal Sliding Mode Method" Mathematics 11, no. 1: 168. https://doi.org/10.3390/math11010168
APA StyleAlsaadi, F. E., Yasami, A., Alsubaie, H., Alotaibi, A., & Jahanshahi, H. (2023). Control of a Hydraulic Generator Regulating System Using Chebyshev-Neural-Network-Based Non-Singular Fast Terminal Sliding Mode Method. Mathematics, 11(1), 168. https://doi.org/10.3390/math11010168






