Mathematical and Physical Analyses of Middle/Neutral Surfaces Formulations for Static Response of Bi-Directional FG Plates with Movable/Immovable Boundary Conditions

Abstract

This article is prompted by the existing confusion about correctness of responses of beams and plates produced by middle surface (MS) and neutral surface (NS) formulations. This study mathematically analyzes both formulations in the context of the bending of bi-directional functionally graded (BDFG) plates and discusses where the misconceptions are. The relation between in-plane displacement field variables on NS and on MS are derived. These relations are utilized to define a modified set of boundary conditions (BCs) for immovable simply supported plates that enables either formulation to apply fixation conditions on the refence plane of the other formulation. A four-variable higher order shear deformation theory is adopted to present the displacement fields of BDFG plates. A 2D plane stress constitution is used to govern stress–strain relations. Based on MS and NS, Hamilton’s principles are exploited to derive the equilibrium equations which are described by variable coefficient partial differential equations. The governing equations in terms of stress resultants are discretized by the differential quadrature method (DQM). In addition, analytical expressions that relate rigidity terms and stress resultants associated with the two formulations are proved. Both the theoretical analysis and the numerical results demonstrate that the responses of BDFG plates based on MS and NS formulations are identical in the cases of clamped BCs and movable simply supported BCs. However, the difference in responses of immovable simply supported BCs is expected since each formulation assumes plate fixation at different planes. Further, numerical results show that the responses of immovable simply supported BDFG plates obtained using the NS formulation are identical to those obtained by the MS formulation if the transferred boundary condition (from NS- to MS-planes) are applied. Theoretical and numerical results demonstrate also that both MS and NS formulations are correct even for immovable simply supported BCs if fixation constraints at different planes are treated properly.

1. Introduction

In comparison to conventional materials which have homogenous microstructures, functionally graded materials (FGMs) have heterogeneous constituents and their properties vary continuously along spatial direction(s) [1]. FGMs can be designed to achieve the required mechanical, thermal, electrical, and magnetic properties by grading their constituents with suitable metal/ceramics materials. FGM was originated during the space-plane project in Japan, 1984 [2]. Currently, FGMs are used in many real applications such as aerospace, biomechanics, medical devices [3], marine, heat exchanger [4], MEMS and NEMS [5], shape memory alloys, thin films, and AFM [6].

In some applications such as aerospace craft, nuclear and shuttles, distributions of the stress or thermal field in the structural elements of such advanced machines can be in two or three directions, and thus, the conventional 1D FGMs are not sufficient. As a consequence, there is a need for multi-directional FGMs [7]. Nemat-Alla [8] proposed a 2D (two directional) FGM which withstands super-high temperatures and gives more reduction in thermal stress. Lu et al. [9] exploited the state space-based differential quadrature method to derive semi-analytical 3D elasticity solutions for multi-directional orthotropic FG plates. Pan [10] developed an enriched improved complex variable element-free Galerkin method for efficient fracture analysis of orthotropic materials. Esmaeilzadeh et al. [11,12] exploited the dynamic relaxation method in analyzing the dynamic of stiffened 2D FG porous plates under a moving load. Do et al. [13] exploited a non-uniform rational B-spline basis function for describing material distribution varying through 3D FG plates and used natural frequency or buckling load as the objective function for maximization. Ghatage et al. [14] presented an exhaustive review on modelling and analysis of multi-directional FG beam/plate/shell structures.

Chen et al. [15] studied the nonlinear forced vibration of the bi-directional functionally graded (BDFG) plate with global and localized geometrical imperfections by using the pseudo-arclength continuation technique. Li et al. [16] studied buckling and post-buckling performance of variable stiffness composite plates with cutouts via classical plate theory with the nonlinear von Karman strain. Luo et al. [17] presented buckling analysis of variable stiffness composite plates with elliptical cutouts using an efficient radial basis point interpolation method based on a naturally stabilized nodal integration scheme. Karamanli et al. [18] developed a finite element model to study the mechanical responses of multi-directional FG strain gradient microplates using a quasi-3D shear theory. Assie et al. [7] developed a computational model based on unified higher order shear theories to evaluate the static buckling of BDFG porous plates resting on elastic foundation based on unified shear theories.

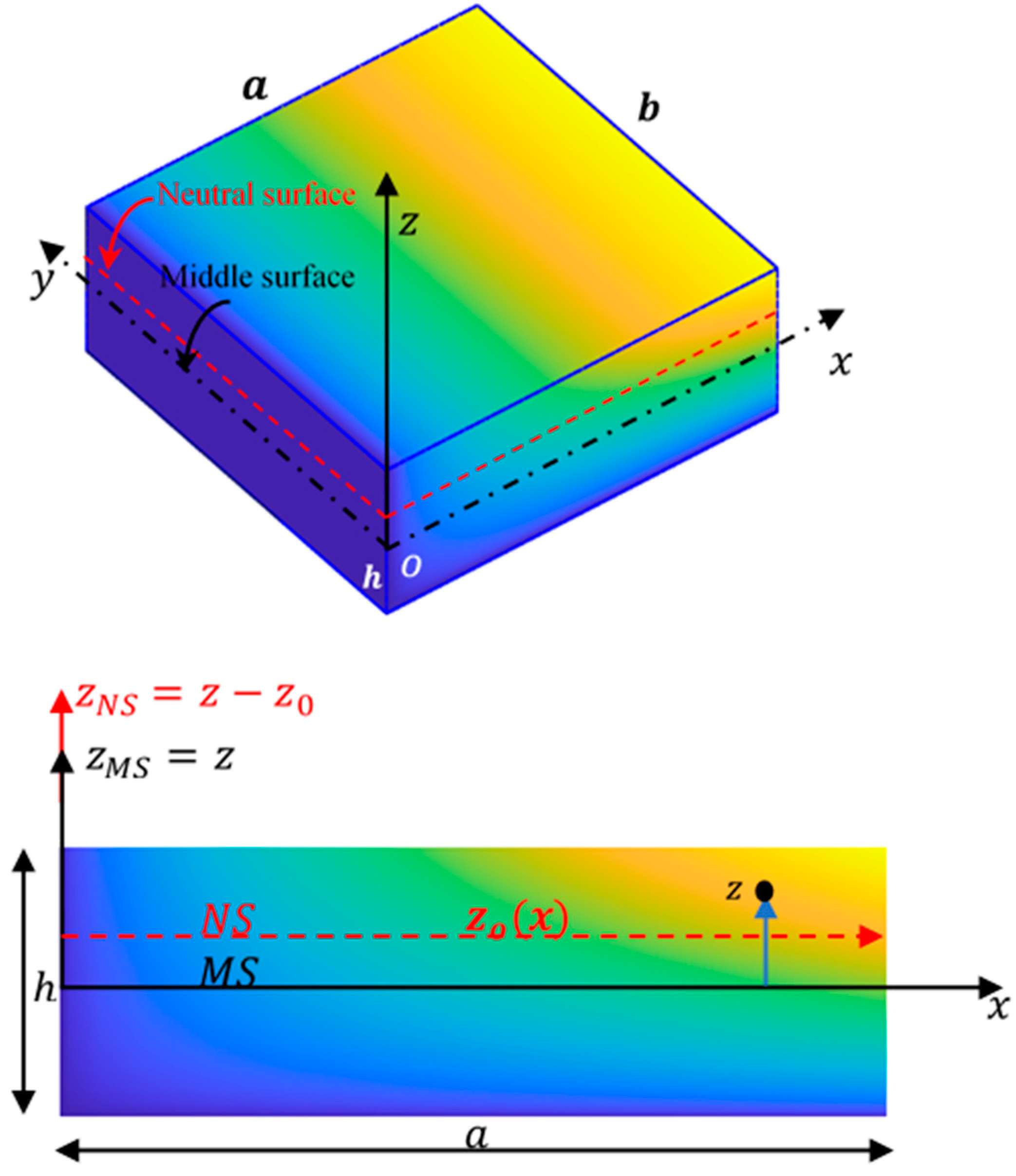
The mid-surface and neutral surface overlay in a homogeneous isotropic plate, while it is the case for the FGMs plate, is not in this case because material properties are graded through the thickness [19]. Hence, there is a strong scientific need to reexamine behaviors of FG structures about the undeformed neutral plane [20,21,22]. The concept of neutral surface that was employed for many analyses leads to more accurate formulation and numerical results [23]. In 2008, Zhang and Zhou [24] derived the governing equations of a FGM thin rectangular plate based on the physical neutral surface and classical laminated plate theory. Zhang [25] studied post-buckling, nonlinear bending and vibration of FGM plates based on a physical neutral surface and high order shear deformation theory. Han et al. [26] and Benferhat et al. [27] examined dynamic instability of the FGM plate on an elastic medium based on the exact neutral surface position. Barati and Shahverdi [28] presented an analytical solution for thermo-mechanical vibration of FG nanoplates under uniform, linear and non-linear temperature rise considering a neutral surface. Farzam-Rad et al. [29] developed a simple quasi-3D shear theory in analyzing a static and free vibration response of FG sandwich plates by using the isogeometric analysis and physical neutral surface. Arefi et al. [23] exploited two-variable sinusoidal shear deformation theory in analyzing the free vibration of a sandwich piezo-elastic nonlocal nanoplate incorporating the neutral surface effect. Lie et al. [30] exploited classical plate theory with the von Karman strain to model large amplitude vibration of matrix cracked hybrid laminated plates containing CNTR-FG layers. Zarastvand et al. [31] presented a comprehensive review on the prediction of acoustic wave transmission features of the multilayered plate. Ghafouri et al. [32] studied the influence of a 3D re-entrant auxetic core on the sound propagation of 3D sandwich panels.

Hashemi and Jafari [33] investigated the nonlinear free and forced vibrations of a 2D-FG plate with temperature-dependent properties. Ali and Azam [19] derived an exact solution for the free vibration of a porous FG plate considering a neutral surface using the dynamic stiffness method. Babaei and Eslami [34] studied the nonlinear bending of infinite length porous FG cylindrical panels subjected to uniform temperature rise and transverse pressure loading. Tati [35] presented a finite element model to explore the bending behavior of FG plates. She et al. [36] developed an exact wave propagation solution of a FG circular plate via the physical neutral surface using Laplace integral transformation. Singh et al. [37] investigated analytically the low-frequency range vibroacoustic response of mode-localized thin FG plates using a physical neutral surface. Peng et al. [38] studied the static and free vibration of the stiffened FGM plate resting on Pasternak foundation by using the moving Kriging approximation and the physical neutral surface. Cuong-Le et al. [39] explored the mechanical response of a sigmoid functionally graded nanoplate via nonlocal strain gradient elasticity theory and an isogeometric numerical solution considering a neutral surface. Kamiński [40] illustrated the sensitivity and randomness in homogenization of periodic fiber-reinforced composites via the response function method. Guminiak and Kamiński [41] studied an application of the stochastic boundary element methods implemented due to three different probabilistic approaches to analyze stability of the rectangular thin elastic and isotropic plates.

Various studies have applied both mid-surface and neutral surface formulations and compared their results; however, they come to conflicting conclusions. Larbi et al. [42] calculated the frequencies of movable simply supported beams based on the neutral plane and showed that the calculated frequencies were in very close agreement with the frequencies obtained from the mid-plane formulation. Eltaher et al. [43] studied FGM beams and showed that the vibration frequencies obtained from mid-plane and neutral plane formulations are different up to about 10%. Yin et al. [44] claimed that the mid-plane formulation is not suitable for vibration analysis of FGM plates and that the neutral plane formulation must be employed instead. Van Do et al. [45] proved that, for simply supported cracked FGM plates, the error in thermal buckling is higher than 15% between the neutral surface and the mid-surface.

Motivated by the existing confusion, few studies have examined the mid-plane versus neutral plane formulations in the context of linear vibration [46,47] and bending [48] of FGM and laminated beams. Wang et al. [46] discussed how the controversial conclusion in some studies that the FGM beam must be based on the neutral plane formulation rather than the mid-plane one for correct solutions. They showed that, for FGM beams with clamped ends and movable simply supported ends, both formulations furnish the same frequency results. They also interpreted the difference in results of immovable simply supported FGM beams due to the assumption of fixation at two different planes. Rather than the middle and neutral plane formulations, Fernando et al. [47] adopted a formulation based on a reference plane where the end supports are applied on. The proposed formulation was used to calculate the vibration frequencies of laminated beams where the end immovable supports were placed at different heights. Their results were in excellent agreement with those obtained by finite element models based on generalized beam, composite shell, or 3D solid elements. Türker [48] investigated the influence of varying support positions through the beam thickness on bending analysis. The results revealed that the flexural rigidity of beams is significantly influenced by the support location.

One main contribution in this work is to remove some misconceptions about MS- and NS-formulations. Without restriction of generality, the analysis is applied to the linear bending of BDFGM plates using higher order shear deformation theories; starting with the fact that changing the coordinate system (from MS to NS) would not change the physics and performance of a plate provided that the boundary conditions are the same in both cases. Once a plate is modelled based on some reference plane, the boundary conditions must be satisfied on that plane. Generally, the MS and NS formulations share the same definition for the transverse displacement $w\left(x,y\right)$ which is independent of the thickness coordinate $z$. Accordingly, the boundary conditions on $w\left(x,y\right)$ and their derivatives have no effect on the results obtained by either formulation. However, attention has to be paid for the constraints involving in-plane displacements $u_0\left(x,y\right),v_0\left(x,y\right)$ since they refer to their values on the mid-plane in the MS formulation but refer to their values on the neutral plane in the NS formulation. In this study and for the first time, firstly, relations between in-plane displacement distributions on the middle- and neutral-planes are proven. Secondly, analytical expressions that relate rigidities and stress resultants associated with the two formulations are derived. Accordingly, the present analysis enables the exact transferring of boundary conditions from one reference plane to the other. The present theoretical analysis proves that MS- and NS-formulations produce identical responses for BDFG plates in cases of clamped and movable simply supported boundaries. However, they produce different responses in the case of immovable simply supported boundaries since each formulation assumes plate fixation at different planes. Further, numerical results show that the responses of an immovable simply supported BDFG plate obtained using the NS formulation are identical to those obtained by MS formulation if the transferred boundary condition (from NS- to MS-planes) are applied.

The problem formulations, constitutive equations, and equivalent stiffnesses relative to mid- and neutral surfaces are discussed in Section 2. Solution methodology including DQM for the governing variable coefficients partial differential equations, and derivation of the proposed modified boundary conditions are presented in Section 3. Section 4 proves the formulation and solution technique used in the analysis with previous works, and provides numerical results that illustrate some important features of neutral surface formulation and the effect of the transmitted boundary conditions on the bending response of the BDFG plate.

2. Theory and Formulation

2.1. Geometrical and Kinematic Relations

A rectangular plate of thickness $h$, length $a$ in the x-direction and width $b$ in the y-direction is shown in Figure 1. The displacement field based on a geometric middle surface MS and the four-variable high shear deformation theory with no shear correction factors can be expressed as:

$$u\left(x,y,z\right)=u_o\left(x,y\right)-z\frac{\partial w_b}{\partial x}-F\left(z\right)\frac{\partial w_s}{\partial x}$$

(1)

$$v\left(x,y,z\right)=v_o\left(x,y\right)-\mathrm{z}\frac{\partial w_b}{\partial y}-F\left(z\right)\frac{\partial w_s}{\partial y}$$

(2)

$$w\left(x,y,z\right)=w_b\left(x,y\right)+w_s\left(x,y\right)$$

(3)

Using the same four variables high shear deformation theory, the displacement field based on a neutral physical surface NS can be expressed as [25,32,49,50,51]:

$$u\left(x,y,z\right)=u_o\left(x,y\right)-\left(z-z_o\right)\frac{\partial w_b}{\partial x}-\left(F\left(z\right)-c_o\right)\frac{\partial w_s}{\partial x}$$

(4)

$$v\left(x,y,z\right)=v_o\left(x,y\right)-\left(z-z_o\right)\frac{\partial w_b}{\partial y}-\left(F\left(z\right)-c_o\right)\frac{\partial w_s}{\partial y}$$

(5)

$$w\left(x,y,z\right)=w_b\left(x,y\right)+w_s\left(x,y\right)$$

(6)

where

• the in-plane displacements $u_o,v_o$ in Equations (1)–(3) are defined at the middle surface, while $u_o,v_o$ in Equation (4) are defined at the neutral surface.
• ${\mathrm{w}}_{\mathrm{b}}{ \mathrm{and} \mathrm{w}}_{\mathrm{s}} \mathrm{stand} \mathrm{for} \mathrm{bending} \mathrm{and} \mathrm{shear} \mathrm{parts} \mathrm{of} \mathrm{the} \mathrm{transverse} \mathrm{displacement}, \mathrm{respectively}.$
• $z_o and$$c_o$ are neutral surface parameters that were evaluated by Wang et al. [52].

$$z_o=\mu \frac{{{\displaystyle \int }}_{-h/2}^{h/2}zE\left(x,z\right)dz}{{{\displaystyle \int }}_{-h/2}^{h/2}E\left(x,z\right)dz}, c_o=\mu \frac{{{\displaystyle \int }}_{-h/2}^{h/2}F\left(z\right)E\left(x,z\right)dz}{{{\displaystyle \int }}_{-h/2}^{h/2}E\left(x,z\right)dz}$$

(7)

where $E\left(x,z\right)$ is the equivalent Young’s modulus that will be identified by Equation (18).

• Factor $\mu$ equals one for the neutral surface (NS) and zero for the mid-surface (MS). Therefore, Equations (1)–(3) can be obtained from Equations (4)–(6).
• F(z) is a shape function that estimates the distribution of transverse shear stress/strain $\left({\mathsf{\tau }}_{\mathrm{xz}},{\mathsf{\tau }}_{\mathrm{yz}}\right)$ and may take several forms. In this work, $\mathrm{F}\left(\mathrm{z}\right)=\frac{4z^3}{3h^2}$ accounts not only for transverse shear strains, but also for a parabolic variation of the transverse shear strains through thickness, and consequently, there is no need to use shear correction coefficients in computing the shear stresses [53,54].

The normal and shear strains associated with the displacement field in Equations (4)–(6) are expressed as follows [1,52]:

$${\epsilon }_x={\epsilon }_x^o-\left(z-z_o\right)\frac{{\partial }^2{w}_b}{\partial x^2}-\left(F\left(z\right)-c_o\right)\frac{{\partial }^2{w}_s}{\partial x^2}$$

(8)

$${\epsilon }_y={\epsilon }_y^o-\left(z-z_o\right)\frac{{\partial }^2{w}_b}{\partial y^2}-\left(F\left(z\right)-c_o\right)\frac{{\partial }^2{w}_s}{\partial y^2}$$

(9)

$${\gamma }_{xy}= {\gamma }_{xy}^0-\left(z-z_o\right)\left(2\frac{{\partial }^2{w}_b}{\partial \mathrm{x}\partial \mathrm{y}}\right)-\left(F\left(z\right)-c_o\right)\left(2\frac{{\partial }^2{w}_s}{\partial \mathrm{x}\partial \mathrm{y}}\right)$$

(10)

$${\gamma }_{yz}=G\left(z\right)\frac{\partial w_s}{\partial y}$$

(11)

$${\gamma }_{xz}=G\left(z\right)\frac{\partial w_s}{\partial x}$$

(12)

where

$$\begin{array}{c}{\epsilon }_x^o=\frac{\partial u_o}{\partial x}+z_{o,x}\frac{\partial w_b}{\partial x}+c_{o,x}\frac{\partial w_s}{\partial x},\\ {\epsilon }_y^o=\frac{\partial v_o}{\partial y} and {\gamma }_{xy}^o=\frac{\partial u_o}{\partial y}+\frac{\partial v_o}{\partial x}+z_{o,x}\frac{\partial w_b}{\partial x}+c_{o,x}\frac{\partial w_s}{\partial x}\end{array}$$

(13)

$$F\left(z\right)=z-f\left(z\right) \mathrm{and} G\left(z\right)=1-F^{\prime }\left(z\right)=f^{\prime }\left(z\right)$$

(14)

2.2. Constitutive Equations

The stress–strain relations (plane stress) considering the 2D shear deformation theory are $\left({\mathsf{\epsilon }}_{\mathit{z}}=0\right):$

$$\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\\ {\tau }_{yz}\\ {\tau }_{xz}\end{array}\right]=\left[\begin{array}{ccccc}{Q}_{11}& Q_{12}& 0& 0& 0\\ Q_{12}& Q_{22}& 0& 0& 0\\ 0& 0& Q_{66}& 0& 0\\ 0& 0& 0& Q_{44}& 0\\ 0& 0& 0& 0& Q_{55}\end{array}\right]\left[\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right]$$

(15)

For isotropic materials, the plane stress stiffnesses are:

$$Q_{11}=Q_{22}=\frac{E}{1-v^2}, Q_{12}=\frac{\nu E}{1-v^2}$$

(16)

$$Q_{44}=Q_{55}=Q_{66}=\frac{E}{2\left(1+\nu \right)}$$

(17)

In a BDFG material, Young’s modulus $E$ is assumed to vary in the z- and x-directions. According to power law with indexes $n_z$, $n_x$ and including porosity, $E$ can be expressed as:

$$E\left(x,z\right)=E_m+\left(E_c-E_m\right){\left(\frac{1}{2}+\frac{z}{h}\right)}^{n_z}{\left(\frac{x}{a}\right)}^{n_x}$$

(18)

Subscripts c and m stand for ceramic and metal, respectively. Poisson’s ratio $\nu$ is assumed to be constant for each constituent.

2.3. Hamilton’s Principles and Equlibrium Equations

The governing equations of equilibrium and associated boundary conditions of the developed linear static model are derived using the static version of Hamilton’s principles, which can be described as:

$${\displaystyle {\int }_0^T}\delta \left(U+V\right)dt=0$$

(19)

where the virtual potential work of applied loads can be expressed in the form, $\delta V$:

$$\delta V=-\underset{A}{{\displaystyle \int }}q\delta \left(w_b+w_s\right)dA$$

(20)

The virtual strain energy $\delta U$ can be evaluated by:

$$\delta U={\displaystyle {\int }_V}\left({\sigma }_x\delta {\epsilon }_x+{\sigma }_y\delta {\epsilon }_y+{\tau }_{xy}\delta {\gamma }_{xy}+{\tau }_{xz}\delta {\gamma }_{xz}+{\tau }_{yz}\delta {\gamma }_{yz}\right)dV$$

(21)

The virtual strain energy, $\delta U$ in terms of stress resultants is derived as

$$\begin{array}{l}\delta U={\displaystyle {\int }_A}[N_x\delta {\epsilon }_x^0+N_y\delta {\epsilon }_y^0+N_{xy}\delta {\gamma }_{xy}^0-M_x^b\frac{{\partial }^2\delta w_b}{\partial x^2}-M_y^b\frac{{\partial }^2\delta w_b}{\partial y^2}-M_{xy}^b\left(2\frac{{\partial }^2\delta w_b}{\partial x\partial y}\right)-M_x^s\frac{{\partial }^2\delta w_s}{\partial x^2}-M_y^s\frac{{\partial }^2\delta w_s}{\partial y^2}\\ - M_{xy}^s\left(2\frac{{\partial }^2\delta w_s}{\partial x\partial y}\right)+S_{yz}^s\frac{\partial \delta w_s}{\partial y}+S_{xz}^s\frac{\partial \delta w_s}{\partial x}]dA\end{array}$$

(22)

Neglecting derivatives of $z_0 and c_0$ with respect to x, the stress resultants can be expressed in terms of generalized displacements $\left(u_o,v_o,w_b,w_s\right)$ in a matrix form as:

$$\left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\\ M_x^b\\ M_y^b\\ M_{xy}^b\\ M_x^s\\ M_y^s\\ M_{xy}^s\end{array}\right]=\left[\begin{array}{ccccccccc}{A}_{11}& A_{12}& 0& B_{11}& B_{12}& 0& B_{11}^s& B_{12}^s& 0\\ A_{12}& A_{22}& 0& B_{12}& B_{22}& 0& B_{12}^s& B_{22}^s& 0\\ 0& 0& A_{66}& 0& 0& B_{66}& 0& 0& B_{66}^s\\ B_{11}& B_{12}& 0& D_{11}& D_{12}& 0& D_{11}^s& D_{12}^s& 0\\ B_{12}& B_{22}& 0& D_{12}& D_{22}& 0& D_{12}^s& D_{22}^s& 0\\ 0& 0& B_{66}& 0& 0& D_{66}& 0& 0& D_{66}^s\\ B_{11}^s& B_{12}^s& 0& D_{11}^s& D_{12}^s& 0& H_{11}^s& H_{12}^s& 0\\ B_{12}^s& B_{22}^s& 0& D_{12}^s& D_{22}^s& 0& H_{12}^s& H_{22}^s& 0\\ 0& 0& B_{66}^s& 0& 0& D_{66}^s& 0& 0& H_{66}^s\end{array}\right]\left[\begin{array}{c}\partial u_o/\partial x\\ \partial v_o/\partial y\\ \partial u_o/\partial y+\partial v_o/\partial x\\ -{\partial }^2{w}_b/{\partial }^{2}x\\ -{\partial }^2{w}_b/{\partial }^{2}y\\ -2{\partial }^2{w}_b/\partial x\partial y\\ -{\partial }^2{w}_s/{\partial }^{2}x\\ -{\partial }^2{w}_s/{\partial }^{2}y\\ -2{\partial }^2{w}_s/\partial x\partial y\end{array}\right]$$

(23)

$$\left[\begin{array}{c}{S}_{yz}^s\\ S_{xz}^s\end{array}\right]=\left[\begin{array}{cc}{A}_{44}^s& 0\\ 0& A_{55}^s\end{array}\right]\left[\begin{array}{c}\partial w_s/\partial y\\ \partial w_s/\partial x\end{array}\right]$$

(24)

Substituting Equations (12)–(20) for $\delta V$ and $\delta U$, respectively, into Equation (19) and performing integration by parts, the equations of the BDFG plate in terms of stress resultants are obtained as:

$$\delta u_o: \frac{\partial N_x}{\partial x}+\frac{\partial N_{xy}}{\partial y}=0$$

(25)

$$\delta v_o: \frac{\partial N_{xy}}{\partial x}+\frac{\partial N_y}{\partial y}=0$$

(26)

$$\delta w_b: \frac{{\partial }^2{M}_x^b}{\partial x^2}+2\frac{{\partial }^2{M}_{xy}^b}{\partial x\partial y}+\frac{{\partial }^2{M}_y^b}{\partial y^2}+q=0$$

(27)

$$\delta w_s: \frac{{\partial }^2{M}_x^s}{\partial x^2}+2\frac{{\partial }^2{M}_{xy}^s}{\partial x\partial y}+\frac{{\partial }^2{M}_y^s}{\partial y^2}+\frac{\partial S_{yz}^s}{\partial y}+\frac{\partial S_{xz}^s}{\partial x}+q=0$$

(28)

Associated with the following boundary conditions:

$$\delta u_0: \left(N_x{\overline{n}}_x+N_{xy}{\overline{n}}_y\right)\delta u_0=0$$

(29)

$$\delta v_o: \left(N_{xy}{\overline{n}}_x+N_y{\overline{n}}_y\right)\delta v_o=0$$

(30)

$$\delta w_b: \left(M_{x,x}^b{\overline{n}}_x+M_{xy,y}^b{\overline{n}}_x+M_{xy,x}^b{\overline{n}}_y+M_{y,y}^b{\overline{n}}_y\right)\delta w_b=0$$

(31)

$$\frac{\partial \delta w_b}{\partial x}: \left(M_x^b{\overline{n}}_x+M_{xy}^b{\overline{n}}_y\right)\frac{\partial \delta w_b}{\partial x}=0$$

(32)

$$\frac{\partial \delta w_b}{\partial y}: \left(M_{xy}^b{\overline{n}}_x+M_y^b{\overline{n}}_y\right)\frac{\partial \delta w_b}{\partial y}=0$$

(33)

$$\delta w_s: \left(M_{x,x}^s{\overline{n}}_x+M_{xy,y}^s{\overline{n}}_x+M_{xy,x}^s{\overline{n}}_y+M_{y,y}^s{\overline{n}}_y+S_{xz}^s{\overline{n}}_x+S_{yz}^s{\overline{n}}_y\right)\delta w_s=0$$

(34)

$$\frac{\partial \delta w_s}{\partial x}: \left(M_x^s{\overline{n}}_x+M_{xy}^s{\overline{n}}_y\right)\frac{\partial \delta w_s}{\partial x}=0$$

(35)

$$\frac{\partial \delta w_s}{\partial y}: \left(M_{xy}^s{\overline{n}}_x+M_y^s{\overline{n}}_y\right)\frac{\partial \delta w_s}{\partial y}=0$$

(36)

where ${\overline{n}}_x$ and ${\overline{n}}_y$ are the components of the outward normal at boundaries.

2.4. Equivalent Stiffnesses Based on Mid-Plane (MS)

To consider the geometric middle surface of the plate, put $z_o and c_o$ as zero-valued ($\mu =0)$ in displacement and strain fields of Equations (4)–(14). Rigidity terms are obtained as functions of x as:

$$\begin{gathered} {\left[(A_{\mathrm{ij}}\left(x\right),B_{\mathrm{ij}}\left(x\right),D_{\mathrm{ij}}\left(x\right),B_{\mathrm{ij}}^s\left(x\right),D_{\mathrm{ij}}^s\left(x\right),H_{\mathrm{ij}}^s\left(x\right))\right]}^{\left(MS\right)}= \\ {\displaystyle {\int }_{-h/2}^{h/2}}{Q}_{\mathrm{ij}}\left(x,z\right)\left[1,z,z^2,F\left(z\right),zF\left(z\right),{\left(F\left(z\right)\right)}^2\right]dz, ij=11,12,22,66 \end{gathered}$$

(37)

$$A_{\mathrm{ij}}^s\left(x\right)={\displaystyle {\int }_{-h/2}^{h/2}}{Q}_{\mathrm{ij}}\left(x,z\right){(G\left(z\right))}^{2}dz, \mathrm{ij}=44, 55$$

(38)

$Q_{\mathrm{ij}}\left(x,z\right)$ and $E\left(x,z\right)$ are defined by Equations (4) and (5), respectively.

2.5. Equivalent Stiffnesses Based on Neutral Physical Plane (NS)

Due to the use of $z_o and c_o \left(\mu =1\right)$ defined by Equation (7) in the displacement field of Equation (4), the plate stiffnesses $B_{ij}\left(x\right) and B_{ij}^s\left(x\right)$ are zero-valued. Subsequently, stretching–bending couplings in Equation (23) die out. Therefore, rigidity terms are modified as functions of x to:

$$\begin{array}{l}{\left[(A_{\mathrm{ij}}\left(x\right),D_{\mathrm{ij}}\left(x\right),D_{\mathrm{ij}}^s\left(x\right),H_{\mathrm{ij}}^s\left(x\right))\right]}^{\left(NS\right)}={\displaystyle {\int }_{-h/2}^{h/2}}{Q}_{\mathrm{ij}}\left(x,z\right)(1,{(z-z_o)}^2,(z-z_o)(F\left(z\right)-\\ c_o),{(F\left(z\right)-c_o)}^2)dz ij=11,12,22,66\end{array}$$

(39)

$$A_{\mathrm{ij}}^s\left(x\right)={\displaystyle {\int }_{-h/2}^{h/2}}{Q}_{\mathrm{ij}}\left(x,z\right){(G\left(z\right))}^{2}dz, \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{ij}=44, 55$$

(40)

2.6. Relations between Stress Resultants Based on MS and NS Formulations

The displacement fields for the MS and NS formulations are defined in Equations (1)–(3) and (4)–(6), respectively. Both formulations define the same transverse displacement $w\left(x,y\right)$ which is assumed to be independent of the thickness coordinate $z$. Attention must be paid for the in-plane displacements $u_0\left(x,y\right),v_0\left(x,y\right)$ that refer to their values on the reference plane of each formulation.

In the NS formulation, Equations (4)–(6), the in-plane displacement distributions can be better written as:

$$u\left(x,y,z\right)=u_o^{NS}\left(x,y\right)-\left(z-z_o\right)\frac{\partial w_b}{\partial x}-\left(F\left(z\right)-c_o\right)\frac{\partial w_s}{\partial x}$$

(41)

$$v\left(x,y,z\right)=v_o^{NS}\left(x,y\right)-\left(z-z_o\right)\frac{\partial w_b}{\partial y}-\left(F\left(z\right)-c_o\right)\frac{\partial w_s}{\partial y}$$

(42)

in which $u_o^{NS}\left(x,y\right) and v_o^{NS}\left(x,y\right)$ are the in-plane displacements at the neutral surface $\left(z=z_0\right)$.

The in-plane displacement distribution on the middle-plane can be obtained by substituting $z=0$ in Equations (41) and (42).

$$u_o^{MS}\left(x,y\right)=u_o^{NS}\left(x,y\right)+z_o\frac{\partial w_b}{\partial x}+c_o\frac{\partial w_s}{\partial x}$$

(43)

$$v_o^{MS}\left(x,y\right)=v_o^{NS}\left(x,y\right)+z_o\frac{\partial w_b}{\partial y}+c_o\frac{\partial w_s}{\partial y}$$

(44)

Equation (3) defines the neutral surface parameters $z_o,c_0$ from which

$$\begin{gathered} {{\displaystyle \int }}_{-h/2}^{h/2}z E\left(x,z\right)dz =z_o{{\displaystyle \int }}_{-h/2}^{h/2}E\left(x,z\right)dz, {{\displaystyle \int }}_{-h/2}^{h/2}F\left(z\right)E\left(x,z\right)dz=c_o{{\displaystyle \int }}_{-h/2}^{h/2}E\left(x,z\right)dz \\ \underset{B_{ij}^{\left(MS\right)}}{\underbrace{{{\displaystyle \int }}_{-h/2}^{h/2}z Q_{ij}\left(x,z\right)dz}} =z_o\underset{A_{ij}}{\underbrace{{{\displaystyle \int }}_{-h/2}^{h/2}{Q}_{ij}\left(x,z\right)dz}}, \underset{B_{ij}^{s\left(MS\right)}}{\underbrace{{{\displaystyle \int }}_{-h/2}^{h/2}F\left(z\right)Q_{ij}\left(x,z\right)dz}}=c_o{{\displaystyle \int }}_{-h/2}^{h/2}{Q}_{ij}\left(x,z\right)dz \\ {B}_{ij}^{\left(MS\right)}= z_o{A}_{ij}, B_{ij}^{s\left(MS\right)}= c_o{A}_{ij}, B_{ij}^{\left(NS\right)}=0, B_{ij}^{s\left(NS\right)}=0, ij=11,12,22,66 \end{gathered}$$

(45)

Note also that, from Equation (39)

$$\begin{gathered} D_{ij}^{\left(NS\right)}={{\displaystyle \int }}_{-h/2}^{h/2}{\left(z-z_0\right)}^2 Q_{ij}\left(x,z\right)dz={{\displaystyle \int }}_{-h/2}^{h/2}{z}^2 Q_{ij}\left(x,z\right)dz-2z_0\underset{z_o{A}_{ij}}{\underbrace{{{\displaystyle \int }}_{-h/2}^{h/2}z Q_{ij}\left(x,z\right)dz}}+z_0^2\underset{A_{ij}}{\underbrace{{{\displaystyle \int }}_{-h/2}^{h/2} Q_{ij}\left(x,z\right)dz}} \\ {D}_{ij}^{\left(NS\right)}=D_{ij}^{\left(MS\right)}-z_0^2{A}_{ij}, similarly D_{ij}^{s\left(NS\right)}=D_{ij}^{s\left(MS\right)}-z_0{c}_0{A}_{ij}, ij=11,12,22,66 \end{gathered}$$

(46)

For the stress resultant, $N_x$, since it depends on the in-plane displacements, its value may depend on the used formulation; however, from Equation (23) and using Equations (43)–(45), note that

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}{N}_x^{\left(MS\right)}=A_{11} \frac{\partial u_0^{MS}}{\partial x}+A_{12} \frac{\partial v_0^{MS}}{\partial y}-B_{11}^{\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}x}-B_{12}^{\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}y}-B_{11}^{s\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}x}-B_{12}^{s\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}y}\\ \hspace{1em}\hspace{1em}\hspace{1em}=A_{11} \frac{\partial \left(u_o^{NS}\left(x,y\right)+{\mathrm{z}}_0\frac{\partial {\mathrm{w}}_{\mathrm{b}}}{\partial x}+{\mathrm{c}}_0\frac{\partial {\mathrm{w}}_{\mathrm{s}}}{\partial x}\right)}{\partial x}+A_{12} \frac{\partial \left(v_o^{NS}\left(x,y\right)+{\mathrm{z}}_0\frac{\partial {\mathrm{w}}_{\mathrm{b}}}{\partial y}+{\mathrm{c}}_0\frac{\partial {\mathrm{w}}_{\mathrm{s}}}{\partial y}\right)}{\partial y}-z_o{A}_{11}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}x}-z_o{A}_{12}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}y}-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{c}_o{A}_{11}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}x}-c_o{A}_{12}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}y}\\ \hspace{1em}\hspace{1em}\hspace{1em} =A_{11} \frac{\partial u_0^{NS}}{\partial x}+A_{12} \frac{\partial v_0^{NS}}{\partial y}=N_x^{\left(NS\right)}\\ \mathrm{That} \mathrm{is}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{N}_x^{\left(MS\right)}=N_x^{\left(NS\right)}, \text{similarly} N_y^{\left(MS\right)}=N_y^{\left(NS\right)}\end{array}$$

(47)

Finally, the relation between bending stress resultants $M_x^{\left(MS\right)}$ and $M_x^{\left(NS\right)}$ is derived. From Equation (23) and using Equations (43)–(46)

$$\begin{gathered} M_x^{b\left(MS\right)}=B_{11}^{\left(MS\right)} \frac{\partial u_0^{MS}}{\partial x}+B_{12}^{\left(MS\right)} \frac{\partial v_0^{MS}}{\partial y}-D_{11}^{\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}x} –D_{12}^{\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}y}-D_{11}^{s\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}x} –D_{12}^{s\left(MS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}y} \\ {M}_x^{b\left(MS\right)}=z_o\underset{N_x^{\left(NS\right)}}{\underbrace{\left(A_{11} \frac{\partial u_o^{NS}}{\partial x}+A_{12} \frac{\partial v_o^{NS}}{\partial y}\right)}}+\underset{M_x^{b\left(NS\right)}}{\underbrace{\left(-D_{11}^{\left(NS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}x}-D_{12}^{\left(NS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{b}}}{{\partial }^{2}y}-D_{11}^{s\left(NS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}x}-D_{12}^{s\left(NS\right)}\frac{{\partial }^2{\mathrm{w}}_{\mathrm{s}}}{{\partial }^{2}y}\right)}} \\ \begin{array}{ccc}{M}_x^{b\left(MS\right)}=M_x^{b\left(NS\right)}+z_o{N}_x^{\left(NS\right)},\text{similarly}\hfill & & M_y^{b\left(MS\right)}=M_y^{b\left(NS\right)}+z_o{N}_y^{\left(NS\right)},\hfill \\ M_x^{s\left(MS\right)}=M_x^{s\left(NS\right)}+c_o{N}_x^{\left(NS\right)},\hfill & & M_y^{s\left(MS\right)}=M_y^{s\left(NS\right)}+c_o{N}_y^{\left(NS\right)},\hfill \end{array} \end{gathered}$$

(48)

It is worth noting that stretching–bending couplings vanish in the governing equations obtained based on the NS formulation because of disappearance of the stiffnesses $B_{ij}\left(x\right) and B_{ij}^s\left(x\right), ij=11,12,22,66$.

3. Numerical Methodology

A set of four partial differential governing equations and associated boundary conditions were developed based on stress resultants to model the static response of BDFG plates in Equations (12) and (13), respectively. The assumption that the material properties change in the x-direction complicates the governing equations since they become variable-coefficients and consequently no analytical solution can be found. In this work, the differential/integral quadrature method (DIQM) [55,56] is developed to numerically solve the governing equations of a rectangular plate $\left(0\le x\le a,0\le y\le b\right)$ with the following boundary conditions.

• Clamped BCs:

$$u_0=v_0=w_b=w_s=\frac{\partial w_b}{\partial x}=\frac{\partial w_s}{\partial x}=0 at x=0,x=a$$

(49)

$$u_0=v_0=w_b=w_s=\frac{\partial w_b}{\partial y}=\frac{\partial w_s}{\partial y}=0 at y=0,y=b$$

(50)

• Simply supported BCs:

Type 1 ($S_m)$ (movable normal in-plane displacement)

$$N_x=v_0=w_b=w_s=M_x^b=M_x^s=0 at x=0,x=a$$

(51)

$$u_0=N_{\mathrm{y}}=w_b=w_s=M_y^b=M_y^s=0 at y=0,y=b$$

(52)

Type 2 ($S_{im})$ (immovable normal in-plane displacement)

$$u_0=v_0=w_b=w_s=M_x^b=M_x^s=0 at x=0,x=a$$

(53)

$$u_0=v_0=w_b=w_s=M_y^b=M_y^s=0 at y=0,y=b$$

(54)

3.1. DQM Implementation for PDE

The DIQM was employed by [56] to solve linear and nonlinear integro-differential equations. It was found that DIQM provides highly accurate results using only a few grid points. It transforms the integro-differential equations into a system of algebraic equations. In this section, the details of DIQM for partial differential equations are presented. Consider a partial differential equation in the unknown function $u\left(x,y\right)$. The 2D domain of the independent variables $0<x<a, 0<y<b$ is discretized by $n$- and $m$-points, respectively. The unknowns $u_{ij}=u\left(x_j,y_i\right), i=1,\cdots ,m, j=1,\cdots ,n$ defined on the rectangular domain are rearranged vector after vector to form the whole unknown vector

$$\mathit{U}={\left[u_{11},u_{21},\cdots u_{m1},u_{12},u_{22},\cdots u_{m2},\cdots ,\cdots ,u_{1n},u_{2n},\cdots u_{mn} \right]}^T$$

(55)

Using classical definitions for DQM in one dimension [57], let $D_x$ be the first order derivative matrix with respect to $x$ of dimension $n\times n$, and let $D_y$ be the first order derivative matrix with respect to $y$ of dimension $m\times m$. To be consistent with the arrangement of unknowns given in Equation (55) for vector $\mathit{U}$, the Kronecker product is used to construct global derivative matrices of dimension $\left(mn\times mn\right)$ as:

$${\mathbb{D}}_x=Kronecker\left(D_x,I\left(m\right)\right)$$

(56)

$${\mathbb{D}}_y=Kronecker\left(I\left(n\right),D_y\right)$$

(57)

where $I\left(n\right)$ and $I\left(m\right)$ are the identity matrices of dimensions $\left(n\times n\right)$ and $\left(m\times m\right)$, respectively. Based on Equations (56) and (57), DQM can approximate higher and mixed partial derivatives such as ${\partial }^{2}u/\partial x^2$, ${\partial }^{2}u/\partial y^2$, ${\partial }^{2}u/\partial x\partial y$ by ${\mathbb{D}}_{xx}\mathit{U}, {\mathbb{D}}_{yy} \mathit{U}$ and ${\mathbb{D}}_{xy}\mathit{U}$, respectively, where ${\mathbb{D}}_{xx}={\mathbb{D}}_x^2, {\mathbb{D}}_{yy}={\mathbb{D}}_y^2, \mathrm{and} {\mathbb{D}}_{xy}={\mathbb{D}}_x{\mathbb{D}}_y$.

3.2. DQM Discretization for PDF

The governing equations for the BDFG plate consist of four variable-coefficient partial differential equations in the unknowns $u_0\left(x,y\right), v_0\left(x,y\right),w_b\left(x,y\right)$ and $w_s\left(x,y\right)$. They are discretized by DQM as the unknown vectors $U,V,W_b \mathrm{and} W_s$, each of dimension $\left(nm\times 1\right)$. Moreover, the variable coefficients $A_{\mathrm{ij}}\left(x\right), B_{\mathrm{ij}}\left(x\right),D_{\mathrm{ij}}\left(x\right),B_{\mathrm{ij}}^s\left(x\right),$ $D_{\mathrm{ij}}^s\left(x\right),$ $H_{\mathrm{ij}}^s\left(x\right),\mathrm{ij}=11,12,22,66$ and $A_{\mathrm{ij}}^s\left(x\right), \mathrm{ij}=44, 55$ are defined for the MS- and NS-formulations in Equations (14) and (15), respectively. These coefficients are computed by IQM and arranged as $\left(nm\times 1\right)$ vectors ${\mathcal{A}}_{\mathrm{ij}}, {ℬ}_{\mathrm{ij}},{\mathcal{D}}_{\mathrm{ij}},{ℬ}_{\mathrm{ij}}^s,{\mathcal{D}}_{\mathrm{ij}}^{\mathrm{s}},{\mathscr{H}}_{\mathrm{ij}}^{\mathrm{s}},ij=11,12,22,66$ and ${\mathcal{A}}_{44}^s, {\mathcal{A}}_{55}^s$. For the convenience of applying DQM to discretize the variable-coefficient partial differential equations, a special matrices multiplication operator is introduced. The operator $‘\circ ’$ is defined such that for a vector $\mathcal{V}$ of dimensions $\left(𝓃\times 1\right)$ and a matrix $ℳ$ of dimensions $\left(𝓃\times 𝓂\right)$ (i.e., each of $\mathcal{V}$ and $ℳ$ must have the same number of rows), $\mathcal{V} \circ ℳ=\mathcal{Y},$ which implies that $\mathcal{Y}$ is a $\left(𝓃\times 𝓂\right)$-matrix, such that ${\mathcal{Y}}_{ij}={\mathcal{V}}_i{ℳ}_{ij}$.

Applying the DQM as described in Section 3.1, the stress resultants can be written as:

$$\left[\begin{array}{c}\begin{array}{c}{\mathit{N}}_x\\ {\mathit{N}}_y\\ {\mathit{N}}_{xy}\end{array}\\ {\mathit{M}}_x^b\\ {\mathit{M}}_y^b\\ {\mathit{M}}_{xy}^b\\ {\mathit{M}}_x^s\\ {\mathit{M}}_y^s\\ {\mathit{M}}_{xy}^s\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{\mathcal{K}}_{N_x}\\ {\mathcal{K}}_{N_y}\\ {\mathcal{K}}_{N_{xy}}\end{array}\\ {\mathcal{K}}_{M_x^b}\\ {\mathcal{K}}_{M_y^b}\\ {\mathcal{K}}_{M_{xy}^b}\\ {\mathcal{K}}_{M_x^s}\\ {\mathcal{K}}_{M_y^s}\\ {\mathcal{K}}_{M_{xy}^s}\end{array}\right]\mathcal{X}$$

(58)

where each of {${\mathcal{K}}_{N_x},{\mathcal{K}}_{N_y},\cdots ,{\mathcal{K}}_{M_{xy}^s}\}$ is a $\left(nm\times 4nm\right)$ matrix,

$$\mathcal{X}={\left[{\mathit{U}}^T,{\mathit{V}}^T,{\mathit{W}}_b^T,{\mathit{W}}_s^T\right]}^T,$$

(59)

$$\begin{array}{ccc}\left[\begin{array}{c}{\mathcal{K}}_{N_x}\\ {\mathcal{K}}_{N_y}\\ {\mathcal{K}}_{N_{xy}}\\ {\mathcal{K}}_{M_x^b}\\ {\mathcal{K}}_{M_y^b}\\ {\mathcal{K}}_{M_{xy}^b}\\ {\mathcal{K}}_{M_x^s}\\ {\mathcal{K}}_{M_y^s}\\ {\mathcal{K}}_{M_{xy}^s}\end{array}\right]& =& \left[\begin{array}{cccc}{\mathcal{A}}_{11}\circ {\mathbb{D}}_x& {\mathcal{A}}_{12}\circ {\mathbb{D}}_y& -({\mathcal{B}}_{11}\circ {\mathbb{D}}_{xx}+{\mathcal{B}}_{12}\circ {\mathbb{D}}_{yy})& -({\mathcal{B}}_{11}^s\circ {\mathbb{D}}_{xx}+{\mathcal{B}}_{12}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{A}}_{12}\circ {\mathbb{D}}_x& {\mathcal{A}}_{22}\circ {\mathbb{D}}_y& -({\mathcal{B}}_{12}\circ {\mathbb{D}}_{xx}+{\mathcal{B}}_{22}\circ {\mathbb{D}}_{yy})& -({\mathcal{B}}_{12}^s\circ {\mathbb{D}}_{xx}+{\mathcal{B}}_{22}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{A}}_{66}\circ {\mathbb{D}}_y& {\mathcal{A}}_{66}\circ {\mathbb{D}}_x& -2{\mathcal{B}}_{66}\circ {\mathbb{D}}_{xy}& -2{\mathcal{B}}_{66}^s\circ {\mathbb{D}}_{xy}\\ {\mathcal{B}}_{11}\circ {\mathbb{D}}_x& {\mathcal{B}}_{12}\circ {\mathbb{D}}_y& -({\mathcal{D}}_{11}\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{12}\circ {\mathbb{D}}_{yy})& -({\mathcal{D}}_{11}^s\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{12}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{B}}_{12}\circ {\mathbb{D}}_x& {\mathcal{B}}_{22}\circ {\mathbb{D}}_y& -({\mathcal{D}}_{12}\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{22}\circ {\mathbb{D}}_{yy})& -({\mathcal{D}}_{12}^s\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{22}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{B}}_{66}\circ {\mathbb{D}}_y& {\mathcal{B}}_{66}\circ {\mathbb{D}}_x& -2{\mathcal{D}}_{66}\circ {\mathbb{D}}_{xy}& -2{\mathcal{D}}_{66}^s\circ {\mathbb{D}}_{xy}\\ {\mathcal{B}}_{11}^s\circ {\mathbb{D}}_x& {\mathcal{B}}_{12}^s\circ {\mathbb{D}}_y& -({\mathcal{D}}_{11}^s\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{12}^s\circ {\mathbb{D}}_{yy})& -({\mathcal{H}}_{11}^s\circ {\mathbb{D}}_{xx}+{\mathcal{H}}_{12}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{B}}_{12}^s\circ {\mathbb{D}}_x& {\mathcal{B}}_{22}^s\circ {\mathbb{D}}_y& -({\mathcal{D}}_{12}^s\circ {\mathbb{D}}_{xx}+{\mathcal{D}}_{22}^s\circ {\mathbb{D}}_{yy})& -({\mathcal{H}}_{12}^s\circ {\mathbb{D}}_{xx}+{\mathcal{H}}_{22}^s\circ {\mathbb{D}}_{yy})\\ {\mathcal{B}}_{66}^s\circ {\mathbb{D}}_y& {\mathcal{B}}_{66}^s\circ {\mathbb{D}}_x& -2{\mathcal{D}}_{66}^s\circ {\mathbb{D}}_{xy}& -2{\mathcal{H}}_{66}^s\circ {\mathbb{D}}_{xy}\end{array}\right]\end{array}$$

(60)

Substituting Equations (58)–(60) into Equation (25)–(28) and applying DQM to discretize the governing differential equations into the following linear algebraic system:

$$\begin{array}{cc}{\left[\begin{array}{c}{\mathbb{D}}_x {\mathcal{K}}_{N_x}+{\mathbb{D}}_y {\mathcal{K}}_{N_{xy}}\\ {\mathbb{D}}_x {\mathcal{K}}_{N_{xy}}+{\mathbb{D}}_y {\mathcal{K}}_{N_y}\\ {\mathbb{D}}_{xx} {\mathcal{K}}_{M_x^b}+2{\mathbb{D}}_{xy} {\mathcal{K}}_{M_{xy}^b}+{\mathbb{D}}_{yy} {\mathcal{K}}_{M_y^b}\\ {\mathbb{D}}_{xx} {\mathcal{K}}_{M_x^s}+2{\mathbb{D}}_{xy} {\mathcal{K}}_{M_{xy}^s}+{\mathbb{D}}_{yy} {\mathcal{K}}_{M_y^s}+{\mathbb{D}}_y S_{yz}^s+{\mathbb{D}}_x S_{xz}^s\end{array}\right]}_{4mn\times 4mn}& \mathcal{X}=\mathit{F}\end{array}$$

(61)

where $F$ is the force vector and

$$S_{yz}^s=\left[O O O {\mathcal{A}}_{44}^s\circ {\mathbb{D}}_y\right], S_{xz}^s=\left[O O O {\mathcal{A}}_{55}^s\circ {\mathbb{D}}_x\right]$$

and $O$ is a zero matrix of dimension $\left(mn\times mn\right)$.

3.3. Remarks on Algebraic Systems of MS and NS Formulations

Equation (61) can be split in the form:

$$\left[\begin{array}{cc}{L}_{ss}& L_{sb}\\ L_{bs}& L_{bb}\end{array}\right]\left[\begin{array}{c}{\mathcal{X}}_{\mathit{s}}=\left\{\begin{array}{c}\mathit{U}\\ \mathit{V}\end{array}\right\}\\ {\mathcal{X}}_{\mathit{b}}=\left\{\begin{array}{c}{\mathit{W}}_b\\ {\mathit{W}}_s\end{array}\right\}\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_s\\ {\mathit{F}}_b\end{array}\right]$$

(62)

where subscripts s and b denote stretching and bending components, respectively. Since the coefficient vectors $\left\{{\mathcal{A}}_{\mathrm{ij}}, {ℬ}_{\mathrm{ij}},{\mathcal{D}}_{\mathrm{ij}},{ℬ}_{\mathrm{ij}}^s,{\mathcal{D}}_{\mathrm{ij}}^{\mathrm{s}},{\mathscr{H}}_{\mathrm{ij}}^{\mathrm{s}},ij=11,12,22,66\right\}$ appearing in the stress resultants Equation (60) are computed differently for the middle and neutral surface formulations (see Equations (37)–(40)), the discretized algebraic systems based on the two formulations are different. The main advantage of the neutral surface formulation (NS) is that the chosen values of $z_0,c_0$ as defined in Equation (7) imply that $\left\{{ℬ}_{\mathrm{ij}}^{\left(NS\right)}={ℬ}_{\mathrm{ij}}^{s\left(NS\right)}=0,ij=11,12,22,66\right\},$ and accordingly, the sub-matrices $L_{sb},L_{bs}$ vanish, and thus the stretching and bending equations are uncoupled. This simplified feature of the NS formulation is a benefit for obtaining analytical solutions. The discretized algebraic systems for the governing equations based on MS and NS formulations can be put in the forms:

$$\left[\begin{array}{cc}{L}_{ss}^{MS}& L_{sb}^{MS}\\ L_{bs}^{MS}& L_{bb}^{MS}\end{array}\right]\left[\begin{array}{c}{\mathcal{X}}_{\mathit{s}}^{MS}\\ {\mathcal{X}}_b^{MS}\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_s\\ {\mathit{F}}_b\end{array}\right]$$

(63)

$$\left[\begin{array}{cc}{L}_{ss}^{NS}& \mathcal{O}\\ \mathcal{O}& L_{bb}^{NS}\end{array}\right]\left[\begin{array}{c}{\mathcal{X}}_s^{NS}\\ {\mathcal{X}}_b^{NS}\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_s\\ {\mathit{F}}_b\end{array}\right]$$

(64)

where $\mathcal{O}$ is a zero matrix of dimension $\left(2mn\times 2mn\right)$. The algebraic systems (Equations (63) and (64)) represent the discretization of the governing equations and need be modified by adding contributions of proper BCs.

It is understood that changing the coordinate system (from MS to NS) would not change the physics and performance of a plate provided that the boundary conditions are the same in both cases. The main objective in this work is to analyze and discuss the following questions. Are solutions based on MS and NS algebraic systems identical? What is the effect of boundary conditions on the solutions?

3.4. Application of Different Boundary Conditions for MS and NS Formulations

It is important to mention that, once the governing equations are derived based on some reference plane, the associated boundary conditions must be satisfied on that plane. That is, the boundary conditions (BCs) must be applied on plane $z=0$ in the MS formulation and on $z=z_0$ plane in the NS formulation. Both of the MS and NS formulations share the same definition for the transverse displacements $w_b\left(x,y\right)$, $w_s\left(x,y\right)$ which are assumed to be independent of the thickness coordinate. Accordingly, the boundary conditions on $w_b\left(x,y\right),w_s\left(x,y\right)$ and their derivatives have no effect on the results obtained by either formulation. However, attention has to be paid for the constraints involving in-plane displacements $u_0\left(x,y\right),v_0\left(x,y\right)$ since they refer to their values on the mid-plane in the MS formulation but refer to their values on the neutral plane in the NS formulation. The relations between in-plane displacement distributions on the middle-plane $u_o^{MS}\left(x,y\right),v_o^{MS}\left(x,y\right)$ and on the neutral plane $u_o^{NS}\left(x,y\right),v_o^{NS}\left(x,y\right)$ are derived in Equations (43) and (44) as:

$$u_o^{MS}\left(x,y\right)=u_o^{NS}\left(x,y\right)+z_o\frac{\partial w_b}{\partial x}+c_o\frac{\partial w_s}{\partial x}$$

(65)

$$v_o^{MS}\left(x,y\right)=v_o^{NS}\left(x,y\right)+z_o\frac{\partial w_b}{\partial y}+c_o\frac{\partial w_s}{\partial y}$$

(66)

In addition, relations between some stress resultants based on the middle and neutral formulations were obtained in Equations (47) and (48) as:

$$N_x^{\left(MS\right)}=N_x^{\left(NS\right)}, \hspace{1em}\hspace{1em}\hspace{1em}{N}_y^{\left(MS\right)}=N_y^{\left(NS\right)}$$

(67)

$$M_x^{b\left(MS\right)}=M_x^{b\left(NS\right)}+z_o{N}_x^{\left(NS\right)}, M_y^{b\left(MS\right)}=M_y^{b\left(NS\right)}+z_o{N}_y^{\left(NS\right)}$$

(68)

$$M_x^{s\left(MS\right)}=M_x^{s\left(NS\right)}+c_o{N}_x^{\left(NS\right)}, M_y^{s\left(MS\right)}=M_y^{s\left(NS\right)}+c_o{N}_y^{\left(NS\right)}$$

(69)

In the following, some theoretical conclusions are derived.

• Note first that for plates with symmetric properties in the thickness-direction, the neutral plane coincides on the middle plane. For such plates, identical responses are expected based on MS and NS formulations for all BCs. As a special case, responses of plates made of pure materials (ceramic or metal) are identical regardless of the used formulation and BCs.
• Clamped BCs (Equation (18)): At a vertical edge $\left(x=0,x=a\right)$, the clamped BCs are given by $u_0=v_0=w_b=w_s=\frac{\partial w_b}{\partial x}=\frac{\partial w_s}{\partial x}=0$. Note that conditions $w_b=w_s=0$ on such vertical lines imply $\frac{\partial w_b}{\partial y}=\frac{\partial w_s}{\partial y}=0$, and since $\frac{\partial w_b}{\partial x}=\frac{\partial w_s}{\partial x}=0$, then using Equations (65) and (66) $u_o^{NS}=v_o^{NS}=0$ implies that $u_o^{MS}=v_o^{MS}=0$ on the vertical edges. A similar conclusion can be derived for horizontal edges. That is, the same BCs are applied in the MS and NS formulations and identical solutions are expected for clamped plates.
• Movable simply supported BCs$S_m$(Equation (19)): For plates with movable simply supported BCs, the tangential in-plane displacement is constrained at the boundaries while the normal in-plane displacement is unconstrained. At a vertical edge $\left(x=0,x=a\right)$, the $S_m$ BCs are given by $N_x=v_0=w_b=w_s=M_x^b=M_x^s=0$. Conditions $w_b=w_s=0$ on vertical lines imply $\frac{\partial w_b}{\partial y}=\frac{\partial w_s}{\partial y}=0$, then by Equation (66), $v_o^{MS}=0$ implies $v_o^{NS}=0$. On horizontal edges, it similarly can be proved that $u_o^{MS}=0$ implies $u_o^{NS}=0$. Using Equations (67)–(69), BCs $N_x^{\left(MS\right)}=M_x^{b\left(MS\right)}=M_x^{s\left(MS\right)}=0$ implies $N_x^{\left(NS\right)}=M_x^{b\left(NS\right)}=M_x^{s\left(NS\right)}=0$ on all edges. Accordingly, the BCs applied to the discretized algebraic systems (Equations (63) and (64)) are identical, and hence the solutions based on MS and NS formulations would be the same.
• Immovable simply supported BCs$S_{im}$(Equation (20)): At a vertical edge $\left(x=0,x=a\right)$, the $S_{im}$ BCs are given by $u_0=v_0=w_b=w_s=M_x^b=M_x^s=0$. Conditions $w_b=w_s=0$ on vertical lines imply $\frac{\partial w_b}{\partial y}=\frac{\partial w_s}{\partial y}=0$, then by Equation (66), $v_o^{MS}=0$ implies $v_o^{NS}=0$. However, no such claim exists for BCs $u_0=0,M_x^b=0,M_x^s=0$. In other words, $u_o^{MS}=0, M_x^{b\left(MS\right)}=0, M_x^{s\left(MS\right)}=0$ does not imply $u_o^{NS}=0, M_x^{b\left(NS\right)}=0,M_x^{s\left(NS\right)}=0$. Similar conclusions can be derived in the case of horizontal edges. This means that for immovable simply supported plates, MS and NS formulations solve two different boundary value problems and hence predict different responses. The MS formulation is a solution for a plate whose normal in-plane displacements are constrained at its boundaries in the middle plane $\left(z=0\right)$, while the fixation is assumed at plane $\left(z=z_0\right)$ in the NS formulation.

In summary, for the discussed boundary conditions, MS- and NS-formulations produce identical responses for BDFG plates in cases of clamped $\left(C\right)$ and movable simply supported $\left(S_m\right)$ boundaries. However, they produce different responses in the case of immovable simply supported $\left(S_{im}\right)$ boundaries since each formulation assumes plate fixation at different planes.

3.5. Modified Immovable BCs $(S_{im})$ for MS and NS Formulations

The immovable simply supported classical boundary conditions $({\mathrm{S}}_{\mathrm{im}})$ (Equations (53) and (54)) for both MS and NS formulations are applied on the plate edges at its own reference planes $z=0,z=z_0$, respectively, as shown in Figure 2. That is, the MS formulation computes the plate response if it is constrained at its middle plane, while the NS formulation models plates constrained at the neutral plane. Based on Equations (65)–(69), the boundary conditions $({\mathrm{S}}_{\mathrm{im}})$ can be modified to enable MS and NS formulations to predict the response of BDFG plates constrained at an arbitrary plane. The following modified BCs are special cases.

(a) 

MS formulation with modified BCs:${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\mathit{-}\mathit{m}\mathit{o}\mathit{d}\right)}$

This modified MS formulation is suggested to enable MS formulation to predict the responses of an immovable simply supported plate if it is constrained at its neutral plane $\left(u_o^{NS}=v_o^{NS}=w_b=w_s=M_x^{b\left(NS\right)}=M_x^{s\left(NS\right)}=0 at x=0,a\right)$. The updated BCs in terms of $u_o^{MS},v_o^{MS},M_x^{b\left(MS\right)},M_x^{s\left(MS\right)}$ can be obtained using Equations (65)–(69) as:

$$u_o^{MS}-z_o\frac{\partial w_b}{\partial x}-c_o\frac{\partial w_s}{\partial x}=v_o^{MS}=w_b=w_s=M_x^{b\left(MS\right)}-z_o{N}_x^{\left(MS\right)}= M_x^{s\left(MS\right)}-c_o{N}_x^{\left(MS\right)}=0, at x=0,a$$

(70)

$$u_o^{MS}=v_o^{MS}-z_o\frac{\partial w_b}{\partial y}-c_o\frac{\partial w_s}{\partial y}=w_b=w_s=M_y^{b\left(MS\right)}-z_o{N}_y^{\left(MS\right)}= M_y^{s\left(MS\right)}-c_o{N}_y^{\left(MS\right)}=0, at y=0,b$$

(71)

Dropping the superscripts $\left(MS\right)$, keeping in mind that all field variables and stress resultants refer to the middle-plane, the modified BCs $\left(S_{im\left(MS-mod\right)}\right)$ can be written as:

$$u_0-z_o\frac{\partial w_b}{\partial x}-c_o\frac{\partial w_s}{\partial x}=v_0=w_b=w_s=M_x^b-z_0{N}_x=M_x^s-c_0{N}_x=0, at x=0,x=a$$

(72)

$$u_0=v_0-z_o\frac{\partial w_b}{\partial y}-c_o\frac{\partial w_s}{\partial y}=w_b=w_s=M_y^b-z_0{N}_y=M_y^s-c_0{N}_y=0, at y=0, y=b$$

(73)

(b) 

NS formulation with modified BCs:${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}-\mathit{m}\mathit{o}\mathit{d}\right)}$

Similarly, the NS formulation can model an immovable simply supported plate constrained at the middle plane by applying the following modified BCs $\left(S_{im\left(NS-mod\right)}\right):$

$$u_0+z_o\frac{\partial w_b}{\partial x}+c_o\frac{\partial w_s}{\partial x}={\mathit{v}}_0=w_b=w_s=M_x^b+z_0{N}_x=M_x^s+c_0{N}_x=0 at x=0,x=a$$

(74)

$$u_0=v_0+z_o\frac{\partial w_b}{\partial y}+c_o\frac{\partial w_s}{\partial y}=w_b=w_s=M_y^b+z_0{N}_y=M_y^s+c_0{N}_y=0 at y=0, y=b$$

(75)

4. Numerical Results

Model validation with previous works and influences of gradation indices, the MS and NS formulations, mobile and immobile boundary conditions on the static response of bi-directional functionally graded plate with fully clamped and simply supported edges will be proved and discussed in details through this section. The BDFG square plate with constituents of $Al/{Al}_2{O}_3$ is considered, which has the following material properties: $E_m=70 \mathrm{GPa}; {\nu }_m=0.3; E_c=380 \mathrm{GPa}; {\nu }_c=0.3$.

4.1. Validation

The effects of material gradation indices and load distribution function on the static deflection and normal stress of the BDFG plate with immovable simply supported boundary conditions are presented in

Table 1. (A) Comparison of the non-dimensional maximum deflection $\left(\overline{w}=w_{max}\frac{10E_c{h}^3}{q_0{a}^4}\right)$ and $\left({\overline{\sigma }}_x=\frac{h}{a{q}_0}{\sigma }_x\right)$ of the BDFG $Al/A{l}_2{O}_3$ immovable simply supported square plate $\left(a/h=10\right)$ under uniform/sinusoidal transversal load based on neutral surface formulation ($NS)$. (B) Comparison with Singha et al. [37] for linear bending of immovable simply supported FG plates under uniform transversal load based on NS, MS formulations $\left(\mathit{a}/\mathit{h}=100, {\mathit{n}}_{\mathit{x}}=0\right)$.

(A)
${\mathit{n}}_{\mathit{z}}$	$\overline{\mathit{w}}$			${\overline{\mathit{\sigma }}}_{\mathit{x}}$
	Present	[35]	[58]	Present	[35]	[58]
	Uniformly distributed load
ceramic	0.4665	0.4666	0.4665	2.8917	2.8688	2.8932
1	0.9287	0.9290	0.9287	4.4720	4.4303	4.4745
2	1.1939	1.1952	1.1940	5.2263	5.1689	5.2296
4	1.3882	1.3908	1.3890	5.8870	5.8035	5.8915
Metal	2.5326	-	2.5327	2.8917	-	2.8932
	Lateral sinusoidal load
ceramic	0.2961	0.2961	0.2960	1.9943	1.9679	1.9955
1	0.5890	0.5891	0.5889	3.0850	3.0389	3.0870
2	0.7573	0.7582	0.7573	3.6067	3.5456	3.6094
4	0.8815	0.8831	0.8819	4.0655	3.9813	4.0693
Metal	1.6072	1.6072	1.6070	1.9943	1.9679	1.9955
(B)
${\mathit{n}}_{\mathit{z}}$	MS formulation			NS formulation
	[35]	Present		[35]	Present
Ceramic	0.4064	0.4064		0.4064	0.4064
0.5	0.5984	0.5989		0.6269	0.6282
1	0.7313	0.7300		0.8154	0.8154
1.5	0.8206	0.8188		0.9525	0.9525
2	0.8824	0.8804		1.0449	1.0449
3.3	0.9817	0.9794		1.1672	1.1672
5	1.0651	1.0625		1.2359	1.2359
10	1.2431	1.2401		1.3569	1.3564
Metal	2.2206	2.2205		2.2206	2.2204

A. As shown, by increasing the gradation distribution through the thickness direction, the material constituent changes from the ceramic phase with high stiffness to the metal phase with lower stiffness; therefore, the deflection and normal stress will be increased. It is also seen that the current results are very close to those obtained by [35,58] for the uniform and lateral distributed loads.

To validate the formulation of both MS and NS, numerical results for linear bending of immovable simply supported FG plates under a uniform transversal load with previous published work by Singha et al. [37] are presented in Table 1B. As concluded, the results are identical and very close to 0.5% deviation with those obtained by Singha et al. [37] for MS and NS formulations. It is seen that the deflection is identical for the MS and NS formulations in the case of pure ceramics/pure metal. However, for graded material, the static deflection for the MS formulation is an under-estimation for the NS formulation. Therefore, the formulation of NS is recommended in design and analysis of the BDFG plate, rather than the MS formulation.

4.2. Parametric Studies

4.2.1. Influence of the $\left(E_c/{\mathrm{E}}_{\mathrm{m}}\right)$ Ratio on ${\mathrm{z}}_0$ and ${\mathrm{c}}_0$

Influence of material orthotropy $\left(E_c/E_m\right)$ and gradation indexes $\left(n_z,n_x\right)$ of a BDFG plate on the values of the neutral surface parameters $(z_0\left(x\right)$, $c_0\left(x\right))$ are illustrated in Figure 3 and

Table 2. Maximum values of $z_0/h$ and $c_0/h$ at different $n_z$ and $E_c/E_m$ ratios $\left(n_x=1\right)$.

${\mathit{n}}_{\mathit{z}}$	${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	${\mathit{z}}_{\mathit{o}}/\mathit{h}$	${\mathit{c}}_{\mathit{o}}/\mathit{h}$	${\mathit{z}}_{\mathit{o}}/\mathit{h}$	${\mathit{c}}_{\mathit{o}}/\mathit{h}$	${\mathit{z}}_{\mathit{o}}/\mathit{h}$	${\mathit{c}}_{\mathit{o}}/\mathit{h}$
0.0	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
0.2	0.0214	0.0047	0.0337	0.0074	0.0381	0.0083
0.5	0.0401	0.0083	0.0669	0.0138	0.0772	0.0160
1	0.0556	0.0111	0.1000	0.0200	0.1190	0.0238
2	0.0625	0.0125	0.1250	0.0250	0.1563	0.0313
4	0.0556	0.0119	0.1250	0.0268	0.1667	0.0357
5	0.0510	0.0113	0.1190	0.0265	0.1623	0.0361
10	0.0347	0.0088	0.0893	0.0226	0.1303	0.0330

. It is understood that $E_c/E_m=1$ indicates that the plate is made of homogeneous material, and hence, $z_0\left(x\right)=c_0\left(x\right)=0$. Increasing the ratio $E_c/E_m$ increases the neutral surface parameters. For $n_x=1, n_z=\left\{0.5,1,2\right\}$, it is observed that increasing $n_z$ increases the values of $z_0\left(x\right)$ and $c_0\left(x\right)$. Table 2 reports the maximum values of $z_0/h$ and $c_0/h$ for different $n_z$ and $E_c/E_m$ ratios.

4.2.2. A Note on the Neutral Surface Formulation

The analysis given in Section 3.3 shows that discretization of the governing differential equations obtained based on the neutral surface formulation results in an uncoupled system of algebraic equations Equation (64). Due to uncoupling, two sub-systems, $L_{ss}^{NS} {\mathcal{X}}_s^{NS}={\mathit{F}}_s and L_{bb}^{NS} {\mathcal{X}}_b^{NS}={\mathit{F}}_b$, can be solved separately for the stretching displacements ${\mathcal{X}}_s^{NS}={\left[{\mathit{U}}^T,{\mathit{V}}^T\right]}^T$ and the transverse deflection ${\mathcal{X}}_b^{NS}={\left[W_b^T,W_s^T\right]}^T$, respectively. This feature of the neutral formulation is important to understand the responses of movable and immovable simply supported plates based on the NS formulation. Figure 4 presents the dimensionless displacement distributions $\left({\overline{u}}_0=\frac{u_0}{a}, {\overline{v}}_0=\frac{v_0}{a}, \widehat{w}=w\frac{100E_c{h}^3}{12\left(1-{\nu }^2\right)q_0{a}^4}\right)$ based on neutral surface formulation ($NS)$ for the (a) movable and (b) immovable simply-supported BDFG $Al/A{l}_2{O}_3$ square plate $\left(a/h=10,{ \mathrm{n}}_{\mathrm{z}}=1, n_x=1\right)$ under a uniform load. It is observed from Figure 4 that the computed transverse deflections $\widehat{w}\left(x,y\right)$ are identical for the movable and immovable boundary conditions. Such an observation can be found also in the literature (see, e.g., columns 4,5 of Table 4 in [35]. These two columns reported identical results for the maximum deflection based on the NS formulations for immovable and movable simply supported FGM plats, respectively. This observation can be interpreted because of the bending–stretching uncoupling in the NS formulation (see Equation (64)), and since the difference in these boundary conditions $\left\{S_m, S_{im}\right\}$ occurs in the in-plane displacement $\left(u_0,v_0\right)$ within the stretching subsystem only, it does not affect the bending subsystem. That is, for movable and immovable plates, the NS formulation produces the same transversal deflection but different in-plane displacements. It is observed also from Figure 4 that displacement distributions are non-symmetric in the x-direction due to the variation in material properties in the x-direction $\left(n_x\ne 0\right)$.

4.2.3. Influence of Middle and Neutral Surface Formulations on Transverse Deflection and Stresses

A BDFG square plate $\left(n_x=1, n_z=\left\{0,1,2,5,10\right\}\right)$ subjected to bi-sinusoidal load is considered under different boundary conditions. The obtained results of deflection and stresses based on $\mathrm{MS}$ and NS formulations are compared for different $E_c/E_m and a/h$ ratios. The following non-dimensional deflection $\overline{w}$ and stresses ${\overline{\sigma }}_x and {\overline{\tau }}_{xz}$ are defined as:

$$\overline{w}=w_{max}\frac{100E_c{h}^3}{12\left(1-{\nu }^2\right)q_0{a}^4}, {\overline{\sigma }}_x=\frac{h^2}{a^2{q}^2}{\sigma }_x\left(\frac{a}{2},\frac{b}{2},\frac{h}{2}\right), {\overline{\tau }}_{xz}=\frac{h^2}{a^2{q}^2}{\tau }_{xz}\left(0,\frac{b}{2},0\right)$$

(76)

Results of non-dimensional deflection $\overline{\mathit{w}}$ for both formulations $\left(\mathrm{MS},\mathrm{NS}\right)$ are compared in

Table 3. Non-dimensional deflection $\overline{w}$ of a BDFG square clamped plate subjected to sinusoidal load based on middle surface formulation $C_{\left(MS\right)}$ and neutral surface formulation $C_{\left(NS\right)}$ at $n_x=1$ for different $E_c/E_m and a/h$ ratios.

${\mathit{n}}_{\mathit{z}}$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	$\mathit{a}/\mathit{h}$	${\mathit{C}}_{\left(\mathit{M}\mathit{S}\right)}$	${\mathit{C}}_{\left(\mathit{N}\mathit{S}\right)}$	${\mathit{C}}_{\left(\mathit{M}\mathit{S}\right)}$	${\mathit{C}}_{\left(\mathit{N}\mathit{S}\right)}$	${\mathit{C}}_{\left(\mathit{M}\mathit{S}\right)}$	${\mathit{C}}_{\left(\mathit{N}\mathit{S}\right)}$
0	10	0.1423	0.1423	0.1771	0.1771	0.1988	0.1988
1		0.1716	0.1716	0.2601	0.2600	0.3198	0.3197
2		0.1798	0.1798	0.2918	0.2917	0.3782	0.3780
5		0.1884	0.1884	0.3231	0.3231	0.4359	0.4358
10		0.1947	0.1947	0.3454	0.3454	0.4744	0.4744
0	100	0.1236	0.1236	0.1533	0.1533	0.1720	0.1720
1		0.1492	0.1492	0.2277	0.2277	0.2816	0.2815
2		0.1556	0.1556	0.2531	0.2530	0.3297	0.3295
5		0.1620	0.1620	0.2749	0.2749	0.3693	0.3692
10		0.1675	0.1675	0.2933	0.2933	0.3988	0.3988

,

Table 4. Non-dimensional deflection $\overline{w}$ of a BDFG square movable simply supported plate subjected to sinusoidal load based on neutral surface formulation $S_{m\left(MS\right)}$ and middle surface formulation $S_{m\left(NS\right)}$ at $n_x=1$ for different $E_c/E_m and a/h$ ratios.

${\mathit{n}}_{\mathit{z}}$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	$\mathit{a}/\mathit{h}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$
0	10	0.3657	0.3657	0.4528	0.4528	0.5022	0.5022
1		0.4417	0.4417	0.6709	0.6710	0.8259	0.8262
2		0.4615	0.4615	0.7487	0.7488	0.9716	0.9721
5		0.4819	0.4819	0.8202	0.8203	1.1021	1.1023
10		0.4982	0.4982	0.8762	0.8762	1.1951	1.1952
0	100	0.3464	0.3464	0.4280	0.4280	0.4745	0.4745
1		0.4187	0.4187	0.6376	0.6377	0.7865	0.7868
2		0.4366	0.4366	0.7088	0.7090	0.9217	0.9222
5		0.4547	0.4547	0.7706	0.7707	1.0335	1.0337
10		0.4703	0.4703	0.8225	0.8225	1.1173	1.1174

and

Table 5. Non-dimensional deflection $\overline{w}$ of a BDFG square immovable simply supported plate under sinusoidal load based on middle surface formulation $S_{im-MS}$ and neutral surface formulation $S_{im-NS}$ at $n_z=\left\{0,1,2,5,10\right\},n_x=1$ for different $E_c/E_m and a/h$ ratios.

${\mathit{n}}_{\mathit{z}}$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	$\mathit{a}/\mathit{h}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$
0	10	0.3657	0.3657	0.4528	0.4528	0.5022	0.5022
1		0.4379	0.4417	0.6472	0.6710	0.7791	0.8262
2		0.4569	0.4615	0.7137	0.7488	0.8930	0.9721
5		0.4790	0.4819	0.7924	0.8203	1.0297	1.1023
10		0.4968	0.4982	0.8608	0.8762	1.1505	1.1952
0	100	0.3464	0.3464	0.4280	0.4280	0.4745	0.4745
1		0.4149	0.4187	0.6139	0.6377	0.7397	0.7868
2		0.4320	0.4366	0.6738	0.7090	0.8430	0.9222
5		0.4518	0.4547	0.7428	0.7707	0.9611	1.0337
10		0.4689	0.4703	0.8072	0.8225	1.0729	1.1174

for clamped, movable and immovable simply supported plates, respectively.

The following conclusions can easily be derived from Table 3, Table 4 and Table 5.

• For all values of $E_c/E_m, a/h$ and different boundary conditions, the deflection increases by increasing $n_z$, which is expected due to the decrease of the ceramic volume fraction.
• For all values of $n_z, a/h$ and boundary conditions, the deflection increases by increasing $E_c/E_m$.
• The deflections obtained based on middle and neutral surface formulations are nearly identical (usually to four decimal places) for the cases of clamped and movable simply supported plates. However, considerable deviations between the results of the two formulations are observed in the case of immovable simply supported plates.
• It is observed from Table 4 and Table 5 that the computed transverse deflections based on the NS formulation are identical for the movable and immovable boundary conditions, as discussed in Section 4.2.2.

Next, the influence of the two formulations (MS and NS) on the computed stresses was investigated. Results of non-dimensional axial stress ${\overline{\mathsf{\sigma }}}_{\mathit{x}}$ of BDFG $\left(n_z=\left\{0, 1,2,5,10\right\},n_x=1\right)$ square movable and immovable simply supported plates subjected to bi-sinusoidal load are reported in

Table 6. Non-dimensional axial stress ${\overline{\sigma }}_x$ of BDFG square movable $\left(m\right)$ and immovable $\left(im\right)$ simply supported plates subjected to bi-sinusoidal load based on middle surface formulation $\left(MS\right)$ and neutral surface formulation $\left(NS\right)$ at $n_z=\left\{0,1,2,5,10\right\},n_x=1$ for different $E_c/E_m and a/h$ ratios.

${\mathit{n}}_{\mathit{z}}$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$				${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$				${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	$\mathit{a}/\mathit{h}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$
0	10	0.1981	0.1981	0.1981	0.1981	0.1948	0.1948	0.1948	0.1948	0.1925	0.1925	0.1925	0.1925
1		0.2266	0.2266	0.2311	0.2273	0.2605	0.2605	0.2672	0.2641	0.2816	0.2817	0.2878	0.2880
2		0.2355	0.2355	0.2406	0.2360	0.2838	0.2838	0.2918	0.2876	0.3178	0.3180	0.3245	0.3259
5		0.2499	0.2499	0.2545	0.2501	0.3182	0.3182	0.3283	0.3206	0.3659	0.3659	0.3775	0.3719
10		0.2637	0.2637	0.2672	0.2638	0.3573	0.3573	0.3673	0.3584	0.4238	0.4238	0.4384	0.4271
0	100	0.1963	0.1963	0.1963	0.1963	0.1932	0.1932	0.1932	0.1932	0.1910	0.1910	0.1910	0.1910
1		0.2244	0.2244	0.2290	0.2252	0.2580	0.2581	0.2647	0.2616	0.2790	0.2791	0.2852	0.2854
2		0.2331	0.2331	0.2382	0.2337	0.2808	0.2808	0.2888	0.2846	0.3145	0.3147	0.3211	0.3226
5		0.2474	0.2474	0.2520	0.2476	0.3146	0.3146	0.3247	0.3169	0.3614	0.3614	0.3730	0.3674
10		0.2612	0.2612	0.2647	0.2613	0.3535	0.3535	0.3635	0.3546	0.4189	0.4190	0.4335	0.4222

for different $E_c/E_m and a/h$ ratios. It is clear that in all cases, identical results (up to 4 decimal places) are produced based on either of the two formulations when movable boundary conditions are assumed. However, for the immovable boundary conditions, the non-dimensional axial stress ${\overline{\mathsf{\sigma }}}_{\mathit{x}}$ based on MS and NS may deviate up to 3% relative difference. It is important to note that for the NS formulation, ${\overline{\sigma }}_x$ is different for movable and immovable boundary conditions in spite of the previous observation of identical values of $\overline{w}$. This is understood since ${\overline{\sigma }}_x$ depends not only on the distributions of transverse displacement, but also on the in-plane displacements which are different in the NS formulation for movable and immovable boundary conditions.

Similar results are presented in

Table 7. Non-dimensional stress ${\overline{\tau }}_{xz}$ of BDFG square movable $\left(m\right)$ and immovable $\left(im\right)$ simply supported plates subjected to sinusoidal load based on middle surface formulation $\left(MS\right)$ and neutral surface formulation $\left(NS\right)$ at $n_z=\left\{0,1,2,5,10\right\},n_x=1$ for different $E_c/E_m and a/h$ ratios.

${\mathit{n}}_{\mathit{z}}$		${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=2$				${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=4$				${\mathit{E}}_{\mathit{c}}/{\mathit{E}}_{\mathit{m}}=6$
	$\mathit{a}/\mathit{h}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$
0	10	0.2054	0.2054	0.2054	0.2054	0.1699	0.1699	0.1699	0.1699	0.1488	0.1488	0.1488	0.1488
1		0.2196	0.2196	0.2196	0.2196	0.1941	0.1941	0.1941	0.1941	0.1768	0.1768	0.1768	0.1768
2		0.2269	0.2269	0.2269	0.2269	0.2091	0.2091	0.2091	0.2091	0.1956	0.1956	0.1956	0.1956
5		0.2349	0.2349	0.2348	0.2349	0.2281	0.2281	0.2280	0.2281	0.2221	0.2221	0.2218	0.2221
10		0.2375	0.2375	0.2375	0.2375	0.2354	0.2354	0.2353	0.2354	0.2334	0.2334	0.2331	0.2334
0	100	0.2057	0.2057	0.2057	0.2057	0.1703	0.1703	0.1703	0.1703	0.1494	0.1494	0.1494	0.1494
1		0.2198	0.2198	0.2198	0.2198	0.1944	0.1944	0.1944	0.1944	0.1772	0.1772	0.1772	0.1772
2		0.2271	0.2271	0.2265	0.2271	0.2094	0.2094	0.2095	0.2094	0.1959	0.1959	0.2027	0.1959
5		0.2350	0.2350	0.2354	0.2350	0.2283	0.2283	0.2229	0.2283	0.2224	0.2224	0.2099	0.2224
10		0.2377	0.2377	0.2392	0.2377	0.2356	0.2356	0.2366	0.2356	0.2336	0.2336	0.2286	0.2336

for ${\overline{\tau }}_{xz}$, again showing identical values of the MS and NS formulations for movable boundary conditions. Regarding the NS formulation, it is observed that the values of ${\overline{\tau }}_{xz}$ are identical for movable and immovable plates. This proves, since ${\overline{\tau }}_{xz}$ depends only on the distribution of transverse displacement, the previous conclusion that the NS formulation produces the same transverse distribution $w\left(x,y\right)$ for movable and immovable boundary conditions (see Figure 4).

4.2.4. Numerical Results for MS and NS Formulations under Different Boundary Conditions

The following numerical experiments are performed to demonstrate the theoretical conclusions given in Section 3.4. Detailed responses $\left(w\left(x,y\right),u\left(x,y,z\right),v\left(x,y,z\right)\right)$ of BDFG plates subjected to different BCs are computed based on MS and NS formulations. First, we consider a clamped plate. An FG $Al/A{l}_2{O}_3$ fully clamped square plate $\left(a/h=100,n_z=0.5,n_x=0\right)$ under a uniform transversal load is solved using the neutral surface ($NS)$ formulation. Once the solution $\left(u_o^{NS}\left(x,y\right),v_o^{NS}\left(x,y\right),w\left(x,y\right)\right)$ is obtained, the response at every point $\left(x,y,z\right)$ in the plate can be computed using Equation (16). By substituting this solution in Equation (17), the in-plane displacements at the middle plane $u_o^{MS}\left(x,y\right)$ and $v_o^{MS}\left(x,y\right)$ are computed. The distributions $\left\{u_o^{NS}\left(x,y\right),u_o^{MS}\left(x,y\right)\right\}$, $\left\{v_o^{NS}\left(x,y\right),v_o^{MS}\left(x,y\right)\right\}$ and $w\left(x,y\right)$ are plotted from left to right in Figure 5 using normalization $\left({\overline{u}}_0=u_0/a,{\overline{v}}_0=v_0/a,\overline{w}=w/h\right)$. As can be seen from Figure 5, although the in-plane displacements distributions on the neutral and middle planes are different, they have the same boundary conditions (zero values in this case).

The same clamped plate problem is resolved based on the MS formulation for the solution $\left(u_o^{MS}\left(x,y\right),v_o^{MS}\left(x,y\right),w\left(x,y\right)\right)$, which is substituted in Equation (17) to estimate the displacements distributions on the neutral plane ($u_o^{NS}\left(x,y\right)$ and $v_o^{NS}\left(x,y\right)$). The obtained solutions were found identical to those given in Figure 4. This is expected since, although each formulation provides its own governing equations, they both apply the same physical laws and are subjected to the same BCs as was discussed in Section 3.4 for the case of clamped plates. The above experiment is repeated for a movable simply supported ($S_m)$ plate. The results generated by NS and MS formulations are identical and are presented in Figure 6. Note that, according to the discussion in Section 3.4 for $S_m$ BCs, at edges $x=0,x=a$, the condition $v_o^{MS}=0$ implies $v_o^{NS}=0$. Similarly, on horizontal edges $y=0,y=b$, condition $u_o^{MS}=0$ implies $u_o^{NS}=0$. Next, the above experiment is repeated for the case of an immovable simply supported $\left(S_{im}\right)$ BDFG plate. Figure 7 presents the obtained solutions based on MS and NS formulations showing different responses especially for in-plane displacements.

The observation of non-equal solutions of MS and NS formulations for $S_{im}$ FG plates were expected theoretically in Section 3.4, and was interpreted as a result of the application of non-identical BCs. To examine this interpretation, the modified BCs suggested in Section 3.5 are applied. That is, the discretized governing equations based on the MS formulation are updated by applying the modified boundary conditions (Equation (28)). The obtained solutions are presented in Figure 8a. On the other side, the algebraic system corresponding to the neutral surface formulation is updated by applying the modified BCs (Equation (29)). Upon solution of the updated algebraic system, the responses are plotted in Figure 8b. It is observed from Figure 7a and Figure 8b that, for $\left(S_{im}\right)$ BCs, the MS formulation with the proposed modified BCs produces an identical solution to that of the NS formulation. Moreover, Figure 7b and Figure 8a show that the NS formulation with the modified BCs (Equation (29)) produces an identical solution to that of the classical MS formulation. These observations demonstrate the conclusion that both MS and NS formulations are correct when they apply the same physical boundary conditions even for $\left(S_{im}\right)$ BCs if the fixation constraint at different planes is treated properly.

Similar results are reported in

Table 8. Non-dimensional deflection $\overline{\mathit{w}}$ of an $\mathit{A}\mathit{l}/\mathit{A}{\mathit{l}}_2{\mathit{O}}_3$ square immovable simply supported plate under uniform load based on the middle surface formulation ${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$ and the neutral surface formulation ${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$, subjected to classical and modified $\left(\mathit{m}\mathit{o}\mathit{d}\right)$ BCs $\left(\mathit{a}/\mathit{h}=100, {\mathit{n}}_{\mathit{x}}=0\right)$.

${\mathit{n}}_{\mathit{z}}$	Classical BCs		Modified BCs
	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{M}\mathit{S}-\mathit{m}\mathit{o}\mathit{d}\right)}$	${\mathit{S}}_{\mathit{i}\mathit{m}\left(\mathit{N}\mathit{S}-\mathit{m}\mathit{o}\mathit{d}\right)}$
Ceramic	0.4064	0.4064	0.4064	0.4064
0.5	0.5989	0.6282	0.6282	0.5989
1	0.7300	0.8154	0.8154	0.7300
1.5	0.8188	0.9525	0.9525	0.8188
2	0.8804	1.0449	1.0449	0.8804
3.3	0.9794	1.1672	1.1672	0.9794
5	1.0625	1.2359	1.2359	1.0625
10	1.2401	1.3564	1.3564	1.2401
Metal	2.2205	2.2205	2.2205	2.2205

, where a square $Al/A{l}_2{O}_3$ immovable simply supported plate under a uniform load is considered. Results of non-dimensional deflection $\overline{w}$ are reported for different values of $n_z$ based on different formulations: middle surface formulation with classical BCs (Equations (53) and (54)) $S_{im\left(MS\right)}$, neutral surface formulation with classical BCs (Equations (53) and (54)) $S_{im\left(NS\right)}$, middle surface formulation with modified BCs (Equations (72) and (73)) $S_{im\left(MS-mod\right)}$, and neutral surface formulation with modified BCs (Equations (74) and (75)) $S_{im\left(NS-mod\right)}$. As was proposed in the analysis in Section 3.5, identical results are obtained using $S_{im\left(MS-mod\right)}$ and $S_{im\left(NS\right)},$ since both model the plate assuming fixation at the neutral plane, whereas each of $S_{im\left(NS-m\right)}$ and $S_{im\left(MS\right)}$ apply the BCs at the middle plane. These results demonstrate that, for the $S_{im}$ plates, the modified BCs enable either formulation to obtain an identical response of the other formulation.

5. Conclusions

This research is motivated by the conflicting conclusions in the literature about the correctness of the mid-plane and neutral plane formulations for modelling FGM beams and plates. The paper develops two mathematical formulations of the BDFG plate based on MS and NS, then presents a critical examination of the two formulations under different boundary conditions. A kinematic relation is assumed with the four-variable higher order shear deformation theory. Hamilton’s principle is developed to get the equilibrium equations based on MS and NS, which are solved by the differential quadrature method (DQM). Both the theoretical analysis and the numerical results demonstrate that:

➢

The responses of BDFG plates based on the MS and NS formulations are different for immovable simply supported $\left(S_{im}\right)$ BCs in contrast with the cases of clamped BCs and $\left(S_m\right)$ BCs, where the responses are identical for both formulations.

➢

For immovable simply supported FGM plates, the NS and MS formulations solve two different boundary value problems since $S_{im}$ BCs on the neutral plane are different from that at the middle plane. Therefore, the solutions generated using the NS and MS formulations for immovable SS plates are different.

➢

The relation between displacement field variables of MS and NS are derived. Once the solution is obtained on either the MS- or NS-plane, this relation is utilized to compute the in-plane displacements on the other plane. In addition, this relation was the key for defining the modified BCs that enable either formulation to obtain the same response of $S_{im}$ plates using the other formulation.

➢

Based on the NS formulation, due to stretching–bending uncoupling, the computed transverse deflection distributions are identical for $S_m$ and $S_{im}$ boundary conditions. However, in-plane displacement distributions are different.

➢

Both the MS and NS formulations are correct when they apply the same physical boundary conditions, even for $\left(S_{im}\right)$ BCs if the fixation constraint at different planes is treated properly.