Abstract
Experimental and computational data and field data obtained from measurements are often sparse and noisy. Consequently, interpolating unknown functions under these restrictions to provide accurate predictions is very challenging. This study compares machine-learning methods and cubic splines on the sparsity of training data they can handle, especially when training samples are noisy. We compare deviation from a true function f using the mean square error, signal-to-noise ratio and the Pearson coefficient. We show that, given very sparse data, cubic splines constitute a more precise interpolation method than deep neural networks and multivariate adaptive regression splines. In contrast, machine-learning models are robust to noise and can outperform splines after a training data threshold is met. Our study aims to provide a general framework for interpolating one-dimensional signals, often the result of complex scientific simulations or laboratory experiments.
Keywords:
machine learning; deep neural networks; MARS; splines; interpolation; feedforward neural networks; noisy data; sparse data MSC:
68T07
1. Introduction
Modelling the behaviour of non-linear systems is challenging. Therefore, data-driven methods have become prevalent, providing an alternative to modelling complex systems [1,2,3,4].
Surrogate and reduced order models are common in engineering [5,6,7]. Moreover, there is an increasing interest in exploring artificial intelligence approaches in complex engineering science and addressing technology problems where experimental data are scarce and fine-grain simulations are computationally expensive or prohibitive. Throughout the paper, we refer to a limited amount of data as scarce data. Machine-learning (ML) and deep-learning (DL) methods, such as multivariate adaptive regression splines (MARS) and deep feedforward neural networks (FFN) are data-driven approaches. They rely on big datasets to approximate linear and non-linear functions. However, experimental or field data may be scarce in many applications due to the inability to conduct detailed physical experiments or to instrumentation constraints.
Moreover, data obtained from fine-grain simulations, e.g., large eddy or direct numerical simulations of turbulence [8], can be expensive in terms of computing time and storage [9]. Under the scarcity restriction, many ML models may under-perform in capturing meaningful patterns in the data.
Previous investigations have attempted to compare artificial neural networks and MARS in pattern recognition and forecasting tasks for various applications. For example, researchers have sought to discover patterns of breast cancer via both neural networks and MARS [10]. MARS and neural networks were compared on the runoff forecasting in the Himalayan region where limited data are available [11]. Other studies have also performed direct comparisons between MARS and neural networks for the forecasting of sales, and tourism [12,13].
Simpler techniques, such as splines, refer to a wide range of functions used in applications where data interpolation or smoothing is necessary. They are piecewise polynomial functions with a local elementary form while being globally flexible and smooth. Specifically, cubic splines are a particular type with parameters up to third-order polynomials that must satisfy certain restrictions, which we will explain later. Splines have been extensively used in interpolating functions for unseen inputs based on sparse observations and creating efficient surrogate models [14,15]. Splines have also been used in aerospace engineering for airfoil design [16] and for designing radar-based collision risk models in high-density terminal areas [17].
Furthermore, research in the field suggests that rectified linear unit (ReLU)-based deep neural networks (DNN) [18] can be viewed as a hierarchical or deep spline [19,20,21,22]. Hence, the question arises as to when spline interpolation is more favourable than an interpolation via DNN. However, DNN, MARS and spline interpolation comparisons have yet to be directly presented. Moreover, studies have yet to be conducted on the effects of sparsity and noise in the training data on NN, MARS or spline performance.
The motivation for this study emerged from engineering applications in which sound and vibration can lead to acoustic fatigue of structures, e.g., Figure 1. Aerodynamic turbulence induces pressure fluctuations on the structure’s walls, manifested as noise. In practice, we analyse the wall pressure fluctuations averaged in the spanwise direction, thus making them one-dimensional, and study their behaviour in time. These continued pressure fluctuations can lead to acoustic fatigue with significant effects on structural integrity. Turbulence is challenging to predict both experimentally and computationally. For example, in high-speed aircraft applications, the flow features turbulence, shock waves, and shock-boundary layer interaction [23,24,25,26], which facilitate flutter. Due to instrumentation constraints, experimental wind-tunnel measurements also become more challenging at supersonic speeds.
Figure 1.
Various engineering applications are featuring acoustic-wall effects and vibration induced by aerodynamic loading: high-speed aircraft, turbomachinery, wind turbines, and high-speed trains.
On the other hand, fine-grain numerical simulations that capture turbulence and acoustic effects take several days or weeks on several high-performance computing cores. Moreover, such simulations are limited to simpler geometries, such as flat panels or ramps, rather than complete aircraft geometries.
Similar challenges exist in other engineering applications, such as wind turbines, high-speed trains and turbomachinery. For example, aeroelasticity has become a significant challenge for large offshore wind turbines. The average hub height for offshore turbines can be up to 150 m, with a mean rotor diameter of 127.5 m. Structural vibration and fatigue are critical mechanical issues for large wind turbines. Again, experiments are difficult to perform, and field data can also be limited. ML methods can be beneficial in calculating the vibrational properties of wind turbines; thus, knowing their limitations is essential.
Our work aims to fill a research gap by directly comparing cubic spline, DNN and MARS interpolation under varied observational data sparsity and noise levels. Furthermore, we aim to provide guidelines on the performance of different methods. The most important factors taken into account are the level of noise in the dataset, the availability of observational data and the complexity of the modelled function.
2. Methods
2.1. Feedforward Neural Networks
Deep feedforward neural networks (FNN) can be considered the simplest deep learning architecture. A feedforward network is a multilayer network where units (neurons) are connected without cycles directly to the next layer. If the network is also densely connected, then each neuron of layer is connected directly to every neuron of layer . For historical reasons, this architecture is sometimes called a multilayer perceptron, which is, however, a misnomer due to units in modern networks being non-linear, unlike the traditional perceptron unit, which is purely linear.
The goal of a feedforward neural network is to approximate a function by creating a mapping and optimizing the values of the parameters . An FNN is a composition of multiple functions . These vector-to-vector functions accept an input vector and map it into an output vector . An acyclic graph and a weight function over the edges, , are often used to describe how these functions are composed. For example, a neural network might consist of n functions connected in a chain to form an overall function
In such a case, is called the first layer of the network, is called the second layer and so on. The number of layers, , present in a network is an architectural design decision and can vary depending on the application. However, it is generally accepted that deeper neural networks have a stronger approximation ability than shallower ones [27,28]. The first and final layers of the network are called the input and output, respectively. All intermediate layers are called hidden layers, and their functionality is often unknown, which is why neural networks are considered black-box models.
Training data points are noisy approximate examples of . Each training point consists of a value x inside ’s domain and a label . Training examples directly command what the output layer must do. It must produce an output close to for every input x. In contrast, the learning algorithm decides how to utilize each layer to approximate with minimum error. When labels represent classes (categories), the problem is a classification problem. On the other hand, when takes continuous numerical values, the problem is a regression, as in our case.
Layers consist of units called neurons. The number of neurons a layer has is also an architectural design decision. However, past research has shown that deep networks can approximate a problem with the same accuracy as shallow networks but with a significantly lower number of training parameters and Vapnik–Chervonenkis (VC) dimensions (a measure of the capacity of a set of function) [27,28]. A neuron represents a vector-to-scalar function, and all neurons of a layer act in parallel. Inspired by the human brain, each unit receives input from many other units and computes its activation value, similar to how brain neurons function. Each neuron applies an activation function to a weighted sum of its inputs and a learnable bias term b.
in the case of a sigmoid activation function, the neuron’s output becomes
The activation function for each application is a hyperparameter choice often achieved through a trial-and-error approach. However, Sigmoid and ReLU activations have been a common choice with other variations, such as leaky ReLU [29], ELU [30], GELU [31], aiming to solve certain drawbacks with varied effectiveness.
We have used feedforward neural networks instead of more complicated architectures, such as RNN or CNN. FNNs have a simpler architecture that facilitates direct comparisons between deep learning and splines. CNNs are not inherently designed for this application since their success is mainly related to computer-vision applications and RNNs are used for sequential data.
For our experiments, we designed two architectures, the small SDNN and the larger LDNN. SDNN is a 10-layer-deep neural network presented in Figure 2. The network has 3421 learnable parameters that need to be optimized. Except for the final layer, all layers consist of 20 neurons and use the leaky ReLU as an activation function since we observed that it helps to avoid constant trivial solutions more than other activations.
Since we are working on a one-variable regression problem, the final layer has only one neuron and uses the identity function as activation.

Figure 2.
SDNN architecture visualized. A 10-layer network, with hidden layers consisting of 20 neurons each. The leaky ReLU activation function is used on every layer. The total number of learnable parameters is 3421.
In contrast, LDNN has nine layers but a total of 25,022,541 (∼25 M) learnable parameters . Hence, this can be considered a medium-sized network by modern standards. Table 1 describes the architecture in detail. The input layer only has one neuron, similar to SDNN, since we only accept one input (not shown in the table). All layers use the leaky ReLU activation function, except that the final layer uses the identity function and has one neuron since we are attempting to regress a single variable.

Table 1.
Architecture of the “large” feedforward network model LDNN.
The size of the SDNN architecture can be considered small, especially by modern standards, where applications in computer vision or natural-language processing use architectures with billions of learnable parameters. On the other hand, the present LDNN architecture can be considered a medium-sized network. Due to the simple nature of our application, we rely on small-to-medium network sizes. Our architectures provide a reasonable basis for benchmarking against splines since it would be unfair to compare a simple technique, such as splines, with a vast, complicated neural network. Furthermore, substantially increasing the network’s size would increase the computational training cost and the training data required to optimize all parameters’ . However, this study focuses on training under sparsity. Note that the model size is usually chosen empirically. Depending on the complexity of a problem, we can design networks, often through a trial-and-error process. However, it is established that deeper neural networks tend to have more modelling capacity [27,28].
2.2. Cubic Splines
A spline is a piecewise polynomial function . Since we want the spline S to be piecewise-defined, the interval is broken into disjoint subintervals,
where
Points are called knots. If knots are equidistantly distributed in the interval , then the spline is called a uniform spline.
where are order polynomials when referring to cubic splines, defined as
for .
Given a set of coordinates , in this case, training data, we compute a set of n splines which must satisfy six conditions:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
The above conditions mean that all data points will be interpolated and that , , are all continuous functions on the interval . Moreover, since , the curve will be smooth across the interval.
Splines have been extensively used in engineering, statistics, and science [16,17,32].
2.3. MARS
Multivariate adaptive regression splines (MARS), first proposed by [33], represent an approach for multivariate non-parametric regression. The interpolation interval is broken into subregions, with the connecting points, called knots, automatically determined by the data. MARS work by computing piecewise curves (splines) of various and differing polynomial degrees. These piecewise curves are called basis functions (BF). The number of basis functions , and the polynomial degree of each, are determined by a two-step search procedure. A MARS model is of the form,
In the above equation, is the coefficient of the constant basis function , while the sum is over the basis functions , each of which has a coefficient . M represents the number of basis functions that make up the MARS model, while is the number of knots. The knot’s location is defined by and is a sign variable that takes the values .
Each function can take on three forms. The intercept is the constant 1. The rest of the basis functions can either be hinge functions or a product of multiple hinge functions. Hinge functions take the form
where C is a constant value called a knot. With the help of the term in the hinge functions, BFs are zeroed out in regions that do not fit the data well.
MARS models are generated through a two-step forward and backward process. During the first step, a forward stepwise algorithm generates many basis functions that overfit the data. Then, a greedy search algorithm, starting with the intercept term , executes an exhaustive search and adds pairs of hinge functions with the maximum reduction in the sum of squares residual error. The addition of new terms (BFs) continues until the maximum number, M, is reached or until the residual is reduced to negligible values.
A backward elimination occurs during the second step. This pruning process aims to reduce the number of basis functions used, limit overfitting on the training dataset and produce models with better generalization ability. During the backward pass, the least effective basis function is removed in each step. Effectiveness is usually calculated with the GCV and the generalized cross-validation criterion [34], described by the formula:
where N is the number of observations, M is the number of basis functions, and p is a penalty term usually chosen as 2 or 3. The term is the number of knots, so the GCV criterion penalizes the addition of basis functions and knots. We can observe the reduction in the GCV value to remove a variable.
MARS has been used extensively in many areas of engineering, economics, and science [10,11,12,13].
2.4. Producing Ground Truth, Sparse and Noisy Data
For the benchmark used here, we utilize two different functions, and . Both target functions are sinusoidal with quickly changing behaviour and multiple local extrema. The exact form of the functions was arbitrarily chosen. However, we bear in mind that fast-paced changes in the signal’s value are more difficult to model; hence, including more high-frequency sinusoidal terms increases the complexity of the function under investigation.
Training data points were produced by sampling with varied timesteps. We simulate sparsity by linearly sampling N points from with a steady timestep in the range . To simulate noisy data, we add random noise to every training sample. The noise value was sampled from the noise distribution
where p is a parameter that controls the noise intensity in each sample. N takes the values {50, 100, 200, 300, 400, 500, 700, 900}, while p {0%, 1%, 5%, 10%}. We combine N and p values to create 32 training scenarios.
Other noise distributions were also tested on a few training scenarios. The results showed no apparent correlation between the type of noise and the models’ performance, but this issue deserves further investigation.
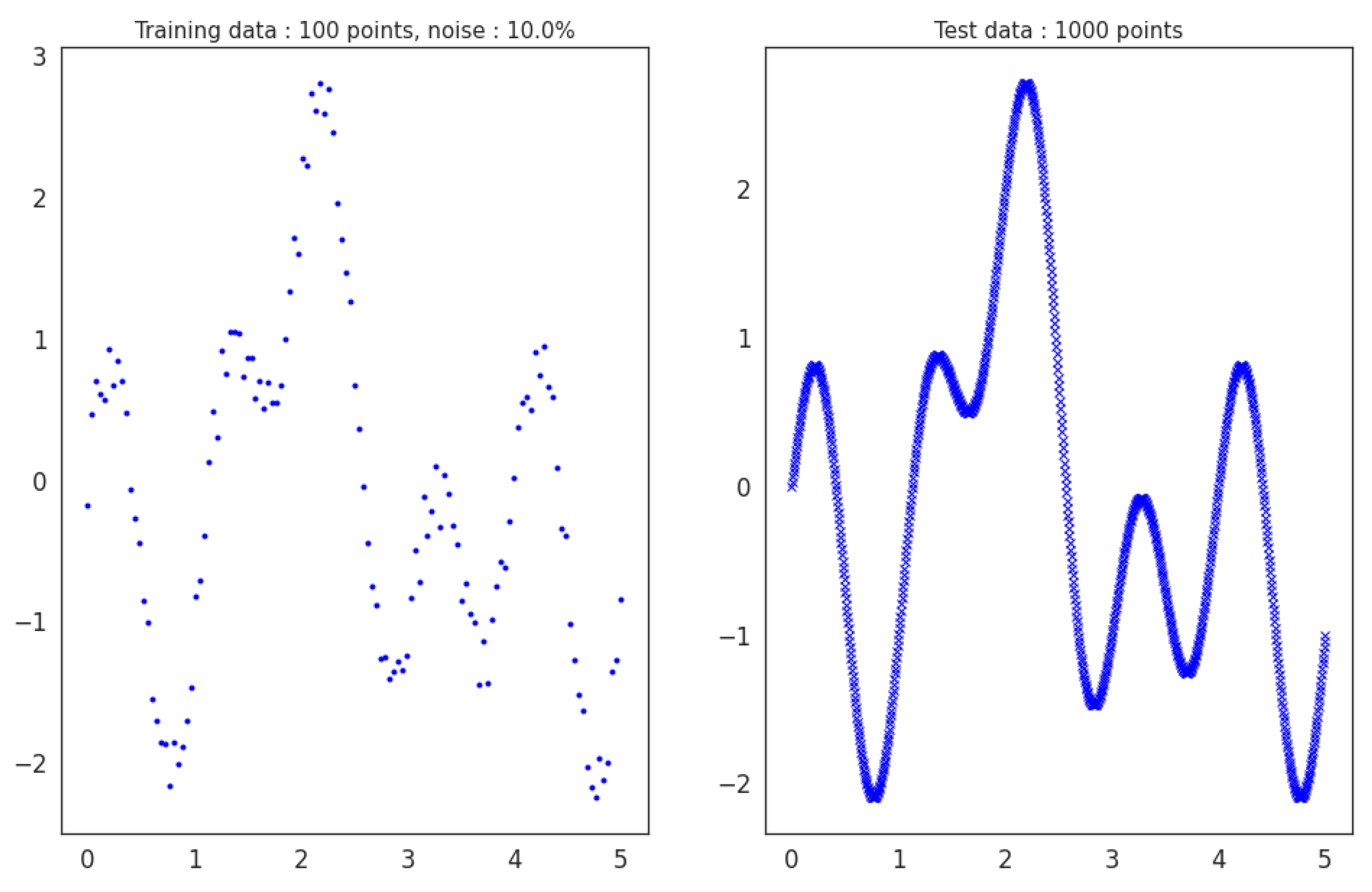
For testing, we sample 1000 noiseless data points from (Figure 3). We use noiseless data for testing because we evaluate how well the methods approximate the true function from noisy data. Finally, the 1000 testing points remain the same across all experiments for a fair and unbiased performance evaluation.
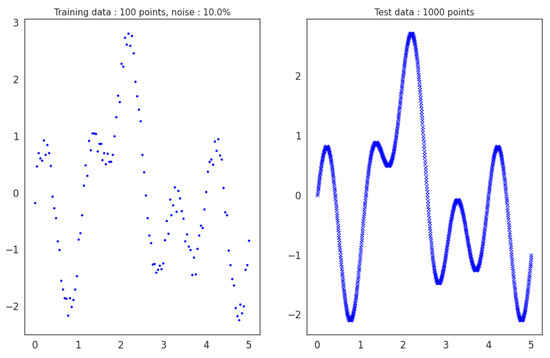
Figure 3.
Training scenario with noise p = 10% and N = 100 training data points. Data is sampled linearly from in the range, and then the noise is added. Training noisy data is on the left, while noiseless test data is on the right.
2.5. DNN Training Parameters
Training neural networks come with a plethora of hyperparameter decisions. These hyperparameters can substantially affect performance. To create a fair basis for our comparison, we modify only the training dataset’s parameters, namely the sparsity N and noise level p, while keeping the network hyperparameters unaltered among different experiments. However, to decide on the final set of hyperparameters used, a few trial-and-error experiments with a random training dataset were conducted to ensure that convergence of the learning algorithm is possible.
Table 2 summarizes the hyperparameter set we decided to use. The optimizer hyperparameter refers to the optimization method used during back-propagation [35] to update the network’s weights and biases. Among the seven optimizers tested, we decided to continue with the Adamax [36] optimizer since it produced the most promising results, offering fast convergence without getting trapped in constant trivial solutions. The learning rate controls the magnitude of each optimization update, with smaller values equating to smaller changes in the network’s parameter after each epoch. The learning rate was set to 0.03 since it provides the learning algorithm with large enough gradient updates without becoming unstable, providing a fast and accurate convergence. We trained all models for 25,000 epochs and applied an exponential learning rate decay with to facilitate accurate convergence to a global minimum. The exponential decay is used to reduce the learning rate gradually and is formulated as
where t is, the iteration number and is the decay factor.

Table 2.
List of the hyperparameters tested. The final choices used across all experiments are written in bold.
Since we aim to regress the true function , we use mean squared error, MSE, as the loss function. Hence, the Adamax optimizer updates parameters so that the MSE between the training labels and model predictions y is minimized. The learning goal is to find the optimal network parameters (weights and biases), formulated as
We also employ an early stopping mechanism, terminating training if validation loss has not improved for 1000 epochs. Finally, we save the model’s best state during each training epoch with the lowest validation error instead of the last epoch.
3. Results and Discussion
We created 32 different sparsity and noise scenarios. These included four levels of noise and eight different levels of sparsity ranging from 50 to 900 training data points. The exact values of the training data are . The noise level p was set as to recreate both low- and high-noise scenarios. We conducted five experiments for every combination of N and p. We present the average values for each training scenario over five experiments to avoid correlation with the noise generator.
For each experiment, we trained four models:
- SDNN.
- LDNN.
- MARS.
- Cubic Splines.
We tracked three metrics: MSE, the (coefficient of determination) and SNR, defined as:
where .
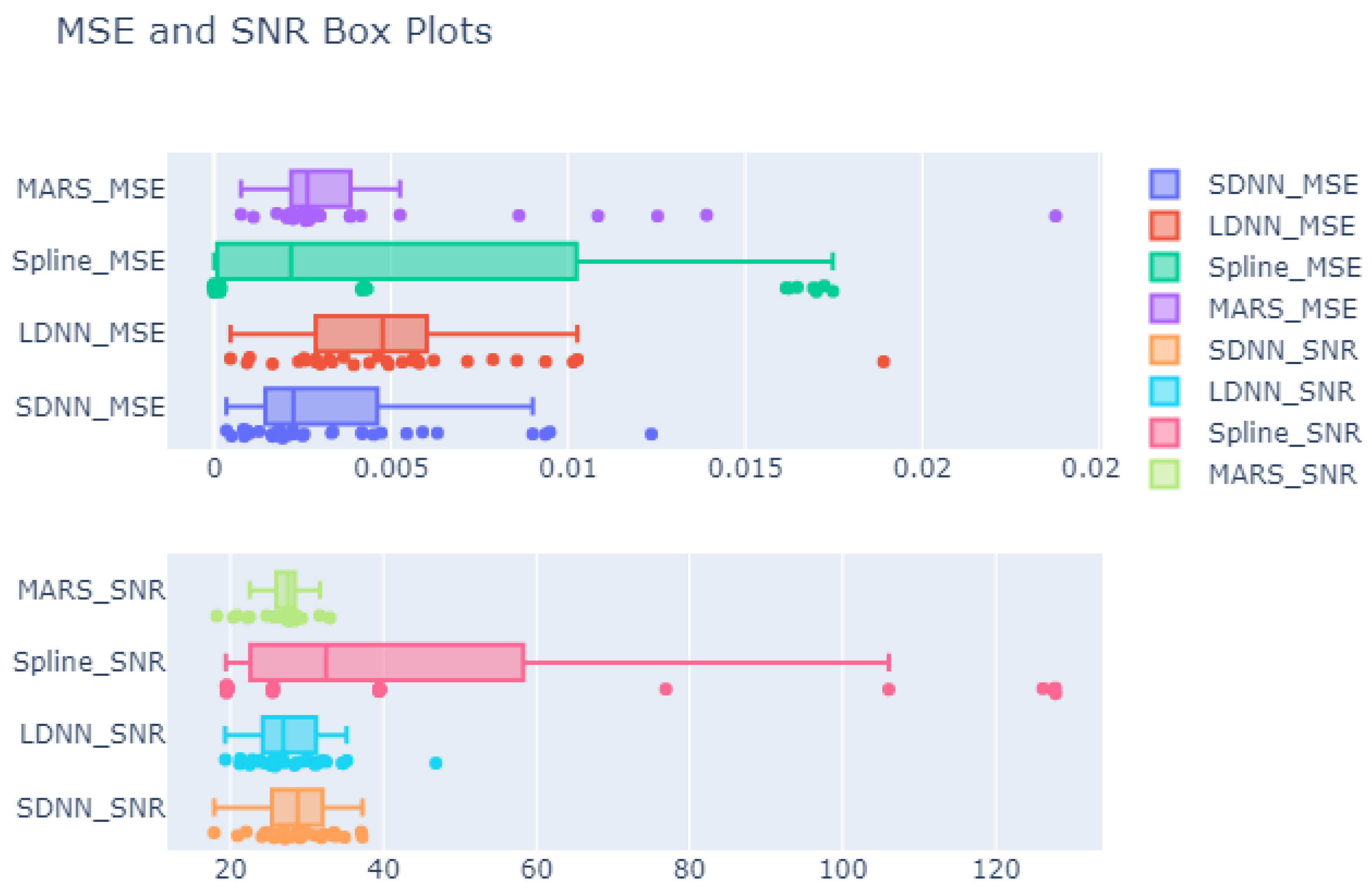
Figure 4 presents the MSE and SNR values attained from all models for all training scenarios. Concerning MSE, the MARS model has the most outlier values, followed by SDNN. On the other hand, the cubic splines model does not have any outliers since all values fall into the range , where represents the difference between the 1st and 3rd quantiles, i.e., the range where 25% to 75% of observations fall:
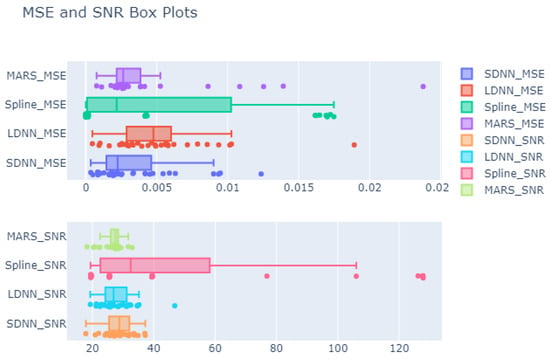
Figure 4.
Boxplots for MSE and SNR values attained from all experiments. The average of five runs is presented. The first row shows the MSE for the SDNN, LDNN, splines and MARS test sets. The second row shows the respective SNR values. The box represents the 1st and 3rd quantiles, while the middle line represents the median value. The left vertical line represents the value , while the right line is . Values outside of the vertical lines are outliers.
The splines model has three separate regions in which most observations are gathered. These regions could coincide with the three noise scenarios: low (0%, 1%), medium (5%) and high (10%). As a result, LDNN presents a relatively steady distribution of MSE without outliers, but with high variance.
The above findings suggest that cubic splines are very sensitive to either noise or sparsity. The SDNN and MARS models are also susceptible to either factor, but less so, since most observations are gathered around the median value, as shown in Figure 4. Finally, the LDNN model is the most insensitive.
Concerning SNR (Figure 4, row 2), the cubic splines model presents the most variance, with values ranging from 20 to 140 dB. We also observe some outlier values above 120 dB. However, these outlier values demonstrate excellent performance in contrast to MSE. MARS also present many outliers, but its variance is generally low. DNNs seem to have a Gaussian-like distribution of values.
The above findings suggest that DNNs are robust to noise and their performance remains relatively steady even under high-noise scenarios. We infer similar conclusions for the MARS models, which, despite the presence of outliers, concentrate most of their values in a small range of around 27 dB in length. Finally, cubic splines seem very sensitive to noise since the SNR values capture a considerable range (≈120 dB).
3.1. MSE
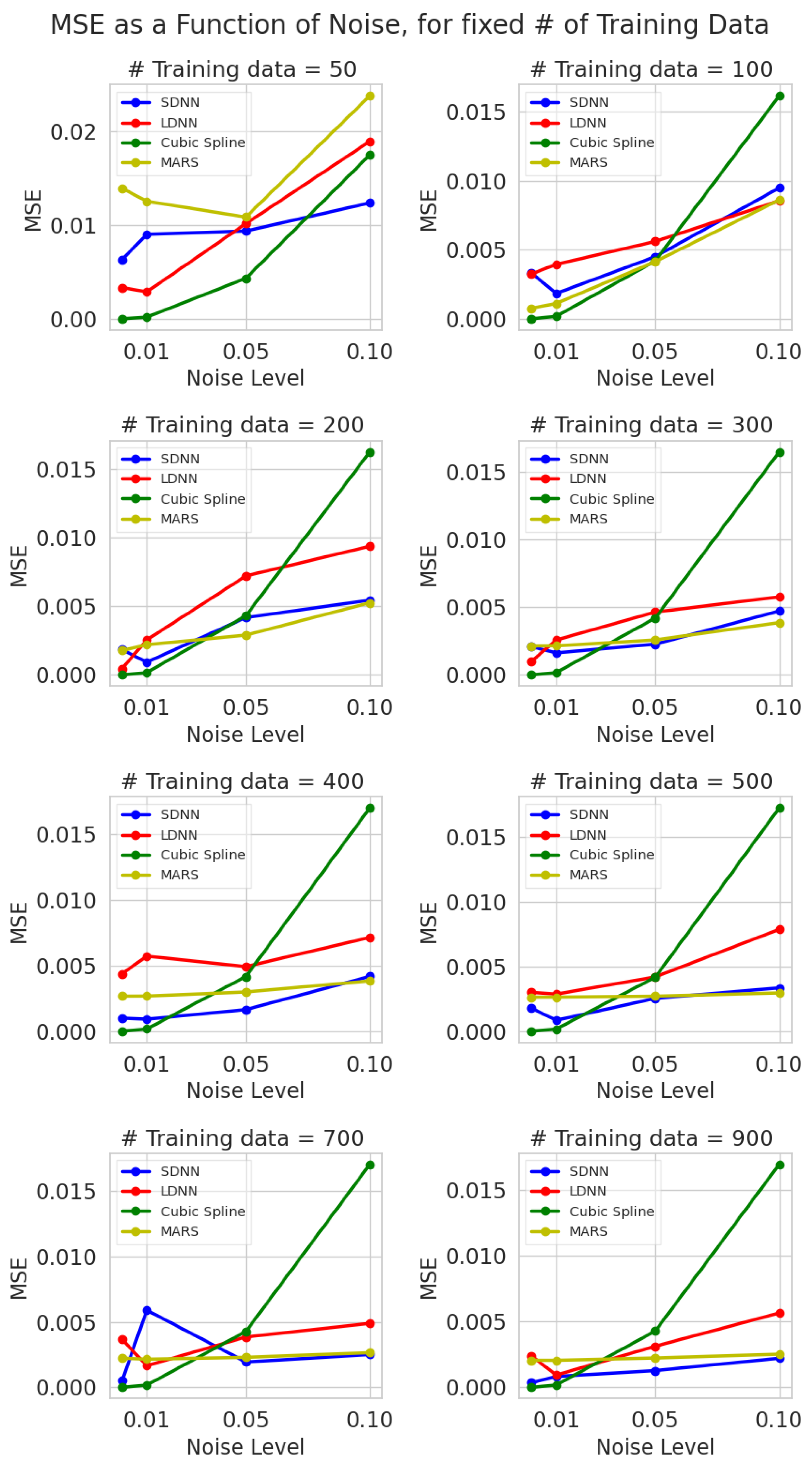
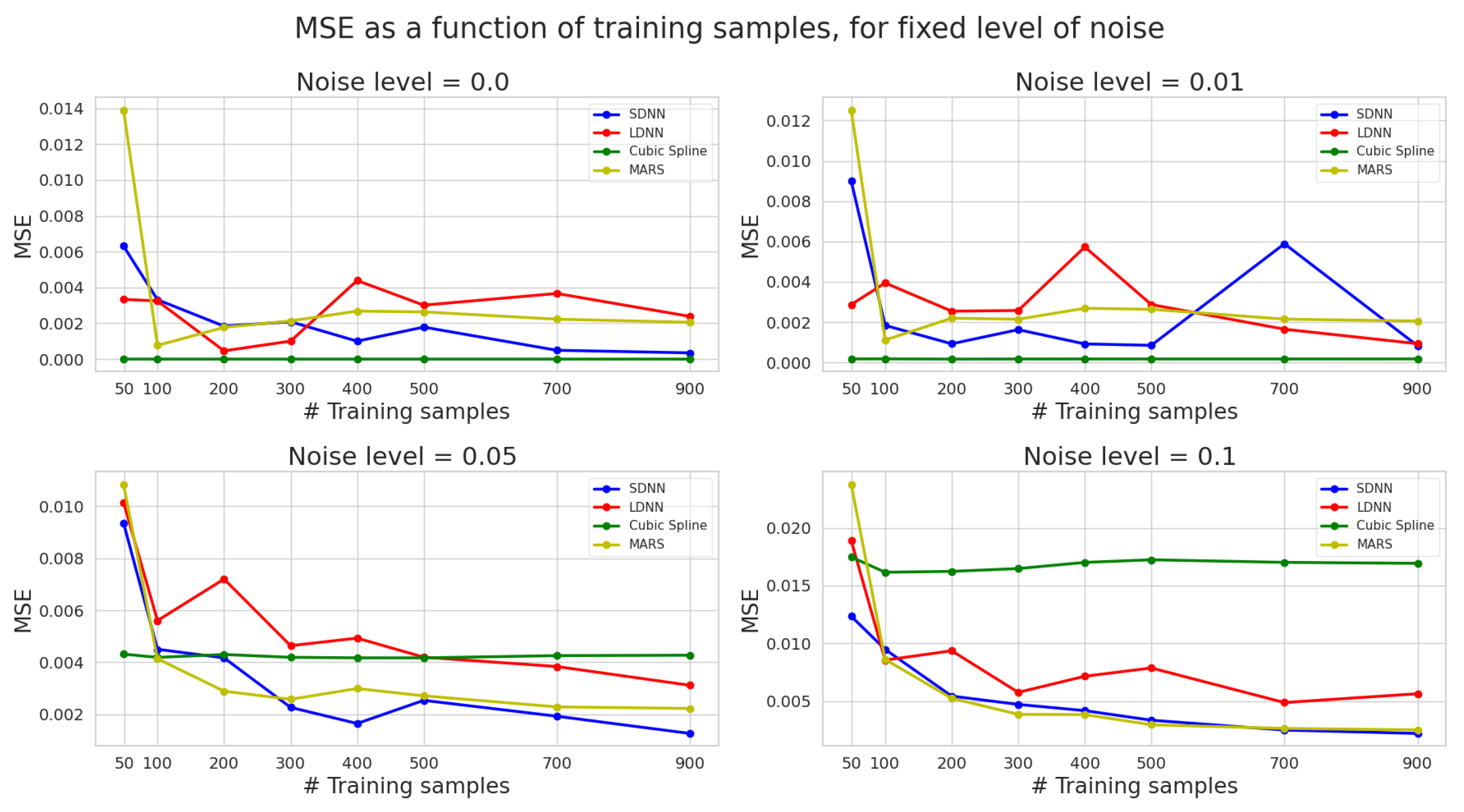
Figure 5 shows the relationship between MSE and training data noise levels. We present MSE vs. noise for all eight different sparsity scenarios. The noise level, in the x axis, is measured as a percentage (Equation (14)).
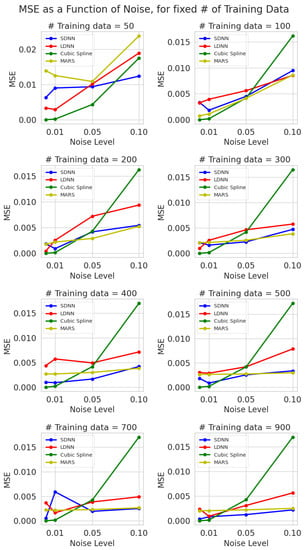
Figure 5.
Test mean squared error vs. noise level (0%, 1%, 5%, 10%) for eight different levels of sparsity (sample training points). The average values over five runs are presented. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
The results reveal that splines are overly sensitive to noisy data. The gap between MSE at 0% noise and 10% noise, irrespective of the training dataset’s size, is the largest observed for any model by a significant margin. This verifies our initial hypothesis that traditional spline techniques are susceptible to noise and that their performance deteriorates as the noise level in the training samples increases.
Moreover, the MSE vs. noise function for SDNN, LDNN and MARS is not always a strictly increasing function, even if it has an increasing trend, as we would expect. This is due to the stochastic nature of the learning algorithms, such as gradient descent. Therefore, initial conditions (weights and bias values) are critical and impact the final convergence of these algorithms. Often, these learning algorithms can get stuck into local minima, especially when the loss function has many local extrema due to a bad weight initialization [37,38,39]. On the other hand, a good initialization, coupled with an optimal hyperparameter set, can provide convergence to a close-to-optimal solution. This explains why we observe unexpected results that break the increasing trend, such as LDNN’s MSE at 400 training samples with a 5% noise level.
Continuing the analysis of Figure 5, we make another important discovery. The variation in MSE values for noise levels for the SDNN, LDNN and MARS models tends to contract as the number of training samples increases. Therefore, the numerical experiments show that the negative effect of noise in the training dataset tends to be eliminated as the training dataset’s size increases. This holds for neural networks and multivariate adaptive regression splines (MARS). These methods are data-driven—the more training data we utilize to train these models, the less error we can expect. However, in some cases, this rule is broken because of the stochastic nature of the learning algorithms.
Our results show that cubic splines outperform all ML methods under low noise (0%, 1%), irrespective of the training dataset’s size. However, the cubic spline performance deteriorated sharply after the 5% noise mark. For higher noise, SDNN and MARS are the best-performing techniques, each challenging the performance of the other.
Figure 6 describes the effect of sparsity on the MSE error of the four models for different noise levels (Appendix A). We can infer some critical conclusions from these graphs. Specifically, cubic splines preserve a steady performance irrespective of the training data used. This confirms that the spline performance is not strongly correlated with sparsity and that splines perform almost equally well under sparse-data restrictions and for non-sparse data. In contrast, DNN and MARS show a strong correlation between the quantity of training data used and their test MSE. It is important to note that increasing the number of training points improves higher noise levels (5%, 10%). The above suggests a saturation point exists, after which using more training data has diminishing returns. This saturation point tends to increase as the noise level increases. However, the trend sometimes breaks due to weight initialization in DNNs. The importance of initialization is even more prominent for larger and deeper DNNs, reflected in more unstable behaviour for LDNN rather than SDNN. The above may cause problems when designing explainable engineering, physics or medical applications solutions.
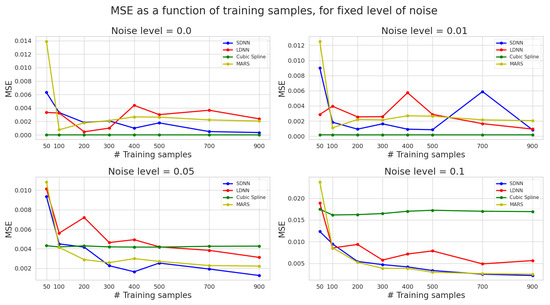
Figure 6.
Test mean squared error vs. the total number of training samples for four different noise levels. The average values over five runs are presented. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
Finally, we make some critical discoveries by observing the crossover points, i.e., the points at which other methods meet or outperform cubic splines’ performance. First, we observe that cubic splines perform best for low noise (0 %, 1%), irrespective of sparsity levels. However, when training data are noisy, splines are outperformed after a threshold of 100 training samples by MAR, and after 200 training samples by SDNN. LDNN needs more than 500 training data points to outperform splines. For very high (10%) noise, splines are outperformed for as few as 50 training data points, indicating their inefficiency in handling noisy observations.
We conclude that cubic splines are more accurate, efficient and less computationally costly when dealing with noiseless or low-noise data. However, ML methods outperform cubic splines when dealing with noisy data, mainly as more training samples are used to train these models. Finally, SDNN exceeds LDNN performance in most cases. A possible explanation is that LDDN is over-parameterized for this problem and is, hence, more prone to overfitting the noise or other irrelevant features instead of the true function. Another explanation is that larger and deeper networks are often more difficult to optimize and a more suitable set of hyperparameters may improve performance.
3.2. SNR
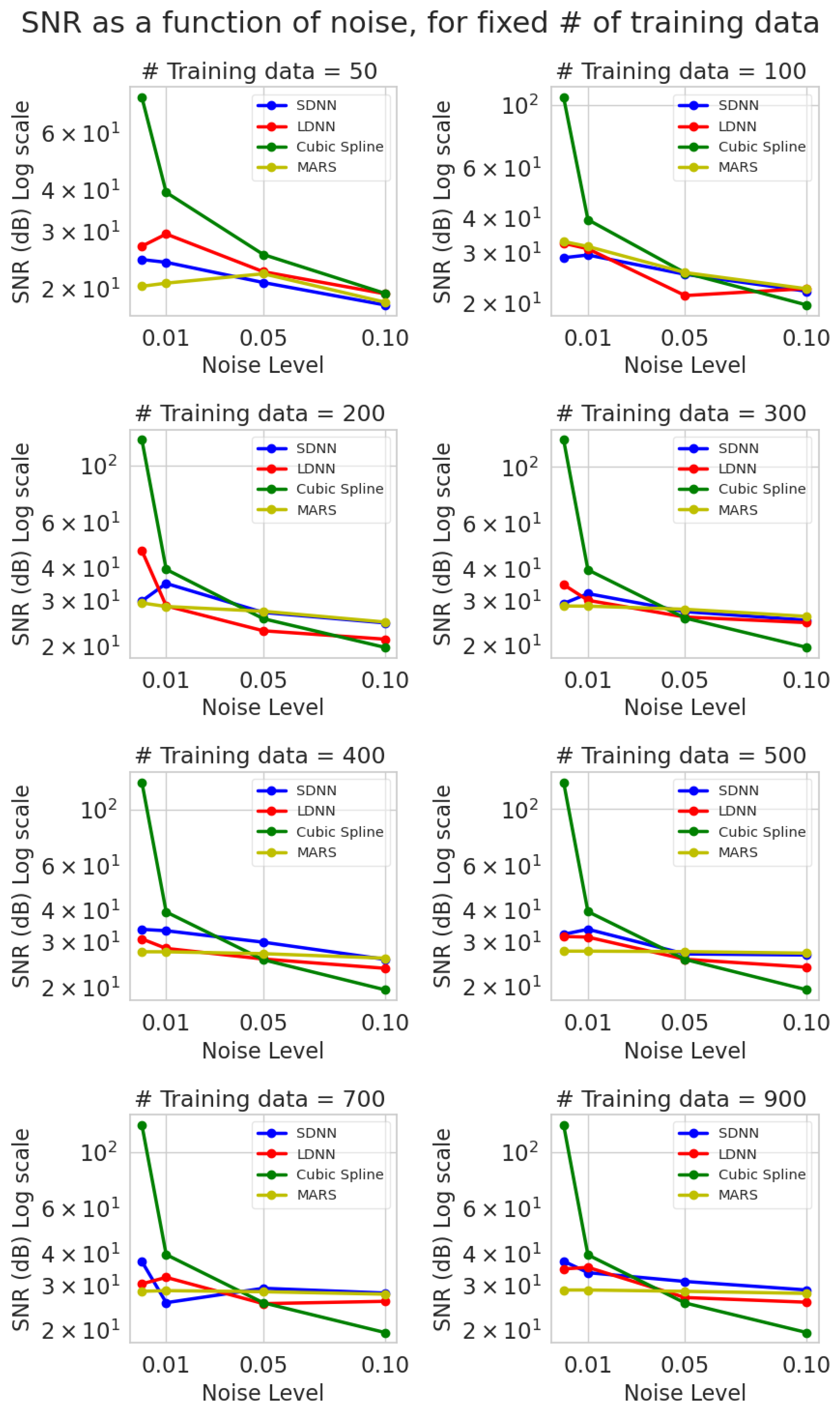
We examined the results regarding the signal-to-noise ratio (SNR), Equation (19). In Figure 7 and Figure 8, the y axis is in log scale and is measured in dB (decibels). The noise level is measured in percentage (Equation (14)) and training data samples are in absolute numbers.
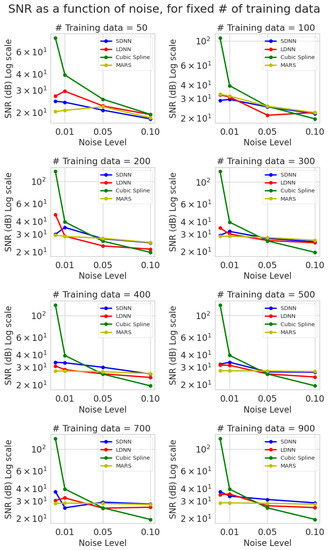
Figure 7.
SNR vs. noise level (0%, 1%, 5%, 10%) for eight different levels of sparsity (sample training points) computed on the test set predictions and ground truth. The average values over five runs are presented. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
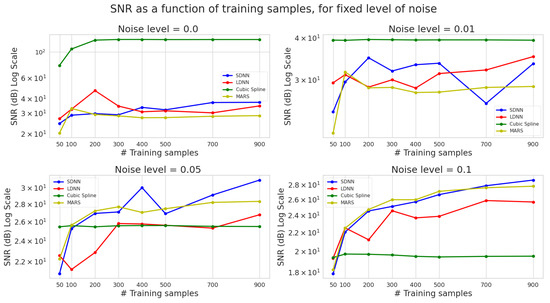
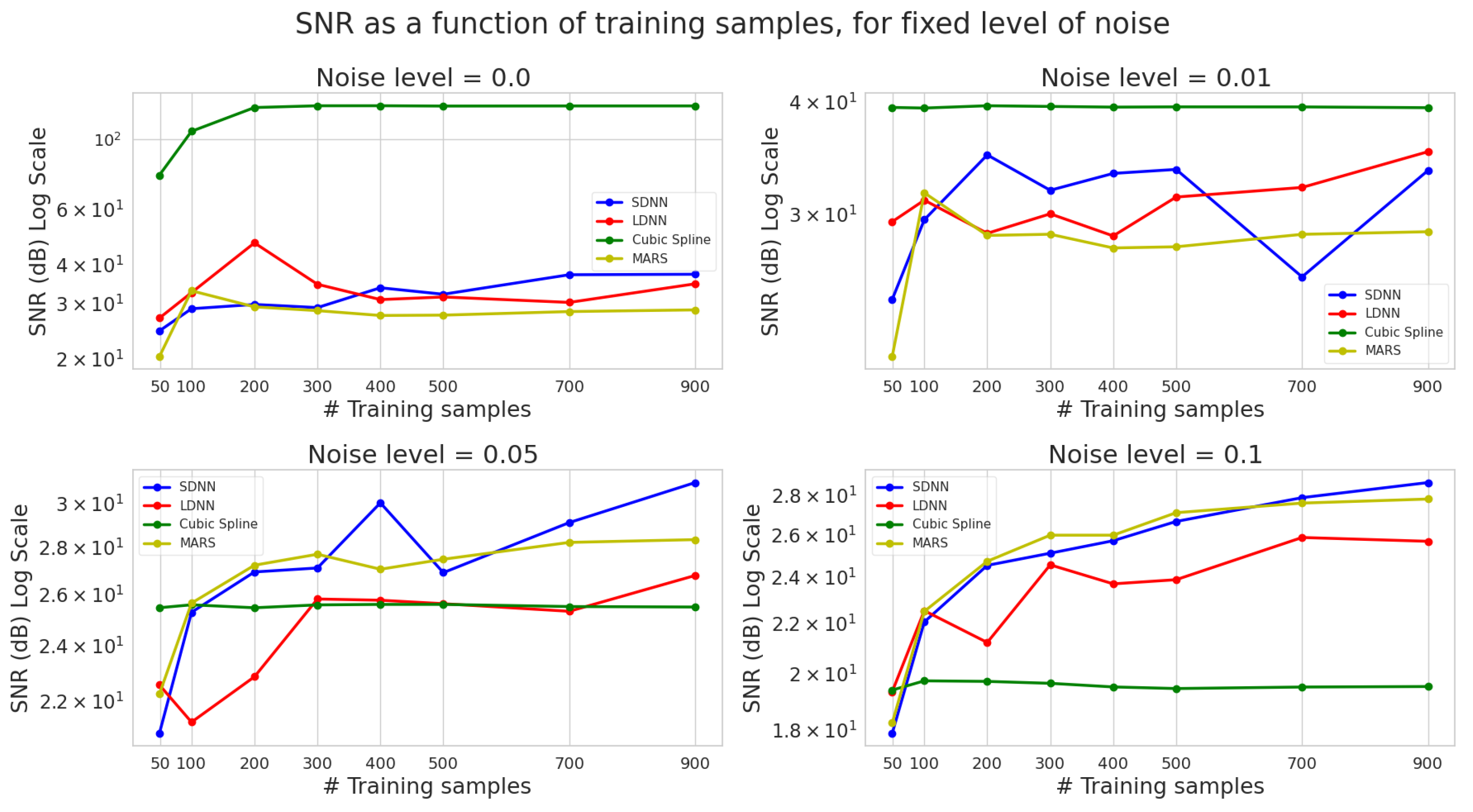
Figure 8.
SNR vs. the total number of training samples for four different noise levels. The average values over five runs are presented. Blue colour represents SDNN, green cubic splines, and yellow MARS.
Splines present a lot of variance in their SNR values from zero to high noise, reaffirming our hypothesis that they are susceptible to noisy data. In contrast, MARS models have the lowest variance, with noise affecting their SNR performance only slightly. This effect tends to limit itself as the number of training samples reduces. Furthermore, the variance for the neural network models also tends to shrink as the number of training examples increases, suggesting that the noise effect is mitigated when many samples are used to train the algorithms (Figure 7). All models follow a descending trend. However, the relation between SNR and noise is strictly decreasing only for the deterministic cubic splines model.
Cubic splines outperform all other methods by a considerable margin when noise levels are low (0%, 1%), but their performance sharply deteriorates above these noise levels. The SNR of cubic interpolation for very sparse data, e.g., 50 or 100, is on par with or outperforms ML methods. The performance of the other models is quite similar. All ML methods are less sensitive to noise and provide almost steady SNR as the number of training samples increases (Figure 7).
In Figure 8, we present the effect of different training dataset sizes on the test set SNR value. Once again, we observe the dominance of cubic splines in the low noise (0%, 1%) scenarios and their insufficient performance under high noise.
SNR is almost independent of the number of training data used for cubic splines. In contrast, we observe a positive correlation between the number of training samples and SNR for DNNs. MARS only evidences such a correlation in higher noise scenarios, suggesting again the existence of saturation points which increase with noise.
The relatively poor performance of LDNN has been attributed to overfitting the noise in the training dataset rather than the true function. The absolute values do not offer any additional conclusions concerning the R-squared coefficient of determination. All models achieve a very high , implying that they follow the trends accurately, but this is only sometimes indicative of their precision. Similar conclusions to MSE can be drawn for R-squared as well.
4. Conclusions
The effort and cost of performing expensive numerical simulations and laboratory experiments could be reduced if we train ML models that use coarse-grained data to produce fine-grained predictions. However, this requires understanding the models’ limitations regarding sparsity conditions. Moreover, non-linear problems in science and engineering entail noise. These factors adversely affect the precision of interpolation methods and surrogate models. Therefore, the present work sheds light on the limitations of various ML and cubic spline methods when data are sparse and noisy. Several conclusions can be drawn from the present study:
- ML methods (DNN and MARS) are significantly more robust to noise than cubic splines. As a result, they can discover the true function hidden under the noise, thus making ML a valuable tool in practical applications.
- Using more data reduces the effect of noise on the interpolation precision. Hence, noisy data should be best modelled using ML models instead of traditional methods, such as splines.
- Cubic splines provide precise interpolation when the data have low noise or are noiseless; they are inaccurate when data is noisy. Under noiseless conditions, splines consistently perform better, irrespective of the number of training samples used, since they are efficient even when data is sparse. Therefore, the cubic spline interpolation can significantly outperform ML models for sparse and noiseless data.
- DNN requires a complicated training procedure that is more time-consuming than splines and MARS. Moreover, DNN’s stochastic nature and sensitivity to hyperparameters increase the uncertainty until an optimal model is discovered. However, a good initialization coupled with an optimal hyperparameter set can provide convergence to a close-to-optimal solution.
- MARS models have the lowest variance regarding SNR, with noise affecting their SNR performance only slightly. Using more data alleviates this effect.
- The importance of initialization is more important for larger and deeper DNNs reflected in more unstable behaviour for LDNN rather than SDNN.
- SDNN exceeds LDNN performance. This is probably due to the over-parametrization of LDDN. Thus, LDNNs are more prone to overfitting the noise.
- Increasing the quantity of training data makes DNN a more attractive option. Further work, however, is required to understand the limitations of the DNN models.
- DNN’s low explainability remains problematic for engineering and medical applications. Thus, further work is required in this area as well.
The present work focused on a hypothetical generalized function with and without noise. However, the conclusions from this study are valuable in guiding further research regarding the splines and ML modelling of pressure-fluctuation histories arising from high-speed aerodynamics and acoustics.
Author Contributions
Conceptualization, D.D.; methodology, D.D. and K.P.; formal analysis, K.P. and D.D.; investigation, K.P. and D.D.; resources, D.D.; writing, K.P. and D.D; supervision, D.D.; project administration, D.D.; funding acquisition, D.D. and S.M.S.; contribution to the discussion, K.P., D.D., S.M.S. and I.W.K. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the Air Force Office of Scientific Research under award numbers FA8655-22-1-7026 and FA9550-19-1-7018. The authors thank Dr David Swanson (Air Force Office of Scientific Research-European Office of Aerospace) for their support. The funding was awarded to D.D. through the University of Nicosia Research Foundation.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NN | Neural network(s) |
| DNN | Deep neural network |
| FNN | Feedforward neural network |
| FFC | Feedforward fully connected |
| RNN | Recurrent neural network |
| CNN | Convolutional neural network |
| ReLU | Rectified linear unit |
| ELU | Exponential linear unit |
| GELU | Gaussian linear unit |
| BF | Basis function |
| MARS | Multivariate adaptive regression splines |
| GCV | Generalized cross-validation |
| SNR | Signal-to-noise ratio |
| MSE | Mean squared error |
Appendix A
Four scenarios show the effects of increased noise and more training samples. We observe an excellent improvement in the neural networks and MARS when training samples are increased from 50 training samples (Figure A1 and Figure A3) to 900 (Figure A2 and Figure A4), compared. In contrast, splines perform similarly (Figure 6), but predictions tend to be more random when more noisy samples are fed as training input.
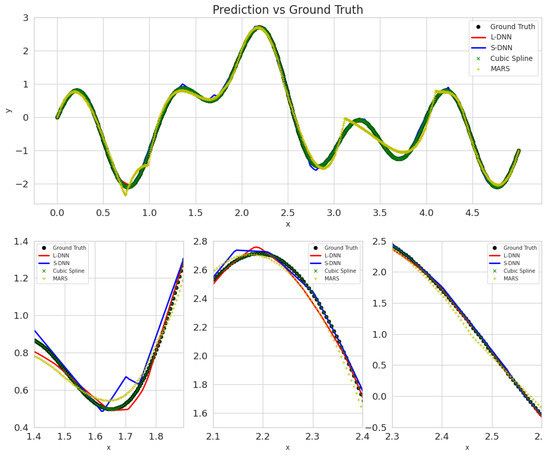
Figure A1.
Predictions’ of all tested methods on the test set for noise = 0%, trained on 50 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
Figure A1.
Predictions’ of all tested methods on the test set for noise = 0%, trained on 50 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
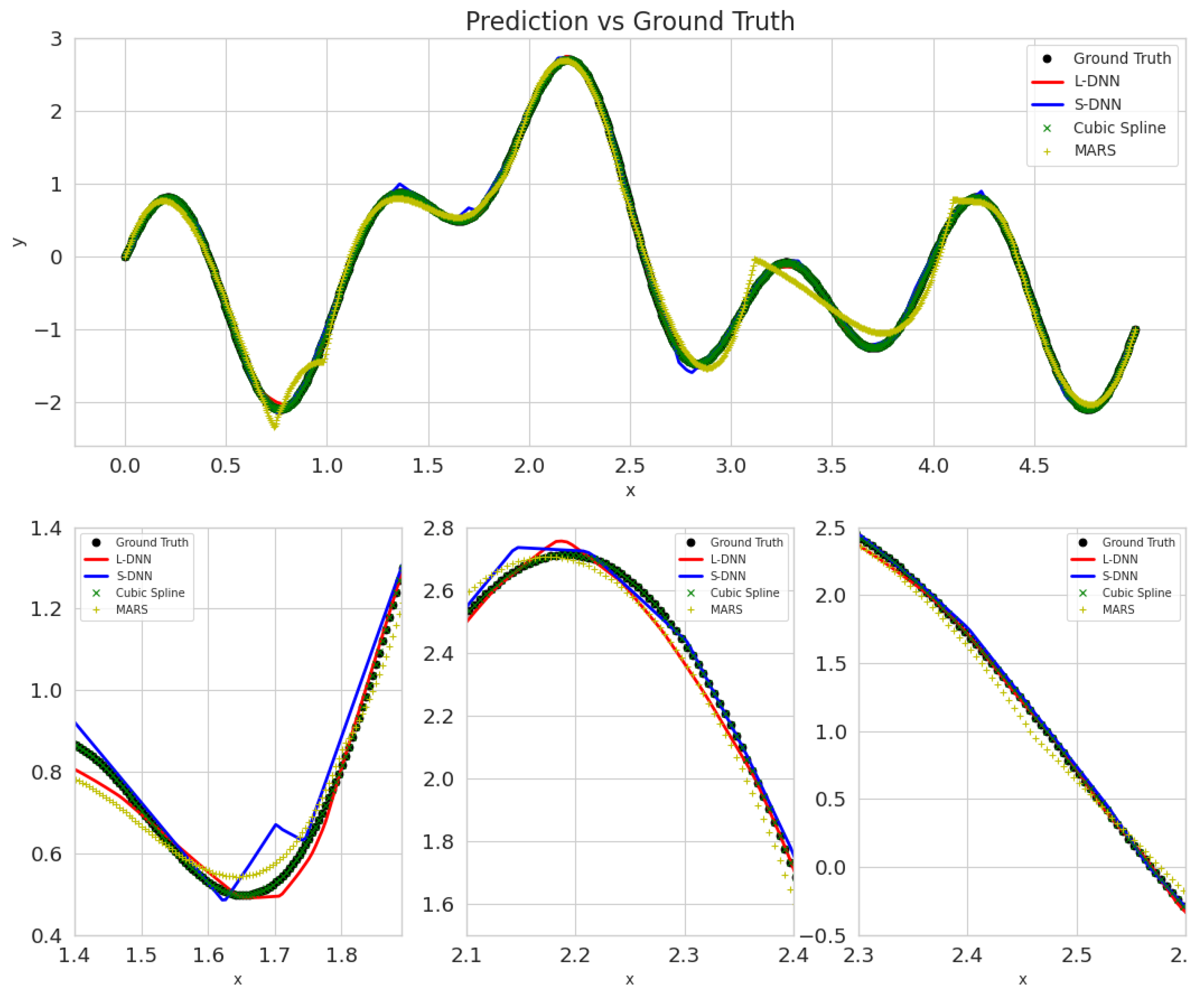
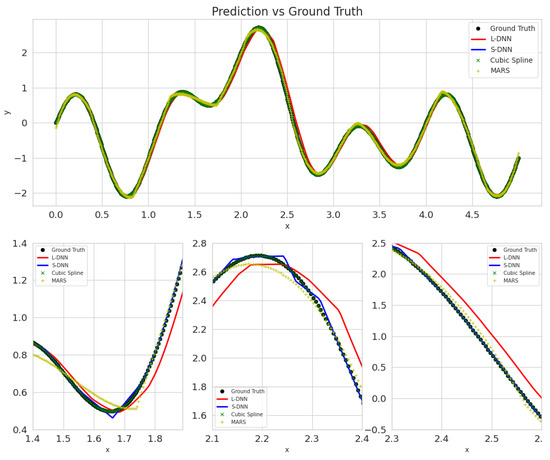
Figure A2.
Predictions’ of all tested methods on the test set for noise = 0%, trained on 900 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
Figure A2.
Predictions’ of all tested methods on the test set for noise = 0%, trained on 900 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
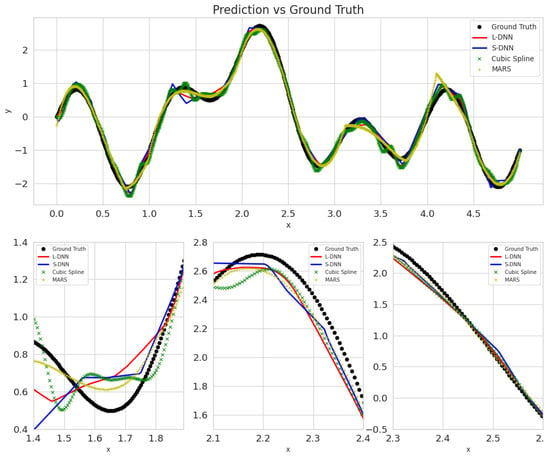
Figure A3.
Predictions’ of all tested methods on the test set for noise = 10%, trained on 50 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
Figure A3.
Predictions’ of all tested methods on the test set for noise = 10%, trained on 50 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
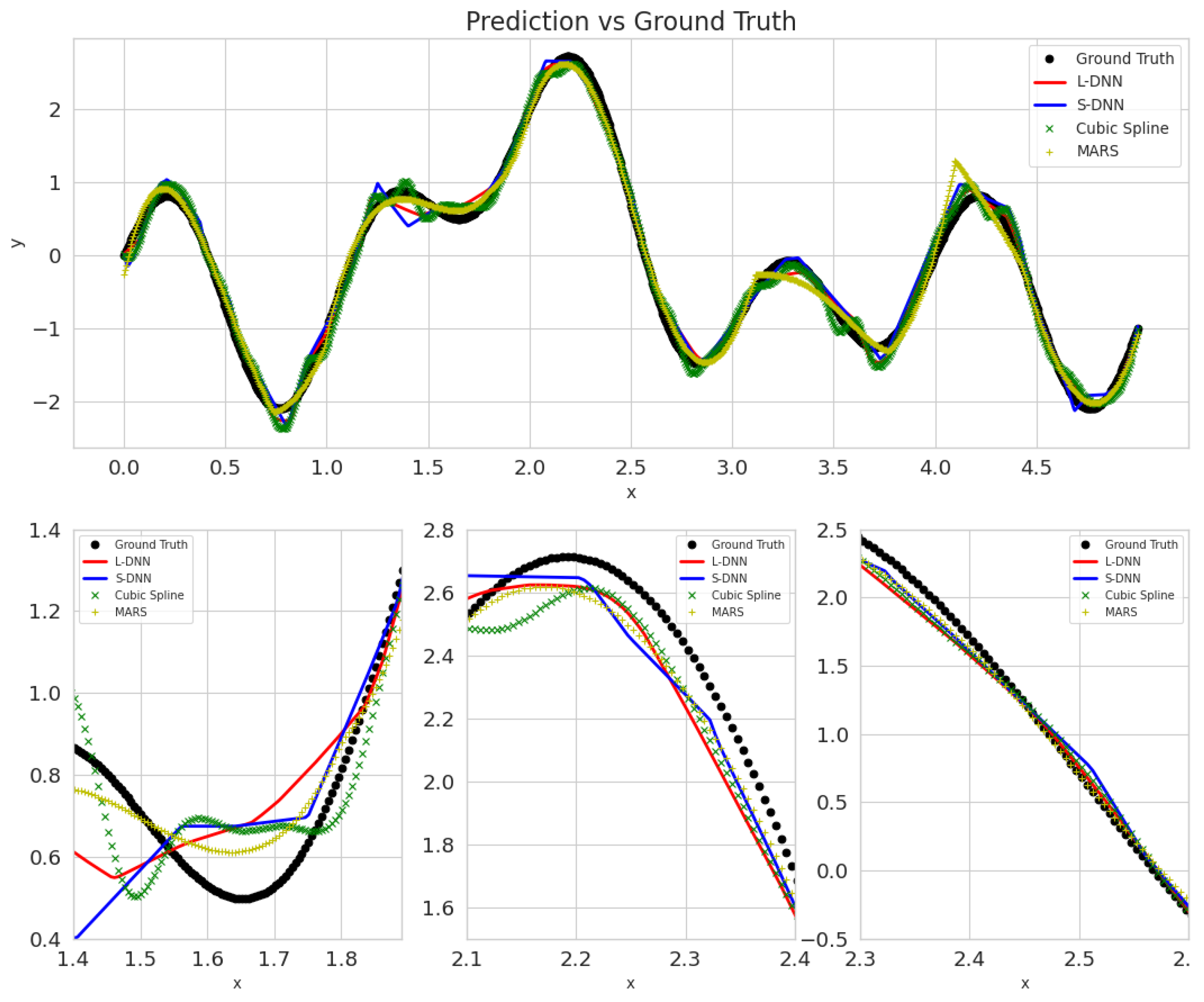
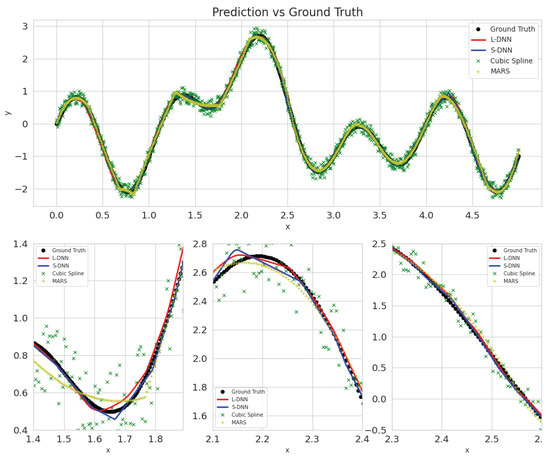
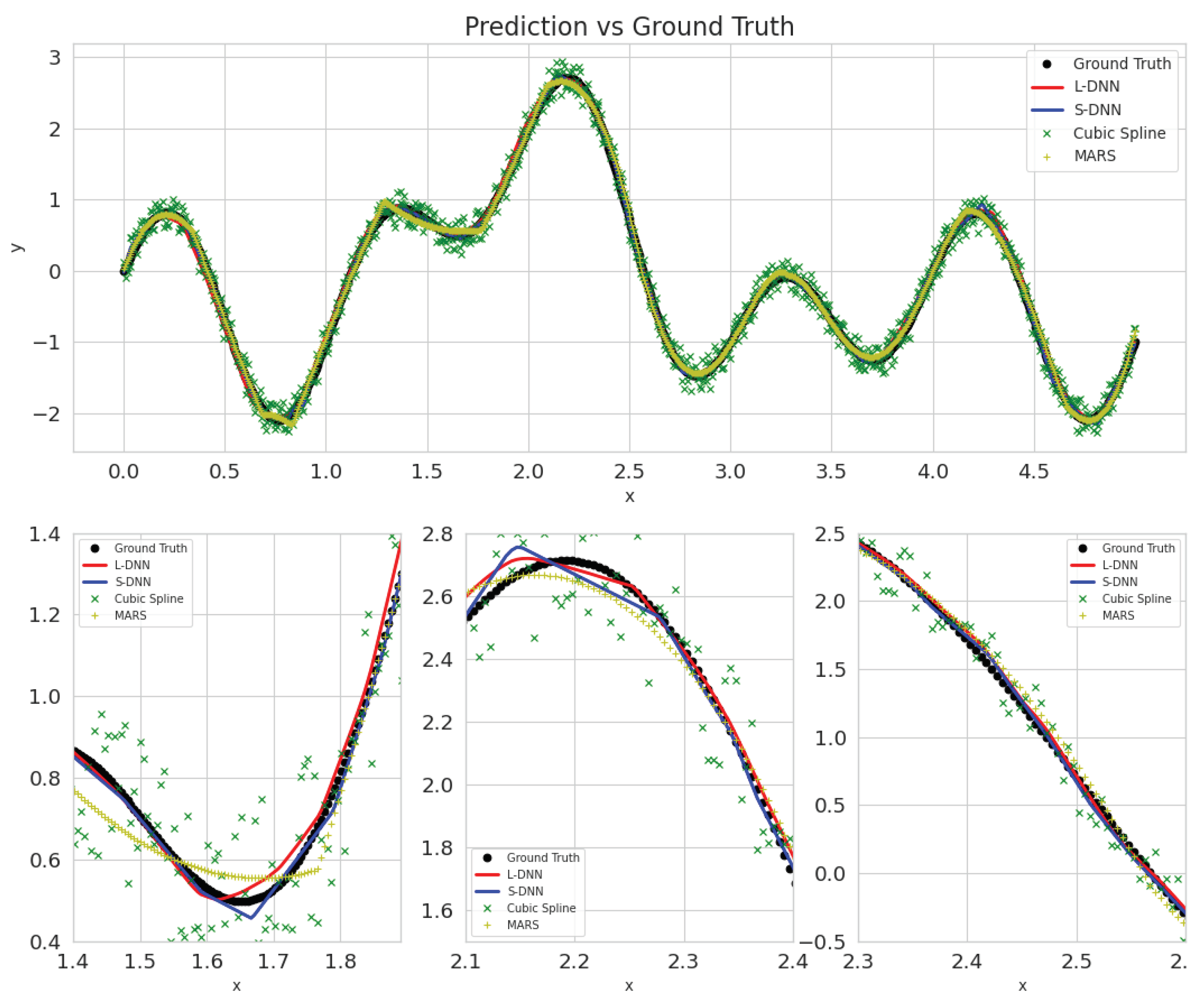
Figure A4.
Predictions’ of all tested methods on the test set for noise = 10%, trained on 900 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
Figure A4.
Predictions’ of all tested methods on the test set for noise = 10%, trained on 900 samples. Blue represents SDNN, red LDNN, green cubic splines, and yellow MARS.
References
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 2019, 31, 015105. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Botu, V.; Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, 115, 1074–1083. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural Network Modeling for Near Wall Turbulent Flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Crowell, A.R.; McNamara, J.J. Model Reduction of Computational Aerothermodynamics for Hypersonic Aerothermoelasticity. AIAA J. 2012, 50, 74–84. [Google Scholar] [CrossRef]
- Brouwer, K.R.; McNamara, J.J. Surrogate-based aeroelastic loads prediction in the presence of shock-induced separation. J. Fluids Struct. 2020, 93, 102838. [Google Scholar] [CrossRef]
- Deshmukh, R.; McNamara, J.J. Reduced Order Modeling of a Flow Past a Cylinder using Sparse Coding. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Ritos, K.; Drikakis, D.; Kokkinakis, I.W.; Spottswood, S.M. Computational aeroacoustics beneath high speed transitional and turbulent boundary layers. Comput. Fluids 2020, 203, 104520. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D.; Charissis, V. Machine-Learning Methods for Computational Science and Engineering. Computation 2020, 8, 15. [Google Scholar] [CrossRef]
- Chou, S.M.; Lee, T.S.; Shao, Y.E.; Chen, I.F. Mining the breast cancer pattern using artificial neural networks and multivariate adaptive regression splines. Expert Syst. Appl. 2004, 27, 133–142. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Sharda, V.N. Comparison of multivariate adaptive regression splines with coupled wavelet transform artificial neural networks for runoff forecasting in Himalayan micro-watersheds with limited data. J. Hydroinform. 2011, 14, 731–744. [Google Scholar] [CrossRef]
- Lu, C.J.; Lee, T.S.; Lian, C.M. Sales forecasting for computer wholesalers: A comparison of multivariate adaptive regression splines and artificial neural networks. Decis. Support Syst. 2012, 54, 584–596. [Google Scholar] [CrossRef]
- Lin, C.J.; Chen, H.F.; Lee, T.S. Forecasting Tourism Demand Using Time Series, Artificial Neural Networks and Multivariate Adaptive Regression Splines:Evidence from Taiwan. Int. J. Bus. Adm. 2011, 2, 14–24. [Google Scholar] [CrossRef]
- Enjilela, E.; Lee, T.Y.; Wisenberg, G.; Teefy, P.; Bagur, R.; Islam, A.; Hsieh, J.; So, A. Cubic-Spline Interpolation for Sparse-View CT Image Reconstruction With Filtered Backprojection in Dynamic Myocardial Perfusion Imaging. Tomography 2019, 5, 300–307. [Google Scholar] [CrossRef]
- da Silva, S.; Paixão, J.; Rébillat, M.; Mechbal, N. Extrapolation of AR models using cubic splines for damage progression evaluation in composite structures. J. Intell. Mater. Syst. Struct. 2021, 32, 284–295. [Google Scholar] [CrossRef]
- Sobester, A.; Keane, A. Airfoil Design via Cubic Splines - Ferguson’s Curves Revisited. In Proceedings of the Collection of Technical Papers-2007 AIAA InfoTech at Aerospace Conference, Rohnert Park, CA, USA, 7–10 May 2007; Volume 2. [Google Scholar] [CrossRef]
- Nieto, F. Radar track segmentation with cubic splines for collision risk models in high density terminal areas. J. Aerosp. Eng. 2014, 229, 1371–1383. [Google Scholar] [CrossRef]
- Fukushima, K. Cognitron: A self-organizing multilayered neural network. Biol. Cybern. 1975, 20, 121–136. [Google Scholar] [CrossRef]
- Unser, M. A Representer Theorem for Deep Neural Networks. J. Mach. Learn. Res. 2019, 20, 1–30. [Google Scholar]
- Parhi, R.; Nowak, R.D. The Role of Neural Network Activation Functions. IEEE Signal Process. Lett. 2020, 27, 1779–1783. [Google Scholar] [CrossRef]
- Parhi, R.; Nowak, R.D. What Kinds of Functions Do Deep Neural Networks Learn? Insights from Variational Spline Theory. SIAM J. Math. Data Sci. 2022, 4, 464–489. [Google Scholar] [CrossRef]
- Balestriero, R.; Baraniuk, R. A Spline Theory of Deep Learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 374–383. [Google Scholar]
- Daub, D.; Willems, S.; Gülhan, A. Experiments on aerothermoelastic fluid–structure interaction in hypersonic flow. J. Sound Vib. 2022, 531, 116714. [Google Scholar] [CrossRef]
- Spottswood, S.M.; Beberniss, T.J.; Eason, T.G.; Perez, R.A.; Donbar, J.M.; Ehrhardt, D.A.; Riley, Z.B. Exploring the response of a thin, flexible panel to shock-turbulent boundary-layer interactions. J. Sound Vib. 2019, 443, 74–89. [Google Scholar] [CrossRef]
- Brouwer, K.R.; Perez, R.A.; Beberniss, T.J.; Spottswood, S.M.; Ehrhardt, D.A. Experiments on a Thin Panel Excited by Turbulent Flow and Shock/Boundary-Layer Interactions. AIAA J. 2021, 59, 2737–2752. [Google Scholar] [CrossRef]
- Kokkinakis, I.; Drikakis, D.; Ritos, K.; Spottswood, S.M. Direct numerical simulation of supersonic flow and acoustics over a compression ramp. Phys. Fluids 2020, 32, 066107. [Google Scholar] [CrossRef]
- Mhaskar, H.N.; Liao, Q.; Poggio, T.A. Learning Real and Boolean Functions: When Is Deep Better Than Shallow. arXiv 2016, arXiv:1603.00988. [Google Scholar]
- Moore, B.; Poggio, T.A. Representation properties of multilayer feedforward networks. Neural Netw. 1988, 1, 203. [Google Scholar] [CrossRef]
- Maas, A.L. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28. [Google Scholar]
- Trottier, L.; Giguère, P.; Chaib-draa, B. Parametric Exponential Linear Unit for Deep Convolutional Neural Networks. arXiv 2016, arXiv:1605.09332. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Bridging Nonlinearities and Stochastic Regularizers with Gaussian Error Linear Units. arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Wegman, E.J.; Wright, I.W. Splines in Statistics. J. Am. Stat. Assoc. 1983, 78, 351–365. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Jin, C.; Ge, R.; Netrapalli, P.; Kakade, S.M.; Jordan, M.I. How to Escape Saddle Points Efficiently. arXiv 2017, arXiv:1703.00887. [Google Scholar]
- Shalev-Shwartz, S.; Shamir, O.; Shammah, S. Failures of Deep Learning. arXiv 2017, arXiv:1703.07950. [Google Scholar]
- Skorski, M. Revisiting Initialization of Neural Networks. arXiv 2020, arXiv:2004.09506. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).