Metaverse and AI Digital Twinning of 42SiCr Steel Alloys

Abstract

Digital twins are the most important parts of Cyber-Physical Systems (CPSs), and play a crucial role in the realization of the Metaverse. Therefore, two important factors: flexibility and adaptability, need to be focused on digital twinning systems. From a virtual perspective, constructing buildings, structures, and mechanisms in the Metaverse requires digital materials and components. Hence, accurate and reliable digital models can guarantee the success of implementation, particularly when it comes to completing physical twins in the real world. Accordingly, four Machine Learning (ML) methods to make digital twins of an advanced 42SiCr alloy considering all of its uncertainties and non-linearities have been employed in this paper. These ML methods accelerate the digitalization of the proposed alloy and allow users to employ them for a wide range of similar metals. Based on this technique, producers can borrow these virtual materials and build their structures in the Metaverse. This way, if the properties of the materials were satisfactory, they might buy them and start manufacturing their products. As a case study, we focus on digital twining of an 42SiCr steel with some influential factors in its mechanical properties, making the nature of the alloy complex. Processes, including heat treatment, may restore the material’s deformability; however, Quenching and Partitioning (Q&P) not only eliminates the impact of cold forming but also provides advanced high-strength steel (AHSS) properties. In this research, the combined impacts of different Q&P treatments were investigated on the mechanical properties of 42SiCr steel alloy. The results have shown the acceptability and accuracy of the proposed ML methods in realizing the digital twins of this complex alloy.

1. Introduction

As has been proved, cyber-physical systems (CPSs) will be the fundamentals of the Metaverse in the future, particularly in Industry 4.0 and 5.0, where automation seeks a software backbone. On the other hand, digital twins play a similar role in both CPSs and the Metaverse platforms [1,2,3,4,5]. Hence, digital twins need to be adaptive and flexible, especially in the case of specific materials such as alloys because these materials are affected by many critical factors, such as temperature, forces, tension, etc. Hence, the digital twinning of these materials will be a challenging task, as the measurement of or calculated characteristics of alloys are completely different from a normal device, machine, or robot equipped with many sensors [1,6]. Another challenging part is related to connecting these alloys to each other to make a mechanism, structure, or building because inaccurate digital twinning of the alloys will lead to bigger problems for the whole system. Another important limitation in the realization of digital twins for materials is that controlling the properties of a manufactured metal is almost impossible and only predicts its dynamic behavior as long as the digitalization of the alloy is successful. Therefore, we need digital twins of materials that can reflect their actual behavior with the highest rate of accuracy. These models can be used to manufacture and build structures.

While our focus is on the digital twinning of the alloys, we need to have a suitable physical twin at first. The development of new or modified steel grades that can undergo advanced heat and other treatments for cost and weight reduction, improved fuel efficiency, and improved mechanical performance is always a result of the sustainability strategy. Therefore, considering these parameters in a physical twin can be useful. In recent decades, there has been strong demand for increased safety and reliability of structures and components exposed to various types of static and cycling service loading. To meet these demands, researchers have modified steel alloys to have better mechanical properties while still meeting environmental and economic requirements [7]. The effectiveness of this technique in producing microstructures with retained austenite (RA) led to its adoption in 2003 [8,9,10,11,12,13,14]. The existence of RA offers the possibility for the optimum strength-to-ductility ratio, which could be accomplished by deformation-induced processes such as the transformation-induced plasticity (TRIP) effect during straining. Currently, Quenching and Partitioning (Q&P) methods are found to be effective in utilizing steels with carbon, and they have been expanded. The Q&P process typically consists of the following four steps: annealing, initial quenching, partitioning, and final quenching. Steel undergoes annealing, also known as partial or complete austenitization, in the first step and then is quenched to a temperature (QT) between the martensite start temperature (Ms) and the martensite finish temperature (Mf), where the austenite can partially transform into the martensite (initial quenching). The steel is then kept at QT or heated to a temperature (PT) that is higher than QT. This will make it possible to redistribute carbon (C) from the surrounding martensite into austenite and to then enrich it (partitioning). It will then be cooled to room temperature (final quenching). If the C enrichment in austenite is insufficient to ensure its thermal stability, fresh martensite may form in the last stage.

In recent years, machine learning (ML) approaches have been widely used as predictive models to analyze and simulate complex systems. The Decision Tree (DT) is a strong and adaptable supervised machine learning algorithm. This is an effective method to recognize the relations between different features of complex signals and perform data classification and prediction accurately. For this reason, it has been found to be a reliable, dependent, and effective ML tool for problem-solving. Yet, the decision tree regressor’s performance is not sufficient at low depth since it cannot capture linear relations. At deeper depths, the decision tree regressor circumvents this restriction, but this leaves it vulnerable to overfitting. A decision tree is made of a leaf node and an internal/decision node, including a foot node. DT uses “the divide and conquer” algorithm. First, a root node is initialized at DT, which is then split into two subsets. Based on the splitting criterion, such as information gain, Gini index for classification tasks, mean square error (MSE) and Poisson for regression tasks, the optimal split is determined. Based on a stopping criterion, splits are categorized either as terminal/leaf nodes or decision/internal nodes. After that, each internal node is handled independently. This procedure continues until there are no more internal nodes to split. The evaluation of materials is a difficult process in and of itself, hence various machine learning and statistical models have been presented to analyze the properties of materials, each with its limitations, providing the opportunity for further research. Creating effective algorithms is one technique to improve the prediction’s accuracy and precision. The alternative is to gradually include more pertinent material parameters in our datasets. In this investigation, we have dealt with the area of improvement in the mechanical properties of Q&P-processed 42SiCr steel (0.43 % C, 2 % Si, 0.59 % Mn, and 1.33 % Cr—weight %) as the physical twin for digitalization.

The fundamentals and basics of digital twins and the Metaverse including modeling and implementing them will be described in Section 2. In addition, some information about modern manufacturing has been embedded in this section and the requirements to realize the Metaverse are brought into this section. The manufacturing process of the proposed alloy, as the physical twin, and extracting the experimental data to be used in ML methods for making digital twins are explained in Section 3. In Section 4, the ML methods and their performances are comprehensively presented. Furthermore, a discussion of the proposed approach, its benefits, limitations, and foundation have been included there.

2. Digital Twin, the Metaverse, ML, and Alloy

A digital twin is a virtual replica of a real-world physical system or product that acts as its imperceptible digital equivalent for practical reasons such as system simulation, testing, maintenance, and monitoring [15,16,17]. This is best understood when it comes to complex systems, where each component has an impact on the linear performance of the system. Materials can be categorized in this classification. Therefore, real-time use and routine synchronization of a digital twin with the appropriate physical system such as alloys can accelerate the process of modeling and monitoring the system. Simultaneously running thorough system verification and validation test scenarios on the digital twin and the physical twin, which is a specific alloy in this research, is a practical litmus test for the effectiveness of the digital twin. When it is highly doubtful to consistently tell the difference between the digital twin and the physical twin, the former is an authentic digital twin. However, due to various elements of the factory layout, the physical behavior of the alloys in the digital twins might change. Several elements contribute to the complexity of the alloys, which depicts the movement of discrete things on conveyors or transport routes in constant and erratic time intervals. Customization leads to significant differences in a product’s physical properties. This raises the possibility of physically produced disruptions that have an impact on both the operation of the production system and the safety of employees or equipment. The physical contact between the structures and the material handling systems are the main sources of these disruptions.

Data-driven devices indicate participation in a digitization and digitalization process enabled by the convergence of IoT, Big Data, and AI and their far-reaching implications, including areas such as digital instrumentation and hyperconnectivity, algorithmization, datafication, and platformization [18,19,20]. These also apply to the overall design of the computer-mediated Metaverse, which is a fictional representation of data-driven smart cities. User interaction, computer vision, AI/blockchain, XR, edge cloud, wireless networks, robotics/IoT and hardware infrastructure are a few of the technology pillars of the Metaverse as a massive ecosystem application.

The Metaverse is coming and it is an undeniable reality that needs to be accepted and extended in all classes of the relevant industries because not only will it play a crucial role in producing and optimizing the products economically, but it will also transform the supply chain. In this respect, the digitalization of the products and relevant infrastructures will be constructive [15,16]. One of these sectors is the digital twining of the materials. For example, each alloy shows its own specific dynamic behavior, which may affect the calculation to produce a product. Hence, having a correct digital version of the alloy can dramatically save resources and enhance safety. Surprisingly, this virtual version can be used and addressed in the Metaverse. Thus, having a realistic vision of this revolutionizing technology can preserve industries. It is not just normative by definition, which refers to a certain preferred perspective on the virtual world, but it is an effective approach to modernizing the production. This is why the investment on this emerging technology and organizing frameworks for developers and researchers to adapt to this area of study is a must. To be exact, it is essential to address the investment on this technology as many large companies will put all of their reputation and power to realize the Metaverse-based platforms as soon as possible, these including Meta, Google, and Amazon, etc. The majority of the mega investors believe that the Metaverse will bring them significant benefits. The process of digital twining for the proposed alloy has been shown in Figure 1.

This research shows how metals, alloys and materials can enter the Metaverse world and how ML-based methods speed up the progress in development of these complex systems [21,22]. As alloys play a vital role in manufacturing, the concentration of this research is to use some intelligent methods for digital twining alloys. This methodology can provide readers and the Metaverse enthusiasts with the means to conduct similar research on a wide range of similar alloys and introduce them to the Metaverse world. Considering the rapid growth of ML-empowered techniques in various aspects of our lives, owing to their effective performance for modeling, predicting, and estimating complex systems, the utilization of these methods to make the digital twins of alloys can be constructive. One of the significant characteristics of ML-based methods is to find the relationship between inputs and outputs of the system. From a systematic perspective, each alloy can have some inputs and outputs that give an overview about the characteristics and dynamic behavior of that alloy. On the one hand, utilization of analytical methods to address an alloy, which experienced many nonlinearities and uncertainties during its production, is problematic. Moreover, this inaccurate style of analyzing alloys needs deep knowledge of mechanical engineering, material engineering, chemical engineering, and physics that employs many of the experts in this field, requires a lot of investment, and is not economical.

Another important problem with conventional methods of modeling complex alloys is the huge latency and time-consuming nature of these methods. More importantly, an alloy’s properties will change with time, environmental conditions, and many micro or macro factors. However, these changes are, in most of the applications, ignorable. However, taking notice of these changes makes no sense in some aerospace programs. Therefore, it is beneficial to adapt the digital version of the systems, materials, and alloys with intelligent approaches, such as ML methods [23,24]. These methods provide industries with a fast and efficient way of modeling complex systems. Most significantly, these methods are the ideal ways to adapt the physical twins of the alloy to the Metaverse. Hence, the digital twins of the alloys can be presented and used with Non-Fungible Tokens (NFTs) in the Metaverse platforms.

In Section 3, to prove the efficiency and applicability of the proposed approach, a specific alloy has been designed and manufactured. Some specific operations have been undertaken in this process to ensure that the studied alloy for digital twining has enough complexity and uncertainty. This process has been described in the next section. In reality, we want to build precise digital twins of an alloy based on its physical twin information, the process of manufacturing, and the relevant properties. This way, this research is conducted based on a comprehensive examination, including the experimental part and the simulation.

3. Physical Twin

3.1. Tested Material

As is emphasized in the previous sections, data play an important role in the digital twining of an ally as well as the application of that in the Metaverse. Therefore, a comprehensive examination of a real process of alloy manufacturing is organized to make sure about the modeling part. Commercial 42SiCr steel sheets were employed and used as the physical twin in this research. The low alloy 42SiCr steel is a modification for a number of materials particularly suited for producing shafts, pins, screws, or springs for transportation vehicles. The principal chemical elements are, in weight percentage, 0.42% C, 2% Si, 0.59% Mn, and 1.33% Cr. Comparing this steel to others in its category, the mechanical qualities are improved by the higher Si content. This may lessen the precipitation of carbides and allow carbon to diffuse into leftover austenite. In addition, pearlite will form as a result of the manganese improving the solubility of carbon in austenite [25]. Additionally, the composition of the material may be able to support the phase changes of the heat treatment Q&P while still offering appropriate cold-forming capabilities in the initial pearlitic state.

Table 1. Chemical composition and CEV of 42SiCr steel used in this work.

Element	C	Si	Cr	Mn	Fe	CEV
wt%	0.42	2.0	1.3	0.68	Bal.	0.82

lists the chemical composition of the 42SiCr steel alloy used in this research as well as the calculated carbon equivalent value (CEV).

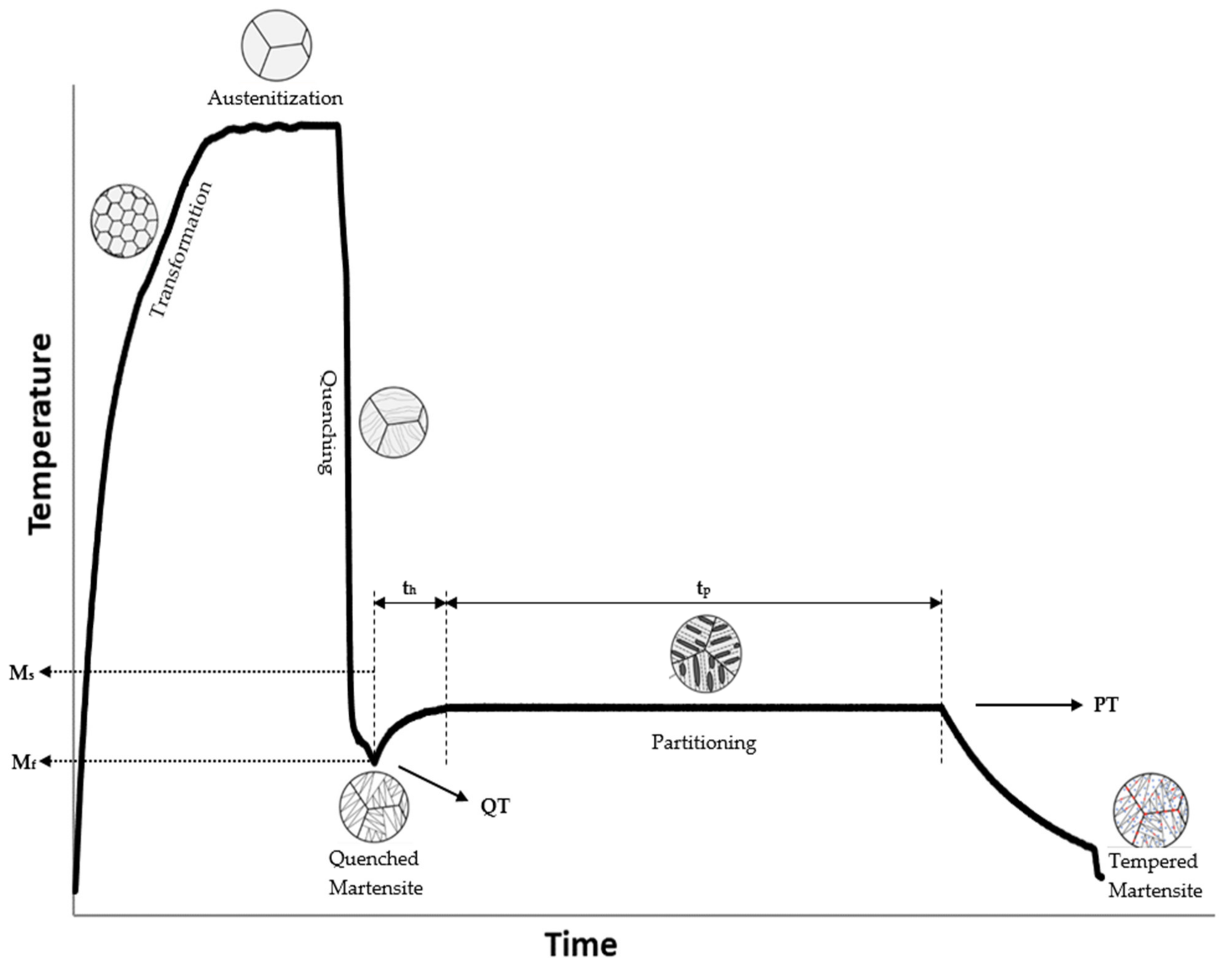
3.2. Q&P Heat Treatment

The Q&P heat treatments were carried out to improve the alloy’s mechanical strength and restore its ductility. Advanced High Strength Steel (AHSS) material properties and increased ductility were achieved by the Q&P treatment. Using this method, the initial pearlitic microstructure is converted primarily into a martensitic microstructure with some retained austenite. To examine the impact of each Q&P parameter on the mechanical characteristics of this material, several combinations of Q&P procedures were used.

As demonstrated in Figure 2, to reach the austenite region, all of the samples were annealed at 950 °C (Austenitization). Later, to keep some fraction of the austenite, it was then partially quenched to the quenching temperature QT, which held just a little bit above the Martensite finish (M_f) temperature. For 42SiCr steel, the martensitic transformation typically starts at around M_s = 298 °C, while M_f is maintained at about 178 °C. The specimens were then heated once more to the partitioning temperature (PT) and kept there for the partitioning time (t_p). This will enable the remaining austenite (RA) to be stabilised through the redistribution of carbon atoms.

Table 2. Q&P process parameters range used in this study.

QT [°C]	PT [°C]	tp [s]	Cooling Rate
RT, 160, 180, 200, 230, 260	RT, 230, 250, 270, 280, 340, 380	0, 120, 300, 400, 500, 600, 700, 800, 1800	0.0325, 0.0625, 0.125, 0.25, 0.5, 1, 2

shows the summary of the Q&P parameters range that were employed in this investigation, and Figure 2 shows the scheme of the Q-P treatment, where:

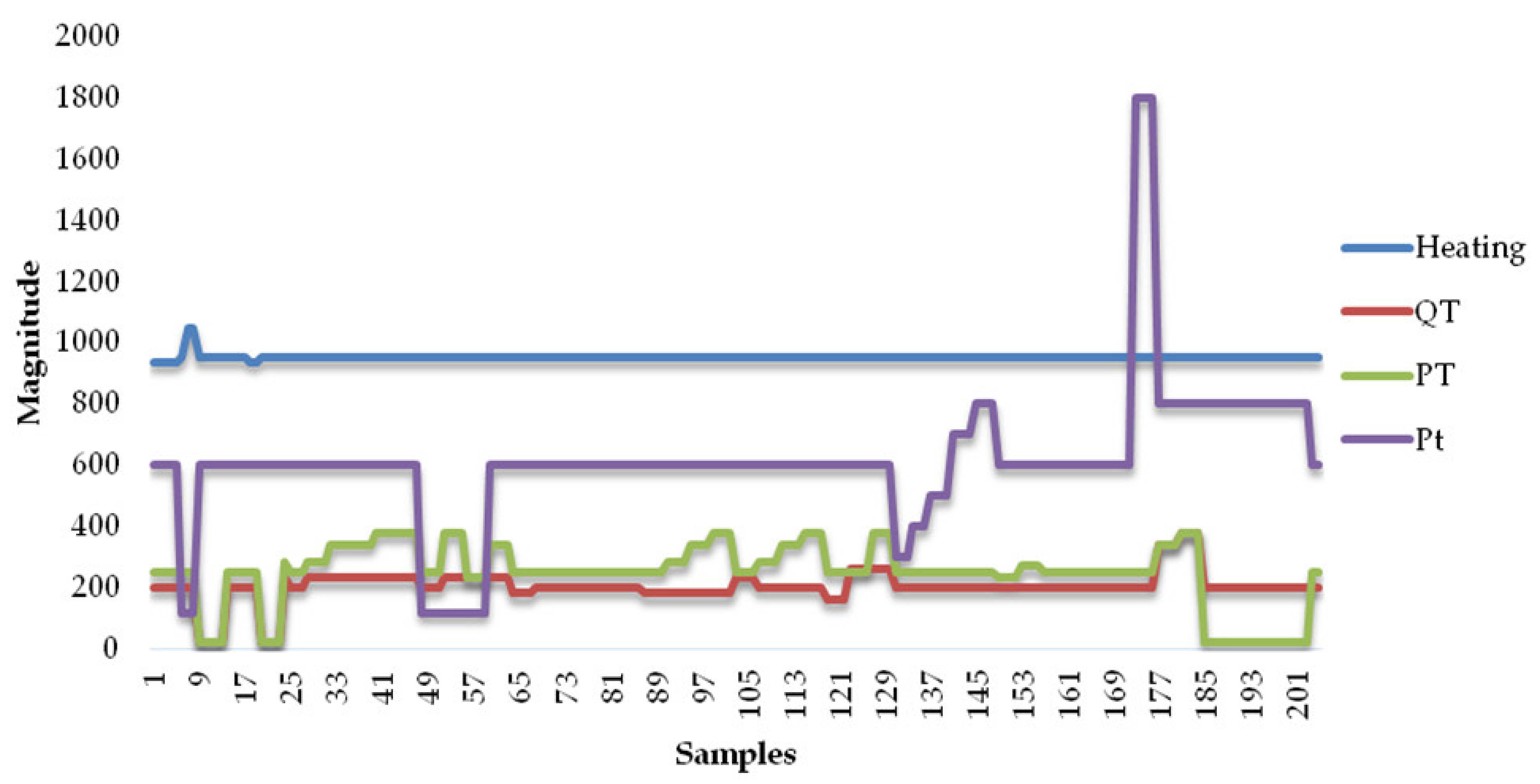
3.3. Testing Preparation and Equipments

Standard tensile samples are made to fit in the tensile machine and have the following dimensions: gauge length 20 mm, width 2 mm, and average thickness 2.5 mm. All of the samples are cut using a water jet cutting technology in a longitudinal manner (parallel to the rolling direction) and ground up. The mechanical tests were carried out utilising a servo-hydraulic MTS thermomechanical simulator and a UHL/VMHT hardness tester (Walter Uhl, Asslar, Germany) (MTS, Minnesota, MN, USA). For the servo-hydraulic MTS, the authors prepared special convertors (UWB, Pilsen, Czech Republic). For all tensile tests, the strain rate was 1 × 10^{3 s−1}. After testing three samples from each state, the average values of ultimate tensile strength (UTS) and elongation to failure (A) were calculated statistically. Hardness tests on the polished sample heads were performed using 10 kg weight and 11-s loading time. The average value was determined by averaging three measurements. Samples of the treated materials were obtained for metallographic examination. The sample preparation process involved using common grinding and polishing techniques. Figure 3 and Figure 4 depict the parameters of the alloy that has been used to make the digital twin.

4. Machine Learning Methods Procedure

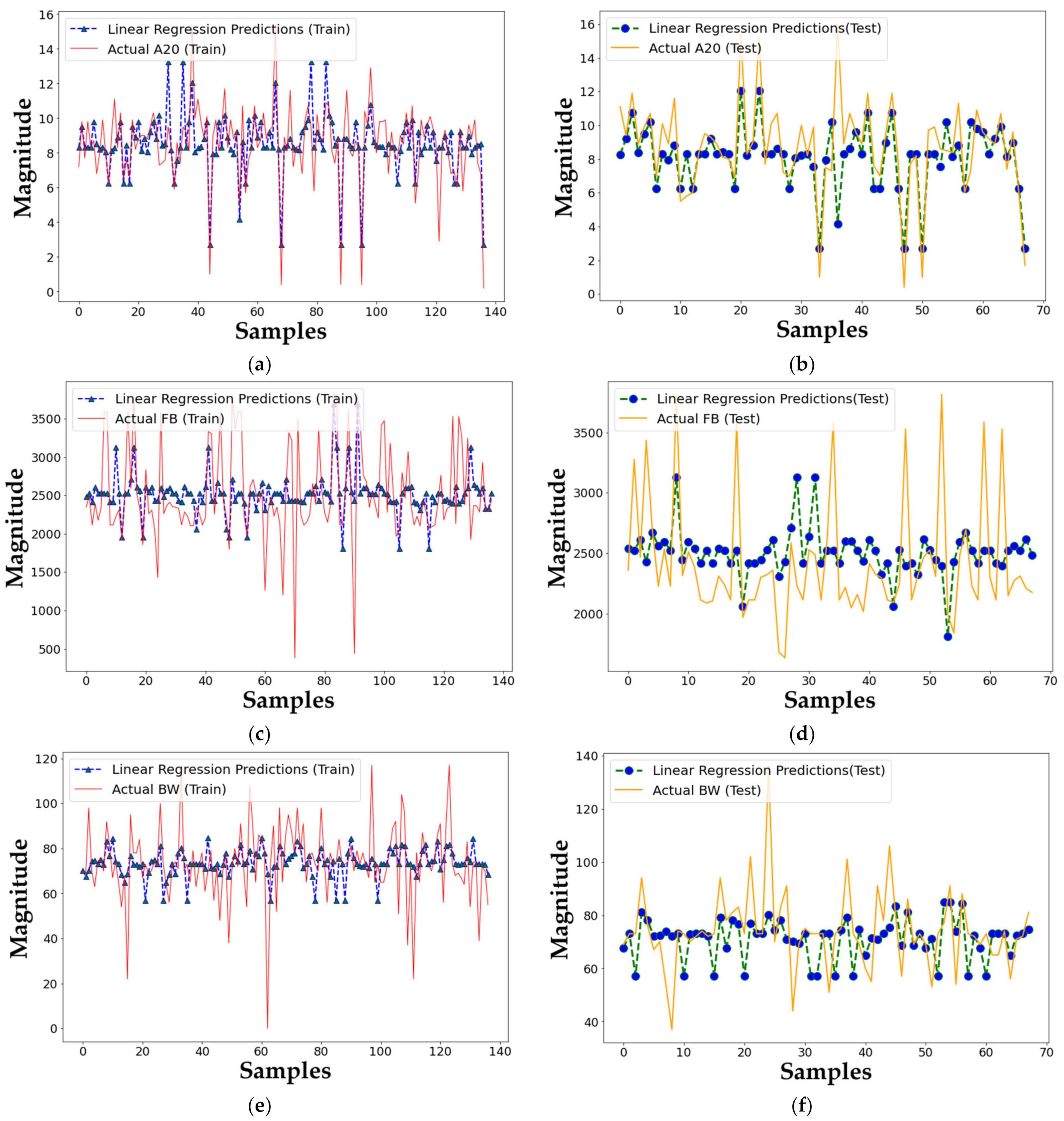
4.1. ML Linear Regression

The first ML method we use to realize the digital twin of the proposed alloy is ML Linear Regression. This linear statistical technique, used for modelling the relationship between a scalar response and at least one explanatory variable (also referred to as dependent and independent variables), can be a good candidate for materials. Figure 5 and Figure 6 depict the performance of this simple and powerful ML method in digital twining the alloy considering the inputs. In the case that there is just one explanatory variable, the method is known as simple linear regression; if there are more, it is known as multiple linear regression [26]. This term also differs from multivariate linear regression, which is used for predictions of multiple correlated dependent variables, as opposed to a single scalar variable. In linear regression, linear predictor functions are used to model relations with the model’s unknown parameters being estimated from the data. These models can be utilized for digital twinning because the digital version of the systems needs to recognize complexity or accuracy. Most frequently, it is assumed that the conditional mean of the response when considering the values of the explanatory variables (or predictors) is an affine function of those values; the conditional median or another quantile is applied less frequently. Similar to all other methods of regression analysis, the concentration of linear regression is on the conditional probability distribution of the response based on the values of the predictors rather than the joint probability distribution of all these variables, which is the focus of multivariate analysis.

The first regression analysis method that underwent in-depth research and saw a lot of use in actual applications was linear regression. This is because models with linear dependence on their unknown variables are simpler to fit than models with non-linear dependence on their variables, and because it is simpler to determine the statistical characteristics of the resulting estimators. This method is based on supervised learning, where it executes a regression operation. Regression uses independent variables to model a goal prediction value. It is mostly used to determine how variables and forecasting relate to one another. Regression models vary according to the number of independent variables they use and the type of relationships they take into account between the dependent and independent variables.

4.2. Decision Tree Regression

Another effective technique for digital twinning of the alloy is Decision Tree Regression (DTR), which has good performance in the estimation of the characteristics of the studied alloy. Its results have been demonstrated in Figure 7 and Figure 8. This supervised learning approach called a decision tree is used in a wide range of regression modelling. This method is used for analyzing the proposed alloy [27].

These trees are used to categorize or regress data using true or false responses to specific queries. When the structure is visualized, it resembles a tree with distinct sorts of nodes at the root, internal, and leaf layers. Figure 9 demonstrates the implementation of this method and its algorithm, which has been changed based on the dynamic of the data. The decision tree begins at the root node and branches out to internal nodes and leaf nodes. The final classification categories or actual values are found in the leaf nodes.

Choosing a feature to serve as the root node is the first step in creating a decision tree. Typically, no one feature can predict the final classes with absolute accuracy; this is known as impurity. This impurity is measured using techniques like Gini, entropy, and information gain, which show how well a feature categorizes the supplied data. At whatever level, the node is chosen as the feature with the least impurity. In order to determine the Gini impurity for a feature with numerical values, the data must first be sorted in ascending order and then the averages of the adjacent values are computed. The Gini impurity is then determined at each chosen average value by organizing the data points according to whether the feature values are smaller or larger than the chosen value and whether the selection accurately categorizes the data. Then, using equation

$$Gini Impurity=1-{\displaystyle \sum }_{i=1}^k{p}_i^2$$

(1)

the Gini impurity is determined. Here, k is the total number of classification categories, and p is the percentage of categories that are present.

For the leaves at each value, the weighted average of the Gini impurity is determined. For that characteristic, the value with the lowest impurity is chosen. To choose the feature and value that will form the node, the procedure is repeated for many features. This process is iterated at each depth level and at each node until all the data is categorised.

Once built, the tree must descend based on the conditions at each node to reach the final value or classification to make a prediction for a data point. When utilizing decision trees for regression, the impurity is measured using variance or the sum of squared residuals.

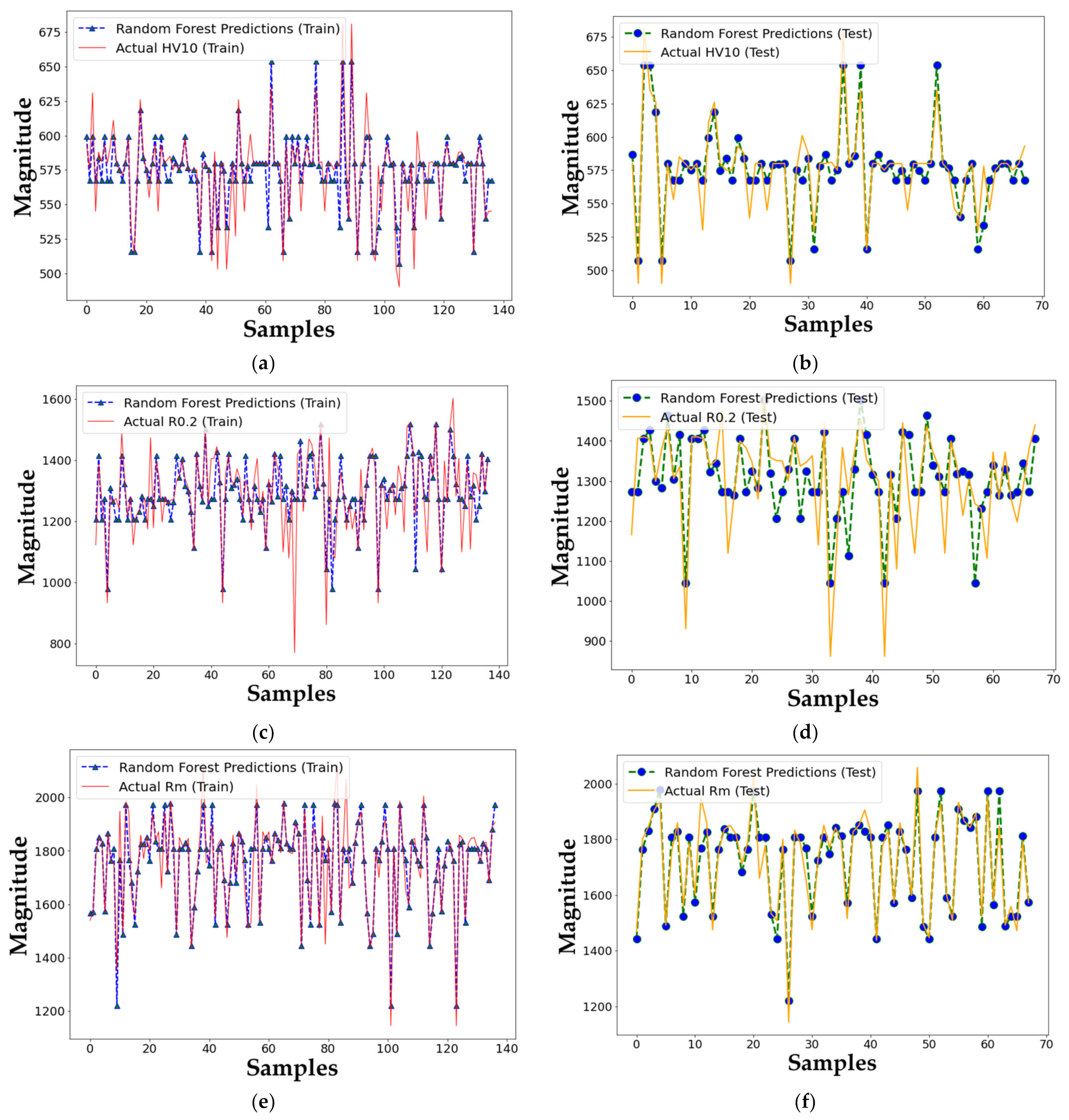
4.3. Random Forest Regression

The third ML method that we used for the implementation of the digital twin of the proposed alloy is Random Forest Regression (RFR). RFR is one of the most widely used algorithms for regression problems due to its simplicity and great accuracy. Therefore, this method can be a suitable tool in digital twining of the materials and alloys [28]. Figure 10 and Figure 11 give useful information about the performance of this method in estimating the desired parameters of the proposed alloy. Multiple decision trees are combined with a voting mechanism in this ensemble technique. It performs more generally than DTR due to randomness. This aids in lowering the variance of the model. It is typically trained using the bagging technique, which combines predictions from various machine learning algorithms to provide predictions that are more accurate than those from a single model. They do not require a lot of parameter adjusting and are less susceptible to dataset outliers. The only RFR parameter normally required for experimentation is the number of ensemble trees. As the average prediction across all decision trees, the predictions are calculated. The fact that the separate models have little association with one another is crucial. RFR is a regressor that uses a voting mechanism to produce predictions based on decision trees. Using divisions between the training samples, RFRs create multi-decision trees. In accordance with the bootstrap sampling method, a portion of the data set is randomly chosen as the training example, and the remaining data is utilized as the validation sample for each decision tree. In order to get the final predictions while regressing unknown samples, the predictions of each decision tree are first generated, and all of the predictions are then aggregated using a simple voting procedure.

RFR’s inherent capacity to automatically fix decision trees’ overfitting issues to their training data sets is its most noticeable advantage. Applying the bagging method and random feature selection, the overfitting issue—which frequently results in erroneous results—is almost entirely solved.

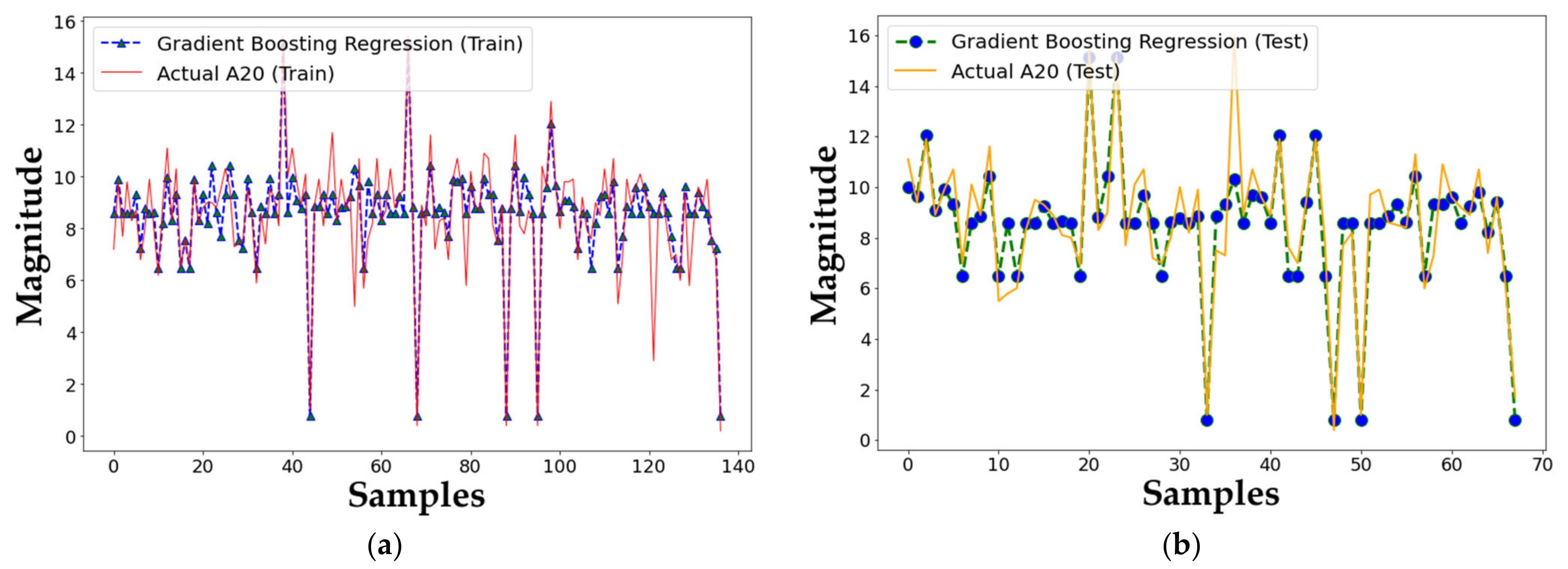
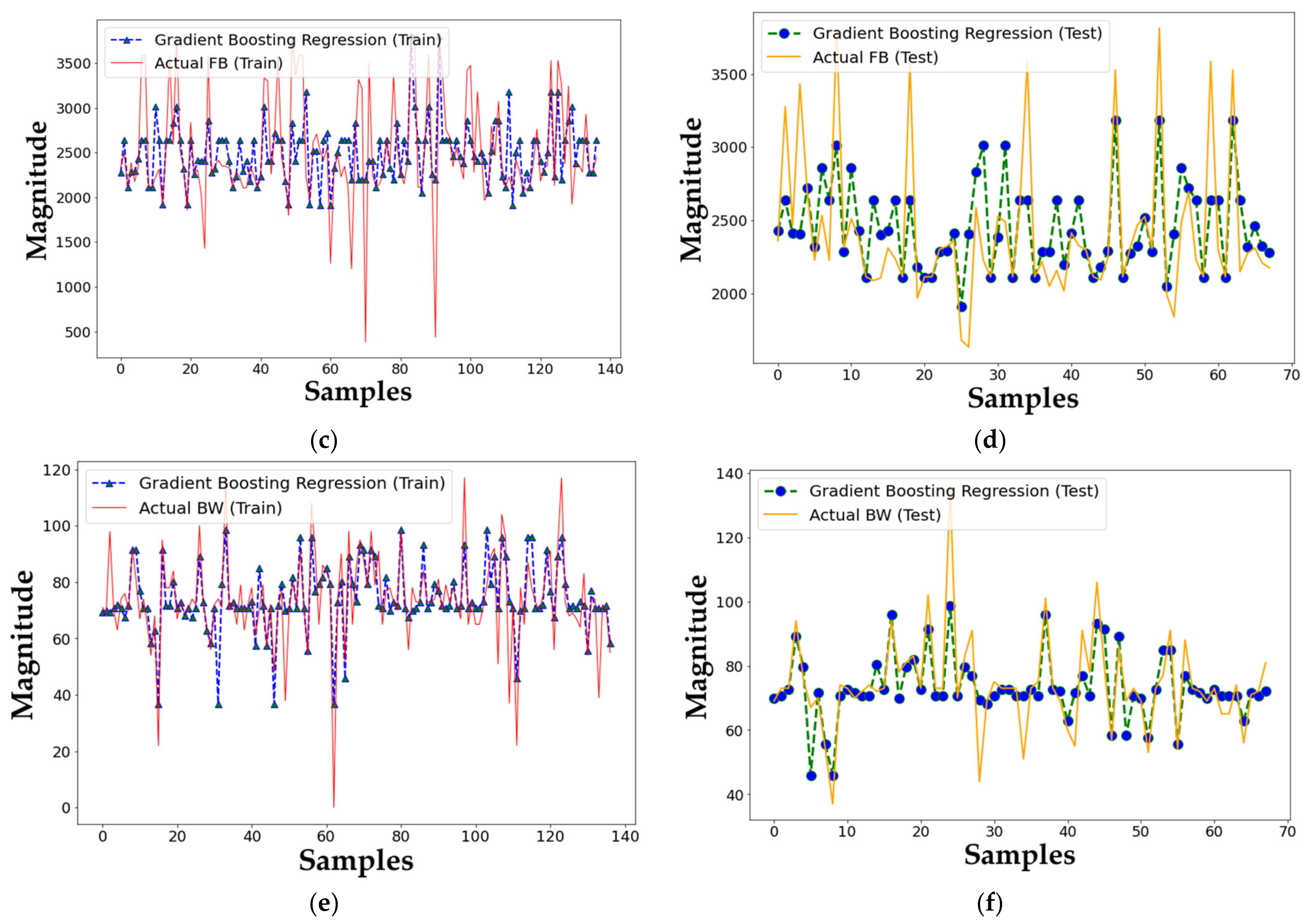
4.4. Gradient Boosting Algorithm

The last ML technique which has been employed in this research for building the digital twin based on the physical twin described in Section 3, is the Gradient Boosting Algorithm (GBA). GBA is an approach for supervised ML that was developed in the past two decades [29].

The boosting ensemble approach employs many weak learners which concentrate on the errors that happen at each step until a robust model for regression and classification is generated. In this paper, the boosting approach is applied to perform regression. While Figure 12 demonstrates the validation of this algorithm in modelling the digital twins of the alloy based on HV10, R0.2 and Rm, Figure 13 depicts the performance of this method for other targets, such as A20, FB, and BW. Gradient Boosting Regression Algorithm has three main parts: the discrepancy between actual and expected values is identified by the loss function. A weak learner is a decision tree that makes a prediction. An additive model is used for minimizing the loss function [29]. To enhance prediction and lower prediction error, each weak learner model tries to correct errors left by preceding weak learner models. Considering a collection of random input parameters $x=\left\{x_1,x_2,\dots x_n\right\}$ and a corresponding response variable $z$,

$$\tilde{F}\left(x\right)={}_{F\left(X\right)}{}^{\mathrm{argmin}}L_{z,x}\left(z, F\left(x\right)\right)$$

(2)

To estimate the approximation function, the loss function is combined with a squared error function as

$$Loss\left(z, F\left(x\right)\right)={\left(z-F\left(x\right)\right)}^2$$

(3)

To determine the gradient of the loss function $Loss\left(z, F\left(x\right)\right)$, the following equation is used [29]:

$${\tilde{z}}_i={\left[\frac{\partial Loss\left(z_i, F\left(x\right)\right)}{\partial F\left(x_i\right)}\right]}_{F\left(x\right)=F_{m-1}\left(x\right)}$$

(4)

The calculation range of the gradient might be generalized if the regression trees $h\left(x_i; b\right)$ with parameter $b$ as weak learners are used. It is often a parameterized function of the input variables $x$ with parameter $b$. To obtain the tree, the following equation may be solved:

$$b_m={}_{b,\beta }{}^{\mathrm{argmin}} {\displaystyle \sum }_{i=1}^N{\left[{\tilde{z}}_i-\beta h\left(x_i,b\right)\right]}^2$$

(5)

where $b_m$ is the weight value also often identified as the expansion coefficient of each weak and $m, \beta$ is the parameters collected at iteration $m$.

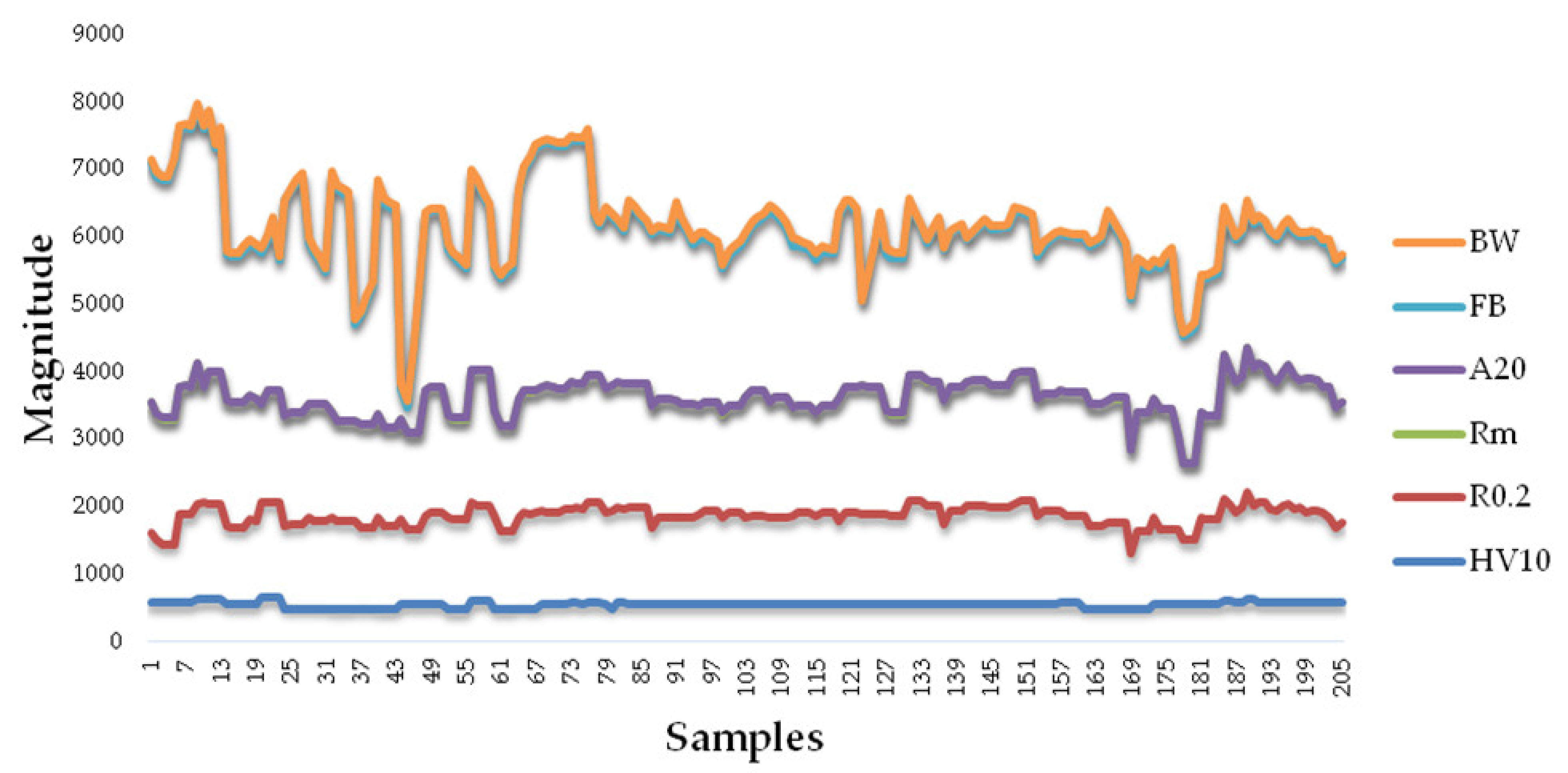
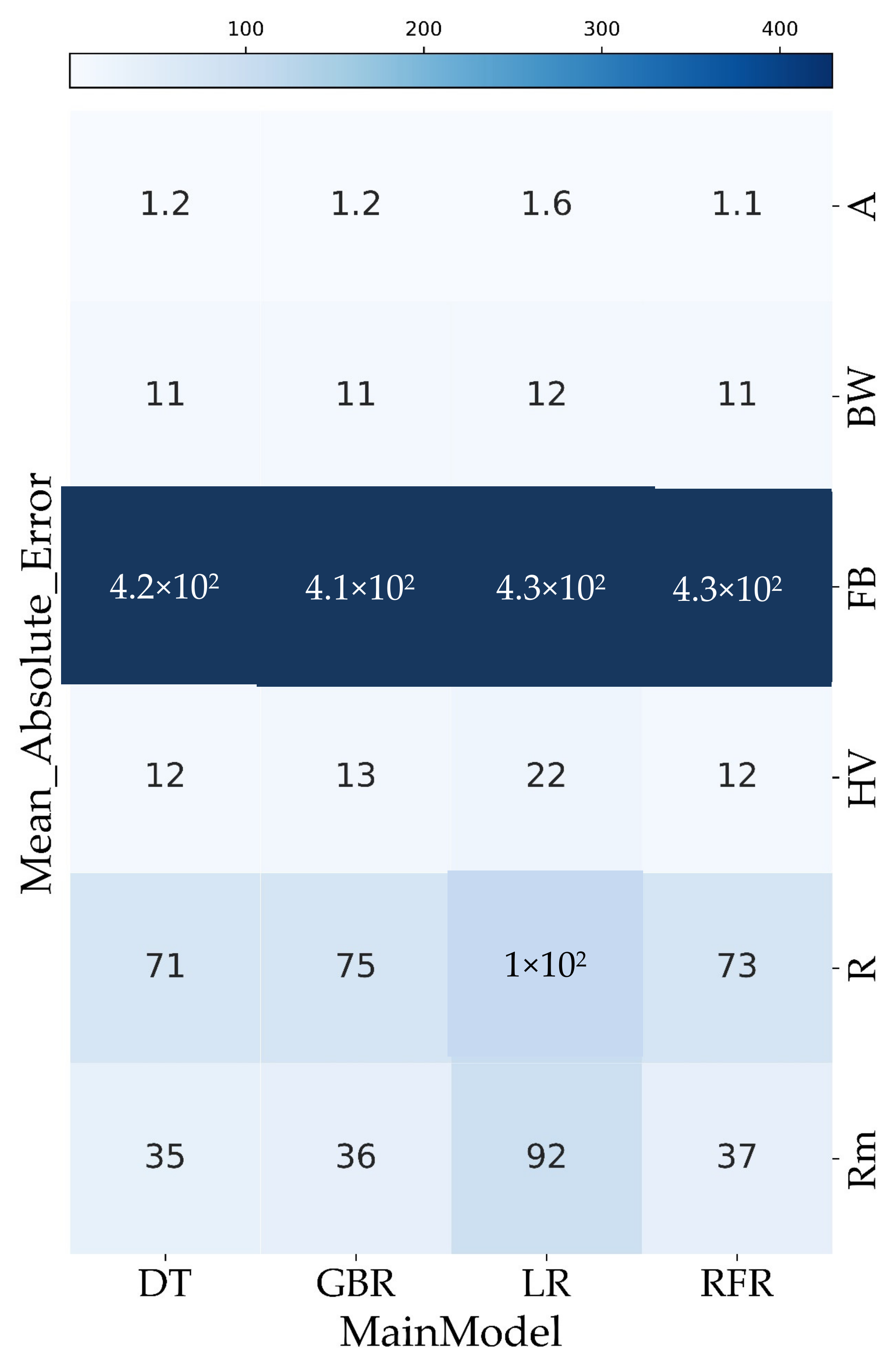
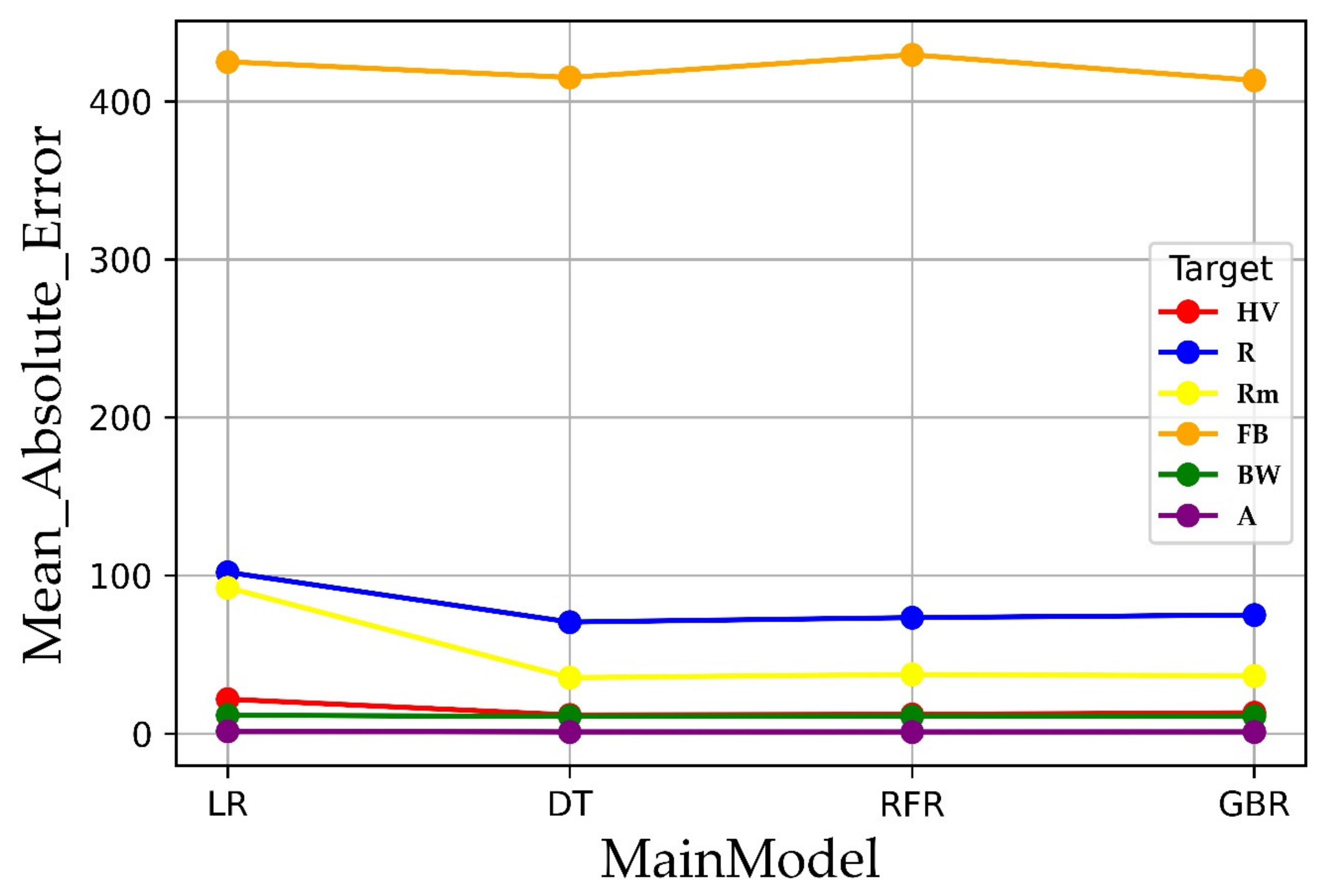
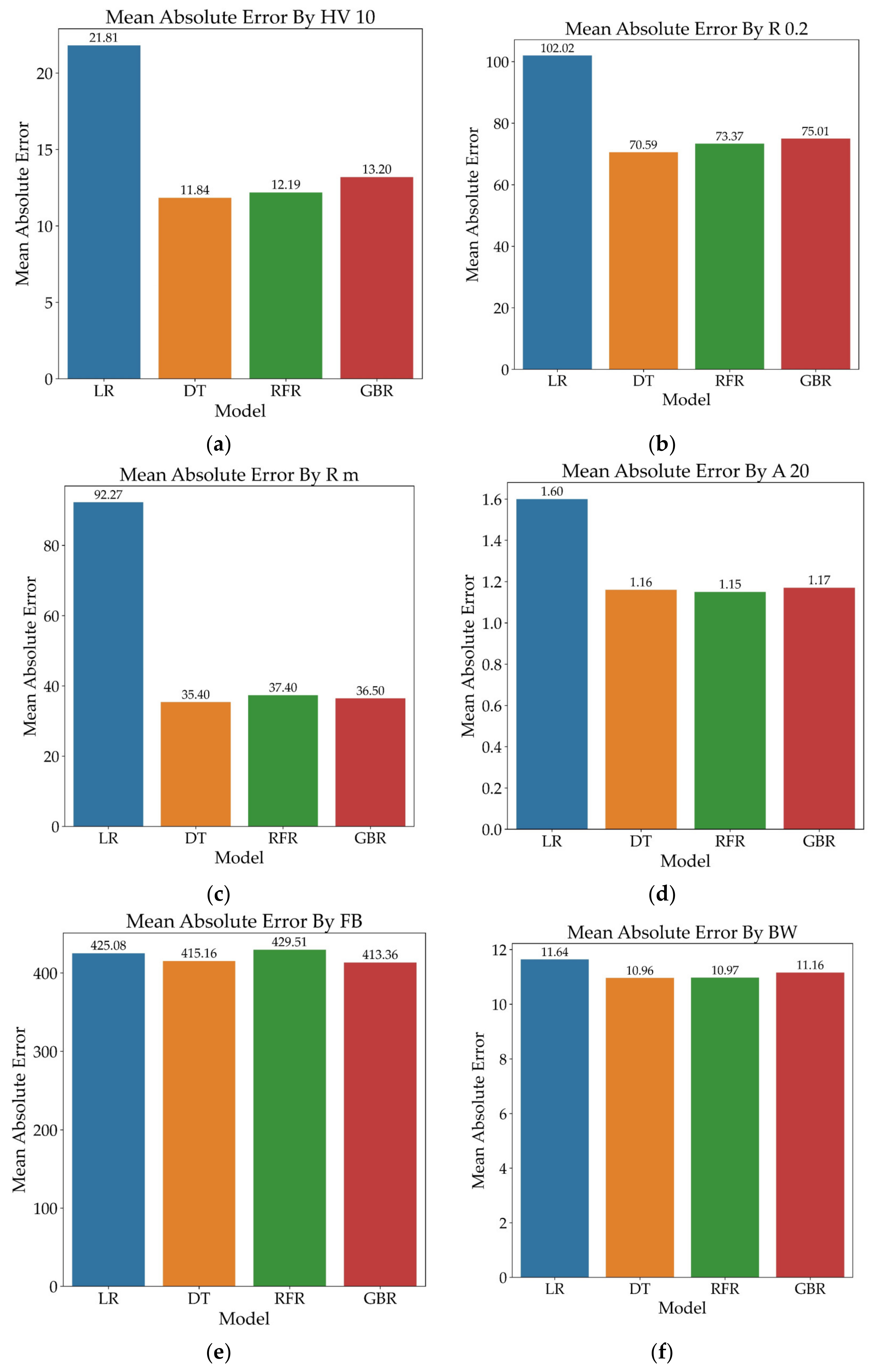
5. Results and Discussion

As a sample of a real-time digital twin, a robot, for instance, could be connected with a number of sensors pertinent to key functional areas. These sensors generate data regarding several performance characteristics of the physical twin, such as load conditions, strain rate, and temperature. Afterwards, a processing system applies this data to the digital twin. Therefore, the evolution of the system design and engineering processes has led to the development of digital twins. Engineering specifications and product drawings have advanced from hand-drawn sketches to computer-aided design further to model-based systems engineering and strict adherence to signals from the physical equivalent. To improve this part, focusing on some studies like the tuning of digital PID controllers and fault diagnosis of an autonomous vehicle with an improved SVM algorithm subject to unbalanced datasets can be constructive [30,31]. However, in the case of materials, the digital twining would be more challenging. Nevertheless, to transfer the material to the Metaverse world, building the digital twins of them is inevitable. In this study, a comprehensive process of the digital twining material with four ML methods, including ML Linear Regression, Decision Tree Regression, Random Forest Regression, and Gradient Boosting Algorithm have been described. While building digital twins of the materials and alloys are the most important part in transferring these materials to the Metaverse, it should be noticed that concentration on simple and more effective methods to achieve this objective is necessary. To evaluate this process, Mean Absolute Model (MAE) has been used. Figure 14 presents the heat map of all used ML-methods to analyze the alloy. This way, RFR estimates A20 with highest rate of accuracy with an MAE of 1.1. On the other hand, RFR and LR shows the worst performance in digital twining FB. However, the other two remaining methods could not have an acceptable output in modeling FB. Figure 15 shows that all proposed methods have desirable performance in modeling A20, while estimating FB was problematic. Figure 16 shows the MAE histogram of the ML methods for each target. Based on this chart, it can be concluded that, in most cases, DT had a successful implementation.

One of the important factors that has been focused on in this research is the connectivity of the models. As many platforms have been implemented based on the AI, digital twining of the materials based on ML methods facilitates this characteristic to present the models in the Metaverse [32]. Numerous new technologies have recently emerged as a result of applications of ML methods, and they can be a backbone for the development of digital twin technology and to enhance the efficiency of cyber-physical systems. AI demonstrates several characteristics that can be used to analyze and model the most complex behavior of the system and create structures in the Metaverse, where the structures built in a virtual environment function like physical ones. This is the reason for their connected nature. Therefore, supplying experimental data to create these models using ML techniques enables the communication between the physical component such as an alloy and its digital equivalent. This connection is the foundation of digital twins; without it, there would be no digital twin technology. This connectedness is produced through intelligent analysis, data mining, and physical items like alloys to model their properties. Nevertheless, these systems’ ability to collect data and analyze information quickly and accurately is another benefit. Digital twin technology based on the ML approach also leads to better connectivity among organizations, products and customers.

From a mechanical viewpoint, due to different processes and specialized applications, alloys can become strongly complex, which can cause physical disturbances. These can result in mistakes or accidents, but they can be controlled by modeling the actual interaction that occurs while the material handling systems are in use. The combination of such a physical simulation model with an experimental model of an alloy based on data mining extends to the idea of a digital twin. The main function of digital twins is to provide decision assistance for real systems by coupling simulation models with operational data. There have been few known instances of digital twins being used in manufacturing outside of the machine tool industry.

6. Conclusions

In this paper, four ML approaches have been employed to digital twining materials with a focus on mechanical properties of a Q&P treated 4SiCr steel alloy. This study can be considered a useful reference for the mechanical and material engineers as to how they can transfer a digital version of their products to the Metaverse using ML. The proposed ML methods include ML Linear Regression, Decision Tree Regression, Random Forest Regression, and the Gradient Boosting Algorithm. This research shows how these classical ML techniques can analyze and model the complex behavior of the proposed alloy and overcome the existing shortage of tangible digital twin implementations in the manufacturing process. The results show the suitable applicability of the proposed method in the digital twining of the proposed alloy.

With regard to the three digital twin functions of prediction, monitoring, and diagnosis, a real-world use case illustrated the flexible advantages of the adopted approaches. It is worthy of note that the method presented here isn’t a full-fledged digital replica of an alloy that exhibits every conceivable behavior linked to a structure. This method can be improved with deep learning methods, although deep learning may not be productive, as in alloys the extraction of the data is very limited.

This study aimed to create digital twins for actual alloys and study the intricate interactions between manufacturing structures in the Metaverse and digital twins. Concentrating on the interconnected features of the understudied alloy characteristics, expansion impacts the accuracy, acceptability, and applicability of the digital twins.