A Data-Driven Process Monitoring Approach Based on Evidence Reasoning Rule Considering Interval-Valued Reliability

Abstract

In the process industry, an alarm system is one of the important ways of condition monitoring. Due to the complexity and irregularity of process information in condition monitoring, there are too many false alarms in the current alarm system. In order to solve the problem of designing an alarm system, this paper proposes a multivariate alarm design method based on the evidence reasoning (ER) rule, considering interval-valued reliability, which can make full use of process information to make accurate alarm decisions. Firstly, the referential evidence matrixes (REMs) are constructed based on the training samples of process variables, and the real-time samples of the process variables are converted into alarm evidence by activating the REMs. Alarm evidence is then fused by the ER rule. In this fusion process, in order to better describe the uncertainty of the process information, the reliability of the alarm evidence is characterized by random variables with certain probability distributions, and it can be adjusted in dynamic intervals according to the real-time change of alarm evidence. Finally, the reactor fault case is implemented in the Tennessee Eastman (TE) process, which shows that the adjustment of interval-valued reliability can adapt to the irregular change of process information and obtains consistent alarm results to further improve the accuracy of alarm decisions.

1. Introduction

With the rapid development of the process industry and the wide application of intelligent information technology, condition monitoring has become a critical part of ensuring the stable, efficient, and safe operation of the process industry [1]. Condition monitoring alerts operators to take appropriate actions to handle possible or potential faults by alarms [2]. Owing to the speedy growth of software and hardware technologies, it is no longer difficult to obtain the sample data of process variables in the process industry, so condition monitoring has become simpler and quicker [3]. However, due to the uncertainty of the industrial environment and the inappropriate design of the condition monitoring system, it will be inevitable to generate a large number of false alarms and missed alarms, so that operators hardly determine the true state of the industrial process ultimately [4]. Therefore, it is very important to design an appropriate alarm method for condition monitoring.

In the traditional condition monitoring method, the alarm threshold is an important parameter, i.e., an alarm is issued based on whether the sampled value of the process variable exceeds the alarm threshold [5]. The higher alarm threshold reduces the number of false alarms, but this may miss critical process state information, resulting in untimely alarms and a large number of missed alarms; the lower alarm threshold triggers more false alarms [6]. Obviously, in practical applications, the alarm design method based on threshold may not be effective in reducing the number of false alarms and missed alarms [7].

In a univariate industrial process, the conventional alarm design methods based on alarm threshold include a time delay method, a filtering method, a deadband method, and so on [8]. Specifically, the time delay method issues an alarm when the sampled value of the process variable exceeds the alarm threshold several times in a row [9]; the filtering method processes the sampled value by the moving variance strategy and then compares the filtered value with the alarm threshold [10]. The deadband method sets high and low alarm thresholds to issue and clear the alarm, and then an alarm is issued when the sampled value is above the high alarm threshold, and an alarm is cleared when the sample value falls below the low alarm threshold [11]. These alarm design methods have improved the alarm thresholds and have achieved some effects in univariate condition monitoring.

In fact, due to the increasing complexity of the industrial process, the multivariate industrial process is gradually replacing the univariate industrial process [12]. The above proposed univariate alarm design methods have some limitations in multivariate industrial processes, such as the inconsistency of alarm results for each variable and the inability to address the complexity of process information. Correspondingly, the multivariable alarm design methods have become a research hotspot in the field of alarm systems, but there is relatively less research on multivariable alarm methods [13]. For example, ref. [14] established objective functions based on the false alarm rate and missed alarm rate of any two process variables and obtained optimal alarm thresholds, respectively, and then designed the alarm system and achieved certain effects compared with univariate alarm systems. In essence, this method only preliminarily extends the idea of univariate threshold optimization to multivariate process, i.e., threshold optimization is performed for multivariate processes, and then the univariate alarm systems are still adopted separately for any one variable [15]. When the number of the process variables are more than two, the order of optimization also needs to be identified. In addition, the alarm results of each variable may be inconsistent or even contradictory, which is a challenge to a certain extent in real application.

In recent years, information fusion theory (IFT) integrates the process information of the multiple variables from various sources to formulate more accurate and consistent decision results though data-driven analysis and has been widely implemented in the domain of pattern recognition, expert systems, and fault diagnosis [16,17]. In IFT, the Dempster-Shafer (DS) theory and evidence reasoning (ER) rule are representative methods [18,19]. Specifically, DS theory translates the data of process variables into corresponding evidence and obtains accurate fusion results through the process of evidence fusion, which reduces the uncertainty of the process information [20,21]. Yang proposed the ER rule based on the DS theory, which further improves the rationality of the evidence fusion process by assigning reliability and weight to evidence [22]. The reliability reflects the inherent property of evidence and is objective, while the weight reflects the importance of the evidence relative to other evidence and is subjective. Since the introduction of reliability, a series of calculation methods for reliability have been proposed, which all describe reliability as a fixed value [23]. On the one hand, reliability reflects the inherent change of the evidence, so it is usually difficult for the fixed value form to describe the uncertainty of the evidence. On the other hand, due to various known or unknown factors, the reliability should change randomly with certain regularity. Therefore, this may be a better way that the reliability can be modeled, in the form of random variables within some uncertain interval.

In view of the above-proposed problems and analysis, this paper proposes an alarm design method via ER rule considering interval-valued reliability, which mainly includes the referential evidence matrix (REM) and is constructed based on the data of training samples, which achieves the transformation of the process variable to the referential alarm evidence, and the real-time sample data activates the REM to obtain alarm evidence. The corresponding interval-valued ER rule is then proposed, which can fuse alarm evidence to get the integrated alarm evidence. Among that, in order to accommodate the change of process variables, the interval-valued ER rule describes the reliability as a random variable and adjusts the changing interval of reliability according to evidence variation. Therefore, the interval-valued reliability adjustment can achieve the efficient integration of the process information. Finally, the accurate alarm decision is made based on integrated alarm evidence.

This paper is organized as follows: Section 2 introduces the theoretical basis of the ER rule; Section 3 presents the alarm design method based on the interval-valued ER rule; Section 4 demonstrates the effectiveness of the proposed method through an example of reactor fault in the TE process; finally, this study is concluded in Section 5.

2. Theoretical Basis

2.1. Theoretical Basis of Dempster-Shafer (DS) Theory

In DS theory, discernment framework Θ = {H₁, H₂, …, H_n} is a set with mutually exclusive propositions, and a power set of Θ, denoted as P(Θ) = 2^Θ = {Ø, H₁, …, H_n, {H₁, H₂}, …, Θ}.

Definition 2.1 

([24]). The mapping $m:P(\Theta )\to [0,1]$ is a basic belief assignment function (BBA) on Θ, which satisfies m(Ø) = 0 and ${\displaystyle {\sum }_{\theta \subseteq P(\Theta )}p(\theta )}=1$.

m(θ) denotes the belief assigned to the proposition θ. In general, the BBA is also referred to as a piece of evidence.

Definition 2.2 

([25]). The Jousselme evidence distance between m₁ and m₂ can be defined by the following equation

$$D_J(m_1,m_2)=\sqrt{\frac{{({\stackrel{\rightharpoonup }{m}}_1-{\stackrel{\rightharpoonup }{m}}_2)}^T\underset{\_}{\underset{\_}{G}}({\stackrel{\rightharpoonup }{m}}_1-{\stackrel{\rightharpoonup }{m}}_2)}{2}}$$

(1)

here $\underset{\_}{\underset{\_}{G}}$ is a $n\times n$ matrix, where n is the number of non-empty set elements in P(Θ), its elements $D(A,B)=\left|A\cap B\right|/\left|A\cup B\right|,\forall A,B\in 2^{\Theta }$, called the Jaccard coefficient. When D_J (m₁, m₂) = 0, the two pieces of evidence are exactly same. On the contrary, when D_J (m₁, m₂) = 1, the two pieces of evidence are completely different. Obviously, the value range of the Jousselme evidence distance is [0, 1].

2.2. Theoretical Basis of Evidence Reasoning (ER) Rule

In ER rule, a piece of evidence e is noted as [26]:

$$e=\{(\theta ,p(\theta ))|\forall \theta \subseteq \Theta ,{\displaystyle {\sum }_{\theta \subseteq \Theta }p(\theta )}=1\}$$

(2)

where the number pair (θ, p(θ)) indicates that belief p(θ) is the degree of support for the proposition θ, and proposition θ can be any element except the empty set in P(Θ). Obviously, here the basic belief assignment function m in DS theory is expressed as evidence e with the form of numbers of pairs in the ER rule.

In the ER rule, evidence is associated with a reliability r and, a weight w, and r$\in$[0, 1], w$\in$[0, 1]. The r denotes the ability of evidence e that provides an accurate judgment to a given question and depends only on the source of evidence. It follows that reliability r is an inherent property of the evidence itself, and it is objective; the w denotes the relative importance of the evidence compared with other evidence, and it is subjective. The w depends on the specific circumstances in which the evidence is used, the users, and the individuals involved in the fusion of evidence. The evidence $\tilde{e}$ with reliability r and weight w is defined as follows

$$\tilde{e}=\{(\theta ,\tilde{m}(\theta ))|\forall \theta \subseteq \Theta ;(P(\Theta ),\tilde{m}(P(\Theta )))\}$$

(3)

where belief $\tilde{m}(\theta )$ indicates the degree of support for θ from the evidence $\tilde{e}$ with reliability and weight, and is defined as follows

$$\tilde{m}(\theta )=\{\begin{array}{c}\hfill 0\hfill \\ \hfill c_{rw}m(\theta )\hfill \\ \hfill c_{rw}(1-r)\hfill \end{array}\begin{array}{c}\hfill \theta =\varnothing \hfill \\ \hfill \theta \subseteq \Theta ,\theta \ne \varnothing \hfill \\ \hfill \theta =P(\Theta )\hfill \end{array}$$

(4)

where m(θ) = wp(θ), c_rw is the normalization factor and is denoted as

$$c_{rw}=\frac{w}{1+w-r}$$

(5)

For the mutually independent evidence, e₁ and e₂, they can be fused through the ER rule, as follows:

$$\begin{array}{c}m{(\theta )}^{e(2)}=[m_1\oplus m_2](\theta )=\{\begin{array}{cc}\hfill 0,\hfill & \hfill \theta =\varnothing \hfill \\ \hfill \frac{\widehat{m}{(\theta )}^{e(2)}}{{\displaystyle {\sum }_{D\subseteq \Theta }\widehat{m}{(D)}^{{}^{e(2)}}}},\hfill & \hfill \theta \subseteq \Theta ,\theta \ne \varnothing \hfill \end{array}\\ \begin{array}{cc}\widehat{m}{(\theta )}^{{}^{e(2)}}=[(1-r_2)m{(\theta )}_1+(1-r_1)m{(\theta )}_2]+{\displaystyle \sum _{B\cap C=\theta }m{(B)}_{1}m{(C)}_2,}& \forall \theta \subseteq \Theta \end{array}\end{array}$$

(6)

It can be used recursively to combine multiple pieces of evidence in any order.

3. The Multivariate Alarm Design Method via the Interval-Valued ER Rule

Here, Section 3.1 first introduces the acquisition of alarm evidence, i.e., the referential evidence matrix (REM) is constructed by casting points that are operation-based on the training set of the process variable, and a real-time sample is transformed into alarm evidence by activating the corresponding REM. Furthermore, in Section 3.2, the interval-valued reliability is adjusted with the change of alarm evidence, and the importance weight of alarm evidence is optimized. In Section 3.3, the interval-valued ER rule fuses alarm evidence coming from multiple process variables and obtains the integrated alarm evidence. Finally, in Section 3.4, the alarm result is obtained based on the integrated alarm evidence. 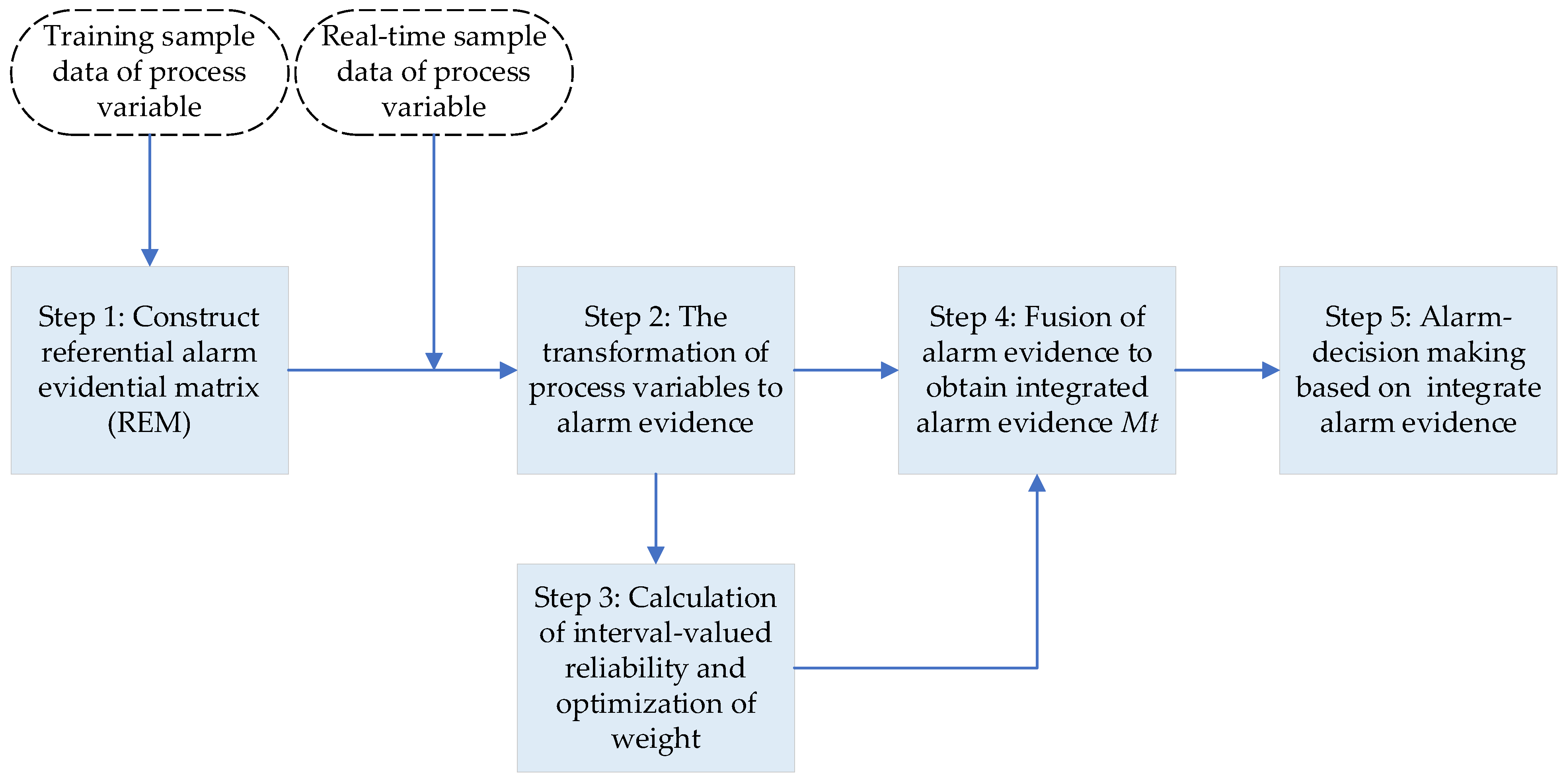The whole process of the designed multivariate alarm method is shown in Figure 1.

Step 1 (The construction of REM): The referential evidence matrix (REM) is constructed by casting points operation based on the training set of process variables, which achieves the accurate transformation of process variable data into referential alarm evidence. More details can be found in Section 3.1.1.

Step 2 (The transformation of process variables to alarm evidence): The real-time sample of the process variable is transformed into alarm evidence by activating the corresponding REM. More details can be found in Section 3.1.2.

Step 3 (The calculation of interval-valued reliability and the optimization of weight): Before using the interval-valued ER rule to fuse alarm evidence, it is important to adjust the reliability intervals and the weights of the corresponding alarm evidence. Therefore, the interval-valued ER rule catering for interval-valued reliability is proposed. Wherein, the reliability of alarm evidence is inscribed by random variables with certain probability distribution characteristics on the interval, and the interval of reliability is adaptively adjusted according to the change of the real-time sample of the process variable, which improves the reasonability of the fusion process. More details are presented in Section 3.2.

Step 4 (The fusion of alarm evidence based on the interval-valued ER rule): On the basis of step 3, this step extends the original ER rule to the interval-valued ER rule, which can fuse alarm evidence to get integrated alarm evidence. More details can be found in Section 3.3.

Step 5 (Alarm-decision making based on integrated alarm evidence): Based on alarm-decision criteria, the alarm decision is made through integrated alarm evidence. More details are shown in Section 3.4.

3.1. The Acquisition of Alarm Evidence

3.1.1. The Construction of REM

Step 1.1: In the context of the alarm system, the discernment framework is defined as Θ = {NA, A}, where “NA” stands for the proposition “no alarm” and “A” represents the proposition “alarm”. Let the set of training samples be V = [x_i(k), y(k)], i = 1, 2, …, I, k = 1, 2, 3, …, K, where I is the number of the process variable, the process variable x_i(k) is the input of the alarm system, and y(k) is the output of the alarm system. Let the reference value set of the input x_i as Oⁱ = {$O_{n_i}^i$|n_i = 1, 2…, N_i}, N_i is the number of reference values of x_i(k), which can be defined based on expert knowledge. The reference value set of the output y(k) is Z = {Z_e, e = 1, 2}, where Z₁ = NA = 0 and Z₂ = A = 1. Therefore, the relationship between the input x_i(k) and the output y(k) can be represented by the corresponding relationship between the input reference values and the output reference values.

Step 1.2: The similarity distribution of x_i(k) in V = [x_i(k), y(k)] relative to the reference values set Oⁱ is calculated by the following information transformation method:

$$Q_O^i(x_i(k))=\{(O_{n_i}^i,{\beta }_{n_i}^i)|n_i=1,2,\dots ,N_i\}$$

(7)

$${\beta }_{n_i}^i=\frac{(O_{n_i+1}^i-x_i(k))}{O_{n_i+1}^i-O_{n_i}^i},{\beta }_{n_i+1}^i=1-{\beta }_{n_i}^i,O_{n_i}^i\le x_i(k)\le O_{n_i+1}^i$$

(8)

$${\beta }_{n_i{}^{\prime }}^i=0n_i{}^{\prime }=1,2,\dots ,N_i,n_i{}^{\prime }\ne n_i,n_i+1$$

(9)

where ${\beta }_{n_i}^i$ represents the similarity of x_i(k) matching input reference value $O_{n_i}^i$.

The similarity distribution of y(k) in V = [x_i(k), y(k)] matching the reference value Z_e is Q(y) = {(Z_e, ${\gamma }_e$)|e = 1, 2}, among them:

$${\gamma }_e=\{\begin{array}{c}1,y(k)=NA\\ 0,y(k)=A\end{array}$$

(10)

$${\gamma }_{e+1}=1-{\gamma }_e$$

(11)

where, ${\gamma }_e$ represents the similarity of y(k) matching the output reference value Z_e.

Therefore, each sample [x_i(k), y(k)] in V is transformed into a similarity distribution with the form $({\beta }_{n_i}^i{\gamma }_e,{\beta }_{n_i+1}^i{\gamma }_e,{\beta }_{n_i}^i{\gamma }_{e+1},{\beta }_{n_i+1}^i{\gamma }_{e+1})$, where ${\beta }_{n_i}^i{\gamma }_e$ represents the joint similarity of x_i(k) matching $O_{n_i}^i$ and y(k) matching Z_e, and the sample cast point table shown in

Table 1. The sample cast point table of [x_i(k), y(k)].

	xi(k)	$O_1^i$	$O_2^i$	$O_3^i$	…	$O_{N_i}^i$	Total
y(k)
Z1		${\delta }_{1,1}^i$	${\delta }_{1,2}^i$	${\delta }_{1,3}^i$	…	${\delta }_{1,N_i}^i$	${\psi }_1^i$
Z2		${\delta }_{2,1}^i$	${\delta }_{2,2}^i$	${\delta }_{2,3}^i$	…	${\delta }_{2,N_i}^i$	${\psi }_2^i$
Total		${\phi }_1^i$	${\phi }_2^i$	${\phi }_3^i$	…	${\phi }_{N_i}^i$	K

is constructed. ${\delta }_{e,n_i}^i$ represents the sum of the similarity of all samples whose input x_i(k) matches $O_{n_i}^i$ and output y(k) matches Z_e. ${\psi }_e^i={\displaystyle {\sum }_{n_i=1}^{N_i}{\delta }_{e,n_i}^i}$ represents the sum of the joint similarity of all output y(k) matching Z_e. ${\phi }_{n_i}^i={\displaystyle {\sum }_{e=1}^2{\delta }_{e,n_i}^i}$ represents the sum of the joint similarity of all input x_i(k) matching $O_{n_i}^i$. Obviously, there is ${\displaystyle {\sum }_{e=1}^2{\psi }_e^i}={{\displaystyle {\sum }_{n_i=1}^{N_i}\phi }}_{n_i}^i=K$.

Step 1.3: According to the sample cast point table, when the value of the process variable x_i(k) is relative to the input reference value $O_{n_i}^i$, the belief that the output y(k) is relative to the output reference value Z_e can be calculate by

$${\lambda }_{e,n_i}^i=\raisebox{1ex}{${\delta }_{e,n_i}^i/{\psi }_e^i$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{e=1}^2({\delta }_{e,n_i}^i/{\psi }_e^i)}$}\right.$$

(12)

and ${\displaystyle \sum _{e=1}^2{\lambda }_{e,n_i}^i}=1$, then the alarm evidence corresponding to the input reference value $O_{n_i}^i$ can be defined as

$$T_{n_i}^i=[{\lambda }_{1,n_i}^i,{\lambda }_{2,n_i}^i]$$

(13)

Therefore, the referential evidence matrix (REM) table as shown in

Table 2. The referential evidence matrix table of input x_i(k).

	xi(k)	$T_1^i$	$T_2^i$	$T_3^i$	…	$T_{N_i}^i$
y(k)		$O_1^i$	$O_2^i$	$O_3^i$	…	$O_{N_i}^i$
Z1		${\lambda }_{1,1}^i$	${\lambda }_{1,2}^i$	${\lambda }_{1,3}^i$	…	${\lambda }_{1,N_i}^i$
Z2		${\lambda }_{2,1}^i$	${\lambda }_{2,2}^i$	${\lambda }_{2,3}^i$	…	${\lambda }_{2,N_i}^i$

can be constructed to describe the relationship between the input x_i(k) and the output y(k).

3.1.2. The Transformation of Process Variables to Alarm Evidence

Step 2: For the real-time sample x_i(t), t = 1, 2, 3, …, it necessarily falls into the interval [$O_{n_i}^i$,$O_{n_i+1}^i$] composed of two reference values, $O_{n_i}^i$ and $O_{n_i+1}^i$, and the referential alarm evidence, $T_{n_i}^i$ and $T_{n_i+1}^i$, corresponding to these two reference values, are activated, and then the alarm evidence $a_t^i$ corresponding to the real-time sample x_i(t) can be obtained by the weighted sum form of $T_{n_i}^i$ and $T_{n_i+1}^i$. $a_t^i$, which is represented as follows:

$$a_t^i=\left\{\left(Z_e,{\beta }_{n_i}^i{\lambda }_{e,n_i}^i+{\beta }_{n_i+1}^i{\lambda }_{e,n_i+1}^i\right),e=1,2\right\}$$

(14)

For ease of understanding, this alarm evidence can be rewritten as follows:

$$\begin{array}{c}{a}_t^i=[a_t^i(NA),a_t^i(A),a_t^i(\Theta )]\\ a_t^i(NA)={\beta }_{n_i}^i{\lambda }_{1,n_i}^i+{\beta }_{n_i+1}^i{\lambda }_{1,n_i+1}^i\\ a_t^i(A)={\beta }_{n_i}^i{\lambda }_{2,n_i}^i+{\beta }_{n_i+1}^i{\lambda }_{2,n_i+1}^i\\ a_t^i(\Theta )=0\end{array}$$

(15)

where $a_t^i(NA)$ and $a_t^i(A)$ denote the belief of “No alarm (NA)” and “alarm (A)” respectively, and $a_t^i(NA)$ + $a_t^i(A)$ = 1.

3.2. The Calculation of Interval-Valued Reliability and the Optimization of Weight

In the original ER rule, the reliability and weight of alarm evidence are generally expressed in the form of a fixed value based on expert knowledge [22,23]. However, since the process variables are constantly changing, the corresponding alarm evidence also changes accordingly. This single fixed reliability and weight in the fusion process may make the fusion results unreasonable. Furthermore, in the original ER rule, the reliability r is defined as the ability of evidence to provide correct results for a particular question and is the objective nature of evidence. On the contrary, the weight w is the importance of the current evidence relative to other evidence and is the subjective nature of evidence. Therefore, reliability is an inherent property which is not affected by other pieces of evidence. In addition, the alarm evidence changes irregularly at each moment, which makes it impossible to calculate the accurate value of the reliability by a functional relationship, so it is a more efficient way to express the reliability of alarm evidence in the form of an interval value. Unlike reliability, the weight of some evidence (a certain process variable) represents the relative importance when it is combined with other evidence (other process variables), hence it can be set as a single value and optimized according to decision objectives.

Through the above analysis for the reliability factor r and the importance weight w, this section designs the interval-valued ER rule catering for interval-type reliability, in which the reliability of each piece of alarm evidence can be adaptively adjusted on a certain interval, and the weight can be obtained by classical optimization algorithms, such as gradient descent algorithm and evolutionary algorithm. This mechanism can ensure the accuracy of the fusion process and improve the efficiency of fusion process.

Step 3: The reliability of alarm evidence is described by a continuous random variable with uniform distribution characteristics on an interval, as shown in the following form

$$r_i\sim U(r_i^{-},r_i^{+})$$

(16)

r_i represents the interval-valued reliability of alarm evidence. $r_i{}^{-}$ and $r_i^{+}$ can be calculated by the following equation

$$r_i^{-}=r_i{}^{\prime }-{\alpha }_i,r_i^{+}=r_i{}^{\prime }+{\alpha }_i$$

(17)

where $r_i{}^{\prime }$ is the optimal reliability obtained by training set. Namely, the sample data of the process variable is defined as the training set and transformed into the alarm evidence $a_t^i$. $r_i{}^{\prime }$ and w_i as the optimal reliability and weight, respectively, are obtained by optimizing distance between the fusion alarm evidence m_t and the standardized evidence {f_NA = (1,0,0), f_A = (0,1,0)}. Specially, m_t is obtained by Equation (6). The optimization process can be realized by genetic optimization algorithms. It should be noted that $r_i{}^{\prime }$ is an optimal fixed value reliability through the training set, and the w_i is used for the entire fusion process. The optimization model based on genetic algorithm is constructed as follows:

$$\begin{array}{c}{\min }_P\zeta (P)={\displaystyle {\sum }_{\tilde{i}=1}^{\tilde{I}}{d}_E(m_t,f^{\tilde{i}})}\\ s.t.\hspace{1em}0\le w_i\le 1,i=1,2,3\\ s.t.\hspace{1em}0\le r_i^{’}\le 1,i=1,2,3\end{array}$$

(18)

where ζ(P) represents the optimization objective function, P = {(w_i, $r_i{}^{\prime }$) | i =1,2,3} represents the parameter set to be optimized, and the value range of w_i and $r_i{}^{\prime }$ is [0, 1]. The d_E indicates the fusion result, that is, the evidence distance between the integrated alarm evidence M_t and the standardized evidence {f_NA = (1, 0, 0), f_A = (0, 1, 0)}. This optimization process can be done through the optimization toolbox in Matlab. Finally, the performance of the model is gradually optimized due to the change of the optimized parameter set.

In Equation (17), α_i is a reliability adjustment factor based on the similarity between pieces of alarm evidence, calculated by the following equation:

$${\alpha }_i=\frac{1-d_i}{{\displaystyle \sum _{i=1}^I(1-d_i)}},i=1,2,\dots ,II\ge 2$$

(19)

where d_i is the distance defined in Equation (1) between the alarm evidence $a_t^i$ and the normalized evidence f_NA, f_A in the discernment framework, shown as follows:

$$d_i=\{\begin{array}{c}{((a_t^i-f_{NA})\ast G\ast {(a_t^i-f_{NA})}^T)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\ast \frac{\sqrt{2}}{2},a_t^i(NA)>a_t^i(A)\\ {((a_t^i-f_A)\ast G\ast {(a_t^i-f_A)}^T)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\ast \frac{\sqrt{2}}{2},a_t^i(NA)\le a_t^i(A)\end{array}$$

(20)

where the alarm evidence can be represented by $a_t^i=[a_t^i(NA),a_t^i(A),a_t^i(\Theta )]$ in Section 2. Thus, the order of G is 3, that is:

$$G=\left[\begin{array}{ccc}1& 0& 0.5\\ 0& 1& 0.5\\ 0.5& 0.5& 1\end{array}\right]$$

(21)

d_i represents the adjustment of interval-valued reliability according to dynamical changing of process variable information. Thus, the interval-valued reliability r_i is a precise description to the statistical property of the alarm evidence in real time.

Remark 1. 

In this section, according to the analysis of reliability described as interval-valued form, interval-valued reliability does not mean that the reliability is chosen as a fixed value or a specific part of interval. The purpose of interval-valued reliability is to portray the variation of reliability with the input information by taking equal probability values in a specific interval. Therefore, among the common probability distributions of continuous random variables, the uniform distribution is more suitable for describing interval-valued reliability due to its characteristic of equal probability distribution.

3.3. The Fusion of Alarm Evidence Based on the Interval-Valued ER Rule

This section extends the original ER rule in Equation (5) to the interval-valued ER rule. According to the interval-valued ER rule, the pieces of alarm evidence $a_t^i=[a_t^i(NA),a_t^i(A),a_t^i(\Theta )]$ from the real-time samples are fused to obtain the integrated alarm evidence M_t = (M_t (NA), M_t(A), M_t(Θ)). The specific process is shown as follows.

Step 4.1: First, the interval-valued ER rule is shown as follows:

$$L_t=\frac{{\displaystyle \prod _{i=1}^I(\frac{w_i{a}_t^i(\theta )}{1+w_i-r_i}+\frac{1-r_i}{1+w_i-r_i})}-{\displaystyle \prod _{i=1}^I(\frac{1-r_i}{1+w_i-r_i})}}{{\displaystyle \sum _{n=1}^2{\displaystyle \prod _{i=1}^I(\frac{w_i{a}_t^i(\theta )}{1+w_i-r_i}+\frac{1-r}{1+w_i-r})}}}\theta \subseteq \Theta ,\theta \ne 0$$

(22)

where the interval-valued reliability r_i and weight w_i of $a_t^i$ can be obtained in Section 3.2. According to the proposed interval-valued ER rule, L_t is the fusion result by fusing alarm evidence. Obviously, L_t is an interval whose optimization model is established as follows:

$$\begin{array}{c}\max /\min L_t=\frac{{\displaystyle \prod _{i=1}^I(\frac{w_i{a}_t^i(\theta )}{1+w_i-r_i}+\frac{1-r_i}{1+w_i-r_i})}-{\displaystyle \prod _{i=1}^I(\frac{1-r_i}{1+w_i-r_i})}}{{\displaystyle \sum _{n=1}^2{\displaystyle \prod _{i=1}^I(\frac{w_i{a}_t^i(\theta )}{1+w_i-r_i}+\frac{1-r}{1+w_i-r})}}}\\ st:r_i~U(r_i^{-},r_i^{+})\end{array}$$

(23)

The extreme value of L_t is calculated by optimizing the above model.

Step 4.2: For making alarm result conveniently, according to mathematical principle, the integrated alarm evidence M_t = (M_t (NA), M_t(A), M_t(Θ)) is obtained by means of mathematical expectations for fusion results L_t.

$$M_t=E(L_t)$$

(24)

$$E(L_t)={\displaystyle \underset{\mathrm{\Omega }}{\iint }\dots {\displaystyle \int L_t{\displaystyle \prod _{i=1}^I\frac{1}{r_i^{+}-r_i^{-}}}d{r}_1\dots d{r}_I}}i=1,2,\dots ,I,I\ge 2$$

(25)

where E(L_t) represents the mathematical expectation of L_t and Ω is an area determined by r_i.

In addition, the proof of the following theorems can verify the interval-valued ER rule proposed in this paper.

Theorem 1. 

Expectation and variance of L_t always exist.

Proof of Theorem 1. 

Assuming i = 2, Equation (25) can be considered as a double integral of r₁ and r₂. According to the property of the double integral, it can be concluded that the integral must exist as long as the integrand is continuous over the definition domain. Obviously, the integrand is a continuous binary elementary function in the equation. Therefore, the expectation and variance of L_t always exist. By analogy, the theorem still applies when $i\ge 3$.□

Theorem 2. 

The original ER rule is a special case of the interval-valued ER rule.

Proof of Theorem 2. 

Supposing i = 2, $r_i^{-}$ and $r_i^{+}$ of intervals tend to a quantitative value, shown as follows

$$\{\begin{array}{c}{r}_1^{-}=r_1^{+}=r_{11}\\ r_2^{-}=r_2^{+}=r_{22}\end{array}$$

(26)

From Equation (22), the fusion equation is expressed as follows

$$\begin{array}{l}{L}_t=\frac{(1-r_2)w_1{a}_t^1(\theta )+(1-r_1)w_2{a}_t^2(\theta )+w_1{w}_2{a}_t^1(\theta )a_t^2(\theta )}{(1-r_2)w_1+(1-r_1)w_2+w_1{w}_2{\displaystyle {\sum }_{\gamma \in \theta }{a}_t^1(\gamma )a_t^2(\gamma )}},\theta \subseteq \Theta ,\theta \ne 0\\ =\frac{a_1{r}_1+b_1{r}_2+c_1}{a_2{r}_1+b_2{r}_2+c_2}=U\end{array}$$

(27)

$$\{\begin{array}{c}{a}_1=-w_2{a}_t^2(\theta );b_1=-w_1{a}_t^1(\theta );c_1=w_1{a}_t^1(\theta )+w_2{a}_t^2(\theta )+w_1{w}_2{a}_t^1(\theta )a_t^2(\theta )\\ a_2=-w_2;b_2=-w_1;c_2=w_1+w_2+w_1{w}_2{\displaystyle {\sum }_{\gamma \in \theta }{a}_t^1(\gamma )a_t^2(\gamma )}\end{array}$$

(28)

In the original ER rule, the fusion result is shown as follows

$$U^{\prime }=\frac{a_1{r}_{11}+b_1{r}_{22}+c_1}{a_2{r}_{11}+b_2{r}_{22}+c_2}$$

(29)

Actually, the expectation of L_t can be further calculated by

$$E(U)={\displaystyle \underset{D}{\iint }\frac{a_1{r}_1+b_1{r}_2+c_1}{a_2{r}_1+b_2{r}_2+c_2}d{r}_{2}d{r}_1}$$

(30)

$$E(U)={\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{\frac{a_1}{a_2}(a_2{r}_1+b_2{r}_2+c_2)-\frac{a_1{b}_2}{a_2}{r}_2-\frac{a_1}{a_2}{c}_2+b_1{r}_2+c_1}{a_2{r}_1+b_2{r}_2+c_2}d{r}_{1}d{r}_2}$$

(31)

where Ω is the region defined by r₁ and r₂.

$$E(U)={\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{a_1}{a_2}d{r}_{1}d{r}_2}+{\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{-\frac{a_1{b}_2}{a_2}{r}_2-\frac{a_1}{a_2}{c}_2+b_1{r}_2+c_1}{a_2{r}_1+b_2{r}_2+c_2}d{r}_{1}d{r}_2}$$

(32)

$$E(U)=\frac{a_1}{a_2}+\frac{1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}{\displaystyle {\int }_{r_2^{-}}^{r_2^{+}}({\displaystyle {\int }_{r_1^{-}}^{r_1^{+}}\frac{(-\frac{a_1{b}_2}{a_2}+b_1)r_2-\frac{a_1}{a_2}{c}_2+c_1}{a_2{r}_1+b_2{r}_2+c_2}}d{r}_1)d{r}_2}$$

(33)

Equation (33) is simplified as follows

$$E(U)=\frac{a_1}{a_2}+\frac{{\displaystyle {\int }_{r_2^{-}}^{r_2^{+}}((a_2{b}_1-a_1{b}_2)r_2+a_2{c}_1-a_1{c}_2)\ln \frac{a_2{r}_1^{+}+b_2{r}_2+c_2}{a_2{r}_1^{-}+b_2{r}_2+c_2}d{r}_2}}{a_2{}^2(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}$$

(34)

According to L’hospital law, Equation (34) can be further calculated by the following equation

$$E(U)=\frac{a_1}{a_2}+\underset{r_1^{+}\to r_1^{-}}{\lim }\frac{\frac{\partial ({\displaystyle {\int }_{r_2^{-}}^{r_2^{+}}((a_2{b}_1-a_1{b}_2)r_2+a_2{c}_1-a_1{c}_2)\ln \frac{a_2{r}_1^{+}+b_2{r}_2+c_2}{a_2{r}_1^{-}+b_2{r}_2+c_2}d{r}_2})}{\partial r_2^{+}}}{{a_2}^2\frac{\partial (r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}{\partial r_2^{+}}}$$

(35)

$$E(U)=\frac{a_1}{a_2}+\underset{r_1^{+}\to r_1^{-}}{\lim }\frac{((a_2{b}_1-a_1{b}_2)r_2^{+}+a_2{c}_1-a_1{c}_2)\ln \frac{a_2{r}_1^{+}+b_2{r}_2^{+}+c_2}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2}}{{a_2}^2(r_1^{+}-r_1^{-})}$$

(36)

Actually, we have

$$\ln \frac{a_2{r}_1^{+}+b_2{r}_2^{+}+c_2}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2}=\ln (1+\frac{a_2(r_1^{+}-r_1^{-})}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2})$$

(37)

When $r_1^{+}\to r_1^{-}$, $\frac{a_2(r_1^{+}-r_1^{-})}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2}$ approaches to 0. Therefore, we have

$$\ln (1+\frac{a_2(r_1^{+}-r_1^{-})}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2})\simeq \frac{a_2(r_1^{+}-r_1^{-})}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2}$$

(38)

Finally, we have

$$E(U)=\frac{a_1}{a_2}+\frac{1}{a_2}\frac{a_2{b}_1{r}_2^{+}+a_2{c}_1-a_1{b}_2{r}_2^{+}-a_1{c}_2}{a_2{r}_1^{-}+b_2{r}_2^{+}+c_2}=\frac{a_1{r}_{11}+b_1{r}_{22}+c_1}{a_2{r}_{11}+b_2{r}_{22}+c_2}=U^{\prime }$$

(39)

Obviously, when $r_i^{-}$ and $r_i^{+}$ of interval tend to the quantitative value, $E(U)=U^{\prime }$. It shows that the original ER rule is a special case of the interval-valued ER rule.

Similarly, when i > 2, the theorem still holds.□

Theorem 3. 

In Equation (22), L_t is a probability function about (r₁, r₂, …, r_I). Taking two pieces of evidence as an example, there exists at least one point$(r_{{\rho }_1},r_{{\rho }_2})$satisfying the following equation.

$$\begin{array}{c}E(U)=G(r_{{\rho }_1},r_{{\rho }_2})\\ st:r_{{\rho }_i}\in \mathrm{\Omega }\end{array}$$

(40)

Proof of Theorem 3. 

Suppose c₁ and C₁ denote the upper and lower bounds of $L_t(r_1,r_2)$, respectively, which can be calculated by the following optimization model:

$$\begin{array}{c}\max /\min L_t(r_1,r_2)\\ st:(r_1,r_2)\in \mathrm{\Omega }\end{array}$$

(41)

When $(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})$ is considered as greater than 0, the following inequality can be obtained:

$$\frac{c_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}\le \frac{L_t(r_1,r_2)}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}\le \frac{C_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}$$

(42)

Based on the property of the double integral, we have

$$\begin{array}{l}{\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{c_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}\le {\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{L_t(r_1,r_2)}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}\\ {\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{L_t(r_1,r_2)}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}\le {\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{C_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}\end{array}$$

(43)

and

$$\begin{array}{l}{\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{c_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}=c_1\\ {\displaystyle \underset{\mathrm{\Omega }}{\iint }\frac{C_1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}d{r}_{1}d{r}_2}=C_1\\ \frac{1}{(r_1^{+}-r_1^{-})(r_2^{+}-r_2^{-})}{\displaystyle \underset{\mathrm{\Omega }}{\iint }{L}_t(r_1,r_2)d{r}_{1}d{r}_2}=E(U)\end{array}$$

(44)

From the above equations, we have

$$c_1\le E(U)\le C_1$$

(45)

From Equation (45), E(U) is a determined value between c₁ and C₁. Obviously, L_t (r₁, r₂) is a continuous function. According to the intermediate theorem of continuous functions on the closed regions, there is at least one point $(r_{{\rho }_1},r_{{\rho }_2})$ on Ω that makes $L_t(r_{{\rho }_1},r_{{\rho }_2})$ equal to E(U). Based on the above derivation, the theorem can be extended to the fusing situation with more than two pieces of evidence.□

3.4. Making Alarm-Decision Based on Integrated Alarm Evidence

Step 5: Through the fusion method in Section 3.3, the integrated alarm evidence M_t = (M_t (NA), M_t(A), M_t(Θ)) can be obtained. The alarm decision is made, according to the following alarm-decision criteria: if M_t (NA) ≥ M_t(A), output y_t(k) = 0, no alarm; if M_t (NA) < M_t(A), output y_t(k) = 1, alarm.

4. Comparative Analysis of Experiment

This section demonstrates the design process of the multivariate alarm method based on the interval-valued ER rule through the following experiment. The Tennessee Eastman (TE) process as a chemical benchmark simulation model as shown in Figure 2, provides a display environment for evaluating process control and monitoring methods and has been widely used as a research platform for continuous process monitoring, regulation, and diagnosis [27]. According to http://web.mit.edu/braatzgroup/links.html (accessed on 13 August 2022), its experimental data can be downloaded. The TE process has 53 process variables and 21 different fault types [28]. The process variables include 12 operational variables and 41 measured variables (22 continuous, 19 component variables). In this benchmark set, each fault in the training set contains 480 samples, and each fault in the test set contains 960 samples, where the fault corresponding to the 161st sample are introduced from the eighth hour, with a sampling interval of 3 min. To address the problem of less training data in the dataset, according to the principle of the TE process and its data characteristics, this experiment combines the original training set with the first 160 samples in the test set under normal conditions to form a new training set. This section takes the reactor fault in the TE process as an alarm example and selects the flow rates of process variables material A, B, and C as input variables x₁(k), x₂(k) and x₃(k), shown as Figure 3, Figure 4 and Figure 5, and the effectiveness of the proposed method is verified by comparison of other traditional alarm design methods and the original ER rule method.

Step 1 (The construction of REM): Firstly, for the three input variables x_i(k), i = 1, 2, 3, this newly composed 640 samples of each sequence are considered as training samples. According to expert knowledge, the reference value sets of the input variable x_i(k) are O¹ = {14, 15.2, 16.4, 17.6, 18.8, 20, 21.2, 22.4, 23.6, 24.8, 26}, O² = {51, 52.4, 53.8, 55.2, 56.6, 58, 59.4, 60.8, 62.2, 63.6, 65}, O³ = {13.1, 13.2, 13.3, 13.4, 13.5, 13.6, 13.7, 13.8, 13.9, 14.0, 14.1}, and the reference value set of the output y(k) is {0,1}. According to Section 3.1.1, the referential evidence matrixes (REMs) are established by Equations (7)–(13), as shown in

Table 3. Table of referential evidence matrix (REM) for variable x₁(k).

y(k)	x1(k)
	14	15.2	16.4	17.6	18.8	20	21.2	22.4	23.6	24.8	26
NA	0.8467	0.9738	0.9658	0.8840	0.6990	0.3356	0.1630	0.0629	0.0356	0	0
A	0.1533	0.0262	0.0342	0.1160	0.3010	0.6644	0.8370	0.9371	0.9644	1	1

,

Table 4. Table of referential evidence matrix (REM) for variable x₂(k).

y(k)	x2(k)
	51	52.4	53.8	55.2	55.6	58	59.4	60.8	62.2	63.6	65
NA	0	0	0	0	0.0069	0.0640	0.4755	0.8634	0.9454	0.9637	1
A	1	1	1	1	0.9931	0.9360	0.5245	0.1366	0.0546	0.0363	0

and

Table 5. Table of referential evidence matrix (REM) for variable x₃(k).

y(k)	x3(k)
	13.1	13.2	13.3	13.4	13.5	13.6	13.7	13.8	13.9	14.0	14.1
NA	0	0	0	0	0.0011	0.0869	0.6442	0.9489	0.9724	0.9705	0.9966
A	1	1	1	1	0.9989	0.9131	0.3558	0.0511	0.0276	0.0295	0.0034

, and the alarm evidence $a_t^i$ corresponding real-time sample is obtained by activating the corresponding REM. According to Section 3.2, the optimal reliabilities and weights of the alarm evidence are obtained, i.e., ${r_1}^{\prime }$ = 0.74, ${r_2}^{\prime }$ = 0.70, ${r_3}^{\prime }$ = 0.60 and w₁ = 0.92, w₂ = 0.86, w₃ = 0.90.

Meanwhile, based on the above training set, some traditional alarm design methods are selected as comparison methods to obtain the optimal alarm threshold, such as the 3σ method commonly used in industry, the filtering method, the time delay method, the FAP-MAP method based on multivariate alarm threshold optimization [29]. Among the traditional alarm design method, the FAP-MAP method constructs the objective function $\underset{x_0,y_0}{{\displaystyle \min }}\{w_1(P_{x,f}+P_{y,f})+w_2(P_{x,m}+P_{y,m})\}$, where P_x,f and P_y,f are the false alarm rate (FAR) for variables x and y, respectively; P_x,m and P_y,m are the missed alarm rate (MAR) of variables x and y respectively; w₁ and w₂ are the weight factors, generally w₁ = w₂ = 0.5; x₀ and y₀ are the optimal thresholds [14]. In each traditional alarm design method, the optimal thresholds of corresponding variable are shown in

Table 6. Optimal threshold values of each variable.

Variable	The 3σ Method	The Filtering Method	The Time Delay Method	The FAP-MAP Method
1	22.85	22.64	22.60	22.43
2	57.50	57.61	57.59	57.62
3	13.58	13.62	13.59	13.65

.

Step 2 (The transformation of process variables to alarm evidence): Next, the alarm system based on the interval-valued ER rule is designed. According to the simulation platform http://depts.washington.edu/control/LARRY/TE/download.html (accessed on 13 August 2022), the test set of input variable x_i(k) is randomly generated, including 900 samples. The first step is to obtain the alarm evidence at each moment. The reference values of input and output are obtained in the training experiment. According to the REM shown in Table 3, Table 4 and Table 5, the real-time samples are transformed into corresponding alarm evidence.

Step 3 (The calculation of interval-valued reliability and the optimization of weight): Furthermore, the optimal reliabilities and weights of alarm evidence are obtained by Equation (18) in the training experiment, and the reliability adjustment factor α_i corresponding to alarm evidence at each moment is calculated by Equations (19)–(21), and the interval of r_i is obtained combining Equation (17).

Step 4 (The fusion of alarm evidence based on the interval-valued ER rule): According to Section 3.3, the original ER rule Equation (6) is extended to the interval-valued ER rule Equation (22), which can fuse the alarm evidence $a_t^i$ (i = 3) to get integrated alarm evidence L_t. L_t is an interval, whose optimization model is established by Equation (23). The extreme value of L_t is calculated by optimizing the model. For making alarm results conveniently, according to mathematical principle, the integrated alarm evidence M_t = (M_t (NA), M_t(A), M_t(Θ)) is obtained by Equations (24) and (25). M_t is obtained based on the interval-valued ER rule.

Step 5 (Alarm-decision making based on integrated alarm evidence): Finally, based on the alarm-decision criteria of Section 3.4, the alarm decision is made through M_t = (M_t (NA), M_t(A), M_t(Θ)), and missed alarm number (m(MA)) is 31 and false alarm number (m(FA)) is 1. In addition, another alarm system based on the original ER rule is designed as a comparative experiment. Repeat the above experimental steps, when using Equation (23) to fuse the alarm evidence $a_t^i$, the optimal fusion weights {w₁ = 0.92, w₂ = 0.86, w₃ = 0.90} and optimal reliabilities {${r_1}^{\prime }$ = 0.74, ${r_2}^{\prime }$ = 0.70, ${r_3}^{\prime }$ = 0.60} are obtained according to the training set, and the results are m(MA) = 79 and m(FA) = 9 respectively.

Table 7. A part of interval-valued reliability under the interval-valued ER rule.

Parameter		k
		1	2	3	…	898	899	900
Interval reliability	r1	[0.489,0.997]	[0.472,1.00]	[0.475,1.00]	…	[0.463,1.00]	[0.555,0.932]	[0.490,0.997]
	r2	[0.439,0.961]	[0.448,0.952]	[0.439,0.961]	…	[0.362,1.00]	[0.381,1.00]	[0.418,0.982]
	r3	[0.331,0.870]	[0.332,0.869]	[0.343,0.858]	…	[0.423,0.778]	[0.290,0.911]	[0.325,0.876]

shows a part of the interval-valued reliability under the interval-valued ER rule. As can be shown in Table 7, the interval-valued reliability r_i dynamically changes according to the input information in real-time. It is obvious that this is more in line with the actual change of the input variable. On the contrary, whether the optimal values of reliability are obtained based on expert knowledge or based on optimization of the training set, reliabilities of the original ER rule are quantitative values in each fusion, which limits the performance of designing alarm system based on the ER rule to a certain extent.

In order to show the effectiveness of the proposed method, use the above proposed simulation platform to randomly generate 100 test sets, and each test set includes 900 samples. Repeat the above experimental steps and perform multiple test experiment. Calculate the average of m(MA) and m(FA) for each variable, shown in Figure 5 and Figure 6.

As shown in Figure 6 and Figure 7, under the 3σ method, m(MA) = 604.3 and m(FA) = 2.5 for x₁, m(MA) = 356.1 and m(FA) = 3.6 for x₂, m(MA) = 180.7 and m(FA) = 3.8 for x₃; all results are higher than the interval-valued ER rule method, especially the m(MA) of x₁ is very high, so the 3σ method is inappropriate in practical applications, while m(MA) = 30.1 and m(FA) = 0.6 under the interval-valued ER rule method, which is far below the 3σ method. Under the filtering method, m(MA) = 542.5 and m(FA) = 2.5 for x₁, m(MA) = 302.4 and m(FA) = 3.2 for x₂, m(MA) = 123.7 and m(FA) = 3.9 for x₃. The filtering method has some advantages over the 3σ method, but m(MA) and m(FA) of the filtering method is still relatively high compared with the interval-valued ER rule method. Under the time delay method, m(MA) = 529.2 and m(FA) = 2.4 for x₁, m(MA) = 311.3 and m(FA) = 3.2 for x₂, m(MA) = 141.4 and m(FA) = 3.4 for x₃. The performance of the time delay method is similar to that of the filtering method. Under the FAP-MAP method, m(MA) = 506.3 and m(FA) = 3.1 for x₁, m(MA) = 281.6 and m(FA) = 3.3 for x₂, m(MA) = 130.7 and m(FA) = 3.7 for x₃. The performance of the FAP-MAP method is the best among the traditional methods, but it also has a certain gap with the interval-valued ER rule method. According to the above results, traditional alarm design methods expose the limitations in multivariate industrial processes, i.e., traditional alarm design methods only consider the alarm results of univariate and lack the ability to handle multivariable alarms simultaneously, which makes the alarm result lack consistency. On the contrary, the interval-valued ER rule method obtains consistent results compared with traditional alarm design methods for multivariate alarm system. It can be seen from Figure 6 and Figure 7 that m(MA) and m(FA) under the interval-valued ER rule method are the lowest compared with traditional alarm design methods, and they are 30.1 and 0.6 respectively. In the interval-valued ER rule method, the alarm evidence is obtained through the data-driven REM, which can be considered as a lossless conversion from process variables to alarm evidence and accurately describes the statistical characteristics of the sample data, so this can significantly reduce m(FA) and m(MA).

In addition, as shown in Figure 6 and Figure 7, the m(MA) = 80.2 and m(FA) = 2.5 for the original ER rule method, and the m(MA) and m(FA) under the interval-valued ER rule method are reduced of 50.1 and 1.9 respectively compared with the original ER rule method. On the one hand, because fixed reliability lacks the ability to handle objective uncertainty, the effectiveness of the original ER rule method is certainly not as good as the interval-valued ER rule method. On the other hand, the interval-valued ER rule can accurately describe process variables by the adjustment of interval-valued reliability. The reliability of alarm evidence is described by the form of random variables, which makes the interval-valued ER rule possess the ability to maximize the process of input information. In summary, the alarm design method based on the interval-valued ER rule can greatly reduce both m(MA) and m(FA).

However, the alarm design method based on the interval-valued ER rule also has certain weaknesses. Due to the limitation of ER algorithm, when the dimensionality of process variables increases, the computational difficulty also rises correspondingly. To address the above weaknesses, in future work, we consider introducing dimensionality reduction methods as well as vectorization methods to reduce the dimensionality of process variables and filter out the appropriate process variables, which can reduce the computational difficulty and obtain the most rational alarm result.

5. Conclusions and Discussion

In view of the accurate transformation from process variable to alarm evidence and the reasonability of alarm result, this paper proposes an alarm design method based on the interval-valued ER rule. Its main contributions are as follows: (1) The REM is constructed based on training sample data of multiple process variables, and the real-time sample of the process variable activates REM to obtain the alarm evidence respectively, which achieves the accurate transformation of process variable data into alarm evidence. (2) The interval-valued ER rule is proposed, which fuses alarm evidence corresponding to process variable data, and obtains the integrated alarm evidence. Among that, the reliability of alarm evidence is inscribed by random variables with certain probability distribution characteristics on the interval, and the interval of reliability is adaptively adjusted according to the change of real-time sample of the process variable, which improves the reasonability of the fusion process. (3) The case study shows that the alarm design method based on the interval-valued ER rule can make full use of the contradictory, redundant, and complementary information of each process variable, and obtain more accurate and consistent alarm results compared with the traditional alarm design method in practical applications.