Fractional-Order Variational Image Fusion and Denoising Based on Data-Driven Tight Frame
Abstract
1. Introduction
- Motivated by a fractional-order total variational denoising model and a data-driven tight frame variational model for image fusion, a variational fusion model capable of handling noisy images is constructed. The denoised images and analysis operator are obtained by this model.
- The new three-step method is constructed. The method combines FOTV and DDTF models for simultaneously denoising and fusing images, and it can find the complementary information from the noisy source images to obtain the final fused images and suppress the noise output. This is the first time that a fractional-order variational model is used to denoise and fuse images disturbed by Poisson noise.
- We evaluate this method on different types of images. The experiments show that the proposed method is more effective.
2. Materials and Methods
2.1. Related Materials
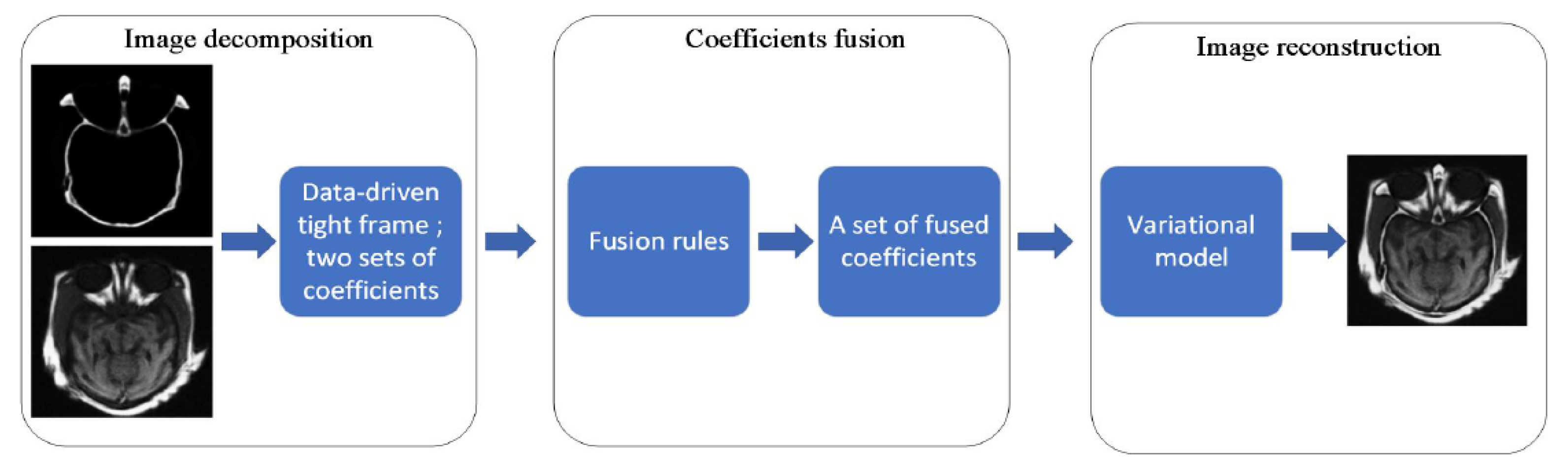
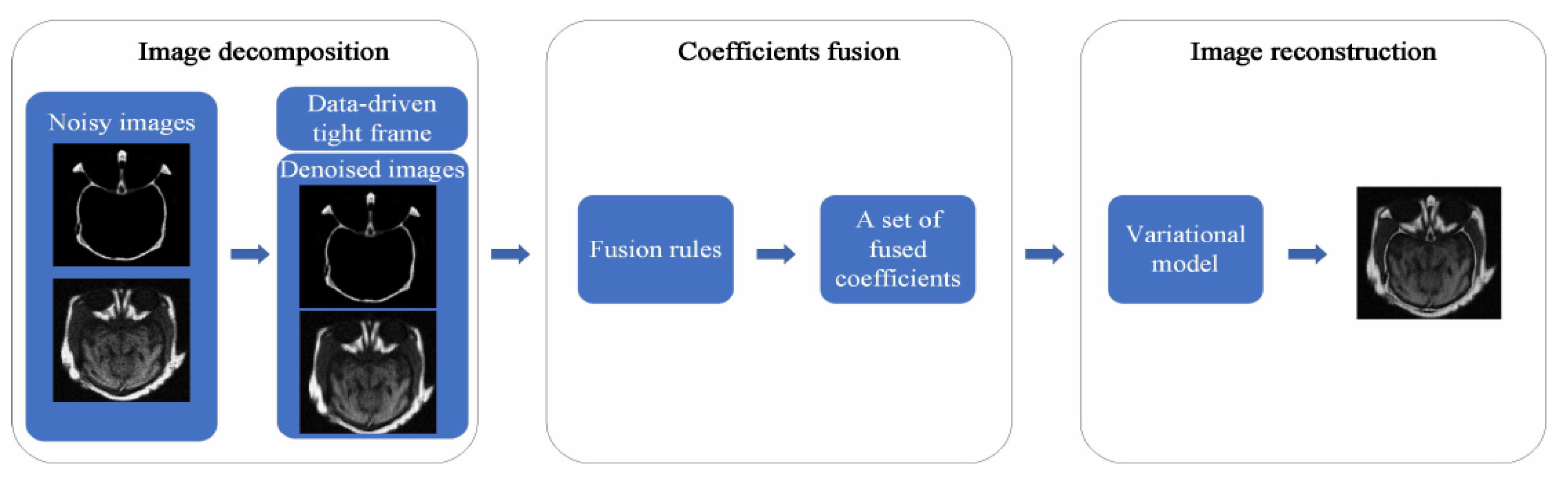
2.2. The Proposed New Three-Step Method
3. Algorithm
3.1. Image Decomposition
- The u-subproblem: for fixed , we solve
- The v-subproblem: for fixed , we solve
- The W-subproblem: for fixed , we solve
| Algorithm 1: The image decomposition step algorithm |
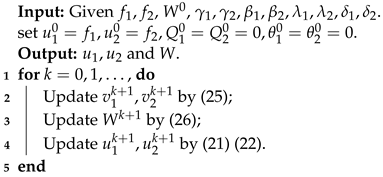 |
3.2. Image Reconstruction
| Algorithm 2: The algorithm for image reconstruction |
 |
4. Numerical Experiments
4.1. Evaluation Metrics
4.2. Selection of Parameters
4.3. Numerical Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Cao, S.; Wan, W.; Huang, S. Multi-modal medical image super-resolution fusion based on detail enhancement and weighted local energy deviation. Biomed. Signal Process. Control 2023, 80, 104387. [Google Scholar] [CrossRef]
- Gharbia, R.; Hassanien, A.; El-Baz, A.; Elhoseny, M.; Gunasekaran, M. Multi-spectral and panchromatic image fusion approach using stationary wavelet transform and swarm flower pollination optimization for remote sensing applications. Future Gener. Comput. Syst. 2018, 88, 501–511. [Google Scholar] [CrossRef]
- Paramanandham, N.; Rajendiran, K. Infrared and visible image fusion using discrete cosine transform and swarm intelligence for surveillance applications. Infrared Phys. Technol. 2018, 88, 13–22. [Google Scholar] [CrossRef]
- Nandi, D.; Ashour, A.; Samanta, S.; Chakraborty, S.; Salem, M.; Dey, N. Principal component analysis in medical image processing: A study. Int. J. Image Min. 2015, 1, 65–86. [Google Scholar] [CrossRef]
- Du, J.; Li, W.; Xiao, B. Anatomical-functional image fusion by information of interest in local laplacian filtering domain. IEEE Trans. Image Process. 2017, 26, 5855–5866. [Google Scholar] [CrossRef] [PubMed]
- Prakash, O.; Park, C.; Khare, A.; Jeon, M.; Gwak, J. Multiscale fusion of multimodal medical images using lifting scheme based biorthogonal wavelet transform. Optik 2019, 182, 995–1014. [Google Scholar] [CrossRef]
- Hermessi, H.; Mourali, O.; Zagrouba, E. Multimodal medical image fusion review: Theoretical background and recent advances. Signal Process 2021, 183, 108036. [Google Scholar] [CrossRef]
- Burt, P.; Adelson, E. The Laplacian pyramid as a compact image code. Readings Comput. Vision. 1983, 31, 532–540. [Google Scholar] [CrossRef]
- Petrovic, V.; Xydeas, C. Gradient-based multiresolution image fusion. IEEE Trans. Image Process. 2004, 13, 228–237. [Google Scholar] [CrossRef]
- Ioannidou, S.; Karathanassi, V. Investigation of the dual-tree complex and shift-invariant discrete wavelet transforms on quickbird image fusion. IEEE Geosci. Remote. Sens. Lett. 2007, 1, 166–170. [Google Scholar] [CrossRef]
- Yang, L.; Guo, B.; Ni, W. Multimodality medical image fusion based on multiscale geometric analysis of contourlet transform. Neurocomputing 2008, 72, 203–211. [Google Scholar] [CrossRef]
- Wang, L.; Li, B.; Tian, L. Multi-modal medical image fusion using the inter-scale and intra-scale dependencies between image shift-invariant shearlet coefficients. Inf. Fusion 2014, 19, 20–28. [Google Scholar] [CrossRef]
- Singh, S.; Singh, H.; Bueno, G.; Deniz, O.; Singh, S.; Monga, H.; Hrisheekesha, P.N.; Pedraza, A. A review of image fusion: Methods, applications and performance metrics. Digit. Signal Process. 2023, 137, 104020. [Google Scholar] [CrossRef]
- Chan, T.; Shen, J.; Vese, L. Variational PDE models in image processing. Not. Am. Math. Soc. 2003, 50, 14–26. [Google Scholar]
- Chan, T.; Shen, J. Mathematical models for local non-texture inpainting. SIAM J. Appl. Math. 2002, 62, 1019–1043. [Google Scholar]
- Rahman, M.; Zhang, J.; Qin, J.; Lou, Y. Poisson image denoising based on fractional-order total variation. Inverse Probl. Imaging 2020, 14, 77–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X. Variational bimodal image fusion with data-driven tight frame. Inf. Fusion 2020, 55, 164–172. [Google Scholar] [CrossRef]
- Thakur, R.K.; Maji, S.K. Multi scale pixel attention and feature extraction based neural network for image denoising. Pattern Recognit. 2023, 141, 109603. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, C.; Yang, L.; Yang, Z. Salt and pepper noise removal method based on graph signal reconstruction. Digit. Signal Process. 2023, 135, 103941. [Google Scholar] [CrossRef]
- Singh, A.; Kushwaha, S.; Alarfaj, M.; Singh, M. Comprehensive overview of backpropagation algorithm for digital image denoising. Electronics 2022, 11, 1590. [Google Scholar] [CrossRef]
- Kushwaha, S.; Singh, R.K. Optimization of the proposed hybrid denoising technique to overcome over-filtering issue. Biomed. Eng. Biomed. Tech. 2019, 64, 601–618. [Google Scholar]
- Tikhonov, A.; Goncharsky, A.; Stepanov, V.; Yagola, A. Numerical Methods for the Solution of Ill-Posed Problems; Mathematics and its Applications; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1995; 328p. [Google Scholar]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Chan, T.; Marquina, A.; Mulet, P. High-order total variation-based image restoration. SIAM J. Sci. Comput. 2000, 22, 503–516. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, M.; Wu, Z.; Deng, C. High-order total bounded variation model and its fast algorithm for Poissonian image restoration. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Lysaker, M.; Lundervold, A.; Tai, X. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time. IEEE Trans. Image Process. 2003, 12, 1579–1590. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Feng, X. Fractional-order anisotropic diffusion for image denoising. IEEE Trans. Image Process. 2007, 16, 2492–2502. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y. Fractional differential analysis for texture of digital image. J. Algorithms Comput. Technol. 2007, 1, 357–380. [Google Scholar]
- Zhang, J.; Chen, K. A total fractional-order variation model for image restoration with nonhomogeneous boundary conditions and its numerical solution. SIAM J. Imaging Sci. 2015, 8, 2487–2518. [Google Scholar] [CrossRef]
- Liu, L.; Xu, L.; Fang, H. Infrared and visible image fusion and denoising via l2-lp norm minimization. Signal Process. 2020, 172, 107546. [Google Scholar] [CrossRef]
- Goyal, S.; Singh, V.; Rani, A.; Yadav, N. Multimodal image fusion and denoising in NSCT domain using CNN and FOTGV. Biomed. Signal Process. Control. 2022, 71, 103214. [Google Scholar] [CrossRef]
- Li, X.; Zhou, F.; Tan, H. Joint image fusion and denoising via three-layer decomposition and sparse representation. Knowl.-Based Syst. 2021, 224, 107087. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, D.; Zhao, T.; Chen, Y. Fractional calculus in image processing: A review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef]
- Varga, D. Full-Reference image quality assessment based on Grünwald–Letnikov derivative, image gradients, and visual saliency. Electronics 2022, 11, 559. [Google Scholar] [CrossRef]
- Henriques, M.; Valério, D.; Gordo, P.; Melicio, R. Fractional-order colour image processing. Mathematics 2021, 9, 457. [Google Scholar] [CrossRef]
- Mei, J.; Dong, Y.; Huang, T. Simultaneous image fusion and denoising by using fractional-order gradient information. J. Comput. Appl. Math. 2019, 351, 212–227. [Google Scholar] [CrossRef]
- Ullah, A.; Chen, W.; Khan, M.A. A new variational approach for restoring images with multiplicative noise. Comput. Math. Appl. 2016, 71, 2034–2050. [Google Scholar] [CrossRef]
- Jiang, Q.; Jin, X.; Chen, G.; Lee, S.; Cui, X.; Yao, S.; Wu, L. Two-scale decomposition-based multifocus image fusion framework combined with image morphology and fuzzy set theory. Inf. Sci. 2020, 541, 442–474. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.; Kittler, J. Infrared and visible image fusion using a deep learning framework. In Proceedings of the International Conference on Pattern Recognition, Beijing, China, 20–24 August 2018; pp. 2705–2710. [Google Scholar]
- Hossain, M.M.; Hasan, M.M.; Rahim, M.A.; Rahman, M.M.; Yousuf, M.A.; Al-Ashhab, S.; Akhdar, H.F.; Alyami, S.A.; Azad, A.; Moni, M.A. Particle swarm optimized fuzzy CNN with quantitative feature fusion for ultrasound image quality identification. IEEE J. Transl. Eng. Health Med. 2022, 10, 1–12. [Google Scholar]
- Qu, G.; Zhang, D.; Yan, P. Information measure for performance of image fusion. Electron. Lett. 2002, 38, 313–315. [Google Scholar] [CrossRef]
- Piella, G.; Heijmans, H. A new quality metric for image fusion. In Proceedings of the IEEE International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; Volume 3, p. III-173. [Google Scholar]
- Xydeas, C.; Petrovi, V. Objective image fusion performance measure. Electron. Lett. 2000, 36, 308–309. [Google Scholar] [CrossRef]
- Zhao, W.; Lu, H. Medical image fusion and denoising with alternating sequential filter and adaptive fractional order total variation. IEEE Trans. Instrum. Meas. 2017, 66, 2283–2294. [Google Scholar] [CrossRef]
- Wang, G.; Li, W.; Du, J.; Xiao, B.; Gao, X. Medical image fusion and denoising algorithm based on a decomposition model of hybrid variation-sparse representation. IEEE J. Biomed. Health Inform. 2022, 26, 5584–5595. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Xia, X.; He, C.; Ren, Z.; Wang, T.; Lei, B. A Noise-Robust online convolutional coding model and its applications to poisson denoising and image fusion. Appl. Math. Model. 2021, 95, 644–666. [Google Scholar] [CrossRef]


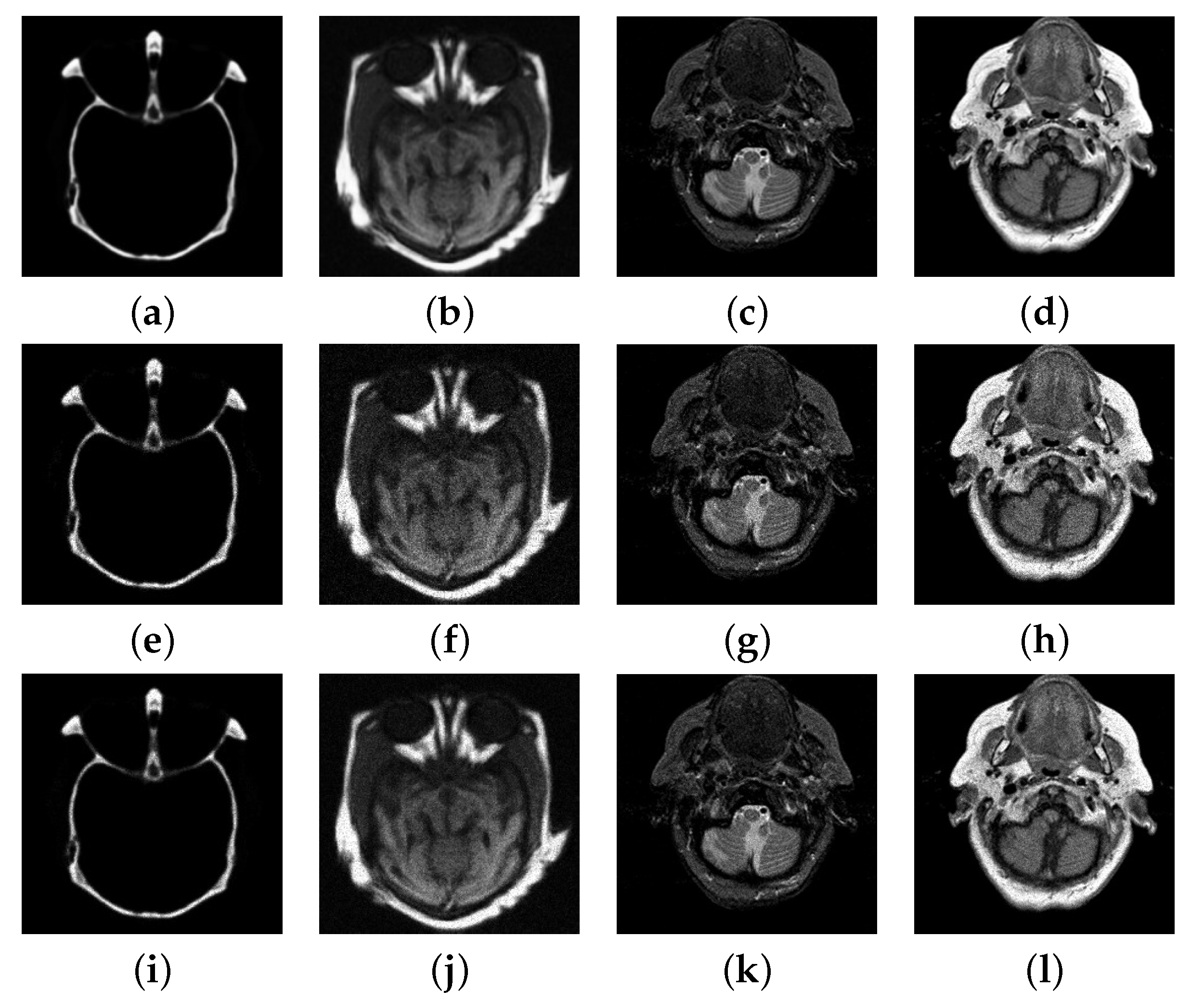







| Test Images | Peak | Noisy | PSNR | |||
|---|---|---|---|---|---|---|
| CT/MRI | 55 | 31.17/24.39 | 31.70/26.79 | 1.83 | 0.50 | 0.56 |
| 155 | 35.70/28.85 | 36.06/28.95 | 2.55 | 0.59 | 0.48 | |
| MR-T1/MR-T2 | 55 | 27.98/23.90 | 29.91/26.15 | 2.61 | 0.40 | 0.53 |
| 155 | 32.41/28.40 | 32.86/28.29 | 3.16 | 0.47 | 0.41 |
| Test Images | Peak | Noisy | PSNR | |||
|---|---|---|---|---|---|---|
| Multifocus1 | 155 | 25.97/25.72 | 28.02/27.50 | 4.00 | 0.40 | 0.39 |
| 255 | 28.17/27.87 | 29.13/28.35 | 4.58 | 0.39 | 0.41 | |
| Multifocus2 | 155 | 25.39/25.41 | 29.72/30.16 | 4.71 | 0.54 | 0.70 |
| 255 | 27.57/27.56 | 30.43/30.55 | 4.77 | 0.60 | 0.66 |
| Method | Index | CT/MRI | MR-T1/MR-T2 | Multifocus1 | Multifocus2 |
|---|---|---|---|---|---|
| proposed | 2.51 | 3.11 | 4.32 | 4.69 | |
| 0.59 | 0.39 | 0.39 | 0.54 | ||
| 0.44 | 0.37 | 0.48 | 0.69 | ||
| DDTF | 2.63 | 2.72 | 3.49 | 3.54 | |
| 0.46 | 0.40 | 0.37 | 0.47 | ||
| 0.33 | 0.28 | 0.25 | 0.46 |
| Test Images | Peak | Noisy | PSNR | |||
|---|---|---|---|---|---|---|
| IR1/VIS1 | 155 | 26.71/26.70 | 27.72/28.89 | 2.18 | 0.23 | 0.40 |
| 255 | 28.90/29.21 | 29.29/30.47 | 2.62 | 0.24 | 0.41 | |
| IR2/VIS2 | 155 | 25.01/25.80 | 27.63/28.30 | 1.67 | 0.29 | 0.24 |
| 255 | 27.18/28.00 | 28.61/29.57 | 2.12 | 0.31 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Liu, J. Fractional-Order Variational Image Fusion and Denoising Based on Data-Driven Tight Frame. Mathematics 2023, 11, 2260. https://doi.org/10.3390/math11102260
Zhao R, Liu J. Fractional-Order Variational Image Fusion and Denoising Based on Data-Driven Tight Frame. Mathematics. 2023; 11(10):2260. https://doi.org/10.3390/math11102260
Chicago/Turabian StyleZhao, Ru, and Jingjing Liu. 2023. "Fractional-Order Variational Image Fusion and Denoising Based on Data-Driven Tight Frame" Mathematics 11, no. 10: 2260. https://doi.org/10.3390/math11102260
APA StyleZhao, R., & Liu, J. (2023). Fractional-Order Variational Image Fusion and Denoising Based on Data-Driven Tight Frame. Mathematics, 11(10), 2260. https://doi.org/10.3390/math11102260




