Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach
Abstract
:1. Introduction
2. Preliminaries
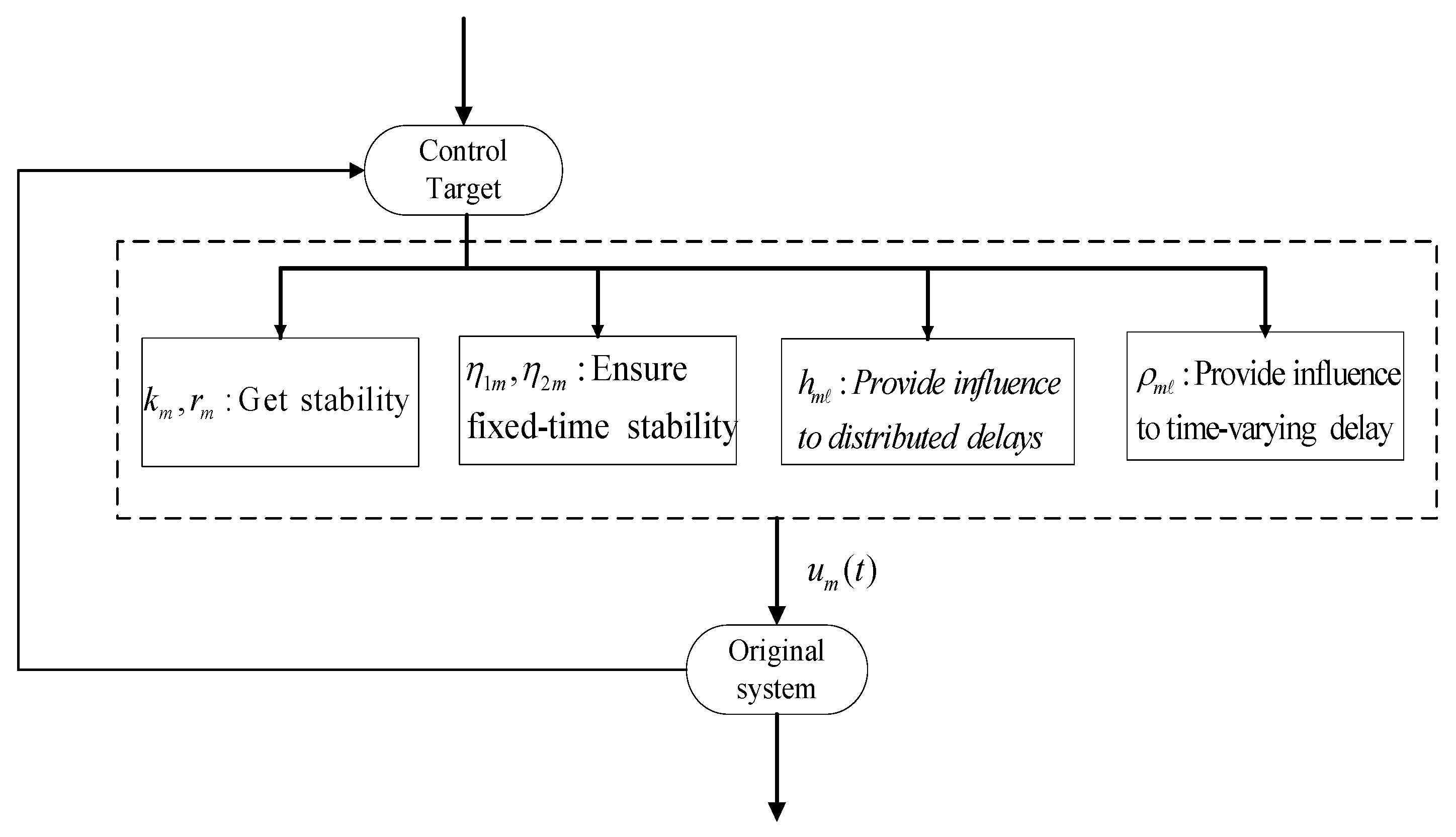
3. Main Results
3.1. FTS of System (4)
3.2. PST of System (4)
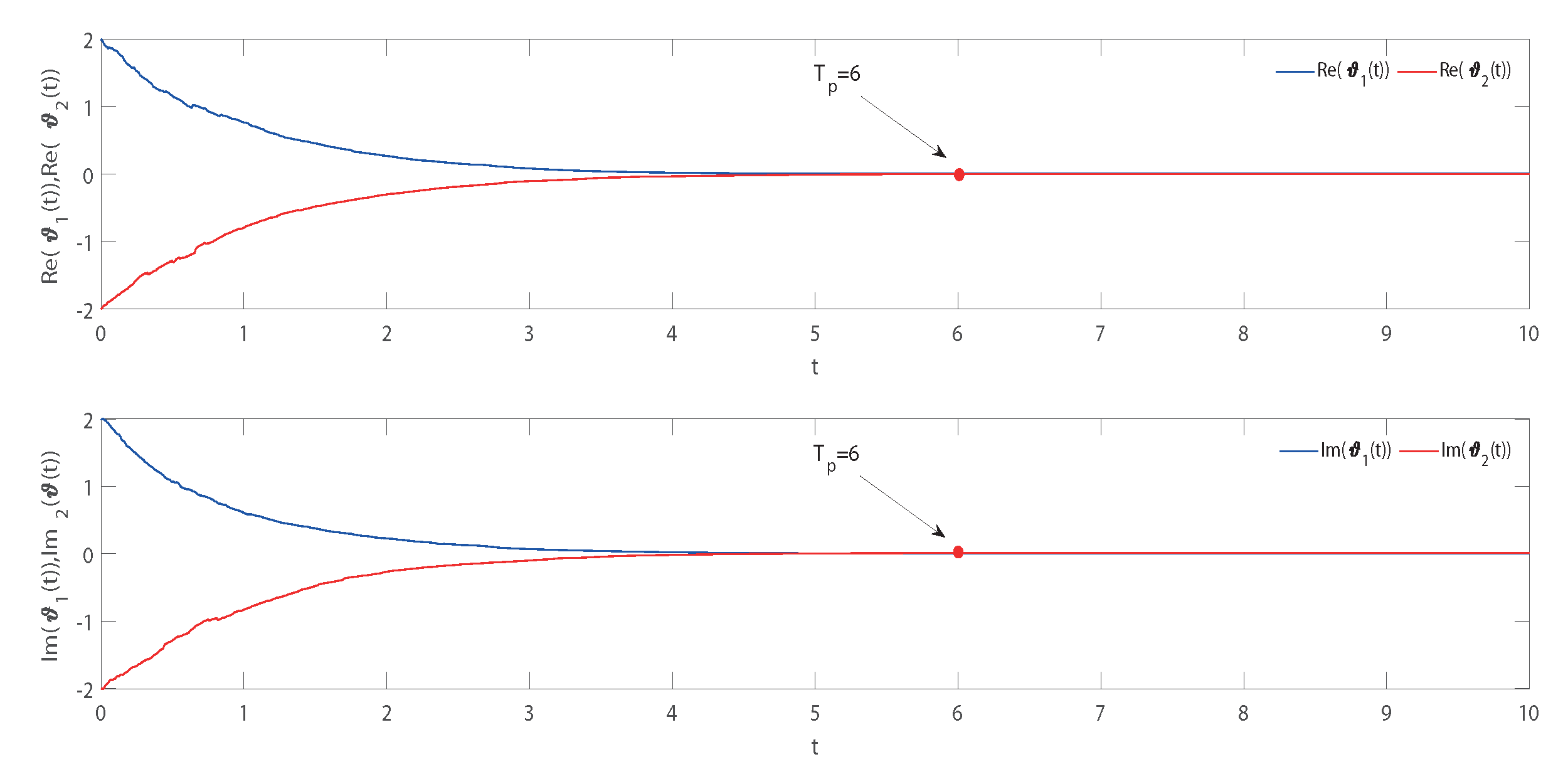
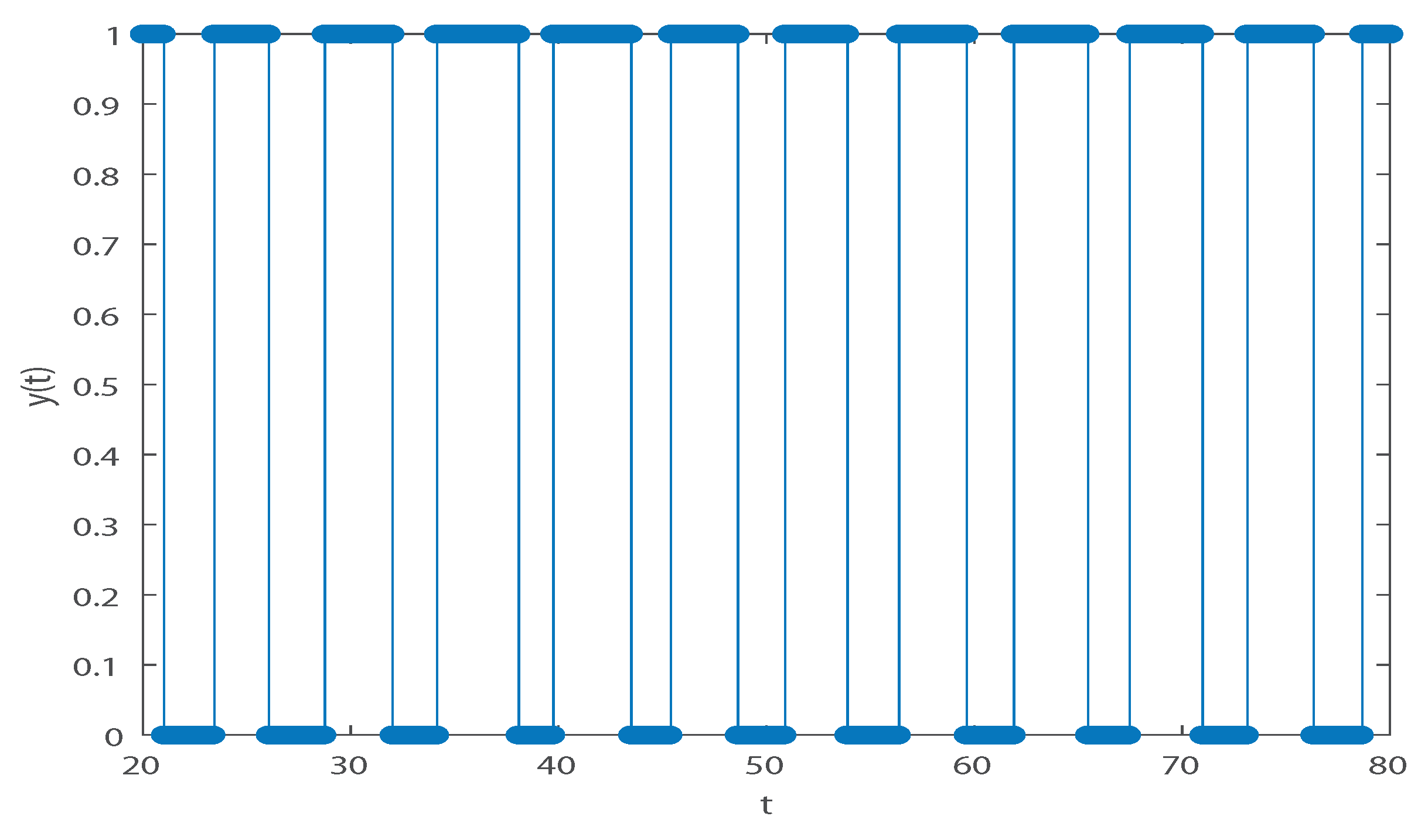
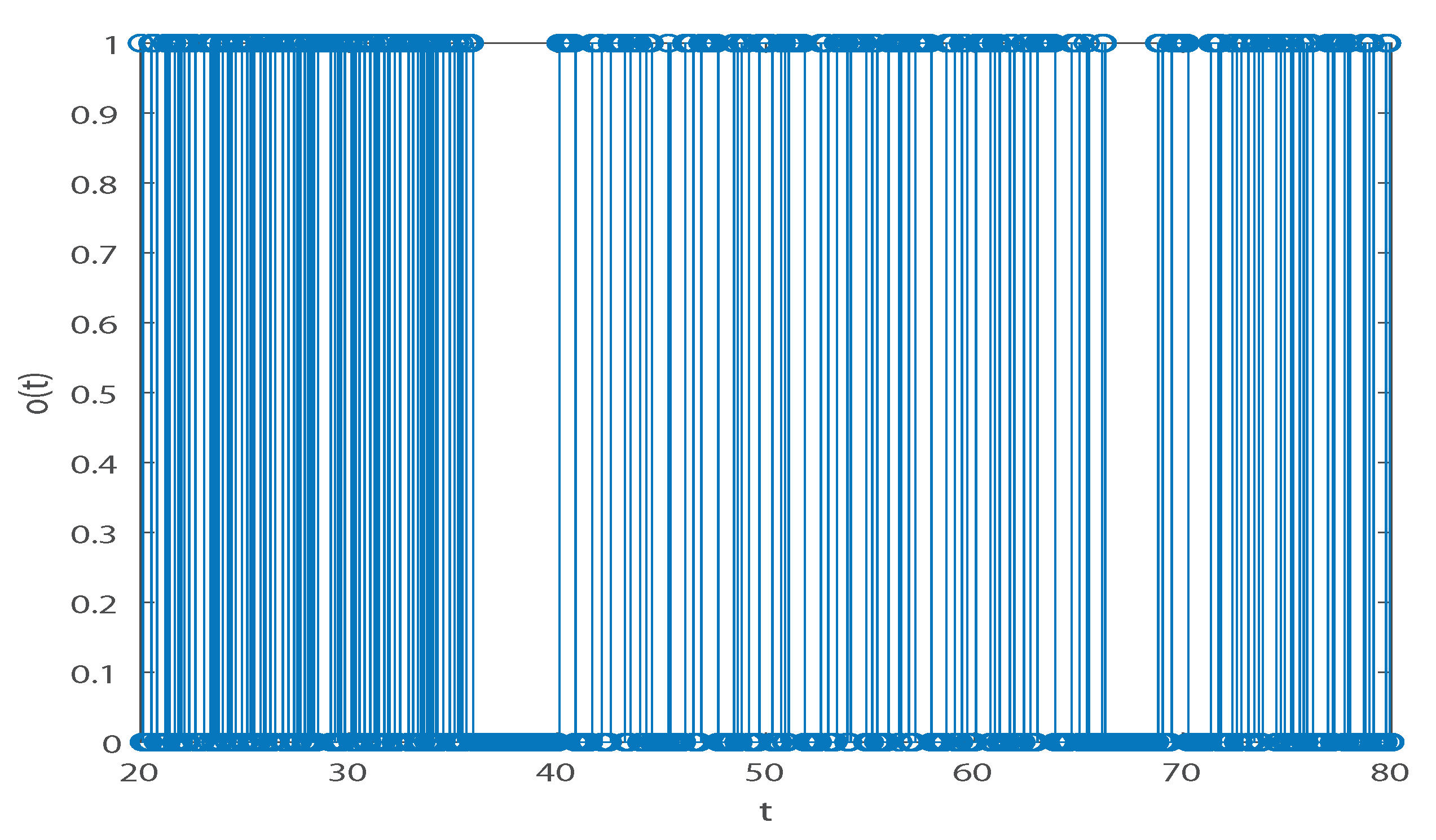
4. Numerical Example


5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Hu, J. Fixed-time stabilization and synchronization for fuzzy inertial neural networks with bounded distributed delays and discontinuous activation functions. Neurocomputing 2022, 495, 86–96. [Google Scholar] [CrossRef]
- Li, H.; Hu, C.; Zhang, G.; Hu, J.; Wang, L. Fixed-/Preassigned-time stabilization of delayed memristive neural networks. Inf. Sci. 2022, 610, 624–636. [Google Scholar] [CrossRef]
- Liu, J.; Shu, L.; Chen, Q.; Zhong, S. Fixed-time synchronization criteria of fuzzy inertial neural networks via Lyapunov functions with indefinite derivatives and its application to image encryption. Fuzzy Sets Syst. 2023, 459, 22–42. [Google Scholar] [CrossRef]
- Gan, Q.; Li, L.; Yang, J.; Qin, Y.; Meng, M. Improved results on fixed-/preassigned-time synchronization for memristive complex-valued neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5542–5556. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, J. New results on fixed/predefined-time synchronization of delayed fuzzy inertial discontinuous neural networks: Non-reduced order approach. Appl. Math. Comput. 2023, 440, 127671. [Google Scholar] [CrossRef]
- Babcock, K.; Westervelt, R. Stability and dynamics of simple electronic neural networks with added inertia. Phys. D Nonlinear Phenom. 1986, 23, 464–469. [Google Scholar] [CrossRef]
- Wheeler, D.W.; Schieve, W. Stability and chaos in an inertial two-neuron system. Phys. D Nonlinear Phenom. 1997, 105, 267–284. [Google Scholar] [CrossRef]
- Song, X.; Man, J.; Ahn, C.K.; Song, S. Finite-time dissipative synchronization for Markovian jump generalized inertial neural networks with reaction–diffusion terms. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 3650–3661. [Google Scholar] [CrossRef]
- Angelaki, D.E.; Correia, M. Models of membrane resonance in pigeon semicircular canal type II hair cells. Biol. Cybern. 1991, 65, 1–10. [Google Scholar] [CrossRef]
- Sheng, Y.; Huang, T.; Zeng, Z.; Li, P. Exponential stabilization of inertial memristive neural networks with multiple time delays. IEEE Trans. Cybern. 2019, 51, 579–588. [Google Scholar] [CrossRef] [PubMed]
- Long, C.; Zhang, G.; Zeng, Z. Novel results on finite-time stabilization of state-based switched chaotic inertial neural networks with distributed delays. Neural Netw. 2020, 129, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Zeng, K.; Wang, L.; Cheng, J. Fixed-time and preassigned-time synchronization of delayed inertial neural networks. In Proceedings of the 2021 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanchang, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 558–563. [Google Scholar]
- Kanakalakshmi, S.; Sakthivel, R.; Karthick, S.; Leelamani, A.; Parivallal, A. Finite-time decentralized event-triggering non-fragile control for fuzzy neural networks with cyber-attack and energy constraints. Eur. J. Control 2021, 57, 135–146. [Google Scholar] [CrossRef]
- Prakash, M.; Balasubramaniam, P.; Lakshmanan, S. Synchronization of Markovian jumping inertial neural networks and its applications in image encryption. Neural Netw. 2016, 83, 86–93. [Google Scholar] [CrossRef]
- Huang, C.; Yang, L.; Liu, B. New results on periodicity of non-autonomous inertial neural networks involving non-reduced order method. Neural Process. Lett. 2019, 50, 595–606. [Google Scholar] [CrossRef]
- Zhang, G.; Zeng, Z. Stabilization of second-order memristive neural networks with mixed time delays via nonreduced order. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 700–706. [Google Scholar] [CrossRef]
- Cao, J.; Wang, J. Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw. 2004, 17, 379–390. [Google Scholar] [CrossRef]
- Guo, Y. Mean square exponential stability of stochastic delay cellular neural networks. Electron. J. Qual. Theory Differ. Equ. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Guo, Y. Globally robust stability analysis for stochastic Cohen–Grossberg neural networks with impulse control and time-varying delays. Ukr. Mat. Zhurnal 2017, 69, 1049–1060. [Google Scholar] [CrossRef]
- Guan, Z.H.; Liu, Z.W.; Feng, G.; Wang, Y.W. Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 2182–2195. [Google Scholar] [CrossRef]
- Guo, Y.; Xin, L. Asymptotic and robust mean square stability analysis of impulsive high-order BAM neural networks with time-varying delays. Circuits Syst. Signal Process. 2018, 37, 2805–2823. [Google Scholar] [CrossRef]
- Maharajan, C.; Raja, R.; Cao, J.; Rajchakit, G.; Alsaedi, A. Novel results on passivity and exponential passivity for multiple discrete delayed neutral-type neural networks with leakage and distributed time-delays. Chaos Solitons Fractals 2018, 115, 268–282. [Google Scholar] [CrossRef]
- Raj, S.; Ramachandran, R.; Rajendiran, S.; Cao, J.; Li, X. Passivity analysis of uncertain stochastic neural network with leakage and distributed delays under impulsive perturbations. Kybernetika 2018, 54, 3–29. [Google Scholar] [CrossRef]
- Sau, N.H.; Thuan, M.V.; Huyen, N.T.T. Passivity analysis of fractional-order neural networks with time-varying delay based on LMI approach. Circuits Syst. Signal Process. 2020, 39, 5906–5925. [Google Scholar] [CrossRef]
- Li, N.; Zheng, W.X. Passivity analysis for quaternion-valued memristor-based neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 639–650. [Google Scholar] [CrossRef]
- Chen, J.; Park, J.H.; Xu, S. Stability analysis for neural networks with time-varying delay via improved techniques. IEEE Trans. Cybern. 2018, 49, 4495–4500. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.m.; Qin, H.y.; Zhong, S.m. Synchronization criteria for neutral-type quaternion-valued neural networks with mixed delays. AIMS Math. 2021, 6, 8044–8063. [Google Scholar] [CrossRef]
- Hirose, A. Applications of complex-valued neural networks to coherent optical computing using phase-sensitive detection scheme. Inf. Sci. Appl. 1994, 2, 103–117. [Google Scholar] [CrossRef]
- Tan, G.; Wang, Z. Further result on H¡Þ performance state estimation of delayed static neural networks based on an improved reciprocally convex inequality. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1477–1481. [Google Scholar]
- Aouiti, C.; Assali, E.A.; Ben Gharbia, I. Global exponential convergence of neutral type competitive neural networks with D operator and mixed delay. J. Syst. Sci. Complex. 2020, 33, 1785–1803. [Google Scholar] [CrossRef]
- Tan, G.; Wang, Z. Generalized dissipativity state estimation of delayed static neural networks based on a proportional-integral estimator with exponential gain term. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 356–360. [Google Scholar] [CrossRef]
- Tan, G.; Wang, Z. Reachable set estimation of delayed Markovian jump neural networks based on an improved reciprocally convex inequality. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2737–2742. [Google Scholar] [CrossRef] [PubMed]
- Nitta, T. Orthogonality of decision boundaries in complex-valued neural networks. Neural Comput. 2004, 16, 73–97. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, Z.; Lin, C.; Chen, J. Fixed-time synchronization for complex-valued BAM neural networks with time-varying delays via pinning control and adaptive pinning control. Chaos Solitons Fractals 2021, 153, 111583. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, S.; Ye, E. Synchronization stability of memristor-based complex-valued neural networks with time delays. Neural Netw. 2017, 96, 115–127. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. Global asymptotic stability and adaptive ultimate Mittag–Leffler synchronization for a fractional-order complex-valued memristive neural networks with delays. IEEE Trans. Syst. Man. Cybern. Syst. 2018, 49, 2519–2535. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, D.; Yang, C.; Fu, J. Synchronization of memristive complex-valued neural networks with time delays via pinning control method. IEEE Trans. Cybern. 2019, 50, 3806–3815. [Google Scholar] [CrossRef]
- Li, X.; Fang, J.a.; Li, H. Master–slave exponential synchronization of delayed complex-valued memristor-based neural networks via impulsive control. Neural Netw. 2017, 93, 165–175. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Fang, J.A.; Li, H. Event-triggered exponential synchronization for complex-valued memristive neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4104–4116. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with both leakage and time-varying delays. Neurocomputing 2017, 245, 86–101. [Google Scholar] [CrossRef]
- Sun, K.; Zhu, S.; Wei, Y.; Zhang, X.; Gao, F. Finite-time synchronization of memristor-based complex-valued neural networks with time delays. Phys. Lett. A 2019, 383, 2255–2263. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Cao, J.; Park, J.H.; Shen, H. H∞ state estimation for switched inertial neural networks with time-varying delays: A persistent dwell-time scheme. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 52, 2994–3004. [Google Scholar] [CrossRef]
- Arbi, A.; Tahri, N. Stability analysis of inertial neural networks: A case of almost anti-periodic environment. Math. Methods Appl. Sci. 2022, 45, 10476–10490. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, K.; Hu, C.; Zhou, Y. Multiple finite-time synchronization of delayed inertial neural networks via a unified control scheme. Knowl. Based Syst. 2022, 236, 107785. [Google Scholar] [CrossRef]
- Aouiti, C.; Cao, J.; Jallouli, H.; Huang, C. Finite-time stabilization for fractional-order inertial neural networks with time varying delays. Nonlinear Anal. Model. Control 2022, 27, 1–18. [Google Scholar] [CrossRef]
- Huang, D.; Jiang, M.; Jian, J. Finite-time synchronization of inertial memristive neural networks with time-varying delays via sampled-date control. Neurocomputing 2017, 266, 527–539. [Google Scholar] [CrossRef]
- Guo, Z.; Gong, S.; Huang, T. Finite-time synchronization of inertial memristive neural networks with time delay via delay-dependent control. Neurocomputing 2018, 293, 100–107. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, E.; Sánchez-Torres, J.D.; Loukianov, A.G. On optimal predefined-time stabilization. Int. J. Robust Nonlinear Control 2017, 27, 3620–3642. [Google Scholar] [CrossRef]
- Kong, F.; Zhu, Q.; Huang, T. New fixed-time stability lemmas and applications to the discontinuous fuzzy inertial neural networks. IEEE Trans. Fuzzy Syst. 2020, 29, 3711–3722. [Google Scholar] [CrossRef]
- Khalil, H.; Grizzle, J. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Feng, L.; Yu, J.; Hu, C.; Yang, C.; Jiang, H. Nonseparation method-based finite/fixed-time synchronization of fully complex-valued discontinuous neural networks. IEEE Trans. Cybern. 2020, 51, 3212–3223. [Google Scholar] [CrossRef]
- Guo, R.; Xu, S.; Ma, Q.; Zhang, Z. Fixed-time synchronization of complex-valued inertial neural networks via nonreduced-order method. IEEE Syst. J. 2021, 16, 4974–4982. [Google Scholar] [CrossRef]
- Ramajayam, S.; Rajavel, S.; Samidurai, R.; Cao, Y. Finite-Time Synchronization for T–S Fuzzy Complex-Valued Inertial Delayed Neural Networks Via Decomposition Approach. Neural Process. Lett. 2023, 1–19. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Z. New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach. Mathematics 2023, 11, 1378. [Google Scholar] [CrossRef]
- Yu, T.; Cao, J.; Rutkowski, L.; Luo, Y.P. Finite-time synchronization of complex-valued memristive-based neural networks via hybrid control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3938–3947. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Zhang, G.; Li, Y. Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach. Mathematics 2023, 11, 2275. https://doi.org/10.3390/math11102275
Yao Y, Zhang G, Li Y. Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach. Mathematics. 2023; 11(10):2275. https://doi.org/10.3390/math11102275
Chicago/Turabian StyleYao, Yu, Guodong Zhang, and Yan Li. 2023. "Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach" Mathematics 11, no. 10: 2275. https://doi.org/10.3390/math11102275
APA StyleYao, Y., Zhang, G., & Li, Y. (2023). Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach. Mathematics, 11(10), 2275. https://doi.org/10.3390/math11102275





