Exponentially Convergent Numerical Method for Abstract Cauchy Problem with Fractional Derivative of Caputo Type
Abstract
1. Problem Formulation and Introduction
| Algorithm 1 Algorithm for computing the homogeneous part approximation . |
| INPUT: , , , |
| OUTPUT: |
|
| Algorithm 2 Algorithm for computing the inhomogeneous part approximation . |
| INPUT: , , , |
| OUTPUT: |
|
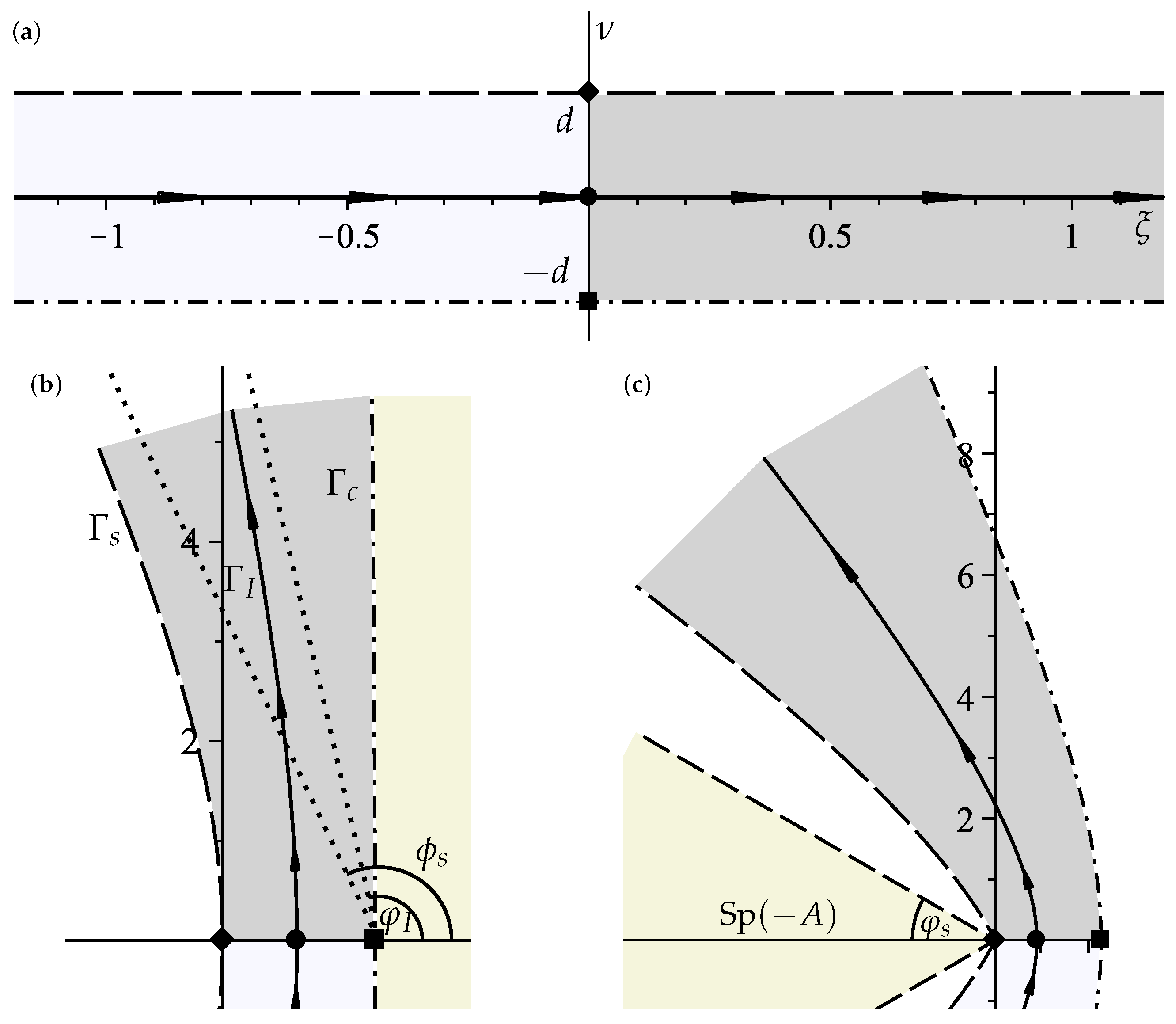
2. Contour of Integration
3. Numerical Method
3.1. Alternative Propagator Representation
3.2. Propagator Approximation
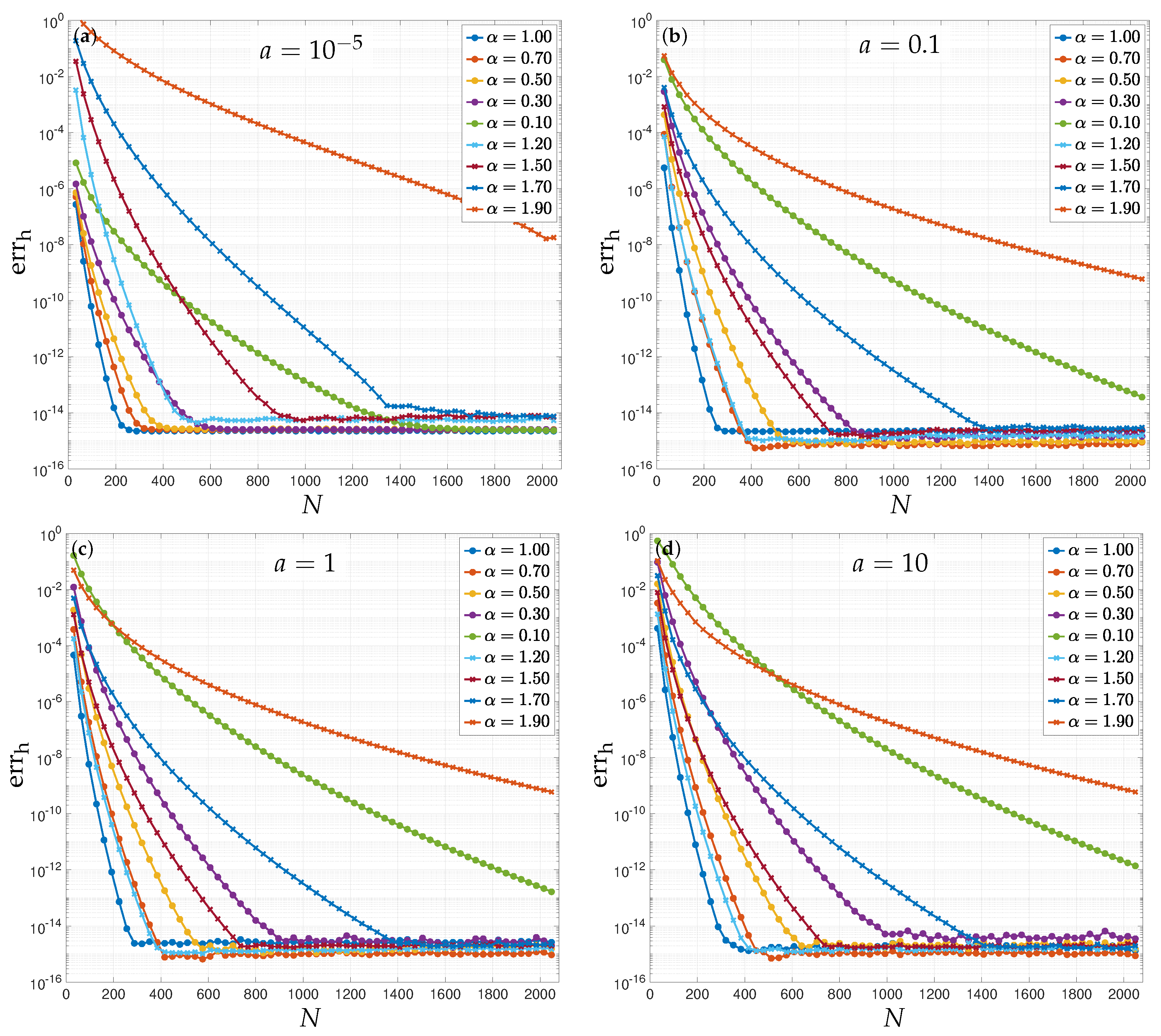
3.3. Numerical Scheme for Homogeneous Part of Solution
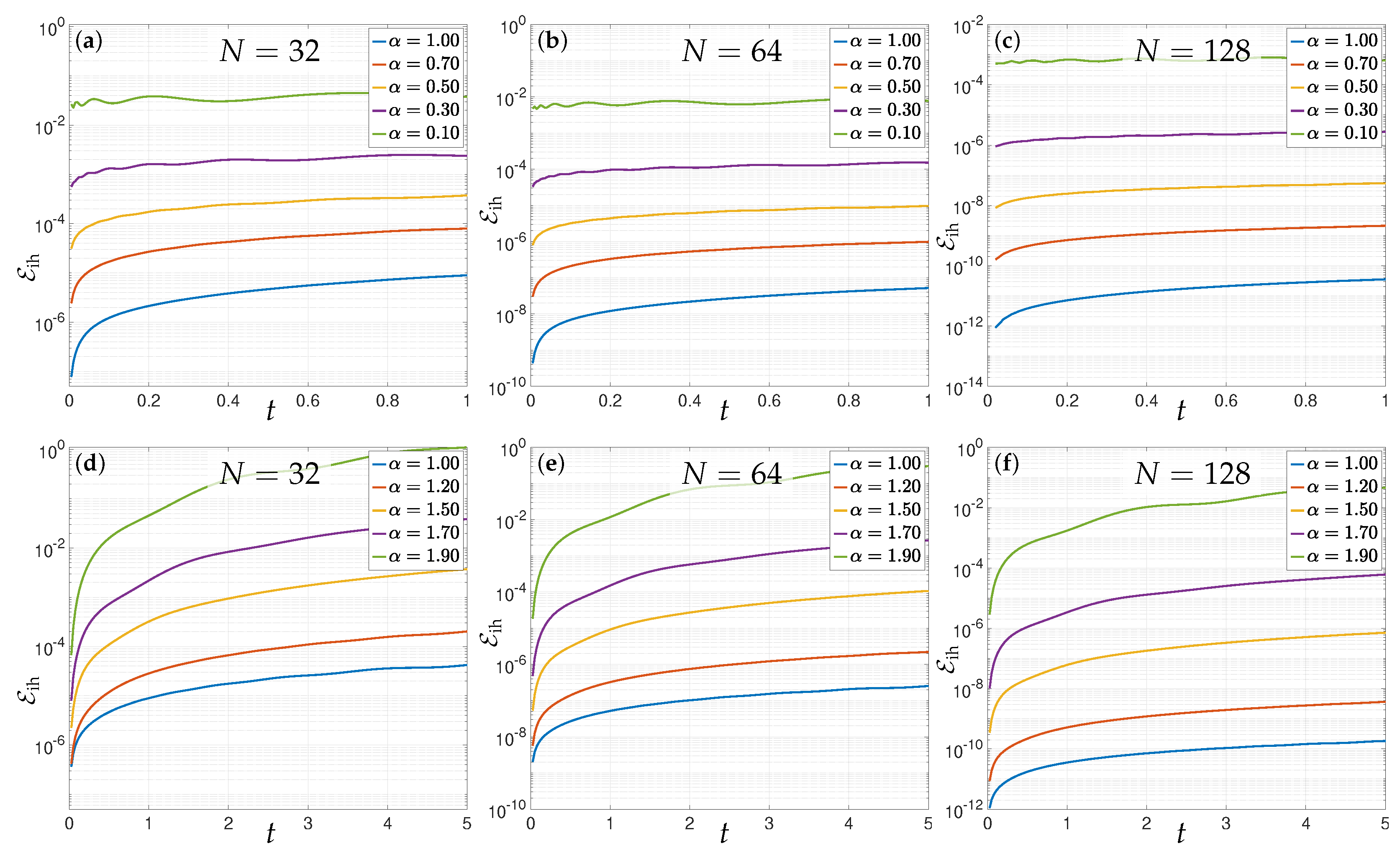
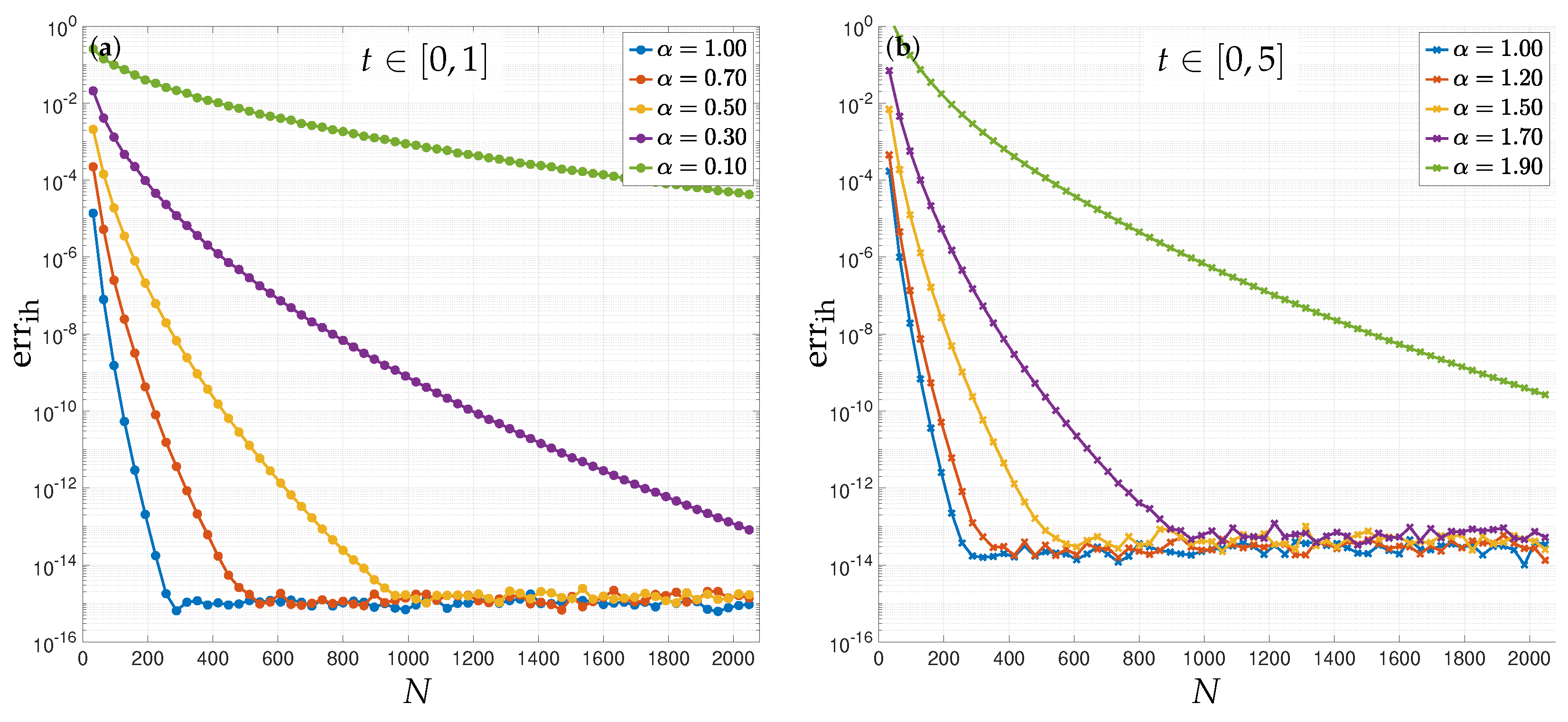
3.4. Numerical Scheme for the Inhomogeneous Part
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilbas, A.; Srivastava, H.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Gavrilyuk, I.; Makarov, V.; Vasylyk, V. Exponentially Convergent Algorithms for Abstract Differential Equations; Frontiers in Mathematics; Birkhäuser/Springer Basel AG: Basel, Switzerland, 2011; pp. viii+180. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Dzherbashian, M.; Nersesian, A. Fractional derivatives and Cauchy problem for differential equations of fractional order. Fract. Calc. Appl. Anal. 2020, 23, 1810–1836. [Google Scholar] [CrossRef]
- Kochubei, A.N. The Cauchy problem for evolution equations of fractional order. Differ. Uravn. 1989, 25, 1359–1368. [Google Scholar]
- Bazhlekova, E. The abstract Cauchy problem for the fractional evolution equation. Fract. Calc. Appl. Anal. 1998, 1, 255–270. [Google Scholar]
- Keyantuo, V.; Lizama, C.; Warma, M. Spectral criteria for solvability of boundary value problems and positivity of solutions of time-fractional differential equations. Abstr. Appl. Anal. 2013, 2013, 614328. [Google Scholar] [CrossRef]
- Bazhlekova, E. Fractional Evolution Equations in Banach Spaces. Ph.D. Thesis, Department of Mathematics and Computer Science, Eindhoven University of Technology, Eindhoven, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Sytnyk, D.; Wohlmuth, B. Abstract fractional Cauchy problem: Existence of propagators and inhomogeneous solution representation. Fractal Fract. submitted.
- Eidelman, S.D.; Kochubei, A.N. Cauchy problem for fractional diffusion equations. J. Differ. Equ. 2004, 199, 211–255. [Google Scholar] [CrossRef]
- Umarov, S. Fractional Duhamel principle. In Handbook of Fractional Calculus with Applications; De Gruyter: Berlin, Germany, 2019; Volume 2, pp. 383–410. [Google Scholar] [CrossRef]
- Fujita, H.; Saito, N.; Suzuki, T. Operator Theory and Numerical Methods; Elsevier: Heidelberg, Germany, 2001. [Google Scholar]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Diethelm, K.; Karniadakis, G. Fundamental approaches for the numerical handling of fractional operators and time-fractional differential equations. In Handbook of Fractional Calculus with Applications; De Gruyter: Berlin, Germany, 2019; Volume 3, pp. 1–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Garrappa, R.; Stynes, M. Good (and not so good) practices in computational methods for fractional calculus. Mathematics 2020, 8, 324. [Google Scholar] [CrossRef]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Garrappa, R. Trapezoidal methods for fractional differential equations: Theoretical and computational aspects. Math. Comput. Simul. 2015, 110, 96–112. [Google Scholar] [CrossRef]
- Stynes, M. Singularities. In Handbook of Fractional Calculus with Applications; Karniadakis, G.E., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 3, pp. 287–306. [Google Scholar] [CrossRef]
- Stynes, M. A Survey of the L1 Scheme in the Discretisation of Time-Fractional Problems. Numer. Math. Theory Methods Appl. 2021, 15, 1173–1192. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. Numerical methods for time-fractional evolution equations with nonsmooth data: A concise overview. Comput. Methods Appl. Mech. Eng. 2019, 346, 332–358. [Google Scholar] [CrossRef]
- Cuesta, E.; Lubich, C.; Palencia, C. Convolution quadrature time discretization of fractional diffusion-wave equations. Math. Comput. 2006, 75, 673–696. [Google Scholar] [CrossRef]
- Baffet, D.; Hesthaven, J.S. A Kernel Compression Scheme for Fractional Differential Equations. SIAM J. Numer. Anal. 2017, 55, 496–520. [Google Scholar] [CrossRef]
- Fischer, M. Fast and Parallel Runge–Kutta Approximation of Fractional Evolution Equations. SIAM J. Sci. Comput. 2019, 41, A927–A947. [Google Scholar] [CrossRef]
- Guo, L.; Zeng, F.; Turner, I.; Burrage, K.; Karniadakis, G.E. Efficient Multistep Methods for Tempered Fractional Calculus: Algorithms and Simulations. SIAM J. Sci. Comput. 2019, 41, A2510–A2535. [Google Scholar] [CrossRef]
- Khristenko, U.; Wohlmuth, B. Solving time-fractional differential equations via rational approximation. IMA J. Numer. Anal. 2022, 1–27. [Google Scholar] [CrossRef]
- McLean, W.; Thomée, V. Maximum-norm error analysis of a numerical solution via Laplace transformation and quadrature of a fractional-order evolution equation. IMA J. Numer. Anal. 2009, 30, 208–230. [Google Scholar] [CrossRef]
- McLean, W.; Thomée, V. Numerical solution via Laplace transforms of a fractional order evolution equation. J. Integral Equ. Appl. 2010, 22, 57–94. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Ayton, L.J. A contour method for time-fractional PDEs and an application to fractional viscoelastic beam equations. J. Comput. Phys. 2022, 454, 110995. [Google Scholar] [CrossRef]
- Vasylyk, V.; Gavrilyuk, I.; Makarov, V. Exponentially Convergent Method for the Approximation of a Differential Equation with Fractional Derivative and Unbounded Operator Coefficient in a Banach Space. Ukr. Math. J. 2022, 74, 171–185. [Google Scholar] [CrossRef]
- Gavrilyuk, I.; Makarov, V. Exponentially convergent algorithms for the operator exponential with applications to inhomogeneous problems in Banach spaces. SIAM J. Numer. Anal. 2005, 43, 2144–2171. [Google Scholar] [CrossRef]
- Weideman, J.A.C. Optimizing Talbot’s contours for the inversion of the Laplace transform. SIAM J. Numer. Anal. 2006, 44, 2342–2362. [Google Scholar] [CrossRef]
- Weideman, J.; Trefethen, L. Parabolic and hyperbolic contours for computing the Bromwich integral. Math. Comput. 2007, 76, 1341–1356. [Google Scholar] [CrossRef]
- Pang, H.K.; Sun, H.W. Fast numerical contour integral method for fractional diffusion equations. J. Sci. Comput. 2016, 66, 41–66. [Google Scholar] [CrossRef]
- Hochbruck, M.; Ostermann, A. Explicit Exponential Runge–Kutta Methods for Semilinear Parabolic Problems. SIAM J. Numer. Anal. 2005, 43, 1069–1090. [Google Scholar] [CrossRef]
- López-Fernández, M.; Lubich, C.; Palencia, C.; Schädle, A. Fast Runge–Kutta approximation of inhomogeneous parabolic equations. Numer. Math. 2005, 102, 277–291. [Google Scholar] [CrossRef]
- Gander, M.J.; Güttel, S. PARAEXP: A Parallel Integrator for Linear Initial-Value Problems. SIAM J. Sci. Comput. 2013, 35, C123–C142. [Google Scholar] [CrossRef]
- Bohonova, T.Y.; Gavrilyuk, I.P.; Makarov, V.L.; Vasylyk, V. Exponentially Convergent Duhamel-Like Algorithms for Differential Equations with an Operator Coefficient Possessing a Variable Domain in a Banach Space. SIAM J. Numer. Anal. 2008, 46, 365–396. [Google Scholar] [CrossRef]
- González, C.; Thalhammer, M. Higher-order exponential integrators for quasi-linear parabolic problems. Part II: Convergence. SIAM J. Numer. Anal. 2016, 54, 2868–2888. [Google Scholar] [CrossRef]
- Fritz, M.; Rajendran, M.L.; Wohlmuth, B. Time-fractional Cahn–Hilliard equation: Well-posedness, degeneracy, and numerical solutions. Comput. Math. Appl. 2022, 108, 66–87. [Google Scholar] [CrossRef]
- McLean, W.; Thomee, V. Time discretization of an evolution equation via Laplace transforms. IMA J. Numer. Anal. 2004, 24, 439–463. [Google Scholar] [CrossRef]
- Thomée, V. A high order parallel method for time discretization of parabolic type equations based on Laplace transformation and quadrature. Int. J. Numer. Anal. Model. 2005, 2, 121–139. [Google Scholar]
- Weideman, J.A.C. Improved contour integral methods for parabolic PDEs. IMA J. Numer. Anal. 2010, 30, 334–350. [Google Scholar] [CrossRef]
- Rieder, A. Double exponential quadrature for fractional diffusion. Numer. Math. 2023, 27, 1–52. [Google Scholar] [CrossRef] [PubMed]
- López-Fernández, M.; Palencia, C.; Schädle, A. A spectral order method for inverting sectorial Laplace transforms. SIAM J. Numer. Anal. 2006, 44, 1332–1350. [Google Scholar] [CrossRef]
- Ashyralyev, A. A note on fractional derivatives and fractional powers of operators. J. Math. Anal. Appl. 2009, 357, 232–236. [Google Scholar] [CrossRef]
- Li, M.; Chen, C.; Li, F.B. On fractional powers of generators of fractional resolvent families. J. Funct. Anal. 2010, 259, 2702–2726. [Google Scholar] [CrossRef]
- Martinez, C.; Sanz, M. The Theory of Fractional Powers of Operators; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Computer Science and Applied Mathematics; Academic Press: Boston, MA, USA, 1984. [Google Scholar]
- Stenger, F. Numerical Methods Based on Sinc and Analytic Functions; Springer Series in Computational Mathematics; Springer: New York, NY, USA, 1993; Volume 20, pp. xv+565. [Google Scholar] [CrossRef]
- Gavrilyuk, I.; Makarov, V.; Vasylyk, V. A new estimate of the Sinc method for linear parabolic problems including the initial point. Comput. Methods Appl. Math. 2004, 4, 163–179. [Google Scholar] [CrossRef]
- Lubich, C. Convolution quadrature revisited. BIT Numer. Math. 2004, 44, 503–514. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical evaluation of two and three parameter Mittag–Leffler functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Seybold, H.; Hilfer, R. Numerical algorithm for calculating the generalized Mittag–Leffler function. SIAM J. Numer. Anal. 2009, 47, 69–88. [Google Scholar] [CrossRef]
- McLean, W. Numerical evaluation of Mittag–Leffler functions. Calcolo 2021, 58, 7. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Gupta, V. A brief survey on numerical methods for solving singularly perturbed problems. Appl. Math. Comput. 2010, 217, 3641–3716. [Google Scholar] [CrossRef]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems, 2nd ed.; Springer Series in Computational Mathematics 24; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gavrilyuk, I.P.; Makarov, V.L.; Sytnyk, D.O.; Vasylyk, V.B. Exponentially Convergent Method for the m-Point Nonlocal Problem for a First Order Differential Equation in Banach Space. Numer. Funct. Anal. Optim. 2010, 31, 1–21. [Google Scholar] [CrossRef]
- Makarov, V.L.; Sytnyk, D.O.; Vasylyk, V.B. Existence of the solution to a nonlocal-in-time evolutional problem. Nonlinear Anal. Model. Control 2014, 19, 432–447. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. A modified quasi-boundary value method for the backward time-fractional diffusion problem. ESAIM Math. Model. Numer. Anal. 2014, 48, 603–621. [Google Scholar] [CrossRef]
- Jin, B.; Rundell, W. A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 2015, 31, 035003. [Google Scholar] [CrossRef]
- Zhokh, A.; Strizhak, P. Macroscale modeling the methanol anomalous transport in the porous pellet using the time-fractional diffusion and fractional Brownian motion: A model comparison. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104922. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sytnyk, D.; Wohlmuth, B. Exponentially Convergent Numerical Method for Abstract Cauchy Problem with Fractional Derivative of Caputo Type. Mathematics 2023, 11, 2312. https://doi.org/10.3390/math11102312
Sytnyk D, Wohlmuth B. Exponentially Convergent Numerical Method for Abstract Cauchy Problem with Fractional Derivative of Caputo Type. Mathematics. 2023; 11(10):2312. https://doi.org/10.3390/math11102312
Chicago/Turabian StyleSytnyk, Dmytro, and Barbara Wohlmuth. 2023. "Exponentially Convergent Numerical Method for Abstract Cauchy Problem with Fractional Derivative of Caputo Type" Mathematics 11, no. 10: 2312. https://doi.org/10.3390/math11102312
APA StyleSytnyk, D., & Wohlmuth, B. (2023). Exponentially Convergent Numerical Method for Abstract Cauchy Problem with Fractional Derivative of Caputo Type. Mathematics, 11(10), 2312. https://doi.org/10.3390/math11102312






